TEMA 5 DA2

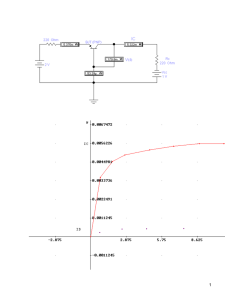
Diseño Análogo 2 – Tema # 5
Circuitos mosfet de DC
Para estos circuitos se hará caso omiso de la
modulación de la longitud del canal 𝜆 = 0 y
𝑉𝑂𝑉 = 𝑣𝐺𝑆 − 𝑉𝑡
Diseñe el circuito de la figura 5.2 para obtener una
corriente 𝐼𝐷 = 80𝜇𝐴, Encuentre el valor requerido
para 𝑅 y el voltaje de dc de 𝑉𝐷 , el transistor NMOS
tiene 𝑉𝑡 = 0.6𝑉 𝜇𝑛 𝐶𝑜𝑥 = 200 𝜇𝐴⁄𝑉 2 , 𝐿 = 0.8𝜇𝑚
y 𝑊 = 4𝜇𝑚, Omita el efecto de modulación de
longitud de canal.
Ejemplo 4,2 pág. 263
Diseñe el circuito de la figura 5.1 para que
transistor opere a 𝐼𝐷 = 0.4𝑚𝐴 y 𝑉𝐷 = 0.5𝑉.
transistor NMOS tiene 𝑉𝑡 = 0.7 𝑉, 𝜇𝑛 𝐶𝑜𝑥
100 𝜇𝐴⁄𝑉 2 𝐿 = 1𝜇𝑚 y 𝑊 = 32𝜇𝑚. Omita
efecto de modulación de longitud de canal.
el
el
=
el
Figura 5.2
En este caso como 𝑉𝐷 = 𝑉𝐺 entonces siempre
𝑉𝐷𝑆 > 𝑉𝐺𝑆 − 𝑉𝑡
Y el transistor estará en saturación
𝐼𝐷 =
Figura 5.1
Entonces el transistor esta en saturación
𝐿
80𝜇𝐴 =
100
2
(𝑉𝐺𝑆 − 𝑉𝑡 )2
4𝜇𝑚
𝜇𝐴⁄𝑉 2 0.8𝜇𝑚 (𝑉𝑂𝑉 )2
𝑉𝐺 = 𝑉𝐷 = 1𝑉
𝑉𝐷𝑆 > 𝑉𝐺𝑆 − 𝑉𝑡
2
𝐿
𝑉𝐺𝑆 = 𝑉𝑂𝑉 + 𝑉𝑡 = 0.4𝑉 + 0.6V = 1V
0.5 ? 0 − 0.7𝑉
𝜇𝑛 𝐶𝑜𝑥 𝑊
2
𝑉𝑂𝑉 = 0.4
𝑉𝐷𝑆 ? 𝑉𝐺𝑆 − 𝑉𝑡 → 𝑉𝐷 ? 𝑉𝐺 − 𝑉𝑡
𝐼𝐷 =
𝜇𝑛 𝐶𝑜𝑥 𝑊
32𝜇𝑚
1𝜇𝑚
𝑉𝐷𝐷 −𝑉𝐷
𝐼𝐷
=
3𝑉−1𝑉
80𝜇𝐴
= 25𝐾Ω
Ejercicio 4.12 pág. 265
(𝑉𝐺𝑆 − 𝑉𝑡 )2
0.4𝑚𝐴 = 100 𝜇𝐴⁄𝑉 2
𝑅=
(𝑉𝑂𝑉 )2
𝑉𝑂𝑉 = 0.5𝑉
En la figura 5.3 se muestra un circuito en el cual el
lado derecho es equivalente al desarrollado
anteriormente con los mismos valores encuentre la
corriente y el voltaje en el drenaje de Q2
𝑉𝐺𝑆 = 𝑉𝑂𝑉 + 𝑉𝑡 = 0.5𝑉 + 0.7V = 1.2V
𝑉𝑆 = 𝑉𝐺 − 𝑉𝐺𝑆 = 0 − 1.2𝑉 = −1.2𝑉
𝑅𝑆 =
𝑉𝑆 −(−2,5𝑉)
𝑅𝑆 =
𝑉𝐷𝐷 −𝑉𝐷
𝐼𝐷
𝐼𝐷
=
=
−1.2𝑉−(−2,5𝑉)
2,5−0.5
0.4𝑚𝐴
0.4𝑚𝐴
= 3,25𝐾Ω
= 5𝐾
Ejercicio 4,3 pág. 264
Figura 5.3
1
Como la corriente en el gate de Q2 es cero entonces
el transistor Q1 tiene los mismos valores del
circuito anterior
𝑉𝐺 = 𝑉𝐷 = 1𝑉
Si suponemos que el otro Q2 está en saturación
entonces tendrán la misma corriente de Q1
𝐼𝐷1 = 𝐼𝐷2
𝜇𝑛 𝐶𝑜𝑥 𝑊
(𝑉𝐺𝑆 − 𝑉𝑡 )2 = 𝐼𝐷 = 80𝜇𝐴
=
2 𝐿
Entonces el voltaje
𝑉𝐷2 = 𝑉𝐷𝐷 − 𝑅2 𝐼𝐷2 = 3 − (20𝐾Ω)80𝜇𝐴 = 1.4𝑉
𝑣𝐷𝑆 > 𝑣𝐺𝑆 − 𝑉𝑡 condición de saturación
𝑅𝐷 =
𝑉𝐷𝐷 −𝑉𝐷
𝐼𝐷
5𝑉−0.1𝑉
= 0.395𝑚𝐴 = 12.4𝐾Ω
Para encontrar la resistencia efectiva entre drenaje
y fuente
𝑉𝐷𝑆
𝑟𝐷𝑆 =
𝐼𝐷
0.1𝑉
= 0.395𝑚𝐴 = 253Ω
Ejemplo 4.5 pag.266
Analice el circuito mostrado en la figura 5.5 para
determinar el voltaje en todos los nodos y las
corrientes en todas las ramificaciones. Sean 𝑉𝑡 =
𝑊
1𝑉 y 𝑘′𝑛 𝐿 = 1𝑚𝐴/𝑉 2 . Pase por alto el efecto de
la modulación del canal.
1.4 > 1 − 0.6 Cumple la condición y hemos
terminado.
Ejemplo 4.4 pág. 265
Diseñe el circuito de la figura 5.4 para establecer
un voltaje de drenaje de 0.1V. ¿Cuál es la
resistencia efectiva entre el drenaje y la fuente en
𝑊
su punto de operación? Sean 𝑉𝑡 = 1𝑉 y 𝑘′𝑛 𝐿 =
1𝑚𝐴/𝑉 2 .
Figura 5.5
Para esta configuración no se tiene muy claro el
modo de operación por tal motivo deberemos
suponer uno y luego comprobar.
Si suponemos saturación tenemos
𝐼𝐷 =
𝑘′𝑛 𝑊
2 𝐿
(𝑉𝐺𝑆 − 𝑉𝑡 )2
Figura 5.4
Donde
Miremos en qué modo de operación se encuentra
𝑉𝐺 = 𝑉𝐷𝐷 𝑅
𝑉𝐷𝑆 ? 𝑉𝐺𝑆 − 𝑉𝑡 → 𝑉𝐷 ? 𝑉𝐺 − 𝑉𝑡
𝑉𝑆 = 𝐼𝐷 𝑅𝑆 = 𝐼𝐷 6𝐾Ω
0.1𝑉 < 5𝑉 − 1𝑉 triodo
𝐼𝐷 = 𝜇𝑛 𝐶𝑜𝑥
𝐼𝐷 =
𝑊
𝐿
((𝑉𝐺𝑆 − 𝑉𝑡 )𝑉𝐷𝑆 −
𝑉𝐷𝑆 2
2
1𝑚𝐴
𝑉 2 ((5 − 1)0.1 −
(0.1)2
2
= 0.5𝑉𝐷𝐷 = 5𝑉
Remplazando estos valores en la ecuación de la
corriente tenemos
)
= 0.395𝑚𝐴
)
𝑅𝐺2
𝐺1 +𝑅𝐺2
1
𝐼𝐷 = 2 1𝑚𝐴/𝑉 2 (5 − 𝐼𝐷 6𝐾Ω − 1)2
𝐼𝐷 = 0.5𝑚𝐴/𝑉 2 (42 − 2(4)𝐼𝐷 6𝐾Ω + (𝐼𝐷 6𝐾Ω)2 )
𝐼𝐷 = 8 − 24𝐼𝐷 + 18𝐾𝐼𝐷 2
2
18𝐾𝐼𝐷 2 − 25𝐼𝐷 + 8𝑚 = 0
Ejercicio 4.15 pág. 267
Utilizando la formula general
Rediseñe el circuito para los siguientes requisitos:
𝑉𝐷𝐷 = +5𝑉, 𝐼𝐷 = 0.32𝑚𝐴, 𝑉𝑆 = 1.6𝑉, 𝑉𝐷 = 3.4𝑉
con una corriente de 1𝜇𝐴 a través del divisor de
voltaje 𝑅𝐺1 , 𝑅𝐺2 . Suponga el mismo MOSFET del
ejemplo 4,5.
𝐼𝐷 =
25 ±√252 −4(18𝐾)(8𝑚)
2(18𝐾)
𝐼𝐷1 =
25+7
𝐼𝐷2 =
25−7
36𝐾
36𝐾
=
25 ±7
36𝐾
= 0.89𝑚𝐴
𝐼𝐷 =
= 0.5𝑚𝐴
2 𝐿
(𝑉𝐺𝑆 − 𝑉𝑡 )2
1
Como se tienen dos valores, uno de ellos permitirá
la creación del canal el otro no. realizando la
comprobación se tiene que
𝑉𝑆1 = 𝐼𝐷1 𝑅𝑆 = (0.89𝑚𝐴)6𝐾Ω = 5.34V Que es
mayor que el voltaje de la compuerta impidiendo
así la creación del canal.
𝑉𝑆2 = 𝐼𝐷2 𝑅𝑆 = (0.5𝑚𝐴)6𝐾Ω = 3V
Este valor de corriente es el correcto
𝑉𝐷 = 𝑉𝐷 − 𝐼𝐷 𝑅𝐷 = 10 − (0.5𝑚𝐴)6𝐾Ω = 10 − 3V = 7V
Y por último la corriente que circula por el divisor
𝑅𝐺1 y 𝑅𝐺2 es
𝐼=
𝑘′𝑛 𝑊
𝑉𝐷𝐷
𝑅𝐺1 + 𝑅𝐺2
=
10
10𝑀+10𝑀
= 0,5𝜇𝐴
Ejercicio 4.14 pág. 267
Para el circuito anterior ¿cuál es el valor más
grande que puede tener 𝑅𝐷 mientras el transistor
permanece en el modo de saturación?
0.32𝑚𝐴 = 2 1𝑚𝐴/𝑉 2 (𝑉𝑂𝑉 )2
𝑉𝑂𝑉 = √0.64𝑉 2 = 0.8𝑉
𝑉𝐺𝑆 = 𝑉𝑂𝑉 + 𝑉𝑡 = 0.8𝑉 + 1𝑉 = 1.8𝑉
𝑉𝐺 = 𝑉𝐺𝑆 − 𝑉𝑆 = 1.8𝑉 − 1.6𝑉 = 3.4𝑉
𝑅𝐺2 =
𝑉𝐺
𝑅𝐺1 =
𝑉𝐷𝐷 −𝑉𝐺
𝑅𝑆 =
𝐼
𝑉𝑆
𝐼𝐷
=
3.4𝑉
1𝜇𝐴
𝐼
=
= 3.4𝑀Ω
5−3.4
1𝜇𝐴
= 1.6𝑀Ω
1,6𝑉
= 0.32𝑚𝐴 = 5𝐾Ω
Para que el transistor este saturado
𝑉𝐷𝑆 ≥ 𝑉𝐺𝑆 − 𝑉𝑡 → 𝑉𝐷 ≥ 𝑉𝐺 − 𝑉𝑡
𝑉𝐷 ≥ 3.4𝑉 − 1𝑉 → 𝑉𝐷 ≥ 2.4𝑉
Si elegimos un 𝑉𝐷 = 3.4𝑉 estará en saturación
𝑅𝐷 =
𝑉𝐷𝐷 −𝑉𝐷
𝐼𝐷
5−3.4
= 0.32𝑚𝐴 = 5𝐾Ω
Para que el transistor siga en saturación
𝑉𝐷𝑆 ≥ 𝑉𝐺𝑆 − 𝑉𝑡
Ejemplo 4,6 pág. 268
Si aumentamos 𝑅𝐷 el voltaje 𝑣𝐷𝑆 aumentara por lo
tanto el limite estará dado por
Diseñe el circuito de la figura 5.6 para que el transistor
opere en saturación con 𝐼𝐷 = 0.5𝑚𝐴 y 𝑉𝐷 = +3𝑉. Si
𝑉𝐷𝑆 = 𝑉𝐺𝑆 − 𝑉𝑡
𝑉𝐷𝑚𝑎𝑥 = 𝑉𝐺 − 𝑉𝑡
𝑉𝐷𝑚𝑎𝑥 = 5 − 1 = 4
Como la corriente de drenaje sigue siendo los
mismos 0.5𝑚𝐴
el transistor PMOS tiene un 𝑉𝑡 = −1𝑉 y 𝑘′𝑝
𝑊
𝐿
=
1𝑚𝐴/𝑉 2 . Si desprecia la modulación de canal.
¿Cuál es el mayor valor que puede tener 𝑅𝐷
mientras se mantiene la operación en la región de
saturación?
10−4
𝑅𝐷𝑚𝑎𝑥 = 0.5𝑚𝐴 = 12𝐾Ω
3
𝑅𝐷𝑚𝑎𝑥 =
𝑉𝐷𝑚𝑎𝑥
𝐼𝐷
4𝑉
= 0.5𝑚𝐴 = 8𝐾Ω
Ejemplo 4.7 pág. 269
Los transistores NMOS y PMOS del circuito de la
𝑊
𝑊
figura 5.7 son coincidentes
𝑘′𝑛 𝐿 = 𝑘′𝑝 𝐿 =
1𝑚𝐴/𝑉 2 , 𝑉𝑡𝑛 = −𝑉𝑡𝑝 = 1𝑉 suponiendo 𝜆 = 0
para ambos dispositivos, encuentre las corrientes
del drenaje 𝑖𝐷𝑁 e 𝑖𝐷𝑃 , además del voltaje 𝑣𝑂 para
𝑣𝐼 = 0𝑉, +2.5𝑉 𝑦 − 2.5𝑉.
Figura 5.6
Como el MOSFET debe operan en saturación se
tiene que:
𝐼𝐷 =
𝑘′𝑛 𝑊
2 𝐿
(𝑉𝐺𝑆 − 𝑉𝑡 )2
1
0.5𝑚𝐴 = 2 1𝑚𝐴/𝑉 2 (𝑉𝑂𝑉 )2
𝑉𝑂𝑉 = ±1𝑉
Elegimos 𝑉𝑂𝑉 = −1𝑉 por ser un transistor PMOS
donde se requiere un voltaje negativo para inducir
canal.
Figura 5.6
𝑣𝐼 = 0𝑉
𝑉𝐺𝑆 = 𝑉𝑂𝑉 + 𝑉𝑡 = −1𝑉 + (−1𝑉) = −2𝑉
a)
𝑉𝐺 = 𝑉𝐺𝑆 + 𝑉𝑆 = −2𝑉 + 5𝑉 = 3𝑉
Con 0V en la entrada los dos transistores tendrán
respectivamente
Como no se indica en el enunciado que corriente
debe pasar por las resistencias 𝑅𝐺1 y 𝑅𝐺2 podemos
suponer una corriente de 1𝜇𝐴
𝑉𝐺𝑆𝑁 = 0𝑉 − (−2.5𝑉) = 2.5𝑉
𝑅𝐺2 =
𝑉𝐺
𝑅𝐺1 =
𝑉𝐷𝐷 −𝑉𝐺
𝐼
3𝑉
= 1𝜇𝐴 = 3𝑀Ω
𝐼
5−3
= 1𝜇𝐴 = 2𝑀Ω
Ahora
𝑅𝐷 =
𝑉𝐷
𝐼𝐷
3𝑉
= 0.5𝑚𝐴 = 6𝐾Ω
Para encontrar la 𝑅𝐷𝑚𝑎𝑥 y que siga operando en
saturación es cuando
𝑉𝐷𝑆 = 𝑉𝐺𝑆 − 𝑉𝑡
𝑉𝐺𝑆𝑃 = 0𝑉 − 2.5𝑉 = −2.5𝑉
En este caso las corrientes 𝑖𝐷𝑁 e 𝑖𝐷𝑃 son iguales y
por lo tanto no hay corriente circulando por la
resistencia de 10K lo que genera un voltaje de
𝑣𝑂 = 0𝑉, generando asi que la compuertas estén al
mismo potencial que el drenaje es decir que los dos
transistores operaran en saturación.
𝑖𝐷𝑁 = 𝑖𝐷𝑃 =
𝑘′𝑛 𝑊
2 𝐿
(𝑉𝐺𝑆 − 𝑉𝑡 )2
1
1𝑚𝐴
2
= 𝑉 2 (2.5𝑉−1𝑉)2 = 1.125𝑚𝐴
𝑉𝐷𝑚𝑎𝑥 = 𝑉𝐺 − 𝑉𝑡 = 3𝑉 − (−1𝑉) = 4𝑉
4
b) Con 𝑣𝐼 = 2.5𝑉
𝑉𝐺𝑆𝑃 = 2.5𝑉 − 2.5𝑉 = 0𝑉 Estará por lo tanto
en corte y el circuito resultante es el siguiente
𝐼𝐷𝑁 = 0𝐴
𝑣𝑂 = 2.44𝑉
𝐼𝐷𝑃 = 0.244𝑚𝐴
Figura 5.7
En este circuito el voltaje 𝑣𝑂 será negativo por la
dirección de la corriente entonces
𝑉𝐷𝑆 ≤ 𝑉𝐺𝑆 − 𝑉𝑡 , 𝑉𝐷 ≤ 𝑉𝐺 − 𝑉𝑡 , 𝑉𝐷 ≤ 1.5𝑉
Por lo tanto esta en la región de tríodo
𝐼𝐷𝑁 = 𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
((𝑉𝐺𝑆 − 𝑉𝑡 )𝑉𝐷𝑆 −
𝑉𝐷𝑆 2
2
El mosfet como amplificador y como interruptor
)
Suponiendo un 𝑉𝐷𝑆 pequeño
𝐼𝐷𝑁 = 𝑘′𝑛
𝑊
𝐼𝐷𝑁 = 𝑘′𝑛
𝑊
𝐿
𝐿
(𝑉𝐺𝑆 − 𝑉𝑡 )𝑉𝐷𝑆
(𝑉𝐺 − 𝑉𝑆 − 𝑉𝑡 )(𝑉𝐷 − 𝑉𝑆 )
𝐼𝐷𝑁 = 1𝑚𝐴/𝑉 2 (2.5 − (2.5) − 1)(𝑉𝐷 − (−2.5))
𝐼𝐷𝑁 = 4𝑚𝐴(𝑉𝐷 + 2.5)
Y el circuito nos da la segunda ecuación
0−𝑉
𝐼𝐷𝑁 = 10𝐾Ω𝐷
Igualando
0−𝑉𝐷
10𝐾Ω
Figura 5.8
= 4𝑚𝐴(𝑉𝐷 + 2.5)
A continuación se estudiara la característica de
transferencia de un MOSFET para tener mayor
claridad en como aplicar adecuadamente la técnica
de polarización para que este dispositivo opere
como amplificador, además se observará en que
regiones el MOSFET puede operar como
interruptor
Operación a
transferencia
gran
señal:
Característica
de
La configuración que se utilizara para observar el
comportamiento de este dispositivo será un
circuito de fuente común mostrado en la figura 5.9
y en la figura 5.10 se muestra una construcción
grafica que ayudará a obtener la característica de
transferencia del amplificador
𝑉
− 40𝐷 −𝑉𝐷 = 2.5
40
𝑉𝐷 = 𝑣𝑂 = − 41 2.5 = −2.44
𝐼𝐷𝑁 =
0−(−2.44)
10𝐾Ω
= 0.244𝑚𝐴
c) Con 𝑣𝐼 = 2.5𝑉
Para este caso la operación es similar a la anterior,
el que entra en corte es 𝑄𝑁 el circuito equivalente
se muestra en la figura 5.8 y los resultados serán
Figura 5.9
5
Como podemos observar la curva tiene la forma de
un inversor lógico digital en donde los modos de
operación de corte y tríodo son usados para la
operación como interruptor y el de saturación para
amplificación.
Si 𝑣𝐼 < 𝑉𝑡 el transistor no tiene un canal inducido
(Corte) por lo tanto 𝑖𝐷 = 0𝐴 y 𝑣𝐷 = 𝑉𝐷𝐷 (segmento
XA en la figura 5.11)
El punto A es cuando el transistor sale de corte y
entra en saturación esto se da cuando el voltaje
𝑉𝐺𝑆 = 𝑉𝑡
El punto B es cuando el transistor está en la
frontera de saturación y tríodo
Figura 5.10
En el circuito de la figura 5.9 se puede obtener la
ecuación
𝑣𝑂 = 𝑣𝐷𝑆 = 𝑉𝐷𝐷 − 𝑖𝐷 𝑅𝐷
1
𝑖𝐷 = − 𝑅 (𝑣𝐷𝑆 − 𝑉𝐷𝐷 )
𝐷
A esta recta se le conoce como la linea de carga, ya
con esta podemos encontrar los puntos A,Q,B,C
que determinan la caracteristica de transferencia
de la figura 5.11
𝑉𝐷𝑆 = 𝑉𝐺𝑆 − 𝑉𝑡
𝑣𝑂𝐵 = 𝑣𝐼𝐵 − 𝑉𝑡
En el intervalo AB el transistor está saturado 𝑣𝐼 ≥
𝑉𝑡 y 𝑣𝑂 ≥ 𝑣𝐼 − 𝑉𝑡 si despreciamos la modulación
del canal
1
𝐼𝐷 = 2 𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
(𝑉𝐼 − 𝑉𝑡 )2
1
𝑣𝑂 = 𝑉𝐷𝐷 − 𝑖𝐷 𝑅𝐷 = 𝑉𝐷𝐷 − 2 𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
(𝑣𝐼 − 𝑉𝑡 )2 𝑅𝐷
Si el dispositivo se polariza en un lugar cerca de la
parte media de la curva, por ejemplo el punto Q es
una polarización apropiada debido a que permite
buenas excursiones de la señal tanto positivas
como negativas
Para obtener la ganancia del amplificador en este
punto, encontramos la pendiente de la recta
tangente en Q
𝐴𝑉 =
𝐴𝑉 =
𝑑𝑣𝑂
|
𝑑𝑣𝐼 𝑉 =𝑉
𝐼
𝐼𝑄
1
2
𝐴𝑉 = −𝜇𝑛 𝐶𝑜𝑥
Figura 5.11
𝑊
𝐿
𝑑(𝑉𝐷𝐷 − 𝜇𝑛 𝐶𝑜𝑥 (𝑣𝐼 −𝑉𝑡 )2 𝑅𝐷 )
𝑑𝑣𝐼
𝑊
𝐿
|
𝑉𝐼 =𝑉𝐼𝑄
(𝑉𝐼𝑄 − 𝑉𝑡 )𝑅𝐷
Note que la ganancia depende directamente del
valor de 𝑅𝐷 , de los parámetros del MOSFET y el
voltaje de DC de la compuerta.
6
En el segmento BC el transistor se encuentra en la
región de tríodo
𝑣𝐼 ≥ 𝑉𝑡 y 𝑣𝑂 ≤ 𝑣𝐼 − 𝑉𝑡
𝑖𝐷 = 𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
((𝑣𝐼 − 𝑉𝑡 )𝑣𝑂 −
𝑣𝑂
2
)
𝑣𝐼 = 1𝑉 𝑣𝑂 = 10𝑉
c) Punto B
𝑊
𝐿
((𝑣𝐼 − 𝑉𝑡 )𝑣𝑂 −
𝑣𝑂 2
2
𝑣𝐼 = 𝑉𝐼𝐵 = 𝑉𝑂𝐵 + 𝑉𝑡 = 𝑉𝑂𝐵 + 1
) 𝑅𝐷
Si 𝑣𝑂 es pequeño
𝑣𝑂 = 𝑉𝐷𝐷 − 𝜇𝑛 𝐶𝑜𝑥
𝑣𝑂 =
𝑣𝑂 =
𝑊
𝐿
((𝑣𝐼 − 𝑉𝑡 )𝑣𝑂 )𝑅𝐷
𝑊
𝐿
𝑟𝐷𝑆
𝑊
𝐿
(𝑉𝐼𝐵 − 𝑉𝑡 )2 𝑅𝐷
1
(1+𝜇𝑛 𝐶𝑜𝑥 (𝑣𝐼 −𝑉𝑡 )𝑅𝐷 )
𝑅
(1+ 𝐷 )
1
𝑉𝑂𝐵 = 𝑉𝐷𝐷 − 2 𝜇𝑛 𝐶𝑜𝑥
𝑉𝑂𝐵 = 10𝑉 − 2 1𝑚𝐴/𝑉 2 (𝑉𝐼𝐵 − 1𝑉)2 18𝐾Ω
𝑉𝐷𝐷
𝑉𝐷𝐷
𝑣𝐼 = 0𝑉 𝑣𝑂 = 10𝑉
b) Punto A
2
𝑣𝑂 = 𝑉𝐷𝐷 − 𝑖𝐷 𝑅𝐷
𝑣𝑂 = 𝑉𝐷𝐷 − 𝜇𝑛 𝐶𝑜𝑥
a) Punto X
= 𝑉𝐷𝐷 𝑟
𝑟𝐷𝑆
𝐷𝑆 +𝑅𝐷
Que es claramente el voltaje que cae en el divisor
de tensión cuando el canal se comporta como una
resistencia constante.
𝑉𝑂𝐵 = 10 − 9(𝑉𝑂𝐵 + 1 − 1)2
9𝑉𝑂𝐵 2 + 𝑉𝑂𝐵 − 10 = 0
𝑉𝑂𝐵 =
−1±√1−4(9)(−10)
18
=
−1±19
18
𝑉𝑂𝐵1 = −1.11𝑉 (No tiene sentido físico debido a que el
mínimo voltaje presente en el circuito es 0V)
𝑉𝑂𝐵2 = 1𝑉
𝑉𝐼𝐵 = 𝑉𝑂𝐵 + 1 = 1 + 1 = 2𝑉
d) Punto C
𝑉𝐼𝐶 = 10𝑉
Suponiendo que 𝑣𝑂 en este punto es muy pequeño
𝑉𝑂𝐶 =
𝑉𝐷𝐷
𝑊
(1+𝜇𝑛 𝐶𝑜𝑥 (𝑉𝐼𝐶 −𝑉𝑡 )𝑅𝐷 )
𝐿
10
𝑉𝑂𝐶 = (1+1𝑚(18𝐾)(10−1)) = 0.061𝑉
Figura 5.12
Ejemplo 4.8 pag.277
Para que el análisis anterior sea más concreto,
considere un ejemplo numérico. Específicamente,
se verá el caso del circuito de CS de la figura 5.9.
𝑊
Para 𝑘′𝑛 𝐿 = 1𝑚𝐴/𝑉 2 , 𝑉𝑡 = 1𝑉 𝑅𝐷 = 18𝐾Ω y
𝑉𝐷𝐷 = 10𝑉.
Primero determinemos las coordenadas de los
puntos importantes de la curva de transferencia
Como 𝑉𝑂𝐶 es muy pequeño con relación a 𝑣𝐼 − 𝑉𝑡
lo que confirma la suposición y permite eliminar el
término cuadrático.
Ahora para la elección del punto Q vemos que el
transistor se encuentra en saturación en un
intervalo de 𝑣𝑂 de 10V a 1V, un buen punto para
polarizarlo es en 𝑉𝑂𝑄 = 4𝑉, pues este punto
genera una mejor ganancia que los 5.5V que serán
equivalentes a la mitad del intervalo.
Para operar en 4V 𝐼𝐷 debe ser
7
𝐼𝐷 =
𝑉𝐷𝐷 −𝑉𝑂
=
10−4
1
𝑊
2
𝐿
(𝑉𝑂𝑉 )2
𝑅𝐷
𝐼𝐷 = 𝜇𝑛 𝐶𝑜𝑥
𝑉𝑂𝑉 = √1
18𝐾
𝐼𝐷
= 0.333𝑚𝐴
0.333𝑚𝐴
𝑊
𝜇 𝐶
2 𝑛 𝑜𝑥 𝐿
= √0.5(1𝑚𝐴/𝑉 2 ) = 0.816𝑉
𝑉𝐼𝑄 = 𝑉𝑂𝑉 + 𝑉𝑡 = 0.816 + 1 = 1.816𝑉
La ganancia en este punto es
𝐴𝑉 = −𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
(𝑉𝐼𝑄 − 𝑉𝑡 )𝑅𝐷 = −1(18)(0.816)
diferentes lo que indica que el segmento de la
curva no es perfectamente lineal, esta corriente
será convertida en voltaje por la resistencia 𝑅𝐷 lo
que generará excursiones de voltaje desde
𝑣𝑂 = 𝑉𝐷𝐷 − 𝑖𝐷 𝑅𝐷 = 10 − 0.275𝑚(18𝐾) = 5.05𝑉
𝑣𝑂 = 𝑉𝐷𝐷 − 𝑖𝐷 𝑅𝐷 = 10 − 0.397𝑚(18𝐾) = 2.85𝑉
De acuerdo a lo anterior el incremento positivo es
(5.05 − 4) = 1.05𝑉 mientras que el negativo
(4 − 2.85) = 1.15𝑉
Gráficamente esta situación se representa en la
figura 5.13
𝑉
𝐴𝑉 = −14.69 𝑉
Si hubiésemos polarizado en 5.5V obtendríamos los
siguientes resultados
𝐼𝐷 =
𝑉𝐷𝐷 −𝑉𝑂
𝑅𝐷
1
𝐼𝐷 = 2 𝜇𝑛 𝐶𝑜𝑥
𝑉𝑂𝑉 = √1
𝜇
=
10−5.5
𝑊
(𝑉𝑂𝑉 )2
𝐿
18𝐾
𝐼𝐷
= 0.25𝑚𝐴
0.25𝑚𝐴
𝑊
𝐶
2 𝑛 𝑜𝑥 𝐿
= √0.5(1𝑚𝐴/𝑉 2 ) = 0.707𝑉
𝑉𝐼𝑄 = 𝑉𝑂𝑉 + 𝑉𝑡 = 0.707 + 1 = 1.707𝑉
La ganancia en este punto es
Figura
𝐴𝑉 = −𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
(𝑉𝐼𝑄 − 𝑉𝑡 )𝑅𝐷 = −1(18)(0.707)
5.13
Polarización en circuitos amplificadores MOS
𝑉
𝐴𝑉 = −12.7 𝑉
Miremos por ejemplo que pasa con una señal
triangular que es polarizada a 1.816V y esta tiene
una amplitud de 150mV pico a pico
Entonces las corrientes que se generan en los serán
1
𝑣𝐺𝑆 = 1.741, 𝐼𝐷 = 2 1𝑚(1.741 − 1)2 = 0.275𝑚𝐴
1
𝑣𝐺𝑆 = 1.816, 𝐼𝐷 = 2 1𝑚(1.816 − 1)2 = 0.333𝑚𝐴
1
𝑣𝐺𝑆 = 1.891, 𝐼𝐷 = 2 1𝑚(1.891 − 1)2 = 0.397𝑚𝐴
Se puede notar que el incremento negativo de la
corriente fue (0.333𝑚𝐴 − 0.275𝑚𝐴) = 0.058𝑚𝐴
(0.397𝑚𝐴 −
mientras que el positivo es
0.333𝑚𝐴) = 0.064𝑚𝐴, que son ligeramente
Como se vio en el ejemplo anterior el punto de
operación Q es el que permitirá o no la oscilación
de la señal además influirá directamente en la
ganancia del amplificador. Un punto de operación
adecuado se caracteriza por una corriente de
drenaje en DC estable y predecible 𝐼𝐷 y un voltaje
de drenaje a fuente 𝑉𝐷𝑆 que asegure la operación
en la región de saturación para todos los niveles de
señal de entrada esperados.
Polarización mediante la fijación de 𝑽𝑮𝑺
Un método que a simple vista parece bueno para la
polarización es fijar un 𝑉𝐺𝑆 constante, este por lo
tanto fijara una 𝐼𝐷 contante
1
𝐼𝐷 = 2 𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
(𝑉𝐺𝑆 − 𝑉𝑡 )2
8
El problema de realizar esta polarización es que
𝑊
𝜇𝑛 𝐶𝑜𝑥 𝐿 no es igual para todos los transistores de
hecho
cambian
significativamente
entre
transistores de la misma familia, además los
parámetros 𝜇𝑛 y 𝑉𝑡 dependen de la temperatura,
esto hará que a para iguales 𝑉𝐺𝑆 se tendrán
diferentes corrientes de drenaje como lo muestra
la figura 5.14
fuente, esto a su vez reducirá la corriente de
drenaje, lo que indica un efecto contrario al
supuesto.
𝑉𝐺𝑆 = 𝑉𝐺 − 𝑅𝑆 𝐼𝐷
1
𝐼𝐷 = − 𝑅 (𝑉𝐺𝑆 − 𝑉𝐺 )
𝑆
Lo que genera una recta de cómo se indica en la
figura 5.15 en donde se puede apreciar que para
dos MOSFET diferentes las corrientes son mas
similares.
Ejemplo 4.9 pág. 283
Figura 5.14
Como se ve en la grafica la diferencia entre
corrientes es muy significativa lo que hace que esta
no sea una buena polarización,
Polarización mediante la fijación de 𝑽𝑮 y conexión
de una resistencia a la fuente
Es necesario diseñar el circuito de la figura5.15
para establecer una corriente de drenaje de DC
𝐼𝐷 = 0.5𝑚𝐴. el Mosfet está especificado para
𝑊
tener 𝑉𝑡 = 1𝑉 y 𝑘′𝑛 𝐿 = 1𝑚𝐴/𝑉 2 . Omita el efecto
de la modulación del canal, use una fuente de
alimentación 𝑉𝐷𝐷 = 15𝑉, Calcule el cambio de
porcentaje en el valor de 𝐼𝐷 obtenido cuando el
MOSFET se remplaza con otra unidad que tiene la
𝑊
misma 𝑘′𝑛 𝐿 pero un 𝑉𝑡 = 1.5𝑉.
Como regla general de diseño se elige 𝑅𝐷 y 𝑅𝑆 para
que haya una caída de la tercera parte del voltaje
de la fuente de alimentación.
𝑅𝐷 =
𝑉𝐷𝐷 −𝑉𝐷
𝑅𝑆 =
𝑉𝑆
𝐼𝐷
𝐼𝐷
=
15𝑉−10𝑉
0.5𝑚𝐴
= 10𝐾Ω
5𝑉
= 0.5𝑚𝐴 = 10𝐾Ω
1
𝐼𝐷 = 2 𝜇𝑛 𝐶𝑜𝑥
𝑊
𝐿
(𝑉𝑂𝑉 )2
1
0.5𝑚𝐴 = 2 1𝑚𝐴(𝑉𝑂𝑉 )2
𝑉𝑂𝑉 = 1𝑉
𝑉𝐺𝑆 = 𝑉𝑂𝑉 + 𝑉𝑡 = 1 + 1 = 2𝑉
𝑉𝐺 = 𝑉𝐺𝑆 + 𝑉𝑆 = 2 + 5 = 7𝑉
Figura 5.15
Lo que sucede en este circuito es que la resistencia
𝑅𝑆 provee una retroalimentación negativa.
Considere el caso de que por algún motivo 𝐼𝐷
aumenta si 𝑉𝐺 se mantiene constante 𝑉𝐺𝑆
disminuirá debido al aumento en el voltaje de la
Para este caso se eligen las resistencias 𝑅𝐺1 y 𝑅𝐺2
que generen este voltaje, Si decidimos que por el
divisor circulara 1𝜇𝐴 entonces tenemos que
𝑉
7
𝐺
𝑅𝐺2 = 1𝜇𝐴
= 1𝜇𝐴 = 7𝑀Ω
9
𝑅𝐺1 =
𝑉𝐷𝐷 −𝑉𝐺
1𝜇𝐴
=
15−7
1𝜇𝐴
Polarización empleando una fuente de corriente
constante.
= 8𝑀Ω
Si el transistor NMOS se remplaza por uno que
tenga un 𝑉𝑡 = 1.5𝑉
1
𝐼𝐷 = 2 1𝑚(𝑉𝐺𝑆 − 1.5)2
𝑉𝐺 = 𝑉𝐺𝑆 + 𝐼𝐷 𝑅𝐷
En la figura se muestra este tipo de polarización, al
lado izquierdo el amplificador polarizado con una
fuente de corriente constante, y al izquierdo la
manera en cómo realizar la fuente de corriente
constante por medio de un espejo de corriente.
∆𝐼𝐷 = 0.455 − 0.5 = −0.045𝑚𝐴
7 = 𝑉𝐺𝑆 + 10𝐾𝐼𝐷
Con estas dos ecuaciones y aplicando FG se tiene
𝐼𝐷 = 0.455𝑚𝐴
Que es
−0.045
0.5
𝑥100 = −9% de cambio
Polarización
mediante
retroalimentación
un
resistor
de
En este circuito se hace uso de una resistencia de
retroalimentación conectada entre el drenaje y la
compuerta lo que garantiza que el transistor este
en saturación, además esta resistencia debe ser
grande para que el amplificador tenga una
resistencia alta a la entrada.
Es claro que al trabajar con una corriente constante
se logra el objetivo de la polarización, ahora
miremos como opera el circuito de la derecha
llamado espejo de corriente.
Al tener conectado 𝑄1 el drenaje y la compuerta
este estará saturado entonces
1
𝑊
En este circuito entonces tenemos que:
𝐼𝐷1 = 2 𝜇𝑛 𝐶𝑜𝑥 ( 𝐿 ) (𝑉𝐺𝑆 − 𝑉𝑡 )2
𝑉𝐺𝑆 = 𝑉𝐷𝑆 = 𝑉𝐷𝐷 − 𝑅𝐷 𝐼𝐷
Además la corriente será también
1
𝐼𝐷 = − 𝑅 (𝑉𝐺𝑆 − 𝑉𝐷𝐷 )
𝐷
Que es idéntica a la
ecuación de la corriente del circuito anterior
excepto porque 𝑅𝑆 ya es 𝑅𝐷 y 𝑉𝐺 es 𝑉𝐷𝐷 entonces
esta polarización también genera mayor
estabilidad.
1
𝐼𝐷1 = 𝐼𝑅𝐸𝐹 =
𝑉𝐷𝐷 +𝑉𝑆𝑆 −𝑉𝐺𝑆
𝑅
Y mientras el transistor 𝑄2 este en saturación
1
𝑊
𝐼𝐷2 = 2 𝜇𝑛 𝐶𝑜𝑥 ( 𝐿 ) (𝑉𝐺𝑆 − 𝑉𝑡 )2
2
Como comparten el mismo 𝑉𝐺𝑆 y si los parámetros
del transistor son iguales exceptuando las
longitudes del canal tenemos que
𝐼 = 𝐼𝑅𝐸𝐹
𝑊
𝐿 2
𝑊
( )
𝐿 1
( )
Figura 5.16
10