trabajo completo PDF - 24° Jornadas Argentinas de Ingeniería

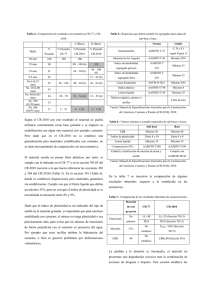
EFECTOS DINÁMICOS EN IMPACTOS DE BARCAZAS CON
PILAS DE PUENTES
Federico Pintoa
F. José Luperib
Carlos A. Pratoa
a
Departamento de Estructuras, F.C.E.F.yN., Universidad Nacional de Córdoba.
b
Estudiante Doctoral, F.C.E.F.yN., Universidad Nacional de Córdoba
Casilla de Correo 916, Córdoba, 5000, Argentina, [email protected]
Resumen
El diseño de puentes sobre vías navegables está frecuentemente dictado por el
riesgo de colisión de embarcaciones con las pilas. Actualmente, esta hipótesis de
carga es tenida en cuenta mediante normativas establecidas por la Asociación
Americana de Carreteras, AASHTO, las cuales recomiendan la utilización de cargas
estáticas equivalentes. Estas cargas equivalentes sólo consideran los efectos
dinámicos de la embarcación y no consideran la flexibilidad de las pilas, ni los
posibles efectos de la forma y tamaño del cabezal en las fuerzas máximas
resultantes en las estructuras que reciben el impacto. Recientemente se ha
avanzado en el desarrollo de técnicas analíticas que permiten estimar historias de
cargas más apropiadas, las cuales pueden ser incorporadas en modelos dinámicos
de estructuras de puentes a fines de realizar análisis más detallados de las fuerzas
desarrolladas debido al proceso dinámico de colisión. Este artículo presenta el
análisis numérico de una pila de un puente propuesto sobre el Río Paraná, en el cual
se consideran estados de carga correspondientes a la normativa AASHTO vigente e
historias de cargas desarrolladas mediante técnicas analíticas propuestas
recientemente en la literatura. Los resultados permiten identificar la importancia de
los fenómenos dinámicos y forma de cabezal, tanto en las fuerzas desarrolladas
como en los desplazamientos máximos
Palabras-clave: Puentes, impacto, embarcación, barcaza, efectos dinámicos
Abstract
The design of bridge structures across navigable waterways is frequently dictated by
the risk of vessel collision against pier structures. This loading condition is currently
accounted for in bridge design following the guidelines of the American Association
of State Highway and Transportation Officials, AASHTO, which are based on
equivalent static loads. These equivalent static loads, however, account only for
dynamic effects on the vessel, but do not consider the flexibility of the pier structure
nor possible size and shape effects of the loaded area on the maximum forces
developed by the impacted structure. Recent barge collision studies have developed
updated methodologies in order to derive time histories of impact loading for dynamic
barge collision analysis of bridge structures. This paper presents barge collision
analyses for a main pier of a recently proposed bridge over the Paraná River
following the AASHTO method, as well as time history analyses considering impact
loads obtained following recently proposed dynamic methods. Results are
instrumental in highlighting the importance of the dynamic effects of the impact loads
and geometry of the impacted are, both on displacements and internal forces.
Keywords: Bridge, impact, Barge, dynamic effects
1. Introducción
La cuantificación del riesgo de colapso debido a colisión de embarcaciones en
puentes sobre vías navegables es un aspecto crucial en la determinación de luces
libres, así como tipología y dimensión de fundaciones de estas estructuras
(AASHTO, 2008). La frecuencia de estos eventos no es despreciable: la literatura
internacional (AASHTO, 1991; Larssen, 1993) indica que ocurre en promedio un
evento colisión por año con consecuencias serias.
Cabe destacar el colapso del puente Sunshine Skyway sobre la Bahía de Tampa en
Florida (EEUU) en el año 1980, debido al impacto de un barco con la consecuente
pérdida de 35 vidas humanas. Luego de este evento catastrófico, se realizó en 1983
un coloquio internacional sobre colisión de embarcaciones en estructuras de puentes
en el seno de la Asociación Internacional de Ingenieros Estructurales y Especialistas
en Puentes (IABSE, por sus siglas en inglés) a fines de abordar la problemática
desde la perspectiva del diseño.
Meier-Dörnberg realizó experimentos a escala natural y reducida a fines de
cuantificar la relación entre fuerzas de impacto desarrolladas y energía disipada
sobre barcazas típicas europeas (Meier-Dörnberg, 1983). En base a los trabajos
realizados por Meier-Dörnberg sobre barcazas y a trabajos previos de Woisin (1976)
sobre impactos en proas de barcos, se elabora en 1991 la primera “Especificación
Guía” de la AASHTO con recomendaciones de diseño a fines de cuantificar fuerzas
de impacto en estructuras de puentes. Esta “Especificación Guía”, ha sido
incorporada en los reglamentos actuales de la AASHTO (2008) sin mayores
modificaciones, considera al problema de colisión de barcazas como un estado de
carga estática equivalente, en base al trabajo original realizado por Meir-Dornberg.
A nivel nacional, cabe destacar que los reglamentos de diseño no tienen en cuenta
el riesgo de colisión en forma explícita, mientras que los proyectos de obras
nacionales de envergadura sobre vías navegables consideran generalmente las
prescripciones de la normativa AASHTO (Pinto et al., 2008).
Desde los trabajos pioneros de Meier-Dörnberg en 1983 hasta comienzos del 2000
no hubo significativos avances en la determinación de fuerzas de colisión debido a
impactos de barcazas, mientras que sí hubo algunos avances en la cuantificación de
efectos dinámicos debido a impactos de barcos (por ejemplo, Pedersen 1993).
Trabajos recientes realizados en la Universidad de Florida (EEUU) (Consolazio y
colaboradores 2008) han avanzado considerablemente las metodologías de diseño
empleadas en las últimas décadas en base a ensayos de impacto a escala real
(Consolazio y Cowan 2003). Estos trabajos proponen relaciones carga deformación
para la proa de la barcaza en base a análisis numéricos refinados, validados en fase
experimental. Mediante estas relaciones carga deformación, es posible realizar
análisis acoplados de respuesta a impacto y, a partir de estos, los autores han
propuesto una metodología para estimar historias de fuerzas apropiadas para el
diseño de puentes frente a impactos de barcazas considerando los efectos
dinámicos.
La metodología propuesta por Consolazio y colaboradores (2008) difiere
sensiblemente de las recomendaciones de AASHTO (2008), por lo cual es de interés
establecer las diferencias obtenidas mediante ambas técnicas de análisis para los
puentes típicos sobre el Río Paraná. El objetivo del presente trabajo es analizar las
diferencias entre las metodologías e ilustrar las diferencias más salientes entre los
resultados obtenidos mediante ambas técnicas para una pila correspondiente a un
anteproyecto realizado para un puente sobre el Río Paraná.
2. Fuerza estática equivalente de AASHTO
Se considera que las barcazas que circulan frecuentemente por el Río Paraná son
de características similares a las “Jumbo Hopper” descriptas en la norma AASHTO
(2008), las cuales tienen las dimensiones indicadas en la Figura 1.
Meier-Dörnberg realizó dos ensayos dinámicos sobre barcazas a escala 1:4.5 y un
ensayo estático en una barcaza en escala reducida 1:6 (Meier Dörnberg, 1983). Los
ensayos dinámicos consistieron en aplicar un impacto mediante un martillo pendular
sobre la proa de una barcaza inmóvil. Uno de los ensayos fue realizado mediante un
martillo con cabeza de impacto cilíndrica de 1.7 m de diámetro, mientras que el otro
utilizó una cabeza de impacto en ángulo de 90 grados. El ensayo de carga estática
utilizó un martillo de 2.3 m.
La Figura 2 muestra los resultados de Meier-Dörnberg correspondientes a 5
procesos de carga y descarga realizados durante el ensayo estático y 3 procesos de
carga y descarga realizados durante el ensayo dinámico con martillo en ángulo.
Dado que los resultados obtenidos por este investigador no difieren sensiblemente
para el caso estático y dinámico, la AASHTO (1991) propone la utilización de una
envolvente, también indicada en la Figura 2, que define el comportamiento carga
deformación de la proa de la barcaza tanto para casos estáticos como dinámicos. De
esta manera, surge el concepto de carga “estática equivalente”, la cual tiene en
cuenta los efectos dinámicos de la proa de la barcaza pero no necesariamente los
de la estructura a impactar.
Figura 1 Dimensiones de barcaza típica
14
Ensayos estáticos
Ensayos dinámicos
Envolvente
12
Carga [MN]
10
8
6
4
2
0
0
1
2
3
4
Deformación [m]
Figura 2 Envolvente carga-deformación utilizada por norma ASHTO (1991, 2008)
Cabe destacar que la curva carga deformación propuesta por AASHTO es
independiente de la forma y dimensión de la pila o cabezal impactado, mientras que
para barcazas de ancho superior a la Jumbo Hopper esta norma aumenta las cargas
mediante un factor igual a la relación de anchos entre barcazas.
La metodología empleada por la norma AASHTO consiste en determinar una fuerza
de impacto “estática equivalente”, la cual es determinada en base a la energía
cinética inicial de la barcaza. Considerando que toda la energía cinética de la
barcaza es transformada en trabajo de deformación elastoplástico de la estructura
de proa, es posible obtener la fuerza “estática equivalente” igualando el área por
debajo de la curva carga-deformación de la Figura 2 al valor de la energía a disipar.
Cabe destacar que la deformación máxima de proa alcanzada por los ensayos de
Meier Dörnberg es del orden de los 3 m, mientras que el largo total de la estructura
de proa es de 6 m. De esta manera, si se restringe la deformación máxima a un
valor de 6 m (abollamiento total de la proa), la energía disipada por deformación de
la barcaza es del orden de los 60 MNm. Considerando una velocidad de diseño
típica para barcazas aguas abajo sobre el Río Paraná, de 5.3 m/s, esta energía de
abollamiento total de proa corresponde a una masa de 4100 toneladas. Esta masa
es ligeramente inferior a la de dos barcazas cargadas (1700 toneladas), más un
remolcador (típicamente 1500 toneladas), lo cual indica que para el caso más de dos
barcazas navegando a 5.3 m/s, la disipación de energía debería realizarse mediante
un mecanismo de deformación elastoplástica que exceda al abollamiento total de la
proa de la barcaza frontal. Esto no es discutido en la norma AASHTO, mediante la
cual es posible utilizar para el cálculo valores de abolladura ampliamente superiores
a las dimensiones de la proa.
3. Metodología AVIL
3.1 Curvas carga deformación de barcazas
El problema de colisión de barcazas contra puentes ha sido recientemente estudiado
en considerable detalle en la Universidad de Florida (Cosolazio y Cowan 2003,
Consolazio y colaboradores, 2005 y 2008). Se realizaron análisis numéricos
detallados a fines de obtener curvas carga-deformación para proa de barcazas
típicas considerando diversas geometrías de obstáculos a impactar (Consolazio y
Cowan 2003). Estos resultados numéricos fueron luego validados mediante ensayos
a escala natural realizados en el Puente St. George Island (Consolazio y
colaboradores, 2005). A partir de los resultados numéricos y experimentales, se
realizaron distintas metodologías a fines de estimar fuerzas durante colisión de
barcazas con estructuras de puentes.
Los resultados obtenidos por Consolazio y Cowan (2003) están dados en la Figura
3, donde puede observarse que los mismos se limitan a deformaciones menores a 5
m, deformación menor a la longitud total de la estructura de proa de las barcazas.
25
Frente plano
Carga [MN]
20
Frente cilíndrico
15
B = 10.7 m
10
5
B = 0.9 m
0
0
1
2
3
4
5
Deformación [m]
Figura 3. Curvas carga-deformación para barcaza (Consolazio y Cowan, 2003)
Un aspecto muy importante de los resultados obtenidos por Consolazio y Cowan es
que la fuerza pico es sensiblemente afectada por la forma de la pila o cabezal
impactado, produciendo los frentes planos y anchos fuerzas pico muy superiores a
las correspondientes a pilas o cabezales redondeados o de pequeño ancho (Figura
3). Otro resultado importante es que la fuerza pico depende del ancho del objeto,
siendo esta dependencia más pronunciada para el caso de frentes de impacto plano.
A fines de obtener una metodología simplificada de análisis, pero que tenga en
cuenta los resultados indicados en la Figura 3, Consolazio y colaboradores (2008)
proponen una simplificación consistente en representar la curva carga deformación
mediante una curva bilineal, cuya carga de fluencia es igual a la carga pico
determinada en los análisis detallados. Mediante una regresión lineal, y
considerando un posible aumento en la carga de fluencia de un 33% debido a
distinta resistencia del acero (A50 vs. A36 considerado en el análisis), y otras
eventualidades tales como el espesor de las chapas de las estructuras (½” vs. ⅜”),
estos autores proponen la relación carga de fluencia vs. ancho de cabezal o pila
dada en la Figura 4.
30
Carga máxima [MN]
25
20
15
10
5
0
0
2
4
6
8
10
Ancho de cabezal o pila [m]
Figura 4. Fuerzas máximas de diseño
En cuanto a la deformación de fluencia, estos autores sugieren la utilización de una
deformación de fluencia de 1.3 cm para el caso de cabezales o pilas planas y 5.1 cm
para el caso de cabezales o pilas redondeadas.
A fines de ilustrar las diferencias entre las curvas carga deformación recomendadas
por Consolazio y colaboradores (2008) y las de AASHTO (1991, 2008), se realiza
una comparación considerando el caso de un cabezal con frentes plano y circular de
6 m de ancho.
20
Carga [MN]
16
B=6m
12
8
AASHTO
Consolazio et al. (2008) Circular
4
Consolazio et al. (2008) Plano
0
0
1
2
3
4
Deformación [m]
Figura 5. Comparación de curvas carga deformación para cabezal de 6 m de
ancho
La Figura 5 muestra que de acuerdo a la metodología de Consolazio y
colaboradores (2008) existe un gran beneficio en la utilización de cabezales o pilas
redondeadas, ya que las fuerzas máximas se reducen en un 50%,
aproximadamente. Por otra parte, cabe destacar que la curva indicada por AASHTO
(1991, 2008) indica fuerzas similares que las obtenidas para el caso de pila circular,
pero menores a las correspondientes a frente plano.
3.2 Determinación de historia de cargas
Dentro de las metodologías propuestas que no requieren realizar un modelo
acoplado de interacción barcaza-puente, Consolazio y colaboradores (2008)
desarrollaron la metodología de Fuerza de Impacto Aplicada, o AVIL, por sus siglas
en inglés. Aunque el método no es exacto, estos autores indican que la metodología
produce resultados acordes con métodos de cálculo más sofisticados que
consideran la interacción barcaza-puente en forma rigurosa en los rangos de
impactos de baja (error ~5%), media (error ~5%) y alta energía (error < 1%). El
método AVIL tiene la ventaja que la historia de carga calculada puede ser aplicada
directamente al modelo de puente a fines de realizar un análisis dinámico. La
historia de carga se calcula a través de los principios de conservación de energía y
conservación de cantidad de movimiento, en base a las características de la
embarcación (masa de barcaza, velocidad inicial, relación carga-deformación de la
proa) y algunas características estructurales básicas del puente. En la Figura 6 se
muestra un esquema conceptual del modelo de 2 grados de libertad considerado
para la formulación de este método.
Figura 6. Modelo de Barcaza-Pila-Suelo
La metodología propuesta diferencia los impactos que mantienen a la barcaza en el
rango elástico de aquellos que producen incursiones en el rango elastoplástico.
Dado que el presente trabajo trata de impactos a velocidades importantes, sólo se
considerarán estos últimos. De esta manera, la carga máxima instantánea que la
barcaza produce sobre el cabezal o pila es igual a la carga de fluencia descripta en
el apartado anterior.
La metodología simplifica a la historia de cargas en tres etapas; una primera etapa
en la cual las cargas en la proa de la barcaza aumentan hasta que se produce
fluencia, una segunda etapa durante la cual la carga se mantiene constante e igual a
la carga de fluencia, y una tercera etapa de descarga al final del proceso de colisión.
Se considera que la primera y tercer etapas se producen en forma perfectamente
elástica, y se asumen variaciones del tipo de un cuarto de onda de la función seno
en la historia de cargas (Figura 7).
La duración de la primera y tercer etapas del proceso es determinada en función de
consideraciones sobre conservación de momento lineal y de energía, mientras que
la duración de la segunda etapa es determinada mediante consideraciones sobre
conservación de momento lineal y que la velocidad es nula al final de esta etapa
(Consolazio y colaboradores, 2008).
Figura 7. Historia de carga para caso no-lineal.
3.3 Verificación de historia de carga
Con el fin de obtener una evaluación independiente de la historia de cargas obtenida
mediante la metodología AVIL, se utiliza en este trabajo un modelo unidimensional
de masas y resortes no-lineales basado en la metodología originalmente propuesta
por Yuan y Harik (2008). Este modelo de múltiples grados de libertad (MGL) tiene en
cuenta la interacción entre barcazas mediante vínculos elastoplásticos
representativos de las eslingas de vinculación con las barcazas adyacentes. La pila
se modela mediante un voladizo con dos masas puntuales, un resorte lineal y un
resorte rotacional. La primera masa corresponde a la superestructura y la segunda a
la pila o cabezal y los resortes corresponden a la rigidez que aporta la
superestructura (Yuan y Harik, 2008; Luperi y colaboradores, 2010).
Figura 8. Modelo unidimensional de masas y resortes no-lineales
Para el comportamiento de la proa se adopta una relación elástica-perfectamente
plástica según lo propuesto por Consolazio y colaboradores (2008). Para barcazas
en la misma fila, el comportamiento a compresión es diferente al comportamiento a
tracción; ya que a compresión actúa la rigidez del cuerpo de la barcaza, descripta
mediante una relación elasto-plástica con endurecimiento. A tracción, por otra parte,
actúan los cables de acero que son amarrados entre barcazas, comportamiento
definido mediante una relación elástica-perfectamente plástica. La fuerza de fluencia
para el caso de tracción es inferior a la fuerza de fluencia a compresión. En la Figura
9 se muestra un esquema de estas relaciones.
Figura 9. Comportamiento de proa y vínculos entre barcazas
4. Ejemplo de aplicación
4.1. Generalidades
A fines de ilustrar las diferencias entre las metodologías de fuerza estática
equivalente y de historia de fuerzas (AVIL y MGL), se considera un caso
correspondiente a la alternativa de tablero de hormigón del anteproyecto de un
puente sobre el Río Paraná, a la altura de las localidades Reconquista (Provincia de
Santa Fe) y Goya (Provincia de Corrientes). La Figura 10 muestra una vista del
cruce principal del puente, mientras que en la Figura 11 se da una vista lateral de
una de las pilas principales a ser analizada.
La estructura principal consiste en un puente atirantado, de 390 m de luz principal y
luces laterales de 180 m. Tanto las pilas como el tablero de la alternativa
considerada en este ejemplo son de hormigón armado, siendo la pila hueca en toda
su altura. Las fundaciones consisten en grupos de pilotes de hormigón, empotrados
en cabezales flotantes de hormigón.
Estudios de tráfico para puentes similares sugieren para el impacto de diseño la
consideración de un convoy de cuatro barcazas tipo Jumbo Hopper de ancho por
cuatro de fondo (Pinto y colaboradores, 2008), si bien estudios recientes sugieren la
posibilidad de la presencia de convoyes de mayor envergadura, a fines de realizar
los estudios comparativos propuestos en este trabajo, se consideran convoyes de
cuatro barcazas de fondo.
Existe controversia a nivel internacional en cuanto a la contribución de las filas
laterales que no impactan directamente con el cabezal (Figura 12) (Yuan y Harik,
2008). Si bien la opinión de los autores es que existe una importante contribución de
las mismas a la respuesta de la estructura impactada, éstas no serán consideradas
en el presente estudio a fines de limitar la discusión a los efectos dinámicos del
proceso de impacto. De esta manera, se considerará solamente una fila de cuatro
barcazas tipo Jumbo Hopper, empujadas por un remolcador (Figura 13).
Figura 10. Vista del cruce propuesto
Figura 11. Vista lateral de pila de puente
Figura 12. Vista en planta de impacto contra el cabezal
Figura 13. Caso a analizar
4.2. Historia de cargas
La masa de cada barcaza cargada es de 1900 toneladas, mientras que la masa del
remolcador es de 1500 toneladas. Se considera una velocidad inicial de impacto de
5.3 m/s, la cual es una estimación en base a la velocidad máxima en condiciones
normales aguas abajo para el cruce sobre el mismo río a la altura de las ciudades de
Resistencia (Provincia de Chaco) y Corrientes (Pinto, 2008). Ignorando posibles
contribuciones de masa hidrodinámica (AASHTO 1991, 2008) a efectos de realizar
una comparación entre distintos métodos, la energía cinética total del conjunto de
barcazas y remolcador resulta igual a 128 MNm.
Siguiendo la metodología indicada por AASHTO (1991, 2008), se obtiene una
deformación de la proa de la barcaza igual a 9.9 m y una carga pico del orden de los
21.9 MN. Cabe destacar que el valor de deformación resulta mayor a la longitud de
proa, y el valor de carga obtenido largamente excede el valor máximo alcanzado en
los ensayos de Meier-Dörnberg (1983) (Figura 2). Dado que la norma AASHTO
propone la utilización de esta carga como carga “estática equivalente” se considera
que la misma permanece constante en el tiempo (Figura 14).
Figura 14. Historia de cargas
Siguiendo la metodología AVIL (Consolazio y colaboradores, 2008), la carga máxima
obtenida resulta igual a 17.3 MN, mientras que la variación temporal (Figura 14)
resulta tal que se asemeja a una carga tipo rectangular. La Figura 15a muestra un
detalle de la historia de cargas al inicio del proceso de colisión, donde puede verse
que el tiempo para alcanzar la carga máxima resulta igual a 0.025 s, mientras que la
totalidad del proceso de carga es del orden de los 3 s (2.93 s impulso rectangular
equivalente).
Cabe destacar que la carga máxima obtenida mediante AASHTO resulta un 27%
superior a la carga máxima obtenida mediante el método AVIL. Sin embargo,
AASHTO ignora la variación temporal, lo cual puede producir efectos dinámicos que
resulten en esfuerzos más severos para el caso del método AVIL.
La historia de carga según la norma DIN tiene una duración de 3.9 segundos, con
una fuerza promedio de 13 [MN], un 40 % menos que la fuerza estática del método
AASHTO.
La Figura 15b muestra un detalle de la porción final del proceso de carga, donde
puede verse que el modelo de MGL indica una variación menos suave que el
modelo AVIL, siendo la duración total muy similar para ambos procesos.
(a)
(b)
Figura 15. Detalle de (a) comienzo y (b) finalización de proceso de carga
(a)
(b)
Figura 16. (a) Transformada de Fourier y (b) Espectro de respuesta de función de
carga,
La Figura 16a muestra la transformada de Fourier de la función de carga, donde
puede verse que el contenido de frecuencias obtenido mediante el modelo de MGL y
mediante la metodología AVIL son esencialmente coincidentes, con diferencias sólo
en el rango de frecuencias mayores a 4 Hz, rango para el cual el contenido es de
todas maneras bajo. La Figura 16b muestra el espectro de respuesta elástica para
un amortiguamiento del 5%, donde puede verse que no existen diferencias
perceptibles entre ambos procedimientos de determinación de cargas para el caso
considerado. La Figura 16b permite identificar, por otra parte, que la fuerza elástica
máxima generada para un sistema de 1GLD es del orden del doble del valor máximo
alcanzado durante el proceso (17.3 MN), para sistemas cuyos períodos naturales
son menores al doble de la duración del impacto. Para un sistema de 1GLD
amortiguado, con baja relación de amortiguamiento, ξ, la fuerza elástica máxima
para un impulso rectangular perfecto, para períodos menores al doble de la
duración, resulta:
Ku max = P  2 − ( π − 1) ξ  (1)
Esta expresión simplificada arroja valores virtualmente coincidentes a los
observados en la Figura 16b, lo que indica que el proceso de carga puede ser
aproximado mediante un impacto rectangular ideal. Por lo tanto, se espera que el
factor de amplificación dinámica sea del orden de dos para el caso no amortiguado,
y para estructuras cuyo período natural sea menor a 6 s.
4.3. Modelo Numérico de Superestructura
A fines de estudiar la respuesta de una de las pilas principales de la estructura en
consideración, se considera un modelo del puente principal completo, el cual
consiste en dos pilas principales, dos pilas de retención intermedias y dos extremas.
Dado que el modelo sólo es utilizado en este trabajo a fines de representar la
respuesta frente a un impacto lateral de embarcación a nivel de pila principal, el
tablero es modelado mediante una viga con propiedades de rigidez y masa
equivalentes, mientras que los obenques han sido incorporados mediante
condiciones de inextensibilidad en el punto de conexión de los mismos con el
tablero. Las propiedades geométricas y mecánicas corresponden a los valores
utilizados en el anteproyecto de la alternativa de hormigón para el cruce en cuestión.
Las fundaciones de las pilas principales consisten en 46 pilotes de hormigón armado
de 2 m de diámetro. Dado que el análisis realizado se restringe a cargas laterales,
se considera en el modelo una profundidad de pilote equivalente a fines de proveer
igual rigidez lateral que un voladizo equivalente. Esta profundidad equivalente es
obtenida mediante un modelo numérico independiente de un pilote inmerso en
resortes no lineales, representativos de las arenas del Río Paraná. Determinando las
curvas carga deflexión del sistema pilote-resortes, se obtiene la longitud equivalente
de voladizo necesaria para proveer una rigidez equivalente en el modelo estructural.
La Figura 17 muestra la representación del modelo numérico utilizado, donde los
pilotes son modelados mediante elementos de viga, el cabezal es modelado
mediante un emparrillado equivalente, y la pila es modelada mediante segmentos de
viga con deformación de corte.
El proceso de colisión es analizado mediante el programa SAP2000, mediante un
análisis modal considerando los primeros 12 modos naturales de vibración. La
Figura 18 muestra una vista esquemática del primer modo de vibración lateral, el
cual resulta con un período, T = 4.85 s.
Figura 17. Esquema del modelo numérico utilizado
Figura 18. Primer modo de vibración lateral
5. Resultados
La Figura 19 muestra la historia de desplazamientos del centro del cabezal debido al
impacto considerando las cargas obtenidas mediante AASHTO y AVIL. Cabe
destacar que el desplazamiento máximo obtenido mediante la metodología AVIL es
de 26 cm, mientras que el valor obtenido mediante AASHTO es de 19 cm. Es decir
que la metodología AVIL resulta en desplazamientos del orden de un 34% superior a
los obtenidos mediante AASHTO.
A fines de visualizar la diferencia en resultados mediante un modelo
conceptualmente simplificado, puede considerarse un sistema equivalente de un
grado de libertad, con un período igual al período natural de la estructura. En este
caso, la relación duración de carga rectangular equivalente/período natural resulta
igual a tD/T = 2.93/4.85=0.6, lo cual resulta en un factor de amplificación dinámica de
γ= 2 si se considera un problema de impacto no amortiguado sobre un sistema de un
grado de libertad (Figura 20). Dado que las cargas instantáneas máximas obtenidas
mediante AVIL resultan un 22% inferiores a AASHTO, pero que consideran un factor
de impacto del orden de 2, el efecto neto estimado en base a consideraciones
simplificadas resulta del orden de 1.56, es decir un 56 % superior a AASHTO. Esto
se condice con el modelo numérico que indica un desplazamiento debido a la
historia de carga del método AVIL mayor a la AASHTO (diferencia de 44 %).
Desplazamiento (m)
0.3
0.2
0.1
0.0
-0.1
AVIL
AASHTO
-0.2
-0.3
0
2
4
6
8
10
12
14
Tiempo (s)
Figura 19. Historia de desplazamientos de cabezal debido a impacto
Factor de Impacto
2.5
2
P
t
1.5
td
1
td/T=0.60
0.5
0
0.01
0.1
1
td/T
Figura 20. Factor de impacto para un sistema de un grado de libertad
Las Figuras 21 y 22 muestran la historia de momentos flectores y cortes máximos en
pilotes debido al impacto considerando las cargas obtenidas mediante AASHTO y
AVIL. Puede verse que los valores obtenidos mediante AVIL superan en este caso
en un 46% tanto para el caso de momentos flectores como para corte a los
obtenidos mediante AASHTO. La diferencia es nuevamente explicada por una
combinación de diferencia en cargas y efectos dinámicos (factor de impacto).
Momento en Pilotes (MNm)
20
10
0
AVIL
AASHTO
-10
-20
0
2
4
6
8
10
12
14
Tiempo (s)
Figura 21. Historia de momento flector máximo en pilotes debido a impacto
Corte en Pilotes (KN)
800
600
400
200
0
-200
AVIL
AASHTO
-400
-600
0
2
4
6
8
10
12
14
Tiempo (s)
Figura 22. Historia de corte máximo en pilotes debido a impacto
Las Figuras 23 y 24 muestran la historia de momentos flectores y cortes máximos en
la pila considerando metodologías AASHTO y AVIL. En este caso la diferencia es
más notable debido a que la deformación estática involucra esfuerzos muy bajos en
la estructura de pila, mientras que los efectos dinámicos debido a la masa del tablero
y pila producen momentos importantes, notablemente superiores a los obtenidos
mediante la aplicación estática de la carga.
Momento en Pila (MNm)
200
100
0
AVIL
AASHTO
-100
-200
0
2
4
6
8
10
12
14
Tiempo (s)
Figura 23. Historia de momentos en base de pila
8
Corte en Pila (MN)
6
4
2
0
-2
-4
AVIL
AASHTO
-6
-8
0
2
4
6
8
10
12
14
Tiempo (s)
Figura 24. Historia de corte en base de pila
3 CONCLUSIONES
El proceso de colisión de conjuntos de barcazas sobre pilas de puentes genera
historias de fuerza que, para casos de grandes conjuntos de barcazas a altas
velocidades de impacto, pueden asemejarse a impactos rectangulares ideales.
Metodologías recientes que modelan el conjunto de barcazas y la interacción con la
estructura de puente en forma explícita arrojan resultados muy similares a los
obtenidos mediante metodologías simplificadas basadas en balance de energía y
cantidad de movimiento, particularmente para el caso de impacto de alta energía.
Estas metodologías difieren en relación a la norma AASHTO de diseño de puentes
en cuanto a que permiten definir la variación temporal del proceso de carga.
Dado que el proceso de cargas resulta similar a un impulso rectangular ideal, existen
importantes efectos dinámicos, actualmente no explícitamente tenidos en cuenta por
la norma AASHTO. La fuerza máxima instantánea desarrollada se encuentra
limitada por la carga de abolladura de la proa del tren de barcazas. Por lo tanto, para
balancear la cantidad de movimiento del tren mediante el impulso producido durante
el impacto, la duración del proceso de carga resulta tal que el factor de amplificación
dinámica es del orden de dos para estructuras típicas (períodos naturales menores a
6 s). De esta manera, se concluye que los efectos dinámicos son de gran
importancia y no deberían ser ignorados en el análisis de colisión de barcazas.
Para el ejemplo de análisis considerado, las metodologías de análisis que
consideran el proceso dinámico de colisión, evalúan una carga máxima instantánea
21% inferior a la obtenida mediante el método estático propuesto por la AASHTO.
Sin embargo, debido a los importantes efectos dinámicos, los esfuerzos resultantes
en la estructura, así como los máximos desplazamientos obtenidos mediante los
métodos dinámicos, resultan 50% superiores a los obtenidos mediante el método
estático de la AASHTO para el caso de las fundaciones, mientras que la diferencia
es mayor para el caso de la superestructura.
4 REFERENCIAS
[1] AASHTO, “Guide Specification and Commentary for Vessel Collision Design of
Highway Bridges”, American Association of State Highway and Transportation
Officials Washington, D.C., 1991.
[2] AASHTO LRFD Bridge Design Specifications, Customary U.S. Units, 4th Edition,
with 2008 Interim Revisions. American Association of State Highway and
Transportation Officials, Washington, D.C., 2008.
[3] Consolazio, G.R. y Cowan, D.R.. Nonlinear analysis of barge crush behavior and
its relationship to impact resistant bridge design. Computers and Structures, 81(811), pp. 547-557, 2003.
[4] Consolazio, G. R., Cowan, D. R., Biggs, A., Cook, R. A., Ansley, M., y Bollmann,
H. T. Full-Scale Experimental Measurement of Barge Impact Loads on Bridge Piers.
Journal of the Transportation Research Board, Transportation Research Record, No.
1936, pp. 81-93, 2005.
[5] Consolazio, G. R., McVay, M. C., Cowan, D. R., Davidson, M. T., Getter, D. J.,
Development of Improved Bridge Design Provisions for Barge Impact Loading.
Structures Research Report 2008/51117, University of Florida, Civil and Coastal
Engineering, Gainesville FL, EEUU, 2008.
[6] Larsen, O.D., Ship Collision with Bridges. IABSE Structural Engineering
Documents. The Interaction Between Vessel Traffic and Bridge Structures. IABSEAIPC-IVBH, p.53-56, Suiza, 1993.
[7] Luperi, F. J., Pinto, F., Prato, C. A. “Determinación de historia de cargas para
impactos frontales de barcazas sobre pilas de puentes”. Enviado para posible
publicación en el MECOM-CILAMCE 2010.
[8] Meier-Dörnberg, K. E. (1983). Ship Collisions, Safety Zones, and Loading
Assumptions for Structures in Inland Waterways, Verein Deutscher Ingenieure
(Association of German Engineers) Report No. 496, pp. 1-9.
[9] Pedersen, P.T. 1993, Ship Impacts: Bow Collisions, Conference Proceedings
from the Third International Symposium on Structural Crashworthiness and Failure,
University of Liverpool, U.K.
[10] Federico Pinto, Carlos A. Prato and Pedro J. F. Huerta (2008). Vessel Colission
Protection for Chaco Corrientes Bridge By Means Of Energy Absorbing Drilled
Shafts. Mecánica Computacional, Volume XXVII. Number 11. Structural Analysis
and Design.
[11] Yuan, P., Harik, E. I. (2008) “One-Dimensional Model for Multi-Barge Flotillas
Impacting Bridge Piers,” Computer–Aided Civil and Infrastructure Engineering, Vol.
23, No. 6., pp. 437-447.
[12] Woisin, G. The Collision Tests of the GKSS. Yearbook of the Shipbuilding
Technology Society, Vol. 70, pp. 465-487, Berlin, 1976.