ElECCión dE las variablEs

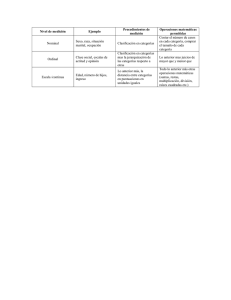
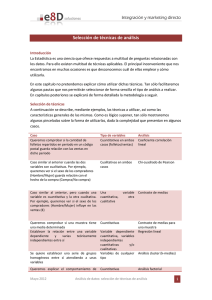
Capítulo 8
Elección de las variables
Elena García Martín, María Satué Palacián, María Pilar Bambó Rubio
1. Introducción
2. TIPOS DE VARIABLES
2. Tipos de variables
a) Cuantitativas y cualitativas
b) Descriptivas y experimentales
c) Principales, secundarias y de confusión
d) Directas e indirectas
3. Escalas de medición
a) Escala nominal o clasificatoria
b) Escala ordinal o escala de rango
a) Variables cuantitativas y cualitativas
Las variables pueden ser clasificadas como cuantitativas (llamadas también intervalares o numéricas)
o cualitativas (o categóricas), dependiendo de si los
valores presentados tienen o no un orden de magnitud natural (cuantitativas), o simplemente un atributo
no sometido a cuantificación (cualitativa).
c) Escala de intervalo
d) Escala de proporción
4. Elección y características de una buena variable
5. Obtención de variables.
6. Aleatorización y enmascaramiento de variables
7. Medida de variables: Fiabilidad y validez
1. INTRODUCCIÓN
Antes de utilizar un método estadístico que nos
permita inferir datos sobre la población a estudiar
debemos elegir y evaluar las variables y escalas de
medición que van a ser utilizadas. En este capítulo se
explicará los tipos de variables, cómo deben ser elegidas y registradas en función del objetivo del estudio
y el método para evaluar su fiabilidad y validez. Una
variable es una característica que al ser medida en
diferentes sujetos es susceptible de adoptar distintos
valores. Cada variable tiene una escala de medida,
que depende de los valores que puede adoptar y que
determina el trato estadístico que va a darse a la información. Elegir una buena variable supone medir
exactamente el efecto que deseamos y optimizar la
potencia de nuestro estudio, por lo que se trata de
una elección importante.
Variables cuantitativas: Son aquellas que sólo
pueden expresarse en cantidades numéricas. Ejemplos clásicos de este tipo de variables serían la talla
y el peso o la PIO y la AV. Debido a la naturaleza
numérica de este tipo de variables, su tratamiento estadístico podrá ser más elaborado que en otro tipo de
variables, incluyendo operaciones aritméticas, lo que
permite una descripción más completa y precisa. Las
variables cuantitativas pueden subdividirse a su vez
en dos subtipos: continuas y discretas.
Variables cuantitativas continuas. En las variables
cuantitativas continuas los valores numéricos que
adoptan las observaciones pueden estar contenidos
dentro de un intervalo, existiendo infinitas posibilidades dentro del mismo. En este caso, las categorías o
clases no vienen dadas de forma natural, sino que deben ser elegidas y el recorrido (conjunto de posibles
valores de la variable) se divide en intervalos que no
se solapen. El análisis de distribución de las variables
cuantitativas continuas es más complejo que el de las
variables cualitativas o el de las cuantitativas discre-
66
tas. Su representación gráfica se realiza mediante histogramas y polígonos de frecuencias (fig. 1). Ejemplo
de estas variables serían el peso o la PIO.
Variables cuantitativas discretas. La distribución
de estas variables es similar a la de las variables cualitativas (que se explicarán más adelante), ya que las
categorías en las que se agrupan los datos vienen
dadas de forma natural por los valores que adquiere la variable. En las variables cuantitativas discretas
los valores numéricos son enteros, sin posibilidad de
que la variable tome valores intermedios. Ejemplos
de este tipo de variables serían el número de hijos o
el número de admisiones en un hospital (fig. 2).
Variables cualitativas: Las variables cualitativas se
utilizan como medida de identificación: aquí los números son etiquetas que identifican particularidades
o clases. Estas observaciones no pueden ser medidas,
pero pueden expresarse cualitativamente y reciben el
8. Elección de las variables
nombre de «atributos». Un «atributo» corresponde
a un valor específico en una variable. Un ejemplo
de variable cualitativa es «sexo», que tiene 2 atributos: varón y mujer. Dependiendo de los valores que
pueda adoptar una variable cualitativa, ésta puede a
su vez ser dicotómica (cuando adopta un sólo valor
entre 2 posibles, sin jerarquía entre sí; por ejemplo:
hombre-mujer, positivo-negativo), o bien, poli o multicotómica, si existe la posibilidad de que adopte
múltiples valores (por ejemplo: nivel socioeconómico, grupos sanguíneos). Las variables cualitativas
también pueden clasificarse en nominales u ordinales. Una variable será nominal cuando los datos
correspondientes no sigan ninguna jerarquía entre
sí. Por ejemplo, la variable «color de ojos» (verde,
azul, negro…), o la variable «raza». Si los valores que
adopta una variable siguen un orden, secuencia o
progresión natural esperable, entonces hablamos de
Fig. 1: Representación mediante histograma de altura de los jugadores de un equipo de baloncesto.
Fig. 2: Representación gráfica del número de hijos por familia en 16 familias encuestadas.
67
8. Elección de las variables
variable cualitativa ordinal (por ejemplo: intensidad
del dolor, respuesta a un tratamiento, estadíos de una
enfermedad) (fig. 3). En los casos en que, a pesar de
este orden jerárquico natural, no es posible obtener
valoración numérica lógica entre dos valores, se habla de variable cuasicuantitativa (1).
b) Descriptivas y experimentales
Una variable descriptiva es aquella en la que los
datos sólo son anotados según han sido observados,
sin conclusiones acerca de una posible influencia o
causalidad. Valen para definir los criterios de inclusión y exclusión de nuestra muestra, para caracterizarla (edad, sexo, etc) y para mostrar los resultados
de los estudios descriptivos. Una variable experimental es aquella que ha sido manipulada por el investigador. Cuando se propone una relación de variables
en forma A causa B, A es la variable independiente y
B la dependiente (porque depende de A). La variable
independiente o predictora (que es la que manipulamos) «causa» la variable dependiente o de desenlace
(que es el resultado que medimos).
Ejemplo 8.1
or ejemplo, si queremos averiguar cómo
P
afecta la adición de sal a la temperatura
de ebullición del agua, la variable «cantidad de sal» sería la variable independiente que será modificada a lo largo del
experimento para observar el cambio en
la variable dependiente «temperatura de
ebullición del agua».
c) Principales, secundarias y de confusión
Las variables principales o primarias son aquellas
que están relacionadas con el objetivo principal de la
investigación mientras que las variables secundarias
son aquellas que no nos proporcionan una respuesta a la pregunta principal que deseamos contestar,
pero que han podido registrarse en el transcurso de
la investigación en forma de objetivos secundarios.
El análisis de estas variables aportará ciertas conclusiones, que deberán interpretarse con cuidado, ya
que el estudio no estaba diseñado para esos posibles
resultados, y por tanto el tamaño muestral podría
no ser suficiente o el tipo de investigación no ser la
adecuada (2). La diferencia entre los objetivos primarios y secundarios se muestra en el capítulo 5. Una
variable o factor de confusión es una variable que
distorsiona el efecto del factor de estudio sobre la variable de respuesta. La figura 4 muestra gráficamente
esta distorsión. Estudiaremos este tipo de efectos en
el capítulo 25, dedicado a la confusión y los sesgos.
d) Directas e indirectas
Las variables directas se definen como resultado
directo clínicamente relevante de la enfermedad en
estudio, por ejemplo la progresión del campo visual
en el glaucoma o el grado de retinopatía diabética
en los pacientes diabéticos. Las variables indirectas
(llamadas también intermedias) no se refieren a los
resultados finales, pero por su fuerte correlación se
utilizan como índices de aquellos (por ejemplo, la
glucemia en pacientes diabéticos o la PIO en pacientes con glaucoma). Otros ejemplos de variables
Fig. 3: Diagrama de sectores en una variable cualitativa ordinal. Se representa la intensidad del dolor en pacientes con aftas
orales.
68
8. Elección de las variables
Fig. 4: Efecto de una variable de confusión.
directas son la mortalidad o la calidad de vida y de
variables indirectas la tensión arterial o el resultado
obtenido en una prueba de esfuerzo.
excluyen mutuamente. La única relación implicada
es la de equivalencia, es decir, los miembros de cualquier subclase consultada deben ser equivalentes.
3. ESCALAS DE MEDICIÓN
b) Escala ordinal o escala de rango
Los tipos de variables que se han explicado presentan cuatro posibles niveles de medición y cada
uno de ellos tiene asociado una serie de pruebas
estadísticas apropiadas. Es por ello muy importante
conocer el tipo de variable que estamos tratando y
la escala de medición que ésta emplea. Las variables
cualitativas se miden habitualmente en dos tipos de
escalas: nominal u ordinal. Las variables cuantitativas
utilizan las escalas de intervalo y de proporción.
Puede suceder que las clases de una escala estén
relacionados entre sí. Relaciones típicas entre clases
son las que dividen la muestra en apartados por altura, preferencias, dificultad, madurez, etc. Las escalas
ordinales son muy utilizadas en encuestas.
a) Escala nominal o clasificatoria
Se emplea cuando los números u otros símbolos
se usan para la clasificación de objetos, personas o
características con el fin de distinguir entre sí los grupos de estudio.
Ejemplo 8.3
ualquier escala que suponga manifesC
tar el grado de preferencia, por un producto, servicio o artículo es ordinal. Otro
ejemplo es la valoración que los pacientes hacen del dolor empleando la Escala
Numérica de Dolor, en la que el sujeto
asigna una puntuación al dolor que padece, que varía desde la ausencia de
dolor (valor 0) al dolor más intenso que
pueda imaginar (valor 10).
Ejemplo 8.2
S on de este tipo la clasificación de los datos por sexos («1=Hombre» «2=Mujer»),
la clasificación de un patrón («1=Normal» «2=Patológico»), o de un rango
(«0=No fuma» «1=Fuma entre 0 y 10
cigarrillos al día» «2=Fuma entre 11 y 20
cigarrillos al día» «3=Fuma más de 20 cigarrillos al día»).
Propiedades formales: En una escala nominal, la
operación de clasificación consiste en partir de una
clase dada y formar un conjunto de subclases que se
Propiedades formales: En la escala ordinal, además de la relación de equivalencia, también existe
la relación de «mayor que», es decir, cada valor es
mayor o menor que el resto de valores de la escala.
c) Escala de intervalo
Se da en una escala ordinal en la que se conoce
la distancia entre dos números cualesquiera. Nuestra
asignación de números a varias clases de objetos es
tan precisa que sabemos la magnitud de las distancias entre todos los objetos de la escala. Una escala
69
8. Elección de las variables
de medida está caracterizada por una medida común
y constante que asigna un número real a todos los
pares de objetos en un conjunto ordenado. En esta
clase de medida, la proporción de dos intervalos es
independiente de la unidad de medida y del punto
cero. En una escala de intervalo, el punto cero y la
unidad de medida son arbitrarios.
Ejemplo 8.4
L a medición de la temperatura mediante
grados centígrados o Farenheit. La unidad de medida y el punto cero en la medición de la temperatura son arbitrarios y
diferentes en ambas escalas. Sin embargo, contienen la misma cantidad y clase
de información. Esto es así porque están
relacionadas linealmente y podemos
transformar la información de una a otra
mediante una fórmula.
Propiedades formales: En una escala de intervalo
se debe especificar la equivalencia (como en una escala nominal), la relación de mayor a menor (como
en una escala ordinal) y la proporción de dos intervalos cualesquiera.
d) Escala de proporción
Se trata de una escala que presenta todas las características de una escala de intervalo y además tiene un punto cero real en su origen. En este tipo de
escala, la proporción de un punto a otro cualquiera
es independiente de la unidad de medida.
Ejemplo 8.5
edición de la tensión arterial o del peso
M
en gramos. Estas escalas tienen un verdadero punto cero.
Propiedades formales: Las características de una
escala de proporción son relación de equivalencia,
relación de mayor a menor, proporción conocida de
dos intervalos, y proporción conocida de dos valores
de la escala.
4. ELECCIÓN Y CARACTERÍSTICAS DE UNA
BUENA VARIABLE
Una vez que el estudio ha identificado el problema que se desea resolver, resulta fundamental elegir
correctamente las variables que vamos a utilizar (tabla I).
Elegir una buena variable es un arte. Algunos de
los errores más frecuentes que se cometen en la elección de variables son los siguientes:
Variables poco sensibles. Si estamos estudiando
el efecto de una terapia sobre la progresión del queratocono, es más difícil demostrar cualquier efecto si
lo medimos en grados evolutivos de la enfermedad
(de I a IV) que si tomamos variables más sensibles (índices o parámetros topográficos), con los que efectos
más pequeños producen cambios mensurables. En
general las variables continuas tienen más potencia
que las dicotómicas o discretas y necesitan menor
tamaño muestral.
Variables con poca relevancia clínica. En ocasiones se recogen variables que son clínicamente poco
importantes para el paciente. En 2010 un ensayo
Tabla I. Características y dificultades para elegir una buena variable
Características de una buena variable
Dificultades para la elección de una buena variable
– Que esté definida con precisión antes de iniciar el estudio
– Que sea apropiada a la pregunta que se desea responder
– Que mida lo que se quiere medir
– Que sea suficientemente sensible para medir el efecto
de interés
– Que su medición sea lo más detallada posible
– Que se pueda medir con un método fiable, preciso y
reproducible
– Que se pueda medir en todos los sujetos y de la misma
manera
– Que sea única. Si hay varias, usar la más relevante y
fiable
– Fenómenos que no pueden medirse objetivamente, necesidad de variables con un componente de subjetividad
– Uso de variables aproximadas o intermedias, porque nos
resulte imposible medir una determinada condición
– Que la variable elegida mida parcialmente el fenómeno
– Uso de variables que no miden el fenómeno de interés
70
8. Elección de las variables
clínico en Lancet medía el efecto analgésico de un
fármaco sobre recién nacidos mediante cambios en
el ECG sin observar diferencias con el grupo placebo. Sin embargo, en una lectura crítica del mismo se
comprobó que si se tomaba como variable el llanto
y los cambios faciales del bebe, los resultados eran
fuertemente positivos. Claramente el segundo grupo
de variables medía mejor el objetivo propuesto y estaba más orientado al beneficio del paciente. Si medimos los resultados de la cirugía de retina, un dato
como la agudeza visual es clínicamente más relevante que el éxito anatómico, etc.
Variables intermedias que no se corresponden
con el objetivo. Muchos estudios toman variables
intermedias como exponentes de mejoría clínica sin
haber demostrado que efectivamente lo sean. Si tomamos una variable intermedia como variable principal deberá ser un marcador directo demostrado del
pronóstico de la enfermedad.
Ejemplo 8.6
S abemos que el control de la glucemia
mejora el pronóstico de la diabetes y lo
mismo sucede con la PIO y el glaucoma,
por lo que inferimos que su normalización da lugar a un mejor pronóstico de
la enfermedad. Pero si dicha relación
no ha sido bien establecida, no debería
tomarse esa variable como variable clínica de respuesta. Por ejemplo, muchos
tratamientos para el ojo seco mejoran
diversos parámetros bioquímicos o anatomopatológicos de la superficie ocular,
pero eso no significa que dichos cambios hayan demostrado tener relevancia
sobre los signos y síntomas del paciente, por lo que no deberían ser tomados
como indicadores de mejoría clínica de
la enfermedad.
5. OBTENCIÓN DE VARIABLES
El investigador debe diseñar un método que permita observar o medir de la forma más exacta posible
las variables seleccionadas para el estudio y obtener
los valores reales que toman las variables en la muestra a estudio. Hay diversas formas para la obtención
de variables en una muestra (4). Algunas son objetivas y otras subjetivas:
– Mediciones biofisiológicas: Es el sistema más
habitual. Por ejemplo la presión intraocular, la agudeza visual, la paquimetría, etc.
– Cuestionarios: Permiten interrogar al sujeto sobre diferentes aspectos, actitudes, sensaciones, etc.
Por ejemplo: un cuestionario sobre calidad de vida
en pacientes con glaucoma crónico simple en tratamiento (ver capítulo 10).
– Técnicas de observación: Mediante el registro de
características observables en el sujeto por parte del
investigador. Puede tener un componente de subjetividad importante, aunque existan clasificaciones previas que pueden orientar en la recogida de datos. Por
ejemplo: el grado de catarata, el efecto Tyndall, etc.
– Escalas: de valoración, combinadas multidimensionales, visuales analógicas, etc.
6. ALEATORIZACIÓN Y ENMASCARAMIENTO DE
VARIABLES
Un estudio aleatorizado o randomizado es aquel
en que los individuos que participan tienen la misma
probabilidad de recibir las diferentes intervenciones a
estudiar, de forma que no se introduzca ningún sesgo
a la hora de establecer el tratamiento a seguir. Debe
ser realizada mediante el azar, lo que en la práctica
significa tablas o series de números aleatorios, generalmente producidos por ordenador (y no otra cosa,
no son válidos según números de historia, fechas de
nacimiento o de consulta, etc.). La aleatorización de
las variables puede ser de diferentes tipos (tabla II).
Tabla II. Tipos de aleatorización
Simple
Cada vez que se incluye un paciente, se obtiene su asignación a una u otra intervención por
el azar, como si lanzáramos una moneda al aire
Restrictiva o por bloques
Estratificada
Se realiza una aleatorización por bloques de un número pequeño de pacientes. Se asegura
que el número de pacientes en cada grupo de sea el mismo
Cuando se realiza una clasificación anterior a la aleatorización, en función de una o varias
características que pueden ser importantes en la evaluación final de los resultados (edad,
sexo)
Por grupos
No se aleatoriza a cada paciente, sino a grupos de pacientes (familias, barrios, centros de
salud...). Útil para tamaños muestrales grandes
71
8. Elección de las variables
Tabla III. Tipos de enmascaramiento
Simple ciego
El paciente desconoce el grupo de tratamiento
Doble ciego
Tanto el sujeto como el médico desconocen la asignación de los pacientes a los grupos
Triple ciego
El paciente, el médico y el responsable de analizar los datos desconocen la asignación de los pacientes a los grupos
Evaluación ciega Será cuando se recurre a un tercero, que desconoce el tratamiento que está recibiendo cada pacienpor terceros
te, para la valoración de la respuesta. Se utiliza cuando no es posible un diseño doble ciego (por
ejemplo, en la realización de técnicas quirúrgicas)
En general se utiliza la técnica simple, reservándose las otras para tamaños muestrales grandes, estudios multicéntricos o comunitarios o, en el caso de la
estratificada, cuando existen variables de confusión
que deseamos controlar para evitar el sesgo. En estos
tipos menos utilizados deben utilizarse técnicas estadísticas especiales.
El enmascaramiento (blinding, masking) consiste
en una serie de medidas (o precauciones) que se toman con el fin de que a lo largo del estudio, bien el
paciente, el médico o ambos, desconozcan la asignación de los tratamientos. Los tipos de enmascaramiento se muestran en la tabla I.
El enmascaramiento es muy importante, de tal
manera que se ha observado que los estudios que utilizan métodos de ocultamiento inadecuados, comparados con aquellos en los que las técnicas de enmascaramiento son apropiadas, asocian un incremento
en la estimación del beneficio medio de un 37% (5).
La validez es el grado en que una medición coincide con la verdad. Por ejemplo, si un estudio quiere
medir la estatura de un grupo de personas y la cinta
7. MEDIDA DE VARIABLES: FIABILIDAD Y
VALIDEZ
Todo proceso de medición está amenazado por
diversas fuentes de error, derivadas tanto de las limitaciones del instrumento de medida, como de la
naturaleza de la magnitud a medir. Es importante diferenciar dos conceptos: validez y fiabilidad (fig. 5).
Fig. 5: Ejemplos con dianas para entender los conceptos
de fiabilidad y validez. A: precisión (+++), validez (0). B:
precisión (0), validez (+). C: precisión (+), validez (0). D:
precisión (+++), validez (+++).
Tabla IV. Enfoques de la fiabilidad o precisión
Estabilidad o constancia
Se realiza una misma prueba en 2 momentos diferentes dejando un intervalo de tiempo
Equivalencia de resultados
Se realizan dos versiones de una misma prueba que pretenden medir lo mismo a través
de diferentes ítems
Consistencia interna o cohe- Mide hasta qué punto los resultados de
rencia
dos pruebas están relacionados
Es el enfoque más usado y al que más
se alude cuando se habla de fiabilidad
o precisión
Variables
cuali- Coeficiente kappa
dicotómicas
Correlación de Pearson
Varibles
cuanti- Correlación intraclase
continuas
72
métrica está mal calibrada, los datos obtenidos son
de por sí falsos.
Se suelen distinguir entre dos modos de controlar la validez de un instrumento de medida: cuando se hace con patrones objetivos (patrón de oro o
«goldstandard») se habla de exactitud (accuracy);
mientras que cuando se controla comparando con
una referencia considerada mejor pero que no puede
considerarse un verdadero patrón de oro se habla de
conformidad (conformity).
Se denomina precisión o fiabilidad al grado en
que una variable tiene el mismo valor cuando se
mide varias veces en la misma muestra. Se ve afectada por el error aleatorio, que se produce al azar,
no afecta a la validez, y puede reducirse aumentando el tamaño muestral. Se distingue entre la reproducibilidad del mismo instrumento/observador en
dos instantes de tiempo diferentes (concordancia o
consistencia interna o intraobservador) y la reproducibilidad del mismo instrumento usado en diferentes
condiciones (concordancia o consistencia externa o
interobservador).
8. Elección de las variables
Cuando nos referimos a la fiabilidad o precisión,
existe cierta confusión, ya que el concepto incluye
tres enfoques diferentes (7) (tabla IV).
BIBLIOGRAFÍA
1. Rubio E, Martinez T, Rubio E, et al. Fundamentos teóricoprácticos de bioestadística para médicos. Ed. Cátedra de
Bioestadística. Universidad de Zaragoza. 1ª Edición.
2. Araujo M. Variables of a study. Medwave 2011;11(03):e4933.
3. Jokin de Irala, Miguel Ángel Martínez-González y Francisco
Guillén Grima ¿Qué es una variable de confusión? Medicina Clínica 2001:10 (117).
4. Polit DF, Hungler B. Investigación científica en ciencias
de la salud, 6ª edición, Mc Graw-Hil Interamericana,
2000.
5. Moher D, Pham B, Jones A, et al. Does quality of reports of
randomised trials affect estimates of intervention efficacy
reported in meta-analyses? Lancet. 1998; 352 (9128): 60913.
6. Feinstein A.R. Clinimetrics, New Haven, Yale University
Press, 1987.
7. Morales P. La fiabilidad de los test y escalas, Madrid, Archivos de la Universidad Pontificia de Comillas, 2007.