Solucionario guía Calor II mezclas y cambios de fase

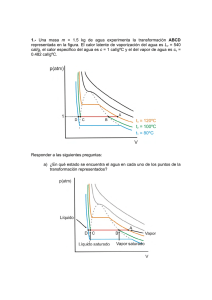
SOLUCIONARIO
GUÍA ESTÁNDAR ANUAL
Calor II: mezclas y cambios
de fase
SGUICES010CB32-A16V1
Solucionario guía
Calor II: mezclas y cambios de fase
Ítem
Alternativa
Habilidad
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
C
B
C
C
D
B
E
C
E
E
B
E
C
E
D
D
A
C
C
A
B
C
B
B
Reconocimiento
Aplicación
Aplicación
Comprensión
Aplicación
Aplicación
Comprensión
ASE
Comprensión
Comprensión
ASE
Aplicación
Aplicación
Aplicación
Comprensión
Comprensión
Comprensión
Comprensión
Comprensión
Aplicación
Aplicación
Comprensión
Comprensión
ASE
Aplicación
Ítem
Alternativa
1
A
Defensa
En la naturaleza las sustancias se presentan en tres fases
principales: sólida, líquida y gaseosa. El hielo es la fase sólida del
agua. Si se le agrega calor (energía), aumenta el movimiento
vibratorio de sus moléculas, llegando a romperse su estructura
molecular para transformarse en agua en estado líquido. Tal
proceso se denomina fusión.
Si se agrega más calor, se aumenta aún más la vibración de sus
moléculas, haciendo que estas finalmente se separen y
comiencen a fluir libremente por todo el espacio disponible; el
líquido pasa entonces a fase gaseosa. Tal proceso se denomina
vaporización.
Por lo tanto, cuando un trozo de hielo se derrite, pasando del
estado sólido al estado líquido, el cambio de fase se denomina
fusión.
2
C
Considerando que todos los cuerpos son del mismo material e
idénticos en forma, que todas las interacciones se produjeron
hasta alcanzar el equilibrio térmico, y que no existen perdidas de
calor en el sistema, tendremos que:
- Al interactuar los cuerpos A y B la suma de sus temperaturas se
distribuye en partes iguales entre los dos cuerpos.
Por lo tanto, ambos cuerpos terminan con una temperatura de 4T
cada uno.
- Al interactuar los cuerpos B y C, nuevamente la suma de sus
temperaturas se distribuye en partes iguales entre los dos
cuerpos.
Por lo tanto, B y C quedan con una temperatura de 7T cada uno.
Así, al final del proceso, el cuerpo B termina con una temperatura
de 7T.
3
B
Como el trozo de azufre se encuentra a la temperatura crítica de
fusión (119 ºC), todo el calor absorbido por el material es utilizado
para producir el cambio de fase.
Para determinar la cantidad de masa que se funde, utilizamos la


expresión del calor latente de fusión  L f 
Q
 , de donde
m
despejamos la masa m. Así, obtenemos
Q  650  cal  
Q 650


 50  g 
 cal    m 
Lf
13
L f  13   
 g 
Por lo tanto, solo 50 gramos del trozo de azufre logran fundirse,
permaneciendo el resto en estado sólido.
4
C
5
C
Inmediatamente después de concluido el proceso de fusión, tanto
la parte líquida como aquella que permanece sólida se encuentran
a la misma temperatura, 119 [ºC]. Todo el calor suministrado a la
masa de azufre se utilizó para producir el cambio de fase,
permaneciendo la temperatura del material constante durante todo
el proceso.
Para determinar el calor absorbido por la masa de agua a menor
temperatura, utilizamos la siguiente expresión.
m1  100  g 


 cal  
cagua  1 

 g º C    Qabsorbido  100 1  x  20 
T1  20  º C  

Tf  x

Para determinar el calor cedido por la masa de agua a mayor
temperatura, utilizamos la siguiente expresión.
m2  200  g 


 cal  
cagua  1 

 g º C    Qcedido  200 1  x  80 

T2  80  º C  

TF  x
Finalmente, al utilizar el principio calorimétrico de mezclas
( Qabsorbido  Qcedido  0 ), obtenemos:
100 1  x  20   200 1  x  80   0
100 x  2.000  200 x  16.000  0
300 x  18.000
18.000
300
 x  60  º C 
x
6
D
Al utilizar el principio calorimétrico de mezclas, tenemos:
Qabsorbido  Qcedido  0
 magua  cagua  T final  Tagua   mlíquido  clíquido  T final  Tlíquido   0
Reemplazando los datos suministrados, nos queda:
200 1 (20  0)  250  clíquido  (20  40)  0
4.000  5.000  clíquido  0
4.000  5.000  clíquido
 clíquido 
7
B
4  cal 
5  g º C 
Considerando el objetivo planteado para la experiencia llevada a
cabo por los alumnos, el orden correcto de los pasos anotados en
el registro de experimentación es:
4. “La temperatura inicial del agua es 20 [ºC].”
3. “Se coloca el recipiente con agua sobre la llama del mechero.”
5. “Se comienza a medir el tiempo con el cronómetro.”
6. “Se evapora completamente el agua.”
2. “Se detiene el cronómetro y se registra el tiempo.”
1. “100 gramos de agua demoran 15 minutos en evaporarse
completamente.”
Por lo tanto, la alternativa correcta es la B.
8
E
Del enunciado sabemos que:
Cuerpo P  calor específico c
Cuerpo Q  calor específico 2c
Cuerpo R  calor específico
c
3
Si se tienen dos cuerpos de igual masa, y se desea elevar la
temperatura de ambos en la misma cantidad, aquel cuyo material
posea un mayor calor específico necesitará absorber una mayor
cantidad de calor.
Por lo tanto, para que Q y R alcancen la misma temperatura, será
necesario entregar una mayor cantidad de calor al cuerpo Q.
9
C
Como la temperatura inicial del agua en ambos recipientes es
mayor a la temperatura ambiente, los cuerpos terminan,
irremediablemente, enfriándose y alcanzando la temperatura del
entorno (15 °C), tal como se indica en el encabezado. Esto nos
permite descartar inmediatamente las opciones 1 y 4, que
muestran curvas de calentamiento y no de enfriamiento.
La variación de temperatura por unidad de tiempo que
experimenta un cuerpo se denomina “tasa de enfriamiento” o
“rapidez de enfriamiento”. Para cuerpos que varían su temperatura
siguiendo la ley de enfriamiento de Newton, la rapidez de
enfriamiento es mayor mientras más acentuada es la diferencia de
temperatura entre el cuerpo y su entorno. Así, al inicio del
proceso, el agua que se encuentra inicialmente a mayor
temperatura (recipiente P) comienza a enfriarse más rápidamente
que el agua que se encuentra a menor temperatura (recipiente Q),
comportamiento que muestra la gráfica de la opción 2.
Por lo tanto, los gráficos que representan correctamente el
comportamiento de la variación de temperatura en el tiempo de los
cuerpos P y Q son el 2 y 3, respectivamente.
10
E
Cuando dos cuerpos o sistemas se encuentran a distinta
temperatura, el cuerpo más caliente cede calor al más frío, el cual
lo absorbe. Este flujo de calor se mantiene hasta que ambos
cuerpos igualan sus temperaturas. Este es el principio de
equilibrio térmico y actúa en muchísimas de las situaciones que
vivimos a diario.
De las alternativas propuestas en el ejercicio, la única que no está
relacionada con el equilibrio térmico es la E, ya que el hecho de
que los fluidos calientes se eleven responde a que los materiales
menos densos flotan en aquellos de mayor densidad. Así, al
calentarse una porción de cierto fluido, se hace menos denso que
el resto del fluido que lo rodea y, por lo tanto, tiende a “flotar”
sobre él, por lo que siempre se desplaza hacia la zona superior.
11
E
La capacidad calórica se define como la cantidad de calor que un
cuerpo debe absorber o ceder, para elevar o disminuir,
respectivamente, su temperatura en 1 [ºC].
Si el jarro contiene más agua que el vaso, la cantidad de calor que
necesitará para, por ejemplo, elevar su temperatura en 1 [ºC], será
mayor que aquella que necesitará el vaso y, por lo tanto, su
capacidad calórica es mayor. Pero, ¿cuánto mayor?
Sabemos que la capacidad calórica se expresa como
Q
C
T
Pero, además, sabemos que
Q  m  c  T
Por lo tanto
Q m  c  T
C

T
T
 C  mc
Es decir, la capacidad calórica depende de la masa del cuerpo y
del calor específico del material que lo conforma. Como las masas
de agua contenidas en el jarro y el vaso cumplen con que
m jarro  5  mvaso (ya que 2.500  g   5  500[ g ] )
entonces, multiplicando ambos lados de la igualdad anterior por el
calor específico del agua, obtenemos
m jarro  cagua  5  mvaso  cagua
Capacidad calórica
del jarro
 C jarro  5  Cvaso
Capacidad calórica
del vaso
12
B
Al utilizar la ecuación de mezclas, tenemos:
Qabsorbido  Qcedido  0
 magua  cagua  Tmezcla  Tagua   mlíquido  clíquido  Tmezcla  Tlíquido   0
 200 1  x  20   100  0,5  ( x  60)  0
 200 x  4.000  50 x  3.000  0
 250 x  7.000
 x  28  º C 
13
E
El calor específico es una propiedad característica de cada
material y no depende de la cantidad de masa. Por lo tanto, si los
cuerpos A y B son del mismo material, el calor específico en
ambos casos es el mismo.
La capacidad calórica se define como la cantidad de calor que un
cuerpo debe absorber o ceder, para elevar o disminuir,
respectivamente, su temperatura en 1 [ºC]. Es característica de
cada cuerpo y depende del material del que está hecho (calor
específico) y de su cantidad de masa. Por ejemplo, una piscina
con agua posee mayor capacidad calórica que un vaso con agua,
aunque ambos están constituidos por el mismo material, agua.
Así, si los cuerpos A y B son del mismo material, pero la masa del
cuerpo A es mayor que la del cuerpo B, entonces la capacidad
calórica de A es mayor que la de B.
La cantidad de calor liberado (o absorbido) por un cuerpo al variar
su temperatura está dada por la expresión
Q  m  c  T
Esta expresión muestra que, al disminuir su temperatura, el calor
liberado por un cuerpo es directamente proporcional a su masa, al
calor específico del material, y a la variación de temperatura que
experimenta. Así, si los cuerpos son del mismo material (igual c) y
se someten a la misma disminución de temperatura (mismo ∆T), el
cuerpo de mayor masa cederá una mayor cantidad de calor; en
este caso, el cuerpo A.
Por lo tanto:
I) Falso
II) Verdadero
III) Verdadero
14
C
Para saber la cantidad de calor necesaria para fundir el hielo,


utilizamos la expresión del calor latente de fusión  L f 
la que obtenemos
Q1  m  L f  100  80  8.000 cal 
Q
 , con
m
Así, para transformar 100 [g] de hielo a 0[ºC] en agua a 0[ºC], se
deben suministrar 8.000[cal].
Para averiguar ahora la cantidad de calor necesaria para elevar la
temperatura del agua de 0 [ºC] a 20 [ºC], utilizamos la expresión
Q  m  c  T , con la cual obtenemos
Q2  100 1 20  2.000 cal 
Así, para elevar la temperatura del agua de 0 [ºC] a 20 [ºC] se
deben suministrar 2.000[cal].
Finalmente, la cantidad total de calor que se debe suministrar para
realizar los dos procesos es
8.000 [cal] + 2.000 [cal] = 10.000 [cal].
15
E
16
D
El calor es energía en tránsito, que fluye desde un lugar más
caliente hacia otro más frío, hasta que las temperaturas de ambos
lugares se igualan, es decir, hasta que se alcanza el equilibrio
térmico.
Al dejar la puerta abierta, el calor del interior de la casa de Alberto
fluyó hacia la atmósfera fría, hasta que las temperaturas se
igualaron. El tamaño de la estufa no tiene importancia, pues el
flujo de calor hacia la atmósfera se producirá mientras la puerta de
la casa se encuentra abierta; la atmósfera es un “foco térmico”,
por lo que puede absorber todo el calor que podamos generar, sin
que su temperatura experimente variación.
El agua puede estar en estado sólido y/o líquido a 0 [ºC], y en
estado líquido y/o gaseoso a 100 [ºC], ya que a estas
temperaturas ocurren los cambios de fase. Por ejemplo, si la
temperatura de ebullición del agua es 100 [ºC], sabemos que la
máxima temperatura que puede alcanzar este elemento en estado
líquido es, precisamente, 100 [ºC]. Una vez que el agua alcanza
esta temperatura, si se le continúa entregando calor comienza a
producirse el cambio de fase, convirtiéndose en vapor, pero
permaneciendo su temperatura constante durante todo el proceso.
Una vez que el agua se ha convertido totalmente en vapor, si se le
continúa entregando calor, la temperatura comenzará a elevarse
por sobre los 100 [ºC].
Por lo tanto:
I) Verdadero
II) Verdadero
III) Falso
17
D
Si dos cuerpos en contacto térmico se encuentran a la misma
temperatura, entonces están en equilibrio térmico. De acuerdo al
gráfico entregado en el ejercicio, para un tiempo t > Q [s] los
cuerpos S y U alcanzan una misma temperatura H y, por lo tanto,
se encuentran en equilibrio térmico.
18
A
19
C
20
C
En el gráfico se observa que, al aumentar la cantidad de calor
suministrado de 400 a 800 calorías, la temperatura del material se
mantiene constante en 60 [ºC], lo que indica que el calor
absorbido se está utilizando para un cambio de fase. Como
inicialmente la sustancia se encuentra en estado líquido, este
cambio de fase corresponde a la ebullición, y la temperatura a la
cual se produce corresponde a su punto crítico de vaporización:
60 [ºC].
La cantidad de calorías absorbidas por el líquido durante el
cambio de fase corresponde a aquel intervalo en el que no hay
aumento de temperatura, es decir, de 400 a 800 calorías.
Por lo tanto, el líquido absorbió: 800 [cal] – 400 [cal] = 400 [cal]
durante el cambio de fase.
Estando en su punto crítico, para que cada gramo del material
pueda cambiar de estado (en este caso de líquido a gas), se debe
entregar una cantidad de calor Q por unidad de masa m, llamada
“calor latente de cambio de fase”, que se expresa como
L
Q
m
Así, el calor latente de vaporización del líquido es
Lv 
21
A
 cal 
Q 400  cal 

 20  
m
20  g 
 g 
Para el proceso de variación de temperatura del acero, utilizamos
la expresión
Q  m  c  T
Reemplazando los datos entregados, obtenemos:
 cal  
c  0,12 

 gº C 

m  400  g 
  Q  400  0,12  80  3.840  cal 

Ti  20  º C 

T f  100  º C  
22
B
Del encabezado sabemos que el cuerpo se encontraba a una
temperatura de D grados, la cual corresponde a su punto de
fusión (o punto crítico de fusión), es decir, la temperatura a la cual
el material puede comenzar a fundirse. Estando en este punto, al
agregar más calor al material este comienza a fundirse, pero
durante el cambio de fase su temperatura permanece constante,
por lo que, al terminar de fundirse, el vibranium líquido sigue a la
misma temperatura que estaba al comenzar el proceso, es decir,
continúa a D grados.
El punto crítico de un material es la temperatura a la cual puede
cambiar de fase, ya sea en un sentido o en el sentido inverso; por
ejemplo, si la temperatura a la que el vibranium puede ser fundido
es D grados, entonces la temperatura a la que podrá ser revertido
el cambio, es decir, a la que podrá ser solidificado, también es D
grados.
Por último, estando en su punto crítico, para que un material logre
cambiar de fase (o para revertir dicho cambio) es necesario
entregarle (o extraerle) una cantidad de calor extra por unidad de
masa, llamada calor latente de cambio de fase. Así, la cantidad de
calor que se le entregó al vibranium para lograr fundirlo deberá ser
la misma que se le extraiga para revertir el cambio y lograr que se
solidifique.
Por lo tanto:
I)
Falso
II)
Falso
III)
Verdadero
23
C
La materia en el mundo que nos rodea la podemos encontrar, en
general, en tres fases: sólida, líquida y gaseosa.
Cada uno de estos estados posee características propias, como
por ejemplo:



Los sólidos tienen una forma bien definida y es difícil
comprimirlos. En ellos las fuerzas intermoleculares son
muy intensas, motivo por el cual sus partículas se
encuentran “muy cerca” unas de otras.
Los líquidos tienen un volumen bien definido, pero su
forma se adapta al recipiente que los contiene. Se tienen,
entonces, fuerzas intermoleculares más débiles; sus
partículas se pueden separan con facilidad y el material
puede fluir.
Los gases no tienen forma ni volumen definido y pueden
fluir libremente, ocupando todo el espacio disponible y
adaptándose completamente al recipiente que los
contiene. Las partículas del gas se encuentran separadas
entre sí y se mueven independientemente unas de otras.
Las fuerzas intermoleculares entre ellas son prácticamente
nulas.
En vista de lo anterior y considerando la información entregada en
el cuerpo del ejercicio, la alternativa correcta es la C.
24
B
Es importante que primero recordemos que durante un cambio de
fase, aun cuando el material absorba o ceda calor, su temperatura
permanece constante. En el gráfico, se observan dos intervalos en
donde esto sucede, aunque el cuerpo se mantiene absorbiendo
calor. En estos intervalos el material experimenta cambios de
fase: entre t1 y t2, y entre t3 y t4.
Así, y tomando en cuenta las tres fases de la materia (sólida,
líquida y gaseosa), podemos afirmar que el material se
encontraba, inicialmente, en fase sólida, experimentando dos
cambios de fase: sólido a líquido y, finalmente, líquido a gaseoso.
De las “leyes del cambio de fase” sabemos que un material debe
alcanzar una temperatura específica (llamada punto crítico) para
poder cambiar de fase. En el gráfico se observan tres intervalos
en donde la temperatura del material aumenta: entre t0 y t1, entre
t2 y t3 y entre t4 y t5. En estos intervalos, el material se encuentra
en una fase determinada, pero está absorbiendo calor y elevando
su temperatura. Así, podemos decir que, entre t0 y t1, el material
se encontraba en fase sólida, pero elevando su temperatura para,
posteriormente, fundirse. En t1 comienza a cambiar de fase,
terminando completamente en estado líquido en t2. El punto crítico
de fusión del material es, por lo tanto, P [ºC]. A partir de este
momento el líquido comienza a calentarse, elevando su
temperatura hasta el instante t3, en donde comienza a
transformarse en vapor. En este punto, su temperatura vuelve a
permanecer constante en R [ºC] (punto crítico de vaporización),
mientras dura el proceso. En el instante t4, el material ya se
encuentra completamente en estado gaseoso. A partir de este
momento, la temperatura comienza a aumentar y el vapor
comienza a calentarse hasta llegar a la máxima temperatura de
Q [ºC], en el instante t5.
Por lo tanto:
I)
Falso
II)
Verdadero
III)
Falso
25
B
Sabemos que
C
Q
T
Por lo tanto
QR  400[cal ]
400
 cal 
 40  
  CR 
TR  10[º C ] 
10
ºC 
QL  280[cal ]
280
 cal 
 40  
  CL 
TL  7[º C ] 
7
 ºC 
Por otro lado, sabemos que
c
C
m
Por lo tanto, el calor específico de R es
 cal  
CR  40   
 cal 
40
 2
 º C   c R 

20
g ºC 
mR  20[ g ] 

Por último, sabemos que el calor específico se define como
c
C
C
m
m
c
Aun cuando conocemos la capacidad calórica del cuerpo L ( CL ),
para determinar su masa necesitamos conocer también su calor
específico, dato que no tenemos. Por lo tanto, no podemos
concluir nada al respecto.
Por lo tanto:
I)
Verdadero
II)
Verdadero
III)
Falso