Taller de Rectas y Planos

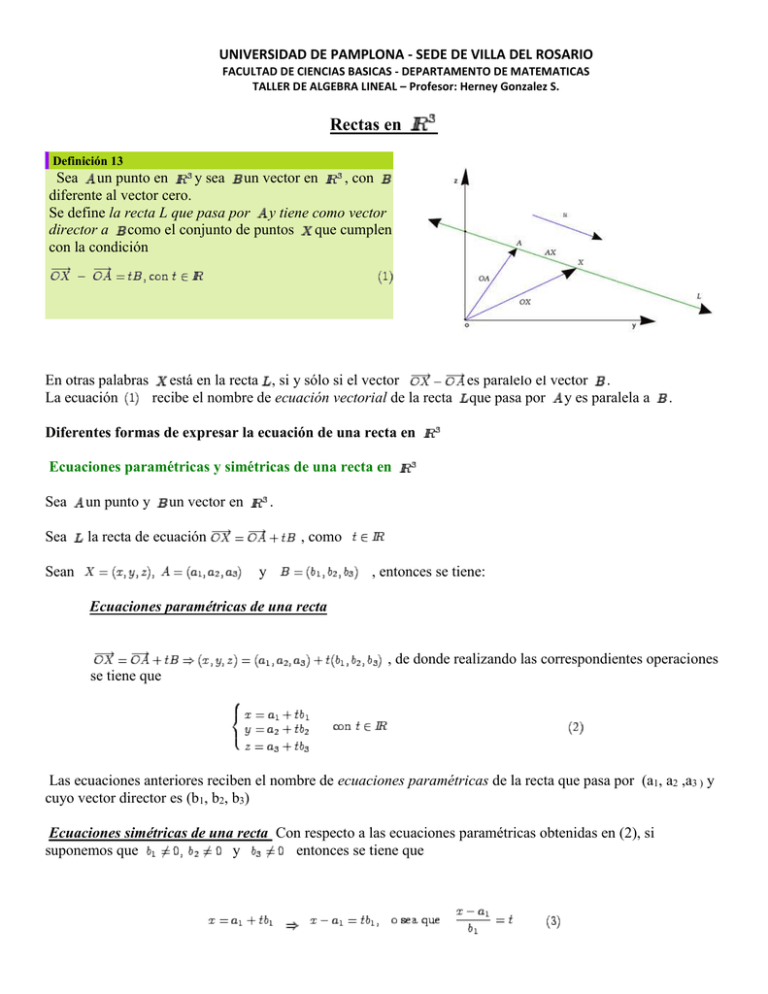
UNIVERSIDAD DE PAMPLONA - SEDE DE VILLA DEL ROSARIO
FACULTAD DE CIENCIAS BASICAS - DEPARTAMENTO DE MATEMATICAS
TALLER DE ALGEBRA LINEAL – Profesor: Herney Gonzalez S.
Rectas en
Definición 13
Sea un punto en
y sea un vector en
, con
diferente al vector cero.
Se define la recta L que pasa por y tiene como vector
director a como el conjunto de puntos que cumplen
con la condición
En otras palabras está en la recta , si y sólo si el vector
es paralelo el vector .
La ecuación
recibe el nombre de ecuación vectorial de la recta que pasa por y es paralela a
.
Diferentes formas de expresar la ecuación de una recta en
Ecuaciones paramétricas y simétricas de una recta en
Sea
un punto y
Sea
la recta de ecuación
Sean
un vector en
.
, como
y
, entonces se tiene:
Ecuaciones paramétricas de una recta
, de donde realizando las correspondientes operaciones
se tiene que
Las ecuaciones anteriores reciben el nombre de ecuaciones paramétricas de la recta que pasa por (a1, a2 ,a3 ) y
cuyo vector director es (b1, b2, b3)
Ecuaciones simétricas de una recta Con respecto a las ecuaciones paramétricas obtenidas en (2), si
suponemos que
y
entonces se tiene que
Como en las ecuaciones
y
el lado izquierdo está igualado a , entonces se cumple que
Las ecuaciones anteriores reciben el nombre de ecuaciones simétricas de la recta que pasa por (a1, a2 ,a3 ) y tiene
como vector director a (b1, b2, b3).
Nota
Si b1 = 0, entonces las ecuaciones simétricas son:
Si b2 =0, entonces las ecuaciones simétricas son:
Si b3 = 0, entonces las ecuaciones simétricas son:
Teorema 11
Sea L una recta de vector director , entonces cualquier vector paralelo a
se puede tomar como vector director de L.
Ejemplo:
Determine las ecuaciones paramétricas y simétricas de la recta que pasa por el punto (-2, 3 1) y tiene como
vector director a (-5, 0, 4).
Solución
Ecuaciones paramétricas
Ecuaciones simétricas
Rectas paralelas y rectas perpendiculares
Definición 14
Dos rectas son paralelas si sus vectores directores son paralelos.
Dos rectas son perpendiculares si sus vectores directores son perpendiculares.
Ángulos entre rectas
Definición
Se define el ángulo que forman dos rectas como el ángulo que determinan
sus vectores directores.
Planos en
Definición 15
Sea
un vector en
diferente de cero. Sea
un punto en
.
Se dice que el conjunto de puntos generan un plano que
contiene al punto , si cumplen que:
Si se denota por
el plano que contiene a
que satisfacen
normal de .
, entonces se dice que
y los puntos
en
es el vector
Note que
lo que afirma es que pertenece al plano que
contiene al punto y cuyo vector normal es si y sólo si el
vector
es perpendicular a
.
Ecuación cartesiana del plano
Si
y
entonces se tiene que:
El resultado anterior se puede resumir así:
Sea  un plano que contiene al
ecuación cartesiana de , viene dada por:
punto y cuyo vector normal es
, entonces la
Ejemplo:
Determine la ecuación cartesiana del plano que contiene el punto
.
Solución
Sean
y
, entonces:
y tiene como vector normal a
Respuesta
La ecuación del plano que se busca es
Ecuación del plano cuando se conocen tres puntos
Note que por la definición de un plano, siempre es posible obtener su ecuación si se conoce un punto plano y el
vector normal a ese plano.
Teorema 13
Sean A, B y C tres puntos en
entonces un vector normal de
y
.
y sea un plano que contiene a A, B y C,
de 𝜋 viene dado por 𝑢𝑥𝑣, donde
En general tres puntos no alineados determinan en forma única un plano,
este hecho permite, dados tres puntos A, B y C , no alineados, calcular la
ecuación del plano que los contiene.
Esto se hace de la siguiente forma:

Sea  el plano que contiene los puntos A, B y C.

Sea 𝑢 = ̅̅̅̅̅
𝐴𝐵 y 𝑣 = ̅̅̅̅
𝐴𝐶

Calcúlese el vector 𝑁, donde 𝑁 = 𝑢𝑥𝑣. Recuérdese que

Si
es un punto de
es un vector perpendicular a
y
, entonces cualquiera de las igualdades
Puede utilizarse para obtener la ecuación de 
Nota
En el caso anterior, el vector 𝑁 puede ser cualquier vector paralelo a 𝑢𝑥𝑣.
Ejemplo:
Determinar la ecuación del plano que contiene los puntos 𝐴 = (2,2,2), 𝐵 = (3,1,1) y. 𝐶 = (6, −4, −6)
Solución
̅̅̅̅ − ̅̅̅̅
Llamaremos (𝑂𝑋
𝑂𝐴)𝑁 = 0
la ecuación buscada, donde
y además se tiene que
.
Respuesta
La ecuación buscada es
Planos paralelos, planos perpendiculares y ángulos entre planos
Definición 16
Sea
un plano, cuyo vector normal es
.
Sea un plano, cuyo vector normal es
.
Se dice que
es paralelo a
si y sólo si
Se diec que es perpendicular a
perpendiculares.
Se define el ángulo formado por
si y sólo si
y
.
Ejemplo:
Sea
Sea
un plano de ecuación .
un plano de ecuación .
Determine el ángulo que forman
Solución
Como vector normal de
Sea
y.
se puede tomar:
Como vector normal de
el ángulo que forman
se puede tomar:
y.
y
son perpendiculares.
y
son
, como el ángulo que forman
y
Entonces
Ejemplo:
Sea
Sea
un plano de ecuación.
un plano de ecuación.
Determine la ecuación del plano que contiene el
Solución
Llámese
y es perpendicular a los planos
el plano de cuya ecuación se busca
y.
y sea la ecuación cartesiana de .
Como
es perpendicular a y a , entonces se tiene que
es perpendicular tanto a
- vector
normal de - como a
- vector normal de
-, por lo que se puede tomar
como el producto
vectorial de
y
De donde.
Sustituyendo el punto dado
en esta ecuación, se tiene que
Respuesta
Por lo que la ecuación buscada es
.
Rectas y planos paralelos, Rectas y planos perpendiculares
Definición 17
Sea
una recta de vector director
es paralela a
si y sólo si
es perpendicular a
y sea
un plano de vector normal .
es perpendicular a
.
si y sólo si es paralelo a
.
Ejemplo:
Determine la ecuación del plano
Contiene los puntos
Es paralelo a la recta
Solución
Sea
Como y
Como
y
que satisface simultáneamente las siguientes condiciones:
, donde
y
de ecuación.
la ecuación de .
están contenidos en , entonces
es paralela a
, entonces
Como
es perpendicular tanto a
producto vectorial de
y
De donde la ecuación de
.
es perpendicular a
es perpendicular a .
, como a
, entonces
lo podemos tomar como el
.
tiene la forma .
Como los puntos y pertenecen al plano , podemos sustituir cualquiera de estos puntos en la ecuación
anterior, para obtener el valor de . Tomemos para esto :
Respuesta
Por lo que la ecuación buscada es
o sea,
.