guia de dinamica tema 4 2010-3

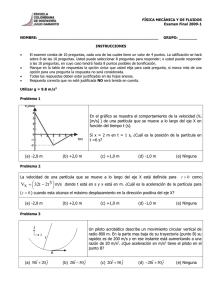
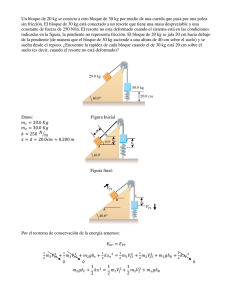
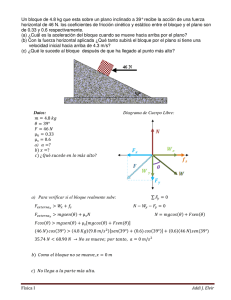
UNIVERSIDAD NACIONAL EXPERIMENTAL
FRANCISCO DE MIRANDA
ÁREA DE TECNOLOGÍA
COMPLEJO ACADÉMICO EL SABINO
DEPARTAMENTO DE FÍSICA Y MATEMÁTICA
UNIDAD CURRICULAR: FÍSICA I. (250302)
PROFESOR FIDIAS GONZÁLEZ – YUSMANIA COELLO
PROFESORES:
GUÍA DE DINÁMICA
Elaborada por: Fidias González – Yusmania Coello
Punto Fijo, Noviembre de 2010
1. De acuerdo con la leyenda, un caballo aprendió las leyes de Newton. Cuando se le pidió que
tirara una carreta, se negó rotundamente argumentando que si el tiraba la carreta hacia
delante, de acuerdo con la tercera ley de Newton habría una fuerza igual hacia atrás. De esta
manera, las fuerzas estarían balanceadas y de acuerdo con la segunda ley de Newton, la carreta
no aceleraría. Pero como usted es más astuto que el caballo, sabe que la carreta se mueve
.Como podría usted razonar con este misterioso caballo, para hacerle entender que debe tirar?
2. Si un bloque de masa m se ubica sobre un plano sin roce, inclinado un ángulo α con respecto
a la horizontal, como se muestra en la Figura 2, partiendo del reposo, resbalara una distancia x
a lo largo del plano en un tiempo t. Verificar que:
1
x = ( gSen α )t 2
2
Figura 2
3. Dos bloques, cada uno de 20 kg están apoyados sobre superficies sin rozamiento en la forma
indicada en la Figura 3. Se considera que las poleas carecen de peso y de rozamiento.
a) Calcular el tiempo requerido para que el bloque A, partiendo del reposo, recorra una
distancia de 4,9 m sobre la superficie del plano.
b) Calcular la tensión de la cuerda que une ambos bloques.
Resp: 3 a) 2s b) 49 N
Figura 3
4. Un bloque de masa 3.M está ubicado a la derecha de otro bloque de masa M, ambos están
apoyados sobre una mesa horizontal lisa y se unen entre sí con una varilla de alambre
horizontal, de masa despreciable. Una fuerza horizontal de magnitud 2.M.g se aplica sobre M
hacia la izquierda. Verificar que la aceleración del sistema es igual a g/2.
5. Si las masas del sistema representado en la Figura 5 son mA = m y mB = 2m Verificar que la
aceleración del bloque A es igual a 2/3 . g y la del bloque B es igual a 1/3 . g. Despreciar todas
las fuerzas de rozamiento, así como las masas de las poleas.
Figura 5
6. En el sistema de la Figura 6, la fuerza F paralela al plano inclinado empuja al bloque de masa
m haciéndolo subir sobre el plano, de coeficiente de roce cinético μ. Verificar que:
a=
F
− g ( µCosα + Senα )
m
Figura 6
7. En el sistema mecánico de la Figura 7, se aplica una fuerza F inclinada un ángulo α sobre el
cuerpo de masa m que se mueve hacia la izquierda, ubicado sobre la mesa horizontal con
coeficiente de roce cinético μ. La polea por donde cuelga otro bloque de masa M no tiene roce
y la cuerda se considera inextensible y de masa despreciable. Demostrar que la aceleración de
los cuerpos es:
a=
F (Cos α + µSen α ) − g ( µm + M )
m+M
Figura 7
8. Un carrito de control remoto de 2,0 kg se mueve rapidez constante de 12 m/s en un círculo
vertical dentro de un cilindro hueco de 5,0 m de radio (Figura 8). .Que magnitud tiene la fuerza
normal ejercida sobre el coche por las paredes del cilindro en los puntos A, B, C y D?
Resp: 8. NA = 77 N, NB = 57 N, NC = 44 N, ND = 38 N
Figura 8
9. Calcular la aceleración de los cuerpos en la figura 9 y la tensión en la cuerda para m1 = 50 g ,
m2 = 80 g y F = 1 N
RESP:
a) 166 cm/s2
917 x 104 Dinas
b) 543 cm/s2
1.22 x 105 Dinas
Figura 9
10. Las masas A y B De la figura 10. Son de 10Kg y 5 Kg respectivamente. El coeficiente de
fricción entre A y la mesa µK = 0,2. Encontrar la mínima masa C para evitar el Movimiento de A
Figura 10
11. Encuentre el valor de la fuerza F y de la fuerza de contacto entre los dos bloques si el
sistema desciende con una aceleración de 3,8 m/22
Datos: m1 = 20 Kg, m2 = 10 Kg y µ= 0,6
Figura 11
GUÍA. UNIDAD IV. R.A SERWAY. “DINÁMICA DE LA PARTÍCULA”
5.3.-Una
Una fuerza dependiente del tiempo, F = (8,00iˆ − 4,00 ˆj ) N (donde t está en segundos), se
aplica a un objeto de 2,00kg inicialmente en reposo. a) ¿En qué tiempo el objeto se moverá con
una velocidad de 15,0m/s? b) ¿A qué distancia está de su posición inicial cuando su velocidad es
15,0m/s? c) ¿Cuál es la distancia
distancia total recorrida por el objeto en este tiempo?
5.18.- Dos fuerzas F1 y F2 actúan sobre una masa de 5,00kg. Si F1=20,0N y F2=15,0N, encuentre
la aceleración en a) y en b) de la figura.
5.32.-Una
Una mujer jala su maleta de 25kg a una velocidad constante
constante y su
correa forma un ángulo θ respecto de la horizontal (ver figura). Jala la
correa con una fuerza de 35N de magnitud. Una fuerza retardadora
horizontal de 22N actúa también sobre la maleta. a) ¿Cuál es el valor de
θ? b) ¿Qué fuerza normal ejerce el piso
pi sobre la maleta?
5.43.- Un hombre de 72 kg está parado sobre una balanza de resorte en un elevador. Partiendo
del reposo, el elevador asciende y alcanza su velocidad máxima de 1,2m/s en 0,80s. Se desplaza
con esta velocidad constante durante los siguientes 5,0s. El elevador experimenta después una
aceleración uniforme en la dirección y negativa durante 1.5s y se detiene. ¿Qué pasa con el
registro de la balanza a) antes de que el elevador empiece a moverse, b) durante los primeros
0,80s, c) mientras el elevador se mueve a velocidad constante y d) durante
du
el tiempo que
desacelera?
5.44.- Una pelota de masa m se deja caer (desde el
reposo) en la azotea de un edificio que tiene una
altura h.. Si un viento que sopla a lo largo de un lado
del edificio ejerce una fuerza horizontal constante
de magnitud F sobre la pelota cuando se suelta (ver
figura), a) demuestre que la pelota sigue una
trayectoria en línea recta. b) ¿Esto significa que la
pelota cae con velocidad constante? Explique. c) Si la
pelota se deja caer con una velocidad inicial vertical
diferente de cero V0, ¿seguirá con una trayectoria en línea recta? Explique. d) Utilizando
m=10,0kg, h=10,0 m, F=20,0N,
=20,0N, y V0=4,00m/s hacia abajo, ¿a qué distancia del edificio la pelota
golpeará el suelo?
5.46.- La masa m1, sobre una mesa horizontal sin
fricción
ión se conecta a la masa m2 por medio de una polea
sin masa P1, y una polea fija sin masa P2 como se
muestra en la figura. a) Si a1, y a2, son las magnitudes de
las aceleraciones de m1 y m2, respectivamente, ¿cuál es
la relación entre estas aceleraciones? Determine
expresiones para b) las tensiones en las cuerdas, y c) las
aceleraciones a1, y a2 en función de m1, m2 y g.
5.50.- ¿Qué fuerza debe aplicarse sobre un bloque A
con el fin de que el bloque B no caiga? El coeficiente
de fricción estática entre los bloques A y B es 0,55 y
la superficie horizontal no presenta fricción.
5.59.-En
En la figura se muestran tres masas conectadas sobre una mesa. La mesa tiene un
coeficiente de fricción de deslizamiento de 0,35. Las tres masas son de 4,0kg 1,0kg y 2,0kg
respectivamente, y las poleas son sin fricción. a) Determine la aceleración de cada bloque y sus
direcciones. b) Determine las tensiones en las dos cuerdas.
5.69.- Un bloque de aluminio de 2,00kg y un bloque de cobre de 6,00kg se conectan mediante
una cuerda ligera sobre una polea sin fricción. Se deja que se muevan sobre un bloque-cuña
bloque
fijo
de acero (de ángulo θ=30.0º),
=30.0º), como se muestra en la figura Determine a) la aceleración de los
dos bloques, y b) la tensión en la cuerda.
µ c AlsobreAcero = 0,47 , µ c CusobreAcero = 0,36
5.71.- Tres carros de equipaje cuyas masas son m1, m2 y m3, son remolcados por un tractor de
masa M a lo largo de la faja de estacionamiento de un aeropuerto. Las ruedas del tractor
ejercen una fuerza de fricción total F sobre el suelo, como se muestra. Para las preguntas
siguientes, exprese sus respuestas en función de F, M, m1, m2 y m3, y g. a) ¿Cuáles
¿Cuál son la
magnitud y la dirección de la fuerza horizontal ejercida sobre el tractor por el suelo? b) ¿Cuál
es el valor más pequeño del coeficiente de fricción estático que evita que las ruedas patinen?
Suponga que cada una de las dos ruedas motrices en el tractor soportan 1/3 de su peso. c)
¿Cuál es la aceleración, a, del sistema (tractor más carros de equipaje)? d) ¿Cuáles son las
tensiones T1, T2, y T3, en los cables de conexión? y e) ¿Cuál es la fuerza neta sobre el carro de
masa m2?
5.73.- Un
n bloque de 2,0kg se sitúa sobre la parte superior de un
bloque de 5,0kg, como muestra la figura. El coeficiente de fricción
cinético entre el bloque de 5,0kg y la superficie es 0,20. Una
fuerza horizontal F se aplica al bloque de 5,0kg. a) Dibuje un
diagrama
rama de cuerpo libre para cada bloque. ¿Qué fuerza acelera al
bloque de 2,0kg? b) Calcule la magnitud de la fuerza necesaria
para jalar ambos bloques hacia la derecha con una aceleración de
3,0 m/s2. c) Encuentre el coeficiente mínimo de fricción estático
entre los bloques tal que el de 2,0kg no se deslice bajo una aceleración de 3,0m/s2.
5.74.- Un bloque de 5,0kg se coloca sobre un bloque de 10kg, (ver
figura). Una fuerza horizontal de 45N se aplica al bloque de 10kg, y el
bloque de 5,0kg se amarra a la pared. El coeficiente de fricción
cinético entre las superficies móviles es 0,20. a) Dibuje el diagrama
de cuerpo libre para cada bloque e identifique las fuerzas de acciónreacción entre los bloques. b) Determine la tensión en la cuerda y la
magnitud de la aceleración del bloque de 10kg.
5.79.- En la figura se muestra un alambre ABC que sostiene un cuerpo
de peso w. El alambre pasa sobre una polea fija en B y se une
firmemente a una pared vertical en A. La línea AB forma un ángulo Φ
con la vertical, y la polea en B ejerce sobre el alambre una fuerza de
magnitud F inclinada un ángulo θ con la horizontal. a) Muestre que si
el sistema está en equilibrio, θ=Φ/2. b) Muestre que F=2wsen(Φ/2) c)
Dibuje una gráfica de F cuando Φ aumenta de 0º a 180º.
5.81.- Las fuerzas F1= (−6iˆ − 4 ˆj ) N y F2 = (−3iˆ + 7 ˆj ) N actúan sobre una partícula de 2kg
inicialmente en reposo en las coordenadas (-2m, +4m). a) ¿Cuáles son las componentes de la
velocidad de la partícula en t=10s? b) ¿En qué dirección se mueve la partícula en t=10s? c) ¿Cuál
es el desplazamiento que realiza la partícula durante los primeros 10s? d) ¿Cuáles son las
coordenadas de la partícula en t =10s?
5.86.- En la figura, el coeficiente de fricción cinético entre los bloques de 2,00kg y 3,00kg es
0,300. La superficie horizontal y las poleas son sin fricción y las masas se liberan desde el
reposo. a) Dibuje un diagrama de cuerpo libre para cada bloque. b) Determine la aceleración de
cada bloque. c) Encuentre la tensión en las cuerdas.
5.89.- Una camioneta acelera cuando desciende
por una colina (ver figura), partiendo desde el
reposo hasta 30,0m/s en 6,00s. Durante la
aceleración, un juguete (m=100g) cuelga de una
cuerda del techo. La aceleración es tal que la
cuerda permanece perpendicular al techo.
Determine: a) el ángulo θ y b) la tensión en la
cuerda
RESPUESTAS A LOS PROBLEMAS PROPUESTOS
(
)
r
r
3. a) t = 3,00 s b) ∆r = 18 iˆ − 9 ˆj m d = ∆r = 20,1 m
r
r
18. a) a = 4 iˆ + 3 ˆj m / s 2 ; a = 5m / s 2 b) a = 5,5 iˆ + 2,6 ˆj m / s 2 ; a = 6,08m / s 2
32. a) θ = 51,06° b) N = 217 ,8 N
43. a) T = 705,6 N b) T = 813,6 N c) T = 705,6 N d) T = 648 N
44. a) Tomando la fuerza del viento como la dirección x, la fuerza resultante sobre la pelota es:
r
r
r F
F = ∑ Fi = F iˆ − mg ˆj = ma ⇒ a = iˆ − g ˆj y esta aceleración es constante en magnitud y
m
dirección por lo tanto la pelota se mueve en la dirección de la aceleración y su trayectoria es una
línea recta. b) No si tiene aceleración no puede caer con velocidad constante. c) Al principio se
moverá hacia abajo pero luego por la aceleración a la que está sometida su trayectoria será una
curva. d) R = 1,16 m
2m1m2 g
4m1m2 g
1
m2 g
46. a) a1 = 2a2 b) T1 =
; T2 =
c) a2 = a1 =
4m1 + m2
4m1 + m2
2
4m1 + m2
50. F = 1960 N
59. a) a = 2,31 m / s 2 hacia abajo para m1, hacia la izquierda para m2 y hacia arriba para m3. b)
T12 = 30,0 N ; T23 = 24,2 N
(
)
(
)
69. a) a = 0,232 m / s 2 b) T = 9,68 N
71. a) La fuerza externa sobre el tractor ejercida por el suelo. La reacción a la fuerza que el
tractor ejerce sobre el suelo, es una fuerza de magnitud F, dirigida hacia la derecha. b)
(m1 + m2 )F
m1 F
3F
F
µ emín =
c) a =
d) T1 =
; T2 =
;
2 Mg
M + m1 + m2 + m3
M + m1 + m2 + m3
M + m1 + m2 + m3
(m1 + m2 + m3 )F
m2 F
T3 =
e) T2 − T1 =
M + m1 + m2 + m3
M + m1 + m2 + m3
73. a) El bloque de 2,0kg es acelerado por la fuerza de roce estático entre los dos bloques b)
F = 34,7 N c) µ emín = 0,306
74. b) T = 9,8 N ; a = 0,58 m / s 2
79. Si el sistema está en equilibrio se cumple para el cuerpo que T = W y para la polea
Fx = FCosθ − TSenφ = 0
∑ Fy = FSenθ + TCosφ − W = 0 de estas ecuaciones resulta θ = φ − θ ⇒ 2θ = φ , donde se ha
usado la identidad trigonométrica Cos(φ − θ ) = Cosφ Cosθ + Senφ Senθ b) Usando la identidad
trigonométrica Senφ = Sen(φ / 2 + φ / 2 ) = 2 Senφ / 2 Cosφ / 2 en la primera ecuación para la
polea, queda efectivamente F = 2W Sen(φ / 2)
r
v
81. a) vt =10 = − 45 iˆ + 15 ˆj m / s b) θ = 162° c) ∆r = − 22 iˆ + 75 ˆj m d) rt =10 = − 227 iˆ + 79 ˆj m
(
)
86. b) a = 5,8m / s c) T1 = 17 N y T2 = 41 N
89. a) θ = 30,7° b) T = 0,843 N
2
(
)
(
)