tema10

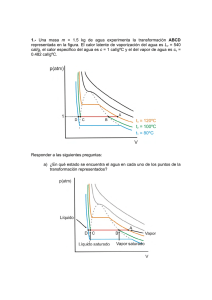
PROBLEMAS TEMA 10
10.1 El fosgeno se disocia según la reacción: COCl2(g) ⇔ CO(g)+Cl2(g). ∆Go viene dado en
función de T por: ∆Go=24100-4TlnT-3.57T (en cal/mol). Suponiendo comportamiento ideal
para la fase gaseosa, calcular: a) El grado de disociación del fosgeno a 250 ºC y P=2 atms. b)
Presión parcial de cada componente en el equilibrio. c) Incremento de entalpía de reacción a 250
ºC.
Solución. a) α = 0.00871; b) p COCl 2 = 1.965 atms, p CO = p Cl 2 = 0.01727 atms, ∆H 0 = 26192 cal.
10.2 Estímese cualitativamente el efecto de un aumento considerable de la presión (por ejemplo
500 atms) sobre el equilibrio gaseoso CO(g)+H2O(g) ⇔ CO2 (g)+H2 (g) a 600 ºC y 1 atm.
Datos
TC(K)
PC(atm)
CO2 (g)
304
72.9
H2 (g)
33.2
12.8
CO(g)
134
34.6
H2O(g)
647
218
Nota. Para H2(g): Tr =T/(TC+8) Pr =P/(PC+8)
Solución. Un aumento de P de 1 a 500 atms, desplaza el equilibrio hacia la izquierda.
10.3 Se desea introducir CO(g) a 10 atms y vapor de agua a 5 atms de presión en una cámara de
reacción a 700 ºC y extraer CO2(g) y H2(g) a presiones parciales de 1.5 atms. ¿Es esto posible
desde el punto de vista termodinámico?. Suponer comportamiento gas ideal. Se sabe que la
constante de equilibrio, a 700 ºC, para la reacción CO(g)+H2O(g) ⇔ CO2(g)+H2(g) es KP = 0.71.
Solución. ∆G = -5.34 cal < 0, por tanto, posible desde el punto de vista termodinámico.
10.4 Para la reacción, I2+ciclopentano ⇔ 2HI+ciclopentadieno, en fase gaseosa ideal, Kp fue
medida espectroscópicamente, en un intervalo de temperatura entre 175 y 415 ºC, y viene dada
por la expresión: logKP =7.55-4843.7/T. a) Calcular ∆Go, ∆Ho y ∆So para la reacción a 300 ºC.
b) Si se mezclan cantidades iguales (en moles) de I2 y ciclopentano a una presión total cte de 1
atm y 300 ºC, ¿cuál será la presión parcial de equilibrio de I2?.
Solución. a) ∆G0 = 2368 cal, ∆H0 = 22155.4 cal, ∆S0 = 34.54 cal/K; b) p I 2 = 0.292 atms.
10.5 La desaminación del ácido aspártico:
Ac. aspártico ⇔ -OOC-CH=CH-COO- + NH +4
es una reacción reversible catalizada por la encima aspartasa. Para el ácido D,L-aspártico la cte
de equilibrio en un cierto margen de temperatura puede expresarse por
2315.5
ln K D , L = 8.19 −
− 0.01025T .
T
Hallar a) una expresión de ∆Ho en función de T, b) ∆So y ∆C oP de la reacción anterior a 25 ºC.
Solución. a) ∆H0 = 4600.89 – 0.02036 T2; b) ∆S0 = 4.13 cal/K, ∆C 0P = -12.134 cal/K.
10.6 En un recipiente previamente evacuado se introdujo sulfato de hierro(II) calentándose a
929 K. Transcurrido cierto tiempo se alcanzaron los siguientes equilibrios:
(1): 2FeSO4(s) ⇔ Fe2O3(s)+SO2(g)+SO3(g)
(2): 2SO3(g) ⇔ 2SO2(g)+O2(g)
La presión en el recipiente alcanzó un valor constante de 635 mmHg. Para la reacción (2) se
cumple la ecuación logKC =14.58-10373/T-2.22 logT. Se pide: a) calcular KP para (2) a 929 K,
b) calcular las presiones parciales del O2(g), SO2(g) y SO3(g), c) calcular KP para (1) a 929 K y
d) Calcular ∆Go a 929 K para la reacción 4FeSO4(s) ⇔ 2Fe2O3(s)+4SO2(g)+O2(g).
Nota.- Suponer comportamiento ideal para la fase gaseosa.
Solución. a) K P2 = 0.05048; b) p SO3 =0.346 atms, p SO 2 =0.4607 atms, p O 2 =0.0286 atms;
c) K p1 =0.1594; d) ∆G0 = 12291.65 cal.
211
10.7 Se deja que una mezcla de hidrógeno y monóxido de carbono en la proporción molecular 2
a 1 alcance el equilibrio, en presencia de un catalizador, a 600 K y 250 atms. Determinar la
proporción de la conversión en metanol según la reacción: 2H2(g)+CO(g) ⇔ CH3OH(g).
Datos
CP (cal/molK)
-6 2
CH3OH(g) 4.39+0.0242T-6.85 10 T
H2(g)
6.95-0.0002T-0.481 10-6T2
CO(g)
6.34+0.00183T-0.28 10-6T2
∆H of (cal/mol) Sof (cal/molK)
-48100
56.63
0
31.21
-26400
47.30
TC (K)
PC (atms)
513.2
33.2
134.4
98.7
12.8
34.6
Nota. Los valores de ∆H of y S of están dados a la temperatura de 298 K.
Solución. El 67 % de CO pasa a CH3OH
10.8 Un reactor ha sido diseñado para operar con una mezcla estequiométrica de CO(g) e H2(g)
con el objeto de producir CH3OH(g) a una presión total de 208 atms. Con ayuda de un
intercambiador de calor la reacción tiene lugar a temperatura cte de 350 K. Se pide: a)
Porcentaje de CO(g) convertido en CH3OH(g). b) Calor extraído por el intercambiador en el
caso de introducir en el reactor 100 moles de CO(g) y 200 moles de H2(g).
Datos (Los valores siguientes de ∆H of y S of están dados a la temperatura de 298 K)
CP (cal/molK)
H2(g)
CO(g)
CH3OH(g)
6.65+0.7 10-3T
6.89+0.03 10-3T
2+0.03T
∆H of (cal/mol)
S of (cal/molK)
TC (K)
PC (atms)
0
-26420
-48100
31.25
47.3
30.3
33.2
134.4
513.2
12.8
34.6
98.7
T
P
y Pr =
TC + 8
PC + 8
Solución. a) 78.4 %; b) –1.763 106 cal.
Para el H2(g) tomar Tr =
10.9 En la manufactura del formaldehido se hace reaccionar una mezcla de aire con vapor de
metanol sobre un catalizador de plata. En este proceso la plata pierde lentamente su lustre
metálico y se desintegra parcialmente. Utilizando los datos siguientes, examínese si esto puede
ser debido (desde un punto de vista termodinámico) a la formación de óxido de plata.
Datos. T de operación: 550 ºC. P gaseosa del aire: 1 atm. ∆G of ,Ag 2O = -2590 cal/mol (a 25ºC).
∆H of ,Ag 2O = -7310 cal/mol (a 25 ºC).
Pueden utilizarse las siguientes capacidades caloríficas a presión cte: CP(Ag) =6.4 cal/molK,
CP(Ag2O) =15.7 cal/molK y CP(O2) =7.5 cal/molK.
Solución. ∆G = 7266.01 cal > 0, por tanto el proceso sugerido no puede ser espontáneo.
10.10. Para la reacción NiO(s)+CO(g) ⇔ Ni(s)+CO2(g) se tiene KP(a 936K)=4540 y KP (1125)
= 1580. Suponiendo una relación lineal para la dependencia de KP con T y comportamiento
ideal para la fase gaseosa, se pide:
a) ∆G0, ∆H0 y ∆S0 para la reacción a 1000 K.
b) ¿Se oxidaría el Ni(s) en una atmósfera cuya composición fuera 20% de CO2, 5 % CO y 75 %
de N2 a 1000 K?.
Solución. a) ∆G0 = -1623.9 cal, ∆H0 = -8792.4 cal, ∆S0 = 7.44 cal/K. b) No se oxidaría.
212
10.11 Las especies químicas C, H2O, CO y H2 pueden reaccionar según
C(s)+H2O(g) ⇔ CO(g)+H2(g).
Calcular el incremento de energía libre asociado a la reacción de H2O(g) a 100 atms con C(s)
para formar CO(g) y H2(g) a 50 atms de presión parcial cada uno de ellos. El proceso tiene lugar
a la temperatura de 800 K. De acuerdo con el valor obtenido para ∆G, decidir si el proceso es o
no espontáneo.
Datos
C(s)
H2O(g)
CO(g)
H2(g)
∆H of (cal/mol)
S of (cal/molK)
CP (cal/molK)
φ•
0
-57800
-26420
0
1.36
45.11
47.30
31.21
2.6+0.0026T
7.2+0.0023T
6.3+0.0018T
6.9-0.0002T
0.82
1.1
1.05
Solución. ∆G = 10843.3 cal > 0, por tanto, no espontáneo.
10.12 Se han obtenido, a 973 K, los valores de las constantes de equilibrio siguientes:
(1) Fe(s) + H2O(g) ⇔ FeO(s) + H2(g) K1 = 2.35
(2) Fe(s) + CO2(g) ⇔ FeO(s) + CO(g) K2 = 1.52
K3 = 1.55
(3) C(s) + H2O(g) ⇔ CO(g) H2(g)
Utilizando el concepto de energía libre y suponiendo comportamiento de gas ideal se pide:
a) ¿Podrá una mezcla que consiste en proporciones equimoleculares de vapor de agua e
hidrógeno a 1 atm de presión total, producir FeO(s) a partir del Fe(s) y a 973 K?. ¿Cuál será el
efecto de aumentar la presión?
b) ¿Tenderá a depositar C(s) a 973 una mezcla consistente en 12% molar de CO(g), 9% molar
de CO2(g) y 79% molar de un gas inerte a una presión total de 1 atm?. ¿Por encima o por debajo
de qué presión sucederá esto desde el punto de vista termodinámico?.
Solución. a) La reacción (1) resulta espontánea en el sentido que está escrita. Un aumento de P
no surge ningún efecto. b) No se formará C(s) a no ser que P > 2.5 atms.
10.13. Para la reacción en fase gaseosa C 2 H 6 (g) ⇔ C 2 H 4 (g ) + H 2 (g) , a 900 K, la constante de
equilibrio es K = 0.0502. Una mezcla que inicialmente contiene 20% molar de C2H6(g), 25%
molar de C2H4 y 55% molar de H2 se hace pasar por un reactor catalítico a 400 K y 150 atms de
presión. Se pide: a) ¿cuál es el sentido espontáneo en que se produce la reacción?. b) ¿Cuál será
la composición del gas que sale del reactor?.
Datos
PC (atms)
TC (K)
C2H6(g)
48.8
305.2
C2H4(g)
50.7
282.8
H2(g)
12.8
33.2
Nota.- Para el H2 tomar Tr =T/(TC + 8) y Pr =P/(PC + 8)
Solución. a) Sentido espontáneo de derecha a izquierda. b) x C 2 H 6 = 0.599, x C 2 H 4 = 0.000389,
x H 2 = 0.4.
213