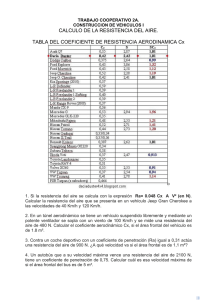
5 1. OBJETIVO DEL PROYECTO El objetivo del presente proyecto

5
1. OBJETIVO DEL PROYECTO
El objetivo del presente proyecto es el diseño de los diferentes elementos necesarios
para la construcción de un kart de pista.
Un kart es un vehículo terrestres con o sin carrocería, cuatro ruedas no alineadas que
están en contacto con el suelo, dos aseguran la conducción y las otras dos la
locomoción.
Las partes principales son el chasis (incluida la carrocería), los pneumáticos y el motor.
El proyecto pretende, una vez construido el vehículo, facilitar a cualquier persona
interesada en el karting disponer de un vehículo fiable y homologado, entiendo por
homologación la constatación oficial CIK-FIA (Comisión Internacional de Karting de la
Federación Internacional de Automovilismo) que un modelo de chasis, motor o de un
material determinado está construido en serie suficiente para poderse incluir dentro de
las categorías del reglamento de dicha federación.
6
2. MOTIVACIÓN Y PROPÓSITO
Cada día más, multitud de personas aficionadas al mundo del motor, quieren poner en
práctica sus habilidades de conducción sin poner en peligro su integridad física y la de
los otros en las carreteras.
Un kart es un medio ideal para disfrutar del deporte del motor, sin riesgos y con una
inversión pequeña en relación a las otras modalidades del deporte del motor. El
mercado no ofrece una gran gama de este tipo de vehículos. Por esta razón
conjuntamente con nuestro interés hacia el mundo de la mecánica se optó por un diseño
más personalizado de este tipo de vehículos.
Por otra parte uno de los propósitos de la realización de este proyecto es poner en
práctica los conocimientos académicos en un tema que causa gran inquietud a los
autores.
7
3. NECESIDADES QUE HA DE CUBRIR
Con tal de realizar este proyecto se ha hecho un balance de las necesidades que ha
cubrir un kart.
Su principal utilidad será la de vehículo de ocio en un circuito preparado, donde será
capaz de desarrollar al máximo sus prestaciones. También podrá ser utilizado como
vehículo de competición dentro de la categoría Formula E dictada por la CIK-FIA
(Comisión Internacional de Karting de la Federación Internacional de Automovilismo).
En su diseño se han contemplado todos los requisitos obligatorios para su
homologación.
Con el propósito de satisfacer estas necesidades se ha optado por la siguiente
configuración:
•
El chasis se ha construido con tubo de acero semi-rígido de acero F-114 de
diámetro exterior de 2 8mm. e interior de 24 mm. Para su diseño se han tenido
en cuenta las fuertes solicitaciones a las que estará sometido, y se ha dotado de
una forma estructural que mejore la absorción de estas.
Las características del material son:
o Acero correspondiente a la norma UNE 36 051-2:1991.
o Tratamiento térmico: trempado 825 ÷ 845ºC en agua.
Revenido 450 ÷ 650ºC.
o Composición química: %C = 0,40 ÷ 0,46.
%Si ≤ 0,35
%Mn ≤ 0,80
8
%Cr ≤ 0,50
Pmáx. = 0,035
Smáx. = 0,035
o Características mecánicas mínimas:
•
ƒ
Tensión a la rotura: 90 kgF/mm2
ƒ
Tensión en el límite de elasticidad: 70 kgF/mm2
ƒ
Alargamiento: 8%
ƒ
Resiliencia: 6 kgF/cm2
ƒ
Dureza HR: 247 ÷ 277
El motor que mejor obedece las exigencias demandadas es un motor de dos
tiempos de 249,3 cm3 con admisión directa al cárter y válvula de escape, con un
sistema de refrigeración líquida, de la casa GAS GAS. Proporciona una potencia
máxima de 51,2 CV a 8500 r.p.m. y un par máximo de 4,7 kg · m (46,107 N · m)
a 7500 r.p.m.
•
Se han seleccionado unos pneumáticos de la marca Maxxis Tires. Las ruedas
posteriores montan pneumáticos 11x7,10-5 y las anteriores lo hacen con 10x4,55, que se corresponden al modelo HG3 de dicha marca.
Se han montado sobre llantas de aluminio de 5” con una disposición de tres
taladros para espárragos de M10.
•
El sistema de dirección es directo mecánico mediante bielitas con rotulas a
derecha y a izquierdas para el posterior reglaje da la dirección. La dirección
estará accionada por un volante de forma totalmente circular cumpliendo así la
normativa.
9
•
Se colocará una plancha de acero entre el asiento del conductor y el frontal del
vehículo, tal como marca la reglamentación, por motivos de seguridad referentes
a las extremidades inferiores del piloto.
•
A lo que se refiere a las protecciones del vehículo se dispondrán de parachoques
delantero, trasero y laterales. Los parachoques deben ser de acero y estar
homologados con la carrocería. Su constitución será la dictaminada por la
norma.
•
La carrocería está constituida por dos pontones laterales, un carenado y un
plafón frontal, que deberán estar homologados por el CIK-FIA.
El material utilizado para su construcción será plástico de tipo expandido y no
presentará ningún canto vivo en caso de fractura.
3.1. FICHA TÉCNICA
3.1.1. motor
•
Cilindrada: 249,3 cm3
•
Tipo: Monocilíndrico de dos tiempos con admisión por láminas directamente al
cárter y válvula de escape.
•
Número de cilindros: Uno.
•
Sistema de refrigeración: Líquida.
•
Diámetro x carrera: 66,4 x 72
•
Carburador: Keihin* PWK 38 mm.
•
Encendido: Kokusan digital CDI Multispark.
•
Engrase motor: por mezcla.
10
3.1.2. transmisión
•
Embrague: multidisco con mando hidráulico.
•
Caja de cambios: 6 velocidades.
•
Tracción: trasera mediante cadena.
3.1.3. dirección
•
Tipo: directa mecánica mediante bielitas con rotulas a derechas y a izquierdas.
3.1.4. frenos
•
Tipo: hidráulico de bomba de tándem.
•
Delanteros: dos discos autoventilados y perforados.
•
Traseros: un disco autoventilado y perforado.
3.1.5. ruedas
•
Llantas: de aluminio de 5”.
•
Pneumáticos: modelo HG3 de la marca MAXXIS TIRES.
•
Dimensiones pneumáticos: delanteros 10x4,5-5
traseros 11x7,10-5
11
4. CONCEPTOS GENERALES DE UN VEHÍCULO AUTOMÓVIL
4.1. CONCEPTO DE DERRAPE Y RODADURA
Cuando un cuerpo reposa sobre una superficie, se opone a su desplazamiento una
resistencia tangencial que tiende a impedir el derrape. Esta resistencia recibe el nombre
de adherencia o rozamiento.
En el caso de un vehículo las ruedas se apoyan sobre el terreno y la adherencia se puede
representar como una fuerza entre las dos superficies de contacto de sentido contrario al
movimiento del vehículo.
Al derrape del vehículo se le puede aplicar la Ley de Coulomb: “la resistencia al derrape
es proporcional a la carga nominal que actúa sobre la superficie de contacto de los dos
cuerpos”.
4.2. RESISTENCIA AL MOVIMIENTO DE UN VEHICULO
Para que un vehículo se desplace con una cierta velocidad es necesario que la potencia
del motor sea la suficiente para vencer todas las resistencias que se oponen al
movimiento del vehículo. Las más importantes son:
•
Resistencia a la rodadura
•
Resistencia debida a la pendiente del terreno
•
Resistencia del aire
12
4.2.1. resistencia a la rodadura
Si Q es el peso total del vehículo y µr el coeficiente de rodadura correspondiente, la
resistencia al movimiento por rodadura será:
Rr = µr · Q
Al vencer esta resistencia se absorbe una potencia de valor:
Nr = Rr · v/75 ·3.6 = µr · Q · v/270 (C.V.)
v = velocidad del vehículo en km/h
4.2.2. resistencia debida a la pendiente
Se define como pendiente a la tangente del ángulo del plano inclinado que forma con la
carretera.
B
L
h
A
C
L’
Para ángulos pequeños se verifica que L’ ≈ L; tan α ≈ sen α; cos α ≈ 1
En la práctica se suele expresar la pendiente en %, es decir L = 100.
i = sen α = h/100
13
Rp
Q’
Q
Se verifica:
Rp = Q · sen α = Q · i
Para vencer la resistencia se absorbe una potencia:
Np = Rp · v/270 = Q · sen α · v/270 = Q · i · v/270 (C.V.)
4.2.3. resistencia por rodadura y pendiente
La resistencia por rodadura viene dada por:
Rr = µr · Q’ = µr · Q · cos α
La resistencia total por rodadura y pendiente es:
Rr + Rp = µr · Q · cos α + Q · sen α = Q · cos α · (µr + tan α)
Como para ángulos pequeños se verifica: i = tan α ≈ sen α; cos α = 1
Rr + Rp = Q · (µr + i)
La potencia absorbida por esta resistencia es:
Nrp = Q · (µr + i) · v/270 (C.V.)
14
4.2.4. resistencia del aire
Se ha comprobado experimentalmente que la resistencia Ra que ofrece el aire a un
vehículo es proporcional a la superficie recta transversal S del vehículo y al cuadrado de
su velocidad v.
Ra = K · S · v2 (kg)
K es el coeficiente de proporcionalidad que depende del vehículo, sus valores normales
son:
Camiones
0,05
Autotrenes
0,095
Autobuses normales
0,038
Autobuses de perfil aerodinámico
0,019
Coches
0,022 ÷ 0,035
Coches de perfil aerodinámico
0,010 ÷ 0,019
La sección transversal S del vehículo se obtiene de la vía del vehículo e y de la altura
máxima de este a, es decir:
S=a·e
a
e
15
4.2.5. adherencia
Fadh = µa · Q’ = µa · Q · cos α; µa = Fa /Q · cos α
F’a = µa · Q’1 = µa · R1 · cos α; µa = Fa / R1 · cos α
F’’a = µa · Q’2 = µa · R2 · cos α; µa = Fa / R2 · cos α
Si F = Q · sen α < Fa el vehículo no derrapará.
Si F = Q · sen α > Fa el vehículo derrapará.
Si F = Q · sen α = Fa el vehículo estará en posición de equilibrio.
4.2.6. valores del coeficiente de adherencia
El
coeficiente
de
adherencia
es
un
número
abstracto
que
se
determina
experimentalmente, dado que depende de la naturaleza del terreno y del estado de los
pneumáticos del terreno.
La tabla siguiente corresponde a vehículos con pneumáticos en buen estado:
Naturaleza del suelo
Coeficiente de adherencia (µa)
Carretera de cemento
0,8
Empedrado seco
0,7
Asfalto seco
0,6 ÷ 0,75
Carretera húmeda
0,3 ÷ 0,4
Carretera mojada
0,25
Carretera alquitranada grasosa
0,15 ÷ 0,20
Carretera con barro
0,15
Carretera con hielo
0,08 ÷ 0,01
16
4.2.7. rodadura
Se dice que un vehículo rueda sobre un terreno cuando el espacio recorrido por sus
ruedas es igual a su desarrollo, es decir, se verifica que:
e=2·π·R·n
Siendo n el numero de vueltas que han dado las ruedas para recorrer e.
Si por el contrario las ruedas pasan de la posición A la posición B sin girar, se dice que
el recorrido ha sido por derrape.
A
e
B
4.2.8. movimiento por rodadura
Es sabido que el par que desarrolla el motor obtiene su mayor valor en las ruedas
motrices, cosa que depende de las desmultiplicaciones de la caja de cambio.
A consecuencia de este par se crea en las ruedas motrices una fuerza tangencial T que
hace que el vehículo se ponga en movimiento. Si esta fuerza es mayora que la fuerza de
adherencia Fa de las ruedas motrices el vehículo derrapara sobre el terreno. En cambio,
si como es normal, la fuerza tangencial es menor que la de adherencia el vehículo rodará
debido a que las ruedas motrices se crea un par, denominado, de rodadura, que hace que
las ruedas se muevan de esta manera:
17
T
T
Fa
Q
r
-j
Q
F’
-F’
-Q
rc
A
j
-j
-Fr
Q
Fa
B
e
Los pneumáticos en contacto con el terreno sufren un deformamiento de forma elíptica
como consecuencia de la carga que gravitan sobre ellas, y se apoyan sobre el terreno en
una zona comprendida entre los puntos A y B.
En el punto A está aplicada la fuerza de adherencia Fa que impide el derrape de la rueda
sobre el terreno. La línea de aplicación de la carga Q que gravita sobre la rueda pasa por
el punto medio entre A y B. Como consecuencia de las fuerzas Fa y T la carga Q
adquiere el valor de j, y su línea de aplicación pasa por el punto A.
Esta fuera j es la resultante de la carga Q y otra fuerza F’ aplicada en el centro de la
rueda, que es la que vence la resistencia creada en A, y que recibe el nombre de fuerza
motriz o de tracción. A la fuerza F’ se le denomina resistencia a la rodadura, por
oponerse al movimiento de la rueda, y se representa por Fr .
18
Cuando las fuerzas están aplicadas en A, siendo e la mitad de la distancia A – B y rd el
radio de la rueda bajo la carga estática (se considera rd = 0,9 · r, siendo r el radio de las
ruedas sin carga y rd el radio dinámico de la rueda), se verifica:
•
Momento de – Q respecto A = + Q · e
•
Momento de – F’ respecto A = - F’ · rd
Como el momento de la resultante –j es nulo también tiene que serlo la suma de los
momentos de las componentes:
Q · e - Fr · rd = 0
Fr / Q = e / rd
Según se observa en la figura anterior la relación entre Fr y Q es la tangente del ángulo
de rodadura. A la relación e / rd se le denomina coeficiente de rodadura, µr . Así
tenemos:
Fr / Q = e / rd = µr
Por lo tanto el coeficiente de rodadura es la relación entre el brazo de palanca e del par
de rodadura y el radio dinámico rd .
4.2.9. condiciones de adherencia y rodadura
Para que se produzca la rodadura es necesario que la fuerza de adherencia Fa sea mayor
que la fuerza de rodadura Fr , es decir que el coeficiente de adherencia µa sea mayor que
el de rodadura µr .
Fa = µa · Q
Fr = µr · Q
19
4.2.10. valores del coeficiente de rodadura
Se obtienen de la misma forma que los de adherencia, experimentalmente dependen de
muchos factores, tales como la presión del pneumático y estado del mismo, naturaleza
del terreno, velocidad del vehículo, etc.
Naturaleza del suelo
Coeficiente de rodadura (µr)
Carretera de cemento
0,0125
Empedrado seco
0,015
Asfalto
0,02 ÷ 0,03
Terreno natural duro
0,08
Terreno de consistencia media
0,110
Terreno arenoso
0,15 ÷ 0,30
Para los cálculos se puede adoptar un coeficiente comprendido entre 0,02 y 0,03.
Como que esta sección es por exceso, para que el error cometido resulte el mínimo
posible, se le aplicará un coeficiente c cuyo valor varía entre 0,85 y 0,95. Por lo tanto:
S=c·a·e
Nota: en el presente caso existen dos tipos de vías, la anterior, correspondiente a las
ruedas del eje delantero i la posterior, correspondiente a las ruedas del eje trasero.
Consideraremos como base e la de la sección transversal recta de la vía posterior, que es
mayor que la de la vía anterior.
Si se expresa la velocidad del vehículo en km/h tenemos:
v’ (m /s)
v = 3,6 · v’
v’ = v/3,6
v’2 = v2 /13
20
La resistencia del aire en función de la velocidad en km/h es por lo tanto:
Ra = K · S · (v2 /13)
(kg)
Resistencia total que se opone al movimiento de un vehículo:
Tr = Rr + Rp + Ra = Q · (µr + i) + K · S · (v2 /13)
(kg)
Este valor dependerá de la velocidad del vehículo en cada momento así como de la
pendiente de la superficie por la que se desplaza.
La potencia necesaria para vencer esta resistencia es la que se necesita en las ruedas
motrices. La potencia del motor ha de ser mayor, ya que como es sabido, existen
perdidas por rozamiento en todos los elementos que forman la transmisión.
Aplicación:
Resistencia a la rodadura:
Rr = µr · Q
µr = 0,02 ÷ 0,03
Rr = 0,025 · 180 = 4,5 kg
Resistencia a la pendiente:
Rp = Q · sen α = (180 · sen α)
Resistencia al aire:
Ra = K · S · v’2
K: coches = 0,022 ÷ 0,035
S = c · a · e / c = 0,085 ÷ 0,95
(kg)
21
S = 0,9 · 0,645 · 1,37 = 0,7953 m2
Ra = 0,0285 · 0,7953 · v’2
Ra = 0,023 · v’2
Resistencia total:
Tr = Rr + Rp + Ra = 4,5 + (180 · sen α) + (0,023 · v’2)
4.3. ARRANQUE.
ARRANQUE
ADHERENCIA
DEL
VEHICULO
EN
EL
Para que el vehículo se mueva es necesario que el esfuerzo tangencial creado en la
periferia de las ruedas motrices sea menor que el esfuerzo por adherencia de dichas
ruedas.
El esfuerzo tangencial viene dado por la expresión:
T = [ (2 · ρ) / (rc · rd · D) ] · Mm
Siendo:
ρ : rendimiento de la transmisión
rc : relación de la caja de cambios
rd : relación de la transmisión
Mm : Momento motor
La carga total que gravita sobre las ruedas del eje motriz en el momento del arranque es:
R’B = RB + 0,242 · [ (2 · ρ · Mm) / (rc · rd · D) ]
La adherencia de las ruedas motrices viene dada por: µ’a · R’B
22
Por tanto para que las ruedas motrices no derrapen es necesario que esta adherencia sea
superior al esfuerzo tangencial T:
µ’a · R’B > (2 · ρ · Mm) / (rc · rd · D)
µa · [ R’B + 0,381 · (2 · ρ · Mm) / (rc · rd · D) ] > (2 · ρ · Mm) / (rc · rd · D)
µa · R’B + µa · 0,381 · (2 · ρ · Mm) / (rc · rd · D) > (2 · ρ · Mm) / (rc · rd · D)
RB > (2 · ρ · Mm) / (rc · rd · D · µa) – [ 0,381 · (2 · ρ · Mm) / (rc · rd · D)
RB > [ (2 · ρ · Mm) / (rc · rd · D) ] · (1/ µa – 0,381)
Por lo tanto, para que el vehículo pueda arrancar necesita que la carga total sobre el eje
posterior correspondiente al vehículo parado sea mayor que la expresión del segundo
miembro de la inecuación.
RB > [ (2 · 0,85 · 4,7) / (29/14 · 13/26 · 0,2794) ] · (1/0,5 – 0,381)
RB > 11,18 kp
Condición que en el presente caso se cumple ya que sobre el eje posterior, con el
vehículo parado gravitan 135 kp.
4.4. PENDIENTE MÁXIMA SUPERABLE
Par motor máximo:
Mmotor máx. = 4,7 kg · m ≡ 46,107 N · m
Fuerza de tracción máxima:
Ftrac. máx. = ½ Mm · (rprimario · rcambio 1ª · rpuente) · (ρprimario · ρcambio · ρpuente) · 1/rdin
Ftrac. máx. = ½ 46,107 · (57/20 · 29/14 · 26/13) · (0,95 · 0,90 · 0,97) 1/0,12573
Ftrac. máx. = 448,87 kp
23
Fpendiente máx. ≡ Ftrac. máx. = P · (fr · cos αmáx + sen αmáx)
448,87 = (180 · 9,81) · (0,025 · cos α + sen α)
0,2542 = 0,025 · cos α + sen α
siendo el primer término de la serie: cos α = 1 – ½ sen2 α
0,2542 = 0,025 (1 – ½ sen2 α) + sen α
α ≈ 14º
4.5. ESTABILIDAD
R1
R’1
h
R2
R’2
c.d.g.
D
f
Rp
Q’
p
D
s
Q
R1 y R2: reacciones de la carga total sobre los ejes anterior y posterior en un plano
horizontal.
R’1 y R’2: reparto de carga total sobre los ejes anterior y posterior en un plano
inclinado.
24
f, s, h: situación del c. d. g. del vehículo.
Rp: resistencia al movimiento del vehículo debido a la pendiente.
Se considera el vehículo con todas las ruedas frenadas.
Q = carga + tara
Para que el vehículo se encuentre en posición estable se ha de verificar: R’1 > 0
∑MT = 0
R’1 · p + Rp · h – Q’ · s = 0
R’1 = Q’ · s/p - Rp · h/p
Q’ = Q · cos α
Rp = Q · sen α
R’1 = (Q · cos α · s/p) – (Q · sen α · h/p) = (Q · cos α / p) · (s – h · tg α)
Para que R’1 > 1 se ha de cumplir:
s – h · tg α > 0;
h< s/tg α;
tg α < s/h
Por lo que a la adherencia se refiere, es conocido que para que un vehículo no derrape es
necesario que la pendiente sea menor que el coeficiente de adherencia, lo que significa:
tg α < µa
Por lo tanto, para que el vehículo no bascule ni derrape se tiene que cumplir:
µa < tg α < s/h
Si se coge como coeficiente de adherencia el de asfalto seco (0,6) y conociendo la
pendiente del presente caso, s = 262 mm y h = 225 mm, nos queda:
0,6 < tg α < 1,16
25
4.6. REPARTO DE CARGAS
4.6.1. reparto de cargas (estudio estático)
a
h
b
A
B
RA
P=m·g
RB
l
Q = peso + tara = 100 + 80 = 180 kg
P = Q · g = 180 kg · 9,81 m/s2 = 1765,8 N ≡ 180 kp
Cogiendo momentos respecto el punto A: (sentido horario positivo)
P · a - RB · l = 0
RB = (P · a) / l = (180 · 0,787) / 1,049 = 135 kp
RA = P - RB = 180 – 135 = 45 kp
Reparto de pesos estáticos en los ejes:
eje anterior:
eje posterior:
(5/180) · 100 = 25%
(135/180) · 100 = 75%
26
4.6.2. reparto de cargas en el arranque
Al frenar o arrancar un vehículo aparece una fuerza de inercia que se opone a la fuerza
que tiende a poner en movimiento o a detener el vehículo y modifica la carga sobre los
ejes.
Al arrancar un vehículo la fuerza de inercia I origina que sobre el eje posterior gravite
más carga que cuando el vehículo está parado. Lo contrario sucede sobre el eje anterior,
dado que el peso que se traspasa sobre el eje posterior reduce el que gravite sobre el eje
anterior. Por lo tanto, si las cargas sobre el vehículo parado son las siguientes:
eje anterior:
RA = 45 kp
eje posterior:
RB = 135 kp
En el momento de arrancar estas cargas se transforman en unas diferentes, R’A y R’B.
a
b
I
h
A
B
R’A
Q
R1
R’B
l
∑MA = 0
- R’B · 1,049 + (1765,8 · 0,787) + I · 0,4 = 0
- 1,049 R’B + 1389,6846 + 0,4 · I = 0
27
R’B = RB + 0,381 · I
∑MB = 0
R’A · 1,049 – (1765,8 · 0,422) + 0,4 · I = 0
R’A = RA – 0,381 · I
El eje posterior sufre un incremento de carga (0,381 I) respecto a la del vehículo parado,
y el eje delantero queda descargado con el mismo peso.
•
Determinación del esfuerzo de inercia.
El esfuerzo tangencial en las ruedas motrices viene dado por la expresión:
T = (2 · ρ / rc · rd · D) · Mm
R’A
R’B
c.d.g.
h
I
A
B
Q
a
b
l
Cogiendo momentos respecto del c.d.g.: (sentido horario positivo)
R’B · 0,262 – 0,4 · T - R’A · 0,787 = 0
0,262 · R’B – 0,4 · T – (Q - R’B) · 0,787 = 0
R’A = Q - R’B
28
R’B = 1324,77 + 0,381 · T
R’B = RB + 0,381 · T
R’A = RA – 0,381 · T
Si se comparan los resultados obtenidos con los obtenidos anteriormente de R’A y R’B se
deduce:
R’B = RB + 0,381 · I
R’B = R’B + 0,381 · T
R’A = RA – 0,381 · I
R’A = R’A – 0,381 · T
I=T
R’B = RB + 0,381 · (2 · ρ · Mm) / (rc · rd · D)
R’A = R’A – 0,381 · (2 · ρ · Mm) / (rc · rd · D)
La fuerza de inercia será más grande cuando las reducciones de la caja de cambio sean
mayores y cuando más mayor sea el par motor.
Aplicando todo lo expuesto se deduce que el reparto de cargas en el momento de
arrancar en primera velocidad y con el máximo par motor será el que se expone a
continuación:
RA = 45 kp
rc = 29/14
RB = 135 kp
rd = 13/26
Mm = 4,7 kg · m
D = 0,2794
ρ = 0,85
R’B = 135 + 0,381 · [ (2 · 0,85 · 4,7) / (29/14 · 26/13 · 0,2794) ] = 137,5 kp
R’A = 45 - 0,381 · [ (2 · 0,85 · 4,7) / (29/14 · 26/13 · 0,2794) ] = 42,5 kp
29
4.6.3. reparto de cargas en la frenada
En este caso la fuerza de inercia actúa en sentido contrario al explicado anteriormente, y
por lo tanto se produce un incremento de carga en el eje anterior respecto a cuando el
vehículo se encuentra parado, y lo contrario sucede para el eje posterior.
a
b
c.d.g.
Fi
h
A
frA
R’’A
frB
R’’B
Q
l
∑MA = 0
- I · 0,4 + Q · 0,787 – R’’B · 1,049 = 0
1,049 · R’’B = 0,787 · 1765,8 – 0,4 · I
R’’B = RB – 0,381 · I
∑MB = 0
R’’A · 1,049 – 0,4 · I – 0,262 · Q = 0
R’’A = RA + 0,381 I
B
30
•
Determinación del esfuerzo de inercia I debido al peso del vehículo (peso +
tara).
Ecuación de un movimiento uniforme retardado:
v = v0 – J · t
siendo:
v: velocidad final
v0: velocidad inicial
J: deceleración
t: tiempo que tarda en pararse el vehículo
En la detención de un vehículo se verifica:
v=0
v0 = J · t
J = v0 / t
El valor de la fuerza de inercia en función de la deceleración y de la carga es:
I = (Q / g) · J
El reparto de cargas en el momento de la frenada es:
R’’A = RA + 0,381 · I = RA + 0,381 · Q/g · J
R’’B = RB - 0,381 · I = RB - 0,381 · Q/g · J
Para el estudio se supondrá una deceleración de J = 5 m/s2.
R’’A = 45 + 0,381 · (180 / 9,81) · 5 = 79,9 kp
R’’B = 135 – 0,381 · (180 / 9,81) · 5 = 100,1 kp
De esta forma, por ejemplo cuando el vehículo circule a su velocidad máxima que es,
aproximadamente, de 90 km/h ≡ 25 m/s tardará en pararse con un coeficiente medio µ =
0,5:
31
J = v0 / t
t = v0 / J
t = 25 / 5 = 5 s
También se podría haber obtenido el reparto de cargas basándonos en otro
razonamiento, igual de válido.
P = tara + peso = 180 kg
δmáx = 5 m/s2
Fuerza de inercia: Fi = m · δ = 91,7 kp
∑MA = 0
P · a - Fi · h – R’’B · I
R’’B = 100,1 kp
R’’A = 79,9 kp
El reparto de pesos en los ejes será:
eje anterior:
(79,9/180) · 100 = 44%
eje posterior:
(100,1/180) · 100 = 56%
4.6.4. reparto de cargas en pendiente
Las cargas varían cuando el vehículo está situado sobre una superficie con pendiente.
En la figura mostrada a continuación se puede observar como las reacciones sobre las
ruedas del vehículo se ven afectadas por el ángulo de inclinación del terreno por el que
circula el vehículo.
32
RA
R1
400
RB
R2
c.d.g.
D
Rp
787 Q’
D
Q
1049
262
∑MA = 0
-
R2 · 1,049 + Q · 0,787 + Rp · 0,4 = 0
Q’ = Q · cos α
Rp = Q · sen α
(- 1,049 · R2) + (0,787 · Q · cos α) + (0,4 · Q · sen α) = 0
R2 = 135 · 04 · cos α + 68,6 · sen α
R2 = RB · cos α + 68,6 · sen α
∑MB = 0
1,049 · R1 – 0,262 · Q’ + 0,4 · RP = 0
R1 = 44,9 · cos α – 68,6 · sen α
R1 = RA · cos α – 68,6 · sen α
33
4.7. DIAGRAMA DE VELOCIDAD – REGIMEN DEL MOTOR
En este tipo de diagrama, se distribuye en abcisas la velocidad del vehículo en
kilómetros por hora y en ordenadas, el régimen de giro del motor en revoluciones por
minuto.
Las dos variables, presentes en el diagrama, se relacionan linealmente mediante la
siguiente ecuación:
v = nm · [ 1 / (rprimario · rcambio · rpuente) ] · 2 · π · rdin · (60/1000)
donde:
(km/h)
v ≡ velocidad del vehículo en km/h
nm ≡ régimen del motor en rev/min
rprimario ≡ relación de transmisión en el eje primario
rpuente ≡ relación de transmisión del puente
rcambio ≡ relación de transmisión del cambio
rdin ≡ radio dinámico del pneumático (m)
Substituyendo valores en la igualdad se obtiene una ecuación en la que se logra poner la
velocidad en función de la relación del cambio.
nm = 8500 r.p.m. (régimen del motor a potencia máxima)
rprimario = 57/20
rpuente = 26/13
rdin = 0,9 · rrueda trasera = 0,9 · 139,7 = 125,73 mm = 0,12573 m
v = 8500 · [ 1 / (57/20 · rcambio · 26/13) ] · 2 · π · 0,12573 · (60/1000)
34
Nº de marcha
Relación
Velocidad (km/h)
1ª
29/14
34,13
2ª
26/16
43,5
3ª
24/18
53,03
4ª
22/20
64,26
5ª
21/23
77,42
6ª
19/24
89,25
VELOCIDAD - RÉGIMEN MOTOR
10000
9000
Régimen Pot Máx
8000
Régimen Par Máx
1ª
2ª
3ª
4ª
5ª
6ª
r.p.m.
7000
6000
5000
4000
3000
2000
1000
0
0
20
40
60
80
100
120
km/h
Para aprovechar al máximo el rendimiento del carburante así como la vida del motor, el
régimen de giro del motor deberá ser lo más próximo a la velocidad de régimen de par
máximo (ωm). Para obtener la máxima aceleración el régimen de giro del motor deberá
ser lo más próximo a la velocidad de régimen de potencia máxima (ωP). El mantener el
35
régimen de giro del motor próximo a lo deseado mientras aumenta la velocidad del
vehículo se logra con una transmisión de varias velocidades.
En la gráfica se han representado las relaciones de velocidades y las correspondientes
relaciones de transmisión de la caja de cambios. Si se mantiene la primera velocidad, la
velocidad del motor (en función de la del kart) está definida por la primera curva. Al
cambiar a la segunda velocidad se pasa a la segunda curva, con la cual cosa, si la
velocidad del kart se mantiene constante, la velocidad del motor será menor.
El momento adecuado para cambiar de marcha depende de la intención del conductor.
Si se desea obtener la máxima aceleración, se realizarán los cambios en las velocidades
del kart indicadas en la gráfica. Con eso se conseguirá mantener la velocidad del motor
en las proximidades de la velocidad de máxima potencia y se conseguirá el régimen
máximo de aceleración del kart.
Si se desea optimizar la vida del motor y su rendimiento, el conductor deberá disminuir
el régimen de giro del motor, manteniéndolo próximo al del par máximo. Para ello se
deberán realizar los cambios a una velocidad del kart algo menor.
4.8. MOTOR ADOPTADO
El motor seleccionado para proporcionar potencia al conjunto mecánico es un motor de
la casa GAS GAS dos tiempos y con una cilindrada de 249,3 cm3.
El motor es de admisión por láminas directamente al cárter y válvula de escape. Consta
de un solo cilindro con refrigeración líquida.
El diámetro interior del pistón es de 66,4 mm y tiene una carrera de 72 m. Adopta un
carburador Keihin PWK de 38 mm.
36
Se le acopla una caja de cambios de seis velocidades con embrague hidráulico
multidisco.
El motor es capaz de desarrollar una potencia máxima de 51,2 CV a 8500 r.p.m. y un
par máximo de 4,7 kg · m (46,107 N · m) a 7500 r.p.m.
El motor fue testado en un banco de pruebas TX-200 y los resultados obtenidos se
muestran a continuación:
Marca: GAS GAS
Fecha de ensayo: 27 – 3 – 2002
Relación régimen motor / régimen rodillo: 0,2624692
Presión ambiente: 997 mb
Potencia según equivalencia norma SAE
ENSAYO INERCIAL: RESULTADOS EN MOTOR
Régimen
Potencia motor (C.V.)
Par motor (N · m)
3000
7,4
17,658
3500
13,0
26,487
4000
17,1
31,392
4500
20,1
32,373
5000
24,1
34,335
5500
29,1
38,259
6000
34,1
41,202
6500
39,0
43,164
7000
43,9
45,126
7500
47,9
46,107
37
8000
50,2
45,126
8500
51,2
43,164
9000
48,8
39,240
9500
41,7
31,392
10000
34,5
24,525
10500
26,5
17,658
POTENCIA, PAR - RÉGIMEN MOTOR
60
CV - Nm
50
40
30
20
10
0
0
2000
4000
6000
8000
10000
12000
r.p.m.
Potencia (CV)
Par (Nm)
4.9. REGLAMENTACIÓN CIK-FIA (COMISIÓN INTERNACIONAL
DE KARTING DE LA FEDERACIÓN INTERNACIONAL DE
AUTOMOVILISMO)
En este apartado se mostrarán los puntos más importantes en los cuales se han basado
muchos de los cálculos del diseño del kart, con el objetivo que cumpla la normativa
dictada por la CIK-FIA (Comisión Internacional de Karting de la Federación
Internacional de Automovilismo).
Esta referencia es importante para entender muchas de las soluciones adoptadas en
varios apartados que vienen dictados por la reglamentación vigente.
38
Si se desea ver más información sobre las normas dictadas por dicho organismo, así
como los requisitos que han de cumplir los vehículos para poder participar u otras
informaciones, consultar Anexo 2.
Esta referencia se ha tenido en cuenta en el diseño del kart con la intención de poder
homologar el vehículo una vez acabado su diseño y posterior construcción.
Además cabe la posibilidad de que una vez el proyecto quede homologado, producirlo
en serie ya que cumple todas las normas de seguridad exigidas y sea accesible a toda
clase de usuarios. Si una vez el propietario del mencionado vehículo deseara participar
en carreras reglamentarias de karting podría hacerlo dentro de la categoría para la que
ha sido diseñado este kart, que se trataría de la Fórmula-E.
Todos los puntos expuestos a continuación son una síntesis extraída del anuario
redactado por la CIK-FIA (Anexo 5).
•
Notación de kart: es un vehículo terrestre con o sin carrocería, con cuatro ruedas
no alineadas que están constantemente en contacto con el suelo, de las cuales
dos aseguran la dirección y las otras dos la propulsión. Las partes principales
son el chasis, el motor y el piloto.
• Exigencias:
a) seguridad: los karts sólo están autorizados a correr si se
encuentran en un estado que responda a las normas de
seguridad
y
reglamentación.
se
encuentran
en
conformidad
con
la
39
b) posición de conducción: sobre el asiento, con los pies para
delante.
•
Chasis: todas las piezas principales del chasis deben estar fijadas sólidamente
unas contra las otras. Sólo se admiten conexiones articuladas por el soporte
convencional de la punta del eje y por la dirección. Cualquier otro dispositivo
que tenga la función de articulación queda prohibido.
Construcción tubular en acero de construcción y su flexibilidad corresponde a
los límites de elasticidad de la construcción.
La utilización de titanio está prohibida.
•
Dispositivos amortiguadores: hidráulicos, pneumáticos o mecánicos están
prohibidos en la totalidad del vehículo.
Fórmula-E (250 c.c.)
Motor: cilindrada máxima 250 c.c.
Motor refrigerado por aire o por líquido (dos cilindros como
máximo).
Caja de cambios mínima de tres velocidades.
Producción en serie.
Pneumáticos libres CIK-FIA.
Especificaciones técnicas:
Distancia entre ejes: mínima 101 cm
máxima 127 cm
Vía: como mínimo 2/3 de la distancia utilizada entre ejes.
40
Longitud total: máxima 182 cm; Fórmula-E, máxima 210
cm.
Paragolpes: una protección delantera, trasera y lateral.
Paragolpes delantero: altura máxima respecto del suelo
20 cm.
Paragolpes trasero: altura máxima respecto del suelo 20
cm.
Bandeja: ha de existir un material rígido desde el asiento
del conductor hasta el frontal del vehículo.
Todo dispositivo de suspensión, elástico o articulado
queda prohibido.
Pneumáticos con o sin cámara de aire.
Diámetro de la llanta como máximo 8”.
Diámetro máximo de la rueda delantera 280 mm y de la
trasera 300 mm.
Ancho máximo de las ruedas 250 mm.
Frenos: sistemas de operación independientes anterior y
posterior que en el caso de que uno no funcione el otro
garantice el funcionamiento. Los frenos obligatoriamente
han de ser hidráulicos.
Dirección: accionada por un volante totalmente circular.
Transmisión: se ha de efectuar siempre sobre las ruedas
traseras, el método es libre, pero todo tipo de diferencial
está prohibido.
41
5. CÁLCULOS DE COMPROVACIÓN
5.1. CHASIS
5.1.1. cálculo del centro de gravedad (c.d.g.) de la estructura
El chasis del kart es una estructura tubular donde todos los tubos son de sección
constante y el acero tiene también una densidad constante.
En este apartado encontraremos el c.d.g. del chasis como estructura unitaria. Entonces
teniendo en cuenta el peso del piloto y del motor, que son las otras masas más
significativas del conjunto, se calculará el c.d.g. del kart como objeto espacial.
•
barra
Cálculo del c.d.g. de la estructura tubular
L (mm)
Xc.d.g.
Yc.d.g.
Zc.d.g.
Qyz = X·L
Qxz = Y·L
Qxy = Z·L
OE
669,00
334,50
0
0
223,8·103
0
0
AG
669,00
334,50 640,00
0
223,8·103
428,1·103
0
CF
579,00
379,50 520,00
0
219,7·103
301,1·103
0
CB
120,00
160,00 580,00
0
19,2·103
69,6·103
0
EG
640,00
669,00 320,00
0
428,2·103
204,8·103
0
CD
533,67
220,00 259,90
0
117,4·103
138,7·103
0
LK
400,00
1430,00 320,00
0
572,0·103
128,0·103
0
GK
770,40
1022,80 575,79
0
788,0·103
443,6·103
0
EL
770,40
1022,80
64,21
0
788,0·103
49,5·103
0
PJ
274,88
1190,00 443,65
0
327,1·103
122,0·103
0
RP
274,88
1190,00 196,35
0
327,1·103
54,0·103
0
ML
236,56
1094,40
49,65
258,9·103
8,4·103
11,7·103
35,52
42
MN
247,66
1319,40
71,00
49,77
326,8·103
17,6·103
12,3·103
HI
236,56
1094,40 604,48
49,64
258,9·103
143,0·103
11,7·103
IK
247,66
1319,40 569,00
49,77
326,8·103
141,0·103
13,3·103
∑
6669,70
5,2·106
2,25·106
49,1·106
-
-
-
Qyz = Xc.d.g. · L
Xc.d.g = 5,2 · 106 / 6669,7 = 780,470 mm
Qxz = Yc.d.g. · L
Yc.d.g = 2,25 · 106 / 6669,7 = 337,230 mm
Qxy = Zc.d.g. · L
Zc.d.g = 49,1 · 106 / 6669,7 = 7,367 mm
(Xc.d.g, Yc.d.g, Zc.d.g) ≈ (780, 337, 7)
43
•
Cálculo del peso del chasis
Superficie con øext = 28 mm
Se = π · øe2/4 = 6,16 · 10-4 m2
Superficie con øint = 24 mm
Si = π · øi2/4 = 4,5 · 10-4 m2
Superficie tubo:
St = Se - Si = 1,6 · 10-4 m2
Longitud total de tubo:
Lt ≈ 6670 mm
Volumen total de tubo:
Vt = St · L = 1,1 · 10-3 m3
Densidad del acero:
ρsteel = 7800 kg/m3
Masa del tubo:
mtubo = 7800 kg/m3 · 1,1 · 10-3 m3 = 8,5 kg
Se tendrán en cuenta las fijaciones, que forman parte de la estructura, y se aplicará un
coeficiente de seguridad no definido, por lo que se adoptará para los cálculos una masa
de la estructura de 15 kg.
Se adoptará un peso del conductor de 90 kg, superior a la media, teniendo en cuenta que
de este modo es como si se aplicara un coeficiente de seguridad por el desconocimiento
del peso real del conductor que ocupe el vehículo.
44
Sabiendo que el peso del motor es de 30 kg y una vez conocidos los pesos del conductor
y el de la estructura (90kg y 15 kg respectivamente) se procederá al cálculo del c.d.g.
del conjunto.
X · Wt = ∑ni=1 = Xi · Wi
X · 180 = (780,47 · 15) + (90 · 575) + (30 · 414,5)
X = 421,6 mm
Y · Wt = ∑ni=1 = Yi · Wi
Y · 180 = (337,230 · 15) + (90 · 320) + (30 · 580)
Y = 285 mm
Z · Wt = ∑ni=1 = Zi · Wi
Z · 180 = (7,367 · 30) + (90 · 500) + (30 · 400)
Z = 320 mm
5.1.2. selección de diámetro de tubos
Para comprobar el diámetro de los tubos que forman la estructura del bastidor se hará un
estudio de las solicitaciones que ejercen sobre ella. Se estudiará el caso más crítico por a
lo que a fuerzas que sufre la estructura se refiere, este caso corresponde a la frenada
brusca.
45
Q = 1765,8 N
δmáx = 5 m/s2
Fi = m · δ = 180 · 5 = 900 N ≡ 91,7 kp
Sabiendo que las reacciones que actúan sobre los ejes en el caso de frenada brusca así
como las fuerzas de frenada para cada uno de ellos son:
R’’A = 79,9 kp
R’’B = 100,1 kp
frA = µ · R’’A = 0,5 · 79,9 = 39,95 kp
frB = µ · R’’B = 0,5 · 100,1 = 50,05 kp
46
M (x) = 80 · x
x=0
x = 78,7
MA = 0
MC = 6296 kp · cm
La máxima flexión se produce en las secciones alineadas con el c.d.g.
Utilizando la ecuación general de la resistencia:
C · (Mf máx / W) = σfluencia / Cu
Al ser el chasis de acero, que se trata de un material dúctil, el criterio de fallo es la
σfluencia:
C=2
Cu = 2
α=2
W = [ 0,1 · (D4 - d4) ] / D
2 · [ 6296 / [ 0,1 · (D4 - d4) / D ] ] = 80 / 2
El diámetro exterior del tubo es de 28 mm (øext).
2 · (6296 / W) = 80 / 2
W = 314,8 mm2
d ≡ øint = 26 mm
De este modo obtenemos que la solución adoptada a un tubo de diámetro exterior 28
mm y diámetro interior 24 mm es válida.
5.1.3. unión de los tubos
La unión de los diferentes tubos que componen el chasis se realiza mediante soldadura.
Esta variará según si se está produciendo en una producción en serie o si es una
producción unitaria y por tanto amateur. En el primer caso se realizará una soldadura
láser y robotizada, en el segundo de los casos, obviamente, se empleará otro tipo de
47
soldadura como puede ser la soldadura SMAW (soldadura por arco eléctrico con
electrodo revestido), la MIG (soldadura por arco metálico protegido con gas) o una TIG
(soldadura por arco eléctrico con electrodo de tungsteno protegido con gas inerte).
5.1.4. proceso de pintado
A continuación se expondrá el proceso que debe seguir este bastidor en caso de
fabricarse en producción en serie dentro de una instalación de pintura.
La estructura llega soldada y el primer proceso a realizar es la de preparación de la
pieza, que consta de diferentes fases y sirve para dejar la estructura preparada para
aplicarle, posteriormente, las capas de pintura precisas.
Este proceso de preparación consta de un desengrase inicial para extraerle todas las
posibles impurezas de lubricantes empleados en fases anteriores. Seguidamente se le
aplica un fosfato que posteriormente facilitará el proceso de pintado y se acaba esta
preparación con un lavado de chasis.
Seguidamente se le aplica una capa de imprimación que consta de un producto
anticorrosivo y a posteriori se le aplican dos capas de pintura, de color a escoger por el
fabricante según demandas.
Finalmente el chasis deberá pasar por un secado en horno a una temperatura
comprendida entre 140ºC y 160ºC.
48
5.2. TRANSMISIÓN
5.2.1. selección de las ruedas dentadas
La transmisión secundaria se realiza mediante dos ruedas dentadas por cadena simple de
rodillos.
El piñón consta de 13 dientes y el plato de 26 dientes. El piñón forma parte del conjunto
del motor, por lo tanto el paso de la cadena es un dato conocido de valor p = 15,875.
Diámetro primitivo:
dp = p · cosec α = p · cos 180/Z
Tablas norma UNE 18011-p2 (Anexo 4)
Nº de dientes (z)
cosec α
Piñón
Z1 = 13
4,197
Corona
Z2 = 26
8,296
Piñón:
dp1 = 15,875 · 4,197 = 66,627 mm
Corona:
dp2 = 15,875 · 8,296 = 131,669 mm
Diámetro de fondo y exterior:
df = dp – d
de = df + 1,25 · p
49
Piñón:
df = 66,627 – 10,16 = 56,467 mm
de = 56,467 + 1,25 · 15,875 = 76,311 mm
Corona:
df = 131,699 – 10,16 = 121,539 mm
de = 121,539 + 1,25 · 15,875 = 141,383 mm
De este modo se seleccionan las ruedas dentadas correspondientes:
Rueda dentada Z = 13 UNE 18011 (11S x 0,92 UNE 18002)
Rueda dentada Z = 26 UNE 18011 (11S x 0,92 UNE 18002)
5.2.2. selección de la cadena de rodillos
Se estudiará el caso de cadena SIMPLE núm. 11. Siendo sus características según
norma: (Anexo 2)
paso:
A = 15,875 mm
ørodillo:
B = 10,16 mm
ancho interior mínimo:
C = 9,65 mm
ancho tras la malla:
F = 14,73 mm
50
Longitud de la cadena:
Lc = (2· L/p) + [ (Z1 + Z2)/2 ] + [ p · (Z2 - Z1)2 / (4 · π2 · L) ]
L: distancia entre centros
Lc: número de eslabones o mallas de la cadena
p: paso de la cadena
Lc = (2 · 200/15,875) + [ (13 + 26) / 2 ] + [ 15,875 · (26 – 13)2 / (4 · π2 · 200) ]
Lc = 45,0366 eslabones
El resultado obtenido se aproxima al número par más cercano, por lo que:
Lc = 46 eslabones
Una vez conocido el número exacto de eslabones de la cadena se puede proceder al
cálculo exacto entre ejes:
46 = (2 · L/15,875) + [ (13 + 26) / 2 ] + [ 15,875 · (26 – 13)2 / (4 · π2 · L) ]
L = 207,747 mm
51
La longitud de la cadena será:
Lcadena = 46 · 15,875 = 730,25 mm ≈ 0,73 m
Cálculo del ángulo β:
β = arcsen (R2 – R1) / L
R1: radio primitivo del piñón.
siendo:
R2: radio primitivo del plato.
β = arcsen (65,8495 – 33,3135) / 2 = 3,56976 º
La cadena seleccionada es:
Cadena de rodillos 11S x 0,73 UNE 18002
5.3. EJE POSTERIOR
En este apartado se dimensionará el eje basándose en los casos más desfavorables de
solicitaciones en los que se puede ver afectado. Estos casos son los siguientes:
•
máxima tracción
•
máxima frenada
Una vez estudiados los casos más críticos y seleccionado un diámetro de eje se
procederá a seleccionar los rodamientos correspondientes a cada punto de apoyo de este
eje con el chasis.
5.3.1. cálculo a máxima tracción
En este apartado se dimensionará el eje posterior del kart, o sea, el eje tractor teniendo
en cuenta las solicitaciones que sufre durante el arranque del vehículo en primera
velocidad.
52
Según los cálculos anteriores en el momento de arrancar en primera velocidad y con el
par máximo del motor el reparto de carga en el eje posterior es de R’B = 137,5 kp lo que
significa que a cada rueda le corresponden:
R’B = RA + RF
RA = 68,75 kp
RF = 68,75 kp
Par eje tractor:
Meje tractor = Mmotor · rprimario · rcambio · rcadena
Meje tractor = 4,7 · 57/20 · 29/14 · 26/13 = 55,49 kg · m
Suponiendo un rendimiento de la transmisión:
η = 0,85
El momento torsor total sobre el eje será:
Meje tractor = 47,17 kg · m
Par neto que recibe cada rueda:
Mrueda = ½ · Meje = 23,6 kg · m
El esfuerzo tangencial de cada rueda motriz será:
Mrueda = Trueda · rrueda
rrueda = drueda / 2 = 279,4 / 2 = 139,7 mm
Trueda = Mrueda / rrueda
Trueda = 23,6 / 0,1397 = 168,93 kp
53
El momento del eje tractor corresponde al momento torsor que será constante en todo el
eje, lo que significa que:
Meje tractor ≡ Mt2 = 47,17 kg · m
A continuación se procederá al cálculo de las solicitaciones que recibe el eje posterior
debido a la transmisión por cadena de rodillos simples:
El diámetro primitivo de la corona situada sobre el eje posterior así como el del piñón
de salida del motor son:
dp2 = 131,7 mm
dp1 = 66,6 mm
El ángulo de abrazamiento de las dos circunferencias primitivas correspondientes a la
corona y al piñón es:
β = 3,56976 º
Mt2 = Ft2 · r2 = Ft2 · dp2/2
Ft2 = 2 · (Mt2 / dp2)
Ft2 = 2 · (47,17 / 0,1317) = 716,3 kp
54
tg β = Fr2 / Ft2
Fr2 = Ft2 · tg β = 716,3 · tg 3,56976 º
Fr2 = 44,7 kp
Seguidamente se calculará el esfuerzo resistente que actúa en sentido opuesto al motriz
calculado anteriormente.
El valor de la fuerza de adherencia en las ruedas motrices es:
Fadh/rueda = 34,375 kp
Estudio de las solicitaciones sobre el eje según el plano de trabajo correspondiente al
formado por XY (plano XY):
55
56
RB isos + RD isos = 717 kp
∑MD = 0 (sentido horario positivo)
4118 + RB isos · 52 = - 717 · 5 = 0
4118 + 52 · RB isos – 3585 = 0
57
∑MD = 0 (sentido horario positivo)
- 4118 - RE isos · 12 = 0
RE isos = - 343,167 kp
RD isos = 343,167 kp
M (x) = 343,167 · x
MD = 0
x=0
x = 12
ME = 4118 kp · cm
AT = 12 · 4118 / 2 = 24708 cm2
Aplicando el Teorema de los Tres Momentos
(4118 · 52) + [ 2 Mn · (52 + 12) ] + (4118 · 12) =
= - 6 · 191315,5 · (24,23 / 52) – 6 · 24708 · (4 / 12)
214316 + 128 · Mn + 49416 = - 534873,9883 – 49416
128 · Mn + 263552 = - 584289,9883
Mn = - 6623,76 kp · cm ≈ - 6624 kp · cm
58
RB + RD = 45
∑MD = 0 (sentido horario positivo)
2105 + RB · 52 – 45 · 5 = 0
RB = - 36,15 kp
RD = 81,15 kp
M (x) = - 36,15 · x + 2105
x=0
MB = 2105 kp · cm
59
x = 47
MC = 405,95 kp · cm
M (x’) = - 36,15 · x’ + 2105 – 45 (x’ – 47) = - 81,15 · x’ + 4220
x’ = 47
MC = 405,95 kp · cm
x’ = 52
MD ≈ 0
S1 = (47 · 2105) / 2 = 49467,5 cm2
S2 = (5 · 405,95) / 2 = 1014,875 cm2
ST = S1 + S2 = 50482,375 cm2
X · 50482,375 = (15,67 · 49467,5) + (48,67 · 1014,875)
X = 16,33 cm
∑MD = 0 (sentido horario positivo)
RE · 12 – 2105 = 0
RE = - 175,42 kp
RD = 175,42 kp
60
M (x) = 175,42 · x
x=0
x = 12
MD = 0
ME = 2105 kp · cm
AT = (12 · 2105) / 2 = 12630 cm2
Aplicando el Teorema de los Tres Momentos:
(2105 · 47) + (2 · Mn · 64) + (2105 · 12) =
= - 6· 50482,375 · (16,33 / 52) – 6 · 12630 · (4 / 12)
Mn = - 1911 kp · cm
RB = - 36,15 – 1911/52 = - 72,9 kp ≈ - 73 kp
RBDD = 81,15 – 1911/52 = 44,4 kp ≈ 44 kp
RDED = 175,42 + 1911/12 = 334,67 kp ≈ 335 kp
RE = -175,42 + 1911/12 = - 16,17 ≈ -16 kp
Plano XY
61
RB = - 138 kp
RBDD = 579 kp
RDED = 895 kp
RE = 209 kp
MB = 4118 kp · cm
MC = 3636,25 – 5978,1 = - 2350,85 kp · cm
MD = - 6624 kp · cm
ME = 4118 kp · cm
Plano ZX
RB = - 73 kp
RBDD = 44 kp
RDED = 335 kp
RE = - 16 kp
62
MB = 2105 kp · cm
MC = 405,95 – 1727,25 = - 1321 kp · cm
MD = - 1911 kp · cm
ME = 2105 kp · cm
MB = (MB xy2 + MB zx2)1/2 = (41182 + 21052)1/2 = 4624,8 kp · cm ≈ 4625 kp · cm
MC = [ (- 2350,85)2 + (- 1321,3)2 ]1/2 = 2696,73 kp · cm ≈ 2697 kp · cm
MD = [ (- 6624)2 + (- 1911)2 ]1/2 = 6894,15 kp · cm ≈ 6894 kp · cm
ME = (41182 + 21052)1/2 = 4624,82 kp · cm ≈ 4625 kp · cm
•
Dimensionado del eje a fatiga
Se analizarán las secciones que soportan mayores solicitaciones, que en este caso es la
sección D, según varios tipos de ciclos.
Eje construido con acero F114
σr = 90 kp/mm2
σf = 70 kp/mm2
Sobre la sección D por x = 82,5 cm actúan:
Momento flector: M = 6894 kp · cm
Momento torsor: T = 4717 kp · cm
a) Flexión + torsión constante.
Debido a que el eje gira se trata de un ciclo de flexión alternativo simétrico.
Flexión:
Mmed = 0
Mosc = 6894 kp · cm
63
Torsión:
Tmed = 4717 kp · cm
Tosc = 0
•
Diseño del eje a vida infinita:
Tensión a flexión alternativa útil:
σf AU = Ka · Kb · Ke · (0,45 · σR)
Coeficientes modificativos:
- coeficiente de acabado superficial:
mecanizado o estirado en frío según
tablas (Anexo 4).
Ka = 0,7
- coeficiente de tamaño:
según tablas (Anexo 4) para diámetro
de 45 mm tenemos que:
Kb = 0,725
- coeficiente de entalla:
Ke = 1 / [ 1 + q · (Kt – 1) ]
q: coeficiente de sensibilidad a la
entalla, al no haber entalla q = 0
De este modo obtenemos que:
Ke = 1
El límite de fatiga valdrá:
σf AU = Ka · Kb · Ke · (0,45 · σR)
σf AU = 0,7 · 0,725 · 1 · (0,45 · 90) = 20,55 kp / mm2
64
Momento resistente a flexión y a torsión:
Wf = (π/32) · d3 = (π/32) · 4,53 = 8,946 cm3
Wt = 2 · Wf = (π/16) · d3 = (π/16) · 4,53 = 17,92 cm3
•
Estado tensional.
Flexión:
σmed = Mmed / Wf = 0
σosc = Mosc / Wf = 6894 / 8,946 = 7,71 kg/mm2
Torsión:
τmed = Tmed / Wt = 4717 / 17,892 = 2,64 kg/mm2
τosc = Tosc / Wt = 0
Tensión combinada:
σc = σcombinada = [ σ2 + (3 · τ2) ]1/2
σc med = [ σmed2 + (3 · τmed2) ]1/2 = 4,57 kg/mm2
σc osc = [ σosc2 + (3 · τosc2) ]1/2 = 7,71 kg/mm2
Según la teoría de GOODMANN el coeficiente de seguridad en la sección estudiada
será:
65
Coeficiente de seguridad por GOODMANN:
(σc med / σr) + (σc osc / σf AU) = 1/n
(4,57 / 90) + (7,71 / 20,55) = 1/n
coeficiente de seguridad: n = 2,35
Es un coeficiente de seguridad aceptable. De este modo, se acepta como diámetro válido
d = 45 mm.
b) Flexión + torsión variable.
Flexión:
Mmed = 0
Mosc = 6894 kp · cm
Torsión:
Tmed = 2358,5 kp · cm
Tosc = 2358,5 kp · cm
66
Coeficientes modificativos:
- coeficiente de acabado superficial:
Ka = 0,7
- coeficiente de tamaño:
Kb = 0,7
- coeficiente de entalla:
Kc = 1
Límite de fatiga:
σf AU = Ka · Kb · Ke · (0,45 · σR) = 20,55 kp/mm2
Momento resistente a flexión y a torsión:
Wf = 8,946 cm3
Wt = 17,892 cm3
•
Estado tensional.
Flexión:
σmed = Mmed / Wf = 0
σosc = Mosc / Wf = 6894 / 8,946 = 7,71 kp/mm2
Torsión:
τmed = Tmed / Wt = 2358,5 / 17,892 = 1,32 kp/mm2
τosc = Tosc / Wt = 2358,5 / 17,892 = 1,32 kp/mm2
Tensión combinada:
σc med = [ σmed2 + (3 · τmed2) ]1/2 = 2,286 kg/mm2
σc osc = [ σosc2 + (3 · τosc2) ]1/2 = 8,042 kg/mm2
Coeficiente de seguridad por GOODMANN:
(σc med / σr) + (σc osc / σf AU) = 1/n
(2,286 / 90) + (8,042 / 20,55) = 1/n
coeficiente de seguridad: n = 2,4
67
Es un coeficiente de seguridad aceptable. Entonces, se acepta como diámetro d = 45
mm.
c) Superposición de dos ciclos.
Torsión: un solo ciclo de tensión intermitente pulsatorio.
Flexión:
- considerando que el eje no gira y la carga varía desde cero hasta un
máximo.
- considerando que el eje gira y la carga es constante: ciclo alternativo
simétrico.
Flexión:
Mmed = 3447 kp · cm
Mosc = 10341 kp · cm
Torsión:
Tmed = 2358,5 kp · cm
Tosc = 2358,5 kp · cm
Coeficientes modificativos:
- coeficiente de acabado superficial:
Ka = 0,7
- coeficiente de tamaño:
Kb = 0,725
- coeficiente de entalla:
Kc = 1
Límite de fatiga:
σf AU = Ka · Kb · Ke · (0,45 · σR) = 20,55 kp/mm2
68
Momento resistente a flexión y a torsión:
Wf = 8,946 cm3
Wt = 17,892 cm3
•
Estado tensional.
Flexión:
σmed = Mmed / Wf = 3,853 kp/mm2
σosc = Mosc / Wf = 11,559 kp/mm2
Torsión:
τmed = Tmed / Wt = 1,318 kp/mm2
τosc = Tosc / Wt = 1,318 kp/mm2
Tensión combinada:
σc med = [ σmed2 + (3 · τmed2) ]1/2 = 4,479 kg/mm2
σc osc = [ σosc2 + (3 · τosc2) ]1/2 = 11,872 kg/mm2
Coeficiente de seguridad por GOODMANN:
(σc med / σr) + (σc osc / σf AU) = 1/n
(4,479 / 90) + (11,782 / 20,55) = 1/n
coeficiente de seguridad: n = 1,605
Es un coeficiente de seguridad aceptable. Luego, se acepta como diámetro d = 45 mm.
5.3.2. cálculo en frenada
En este apartado se dimensionará el eje posterior del kart, o lo que es lo mismo, el eje
tractor teniendo en cuenta las solicitaciones que sufre durante la frenada del vehículo.
69
Según cálculos anteriores en el momento de la frenada el reparto de carga en el eje
posterior es de R’’B = 100,1 kp, por lo tanto a cada rueda le tocan:
RA = RF = R’’B / 2 = 50,05 kp
En la siguiente figura se pueden observar todas las solicitaciones que se tendrán en
cuenta por tal de realizar este dimensionado:
70
Plano ZX
RB = - 58,1 kp
RBDD = 0
RDED = 215,7 kp
RE = - 38,5 kp
MB = 1525 kp · cm
MD = - 1495 kp · cm
MP = 15 kp · cm
ME = - 1525 kp · cm
x = 52 cm
MD = 0
AT = (52 · 1525) /2 = 39650 cm2
x = 17,3 cm
71
RD isos + RE isos = 72 kp
∑MD = 0 (sentido horario positivo)
- 72,6 – 1525 + RE isos · 12 = 0
RE isos = - 163,1 kp
RD isos = 91,1 kp
M (x) = 91,1 · x
x=0
MD = 0
x=6
MP = 546,6 kp · cm
M (x’) = 91,1 · x’ + 72 · (x’ – 6) = 163,1 · x’ - 432
x’ = 6
MP = 546,6 kp · cm
x’ = 12
ME = 1525,2 kp · cm
72
RD isos + RE isos = 0
∑MD = 0 (sentido horario positivo)
RE isos · 12 – 1525 = 0
73
RE isos = - 127,1 kp
RD isos = 127,1 kp
AT = 9150 cm2
x = 4 cm
Aplicando el Teorema de los Tres Momentos:
(1525 · 52) + 2 · Mn · 64 + 1525 · 12 = - 6 · 39650 · (17,3 / 52) – 6 · 9150 · (4 / 12)
Mn = - 1525 kp · cm
RB = -29,33 – (1525 / 52) = - 58,7 kp
RBDD = 29,33 – (1525 / 52) = 0
RDED = 127,1 + (1525 / 12 = 254,2 kp
RE = -127,1 + (1525 / 12) = 0
Plano ZX
74
RB = - 58,7 kp
RBDD = 0
RDED = 254,2 kp
RE = 0
MB = 1525 kp · cm
MD = - 1525 kp · cm
MP = 0
ME = 1525 kp · cm
MB = (MB xy2 + MB zx2)1/2 = (15252 + 15252)1/2 = 2156,7 kp · cm ≈ 2157 kp · cm
MD = [ (- 1495)2 + (- 1525)2 ]1/2 = 2135,6 kp · cm ≈ 2136 kp · cm
MP = (152)1/2 = 15 kp · cm
ME = (15252 + 15252)1/2 = 2156,7 kp · cm ≈ 2157 kp · cm
Se analizan las secciones que soportan una mayor solicitación, que en este caso son las
secciones B y E, según diversos tipos de ciclos.
Eje construido con acero F-114:
σr : 90 Kp/mm2
σF : 70 Kp/mm2
Sobre las secciones B y E, en los puntos x = 30,5 cm y x = 94,5 cm, actúan:
Momento Flector:
Mf =2136 cm · Kp
T = 700 cm · Kp
a) Flexión + torsión constante
Debido a que el eje gira, se trata de un ciclo de flexión alternativo simétrico.
Flexión:
Mmed = 0 cm · Kp
Mosc = 2136 cm · Kp
75
Torsión:
Tmed = 700 cm · Kp
Tosc = 0 cm · Kp
•
Diseño del eje para vida infinita
Tensión a flexión alternativa útil:
σfAU = Ka · Kb · Ke · (0,45 · σr)
Coeficientes modificativos:
- Coeficiente de acabado superficial:
Mecanizado o laminado en frío
Ka = 0,7
-
Coeficiente de tamaño:
Según las tablas (Anexo 4) para un diámetro de
45 mm
Obtenemos una Kb = 0,725
- Coeficiente de entalla:
Ke = 1 / [1 + q · (Kt – 1)]
q es el coeficiente de sensibilidad a la entalla,
al no haber entalla, q = 0
Por lo tanto, Ke = 1
Aplicando dichos coeficientes, el límite de fatiga valdrá:
σfAU = Ka · Kb · Ke · (0,45 · σr)
σfAU = 0.7 · 0.725 · 1 · (0,45 · 90)
σfAU = 20,55 Kp/mm2
Momento resistente a la flexión y a la torsión:
Wf = (π/32) · d3 = (π/32) · 4.53
Wf = 8,946 cm3
76
Wt = 2 · Wf = 2 · [(π/32) · d3] = (π/16) · 4.53
Wt = 17,892 cm3
Estado de tensiones:
-
σmed = Mmed / Wf
Flexión:
σmed = 0 Kg/mm2
σosc = Mosc / Wf =2136/8,946
σosc = 2,39 Kg/mm2
-
τmed = Tmed / Wt = 700/17,892
Torsión:
τmed = 0,39 Kg/mm2
τosc = Tosc / Wt
τosc = 0 Kg/mm2
-
Tensión combinada: σc = σcombinada = √ σ2 + 3·τ2
σc med = √ (σmed 2 + 3·τmed 2) = √ (0 + 3·0,392)
σc med = 0,68 Kg/mm2
σc osc = √ (σosc 2 + 3·τosc 2) = √ (2.392 + 0)
σc osc = 2,39 Kg/mm2
Según la teoría de Goodman, el coeficiente de seguridad en la sección será:
σfAU/Cu
σosc
σmed
σF/Cu
σr/Cu
77
Ecuación de la recta de Goodman:
(σc med /σr) + (σc osc /σfAU) = 1/n
(0,68/90) + (2,39/20,55) = 1/n
n=8,07
Coeficiente de seguridad = 8,07
Es un coeficiente aceptable, por lo tanto se acepta d = 45 mm.
b) Flexión variable + Torsión variable
Flexión:
Mmed = 0 cm · Kp
Mosc = 2136 cm · Kp
Torsión:
Tmed = 700 cm · Kp
Tosc = 700 cm · Kp
Coeficientes modificativos:
-
Coeficiente de acabado superficial:
Ka = 0,7
-
Coeficiente de tamaño:
Kb = 0,725
-
Coeficiente de entalla:
Ke = 1
Aplicando dichos coeficientes, el límite de fatiga valdrá:
σfAU = Ka · Kb · Ke · (0,45 · σr)
σfAU = 0.7 · 0.725 · 1 · (0,45 · 90)
σfAU = 20,55 Kp/mm2
Momento resistente a la flexión y a la torsión:
Wf = 8,946 cm3
Wt = 17,892 cm3
78
Estado de tensiones:
-
Flexión:
σmed = Mmed / Wf
σmed = 0 Kg/mm2
σosc = Mosc / Wf =2136/8,946
σosc = 2,39 Kg/mm2
-
Torsión:
τmed = Tmed / Wt = 700/17,892
τmed = 0,39 Kg/mm2
τosc = Tosc / Wt = 700/17,892
τosc = 0,39 Kg/mm2
-
Tensión combinada: σc = σcombinada = √ σ2 + 3·τ2
σc med = √ (σmed 2 + 3·τmed 2) = √ (0 + 3·0,392)
σc med = 0,68 Kg/mm2
σc osc = √ (σosc 2 + 3·τosc 2) = √ (2.392 +3·0,392)
σc osc = 2,48 Kg/mm2
Coeficiente de seguridad utilizando la ecuación de la recta de Goodman:
(σc med /σr) + (σc osc /σfAU) = 1/n
(0,68/90) + (2,48/20,55) = 1/n
n = 7,8
Coeficiente de seguridad = 7,8
Es un coeficiente aceptable, por lo tanto se acepta d = 45 mm.
c) Superposición de dos ciclos
Flexión:
- Considerando que el eje no gira y la carga varía desde cero hasta un
máximo.
79
- Considerando que el eje gira y la carga es constante, ciclo alternativo
simétrico.
Mmed = 1068 cm · Kp
Mosc = 3204 cm · Kp
Torsión:
- Un solo ciclo de tensión intermitente pulsatoria.
Tmed = 350 cm · Kp
Tosc = 350 cm · Kp
Coeficientes modificativos:
-
Coeficiente de acabado superficial:
Ka = 0,7
-
Coeficiente de tamaño:
Kb = 0,725
-
Coeficiente de entalla:
Ke = 1
Aplicando dichos coeficientes, el límite de fatiga valdrá:
σfAU = Ka · Kb · Ke · (0,45 · σr)
σfAU = 0.7 · 0.725 · 1 · (0,45 · 90)
σfAU = 20,55 Kp/mm2
Momento resistente a la flexión y a la torsión:
Wf = 8,946 cm3
Wt = 17,892 cm3
Estado de tensiones:
-
Flexión:
σmed = Mmed / Wf = 1068/8,946
σmed = 1,19 Kg/mm2
σosc = Mosc / Wf =3204/8,946
σosc = 3,58 Kg/mm2
80
-
Torsión:
τmed = Tmed / Wt = 350/17,892
τmed = 0,2 Kg/mm2
τosc = Tosc / Wt = 350/17,892
τosc = 0,2 Kg/mm2
-
Tensión combinada: σc = σcombinada = √ σ2 + 3·τ2
σc med = √ (σmed 2 + 3·τmed 2) = √ (1,192 + 3·0,22)
σc med = 1,24 Kg/mm2
σc osc = √ (σosc 2 + 3·τosc 2) = √ (3,582 +3·0,22)
σc osc = 3,6 Kg/mm2
Coeficiente de seguridad utilizando la ecuación de la recta de Goodman:
(σc med /σr) + (σc osc /σfAU) = 1/n
(1,24/90) + (3,6/20,55) = 1/n
n = 5,3
Coeficiente de seguridad = 5,3
Es un coeficiente aceptable, por lo tanto se acepta d = 45 mm.
5.3.3. cálculo de los rodamientos
Los nombres “cojinete de rozamiento”, o simplemente rodamiento, y “cojinete de
antifricción” se utilizan para describir la clase de soporte de eje en el que la carga
principal se transmite mediante elementos que están en contacto o deslizándose.
Los rodamientos no se rompen por rotura, si no que en un rodamiento sobrecargado se
destruye por los efectos repetitivos que llegan a destruir la estructura molecular del
acero, es decir, rompen por fatiga.
81
Diversos experimentos muestran que dos grupos de cojinetes idénticos probados sobre
cargas diferentes F1 y F2 tendrán unas vidas respectivas L y L’ de acuerdo con la
relación de Palmgreen:
L/L’ = (P’/P)β
L: Número de revoluciones antes de que se produzca la rotura (vida).
P: Carga teórica aplicada
β: Dependerá del tipo de cojinete:
β = 3 (Para cojinetes de bolas)
β = 10/3 (Para cojinetes de rodillos
En los catálogos de fabricantes encontramos la capacidad de carga estática (Co) y la
capacidad de carga dinámica (C). Son capacidades básicas de carga definidas como la
carga radial constante que puede soportar un grupo de cojinetes, aparentemente
idénticos, hasta una duración nominal de un millón de revoluciones del aro interior
(Carga estacionaria y aro interior fijo).
En el caso de que las solicitaciones sean una combinación de carga radial y axial la
ecuación para determinar la capacidad de carga dinámica es:
C = (Feq · fk · fma · fg · fL)/(fn · fT · fH)
Siendo:
Feq = (X · FR) + (Y · FA)
X, Y: Coeficientes de tablas
FR, FA: Fuerza radial y fuerza axial
fk: Factor de esfuerzos dinámicos adicionales
fma: Factor de esfuerzos adicionales del entorno de la propia máquina
fg: Factor de giro; 1 ≤ fg ≤ 1,25; situación de giro del anillo interior fg = 1
fL: Factor de duración; fL = β√(LH /500); LH: duración en horas
82
fn: Factor de velocidad; fn = β√(33,33 /n); n: r.p.m.
fT: Factor de temperatura
fH: Factor de duración de pista
• Lubricación
Estamos ante un caso de lubricación elsatohidrodinámica (EHD), que es el fenómeno
que ocurre cuando se introduce un lubricante entre superficies que están en contacto
rodado puro.
Los objetivos de un lubricante para cojinetes de rodamiento o antifricción se pueden
resumir como los siguiente:
o Formar una película d lubricante entre las superficies deslizantes y
rodantes.
o Ayudar a distribuir y disipar el calor.
o Impedir la corrosión de las superficies del cojinete.
o Proteger las piezas contra la entrada de materias extrañas.
Casi siempre se usan grasas saponificadas con litio (penetración de amasamiento
220÷250; consistencia nº 3; DIN 51 818)
Para lubricar los rodamientos se deberían llenar de grasa los espacios libres del
rodamiento y entre los rodillos.
• Montaje y alojamiento
Se distinguen dos posiciones de rodamientos ajustados uno contra el otro, una posición
en X y otra en O.
83
Un problema de montaje frecuente es aquel en que es necesario un cojinete en cada
extremo de un eje. Generalmente uno de los dos cojinetes tiene la función adicional de
situar o ubicar axialmente el eje.
• Precarga
El objetivo de la precarga es eliminar el juego interno que tienen comúnmente los
cojinetes, con la finalidad de aumentar la duración a fatiga y disminuir la pendiente o
inclinación del eje en el cojinete.
Es aconsejable seguir siempre la recomendaciones de los fabricantes al determinar la
precarga, dado que un valor demasiado alto conduciría a un fallo prematuro.
• Alineamiento
Según se expresa en los catálogos de los fabricantes, el desalineamiento permisible en
los cojinetes de rodillos cónicos y cilíndricos se limita a 0,001 rad. En cojinetes de bolas
el desalineamiento no debe exceder de 0,0087 rad. En el caso de los cojinetes con
ranura profunda el intervalo de desalineación oscila entre 0,0035 y 0,0047 rad.
La vida de un cojinete disminuye significativamente cuando se exceden los limites de
desalineación permisible. Hay, aproximadamente, un 20 % de perdida de vida por cada
0,001 rad de inclinación o pendiente del eje neutro mas allá de los limites permisibles.
• Alojamiento
Para evitar la entrada de polvo y materias extrañas y para retener el lubricante, el
montaje del cojinete incluye un sellado. Los tres principales tipos de sellado son:
o Sellado de fieltro
84
o Sellado comercial
o Sellado de laberinto
Basándonos exclusivamente en nuestro caso, en el que necesitamos guiar o apoyar un
eje en rotación, hacen falta al menos dos rodamientos dispuestos a una cierta distancia
entre si.
Según el caso de aplicación se escoge un rodamiento con apoyo fijo y uno con apoyo
variable, un apoyo con ajuste propio o un apoyo flotante.
• Disposición rodamiento fijo – rodamiento libre
En un eje apoyado por dos rodamientos radiales, debido a las tolerancias de
mecanizado, es muy extraño que las distancias entre los asientos de los apoyos sobre el
eje y las del alojamiento coincidan exactamente. Las distancias también pueden variar
por el calentamiento en servicio. Estas diferencias de distancia se compensan en el
rodamiento libre.
Cuando se trata, como es nuestro caso, de ejes apoyados por mas de dos rodamientos,
solo se coloca un rodamiento fijo para evitar tensiones axiales indebidas
Se coloca una pareja de rodamientos de bolas de contacto angular en la ejecución por
montaje universal con rodamiento fijo, a: disposición en O, b: disposición en X
(FAG26).
En el calculo del dimensionado se examina la seguridad contra la fatiga prematura del
material de las pistas de rodadura y los cuerpos rodantes.
85
La duración L10 según DIN ISO 281 pocas veces indica el tiempo de duración realmente
asequible. El acreditado método de cálculo FAG para la vida asequible considera las
influencias de servicio y del ambiente en el cálculo. El método se guía por la norma
DIN ISO 281 y esta basado en los conocimientos adquiridos a través de investigaciones
sobre la resistencia a la fatiga en rodamientos
• Rodamientos solicitados dinámicamente
Utilizaremos el método normalizado según la DIN ISO 281 para rodamientos
solicitados dinámicamente que parte de la fatiga de material (formación de pittings)
como causa del fallo del rodamiento.
La ecuación que rige la duración es:
L10 = L = (C/P)p [106 revoluciones]
L10: Duración nominal (106 revoluciones)
C: Capacidad de carga dinámica (kN)
P: Carga dinámica equivalente (kN)
p: Exponente de la duración
L10 es la duración nominal en millones de revoluciones adquirida o bien pasado al
menos de un 90% de un lote más o menos grande de rodamientos iguales.
La capacidad de carga dinámica C se indica en unas tablas para cada rodamiento. Una
situación de carga de esta magnitud conduce a una duración L10 de 106 revoluciones.
Al actuar al mismo tiempo una carga radial y una axial, se calcula la carga dinámica
equivalente P. Esta es, en los rodamientos radiales, una carga radial ficticia y en los
rodamientos axiales, una carga axial ficticia, y tiene, respecto a la fatiga, el mismo
efecto que la carga combinada real.
86
P = X · FR + Y · FA (kN)
P: Carga dinámica equivalente (kN)
FR: Carga radial (kN)
FA: Carga axial (kN)
X: Factor radial
Y: Factor axial
C = (Feq · fk · fma · fg · fL)/(fn · fT · fH)
Por lo tanto:
C = (P · fk · fma · fg · fL)/(fn · fT · fH)
Para una duración estimada de 1200 horas, según las tablas (Anexo 4), fL = 1,34
fL = β√(LH /500) = = 3√(1200/500) = 1,34
Para una velocidad media de n = 3375 rpm, según las tablas, fn = 0,25
Si gira el anillo interior fg = 1
fma: 1 ≤ fma ≤ 3. Eje sin choque fma = 1,2
fk: Factor de esfuerzos estáticos (transmisión); 1 ≤ fk ≤ 1,5
fH: Factor de duración de pista; fH = 1
Para nuestro caso escogeremos rodamientos de bolas de contacto angular. En lo que se
refiere al diseño, los rodamientos de este tipo corresponden a una pareja de rodamientos
de bolas de contacto angular en disposición O. El rodamiento puede absorber altas
fuerzas radiales y axiales en los dos sentidos. Los rodamientos de las series 32B y 33B
con tapas de obturación o tapas de protección tienen los dos lados libres de
mantenimiento y posibilitan construcciones sencillas.
87
Según la norma se deben situar dos rodamientos de bolas de contacto angular, con dos
filas DIN 628 volumen 3
Los rodamientos de contacto angular 32B y 33B no tienen ranuras de entrada para las
bolas, por esta razón la capacidad de carga axial es igual en los dos sentidos. Los
rodamientos están llenos de grasa.
Según FAG 171 el ángulo de contacto de las series 32B y 33B es α = 25º.
• Carga dinámica equivalente
La formula para su determinación depende del ángulo de contacto de los rodamientos.
P = FR + 0,92 · FA (kN); para FA/FR ≤ 0,68
P = 0,67 · FR + 1,41 · FR (kN); para FA/FR > 0,68
• Apoyo eje trasero, punto B
o Máxima frenada
Z
-58,1 Kp
X
Y
-58,7 Kp
FR = √ (RBy2 + RBz2)
FR = √(58,12 + 58,72)
FR = 82,6 Kp
88
o Máxima tracción
Z
-138 Kp
X
Y
-73 Kp
FR = √ (RBy2 + RBz2)
FR = √(1382 + 732)
FR = 156,12 Kp
o Curva a tracción máxima
Fc.roda = 33,75 Kp (Fuerza axial en cada rueda)
En total, el eje trasero puede llegar a soportar una fuerza axial de 67,5 Kp debida a la
fuerza centrifuga.
•
Los otros dos apoyos tendrían las siguientes solicitaciones:
Máxima tracción
Apoyo D
Apoyo E
FR = √ (RDy2 + RDz2)
FR = √ (REy2 + REz2)
FR = √(0 + 3792); FR = 379 Kp
FR = √(2092 + 162); FR = 209,6 Kp
89
Máxima frenada
Apoyo D
Apoyo E
FR = √ (RDy2 + RDz2)
FR = √ (REy2 + REz2)
FR = √(215,72 + 254,22); FR = 333,4 Kp
FR = √(38,52 + 0); FR = 38,5 Kp
•
Apoyo B
FR = 156,12 Kp
FA = 0 Kp
FA /FR = 0 < 0,68
P = FR + 0,92 · FA = 156,12 + 0,92 · 0
P = 156,12 Kp = 1,53 kN
C = (P · fk · fma · fg · fL)/(fn · fT · fH)
C = (1,53 · 1,2 · 1,25 · 1 · 1,34)/(0,25 · 1 · 1) = 12,3 kN
C = 12,3 kN
Escogemos un rodamiento FAG serie 3209B
•
Apoyo D
FR = 379 Kp
FA = 0 Kp
FA /FR = 0 < 0,68
P = FR + 0,92 · FA = 579 + 0,92 · 0
P = 579 Kp = 5,68 kN
90
C = (P · fk · fma · fg · fL)/(fn · fT · fH)
C = (5,68 · 1,2 · 1,25 · 1 · 1,34)/(0,25 · 1 · 1) = 45,66 kN
C = 45,66 kN
Escogemos un rodamiento FAG serie 3209B
•
Apoyo E
FR = 209,6 Kp
FA = 33,75 Kp
FA /FR = 33,75/209,6 = 0,16 < 0,68
P = FR + 0,92 · FA = 209,6 + 0,92 · 33,75
P = 240,65 Kp = 2,36 kN
C = (P · fk · fma · fg · fL)/(fn · fT · fH)
C = (2,36 · 1,2 · 1,25 · 1 · 1,34)/(0,25 · 1 · 1) = 18,9 kN
C = 18,9 kN
Escogemos un rodamiento FAG serie 3209B
5.4. SISTEMA DE DIRECCIÓN
5.4.1. principios teóricos
La dirección será del tipo directa mecánica mediante bielitas.
Si se hace girar el volante del vehículo, el tubo de la columna de dirección transmite
este movimiento al mecanismo de dirección. En el mecanismo de dirección el
movimiento de giro se reduce y se transmite en forma de movimiento oscilante de la
91
biela de dirección, a través del varillaje, a las ruedas delanteras que pueden girar en una
u otra dirección de manera que le vehículo pueda ser conducido.
•
Geometría del extremo delantero
Nos referimos a los diferentes ángulos entre las ruedas delanteras, el bastidor y la partes
de fijación. Cada una de estos ángulos es importante ya que si no son correctos, es más
duro el control del vehículo y los pneumáticos se desgastan rápidamente.
•
Angulo de caída
También conocido como ángulo de inclinación. Entendemos por caída la inclinación de
las ruedas respecto la vertical. Cuando la inclinación es hacia fuera, la rueda esta mas
separada de la parte superior y hablaremos de un ángulo de caída positivo. Si por el
contrario, la inclinación es hacia dentro, la caída es negativa.
Así, denominaremos ángulo de caída a la magnitud de la inclinación, medida en grados,
respecto la vertical. Con el vehículo en marcha, un ángulo de caída de valor medio cero,
es el que alarga mas la vida de los pneumáticos.
La finalidad de la caída es dar a las ruedas una ligera inclinación inicial hacia fuera. Con
ello, cuando el vehículo este con el conductor y en marcha, la crac pondrá las ruedas en
posición vertical.
Normalmente se designa mediante la letra γ. En los pneumáticos delanteros el ángulo de
caída es positivo y toma unos valores comprendidos entre 30’ y 1º.
•
Angulo de salida (Inclinación del eje de dirección)
92
Es la magnitud de la inclinación o ángulo hacia dentro que, respecto la vertical, forma el
pivote de dirección o eje de la rotulas. Esta inclinación, denominada salida, favorece la
estabilidad de la dirección, reduce el esfuerzo de dirección y reduce el desgaste de los
pneumáticos. La inclinación del eje de dirección no es ajustable.
Normalmente el ángulo de salida se designa con la letra δ y toma unos valores
comprendidos entre 6º y 7º.
•
Angulo total
El ángulo total o combinado, conocido también como ángulo comprendido, es el ángulo
de caída mas el ángulo de salida. Es importante porque nos determina el punto de
intersección de la rueda y el eje del pivote de dirección. Esto, a la vez, determina si la
rueda tenderá a la convergencia o bien a la divergencia.
•
Angulo de adelantamiento
Además de estar inclinado hacia el centro del coche, el eje de dirección también puede
estar inclinado hacia delante o hacia atrás según la vertical. La inclinación hacia atrás
respecto la vertical se denomina avance positivo. Este avance favorece la estabilidad de
la dirección ya que contribuye a mantener las ruedas orientadas hacia delante en línea
recta. También contribuye a contrarrestar toda la tendencia a no seguir esta dirección.
El ángulo de avance se suele representar con la letra ε y toma unos valores entre 0 y 4º.
•
Concepto de convergencia
Se entiende por convergencia la desviación hacia dentro con que se montan las ruedas
delanteras.
93
Normalmente la convergencia suele ser tan solo una fracción de pulgada, entre 1 y 2
mm. La finalidad de esta es asegurar el paralelismo de las ruedas delanteras durante la
marcha o rodadura, estabilizar la dirección y evitar el patinaje lateral, así como el
excesivo desgaste de los pneumáticos.
•
Divergencia en los virajes
La divergencia en los virajes, denominada también geometría de dirección, se refiere a
la diferencia entre los Angulo formados por cada una de las dos ruedas delanteras con el
bastidor del coche durante los virajes.
Como que la rueda interior gira siguiendo un arco de radio más pequeño que el de la
rueda exterior, cuando el vehículo describe una curva, el eje de la rueda exterior debe
formar un ángulo más agudo con el bastidor del coche, es decir, tiene que divergir un
poco más.
La relación ha de ser tal que la rueda interior en una curva diverja mas que la rueda
exterior. Al rodar sobre una curva las ruedas de un vehículo desarrollan recorridos de
diferente magnitud.
•
Varillaje de dirección
El varillaje de dirección conecta las manguetas con la columna de dirección. Todos los
varillajes han de estar provistos de algún medio para ajustar las longitudes de las barras
de acoplamiento, de manera que se pueda obtener la correcta alienación entre las ruedas
delanteras.
94
Esta alineación da a las ruedas delanteras una ligera convergencia cuando el vehículo
esta parado. A continuación, cuando el vehículo empieza a moverse, esta convergencia
prácticamente desaparece, así como todo juego o deslizamiento en el sistema de
dirección.
En nuestro caso, con tal de ajustar las longitudes de las barras de acoplamiento, se
utilizaran rotulas en los extremos de las varillas de dirección. Una rotula será a derechas
y la otra a izquierdas con tal de que se puedan ajustar bien.
5.4.2. elementos que constituyen el sistema de dirección
•
Volante: ALL KART; ∅ = 31 cm.
•
Columna de dirección: varilla cilíndrica; l = 520 mm; ∅ = 20 mm.
•
Patilla donde van enganchadas las varillas de dirección.
•
Dos varillas de dirección; ∅ = 8 mm; l = 267 mm.
•
Cuatro rotula M8 macho o hembra; dos a derechas y dos a izquierdas
Máximo ángulo que puede describir la rueda estando la dirección al máximo:
A
B
R
E
E
D
O
95
Batalla = 1,035 m
Vía = 0,660 m
tg γ = Batalla/(Vía/2) = 1,035/(0,660/2) = 3,136
γ = 72,316º
DE = R · cosγ = 0,06 · cos 72,316 = 0,0182 m
CD = AB – (2 · DE) = 0,660 – (2 · 0,0182) = 0,6236 m
A
R
B
D
C
(C’A)2 = (AB) 2 + (C’B) 2 – 2 · (AB) · (C’B) · cos α
cos α = [(AB) 2 + (C’B) 2 – (C’A) 2 ] / [2·(AB) ·(C’B)]
cos α = [(0,660) 2 + (0,6236 + 0,069)2 – 0,062] / (2 · 0,660 · (0,6236 + 0,06))
cos α = 0,99663
α = 4,71º
Angulo máximo:
γ – α = 71,316 – 4,706 = 67,61º
A continuación daremos el valor de la diferencia entre las trazas para diferentes valores
del radio de una curva:
96
a
b
O
r
tg α = b/(r – a/2) = 1,035/(r – 0,33)
tg β = b/(r + a/2) = 1,035/(r + 0,33)
r
α
β
λ=α–β
5
12,496
10,989
1,507
10
6,1092
5,722
0,387
20
3,012
2,914
0,098
30
1,998
1,954
0,04
40
1,495
1,470
0,025
50
1,194
1,178
0,016
100
0,595
0,591
0,004
97
5.4.3. cálculo de los elementos del eje delantero
El eje delantero esta sometido a unas solicitaciones que varían continuamente. Para
diseñar sus elementos se estudian tres casos diferentes de funcionamiento del vehículo y
así se escogerán las solicitaciones más críticas.
Los tres casos que se estudiarán son:
-
Vehículo en línea recta a máxima tracción.
-
Vehículo en una curva a máxima tracción
-
Vehículo en línea recta en frenada
a) Vehículo en línea recta a máxima tracción
z
b
Rz
y
a
Ry
Rx
M
c
Fi.di
rdin
x
Fi.rueda
Fr
N
Fr: Fuerza de rodadura; Fr = µr · N
N: Fuerza normal.
M: Fuerza a realizar por la palanca de acoplamiento para vencer las fuerzas que tienden
a hacer virar la rueda.
98
Fi.rueda: Fuerza de inercia asignada a la rueda, mangueta y disco de freno.
Fi.di: Fuerza de inercia asignada al resto de elementos del eje estudiado.
R: Reacción en el punto de unión con el chasis.
Fr = µr · P = 0,025 · 180 = 4,5 Kp
Fr = 44,145 N
N = 45 Kp = 441,45 N
a = 95 mm
b = 50 mm
c = 287 mm
rdin = 114,3 mm
Fi.roda = m · a = 10 · 3,614
Fi.roda = 36,14 N
Fi.di = m · a = 1 · 3,614
Fi.di = 3,614 N
Para calcular la aceleración propulsiva a la velocidad de 90 Km/h:
T = [(2 · ρ)/(rc · rd · D)] · Mm
T: Esfuerzo tangencial en la periferia de las ruedas de tracción.
T = m · ap = (Q/g) · ap
ap = (g/Q) · T = [(2 · ρ · g)/(rc · rd · nm · D · Q)] · Mm (m/s2)
Mm = 716,2 N/ nm
ap = (2 · 716,2 · ρ · g · N)/(rc · rd · D · Q) = (14051,84 · ρ · N)/(rc · rd · D · Q) (m/s2)
ρ: rendimiento de la transmisión. ρ = 0,8
Potencia máxima de 51,2 CV a 8500 rpm
D: Diámetro rueda propulsiva. D = 279,4 mm
rc: Relación de la caja de cambios. 6ª velocidad Æ 19/24
99
rd: Relación de la transmisión. rd = 13/26
Q: Peso total. Q = 180 Kp
ap = (14051,84 · 0,85 · 51,2)/(19/24·13/26 · 8500 · 0,2794 · 180)
ap. max = 3,614 m/s2
Analizaremos las diferentes solicitaciones del caso realizando un equilibrio dinámico de
todas las fuerzas. Para ello desglosaremos el estudio según diversos planos de trabajo
para que se nos reduzcan las incógnitas.
Plano xy
Fr = 44,145 N
x
A
Rx
B
50
Ry
C
M
Fi.rueda = 36,14 N
Fi.di = 3,614 N
y
95
ΣMB = 0 (sentido horario positivo)
(44,145 · 0,095) – (36,14 · 0,095) – (M · 0,05) = 0
M = – 15,21 Kp
Fr – Fi. rueda – Fi. di – Ry = 0
44,145 – 36,14 – 3,614 – Ry = 0
Ry = 4,4 N
Rx = 15,21 N
100
Plano zx
z
Rz
x
Rx
A
M
B=C
O
N
ΣMO = 0 (sentido horario positivo)
– (Rz · 0,095) – (15,21 · 0,0143) + (15,2 · 0,0143) = 0
Rz = 16,47 N
b) Vehículo en una curva a tracción máxima
N = 441,45 N
Fr = 44,145 N
Fi. rueda = 36,14 N
101
Fi = 3,614 N
Fc = 331,1 N
Plano xy
ΣMB = 0 (sentido horario positivo)
(Ff · 0,095) – (Fi. rueda · 0,095) – (M · 0,05) = 0
M = (Ff – Fi. rueda) · 0,095/ 0,05
M = – 155,24 N
Ff – Fi. rueda – Ry – Fi = 0
331,1 – 36,14 – Ry – 3,614 = 0
Ry = 4,4 N
Rx = 315,9 N
ΣMO = 0 (sentido horario positivo)
– (Rz · 0,095) – (Rx · 0,0143) + (M · 0,0143) = 0
Rz = 398,4 N
102
c) Vehículo en frenada en trayectoria recta
N = 783,819 N
Fr = 44,145 N
Fi. rueda = 36,14 N
Fi. di = 3,614 N
Ff = 391,91 N
Plano xy
103
ΣMB = 0 (sentido horario positivo)
(Ff · 0,095) – (Fi. rueda · 0,095) – (M · 0,05) = 0
M = (Ff – Fi. rueda) · 0,095/ 0,05
M = – 675,96 N
Ff – Fi. rueda – Ry – Fi = 0
391,91 – 36,14 – Ry – 3,614 = 0
Ry = 352,16 N
Rx = 675,96 N
Plano zx
ΣMO = 0 (sentido horario positivo)
– (Rz · 0,095) – (Rx · 0,0143) + (M · 0,0143) = 0
– (Rz · 0,095) – (675,96 · 0,0143) + (675,96 · 0,0143) = 0
Rz = 0 N
104
•
Cálculo de los espárragos de unión al chasis
Su diseño se basa en el posible fallo por corte.
Lo estudiaremos según los tres casos también estudiados en el apartado anterior.
Caso a
Formula para determinar el diámetro mínimo
C · τ = 0,6 · σf · Cu
τ: (4/3 Fcorte)/área
Coeficiente de divergencia de carga; C = 2
Coeficiente de seguridad; Cu = 2
Acero al carbono; σf = 90 Kp/mm2
Rx = 15,21 N
Ry = 4,4 N
Rz = 16,47 N
Fuerza de corte
Fcorte = √(Rx2 + Ry2 + Rz2)
Fcorte = √(15,212 + 4,42 + 16,472)
Fcorte = 22,85 N
Aplicando la ecuación para la determinación del mínimo diámetro
2 · τ = 0,6 · 90 · 2
τ = 54 N/mm2
54 = (4/3 · 22,85)/área
área = 0,56 mm2
area = π · (d2/4)
d = 1 mm
105
Caso b
Utilizaremos la misma formula para determinar el diámetro mínimo
C · τ = 0,6 · σf · Cu
τ: (4/3 Fcorte)/área
Coeficiente de divergencia de carga; C = 2
Coeficiente de seguridad; Cu = 2
Acero al carbono; σf = 90 Kp/mm2
Rx = 315,9 N
Ry = 4,4 N
Rz = 398,4 N
Fuerza de corte
Fcorte = √(Rx2 + Ry2 + Rz2)
Fcorte = √(315,92 + 4,42 + 398,42)
Fcorte = 508,46 N
Aplicando la ecuación para la determinación del minimo diámetro
2 · τ = 0,6 · 90 · 2
τ = 54 N/mm2
54 = (4/3 · 508,46)/área
área = 12,55 mm2
area = π · (d2/4)
d = 4 mm
106
Caso C
Nuevamente utilizamos la formula para el diámetro mínimo
C · τ = 0,6 · σf · Cu
τ: (4/3 Fcorte)/área
Coeficiente de divergencia de carga; C = 2
Coeficiente de seguridad; Cu = 2
Acero al carbono; σf = 90 Kp/mm2
Rx = 675,96 N
Ry = 352,16 N
Rz = 0 N
Fuerza de corte
Fcorte = √(Rx2 + Ry2 + Rz2)
Fcorte = √(675,962 + 352,162 + 0)
Fcorte = 716,19 N
Aplicando la ecuación para la determinación del minimo diámetro
2 · τ = 0,6 · 90 · 2
τ = 54 N/mm2
54 = (4/3 · 762,19)/área
área = 18,82 mm2
area = π · (d2/4)
d = 4,9 mm
Los valores obtenidos en los tres casos anteriormente descritos justifican la adopción
del espárrago siguiente:
Tornillo de ajuste hexagonal M10 x 80 Mu DIN 7968-5.6
107
5.5. SISTEMA DE FRENADO
5.5.1. principios teóricos
El efecto de frenado consiste en absorber la energía cinética que posee el coche debido a
su desplazamiento transformándola en energía calorífica debido al rozamiento de los
elementos de frenado (pastillas de freno, discos, etc.).
Si al vehículo se le aplica una fuerza igual y de sentido contrario a la fuerza que provoca
el movimiento se origina en el una deceleración (δ) o aceleración negativa que llega a
anular el movimiento absorbiendo la energía cinética.
El esfuerzo máximo que una rueda puede ejercer sobre el terreno es la fuerza de
adherencia (Fadh) que, según la leyes del rozamiento es igual a la fuerza con que la rueda
pisa el terreno
multiplicado por el cociente de adherencia entre el suelo y el
pneumático. De esta forma tenemos:
Fadh = peso · µ
La fuerza de adherencia vale lo mismo que la fuerza de impulso que induce al
desplazamiento del vehículo. Así se consigue el par de rotación de la rueda.
108
Si queremos que no haya un bloqueo de la rueda en el momento de aplicar la fuerza de
frenado se ha de cumplir:
Ffrenado ≤ Fadh
Esta condición indica que la fuerza de frenado tiene un máximo que si es superado
producirá un bloqueo de las ruedas. Si esto llega a suceder, al no haber rozamiento entre
los elementos de frenado, el vehículo seguirá en movimiento hasta que la energía
cinética sea eliminada por el efecto del rozamiento entre el pneumático y el suelo.
Como se ha comentado anteriormente, al aplicar una fuerza igual y de sentido contrario
a la fuerza inductora del movimiento, aparecerá una deceleración, y por lo tanto, una
fuerza de inercia que toma un valor:
Fi = m · δ
Ffrenado ≤ Fadh
De aquí deducimos:
Finercia ≤ Fadh
δ≤µ·g
Esta expresión nos indica que la máxima deceleración que se puede aplicar es 9,81 m/s2
en el caso extremo de tener un coeficiente de adherencia µ = 1. Por lo tanto, según el
tipo de superficie sobre el que circule el vehículo tendrá unas deceleraciones máximas
asociadas a los diferentes terrenos.
La fuerza de frenado máximo total del vehículo, según si la superficie es asfalto seco o
con hielo tomará unos valores extremos:
109
Asfalto seco: µ = 0,75
Ffrenada max = m · g · µ = 180 · 9.81 · 0,75
Ffrenada max = 1324,35 N
Asfalto con hielo: µ = 0,1
Ffrenada max = m · g · µ = 180 · 9.81 · 0,1
Ffrenada max = 176,58 N
5.5.2. hipótesis de cálculo
Si basásemos los cálculos con un coeficiente de adherencia correspondiente, por
ejemplo a una carretera con hielo o bien alquitranada y grasienta, obtendríamos unas
fuerzas de frenado muy bajas. De esta manera, cuando el vehículo circulase por terrenos
con un coeficiente de adherencia más elevado casi no frenaría.
Por lo tanto, como base para el cálculo, adoptaremos un valor de coeficiente mayor,
µ = 0,5. Así, cuando el vehículo se desplace por un suelo mas deslizante será necesaria
una fuerza de frenado menor.
Para mostrar un ejemplo de lo anteriormente citado, se supone que el vehículo circula
sobre una superficie con un coeficiente de adherencia µ = 0,2, de esta manera se estaría
utilizando :
Para µ = 0,5
Ff.max = 90 Kp
Para µ = 0,2
Ff.max = 36 Kp
% de frenado utilizada = (36/90) · 100 = 40 %
Es decir, sobre carretera mojada o alquitranada se podría utilizar una fuerza de frenado
correspondiente al 40 % de la disponible.
110
Pero, por lo que se refiere al diseño de los frenos, este tipo de vehículos no exige como
condición indispensable el hecho de no superar la fuerza de frenado máxima ya que su
técnica de conducción se basa en utilizar el bloqueo de las ruedas con el consecuente
derrape de las ruedas con tal de realizar a mayor velocidad los virajes.
Por lo tanto, para una µ = 0,5, la deceleración máxima que tendremos será:
δ≤µ·g
δ = 9,81 · 0,5 = 4,905 m/s2
δ = 4,905 m/s2 ≈ 5 m/s2
•
Fuerzas de frenado
Calculamos la fuerza de frenado en cada eje aplicando la ley del rozamiento:
Frozamiento = µ · peso
Eje delantero:
FRA = µ · R’’A = 0,5 · 79,9
FRA = 39,95 Kp
Eje trasero:
FRB = µ · R’’B = 0,5 · 100,1
FRA = 50,05 Kp
Según la normativa incorporaremos dos frenos de disco en cada rueda delantera y un
freno de disco en el eje trasero.
5.5.3. circuito hidráulico
En nuestro caso utilizaremos frenos de tipo hidráulico que constarán de un pedal de
freno, un cilindro principal en tándem, un sistema de conductos, los cilindros de rueda y
los frenos en las ruedas.
111
Por razones de seguridad y exigencias de la CIK, la instalación será de doble circuito.
Así, en caso de que falle uno de los circuitos de frenado el vehículo podrá frenar con el
otro.
El efecto de los frenos hidráulicos se basa en el principio de Pascal que dice que la
presión ejercida en un punto de un fluido cerrado se transmite con la misma intensidad
en todos los sentidos
De esta manera en todos los cilindros de rueda nos actuara la misma presión hidráulica.
En un sistema hidráulico, la relación de fuerzas corresponde a la relación de las áreas de
los émbolos, es decir, sobre la mayor área aparece la mayor fuerza. Las carreras de los
émbolos son inversamente proporcionales a las fuerzas. Así obtenemos:
F1/ F2 = A1/ A2
•
Distribución del circuito de frenado
En nuestra instalación de freno de doble circuito el eje delantero y el trasero forman un
circuito de freno independiente.
•
Cilindro de rueda
En el cilindro de rueda, la presión producida en el cilindro principal acciona el embolo y
produce la fuerza tensora para apretar las zapatas de freno.
Los cilindros de rueda van sujetos al soporte de los frenos, escudo del freno. Los
émbolos de los cilindros de rueda cierran mediante retenes de goma. Unas fundas
guardapolvo impiden la entrada de suciedad.
112
•
Frenos sobre las ruedas
Como frenos sobre las ruedas se utilizarán los de fricción en forma de disco. Serán
frenos de disco parciales con pinza de freno de asiento fijo que contiene don cilindros
de frenado
Aunque en los frenos de disco las temperaturas que se producen localmente son más
altas que en los frenos de tambor, la menor superficie del forro y la mayor fuerza de
apriete hace que los frenos de disco tengan menor fading que los frenos de tambor, ya
que el aire pasa por los dos costados y por el interior del disco, al ser discos ventilados.
Por efecto de la fuerza centrifuga se produce una buena auto limpieza y los restos de la
abrasión y de polvo son expulsados al exterior.
Los discos de freno serán de fundición de hierro con ventilación interior. Dispondrán de
canales de ventilación colocados radialmente y de forma que al girar hagan de
ventilador. Se consigue así que las temperaturas sean más bajas al frenar y que, después
de la frenada, el enfriamiento sea más rápido.
Los forros de freno están formados por un soporte de acero y por el forro propiamente
dicho que sujeto mediante un adhesivo especial. Se pueden calentar hasta 750ºC y hasta
950ºC durante un breve tiempo.
•
Tubuladura, manguitos y líquidos para la instalación de los frenos hidráulicos.
Las diferentes partes de la instalación de frenos hidráulicos se unirán mediante tubos.
Según la norma serán tubos de acero sin costura con sus superficies interna y externa
desoxidadas, pulidas y limpias.
113
Se utilizaran tubos con diámetro exterior de 4,75 mm, 6 mm, 8 mm o 10 mm.
Los manguitos cubrirán los tramos entre la tubuladura fija y las partes del vehículo con
movimiento relativo a la tubuladura.
Al liquido de freno se le exigen unas propiedades especificas que están fijadas por las
especificaciones americanas DOT 3 y DOT 4.
5.5.4. Cálculo de los elementos que constituyen el sistema de
frenado
Primero de todo se describirán todos los elementos que forman el sistema de frenado,
tanto el delantero como el trasero, para posteriormente utilizar estos datos para el
dimensionado de los diversos componentes.
•
Sistema de freno delantero
a) Rueda delantera
Pneumático:
HG3 10 x 4,5-5
Diámetro de la rueda:
Radio de la rueda:
Drueda = 254 mm
Rrueda = 127 mm
Radio dinámico:
Rdin = 0,9 · Rrueda = 114,3 mm
Para el cálculo de los diversos elementos, así como para el cálculo de la fuerza del
embolo, se utilizará el radio dinámico de la rueda.
b) Discos delanteros
Discos de freno DRACKART
Discos flotantes autoventilados y perforados
114
Diámetro exterior:
De = 89 mm
Diámetro interior:
Di = 52 mm
Grosor:
e = 3,2 mm
c) Pastillas de freno
Coeficiente de rozamiento: Adoptaremos un ferodo de la serie F
0,351 < µf < 0,45
Para los cálculos utilizaremos un coeficiente µf = 0,4
Ancho de la pastilla:
b = 6mm
Al disco los abrazan los forros del freno por ambos lados. Así, para calcular la fuerza
que ha de realizar el embolo, Femb, se ha de plantear una ecuación de equilibrio entre el
momento de la fuerza de frenado y la fuerza del embolo, partiendo de la ecuación
mostrada anteriormente:
FR · Rdin = 2 · Ff · Rfr
Sabemos que:
Ff = µf · Femb
115
Femb: Fuerza ejercida por el émbolo
µf: Coeficiente de rozamiento entre los ferodos y la superficie del disco
Sustituyendo nos queda:
FR · Rdin = 2 · µf · Femb · Rfr
Femb = (FR · Rdin)/(2 · µf · Rfr)
Femb = (40 · 0,1143)/(2 · 0,4 · 0,069)
Femb = 82,826 Kp
•
Sistema de freno trasero
a) Rueda trasera
Pneumático:
HG3 11 x 7,1-5
Diámetro de la rueda:
Drueda = 279,4 mm
Radio de la rueda:
Rrueda = 139,7 mm
Radio dinámico:
Rdin = 0,9 · Rrueda = 125,73 mm
Para el cálculo de los diversos elementos, así como para el cálculo de la fuerza del
embolo, se utilizará el radio dinámico de la rueda.
b) Disco trasero
Discos de freno DRACKART
Discos flotantes autoventilados y perforados
Diámetro exterior:
De = 208 mm
Diámetro interior:
Di = 134 mm
Grosor:
e = 12,2 mm
116
c) Pastillas de freno
Coeficiente de rozamiento: Adoptaremos un ferodo de la serie F
0,351 < µf < 0,45
Para los cálculos utilizaremos un coeficiente µf = 0,4
Ancho de la pastilla:
b = 6mm
La fuerza de rozamiento que aparece entre el ferodo y el disco se considera aplicada en
el centro de la pastilla de freno. Así tendremos que:
Rfr: Punto de aplicación de la fuerza de frenado.
R1: Radio interior del ferodo
R2: Radio exterior del ferodo que coincide con el radio exterior del disco
Rfr = (R1 + R2)/ 2
Rfr = (69,5 + 104)/2 = 86,75 mm
Para calcular la fuerza de aplicación en el freno trasero aplicaremos la misma formula
deducida en el caso de los frenos delanteros:
Femb = (FR · Rdin)/(2 · µf · Rfr)
Femb = (50,05 · 0,12573)/(2 · 0,4 · 0,08675)
Femb = 90,41 Kp
117
•
Diseño del circuito de frenado
l: Longitud del punto de fijación del pedal al vástago del cilindro maestro; l = 50 mm
L: Longitud total del pedal de freno; L = 165 mm
Fp: Fuerza aplicada sobre el pedal.
Fcil.maestro: Esfuerzo sobre el vástago que aprieta el cilindro.
Scil.maestro: Sección en cm2 del pistón del cilindro maestro. S = π · r2 = π · 12 = π
Dcil.maestro: Diámetro del pistón del cilindro maestro; Dcil.maestro = 20 mm
Femb1: Fuerza del embolo en los frenos delanteros.
Femb2: Fuerza del embolo en los frenos traseros.
Semb1: Superficie del embolo en los frenos delanteros.
Semb2: Superficie del embolo en los frenos traseros.
118
•
Cálculo de los esfuerzos que se producen en el circuito hidráulico.
Sobre el pedal de freno el piloto puede aplicar una fuerza máxima estimada de
Fp = 40 kp.
La relación de palanca del pedal de freno es:
rp = L/l
rp = 165/50
rp = 3,3
La fuerza transmitida al vástago del cilindro maestro será:
Fcil.maestro = Fp · rp
Fcil.maestro = 40 · 3,3
Fcil.maestro = 132 Kp
El liquido en el circuito hidráulico tendrá una presión de:
P = Fcil.maestro / Scil.maestro
P = 132/π
P = 42,02 bar
Esta presión, basándonos en el principio de Pascal, se mantendrá constante en todos los
puntos del circuito hidráulico.
•
Fuerza de los émbolos sobre los discos de freno
La presión hidráulica de todo el circuito de frenado actúa sobre la cara de los pistones
que están fijados en las pinzas provocando una fuerza sobre la superficie del disco.
Femb = P · Semb
Semb = Pemb/P
119
a) Frenos delanteros
Semb1 = Femb1/P
Femb1 = 82,826 Kp
Semb1 = 82,826/42,02
Semb1 = 1,97 cm2
Semb1 = π · Demb12/4
Demb1 = 15,84 mm
Por lo tanto dispondremos de dos pistones de 16 mm de diámetro para cada pinza del
freno delantero.
b) Freno trasero
Semb2 = Femb2/P
Femb2 = 90,41 Kp
Semb2 = 90,41/42,02
Semb2 = 2,15 cm2
Semb2 = π · Demb22/4
Demb1 = 16,55 mm
Se adopta un pistón de 17 mm de diámetro para la pinza trasera.
•
Cálculo de la carrera del pistón en cada embolo de la pinza de freno
El cilindro maestro tándem consta de dos pistones, ya que se tiene un doble circuito de
frenado. Cada piston tiene una carrera de Lc1 = Lc2 = 5 mm.
120
El volumen que desplace los émbolos de las pinzas ha de ser el mismo que el volumen
que desplace la bomba, tanto para el circuito trasero como el delantero.
Así tendremos que:
Volumen desplazado por las pinzas = Volumen desplazado por el cilindro maestro
Para el circuito de frenos delantero tenemos que:
LD1 = (Scil.maestro · Lc1)/(4 · Semb1)
LD1 = (314,16 · 5)/(4 · 197)
LD1 = 1,99 mm
Para el circuito de frenos trasero tenemos que:
LD2 = (Scil.maestro · Lc2)/(2 · Semb2)
LD1 = (314,16 · 5)/(2 · 215)
LD1 = 3,65 mm
•
Cálculo de la superficie de la pastilla. Balance térmico.
Los frenos deberán transformar la energía cinética del vehículo en energía calorífica.
Pasaremos a estudiar esta cuestión mediante un balance térmico.
Con tal de efectuar este balance, debemos establecer una relación entre la energía
cinética que tiene el vehículo cuando se mueve y la fuerza de apoyo de la rueda. Por
esta razón se determina el momento que genera la fuerza de retardo respecto el eje de la
rueda. Entonces la fuerza de retardo en cada rueda valdrá la mitad del valor que se hay
determinado para el eje.
Comparamos la energía cinética del vehículo con los momentos de la fuerzas verticales
respecto del eje de la rueda debido a que el trabajo es el producto de una fuerza por un
121
desplazamiento, espacio, y el momento de una fuerza se puede asimilar al mismo tipo
de producto.
La energía cinética que se disipará por el sistema de frenado será proporcional al
momento generado en cada rueda por las fuerzas de retardo. Si repartimos la energía
cinética disipada proporcionalmente al momento de frenado de cada rueda, se puede
calcular la superficie del forro contra el disco de freno en función de la energía por
unidad de superficie que puede disipar el material del que esta fabricado el forro del
freno.
La fuerza que realiza el bombín de freno que apreta el elemento rozado contra el disco,
depende del coeficiente de rozamiento entre estos dos, pudiendo llegar a valer cero
cuando se llegan a temperaturas superiores a 800ºC en la superficie del forro. Estas
temperaturas pueden llegar a modificar la estructura del material, fenómeno conocido
como fading. El fading consiste en la acumulación de material del forro sobre los discos
por sobrecalentamiento de la superficie del forro con una consecuente perdida de
efectividad.
Para encontrar la potencia que han de soportar los forros de los frenos, calcularemos
primero la energía cinética del vehículo.
Ec = ½ · m · v2
Para después calcular el tiempo de frenada.
tfrenada = v/(9,81 · µ)
Utilizaremos el radio dinámico de las ruedas para calcular los momentos de las fuerzas
de retardo. La fuerza de retardo es horizontal y la provoca el pneumático sobre el suelo.
Obtendremos así el momento total en cada eje.
122
Suponiendo que el momento total de los dos ejes es igual a la energía cinética del
vehículo, se ha de distribuir esta energía cinética de forma proporcional al momento de
la fuerza de retardo correspondiente a cada rueda.
La energía cinética que habrá de disipar el freno en cada rueda dividida por el tiempo de
frenado nos dará la potencia que habrán de soportar lo forros. Con las características del
material del forro de freno, dadas por el fabricante, se calculará la potencia que son
capaces de disipar por unidad de superficie. Para un forro estándar este valor esta
comprendido entre 1,2 y 1,3 kW/cm2. Así podemos encontrar la superficie del forro
correspondiente.
•
Aplicación. Cálculo de las superficies de los forros.
Como ya sea ha dicho anteriormente, los forros soportan una potencia calorífica
comprendida entre 1, 2 y 1,3 KW/cm2.
Esfuerzos de frenado:
Delantero: FR1 = 40 kp
Trasero: FR2 = 50,05 kp
Radios dinámicos:
Rdin1 = 11,43 cm
Rdin2 = 12,57 cm
Momento de frenado:
Meje del. = 40 · 0,1143
Meje del. = 4,572 kp · m
Meje tras. = 50,1 · 0,1257
123
Meje tras. = 6,298 kp · m
MTOTAL = Meje del. + Meje tras.
MTOTAL = 10,87 kp · m
•
Energía cinética del vehículo
Suponemos que circula a una velocidad máxima de 100 Km/h que seria la velocidad
máxima teórica que podría alcanzar el kart.
100 km/h = 27,778 m/s
Ec = ½ · m · v2
Ec = ½ · 180 · 27,7782
Ec = 69445,56 kp · m
Se repartirá la energía cinética de manera proporcional al momento del eje delantero.
Así la energía la energía a transformar en calor por los frenos de las dos ruedas
delanteras será:
E = (69445,56 · 4,572)/(10,87)
E = 29209,3 kp · m
El tiempo de frenado lo calcularemos mediante la expresión:
tf = v/δ
δ = g · µ = 9,81 · 0,5
δ = 4,905 m/s2
tf = 27,778/4,905
tf = 5,663 s
Conociendo la energía y el tiempo de frenado se calculará la potencia que han de disipar
los frenos delanteros. Esta potencia es el trabajo utilizado por unidad de tiempo, la
124
mitad de esta potencia corresponde al freno de una rueda delantera, debido a que se ha
calculado la fuerza de retardo por el eje, no ocurriendo lo mismo en el eje trasero, donde
solo hay un disco de freno.
W = 29209,3/(2 · 5,663)
W = 2578,96 kp · m/s
Potencia = 2578,96 · 9,81
Potencia = 25299,6 w ≡ 25,3 kW
Superficie total de los forros = 25,3 KW/1,25 kW/cm2
Superficie de un forro: S = 20,24 cm2
Longitud de pastilla: L = S1forro/b
b: anchura de la pastilla. b = 22 mm
L = 20,24/22
L = 9,2 cm
Aplicaremos el mismo procedimiento de cálculo para el eje trasero.
La energía la energía a transformar en calor por los frenos de las dos ruedas delanteras
será:
E = (69445,56 · 6,298)/(10,87
E = 40236,259 kp · m
El tiempo de frenado lo calcularemos mediante la expresión:
tf = v/δ
δ = g · µ = 9,81 · 0,5
δ = 4,905 m/s2
125
tf = 27,778/4,905
tf = 5,663 s
Potencia a disipar por los frenos:
W = 40236,259/(2 · 5,663)
W = 7105,11 kp · m/s
Potencia = 7105,11 · 9,81
Potencia = 69701,13 w ≡ 69,7 kW
Superficie total de los forros = 69,7 KW/1,25 kW/cm2
Superficie de un forro: S = 55,76 cm2
Longitud de pastilla: L = S1forro/b
b: anchura de la pastilla. b = 40 mm
L = 55,76/40
L = 13,94 cm
126
6. MANTENIMIENTO
-
Cada 2 horas de uso, lubricar un poco las siguientes piezas: puntos de freno,
pedales, ejes, piñón y puntos del volante. Usar aceite SAE 30, aconsejado por
Temcuseh.
-
Debe cambiar el aceite en el cárter del motor después de las dos primeras horas
de uso de su motor nuevo, y después de cada 25 horas de empleo a partir de
entonces.
-
Aunque el Convertidor de par haya sido diseñado para durar muchas horas, la
limpieza periódica y la lubricación es necesaria para la vida óptima y el
funcionamiento. Los principios de lubricación y mantenimiento pueden venir
dados por el fabricante, como los rodamientos (Anexo 3).
-
Para aumentar la vida de la cadena, lubricar con aceite de grafito en spray.
-
Es necesario apretar la tuerca de los ejes justo lo necesario para que la rueda gire
libremente sobre él. Si la rueda no gira libremente la tuerca debe ser aflojada.
-
Después de las dos primeras horas de uso, compruebe el ajuste de cadena y
reajústelo si lo cree necesario. Afloje los tornillos que sujetan el motor y deslice
el motor hacia atrás para apretar la cadena nuevamente.
Para no usar el kart durante mucho tiempo:
-
Quitar gasolina del tanque con el motor ya frío y absorbiéndolo. Dejar seco el
carburador dejando apagado el motor.
-
Quitar la bujía y echarle por el hueco unas gotas de aceite al cilindro
y remover despacio el pistón para repartir el aceite y volver a poner la bujía.
127
-
La gasolina almacenada durante mucho tiempo afecta al rendimiento y dificulta
el arranque.
-
La recarga normal de la batería es aconsejable si está parada mucho tiempo.
-
No agotar el combustible con el motor en marcha.
-
No use gasolina que haya tenido guardada excesivo tiempo o piense que haya
podido perder sus propiedades porque esto afectara al rendimiento del kart.
-
La Batería puede generar gases explosivos. Durante el empleo del kart mantenga
cigarrillos, o cualquier producto inflamable lejos del vehículo.
-
Al poner el vehículo nuevamente en marcha, haga una inspección
del mismo.