Para reforzar y ayudarte a comprender de una forma más... propongo los siguientes aspectos

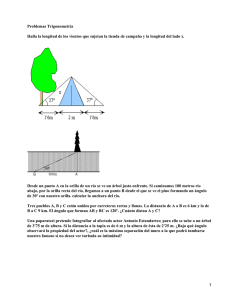
Para reforzar y ayudarte a comprender de una forma más eficaz la temática del segundo período te
propongo los siguientes aspectos
COMPETENCIA: SOLUCIÓN DE PROBLEMAS
1. En los siguientes ejercicios los lados de un triángulo rectángulo se representan con las letras a, b y c,
siendo siempre a la hipotenusa. Los lados del triángulo se representan con las letras A, B y C, siendo
siempre A el ángulo recto, B el ángulo opuesto a b y C el ángulo opuesto a c. Usando exclusivamente
la definición de las razones trigonométricas involucradas en cada caso, calcula el lado que se pide:
a) a = 40 m; B = 30º.
Halla b.
b) a = 40 cm; B = 30º.
Halla c.
c) a = 12 dm; C = 60º.
Halla b.
d) a = 12 Hm; C = 60º. Halla c.
e) b = 20 m; B = 30º.
Halla a.
f) b = 20 mm; B = 45º. Halla c.
g) c = 20 m; B = 30º.
Halla a.
h) b = 20 Km; C = 45º. Halla a
2. Halla los valores de las 5 razones trigonométricas que faltan en cada caso :
Si CosA = 3/5
Si Tan B = 5/2
Si Sec C = 5/6
3.
Una escalera de 14 m de longitud, llega justamente hasta la parte superior de un muro. Si la
escalera forma un ángulo de 60° con el muro, hállese la altura y la distancia a él del pie de la
escalera.
Desde la cúspide de un monumento de 50 m de alto, el ángulo de depresión a un automóvil es de
30º. Calcula la distancia del automóvil al pie del monumento.
4.
Dos senderos de un jardín miden cada uno 18 m y se cruzan formando un ángulo de 60º.
Determina la distancia entre sus extremos.
5.
Determina el perímetro de un triángulo isósceles si su base mide 40 cm y los ángulos que
forman los lados iguales con la base miden 23° cada uno.
6. Una persona observa un árbol a 4m de distancia con un ángulo de elevación de 30º . ¿Cuál es la
altura del árbol?
7. Alex y Víctor están separados por una distancia de 170 m. Cada uno divisa una cometa intermedia
entre ellos. Alex ve la cometa con un ángulo de elevación de 45° y Víctor con un ángulo de 30°. ¿A
qué altura del piso se encuentra la cometa?
8. Calcula la distancia a que se encuentra un observador, cuando el ángulo de elevación de la
cúspide de un monumento de 50 m de altura es de 30º
9. Una escalera de 13,5m de longitud, llega justamente hasta la parte superior de un muro. Si la
escalera forma un ángulo de 60° con el muro, halla la altura y la distancia al del pie de la escalera.
Teoremas del Seno y Coseno
1. Un piloto de vuelo recorre 300 km de Bogotá a Cali, gira el avión 55ª para dirigirse a Cartagena. Si
sabe que entre Cali, Cartagena y Bogotá se forma un ángulo de 22ª. Determina la distancia que
hay de Bogotá a Cartagena?
2. Dos piedras A y B se encuentran a la orilla de una playa a una distancia de 2 km,
y una boya en un punto C. Si la piedra A mide A igual a 79ª y el que está en B
mide un ángulo igual a 43ª, ¿ a qué distancia está la boya de la costa?
3. La diagonal mayor de un paralelogramo mide 35 cm y forma ángulos de 25º y 32º con
los lados. Determina la longitud de los lados del paralelogramo
4. Un carpintero quiere construir una mesa triangular de tal forma que un lado mida 2 m,
otro 1,5 m y el ángulo opuesto al primero debe ser 40ª. Halla el resto de las medidas para
que el carpintero pueda construirla
5. Dos senderos de un jardín miden cada uno 23m y se cruzan formando un ángulo de 43º.
Determina la distancia entre sus extremos y el área ocupada por el jardín
6. Un arquitecto está diseñando el plano de un parque, que será de forma triangular y cuyos lados
serán de 12, 9 y 7 m respectivamente. ¿Cuáles serán los valores de los ángulos en el plano?
COMPETENCIA: RAZONAMIENTO
1. Dentro del paréntesis escribe el signo que tiene la función que se indica:
a. Sen 205
d. Cot637
(
)
(
b. Cos455
)
(
e. Csc321 (
)
c. tan710 (
)
f. Sec238 (
)
)
2. Considera el ángulo θ = - 930 en posición normal. Escribe el valor de verdad de cada proposición.
Argumenta cada respuesta.
a. (
) 5π/6 es su ángulo de referencia
b. (
) θ está ubicado en el segundo cuadrante
c. (
) Cscθ=2
d. (
) Tanθ≤ Senθ
e. (
) θ es coterminal con un ángulo de7π/3
f. (
) Cscθ≤ Secθ
3. Calcula el valor exacto de cada función:
a. sen (-135)
b. Cos1140
c, Sec (1020)
d. Tan1050
4. Encuentra el valor numérico de la expresión
Csc(765º) - Sec(300º)Sen( 695º)
5. Determina si el valor de cada función es positiva, negativa, cero o uno
a. Cos90º ______
b. Tan180º
_____
c. Cos360º ______
d. Cos270º ______
e. Cos 180º ______
f. Sen270º ______
6. Determina el cuadrante al que pertenece el ángulo θ y escribe un ángulo que lo represente, según
las condiciones que se dan:
a. Cscθ positivo y Senθ positivo
_________
_________
b. Tanθ negativo y Secθ positivo _________
_________
c. Senθ positivo y Cotθ negativo
________
__________
7. Teniendo en cuenta las características de las gráficas de las funciones trigonométricas, escribe F o
V según el caso. Justifica tu respuesta
a .(
) las funciones secante y cosecante no poseen asíntotas verticales
c. (
) La función cosecante tiene como dominio el conjunto de los números reales
d. (
) La función secante corta al eje y en el punto (0,1)
e. (
) La gráfica de la cotangente nunca corta al eje x
f. (
) La función secante sólo es negativa en el tercer cuadrante
g.(
) La tangente no posee máximos ni mínimos
8 . Encuentra el valor numérico de cada expresión
a. sen 135º
b. Cos1140º
c. Tan 210º
d. Csc 945º
e. Sec(750º)Cot( 420º) + Sen(240º)
f. Tan (300º) - 2Cos(330º) - Sen(600º)
COMPETENCIA: COMUNICACIÓN
1. Teniendo en cuenta los aspectos que se enumeran a continuación explica que tienen en común
las funciones trigonométricas secante, cosecante y cotangente :
Dominio:
Rango:
Máximos:
Mínimos:
Período:
2. ¿Qué sucede con los valores de las ecuaciones de las asíntotas en las funciones trigonométricas
secante, cosecante y cotangente y los valores de las funciones inversas para estos ángulos
respectivamente?
3. Agrupa en pares e impares las funciones trigonométricas y justifica por qué se definen así.
4. Traza en un mismo plano cartesiano las gráficas de las funciones Seno y Coseno, toma los valores
para ángulos cuadrantales entre 0º y 360º.
5. Realiza un cuadro comparativo donde anotes las semejanzas y diferencias que existen entre estas
dos funciones
semejanzas
diferencias
6. Completa los siguientes enunciados:
______________________ es el intervalo donde ambas funciones son positivas
Cuadrante donde ambas funciones son negativas: ________________
______________________ intervalo donde la función Seno decrece y Coseno crece
d. La función Senθ decrece cuando el ángulo θ va de
______ a __________
Cuando el ángulo θ decrece de 2π a 3π/2 la función Senθ____ de ___ a ____
La función Cosθ crece cuando el ángulo θ va de
______ a __________
¿En que intervalos las dos funciones son decrecientes?
Cuando el ángulo θ decrece de 2π a π3/2 la función Coseno___ de___ a ____
Cuando el ángulo θ toma los valores de _________________ las funciones seno y coseno tienen el
mismo valor.