ejercicios de propiedades de la materia

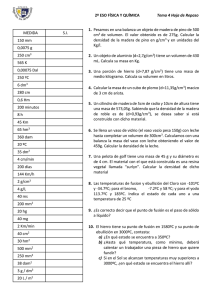
EJERCICIOS DE PROPIEDADES DE LA MATERIA
1
Indicar la medida de cada aparato.
17 ml
5 ml
90 ml
500 ml
16 ml
4 ml
80 ml
b) Si al abrir la llave de la pipeta gotea a un ritmo de 47 gotas/minuto y cada gota son 0,05 ml,
¿cuánto le cuesta vaciarse?
2
Completar la siguiente tabla de densidades:
MASA
2 kg
VOLUMEN
SUSTANCIA
cobre
glicerina
dióxido de carbono
2,5 litros
3
12 m
3
3
3
Datos de densidad a 20ºC: cobre: 8,9 g/cm ; glicerina: 1,6 g/cm ; dióxido de carbono: 1,94 g/dm .
3
Localizar la afirmación correcta:
a) Si 1 litro de alcohol tiene una masa de 800 g, su densidad será 0,8 g/mL.
b) Si la densidad del cuerpo humano es aproximadamente 1,07 kg/dm3, debería flotar en agua
destilada.
c) La densidad de una sustancia es el volumen correspondiente a una masa unidad de dicho
cuerpo.
d) Si la densidad de una sustancia es 12 g/L, significa que 1 m3 de ese cuerpo tiene una masa de
1200 kg.
4
A partir de los siguientes datos:
densidad del benceno: 0,88 g/cm3
densidad del oro: 19,3 g/cm3
a) Decir quién tiene mayor masa: 2 litros de benceno o 100 cm3 de oro.
b) El benceno es inflamable; ¿qué ocurriría si echamos una cerilla a una mezcla de benceno y
agua?
5
Localizar la afirmación correcta.
a) Sistema material es toda suma de dos o más masas.
b) Sustancia es un elemento puro.
c) Materia es todo aquello que se ve.
d) Materia es todo aquello que tiene masa.
6
La densidad del cobre es 8,9 g/cm3. ¿Qué masa corresponde a un lingote de cobre de 35 x 35 x 20
cm?
7
Para calcular la densidad de una sustancia sólida se mide su masa en una balanza y resulta igual a
169,5 g. Según los datos del dibujo:
a) Describe los pasos que se realizan a continuación y calcula la densidad del objeto.
b) ¿Daría el mismo resultado si lo sumergimos en leche?
8
¿Cuál es la masa de 10 cm3 de aceite? ¿Qué volumen ocupa 1 Tm de aceite?
Densidad del aceite: 0,9 g/cm3.
9
Tenemos una canica de cobre cuyo diámetro hemos medido con un calibre y es igual a 2,5 cm.
Sugerir dos métodos para calcular la densidad del cobre si dispones de balanza y probeta.
Dato: volumen de una esfera = 4/3 pr3. Masa de la canica = 72,8 g.
SOLUCIONES
Solución:
a) Bureta: 16,4 ml
Pipeta: 4,7 ml
Probeta: 85 ml
Matraz: 500 ml exactos, ya que está perfectamente aforado.
b) Si la pipeta contiene 4,7 ml son un total de: 4,7/0,05 = 94 gotas.
Como caen 20 gotas/minuto, serán: 94/47 = 2 minutos.
Solución:
Se trata de ir despejando la variable correspondiente de la fórmula de la densidad. Así pues:
COBRE: V = m/d = 2 000/8,9 = 224,7 cm3.
GLICERINA: m = V · d = 2 500 cm3 · 1,6 = 4 000 g = 4 kg.
DIÓXIDO DE CARBONO: m = V · d = 12 000 dm3 · 1,94 g/dm3 = 23 280 g = 23,3 kg.
Solución:
La respuesta correcta es la a).
Solución:
La primera pesada nos permite saber la tara de la probeta, es decir su masa en vacío, que resulta
igual a 50 g. A continuación añadimos el líquido y volvemos a pesar. Por diferencia sabemos la masa
correspondiente al líquido vertido en la probeta. Seguidamente hacemos la lectura directa de volumen
y ya podemos saber la densidad. Veamos los dos casos propuestos:
a) Añadimos agua hasta donde marca la altura de la probeta, hemos añadido 75 mls. Tomando la
densidad del agua, 1 g/ml, resultará un suplemento de masa de 75 g. Así pues, la segunda balanza
deberá medir:
50 + 75 = 125 g.
b) Si la balanza marca 117,5 g, significa que el líquido añadido son: 117,5 g - 50 g = 67,5 g
Puesto que el volumen es el mismo, resultará:
d = m/V = 67,5 g/75 ml = 0,9 g/ml.
Densidad que corresponde, aproximadamente, al aceite.
Solución:
a) 2 litros de benceno son 2 000 cm3 es decir: 2000 · 0,88 = 1760 g
100 cm3 de oro son: 100 · 19,3 = 1930 g. Tiene más masa el oro.
b) La densidad del benceno es menor que la del agua, luego flota sobre ella. Si echamos una cerilla,
se incendiará.
Solución:
La opción correcta es la d).
Solución:
Hallamos el volumen: 35 · 35 · 20 = 24 500 cm3
Así pues: masa = V · d = 24 500 · 8,9 = 218 050g = 218 kg.
Solución:
a) Puesto que no conocemos el volumen del objeto, lo sumergimos en agua y hallamos la diferencia:
75 cm3 - 60 cm3 =15 cm3.
Así pues, la densidad será:
d = m/V = 169,5 g/15 cm3 = 11,3 g/cm3.
Densidad que corresponde al plomo.
b) El resultado es independiente del líquido de que se trate, ya que éste sólo sirve para hallar el
volumen del objeto, el cual se corresponde con el volumen de líquido desalojado.
Solución:
10 cm3 de aceite son: 0,9 · 10 = 9 g.
Las unidades de la densidad se pueden poner también: 0,9 g/cm3 = 0,9 kg/dm3.
1 Tm = 1000 kg, equivalentes a: 1000/0,9 = 1111,1 dm3.
Solución:
Primera posibilidad: calculamos su masa con la balanza y se supone que nos da 72,8 g. A
continuación, tomamos el dato del radio (1,25 cm) y hallamos su volumen:
V = 4/3 p r3 = 4/3 p· (1,25)3 = 8,2 cm3.
De ahí calculamos su densidad:
d = m/V = 72,8 g/8,2 cm3 = 8,9 g/cm3.
La otra posibilidad consiste en medir directamente su volumen por desplazamiento del volumen de
un líquido en la probeta. Sumergimos la bola, restamos del volumen anterior y hallamos el dato
experimental de volumen. Junto con el valor de la masa obtenido con la balanza, el cálculo de la
densidad es inmediato.