ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA

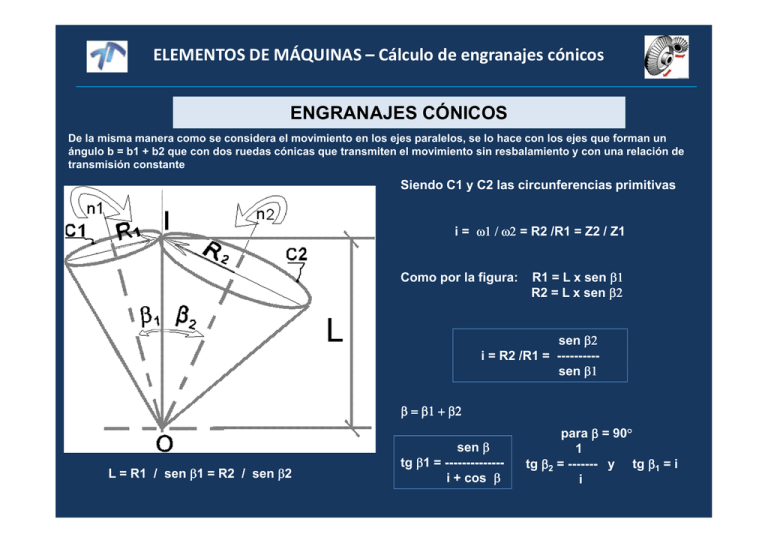
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
ENGRANAJES CÓNICOS
De la misma manera como se considera el movimiento en los ejes paralelos, se lo hace con los ejes que forman un
ángulo b = b1 + b2 que con dos ruedas cónicas que transmiten el movimiento sin resbalamiento y con una relación de
transmisión constante
Siendo C1 y C2 las circunferencias primitivas
i = ω1 / ω2 = R2 /R1 = Z2 / Z1
Como por la figura:
R1 = L x sen β1
R2 = L x sen β2
sen β2
i = R2 /R1 = ---------sen β1
β = β1 + β2
L = R1 / sen β1 = R2 / sen β2
sen β
tg β1 = -------------i + cos β
para β = 90°
1
tg β2 = ------- y tg β1 = i
i
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
Para estudiar el movimiento en los engranajes de ejes paralelos, cortábamos con un plano normal a
ambos ejes de giro de las ruedas, y sobre las circunferencias primitivas analizábamos los tipos de
curvas de los dientes (Curvas conjugadas, en especial la evolvente) luego proyectando
paralelamente a los ejes obteníamos cada diente.
En el caso de los engranajes cónicos LA SECCIÓN NORMAL A AMBOS EJES ES UNA ESFERA CON
CENTRO EN EL PUNTO DE INTERSECCIÓN DE LOS MISMOS y la intersección con esta esfera nos
dará las circunferencias primitivas C1 y C2 en contacto en I siendo OI la generatriz de la esfera, los
ejes cortan a la esfera en O1 y O2
Si ahora analizamos los tipos de curvas, nos encontramos que debemos trabajar sobre una
superficie esférica visto desde el centro O, esto no es posible por no ser la superficie de la espera
desarrollable, (No está generada por una recta)
Debido a este inconveniente, es que con mucha inteligencia, se utiliza el método de los cono
complementarios ó método de Tredhold
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
Nomenclatura y normalización
La longitud b del diente debe ser igual o menor que 1/3L ó de 6M a 10M.
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
Fuerzas y tensiones en los dientes
TANGENCIAL
Fx = Fn cos α = Ft = 71.620 N / n1 Rpe1
NORMAL
Fn = Ft / cos α
RADIAL-AXIAL
Fy = Ft tang α sen β1
AXIAL -RADIAL
Fz = Ft tang α cos β1
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
Métodos de cálculo: Wilfred Lewis (1892)
dF = σt pl y dl
Momento torsor respecto eje engranaje:
dF . r = σt pl y dl r
Variables proporcionales a la distancia desde el
vértice del cono primitivo:
r R
=
l L
⇒ r=
Rl
L
y
pl pc
=
l
L
pl =
⇒
2
dF =
p l
Rl
l
σ t c y dl = R σ t pc y   dl
L
L
L
pc l
L
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
2
Rl
p l
l
dF =
σ t c y dl = R σ t pc y   dl
L
L
L
Integrando r variando de 0 a R y l variando entre L y L – b:
R σ t pc y L 2
M t = Ft .R =
l dl = R σ t pc b
2
∫
L
−
b
L
 b b2 
y 1 − + 2 
 L 3L 
 b b2 
Ft = σ r b pc y 1 − + 2 
 L 3L 
b máximo 1/3L, b2/3L2 = 1/27 se desprecia sin error apreciable y teniendo en cuenta la tensión admisible:
 L −b
Fb = σ adm b pc y 

 L 
pc
y
Ft
L
paso circunferencial en extremidad mayor
factor de forma con número virtual zv de dientes
fuerza tangencial en extremidad mayor
generatriz cono primitivo
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
Número virtual de dientes (Zi)
2 π R1-2 = Z1-2 p
2 π ρ1-2 = Zi (1-2) p
ρ1-2 = R1-2 / cos β1−2
Z1
Zi1 = ---------cos β1
Z2
Zi2 = ---------cos β2
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
ecuación de Lewis para cálculos preliminares de diseño
Fb ≥ Ft
Partimos de la igualdad:
Fb = b[cm] y pe[cm] σadm[Kg/cm2] (L – b)/L)= Ft [Kg] = 71620 N[HP] / (n[rpm] Re[cm])
se considera como buena la siguiente proporción:
como Dp = ( pe / π ) Z
2 pe < b < 3 pe ó
6 M < b < 10 M
Es decir, b = ρ pe
Fb = ρ y pe2 σadm (L – b)/L)
Ft = 71620 N / [ n ( pe Z / 2 π ) ]
Ft = 450.000 N / ( n pe Z )
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
Fb = F t
Fb = ρ y pe2 σadm (L – b)/L)
Ft = 450.000 N / ( n pe Z )
N [ HP]
L
pe [ cm] = 76,6 3
σ adm [Kg / cm2 ] y ρ Z n[ rpm] L − b
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes cónicos
Esfuerzos en los apoyos
TANGENCIAL
Fx = Fn cos α = Ft
NORMAL
Fn = Ft / cos α
RADIAL-AXIAL
Fy = Ft tang α sen β1
AXIAL -RADIAL
Fz = Ft tang α cos β1
= 71.620 N / n1 Rmed1
Rmed = R- (b/2) sen β
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes: AGMA
Métodos de cálculo: Flexión en la base
Lewis
Lewis-Barth
Buckingham
Norma AGMA
Métodos de cálculo: fatiga superficial
Buckingham
Norma AGMA
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
NORMAS P/CALCULO RESISTENCIA
OBJETIVOS
Organizaciones
-orientar
-coordinar
-simplificar
-unificar
-reducir costos en tiempo y trabajo
-AGMA (EEUU-1916) 218.01, 2001C95
-DIN (Alemania-1917) 3990
-JGMA (Japón)
402 a 405
-GOST (Rusia)
21354-86
-ISO (Internacional-1947: institutos estandarización
de países: ANSI, IRAM, etc.)
6336
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
F
F1
F2
30
30
o
lsn’
l s’
o
hsn
hs
Geometría y Fuerzas para normas ISO; DIN & JGMA
F1
F2
ls’
ls2’
ls1’
hs
hs1
hs2
Geometría y Fuerzas para normas AGMA
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Métodos de cálculo: norma AGMA
American Gear Manufacturers Association, Asociación Americana de Fabricantes de Engranajes
“Este estándar de AGMA y publicaciones relativas están basados en datos, condiciones o
aplicaciones típicos o promedio. Los estándares están sujetos a mejoramiento, revisión o
anulación continuos, según lo dicte la experiencia acrecentada. Cualquier persona que consulte
publicaciones técnicas de AGMA deberá cerciorarse de que obtenga la información más reciente
disponible de la asociación acerca del tema en cuestión.”
“El conocimiento y el juicio que se requieren para evaluar los diversos factores nominales vienen
de años de experiencia que se ha ido acumulando en el diseño, fabricación y operación de
unidades de engranaje. Los factores empíricos dados en este estándar son de naturaleza
general. Las normas de aplicación de AGMA pueden utilizar otros factores empíricos que se
adecuen más estrechamente al uso particular. Esta norma está orientada al diseñador
experimentado de engranes, capaz de seleccionar valores razonables para estos factores. No
está dirigido hacia el uso masivo de la ingeniería pública en general.”
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
• Dos ecuaciones fundamentales válidas para engranajes
rectos, helicoidales, doble helicoidales y cónicos:
– Para el esfuerzo flexionante
Wt Ka Pd Ks Km KB KI
σt =
Kv
F
J
– Para la resistencia a la picadura (contacto)
σc = Cp
Wt Ca Cs Cm C f
Cv D F I
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Para el esfuerzo flexionante
Las suposiciones para las cuales la ecuación fue derivada son:
- La relación de contacto está entre 1 y 2
- No hay interferencia ni rebaje del diente por encima del inicio teórico del flanco activo.
- Hay juego circunferencial.
- Los radios de acuerdo del diente son estándar.
-Se desprecian las fuerzas de rozamiento.
(El método analizado a continuación es válido para engranajes externos)
Modifica la ecuación de Lewis teniendo en cuenta, entre otra cosas:
- Efecto de la fuerza radial
- Concentración de tensiones en la base del diente
- Los efectos de tener varios dientes en contacto
- Carga aplicada en forma dinámica
- Distribución no uniforme en el ancho del engranaje
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Lewis-Barth:
Ft ≤ Fb = b y p σadm K´v
σt = Ft / b y p K´v ≤ σadm
Ft 1 1
σt =
K ´v b p y
Para adecuar nomenclatura y comparar:
- Ft
-b
-p
-πy
lo llamo Wt
lo llamo F
utilizo en su lugar P d = π / p
lo llamo J´
Wt Pd 1
σt =
K ´v F J ´
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Lewis-Barth
AGMA
Wt Pd 1
σt =
K ´v F J ´
Wt Ka Pd Ks Km KB KI
σt =
Kv
F
J
Hay tres grupos de términos:
- el primero está relacionado con la carga
- el segundo con el tamaño de los dientes
- el tercero con la distribución de esfuerzos
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Cuidado con las unidades!!
σ t [lb / pu lg
σ t [ Kg
/ cm
2
]
2
Wt Pd Ka Ks Km KB KI
]=
F
Kv J
=
Wt Ka Ks Km KB KI
F m
Kv J
Carga tangencial transmitida:
Wt [ lb ] =
33000 N [ HP ] 126000 N [ HP ]
=
V [ pie / min]
n[ rpm ] D[ pu lg]
Diametral Pitch:
Pd [1 / pu lg]
US
SI
Ancho:
F [ pu lg]
Módulo:
Wt [ Kg ] =
71620 N [ HP ]
n[ rpm ] R[ cm ]
m[cm ]
F [cm ]
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Ka
Kv
FFFF
PPPPdddd
WWWW
σt =
t
Ks KmKBKI
J
Los factores empíricos K, reflejan cada uno el daño extra causado por
un efecto particular no uniforme identificable separadamente:
Sistema impulsado
Sistema motriz
Factor de sobrecarga (Ka): Wt es el valor promedio
de la carga transmitida, la carga máxima real puede
ser varias veces mayor debido a choques.
Factor dinámico (Kv): fuerzas internas
generadas por imprecisiones en fabricación
y engrane de los dientes (exactitud perfil
diente, elasticidad material y velocidad). Es
función del grado de calidad Qv del
engranaje (tolerancia de fabricación).
Uniforme
Choques
moderados
Choques
intensos
Uniforme
1,00
1,25
≥ 1,75
Choques ligeros
1,25
1,50
≥ 2,00
Choques medianos
1,50
1,75
≥ 2,25
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
B
 

  A 
1
 

  A +V 2 
K v = Cv = 

A

1
 A + 200V 2
(
)

V in ft/min




B
V in m/s
A = 50 + 56(1 − B)
2
(12 − Qv ) 3
B=
4
for 6 ≤ Qv ≤ 11
Velocidad máxima para cada calidad:
Vmax =  A + ( Qv − 3) 
2
 A + ( Qv − 3) 
=
200
ft/min
2
m/s
Para V mayor que los valores máximos
dados, utilice engranajes de mayor
calidad
Qv ≤ 5
50
V in ft/min, V < 2500 ft/min
50 + V
50
=
V in m/s, V < 13 m/s
50 + 200V
Kv =
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
FFFF
PPPPdddd
KKKKaaaa vvvv
ttttKKKK
WWWW
σt =
Ks Km KB KI
J
Factor de tamaño (Ks): considera falta de uniformidad de las propiedades del material.
(p, d, b, relación del tamaño entre los dientes y el diámetro de la rueda, esfuerzos,
profundidad del temple superficial )
La recomendación de la AGMA es que se utilice un factor igual a la unidad “para la mayoría de los
engranajes siempre que se haga una elección adecuada del acero para el tamaño de la pieza y el
tratamiento térmico y el proceso de templado o endurecimiento.”
Factor de distribución de carga (Km): toma en cuenta desalineamientos (de
los ejes, inexactitudes de los dientes, deflexiones elásticas causadas por la
carga en ejes o árboles, cojinetes o en el alojamiento). Los errores pueden
combinarse de tal manera que el contacto con el engranaje oponente sea
menor que el ancho íntegro de la cara, o que el contacto sea completo, pero
carente de uniformidad.
Pd
M
Ks
≥5
≤5
1.00
4
6
1.05
3
8
1.15
3
12
1.25
1.25
20
1.40
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
KKKKmmmm
KKKKssssFFFF
PPPPdddd
KKKKaaaa vvvv
ttttKKKK
WWWW
σt =
Factor de geometría (J): evalúa la forma (o perfil) del diente, la posición
en la cual se le aplica la carga más peligrosa, concentración de tensiones
y repartición de la carga entre uno o más pares de dientes
KB KI
J
J = Y / ( Kf mN )
Y : factor de forma
Kf : factor de concentración de tensiones
mN: relación de repartición de carga en los dientes
(Para rectos = 1)
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
KKKKmmmm
KKKKssssFFFF
PPPPdddd
KKKKaaaa vvvv
ttttKKKK
WWWW
El factor de flexión del aro KB considera los casos de engranes de gran
diámetro, hechos con un aro y radios en lugar de un disco sólido; dicho aro
posee un espesor delgado en comparación con la altura de los dientes. La
AGMA define una relación entre el espesor del aro y la altura de los dientes:
relación de respaldo
mB =
tR
ht
tR= espesor aro desde raíz del diente
ht= altura completa del diente
Para la relación mB no se recomienda
valores menores de 0.5
JJJJ
σt =
KB KI
k B = −2mB + 3.4 for 0.5 ≤ mB ≤ 1.2
= 1 for mB > 1.2
= 1 for solid gears
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
KKKKBBBBJJJJ
KKKKmmmm
KKKKssssFFFF
PPPPdddd
KKKKaaaa vvvv
ttttKKKK
WWWW
σt =
KI
El factor de engranaje intermedio KI considera que un
engranaje de este tipo está sujeto a la vez a más ciclos
de esfuerzo por unidad de tiempo, y a cargas
alternantes más elevadas:
KI = 1.42 para engranajes intermedios
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
KL
σ t ≤ σ adm σ
= σ at
adm[ lb / pu lg ]
2
Esfuerzo admisible según el material (en tablas)
KT KR
Es un esfuerzo de diseño con 10 millones de ciclos (107 ) de
operación con carga y 99% de confiabilidad (1 falla c/100
muestras).
Cuando está sujeto a sobrecargas intensas, momentáneas y
poco frecuentes, se determina por sus propiedades de
resistencia al límite de fluencia
Confiabilidad
Factor de confiabilidad (KR): asegurar alta confiabilidad, o
en algunos casos permitie diseñar con ciertos riesgos
calculados
KR
0,9
0,85
0,99
1,00
0,999
1,25
0,9999
1,50
Factor de Confiabilidad KR (fatiga)
Confiabilidad
Alta
Diseño normal
KR
>=3,00
1,33
Factor de Confiabilidad KR (fluencia)
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
KKKKRRRR
2
σσσσ at
σ adm[lb / pu lg ] =
KL
KT
Factor de duración (KL): las resistencias están basadas en 107 ciclos de carga en los dientes. El objetivo del factor de
duración consiste en modificar dichas resistencias para obtener duraciones distintas.
Cuando el criterio sea el de la resistencia a la fluencia el factor de duración vale 1.
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
KT
KKKKRRRR
KKKKLLLL
2
σσσσ at
σ adm[lb / pu lg ] =
+
TTTTFFFF
KT =
620
460
Factor de temperatura (KT): ajusta valor del esfuerzo admisible tomando en consideración la
temperatura. En los engranajes en los que el aceite o los cuerpos de los engranes trabajan
con temperaturas que no exceden de 250°F (120°C), al factor de temperatura se le puede
asignar el valor de 1. Para acero, con temperaturas de trabajo entre 70 y 150°C:
donde TF es la temperatura
máxima de trabajo del aceite en °F
Actualmente se tiene toda la información necesaria para calcular
el esfuerzo real flexionante y comparar este esfuerzo con el
máximo admisible.
σ t ≤ σ adm
Se deberá utilizar las ecuaciones de resistencia a la flexión separadamente para el piñón y la rueda si son fabricados de materiales diferentes o tienen un
tratamiento térmico diferente. De otro modo, solo se tiene que diseñar el piñón ya que el engranaje más grande tiene mayor factor de geometría J.
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Para el esfuerzo de contacto
Buckingham
σ c = Cp
Ft
b D1 I
Para adecuar nomenclatura y comparar:
- Ft
-b
lo llamo Wt
lo llamo F
σ c = Cp
Wt
F DI
AGMA
σc = Cp
1- Ley de distribución de presiones según Hertz
2-Distribución de la presión hidrodinámica (cuerpos
indeformables)
3-Distribución real de presiones (cuerpos deformados, en
movimiento y actuando una capa de lubricante)
Wt Ca Cs Cm C f
Cv D F I
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
σc = Cp
Wt Ca Cs Cm C f
Cv D F I
Factor de geometría:
Carga tangencial transmitida:
Wt [ lb ] =
33000 N [ HP ] 126000 N [ HP ]
=
V [ pie / min]
n[ rpm ] D[ pu lg]
Coeficiente elástico:
Cp[
lb / pu lg 2 ]
=
1
 1 − ν 12 1 − ν 2 2 

+
π 

E
E
2
 1

Diámetro:
D[ pu lg]
Ancho:
F [ pu lg]
I=
cos a sena mG
2
mG + 1
siendo mG = D2 / D1
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
t
WWWW
IIII
pppp
FFFF
DDDD
CCCC
σc =
Ca C s Cm C f
Cv
Factor de tamaño (Cs) = Ks
Factor de distribución de carga (Cm) = Km
Factor dinámico (Cv) = Kv
Factor de aplicación (Ca) = Ka
Factor de condición superficial (Cf) : depende del acabado superficial
(según sea afectado por el cortado, acepillado, pulimentado,
rectificado, etc.), de los esfuerzos residuales y de los efectos plásticos
(endurecimiento por el trabajo). Puede tomarse como la unidad, a
menos que las pruebas o experiencias en el sitio de trabajo indiquen
otra cosa.
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
σ c ≤ σ ad
σ ad [lb / pu lg
2
]
CL CH
= σ ac
CT CR
Esfuerzo admisible según el material (en tablas)
Factor de temperatura (CT) = KT
Factor de confiabilidad (CR) = KR
Factor de duración (CL): las resistencias están
basadas en 107 ciclos de carga en los dientes.
El objetivo del factor de duración consiste en
modificar dichas resistencias para obtener
duraciones distintas.
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
CCCC
LLLL
CCCC CCCCTTTT
RRRR
2
σσσσ ac
σ ad [lb / pu lg ] =
CH
Factor de relación de dureza (CH) : tiene en cuenta la diferencia
de durezas entre piñón y engrane y se utiliza sólo para el
engrane. Es función de la dureza de los dos engranes y de la
relación de velocidades.
CH = 1 + A(mG − 1)

H Bp
< 1.2
0 if
H Bg


H Bp
H Bp

− 8.29(10 −3 ) if 1.2 ≤
≤ 1.7
A = 8.98(10 −3 )
H Bg
H Bg


H
6.98(10−3 ) if Bp > 1.7
H Bg

C H = 1 + B (450 − HBg )
Para piñones endurecidos superficialmente con dureza > 48 RC
y para una dureza del engrane entre 180 y 400 HB:
7.5(104 )e −0.0112 Rq (US units)
B=
−0.052 Rq
4
(SI units)
7.5(10 )e
Rq = RMS rugosidad superficial del diente del piñón en µin rms
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes : AGMA
Actualmente se tiene toda la información necesaria para calcular el esfuerzo de contacto y comparar este
esfuerzo con el máximo admisible. Los coeficientes de seguridad previstos para esfuerzos de flexión y
recomendados en las normas AGMA son iguales que los orientados para los esfuerzos de contacto.
σ c ≤ σ ad
Las mismas expresiones son válidas para engranajes helicoidales; fundamentalmente varían los coeficientes de
forma (J), de montaje (Km) y dinámico (Kv), debido a la nueva geometría y sus ventajas (menor efecto dinámico) y
desventajas (fuerza axial). Al coeficiente de geometría (I) del cálculo al desgaste hay que calcularlo debido a que
el ángulo de la hélice no está normalizado.
También son válidas para engranajes cónicos; fundamentalmente varían los coeficientes de forma (J), de montaje
(Km) y de tamaño (Ks), debido a la nueva geometría y al montaje. El coeficiente elástico (Cp) y de geometría (I) ya
que se utilizan las ecuaciones de Hertz para dos esferas en contacto. La fuerza de trabajo se calcula actuando en
el diámetro primitivo exterior.