LAB 6 - Uprm

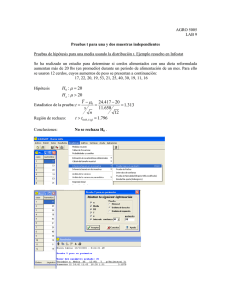
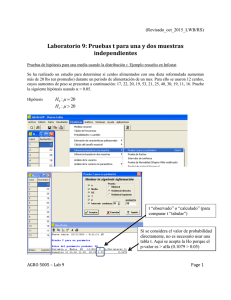
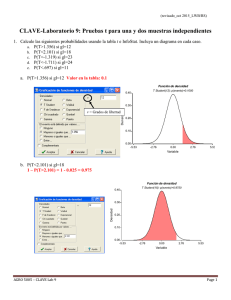
(Revisado ago 2015_LWB/RS)
Laboratorio 6: Distribución Normal
1. La tabla 1 del texto presenta la probabilidad de que un valor aleatorio de Z = (Y-µ)/ sea menor que
el valor tabulado z (área bajo la curva entre menos infinito y z). Use la tabla de z para determinar las
siguientes probabilidades. Incluya un gráfico en cada caso, sombreando el área que representa cada
probabilidad.
a. P(Z<-2)=
b. P(Z>2.56)=
c. P(Z<-1.23)=
d. P(Z<2.25)=
e. P(-1.63<Z<2.57)=
f. P(-1.70<Z<-0.25)=
g. P(1.42<Z<1.89)=
2. En InfoStat, se puede usar el menú Estadisticas>Probablidades y Cuantiles para calcular
probabilidades en la distribución normal. Use InfoStat para determinar las siguientes probabilidades y
compare sus resultados con el ejercicio 1.
a. P(Z<-2)=
b. P(Z>2.56)=
c. P(-1.63<Z<2.57)=
d. P(-1.70<Z<-0.25)=
e. P(1.42<Z<1.89)=
3. Use la tabla de z para encontrar el valor de a cuya probabilidad sea la especificada. Incluya un
diagrama en cada caso. (ayuda: la dirección de la flecha indica el lado de la distribución que debe
ser sombreada. Esta área sombreada corresponde a la probabilidad indicada)
a. P(Z<a)=.84
b. P(Z>a)=.19 (ayuda: es la misma a de P(Z< a)=0.81)
c. P(Z<a)=.23
d. P(Z>a)=.65 (ayuda: es la misma a de P(Z< a)=0.35)
e. P(-a<Z<a)=.90
4. Use InfoStat para encontrar el valor de a cuya probabilidad sea la especificada. Compare sus
resultados con el ejercicio 3.
a. P(Z<a)=.84
b. P(Z>a)=.19
c. P(-a<Z<a)=.90
5. Otra alternativa para buscar probabilidades en Infostat es usar el menú Aplicaciones > Didácticas >
Gráficos de funciones de densidad continuas. Aquí no sólo obtenemos las probabilidades sino
también las gráficas. Para superponer varias gráficas, es posible usar la opción clonar (herramientas
gráficas). Se obtendrá una copia (clon) de la serie gráfica original. Si seleccionamos esta nueva serie
podemos cambiar sus parámetros y comparar ambas distribuciones. Grafique en un mismo gráfico las
funciones correspondientes a las siguientes tres distribuciones normales:
   10,  2  1 ,    10,  2  3 ,    9,  2  3 .
AGRO 5005 – Lab 6
Page 1
(Revisado ago 2015_LWB/RS)
6. Usando la definición de cuartiles (valores de la variable que dejan un 25% o un 75% de la
distribución a la izquierda), calcule los valores de Q1 y Q3 en la distribución normal estandarizada.
¿Cuál es el valor del RIC (Recorrido Intercuartílico)? Use la tabla e Infostat.
Para encontrar probabilidades asociadas con una distribución normal general se debe primero transformar
el valor de Y en Z usando la siguiente fórmula, y luego usar la tabla de z para encontrar el valor.
z
y

Ejemplo:
P(Y<115) = P(Z < [115-100)/6] )= P(Z<2.50) = 0.9938.
El problema inverso (encontrar un valor de Y que acumule cierta probabilidad), se resuelve calculando
primero el valor de Z y después resolviendo la ecuación z 
y

de la siguiente manera:
y = z + 
Ejemplo: Dado Y ~ N(100, 36), Encontrar a tal que P(Y<a)=0.6591:
A partir de la tabla de Z, vemos que P(Z<.41)=.6591. Entonces a = (.41)(6) + 100 = 102.46.
7. Para Y ~ N (  100,   36) , calcule las siguientes probabilidades. Incluya un diagrama en cada
caso. Use tablas e InfoStat.
a. P(93<Y<102)=
b. P(90<Y<95)=
c. P(Y>103)=
d. P(Y<98)=
2
8. Para la misma situación Y ~ N (  100,   36) , calcular los valores de a. Incluya un diagrama en
cada caso. Use tablas e InfoStat.
a. P(Y>a)= .25
b. P(Y<a)= .08
c. P(Y>a)= .72
d. P(Y<a)= .995
2
AGRO 5005 – Lab 6
Page 2
(Revisado ago 2015_LWB/RS)
9. Un programa de selección en maíz trata de obtener plantas no demasiado altas. Suponga que la altura
de las plantas sigue una distribución normal con media 160 cm y desviación estándar 21 cm.
a. ¿Qué proporción de las plantas van a ser eliminadas si se decide descartar todas las
plantas cuya altura exceda 180 cm? (ayuda: P(Y>180) =?)
b. ¿A partir de qué altura se deberían descartar las plantas si se desea eliminar el 20% del
lote con las plantas más altas? (ayuda: P(Y>a) = 0.20)
10. La cantidad de oxígeno disuelto en el agua de los ríos depende de la temperatura, la cantidad de
materia orgánica en descomposición, de la presencia de contaminantes, etc. El Council of
Environmental Quality (CEQ) considera que un contenido de oxígeno disuelto menor de 5 mg/l es
indeseable porque no sería capaz de sostener la vida acuática. Suponga que una planta industrial
descarga sus residuos en el río y las mediciones de oxígeno disuelto aguas abajo de la descarga
tienen una distribución normal con media de 6.5 mg/l y desviación estándar de 0.6 mg/l.
a. ¿Qué proporción de los días será el contenido de oxígeno disuelto considerado indeseable
por el CEQ?
b. ¿Hasta qué valor podría caer el contenido de oxígeno disuelto? (ayuda: ¿entre qué valores
de la variable Ud. espera encontrar virtualmente todas las observaciones?)
11. La longitud del caparazón del langostino Thenus orientalis, encontrado comúnmente en los mercados
de Singapur, tiene una distribución aproximadamente normal, con una media de 59.5 mm y una
desviación estándar de 4.6 mm.
a. Si va a seleccionar aleatoriamente un langostino de esta población, ¿qué probabilidad tiene de
que éste tenga una longitud menor de 55mm?
b. Si el gobierno decretara que todos los langostinos que se vendan en el mercado deben tener
una longitud mínima de 50mm, ¿qué proporción de los langostinos serán de un tamaño ilegal
para la venta?
c. Un comerciante tiene una anuncio que dice “Nosotros garantizamos que los todos los
langostinos que vendemos en este negocio son los más grandes disponibles”. ¿Qué longitud
mínima deberían tener para asegurarnos que esto langostinos están en el 10% superior de la
población?
AGRO 5005 – Lab 6
Page 3