15. Funciones definidas a trozos

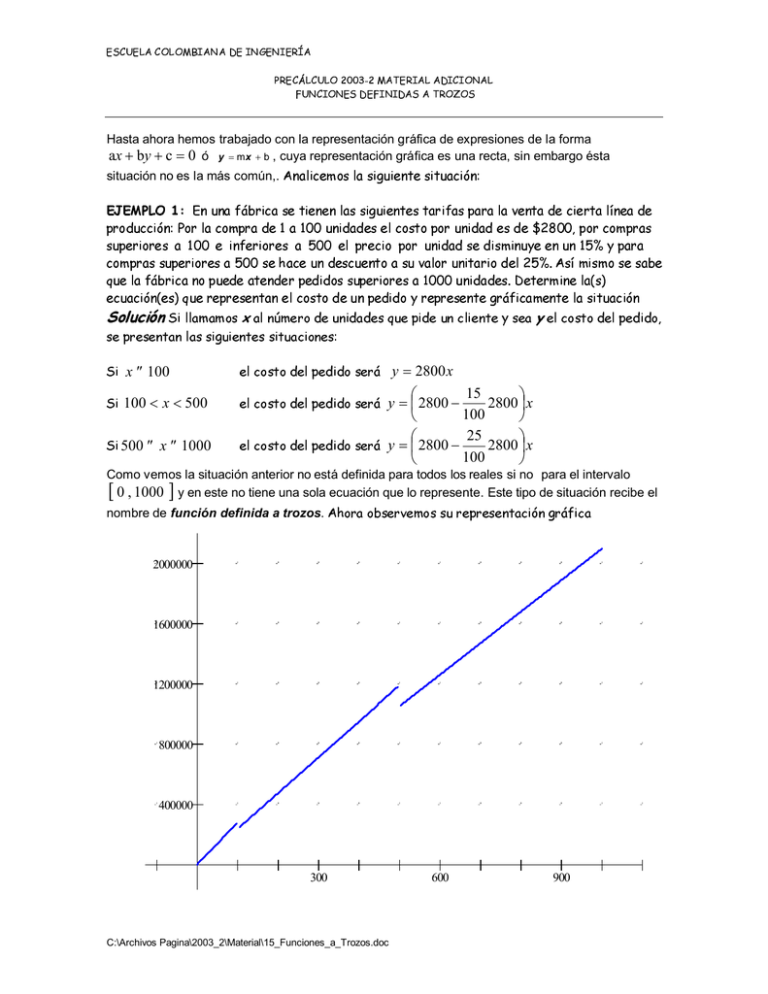
 Hasta ahora hemos trabajado con la representación gráfica de expresiones de la forma
ax + by + c = 0 ó y = m x + b , cuya representación gráfica es una recta, sin embargo ésta
situación no es la más común,.
' (
' )
* + ,
-
.
6 # % &
! # 4 3 D
3 !
4 3 !
# 8
! # 4 3 0 1 2 3 I J K L M N O
V Z
P
D
Q
_ [ Z V Z X a S X
P
Q
P
Q
P
Q
# 9 : :
# % F ! G
H
3
!
! " # $ ! $ # % &
/
4 3
4 3 0 3 # 6 U V
9
! W
S R
V Qe ] QZ X a Z V
$ 9 : :
!
# ! $
\ Z
!
6 # ! $
4
! # 4 3 3
! #
3 !
4 6 6
] X Q\ S \ Z V
^ ] Z
$ 3 0 !
4
@
3
! !
6 ! # $ 3 9 : : :
] X
5 $ 6 6 3 $ ; < = : : > 4
# @ 6 # 6 6 ! C
3 4 3 ! $ _ Q\ Z
# 6 6
# 6 6
5 3
4 3 < ? A
C
# E $ 3 ! 7
b
V Z S
c
9 ? A
" 3 1 0 $ ` R QZ X a Z
3
7 ! 6 4 3 !
@
4 3 ! ! 2 F ! G
! $ # % Z R ` U V a U
\ Z R _ Z \ Q\ U d
V Qa ] S ` Q U X Z V f
Z R ` U V a U
\ Z R _ Z \ Q\ U
V Z [ g
100 < x < 500
Z R ` U V a U
\ Z R _ Z \ Q\ U
V Z [ g
500 ≤ x ≤ 1000
Z R ` U V a U
\ Z R _ Z \ Q\ U
V Z [ g
x ≤ 100
4 3 6 ! # $
4 6 6
X Y T Z [ U
! " # $ !
# 6 6 !
? : :
B $ 6 3
3 4 3 ! $ S T
! 3 !
? : :
4 # 6 R RS T
RS V
3 !
0 1 2 3 y = 2800 x
15


2800  x
y =  2800 −
100


25


2800  x
y =  2800 −
100


Como vemos la situación anterior no está definida para todos los reales si no para el intervalo
0 , 1000 y en este no tiene una sola ecuación que lo represente. Este tipo de situación recibe el
[
]
nombre de función definida a trozos.
U [ S
U j V Z [ k Z T
U V
V ]
[ Z _ [ Z V Z X a S ` Ql X
e [ g m Q` S
h i
2000000
1600000
1200000
800000
400000
300
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
600
900
4200
+
!
7
& ( % " # '
2800
: (
2100
4 +
8
D % '
C
1400
7
) * %
1 2 3 4 5 6 7 8 9 1011121314
x ∈ (2 ; 3 ]
f ( x ) = 2.100 x ∈ ( 3 ; 4 ]
E
? @< 2
% # +%
f (x )
!
" %
' "
C
' -
0 1 2 2
% $ ;'
'
7
A @2 2
% " #
% > ' ! (
) * %
% ,
'
+! , % "
& -
'
7
: (
-
* '
& ' : ' (
'
, !
'
% 3 ' C
" +
x ∈ (1; 2 ]
f ( x ) = 3.500
4 ( '
+5 , 6 & % ( !
" % ( > +
'
+!
% " %
" +# * '
+5 ,
+5 , -
( % & ( % " % , # ' ,
6
- . -/ - & ' ( '
B % & ( % " % , # %
+5 , 6 & % ( !
6 & ' ( '
'
% & ' ( ) * % ' $ % ( !
4 +
8
!
0 < -= 2 2 -
%
$ % F %
" +# * '
) * %
'
% ,
3 ! ( '
$ %
% ,
8
$ +' ( +!
& ! (
% "
* % , # ( %
f ( x ) = 700
6
& ' ( ) * % !
) * %
* '
x ∈ ( 0 ; 1]
$ %
% ,
! F " % ( > '
%
$ %
% ,
& !
7
f ( x ) = 2.800 x ∈ ( 4 ; 13 .5 ]
6
% "
& ' : !
% , # %
7
! " # !
( % & ( % " % , # %
$ %
-3 -2 -1
$ %
'
" % '
. !
700
$ %
% " # * $ +' , # % "
7 8 9
3500
! "
* ,
* !
* " * ' ( +! -
* , '
! , !
' "
" ! '
%
( %
7
# ' "
& ! $ (
8
%
* '
! "
' $ '
' " ; @
f ( x ) = 1.400
* ' " %
> % 3 ;
+5 ,
* , '
G ' ( '
6
% "
( +F +(
' " ; @
 700 x ∈ (0 ; 1]

 1400 x ∈ (1; 2 ]

f ( x ) =  2100
x ∈ (2 ; 3 ]
 2800
x ∈ (3 ; 4 ]

 3500 x ∈ ( 4 ; 13.5 ]
" # '
" +# * '
I 3 ! ( '
4 ( %
+5 ,
% , # ( ' ( %
* % ,
D
+
" %
N
L S Q R
C
$ % 4 +, %
Q
X
X
'
( +F '
'
* , '
4 * ,
4 * ,
O
$ %
%
, !
! ,
+5 ,
!
!
7
F ( %
7
$ %
' : * , ' "
% ' "
+5 ,
% , %
7
!
!
L M
N
4 * ,
'
* , '
función definida a trozos.
+! , % "
# ' F '
4 * ,
$ %
+5 ,
O P Q R
$ % 4 +, +$ ' "
'
# ( ! K ! "
> ' ! ( % " 6 3 ' : '
$ % 4 +, +$ '
'
'
: (
8
) * %
4 +
'
" %
& ( % " % , # ' ,
% ,
! ,
% & ' , !
# ( ! K ! "
L S T L R Q
E
E
f (x )
6Y
Y 6?
2
6?
Y
2
6A
X Z
6A
3
f (x )
2
1
Z
6?
Z
6Y
Z
X Z
X
* , '
2
X Z
X
+F %
<
X Z
X
( %
# ( ' F ' J ' (
' $ '
UV W O M
E
X
! "
7
% "
F +H ,
7
+' 6 & ' ( '
' ( # % " +' , !
1.
# '
Z
−3
6Y
−2
−1
6?
1
2
3
−1
6A
−2
2
6A
Y
2
6?
Y -?
2
6Y
<
−3
2
" # '
% "
4 * ,
( +# '
+5 ,
% "
! , !
f (x ) = [ x
]
+$ '
# '
7
F +H ,
∀x ∈ ℜ
6
!
7
!
'
4 * ,
f (x ) = x 
6
+5 ,
( % $ ! , $ % ' (
3 '
f (x ) = floor (x )
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
5
+'
' F ' J ! 6
4 ! ! (
f (x ) = Int (x )
5
/ , #
C
% "
2.
g (x ) = x − [ x
3 " 5 6 #
#
]
! " # !
$ %
& ' ( )*
+ * , - .
' /
+ *
7
2 3 $ 4 3
f (x )
0
0 1
2
1
−3
−2
−1
1
2
3
−1
−2
−3
3
3.
2
8 3 3 " 5 6 #
−2
−1
1
2
% 3 # 4 #
4 " $ 9 $ % :
1 si x > 0
Sgn ( x ) = 
 − 1 si x < 0
1
−3
3
−1
−2
−3
4.
;
% #
6 # #
N P LU N H
D
GS K
f (x ) = [x ]
V N I O S K
D
Y
W
Y
Z F[
Y
Z
W ]
W ]
W ]
F\
F[
FZ
W ]
W Y
W Y
W Y
<=
> = ? @ A
A B @ A ? =
C A
D
E
F G GH I H
GJ
K LM N LH I O H
O J P GJ
Q H
R J GS T H K F
f (x )
3
FZ
F[
2
F\
]
]
]
]
1
FZ
F[
F\
F\
Z
F[
Z ^[
FZ
$ :
F
f (x )
W X
W
$ !
−3
−2
−1
1
−1
−2
X
Y
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
−3
2
3
5.
H J
GJ
N I L I
S I S LQ J
,8 0
S )
< 3 . 4 8 0
S
!
H L GLI M
*
K H
K L)
@
>
@
A :B
@
A
> D
> D
> D
> @
> @
D
T H Q S I Q H J T
&
f (x ) = x 
, ,- . -
' J LJ
,/
J T T LP J
0 12 3 1- . 4 -
D
:B
D
:A
D
:B
Q H
D ^
( K O J
7 / ,8 9 - 0 :
2
1
:A
:B
−3
−2
−1
:C
A
:B
A EB
1
2
3
1
2
3
−1
−2
?
:A
−3
,/
=
G 3 . H 1I .
JK L M N
K O P M L Q R M
f (x )
@
>
@
A :B
@
A
> D
> D
> D
> @
> @
H 3 / , 0 -
0 1U
5 8 , 1V /
f (x ) = x
3
:A
:B
2
:C
D
:C
D
:B
D
:A
> D
> @
,/
f (x )
=
> ?
=
S T
D
1
:A
:B
−3
:C
:C
A
:B
A EB
−2
−1
−1
−2
?
:A
−3
@
6
5
4
7.
F - /
 x − 2 si x − 2 ≥ 0
f (x ) = x − 2 = 
− (x − 2) si x − 2 < 0
3
2
1
−6 −5 −4 −3 −2 −1
−1
1
2
3
4
5
6
−2
−3
−4
−5
−6
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
H K
3 5 1; 3 -
:C
:C
F - /
>
6 -
3
:A
@
6.
H G R J GS T
4 / 5 ,/
f (x )
D
:C
> D
> @
$ % P S GL+ J
=
> ?
>
" # :
f (x )
=
:
6
8.
5
 x − 2 si − 3 ≤ x ≤ 1
f (x ) = 
:
 − x + 1 si 1 < x
F - /
4
3
2
1
−6 −5 −4 −3 −2 −1
−1
1
2
3
4
5
6
−2
−3
−4
−5
−6
y
6
3
f(x)
9.
x
−9
−6
−3
3
6
9
- 4 - 9 U
1. -
G 3 . H 1I .
/
,/
- < 9 - 0 1I .
4 9 8 V 8 0
9 - 0 < - H 4 17 8
6 8 U
6 -
,/
f (x )
2 9 G 1H / :
6 -
H 8 .
,/
0 3
1. 18 E
−3
−6
−9
−12
45
40
10.
/
G 12 3 9 /
6 - , 0 - 8 9
U
3 - 0 4 9 /
/ ,7 10
-
- .
,
. 17 - , 6 -
G 3 . H 1I .
, / 2 3 /
6 - , 4 1- U
0 - 8 9
/ ,7 10
< 3 - 6 -
/ 5 9 19
8
< 3 - 6 -
- . 4 9 / 9
8
6 -
4 1. /
H - 9 9 / 9
- , 6 - 0 / 2 3 - E
< / ,/ 5 9 / 0
; 3 - ! - 0
,8
; 3 -
3 . 16 / 6 - 0
0 / ,19
" / , ,/ 9
G 3 . H 1I .
U
0 ,/
U
,/
0 4 - 6
3 - 0 4 9 /
- 0 4 .
H - 9 9 / 9
6 - 5 ,/
- .
< 8 E
-
< 3 - 6 -
0 1U
5 I ,1H /
30
,
/ 5 9 19
6 - 0 H 9 1 5 19
G 12 3 9 / :
35
4 1. /
, 2 9 1G 8 :
- .
1. 6 1H / . 6 8
9 - < 9 - 0 - . 4 / . 6 8
- < 9 - 0 1I .
,/
6 -
- .
,8 0
,/
8 0 4 9 / 6 / E #
8
25
20
15
10
5
−5
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
10 20 30 40 50 60 70 80 90 100
11.
.
- , 2 9 G 1H 8
-
, - ! -
7 - 9 4 1H / , 9 - < 9 - 0 - . 4 /
,/
H / . 4 16 / 6
6 -
1 ,I U - 4 9 8 0
/
,8 0
; 3 -
0 -
- . H 3 - . 4 9 /
,/
/ 9 /
8 . 0 3 - ,8
H ,/ 0 - :
,3 - 2 8
6 -
7 /
/
0 3
0 3
H / 0 /
- .
- U < 9 - 0 /
3 .
4 1- U < 8
E
4
< / 9 4 1 H 3 ,/ 9
1/ 9 1/ U
9 - 2 9 - 0 /
/ 9 /
- . 4 /
0 3
8 . 0 3 - ,8
7 /
/
/
6 1H 4 / 9
H / 0 / E
a.
3 4 / .
b.
3 4 1- U < 8
c.
3 , - 0
d.
F
,- ! 8 0
- 0 4 ,/
6 -
,/
H / 0 /
/ 9 /
6 -
8 . 0 3 - ,8 ,/
/ 9 /
2 / 0 4 /
< - . 6 1- . 4 -
8 . 0 3 - ,8
< / 9 /
6 - , 0 - 2 U - . 4 8
6 -
19
/
9 - H 4 /
,/
(3;1,2) (3,15;1)
1
0 -
; 3 -
e.
0 / 5 -
V 8 . /
3 / 9 /
; 3 -
- 0 4 U 4 8 6 8
6 -
8 . 0 3 - ,8
7 17 -
- .
- , H 8 0 4 / 6 8
8 H H 16 - . 4 / , 6 -
,/
/ 3 4 8 < 10 4 /
. 8 9 4 - : - .
H / 0 / 0 3
4 9 / . 0 < 8 9 4 -
3 4 1 ,1V / 9 < 3 6 8
1 .2
(3.15;1)
0 .8
0 .4
8:00
12.
.
F - U
0 14 18
C
@ 6 -
/ . /
6 U
6 - 0 4 1. 8
,/
0 -
G / U
7 1/ ! - : - .
-
5 1; 3 -
; 3 -
, - ! -
- .
D
:
7 - 9 4 1H / ,: -
- , < ,/ . 8
A : - .
/
- . 4 9 -
9 / V I .
/
/
,/
C
H / 6 /
,/
U
, - 0 < / H 18
19 8 2 8 4 E
6 -
- , 9 - H 8 9 9 16 8 E
.
6 -
7 / H / H 18 . - 0
7 1/ ! / 9 - , - ! -
/
3 . /
/
,/
H 8 0 4 /
7 - ,8 H 16 / 6
- .
H / 9 9 8 E
,
< 9 8 U - 6 18
6 -
" 8 9 1V 8 . 4 / , 9 - < 9 - 0 - . 4 -
- , 4 1- U < 8
9 - H 8 9 9 16 8 E
,8 0
6 10 4 / . H 1/
E
/ 4 / ; 3 17 /
@ @
H / 9 4 - 0 1/ . 8
C E " 8 9 / 0
3 4 1 ,1V / 6 /
- 6 9 8
6 -
5:30
3:00
2 9 G 1H / U - . 4 -
H 8 9 9 - 0 < 8 . 6 - .
< / 9 /
1 , 1/
- . H 3 - . 4 9 /
" E - < 9 - 0 - . 4 -
a.
b.
F / . 4 /
9:00
< 3 . 4 8 0
9 - H 8 9 9 16 /
1. 6 1H / . 6 8
,/
- 0 H / ,/
- ! -
6 10 4 / . H 1/
- , 4 1- U < 8
- 0
- ; 3 1 7 / ,-
/
c.
/ 2 /
,/
2 9 G 1H /
; 3 -
9 - < 9 - 0 - . 4 -
4 8 6 8
- ,
7 1/ ! - E
d.
- 4 - 9 U
1. -
,/
- H 3 / H 1I .
; 3 -
9 - < 9 - 0 - . 4 /
,/
f (x )
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
6 10 4 / . H 1/
- .
G 3 . H 1I .
6 - , 4 1- U < 8
, , U
- ,/
e.
- 4 - 9 U
1. -
-
- . 3 . H 1/ 6 8
g.
- 4 - 9 U
1. -
f (7 )
h.
- 4 - 9 U
1. -
< / 9 /
i.
, < 3 . 4 8
j.
, U 8 6 1G 1H / 9
3 -
0 12 . 1 G 1 H / 6 8
U
6 -
1. 2 9 - 0 8 0
< 8 9
A
@
0 8 5 9 -
b.
3 ,- 0
c.
3 . 4 8 0
14.
. /
H / 6 /
0 1
,/
/ 2 /
,/
b.
/ ,H 3 ,-
9 -
6 -
?
6 -
,/
G 3 . H 1I .
6 10 4 / . H 1/
f (x ) :
/
; 3 -
8 5 4 - . 16 8 0
/
@
9 - < 9 - 0 - . 4 /
6 -
,/
7 - . 4 / 0
@
B
- / H 4 / U - . 4 -
- ,
9 - 7 10 4 /
U 0
U 0
U
/ ,2 - 5 9 1 H / U - . 4 -
" : - . 4 9 -
U
- ! - U < ,/ 9
< 8 9
6 -
- < 9 - 0 . 4 - ,/
- ! - U < ,/ 9
< 8 9
- 0
! 3 0 4 1G ; 3 - ,8
G 3 . H 1I . E
@ @
- .
,/
- ,
4 - 9 H - 9 /
U
10 U
/ , ,
1. 2 9 - 0 8 0
6 -
,8 0
< 8 9
@ @ @
A
,/
; 3 1. 4 /
< ,/ . 8
- 0
0 - U / . / ,
,8 0
8
I U 8
" 8 9 /
H / 9 4 - 0 1/ . 8
6 -
?
@ @
< 3 5 , 1H 16 / 6
E 8 0
; 3 -
0 8 .
- ,
- ! - U < ,/ 9 - 0 E
3 4 1 ,16 / 6
0 1
6 - 5 - 9 .
0 -
D
7 - . 6 - .
7 - . 6 - 9 0 -
@ @
C
< / 9 /
- ! - U < ,/ 9 - 0 8 5 4 - . - 9
3 . / 0
3 4 1 ,16 / 6 - 0
0 - U
/ . / ,- 0
6 -
/ ,
8 9 2 / . 1V /
? @
. - .
,/
7 - ,8 H 16 / 6
H / 6 /
6 -
@ @ @
E
,/
3 4 1 ,16 / 6 - 0
G 3 . H 1I .
I
U
3 . /
- . 8 0 :
- H 3 9 0 1I . E
0 1
0 -
, 7 1/ ! -
0 3 < - 9 / .
,/ 0
4 1- . -
? @
3 .
7 / ,8 9
< - 9 0 8 . / 0
6 -
" / H - .
3 . /
D @ @
E
@ @ @
U
9 - 5 / ! /
< 8 9
D
6 - ,
/
G 3 . H 1I .
7 1/ ! - 9 8 0
d.
0 4 / 5 ,- V H /
3 .
U 1U
$
+ % 6 /
- , < 9 - H 18
6 -
,/
- H 3 9 0 1I .
6 - < - . 6 1- . 6 8
6 - ,
.
U - 9 8
6 -
< - 9 0 8 . / 0 E
; 3 -
" / 2 /
6 -
9 - < 9 - 0 - . 4 /
,/
- ,
1. 2 9 - 0 8
4 8 4 / , 6 -
,/
/ 2 - . H 1/
- .
G 3 . H 1I .
6 - ,
.
U - 9 8
2 9 G 1H /
< - 9 0 8 . / 0
6 - 5 - .
19
- .
,/
- H 3 9 0 1I .
< / 9 /
; 3 -
- ,
1. 2 9 - 0 8
6 -
,/
/ 2 - . H 1/
0 - /
8 E
) U - 9 8
- U < 9 - 0 /
; 3 -
2 9 G 1H /
,/
. /
6 -
0 8 .
7 1/ ! - 0
c.
,/
< - 9 0 8 . / E
/ , ,-
6 -
16.
6 -
6 -
2 9 G 1H /
,/ 0
=
6 -
< - 9 4 - . - H -
G 3 . H 1I .
@ @ @
0 -
a.
15.
7 / ,8 9
- ! - U < ,/ 9 - 0
/ 2 - . H 1/
< - 9 0 8 . /
,/
0 - 9 .
U - . 8 0
; 3 1. 2 9 - 0 8 0
,/
D
6 -
f (3 , 5 )
- , 7 / ,8 9
7 - . 4 / 0
,8 0
0 H 9 15 /
- , 9 / . 2 8
f ( − 1)
< 3 5 ,1H / H 1I .
a.
4 1- . -
( 2.5 , 200 )
8 6 1G 1H /
, H 8 0 4 8
1. 18
6 - , < 9 8 5 ,- U /
f.
0 -
13.
, 6 8 U
6 -
- , 6 8 U
4 / - .
6 -
,/ 0
8 2 8 4 & * 10
1. 18
% G 3 . H 18 . - 0
H 8 5 9 /
@ @ @
A
% < 8 9
- , < 9 1U - 9
'
1 ,I U - 4 9 8
# 9 - H 8 9 9 16 8
! I
G 9 / H H 1I .
( $ "
# 0 ≤ x ≤ 10
% , .
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
% - +
% +
* %  2 + 4 t si 0 ≤ t < 2

 6 + 2 t si 2 ≤ t < 4
p (t ) = 
si 4 ≤ t < 12
 14
 50 − 3 t si 12 ≤ t < 16

% +
a.
b.
* " % * . & % . t = 16
% , - t =0
% . & . & . . 17.
5
4
* % % a.
3
b.
!
c.
#
d.
$
e.
$
2
1
-4 -3 -2 -1
-1
1 2 3 4 5
f.
g.
h.
i.
j.
k.
l.
" % % % * .
% % * .
" " " " " " " " " " " " " " " " " " " " " "
* .
" " " " " " " " " " " " " " " " " " " " " "
- . " " " " " " " " " " " " " "
- .
" % " " " " " " " " " " " "
+ %& & & & & & & & & & & &
! % & & & & & & & & & & &
% '
" " " " " " " " " "
% , ' " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " "
) ( ) * + ) ,- .
% * % ! . /0 % % * % ! . /0 % * % ! . /0 ) ( ) * + ) ,- .
) ( ) * + ) ,- .
18. Describa el proceso para obtener la gráfica de
usar tabla de valores.
a.
A partir de la función y = x
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
y = mx + b
b.
- % % - % '
* 1
2 /
/
/
" " " " " "
en un sistema de coordenadas sin
A partir de la función
y = mx + b
19. Una función en términos de valor absoluto en su forma más general se puede escribir de la
forma y = f ( x ) = a x + b + c con
a , b , c ∈ ℜ y a ≠ 0 determine:
a.
Cuál es la constante y de qué tipo para que genere un desplazamiento vertical hacia arriba de
la función g ( x ) = x
b.
Cuál es la constante y de qué tipo para que genere un desplazamiento vertical hacia abajo de
la función g ( x ) = x
c.
Cuál es la constante y de qué tipo para que genere una dilatación de la función g ( x ) = x
d.
Cuál es la constante y de qué tipo para que genere una contracción de la función g ( x ) = x
e.
Cuál es la constante y de qué tipo para que genere una traslación horizontal a la derecha de la
función g ( x ) = x
Cuál es la constante y de qué tipo para que genere una traslación horizontal a la izquierda
de la función g ( x ) = x
f.
g.
Cuál es la constante y de qué tipo para que genere una reflexión respecto al eje x de la
función g ( x ) = x
20. Con cualquiera de los métodos anteriores grafique::
9
8
7
6
f (x ) =
g (x ) = − 2 x − 2
y
l ( x ) = 3 x + 2 en el siguiente sistema
de coordenadas
5
4
3
2
1
-9 -8 -7 -6 -5 -4 -3 -2 -1-1
1
x +1
2
1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
Con base en las gráficas llene la siguiente tabla:
1.
2.
3.
4.
5.
6.
7
8.
9.
10.
11.
12.
f (x )
g (x )
Dominio
Rango
Coordenadas del corte con el eje
x
Coordenadas del corte con el eje
y
Valor máximo de la función
Valor mínimo de la función
Encuentre la ecuación de cada
función como una función definida
a trozos.
Tipo de simetría
Intervalo de:
Crecimiento
Decrecimiento
Valor de la función para:
x =0
x =3
x = −6
x = −3
Para que valores de x es:
La función igual a 2
La función igual a –6
Intervalos donde la función está
por:
Encima del eje x
Debajo del eje x
21. Sea f (x ) = 3 x − 2
−3
∀x ∈ ℜ
Haga la gráfica de f en el sistema de coordenadas con lo aprendido en el taller.
Con base en la gráfica determine:
6
5
a. El valor de:
4
3
f (−1) = ,
2
1
-6 -5 -4 -3 -2 -1-1
-2
-3
-4
f(0) =
1 2
3 4
5 6
f(4) =
b. El valor mínimo de f (x )
-5
-6
c.
El rango de f (x )
d. Determine las ecuaciones de las rectas que conforman la gráfica.
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
l (x )
e. Para que valores de x , es f (x ) < 0 ?
f.
Para que valores de x , es f (x ) > 0 ?
g. Para que valores de x , es f (x ) = 0 ?
h. Ecuación del eje de simetría?
i.
Es
f ( −1) < 3 ,
j.
Si
- 1 ≤ x ≤ 4 entonces 6 ≤ f (x ) ≤ 3
por qué?
4
22. Encuentre la expresión con valor absoluto que
representa la función dibujada en el siguiente plano
cartesiano:
3
2
1
-4 -3 -2 -1
-1
1
2
3
4
-2
-3
-4
-5
23. La gráfica dibujada en el siguiente plano cartesiano se desplaza 3 unidades a la izquierda y se
refleja sobre el eje de las y:
y
4
a. Encuentre la ecuación de la nueva función con
su respectivo dominio).
3
2
1
−6 −5 −4 −3 −2 −1
−1
x
1 2
3 4
b. Encuentre la ecuación de la función en términos
de valor absoluto.
5 6
−2
−3
c. Determine el rango
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
24. Considere la siguiente inecuación − 4 x + 1 ≥ x − 2 .Encuentre el conjunto solución
3
6
5
a.
Utilizando el método gráfico
b.
Utilizando el método de puntos divisorios
4
3
2
1
-6 -5 -4 -3 -2 -1
-1
1
2
3
4
5
6
-2
-3
-4
-5
-6
25. Encuentre el conjunto solución de
x −5 ≤ x +3
6
5
4
a.
Usando el método gráfico.
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
b.
26.
Compare los conjuntos solución, que puede concluir?
y = −2x −2 − 2
y
3
2
1
x
-3
-2
-1
1
2
3
-1
-2
-3
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
1
2
3
4
5
6
−1
2
y = − 2 x + 1 + 4 −1
3
1
−2
4
−3
27.
y
5
x
1
−1
2
3
−2
−3
−4
−5
y
4
28.
3
2
1
−3
−2
−1
x
1
−1
2
3
4
5
6
7
8
−2
−3
−4
29.
30.
a.
b.
c.
d.
f (6 ) f (0 ) f (2 )
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
f (x − 2 ) f (x ) − 2
y
f (x )
1
x −1 + 2
2
y =− −
3
2
1
-3
-2
-1
1
2
3
-1
-2
-3
31.
a.
b.
c.
y1 = x + 1 − 3
y2 = − x −1
3
y
32.
a.
b.
f (x ) = 3 x − 5 − x + 2
∀x ∈ ℜ
f (−4 ),
f (0 )
y
f (6 )
y = k − 4x
3
4
c.
d.
e. Haga la gráfica de f para −10 ≤ x ≤ 30
f. Resuelva la ecuación para f (x ) = 13
33. Determine las ecuaciones de las siguientes familias de funciones:
7
4
6
5
3
4
2
3
2
1
1
-7 -6 -5 -4 -3 -2 -1
-1
1 2 3 4 5 6 7
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
-4
-3
-2
-1
1
-1
2
5
34.
% & # $ ! $ $ # ! " '
ALTURA EN m.s.n.m.
3000
3000
Ipiales
Pasto
2500
2500
Tangua
Chachagui
2000
2000
Piendamó
Rosas
El Pedregal
Popayán
1500
1500
El Tablón
(S de Quilichao
1000
1000
S de Cali
El Bordo
Mojarras
500
500
40
( 80
& + , -
8 6 9 :
5 6 7
5 6 7
8 6 7
( # 7
#
# @
6 G
120
120
. /
160
160
200
200
A
320
320
* 360
360
400
400
" 440
480
440
48
0
DISTANCIA EN km
.
/ 0 1 - /
< < =
B ; ! C 6 :
H
. , 2 1 / 3 + , /
>
. 4
? D > E >
F =
? D I > >
D > D
? ( :
( 6 J K 7
D E L I
D L =
? @ :
5 6 5
D E > >
D I M
? # ;
N :
G
:
# ;
@ :
O 6 @ @ 6 5
8 6 N ; H
7
! C 6 ! C 6 9 B ( 6 5 8 :
8 6 7
# ;
Q
0 U
9 B 6
( # @ # 9 6 ;
I > >
M M <
? P = >
M E =
? ? D M = >
L L I
M > > >
L I =
? F D >
? M = M E ( 6 ; # 5
3
)
280
280
V U W U U
R
X V Y Z
U V
* '
! 6 ; #
240
240
* U U Z U
M F > >
F L I
? D I > >
F = L
? M < > >
F < E
? " W V
C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
[
W V \ U S $ $ $
$T
\ V V U W Z ] Z Q
+ / 0 ,
a.
b.
c.
d.
! R A
A
6
M I
? )
R * ! % & 9 * # e.
* R " # DISTANCIA
0
0
45000
101
101000
135000
182000
ROSAS
182
EL BORDO
229
229000
MOJARRAS
275
275000
EL TABLÓN
338
338000
CHACHAGUI
385
385000
PASTO
410
410000
TANGUA
438
438000
EL PEDREGAL
453
453000
IPIALES
497
497000
%
g.
h.
% % & 2 ] [! ]
% ALTURA (m)
45
+ [ ]
$
DE CALI (m)
& 135
2 Z ] % PIENDAMÓ
# W Y Z POPAYÁN
f.
+ []
] Z DISTANCIA
SANTIAGO DE CALI
( ) DE CALI (Km)
SANTANDER DE QUILICHAO
2 Z ] R " $
CIUDAD
# $ ! # ;
"
% * " $
S # Diferencia
Diferencia
en alturas
en distancia
& T
Pendiente
Pendiente
Corte en y
en %
5 ! % $
! # ' V " & )
& * ) )
& % ( " " @ )
)
% " # N C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
# & % % $
* % )
U U
* )
'
4 [
# i.
) " * ; j.
? $
[ Z M E
? % 6
l.
I a.
b.
6
m.
5 "
% ( " % * L =
% R * I >
? " % & % )
% R
" % D
% M E P >
)
$ 8
% 5 * + \ )
( $
1 Z % & * R
4 [
R " < >
$ # V [
% 2 Z V ]
)
M >
3
U V 2 V ( 0 U
[ U
7
R
$
" )
0 = $< I <
% )
( % & ! R ! " % $ $ $
<
( "
M P D M
! k.
U + \ $
V V U
[
& % * " F >
# W Y Z
"
% * " ! R ) D M
? 5 ! R * ; "
# * " )
M > > >
" C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
8 R )
( )
8 * n.
% * % & ) $
o.
# % % "
# ( ( R C:\Archivos Pagina\2003_2\Material\15_Funciones_a_Trozos.doc
) % 8 # (