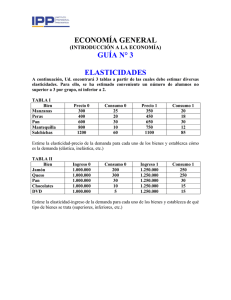
Elasticidad de la demanda por medicamentos en el mercado

Elasticidad de la demanda por
medicamentos en el mercado
farmacéutico privado en Colombia1
The elasticity of drugs demand in Colombia’s
pharmaceutical market
Johanna Vásquez Velásquez*, Karoll Gómez Portilla**
Elkin Castaño Vélez***, José Vicente Cadavid Herrera****
Andrés Ramírez Hassan*****
Recibido: 20/03/2013
Aprobado: 21/05/2013
Este trabajo de investigación fue financiado por el Comité para el Desarrollo de
la Investigación (CODI) de la Universidad de Antioquia y por la Universidad Eafit.
Agradecemos a Juan Esteban Vélez, estudiante de Maestría en Economía, por su
colaboración en el procesamiento de la información estadística. Igualmente, agradecemos los valiosos comentarios y opiniones del grupo de expertos consultados y
la colaboración de Econometría Consultores, la Cámara Farmacéutica de la Asociación Nacional de Empresarios de Colombia (ANDI) y al IMS por facilitar las bases de
datos. Las ideas y opiniones aquí expresadas son responsabilidad de los autores.
*
Docente e investigadora, Grupo de Econometría Aplicada (GEA), Centro de Investigaciones Económicas (CIE), Universidad de Antioquia, Colombia [[email protected]]
**
Docente e investigadora, Universidad Nacional de Colombia, Sede Medellín. Investigadora, Grupo de Econometría Aplicada (GEA), Centro de Investigaciones y
Consultarías (CIC), Universidad de Antioquia, y Centro de Estadística Aplicada a
Estudios Socioeconómicos (Ceaes), Universidad Nacional de Colombia, sede Medellín. [[email protected]]
***
Docente, investigador y coordinador, Grupo de Econometría Aplicada (GEA), Centro de Investigaciones y consultarías (CIC), Universidad de Antioquia, Colombia.
Docente en la Escuela de Estadística, director del Centro de Estadística Aplicada
a Estudios Socioeconómicos (Ceaes), Universidad Nacional de Colombia, sede
Medellín, Colombia [[email protected]]
****
Magíster en Economía Aplicada. Docente e investigador, Economía y Finanzas,
Centro de Investigaciones Económicas y Financieras (CIEF), Universidad EAFIT,
Colombia [[email protected]]
*****
Doctor en Estadística. Docente e investigador, Profesor asociado, Grupo de
Estudios en Economía y Empresa, Escuela de Economía y Finanzas, Centro de
Investigaciones Económicas y Financieras (CIEF), Universidad EAFIT, Colombia
­[[email protected]]
1
ISSN 1657-4206 I Año 17 I No. 36 I enero-junio 2013 I pp. 147-172 I Medellín-Colombia
148
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
Resumen
Esta investigación estimó la elasticidad de la demanda intramolecular, marca y genérico, para tres patologías trazadoras, hipertensión esencial, diabetes e hiperlipidemia,
en el mercado ético y privado colombiano, a partir de una especificación dinámica del
modelo AIDS basado en técnicas de cointegración. La estimación de la elasticidad de la
demanda intramolecular permite concluir que tanto medicamentos de marca como genéricos son inelásticos ante cambios en su precio, son bienes de lujo según elasticidad
gasto y parece existir sustitución intramolecular por el signo obtenido de la elasticidad
de sustitución.
Palabras clave
Elasticidades, mercado farmacéutico, modelo AIDS, cointegración.
Abstract
Based on a dynamic specification of the AIDS model arisen from cointegration techniques,
this research estimated the elasticity of the intra-molecular, brand and generic demand
for three tracer conditions: essential hypertension, diabetes and hyperlipidemia both
in the non-profit and private Colombian market. The estimate of the intra-molecular
demand elasticity allows us to conclude that both brand-name and generic drugs are
inelastic to price changes, they are luxury goods according to expenditure elasticity and
intra-molecular replacement seems to exist due to the elasticity of substitution.
Keywords
Elasticity, pharmaceutics market, AIDS model, cointegration.
Clasificación JEL: D11, D82, I11
149
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
1. Introducción
La industria farmacéutica se caracteriza por la gran inversión que realiza en investigación y desarrollo (I&D) y publicidad; por las altas tasas de renovación y la consecuente
diferenciación de productos, y por la generación de beneficios financieros a las empresas y mejoras en el bienestar de los consumidores al reducir el número de muertes y
los días de incapacidad y de hospitalización. Asimismo, la interacción entre vendedores
y compradores propicia un ambiente de mercado que difiere de otras industrias; particularmente se destaca la participación de varios agentes en la adquisición del bien
de consumo, donde las características de la demanda dependen del sistema de salud
imperante, los problemas de información derivados de la relación principal-agente,2 una
elasticidad del precio de la demanda que en muchas ocasiones depende de la inversión
en publicidad, y los beneficios propios de los monopolios legales que se otorgan a través
de la protección vía patentes (Santerre & Stephen, 2000).
La demanda es guiada por el paradigma estándar de maximización de la utilidad a partir
del consumo de la mejor cesta de bienes que puede adquirir un individuo con completa
información. En este sentido, la decisión de consumo final depende: 1) de las características del producto, 2) del precio, 3) de las características del consumidor, y 4) del uso;
consideraciones que hacen del análisis de elección del consumidor en el mercado de
medicamentos un tema particularmente complejo. Por un lado, las características del
producto y el precio dependen del tipo de productor: marca o genérico, y de la enfermedad que van a tratar; y por el otro, el consumidor y quien decide el consumo, que en
la mayoría de los casos no son la misma persona. Además, los consumidores pueden
actuar en dos tipos de mercados, en el de medicamentos de venta libre, conocidos
mundialmente como OTC (Over The Counter), o en el mercado ético, que funciona bajo
prescripción médica. Dichas características hacen que la demanda sea considerada
como un proceso de múltiples etapas que dependen del sistema de salud imperante
(Merino, 2003).
En cuanto a las posibilidades de sustitución, se han establecido teóricamente dos vías
para una determinada clase terapéutica, esto es, intermolecular e intramolecular. La
primera representa la sustitución entre componentes activos que sirven para la misma
2
La relación principal-agente se establece cuando un agente económico contrata a otro agente para que
tome decisiones económicas.
150
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
enfermedad dada su clasificación anatómica, terapéutica y química conocida mundialmente como ATC (Anatomical Therapeutic Chemical). La segunda se refiere a la posibilidad de comprar el medicamento por su nombre de marca o su denominación genérica
(Stern, 1996).
Otro factor importante que opera del lado de la demanda se refiere a las relaciones de
agencia entre consumidores (principal), médicos y farmaceutas (agentes), y entre los
médicos y el sistema de salud vigente. Dichas relaciones están mediadas por problemas
de información incompleta y asimétrica, lo cual puede generar problemas de demanda
inducida, debido principalmente al desconocimiento que tiene el principal de la efectividad del medicamento elegido y formulado por el agente. Además, puede presentarse
riesgo moral debido al exceso de demanda por medicamentos que puede ser ocasionado por la presencia del tercer pagador en el mercado, y selección adversa por la asimilación de señales de calidad emitidas ya sea por los laboratorios, que obtienen patentes
y producen medicamentos de marca y genéricos, o por las entidades aseguradoras que
son eficientes en la entrega de ellos.
Así y según las consideraciones mencionadas del lado de la demanda, se encontró que
los estudios a nivel internacional se pueden clasificar en dos tipos, los que estiman la
elasticidad precio de la demanda y aquellos que analizan las variaciones en la sustitución de productos cuando los sistemas de aseguramiento restringen los medicamentos
prescritos y distribuidos. En el primer grupo se pueden destacar los estudios realizados
por Fisher, Cockburn, Griliches y Hausman (1997), Merino (2003), Hellerstein (1994); y
en el segundo, los de Onishi (1997), Crawford y Shum (2000). Más recientemente, trabajos como el de Chaudhuri y Golberg (2003) realizan estimaciones de elasticidad de la
demanda con el fin de analizar asuntos como el impacto de las patentes en el bienestar
del consumidor. Por otra parte, en Colombia investigaciones como las de Zuleta y Parra
(1999), Zuleta y Junca (2001), Mejía et al. (2002), Jaramillo y Restrepo (2003) y Archila
et al. (2005), entre otras, se han concentrado en estudiar el impacto que tendría la protección de patentes sobre los precios y el acceso a medicamentos, sin estimar y analizar
elasticidades precio y precio cruzada de la demanda.
El objetivo de este trabajo es estimar la sustitución intramolecular precio, precio cruzada y gasto de la demanda, por marca y genérico, para tres patologías trazadoras,
151
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
hiperlipidemia, hipertensión esencial y diabetes, inscritas en el grupo de medicamentos
ambulatorios y hospitalarios, y comercializados en el mercado privado colombiano.3 El
artículo se desarrolla en cinco partes: la primera presenta las principales características
teóricas de la demanda por medicamentos; en la segunda se realiza una caracterización
del sector en Colombia, incluyendo su marco regulatorio; en la tercera se describe la
metodología utilizada para la elección de patologías trazadoras y medicamentos, además de la especificación del modelo EC AIDS para la estimación de la elasticidad de la
demanda; en la cuarta sección se muestran los principales resultados, y finalmente se
presentan las conclusiones y discusión.
2. Caracterización teórica de la demanda en el mercado de
medicamentos
En el mercado de servicios médicos pueden diferenciarse tres tipos de bienes: los públicos, los privados de bajo costo y los privados de alto costo (Caves, 1991). Los primeros
se refieren a las campañas de promoción y prevención, tales como las jornadas de vacunación para niños menores de cinco años, actividades generalmente realizadas por el
Gobierno o por entidades sin ánimo de lucro. Los segundos se refieren a las consultas
médicas que fácilmente pueden pagarse como gasto de bolsillo y, por último, se crean
los planes de aseguramiento para los bienes privados de alto costo, con el fin de proteger al consumidor de pérdidas financieras catastróficas. Así, cada uno de estos bienes
está asociado a diferentes tipos de enfermedades, por lo que se asocian también a
distintos tipos de medicamentos que pueden ayudar en la recuperación de la salud
después de los episodios de enfermedad.
En este sentido, la demanda de medicamentos podría considerarse como una demanda
derivada de la demanda por servicios médicos, ya que esta última se configura como el
punto de partida para la prescripción médica (mercado ético), distribución y consumo
final. En consecuencia, es necesario describir los bienes o productos que se comercializan en el mercado farmacéutico, el establecimiento de precios y los diversos agentes
que participan en la demanda del bien final.
3
Cáncer de mama y VIH sida, dentro del grupo de medicamentos de alto costo, fueron inicialmente considerados en el estudio. Sin embargo, después de realizar un análisis basado en el ATC para garantizar la
sustitución intermolecular e intramolecular, estos grupos tuvieron que ser descartados.
152
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
2.1. Bienes o productos y precios
La clasificación depende de tres elementos básicos: de la enfermedad que se va a tratar —clase terapéutica—, del ingrediente activo —molécula— y del productor —pionero,
imitador o genérico— (Crawford, 2005). Además, dependiendo de la forma de comercialización del medicamento se pueden considerar dos tipos de mercados: el ético y el de
venta libre. En este sentido, y de acuerdo con la teoría sobre diferenciación de productos
desarrollada por Caves y Williamson (1985), los medicamentos incluidos en una misma
clase terapéutica que contienen el mismo ingrediente activo, independientemente de su
productor: marca o genérico, se consideran teóricamente como sustitutos imperfectos
unos de otros, ya que difieren en sus precios, formas de presentación, concentración,
frecuencia de uso, efectos secundarios y dosis, entre otros atributos. Así, el hecho de
que un consumidor considere dos marcas del mismo ingrediente activo como dos bienes diferentes permiten a cada productor enfrentar una curva de demanda con pendiente negativa y tener poder de mercado.
En cuanto a los precios, estos dependen del tipo de proceso de producción adoptado por
cada empresa, es decir, si es pionera, imitadora o productora de genéricos (Grabowski
& Vernon, 1987). Para las primeras, llevar medicamentos al mercado implica una alta
inversión en I&D que en la mayoría de los casos cuenta con baja probabilidad de éxito
técnico y un gran éxito comercial, debido en parte a la ventaja de la protección de patentes. Por tanto, los precios de venta son altos, con el fin de recuperar la inversión en
I&D.4 Las empresas imitadoras son aquellas firmas que invierten en I&D sobre una familia conocida de productos con el objetivo de desarrollar ventajas marginales sobre la
calidad terapéutica; en algunos casos estos medicamentos tienen usos para patologías
diferentes y generalmente dichos productos entran al mercado con precios de venta
más bajos que los pioneros.
Finalmente, las productoras de genéricos gastan recursos en diseño y formulación, y se
dedican a comercializar medicamentos a los cuales se les venció la protección otorgada
por la patente bajo una versión simple del nombre químico, el cual describe la estructura molecular de su ingrediente activo. En consecuencia, estos productores afectan las
ventas de los pioneros y los imitadores, debido al bajo precio que cobran. Sin embargo,
4
Es importante anotar que los productores innovadores también pueden lanzar al mercado imitadores y
genéricos.
153
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
se ven afectados por las barreras a la entrada generadas por las empresas establecidas
y por la fidelidad a la marca generada en los consumidores.
2.2. Tipos de agentes
Dado que la demanda realizada en el sector farmacéutico se deriva del consumo de
servicios médicos, esta no solo depende del consumidor final, sino del comportamiento
de los médicos, quienes prescriben, y de los farmaceutas que actúan en hospitales y
droguerías de ventas al por menor y son quienes finalmente entregan el medicamento
prescrito. Así, se tendrán como agentes tomadores de decisiones a los médicos y a distribuidores, y a los pacientes como consumidores finales. Las relaciones entre dichos
agentes están mediadas por unas particularidades que son importantes de analizar
desde el punto de vista económico.
En este sentido, pueden distinguirse tres tipos de consumidores: 1) el comprador directo, quien participa en el mercado de OTC o medicamentos de venta libre, para este tipo
de consumidor posiblemente la demanda sea elástica, ya que la posibilidad de elección,
sujeta a su restricción presupuestal, está más ligada al precio; 2) el médico como agente del paciente: este tipo de consumidores participarán en el mercado ético; y 3) los
pacientes con planes de salud que cubren la entrega de medicamentos.
En el caso del mercado ético, el médico elige entre los medicamentos con el mismo ingrediente activo, el que mejor se ajuste a las características del paciente según su enfermedad (Hellerstein, 1998). Luego de la primera decisión, el médico elige el tipo de producto,
ya sea de marca o genérico; en este caso el médico, dependiendo de su sensibilidad a
las variaciones en los precios, puede actuar como agente perfecto o imperfecto de sus
pacientes (Fischer et al., 1997).5 Ahora, bajo la presencia de seguros de salud, el consumidor generalmente no paga el costo total de los medicamentos que consume y además,
médicos y farmaceutas pueden estar obligados a recetar y a distribuir los medicamentos
del plan de salud comprado; según Onishi (1997), este tipo de prácticas en el mercado
han aumentado el grado de sustitución entre medicamentos de marca y genéricos.
5
Serán perfectos si no obtienen beneficios derivados de la elección de los medicamentos que recetan
y consideran el nivel de precios en la prescripción. Por el contrario, serán imperfectos si consideran
que medicamentos con la misma molécula pero bajo nombres distintos en su presentación de marca y
genérico, no son sustitutos y tienen incentivos monetarios o no monetarios para la prescripción de medicamentos específicos.
154
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
3. El sector farmacéutico en Colombia
Desde de 1993 funciona en Colombia el Sistema General de Seguridad Social en Salud
(SGSSS), cuyo principio básico es el aseguramiento universal de la población nacional
bajo dos sistemas o regímenes de aseguramiento: régimen contributivo y régimen subsidiado.6 En 2006 la cobertura del sistema era del 79,27% de la población; 36,28% en el
régimen contributivo y 42,99% en el régimen subsidiado (Así vamos en salud).7 En este
sistema, las empresas aseguradoras o entidades promotoras de salud (EPS) son las
encargadas de la afiliación y de suministrar el plan único de protección integral denominado Plan Obligatorio de Salud (POS) e incluye atención preventiva, médico-quirúrgica
y medicamentos. Dichas empresas contratan a su vez la entrega de servicios de salud
con instituciones prestadoras de servicios de salud (IPS) y/o profesionales.
En cuando a los medicamentos, la ley establece que la prescripción a los afiliados a la
seguridad social se hace bajo su nombre genérico y sujeta al listado establecido, por lo
que dadas las particularidades mencionadas en el sistema de salud colombiano, coexisten dos submercados de medicamentos: 1) el institucional, para los afiliados al sistema
de seguridad social, y 2) el privado. En ambos casos las diferencias más importantes
se presenta en los canales de distribución de medicamentos al consumidor final y las
posibilidades de sustitución.
En el mercado institucional, los medicamentos son entregados por las IPS o por farmacias adscritas a la EPS del afiliado, y la sustitución entre medicamentos solo podría
presentarse entre medicamentos con la misma molécula, las cuales aparecen señaladas en el listado. No obstante, al revisar las moléculas y su clasificación ATC, el listado
de medicamentos al que tienen derecho los afiliados a la seguridad social no cuenta
con moléculas que puedan reemplazarse unas con otras. Por lo tanto, desde el punto
de vista económico no se podría hablar de bienes sustitutos, a nivel intermolecular o
intramolecular, debido a que es obligatoria la prescripción y distribución de medicamentos genéricos y esenciales. Por el contrario, en el mercado privado la sustitución puede
darse entre moléculas o entre productores de marca y genérico, y puede ser realizada
por quien prescribe, quien distribuye o quien consume.
6
En el régimen contributivo está afiliada la población con capacidad de pago y en el subsidiado la población pobre y vulnerable.
7
Información disponible en http://www.asivamosensalud.org/areas/aseguramiento.htm.
155
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
Esquema 1.
Estructura del mercado farmacéutico colombiano
Mercado Farmacéutico Colombiano
Regulación
Ministerio de la Protección Social
Instituto Nacional de Vigilancia
de Medicamentos y Alimentos –Invima–
Comisión Nacional de precios
Consejo Nacional de Seguridad Social en Salud
Mercado Privado
Medicamentos
Sustitución
Compradores
Distribuidores
Consumidor
Marcas y genéricos
Intermolecular e intermolecular
Personas naturales
o jurídicas y mayoristas
Farmacias y almacenes de cadena
Toda la población
Mercado Institucional
Genéricos
Ninguna
EPS, IPS y Secretarías Municipales y Departamentales
Farmacias,Operadores
lógicos e IPS
Afiliados a la seguridad social
Medicamentos
Sustitución
Compradores
Distribuidores
Consumidor
Fuente: elaboración propia, 2009
En el esquema 1 se muestra la organización del mercado de medicamentos en Colombia. Este se encuentra regulado por el Estado a través del Ministerio de la Protección
Social, el cual se encarga de expedir el Manual de Normas Técnicas de Calidad o las
Guías Técnicas de Análisis y desarrollar un programa permanente de información sobre
precios y calidad de los medicamentos, tanto para el mercado institucional como para
el privado. El Instituto Nacional de Vigilancia de Medicamentos y Alimentos (Invima),
La Comisión Nacional de Precios de Medicamentos (CNPM) y el Consejo Nacional de
Seguridad Social en Salud (CNSSS) son algunos organismos adscritos al Ministerio que
se encargan de aspectos específicos, tales como de la vigilancia sanitaria y control
de calidad, el establecimiento de una política de precios y la definición del grupo de
medicamentos esenciales en su presentación genérica, respectivamente, para el buen
funcionamiento del mercado.
156
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
A partir de 2006, con la Circular 004 de septiembre, la Comisión de Regulación de Precios planteó un nuevo modelo de regulación que buscaba proteger a los consumidores
y controlar posibles abusos de posición dominante por parte de productores, importadores y expendedores de medicamentos. Así se determinó el control de precios bajo
tres esquemas: 1) control directo, que se realiza tomando los precios de medicamentos
iguales, en términos de moléculas, concentración, presentación y forma farmacéutica,
y comparando los precios en nueve países de referencia; 2) libertad regulada, con criterios y metodología para que los productores y distribuidores determinen o modifiquen
los precios máximos; y 3) libertad vigilada, cuando los productores y distribuidores determinan libremente los precios, con la obligación de informar en forma escrita sobre
las variaciones y determinaciones de sus precios, de acuerdo a la metodología que la
entidad determine.
4. Metodología
4.1. Descripción general
Con el fin de limitar el grupo e identificar el conjunto de medicamentos a estudiar según
su importancia en términos de la política pública en salud, se consultó a expertos colombianos de distintas instituciones, quienes sugirieron tomar cinco de las patologías
trazadoras identificadas en el Estudio sobre la propiedad intelectual en el sector farmacéutico colombiano, desarrollado por Fedesarrollo y la Fundación Santa Fe de Bogotá.
Tales patologías fueron: hipertensión esencial, diabetes, hiperlipidemias con medicamentos de uso ambulatorio y hospitalario, y cáncer de mama y VIH sida. Para las patologías anteriores se tomaron aquellos componentes activos que estuvieran listados en el
Manual de Medicamentos y Terapéuticas del SGSSS.
La información utilizada fue donada por Econometría Consultores, la Cámara Farmacéutica de la Asociación Nacional de Empresarios de Colombia (ANDI) e IMS y corresponde
al mercado privado.8 Se contó con información mensual para cinco años, comprendidos
entre enero de 2000 y diciembre de 2004, sobre medicamentos que tuvieran registro
8
Aunque en el país existe información sobre prescripción para el mercado institucional, esta es de carácter privado y no pudo ser utilizada.
157
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
sanitario vigente a octubre de 2006 en el Invima y se realizó una actualización de los
nombres de marca asociados a cada componente activo. En este caso y dadas las etapas del proceso de demanda de medicamentos, la primera correspondería a la elección
de componente activo y la segunda a la elección de dicho componente según su nombre
de marca o genérico. En esta investigación, dado que no se contó con información sobre
la prescripción médica y dada la imposibilidad de dicha sustitución dentro del POS, solo
se modeló la sustitución intramolecular.
El IMS reporta los precios unitarios por concentración y las unidades de dosis vendidas
por el canal de distribución minorista privado, el cual se hace a través de las farmacias
colombianas. Esta distribución se realiza de todos los productos y formas farmacéuticas
existentes en el país, los cuales son clasificados según la clase terapéutica. En este
estudio, los precios y las cantidades están en unidades de dosis, por lo que todas las
concentraciones se convierten a una unidad de medida común.9
Se consultaron, además, los códigos de los componentes activos según su código ATC,
el cual fue obtenido del WHO Collaborating Centre for Drug Statistics Methodology, y se
identificaron sus posibles moléculas sustitutivas, por lo que se consideraron finalmente
tres patologías: hipertensión esencial, hiperlipidemia y diabetes10 con medicamentos
regulados por el sistema de libertad vigilada de precios.
Para la hipertensión esencial se tuvieron en cuenta inicialmente tres grupos de medicamentos, para un total de 36 medicamentos, 22% genéricos y 78% de marcas. En el caso
de la diabetes únicamente se contó con un grupo de medicamentos que cumple con
las especificaciones y contiene dos componentes activos sustitutos, para un total de
8 medicamentos. La hiperlipidemia contiene 2 grupos, el primero con 2 componentes
activos y el segundo con 4, esto unido a las marcas arroja un total de 39 medicamentos.
En total, las tres patologías suman un total de 83 medicamentos, que incluyen los componentes activos y las marcas asociadas. En la tabla 1 se presenta la lista de patologías
y medicamentos considerados.
La base de datos fue provista por Econometría Consultores S. A. bajo el consentimiento de la Cámara
Farmacéutica de la Asociación Nacional de Empresarios de Colombia (ANDI) y del (IMS).
10
Después de realizar un análisis basado en el ATC para garantizar la sustitución intermolecular e intramolecular, cáncer de mama y VIH sida tuvieron que ser descartados.
9
158
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
Tabla 1.
Patologías y medicamentos estudiados
Patologías
Medicamentos
Sulfamidas, derivados de la urea
Hiperlipidemia Fibratos
HMG CoA inhibidores y reductores
Hipertensión ACE inhibidores,
esencial
llanos
derivados de Dihydropyridine
Antagonistas del
Angiotensina II,
llanos
Total general
Diabetes
Código
ATC
Componentes
activos
Marcas
Total
No.
Lab.
Concentración industrial
del mercado
A10BB
2
6
8
15
Alta
C10AB
2
26
28
40
Alta
C10AA
4
7
11
30
Alta
C09AA
3
12
15
56
Alta y media
C08CA
2
4
6
29
Alta
C09CA
3
12
15
19
Alta
16
67
83
189
Alta
Fuente: elaboración propia a partir de información del IMS, Invima y clasificación ATC.
Con la información mensual entre enero de 2000 y diciembre de 2004 para series de
precios, cantidades de medicamentos y el PIB real base 2004, se construyeron las cantidades e índices de precios agregados para los medicamentos genéricos y de marca
de cada una de las patologías en estudio. Asimismo, se construyó la serie de gasto total
real y las participaciones en el gasto de genéricos y de marca, así como los índices de
precios de Stone, Laspeyres y Paasche.11
4.2. Especificación del modelo casi ideal de demanda (AIDS)
En cuanto a la evidencia empírica derivada de estudios internacionales se puede concluir que independientemente del objetivo de los trabajos en los últimos años, la espe El índice de precios de Stone se construyó como la suma ponderada del logaritmo de precios de los medicamentos genéricos y los de marca, usando como ponderador la participación promedio de cada uno en el gasto. El índice de precios de Paasche se construyó como la suma ponderada de la razón entre los logaritmos de
los precios de los medicamentos genéricos y los de marca y el precio de estos en el periodo inicial, usando
como ponderador la participación promedio rezagada un periodo de cada uno en el gasto. Finalmente, el
índice de precios de Laspeyres, como la suma ponderada del logaritmo de precios de los medicamentos genéricos y los de marca, usando como ponderador la participación del periodo inicial de cada uno en el gasto.
11
159
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
cificación que ha predominado en el trabajo empírico ha sido la de modelos de elección
discreta. Sin embargo, dicha especificación tiene dificultades, relacionadas, principalmente, con la escasa disponibilidad de información necesaria para su estimación, como
las unidades demandadas por individuo según la prescripción médica. En consecuencia, trabajos recientes como los de Chaudhuri y Goldberg (2003) y Akbulutgiller (2008)
hacen uso de la especificación alternativa de sistemas de demanda casi ideales (AIDS,
por sus siglas en inglés),12 introducida por Deaton y Muellbauer (1980), ya que permite
modelar la demanda realizada por un consumidor representativo para luego obtener
la demanda agregada con relación al gasto. Así mismo, permite la modelación en dos
niveles considerando las posibilidades de sustitución y el orden en el que estas se podrían presentar en el mercado farmacéutico, es decir, primero se estudia la sustitución
intermolecular y luego la intramolecular.
La versión clásica del modelo AIDS, desarrollada por Deaton y Muellbauer (1980), supone que los consumidores tienen un ajuste al equilibrio en cada periodo de tiempo, sin embargo este supuesto es poco realista dado el consumidor, el cual no se ajusta instantáneamente ante cambios en los factores económicos, sino que existen ciertos hábitos que
suelen persistir en el tiempo (Anderson & Blundell, 1982, 1983). En consecuencia, los
resultados de la especificación y estimación de sistemas AIDS cuando se trabajaba con
datos de series temporales fueron criticados desde el punto de vista teórico, debido al
frecuente rechazo de las restricciones de homogeneidad y simetría y al desconocimiento
de las propiedades estadísticas de los datos,13 por lo cual se recurrió a especificaciones
dinámicas para resolver este problema. Anderson y Blundell (1983) proponen un sistema
AIDS en forma de modelo de corrección de errores, el cual es una versión dinámica del
modelo AIDS tradicional que incorpora la posibilidad de desequilibrios a corto plazo. Esa
es la especificación usada en este trabajo y que se describe a continuación.
Si todas las variables en el sistema de demanda son no estacionarias y están cointegradas, es decir, los residuales estimados de él son estacionarios, entonces las funciones
de demanda del modelo AIDS en forma de participaciones en el gasto se puede especificar como:
12
13
Almost Ideal Demand System.
Como por ejemplo la presencia de raíces unitarias en las variables del sistema, lo cual en muchas series
económicas resulta ser una implicación teórica del uso racional de la información disponible por parte
de los agentes económicos.
este trabajo y que se describe a continuación.
este trabajo y que se describe a continuación.
esteSiytrabajo
ydescribe
que
se
describe
continuación.
Si
las
variables
el
sistema
demanda
estacionarias
y están
cointegradas,
este trabajo
quetodas
selas
a continuación.
todas
variables
en en
elasistema
de de
demanda
sonson
no no
estacionarias
y están
cointegradas,
Si todas las variables en el sistema de demanda son no estacionarias y están cointegradas,
decir,
residuales
estimados
son
entonces
las
funciones
es es
decir,
loslos
residuales
estimados
de de
él él
son
estacionarios,
entonces
funciones
de de
Si todas
las
variables
en el sistema
de demanda
son
noestacionarios,
estacionarias
y estánlas
cointegradas,
es decir,
los las
residuales
de de
él demanda
son estacionarios,
entonces las
funciones
de
Si 160
todas
variablesestimados
en el sistema
son no estacionarias
y están
cointegradas,
Silasdemanda
todas
las
en AIDS
el
sistema
de
demanda
son no estacionarias
ycointegradas,
están
cointegradas,
AIDS
en
forma
de
en
el gasto
se
puede
especificar
demanda
Si todases
variables
endel
el modelo
sistema
de en
demanda
noparticipaciones
estacionarias
están
del
modelo
forma
deson
participaciones
enyentonces
el
gasto
se
puede
especificar
decir,
losvariables
residuales
estimados
de
élson
lasen
funciones
de
la
demanda
medicamentos
el estacionarios,
mercado farmacéutico
Colombia
demanda
del modelo
AIDS enpor
forma
de de
participaciones
en el gasto
seprivado
puede
es Elasticidad
decir,
losderesiduales
estimados
élenson
estacionarios,
entonces
lasespecificar
funciones de
JOHANNA
VÁSQUEZ
VELÁSQUEZ,
KAROLL
GÓMEZ
PORTILLA
es los
decir,
los modelo
residuales
estimados
dedeél
son estacionarios,
las funciones
de
como:
es decir,
residuales
estimados
deforma
él son
estacionarios,
entonces
las funciones
de
como:
demanda
del
AIDS
en
participaciones
en el entonces
gasto
se puede
especificar
ELKIN CASTAÑO
VÉLEZ, AIDS
JOSÉ VICENTE
CADAVID
HERRERA,
como:
demanda
del modelo
en forma
de participaciones
en el gasto se puede especificar
demanda
del
modelo
ende
forma
de participaciones
en elsegasto
puede especificar
demanda
del
modelo
AIDSHASSAN
enAIDS
forma
participaciones
en el gasto
puedeseespecificar
ANDRÉS
RAMÍREZ
como:
 x x   i ui ,t 1  ei ,t
wi ,t  i  
 log

 log
pj ,t


ij w j 
,t 1  
ij  log
i
como:




log

w
w
p
u
x

j jijp j ,t  i j ,t log i  PiuPi,t1i,ti eii,,tt1  ei,t (1) (1)(1)
1
jij  j ,t 
como: como:wi ,t   i i ,t i ij 
w

ij  log
j j ,t 1
i ,t
 Pix,t x   i ui ,t 1  ei ,t
j
wi ,t   i 
 ij w j ,t 1 j   ij  log p j ,t14 i  log
(1)

x
14








 i ui ,del



log

log
w
w
p
ei ,t i-ésimo
(1)grupo
x
P
siendo
un
índice
de
precios
agregado;
w
es
la
participación
del
de




P
i i la participación


i ,t índice
i j
ijprecios
j ,t 1 agregado;
j ,t es
t 1 


j ij
i
,
t
P
siendo
un
de
w
i-ésimo
grupo
w
ijde
 ij 
p14log
ei u,t ii-ésimo
w
w j,t ij1log
wiP,t un
 iíndice
i ,
 p logi i logi uPi,t1i ,tdel

t 
i
,t 1  ei(1)
,t grupo(1)
(1) de
j ,t j1 
j ijj ,t wi i esj ,tla participación
siendo
precios
agregado;
de
P i ,t como w  ( p * q ) x , y donde
j
j
 P icalculada
j
j
,t 
14
medicamentos
en
el
gasto
total
medicamentos,
i( p * q
i )grupo
P un índice
siendo
precios
agregado;
participación
de
wi i-ésimo
xi , y donde
medicamentos
en de
el gasto
total
de de
medicamentos,
como del
14wi es lacalculada
i
i
P
siendo
un
índice
de
precios
agregado;
w
es
la
participación
i-ésimo
grupo de
medicamentos en el gasto total de medicamentos,
calculada
como wi  ( pdel
i
14
14
i *q
i ) x , y donde
P
un
índice
de
precios
agregado;
es
la
participación
del
i-ésimo
grupo
de
siendo
14 lawiparticipación
Psiendo
siendo medicamentos
un índice
de
precios
agregado;
w
es
del
i-ésimo
grupo
de
i
un índice
de
precios
agregado;
wlos
essubíndices
la
participación
i-ésimolos
grupo
mejdel
esgasto
el gasto
total.
En
este
caso
subíndices
los
P∑(p*q)
wrepresentan
x , medicamentos
en
total
de
medicamentos,
calculada
como
yde
donde
i los
i  ( pi * q
i ) medicamentos
i,como
j i,representan
esenel
el
gasto
total.
En
este
caso
x x∑(p*q)
w

(
p
*
q
)
x
,
y
donde
medicamentos
el
gasto
total
de
medicamentos,
calculada
i
i
i, j representan
∑(p*q)
gasto
total.
En
este
los calculada
subíndices
x medicamentos
enelel
gasto
total
decaso
medicamentos,
calculada
donde
dicamentos
en
gasto
de
medicamentos,
calculada
como
wcomo
 ( pi w
*iqiilos
) ( xpmedicamentos
medicamentos
eneselelgasto
total
detotal
medicamentos,
como
i, *yqdonde
i ) x ,, yy donde
esi una
gmarca
y marca
m.
Adicionalmente,
es una
cambios
genéricos
representa
iconstante,
, j irepresentan
∑(p*q)
esg el
gasto
total.
En
este caso lossubíndices
los medicamentos
x genéricos
ij representa
y
m.
Adicionalmente,
constante,
loslos
cambios
en en

i subíndices
ij
i
,
j
∑(p*q)
En
este
caso
subíndices
representan
los
medicamentos
x

es
el
gasto
total.
En
este
caso
los
i,j
representan
los
medicamentos

genéricos
g
y
marca
m.
Adicionalmente,
es
una
constante,
representa
los
cambios
en

i
i, j ij representan
∑(p*q)
es el
gasto
los subíndices
los medicamentos
x  es
i, j representan
el gasto
total.
Entotal.
este En
casoeste
loscaso
subíndices
los medicamentos
x  ∑(p*q)
precios
relativos
de
bienes,
esto
elconstante,
impacto
tiene
cambio
en
el precio
genéricos
g gy ymarca
m.m.Adicionalmente,
eses:
una
constante,
representa
losen
cambios
en deldel
 ijij representa
genéricos
marca
Adicionalmente,
es
una
los
cambios
en
ies:
loslos
precios
relativos
de
loslos
bienes,
esto
el
impacto
queque
tiene
un un
cambio
el precio

genéricos
g
y
marca
m.
Adicionalmente,
es
una
constante,
representa
los
cambios
en

i
ij
los
precios
relativos
de
los
bienes,
esto
es:
el
impacto
que
tiene
un
cambio
en
el
precio
del
 i constante,
genéricos
g yrelativos
marca
m.
Adicionalmente,
es impacto
una
constante,
representa
loselcambios
en real
 ij un
 i esto
genéricos
g yprecios
marca
m.
Adicionalmente,
es una
los
cambios
en
que
ij representa
medicamento
j
sobre
la
participación
del
medicamento
i
manteniendo
el
gasto
los
de
los
bienes,
es:
el
tiene
cambio
en
precio
del
j sobre
la
del
medicamento
manteniendo
gasto
los medicamento
precios
dee loses
bienes,
esto es:
elerror
impacto
que tieney iun
cambio
en el elprecio
delreal de
elparticipación
término
de
del modelo
el término
de
corrección
La relativos
expresión
,participación
t los bienes,
i ,t 1 cambio
medicamento
j relativos
sobre
ladeila
del
i manteniendo
manteniendo
elgasto
gasto
real
los
precios
esto
es:medicamento
el impacto
que
tieneuun
en
elreal
precio
del
medicamento
jlos
sobre
participación
del
medicamento
ireal,
el
conslos
precios
relativos
de
los
bienes,
esto
es:
el
impacto
que
tiene
un
cambio
en
el
precio
delbienes
losLaprecios
relativos
de
bienes,
esto
es:
el
impacto
que
tiene
un
cambio
en
el
precio
del

representa
los
cambios
en
el
gastos
los
cuales
son
positivo
para
constante;
y
término
de error del modelo
y ui ,t 1real,
el término
deson
corrección
de real
expresión
ei ,t esyj el
i
medicamento
la participación
del medicamento
i manteniendo
el gasto
sobre
los
cuales
positivo
para
bienes
constante;
i representa los cambios en el gastos
medicamento
j sobre
laende
participación
del
medicamento
i 0son
manteniendo
el
gasto
real
 representa
representa
los
cambios
en
gastos
real,
cuales
positivo
para
bienes
los
1el
 cuales
término
tante; yerrores
los
cambios
enel
el
gastos
real,
para
estimados
elerror
modelo
por
MCO
,son
que
mide
la
velocidad
término
modelo
ycon
deelpositivo
corrección
debienes
Laconstante;
expresión
ui ,itlos
i i  manteniendo
i ,t i es j el
1 manteniendo
medicamento
la
participación
del
medicamento
el
gasto
realde ajuste
medicamento
j yesobre
lasobre
participación
deldel
medicamento
gasto
real
es
una
variable
normales
y
suntuarios,
y
negativo
para
bienes
inferiores.
Finalmente,
p

representa
los
cambios
en
el
gastos
real,
los
cuales
son
positivo
para
bienes
constante;
y
j

1



0
errores
estimados
en
el
modelo
por
MCO
con
,
que
mide
la
velocidad
de
ajuste
isuntuarios,
variable
queque
normales
negativo
para
bienes
Finalmente,
ppositivo
términoyyde
error
del
modelo
término
deson
corrección
de
La expresión
ei ,t yes
ui ,t real,
i yinferiores.
normales
negativo
para
bienes
inferiores.
Finalmente,
esuna
unapara
variable
j es
15
1 el los
eli largo
representa
los
cambios
en
el gastos
cuales
bienes
constante;
yysuntuarios,
una
variable
que
normales
suntuarios,
y negativo
para
bienes
inferiores.
Finalmente,
pson
Además,
la
última
columna
de
lapositivo
matriz
es
borrada,
ya que por
plazo.

eli el
j es positivo
representa
los MCO
cambios
en
el
gastos
real,
los
cuales
para
bienes
constante;
y en

1



0
representa
los
cambios
en
el
gastos
real,
los
cuales
son
para
bienes
constante;
y yi hacia
errores
estimados
modelo
por
con
,
que
mide
la
velocidad
de
ajuste
ij
i
15 el
que
representa
elprecio
precio
del
medicamento
jyyde
es
el operador
para
la
primera

es operador
para
la
diferencia.
representa
del
medicamento
es una
variable
y suntuarios,
ydel
negativo
para
bienes
inferiores.
p jjprimera
Además,
la
última
columna
es
borrada,
que
por que
hacia normales
elestimados
largo
plazo.
 ijpara
es
el
la primera
diferencia.
representa
elelprecio
medicamento
j 1yj
bienes

la
0 matriz
errores
ensuntuarios,
modelo
por
MCO
con
, queFinalmente,
mide
la velocidad
ajuste
una
variable
que
normales
y
y
negativo
para
inferiores.
Finalmente,
p j esyade
i
15

es
el
operador
para
la
primera
diferencia.
representa
el
precio
del
medicamento
j
y
EC
AIDS
es
singular
(Koukouritakis,
2003).
construcción
el
modelo
es
una
variable
normales
y
suntuarios,
y
negativo
para
bienes
inferiores.
Finalmente,
p
una variable
que
normales
suntuarios,
para
bienes
inferiores.
Finalmente,
Además,
la última
la
matriz
es
borrada,
ya corrección
que
por que
hacia La
elylargo
plazo.eyi ,t negativo
es el término
de columna
error
del de
modelo
y ui,t ij1 pel
término
de
de
expresión
j
j es

es
el
operador
para
la
primera
diferencia.
representa
el
precio
del
medicamento
j
y
15
es
elAIDS
término
de error
del de
modelo
y2003).
término
de
corrección
de
La largo
expresión
ei ,t Además,
ui
EC
esúltima
singular
(Koukouritakis,
construcción
el
modelo
,t 1 el
la
columna
la
matriz
es
borrada,
ya
que
por
hacia
plazo.

es
el
término
de
error
del
modelo
y
el
término
de
corrección
de
La elexpresión
es
el
operador
para
la
primera
diferencia.
representa
precio
del
medicamento
j
y
es
el
término
de
error
del
modelo
y
el
término
de
corrección
de
La
eiel
u
e
u
ij
Laexpresión
expresión
es
el
término
de
error
del
modelo
y
el
término
de
corrección
de
erro,t
i ,t 1 i ,t 1
i ,t
en
es
operador
para
primera
diferencia.
representa
elpor
precio
del
medicamento
j el
y operador
13 el modelo
 unitarias
es
para
la
primera
diferencia.
representa
el precio
del
medicamento
yraíces
EC
AIDS
esdejsingular
(Koukouritakis,
2003).
construcción

1



0
errores
estimados
en
modelo
por
MCO
con
,
que
mide
la
velocidad
de
ajuste
Como
ejemplo
lael
presencia
las el
variables
del
sistema,
lo la
cual
en muchas
series económicas
resulta ser una
13
i
Como
por ejemploen
la presencia
de raíces
unitarias
en con
las variables
del
sistema,
lo
cual
en muchas
series económicas
ser una
sistema,
1 por
parte
cual
0, ,los
estimados
modelo
MCO
que
mide
laeconómicas
velocidad
ajuste
res
estimados
modelo
por
MCO
con
que
mide
la
velocidad
deserresulta
ajuste
implicación
teórica
delel
uso
racional
depor
la en
información
disponible
económicos.
13 errores
i lo
Las
teóricas
de
aditividad,
homogeneidad
(funciones
homogéneas
de grado
EC
AIDS
es
singular
(Koukouritakis,
construcción
el
modelo
Como
por
ejemplo
larestricciones
presencia
de
raíces
unitarias
lasMCO
variables
del
en, agentes
muchas
series
resulta
implicación
teórica
racional
depor
la
información
disponible
los
económicos.
14 estimados
Pashardes
1 por
(1993),
1parte
0dei 2003).

0agentes
errores
estimados
endel
eluso
modelo
MCO
con
, deque
mide
ladiferentes
velocidad
ajuste
errores
en
por
con
que
mide
la velocidad
de una
ajuste
i
15
Debido
a los
sesgos
enel
la modelo
estimación
mencionados
por
se
construyeron
índices de
de precios
lineales como el
14 teórica
15
implicación
del
uso
racional
de
la
información
disponible
por
parte
de
los
agentes
económicos.
13
Debido
a
los
sesgos
en
la
estimación
mencionados
por
Pashardes
(1993),
se
construyeron
diferentes
índices
de
precios
lineales
como
13
Además,
lamedir
última
columna
de
lala
matriz
eselborrada,
borrada,
ya
que
por
hacia
elelejemplo
largo
plazo.
 ij es
Las14 restricciones
teóricas
de
aditividad,
homogeneidad
(funciones
de
grado
hacia
largo
plazo.
la
última
columna
de
matriz
ya
que
Como
por
la
presencia
deAdemás,
raíces
unitarias
en la
lasparticipación
variables
deldesistema,
lo cual
en homogéneas
muchas
series
económicas
resulta
serpor
una el el
15
índice
de
precios
de
Stone,
que
permite
los
bienes
de
una
canasta
en
ingreso
empleado
para
adquirirla;
13 índice
Debido
a los
sesgos
endel
lade
estimación
mencionados
Pashardes
(1993),
construyeron
diferentes
índices
de
precios
lineales
como
el
cero
en
precios
ylaelraíces
en
el
gasto
total)
ylos
simetría
(derivadas
precio
cruzadas
simétricas)
Además,
lapor
última
columna
de
ladematriz
es
borrada,
ya para
que
por
hacia
elíndice
largo
plazo.
de
precios
Stone,
permite
medir
la
participación
dese
bienes
una
canasta
el ingreso
empleado
adquirirla;
Como
por
ejemplo
la15
presencia
de
unitarias
en las
variables
del
sistema,
lo
enmuchas
series
económicas
resulta
ser
una el
15que
implicación
teórica
uso
racional
de
información
disponible
por
parte
de
los
agentes
económicos.
ijen
de
precios
de
Laspeyes,
cual
es
invariable
a las
unidades
dela
medida,
ymatriz
elcual
índice
de
precios
de
Paasche.
13 el largo
13 Las
restricciones
teóricas
deunitarias
aditividad,
homogeneidad
(funciones
homogéneas
de
grado
Además,
la
última
columna
de
matriz
es
yaseradquirirla;
que
por
hacia
plazo.
Además,
la
última
columna
de
es
borrada,
ya
que
el
largo
plazo.


índice
de
precios
de
Stone,
que
permite
la
participación
de
los
bienes
de
una
canasta
en
el2003).
ingreso
empleado
para
el por
14
Como
por
ejemplo
lael
presencia
demedir
raíces
unitarias
en
las
variables
del
sistema,
loíndice
cual
en
series
económicas
resulta
ser
una
Como
por
ejemplo
de
raíces
en
las
variables
del
sistema,
lomedida,
cual
en
muchas
series
económicas
resulta
una
índice
de
precios
de
Laspeyes,
el
cual
invariable
adisponible
las
unidades
de
yla
el
de
precios
de
Paasche.
14hacia
implicación
teórica
del
uso
racional
de
laes
información
por
parte
los
agentes
económicos.
ijmuchas
ij borrada,
construcción
modelo
EC
AIDS
es
singular
(Koukouritakis,
Debido
ala
lospresencia
sesgos
en
la
estimación
mencionados
por
Pashardes
(1993),
sede
construyeron
diferentes
índices
de
precios
lineales
como
el
cero
en
precios
y
en
el
gasto
total)
y
simetría
(derivadas
precio
cruzadas
simétricas)
14 precios
EC
AIDS
esunidades
singular
(Koukouritakis,
2003).
construcción
el
modelo
de
delosLaspeyes,
cual
es
invariable
aeconómica
dede
medida,
y el
índice
decanasta
precios
de Paasche.
implicación
del
uso
racional
de
lamedir
información
disponible
parte
de(funciones
los
agentes
económicos.
implicación
teórica
uso
racional
de
información
disponible
por
los
agentes
económicos.
Debido
ateórica
sesgos
enella
estimación
mencionados
porparte
Pashardes
(1993),
se
diferentes
índices
dede
precios
impuestas
por
la
teoría
de
la
demanda,
exigen
cumplimiento
de lascomo
siguientes
Lasíndice
restricciones
teóricas
depermite
aditividad,
homogeneidad
homogéneas
grado
índice
dedel
precios
Stone,
que
lalas
depor
los
bienes
deconstruyeron
una
en
elel
ingreso
empleado
paralineales
adquirirla;
el el
14
14
EC
AIDS
eslaparticipación
2003).
construcción
elLaspeyes,
modelo
cero
precios
yde
en
gasto
total)
ysingular
simetría
(derivadas
precio
cruzadas
simétricas)
Debido
aen
los
en
lael
estimación
mencionados
por
Pashardes
(1993),
sey construyeron
diferentes
índiceslineales
de
precios
lineales
como elel
Debido
aen
losíndice
sesgos
lasesgos
estimación
mencionados
por
Pashardes
(1993),
se(Koukouritakis,
construyeron
diferentes
índices
de
como
el adquirirla;
de
precios
de
Stone,
que
permite
medir
participación
de
los 15
bienes
de
una
canasta
en
elprecios
ingreso
empleado
para
índice
de
precios
de
el
cual
es
invariable
a
las
unidades
de
medida,
el
índice
de
precios
de
Paasche.
—
—
EC
AIDS
es
singular
(Koukouritakis,
2003).
construcción
el
modelo
EC
AIDS
es
singular
(Koukouritakis,
2003).
construcción
el
modelo
impuestas
por
la teoría
económica
de la
demanda,
eldey elcumplimiento
de
las
siguientes
índice
dede
precios
de
Stone,
que
permite
medir
la participación
deexigen
los
bienes
una
canasta
enempleado
el ingreso
empleado
para eladquirirla; el
índice
de precios
de
Stone,
que
permite
medir
la
participación
de
los
bienes
de
una
canasta
en
el
ingreso
para
adquirirla;
—
15
—
índice
precios
de
Laspeyes,
el
cual
es
invariable
a
las
unidades
de
medida,
índice
de
precios
de
Paasche.
condiciones,
las cuales
impuestas
pory elprecios
medio
de cruzadas
lade Paasche.
nohomogéneas
estimación
de grauna de las
cerode precios
eníndice
precios
ydeelen
el invariable
gasto
ysonlas
simetría
(derivadas
precio
simétricas)de
—
15 —
de
precios
Laspeyes,
el cual esatotal)
invariable
unidades
dePaasche.
precios
Las
restricciones
teóricas
de
aditividad,
homogeneidad
(funciones
índice
de
Laspeyes,
cual es
las
unidades
de
medida,
ydeexigen
elmedida,
índice de
de
impuestas
por
la teoría
económica
de
la ademanda,
el índice
cumplimiento
de las siguientes
condiciones,
las
cuales
son
impuestas
por
medio
de
la
no
estimación
de
una
de
las
—yhomogeneidad
15exigen
—
Las por
restricciones
teóricas
aditividad,
(funciones
homogéneas
de grado
ecuaciones
dely sistema:
impuestas
la en
teoría
económica
de
la demanda,
el
cumplimiento
de
las siguientes
cero
precios
elde
gasto
total)
(derivadas
precio
cruzadas
simétricas)
—simetría
15 —
Lasdorestricciones
teóricas
de
aditividad,
homogeneidad
homogéneas
delasgrado
condiciones,
las cuales
sonen
impuestas
porhomogeneidad
medio
de la
no(funciones
estimación
de una de
de
15 —
—
15 —
—
Las cero
restricciones
teóricas
de
aditividad,
(funciones
homogéneas
grado
Las
restricciones
teóricas
de
aditividad,
homogeneidad
(funciones
homogéneas
de grado
ecuaciones
del
sistema:
enlasprecios
yson
en impuestas
el gasto
total)
y simetría
precio
cruzadas
simétricas)
impuestas
poryla
económica
la demanda,
el cumplimiento
de
condiciones,
cuales
por yde
medio
de (derivadas
la(derivadas
no exigen
estimación
de
una desimétricas)
las las sicero
endel
precios
enteoría
el gasto
total)
simetría
precio
cruzadas
ecuaciones
sistema:
ceroimpuestas
en precios
ylaen
total)total)
y la
simetría
(derivadas
precio
cero
en precios
y el
en gasto
el
gasto
yimpuestas
simetría
(derivadas
precio
guientes
condiciones,
las
cuales
son
por
de
lacruzadas
nocruzadas
estimación
de una
por
teoría
económica
de
demanda,
exigen
cumplimiento
desimétricas)
las simétricas)
siguientes
ecuaciones
del sistema:

 i de
1,

 ij 0,
i medio
0elelcumplimiento


impuestas
por laAditividad:
teoría económica
la
demanda,
exigen
de las siguientes
impuestas
la
teoría
económica
de
ladedemanda,
exigen
el cumplimiento
de las
impuestas
por
lateoría
económica
demanda,
cumplimiento
de
lasuna
siguientes
i exigen
de laspor
ecuaciones
del
sistema:
Aditividad:

1,
 iij impuestas
0,
0 medio
condiciones,
las
cuales
son
por
de
lael no
estimación
desiguientes
de las


i lai ipor
i
condiciones,
lasi cuales
son
medio de la no estimación de una de las
i  impuestas
Aditividad:

1,

0,


0



i
ij
i
condiciones,
las
cuales
son
impuestas
por
medio
de
la
no
estimación
de
una
de
las
condiciones,
las
cuales
son
impuestas
por
medio
de
la
no
estimación
de
una
de las
(2)
 iji  0
ecuaciones del iHomogeneidad:
sistema: i

Aditividad:


1,


0,


0
ecuaciones
del
sistema:
j



i
ij
i
Aditividad:
(2)
Homogeneidad:
j  ij i 0
ecuaciones
del sistema:
ecuaciones
deli sistema:
i
(2)
Homogeneidad:


0

ij
Homogeneidad:
(2)
Simetría:
   ji
j   0ij
(2)
Homogeneidad:

ij
Aditividad:


1,


0,


0
Simetría:
 ij   ji j  i
i  ij ij 0,
i i i 0
Simetría:
Aditividad:

1,
ii i1,


Simetría:
 ij


Aditividad:
Aditividad:
i
i
1,
0,
0i 0
ji i

ij 0,
i
i 
ij
i
i
i
i
i
i
Simetría:



ij
ji
A
partir
de
este
modelo
se
pueden
derivar
las ecuaciones
correspondientes
la elasticidad
(2)correspondientes
Homogeneidad:
0
j seij ijpueden
A partir
de este modelo
derivar las ecuaciones
a laaelasti(2)
Homogeneidad:
0

A partir de
este
modelo se
pueden
las ecuaciones correspondientes
a la elasticidad
(2) (2)
Homogeneidad:
Homogeneidad:
j
0ijderivar
 0 , elasticidad
ij 
compensada
oohicksiana,
demanda
de
corto
del
gasto
corto plazo
gasto
preciocorrespondientes
compensada
hicksiana,
demandaordinaria
i , elasticidad
j
A partircidad
de este
modelo
se jpueden
derivar
las ecuaciones
a la elasticidad

,
elasticidad
precio
compensada
o
hicksiana,
demanda
ordinaria
de corto plazoSimetría:
del gasto ij
ji
Simetría:
 ijsei pueden

A partir de este
modelo
las ecuaciones
adela sustitución,
elasticidad las cuales se
ySimetría:
precio
de derivar
la demanda
 ijH , y  ijcorrespondientes
elasticidades
precio compensada
o hicksiana,
demanda
ordinaria
de corto plazo
del
gasto
Simetría:
 ij cruzada
ijjii, jielasticidad
ji
H
y precio
de

,
y
o
elasticidades
de
sustitución,
las
cuales
se

cruzada
Debido
los la
sesgos
en la estimación
mencionados
por Pashardes
(1993),
se construyeron
diferentes
demanda
,
elasticidad
precio
compensada
o
hicksiana,
demanda
ordinaria
de
corto 14plazo
delagasto
ij
ij
i
escriben,
respectivamente,
como
índices
lineales como
precios
de Stone,de
quesustitución,
permite medir las
la participación
y precio
cruzada
deprecios
lamodelo
demanda
 ijH el
, yíndice
elasticidades
cuales
se de los
 ij deosigue:
A partir
dedeeste
se pueden
derivar
las
ecuaciones
correspondientes
a
la
elasticidad
H
bienes
de
una
canasta
en
el
ingreso
empleado
para
adquirirla;
el
índice
de
precios
de
Laspeyes,
escriben,
respectivamente,
como
sigue:
A
partir
de
este
modelo
se
pueden
derivar
las
ecuaciones
correspondientes
a
la
elasticidad
y precio
la modelo
demanda
 ij ,derivar
y derivar
elasticidades
de correspondientes
sustitución, las
se el cual
ij o
A partir
deinvariable
este
modelo
sepueden
las
ecuaciones
lacuales
A cruzada
partir
dede
este
las de
ecuaciones
aelasticidad
la elasticidad
i sesigue:
es
a las
de
medida,
y el
índice
precioscorrespondientes
de Paasche.
escriben,
respectivamente,
como
i ,pueden
elasticidad
precio
compensada
o hicksiana, ademanda
ordinaria
de
corto
plazo
del

i gasto
1unidades

i un del
oi sigue:
, elasticidad
precio
compensada
o hicksiana,
demanda ordinaria
de 15corto
plazo
gasto
 Si
a uno
enprecio
valor
absoluto
se oasume
que las demanda
perturbaciones
desapareescriben,
como
respectivamente,
1toma
 plazo
iw, ielasticidad
cercano
precio
compensada
hicksiana,
ordinaria
de corto
plazo
delvalor
gasto
compensada
o hicksiana,
demanda
ordinaria
de
del grande
gasto
i corto
i , elasticidad

H
cen
rápidamente
y
se
retorna
rápidamente
al
equilibrio.
i
w
y precio
cruzada
de
la
demanda

,
y
o
elasticidades
de
sustitución,
las
cuales
se

i

1

H
ij
ij
i
y precio
cruzada
de la demanda
o elasticidades de sustitución, las cuales se
i i
 ij   H,ijyH, ,y yoij elasticidades
demanda
H la
y precio
de
demanda
de
sustitución,
las
cuales
se
yi precio
de
la
o
elasticidades
de
sustitución,
las
cuales
se


 1cruzada
 wcruzada
(3)



I
w

ij
ij
ij
 como
 ijsigue:
j
  ij  ij
escriben,
wrespectivamente,
H
w
i
i


(3)
     w j
I respectivamente,
 ij 
escriben,
como sigue:
escriben,
respectivamente,
sigue:
escriben,
como
sigue:
 wiji  w como
(3)
I respectivamente,
H 
Homogeneidad: Homogeneidad:
  ij  0
j

j
ij
(2)
0
(2)
Simetría:  ij   Simetría:
ji
 ij   ji
161
Ecos de Economía
Universidad EAFIT
Nº 36 - Año a17la/ enero-junio
correspondientes
elasticidad2013
A partir de este A
modelo
derivar
ecuaciones
partir se
de pueden
este modelo
se las
pueden
derivar las ecuaciones correspondientes a la elasticidad
compensada
o hicksiana,
demanda
ordinaria
de corto plazo del
i , elasticidad
 , elasticidad
precio
compensada
o hicksiana,
demanda ordinaria
de gasto
corto plazo
del gastoprecio
i
y precio cruzaday de
la demanda de
 , ydemanda
sustitución, las
cuales
se las cuales se
 ij o elasticidades
 ijH , y  ij ode
oelasticidades
elasticidades
de sustitución,
sustitución,
ordinaria y precio
precio cruzada
cruzada de la
la demanda
de
las
cuales
se escriben,como
respectivamente,
como sigue:
escriben,
respectivamente,
sigue:
escriben, respectivamente,
como sigue:
H
ij
i  1 
i
wi
i  1 
i
wi
  ij 
  i  j
  wHj 
I   ij1,  w
ij
j
w
 i siendo
I
 wi 
 ijH 
I 
(3)
(3)
(3)
j0, j i  j
1,1,i i
I

siendo
I

siendo

1,
i

j


siendo I   0,0,iiwj2 j w w2 i 
j
i
i
i
0, i  ijj


Si toma un valor grande o cercano
en valor absoluto se asume que las perturbaciones desaparecen rápidamente y se retorna
ij a uno
2
2
toma un valor
cercano
uno en valor
rápidamente al equilibrio. Si 
i ijwo w
1grande
w2 i wi ija 
j se asume que las perturbaciones desaparecen rápidamente y se retorna
i2w
i
j j i absoluto
i w
i iw
 ij alij w
rápidamente
equilibrio.
ijijij wi2  wi wi2 i 
j
j j
i —
 ij   11ij  ijwi wijw j —i 16
— 16 —
i j
1   ij wi w j
siendo pi > 0 implica que i > 1: es un bien de lujo.
15
15
>
0elasticidad
implica
que
>es
1:
es
un
de
lujo.
siendo
siendo
implicaque
que
un
dede
lujo.
i >i 1:
es
unbien
bien
lujo.
siendo
pCon
i p>i 0
laimplica
gasto
se
mide
el bien
cambio
en la participación de los medicament
se
implica que
1: eselun
bienen
delalujo.
siendo pCon
i >la0elasticidad
i >mide
gasto
cambio
participación de los medicamentos i dea un
cambio
porcentual
equivalente
enen
gasto
total dede
medicamentos,
mantenien
Con
elasticidad
gasto
mide
cambio
participación
de
medicamentos
id
Con
la ala
elasticidad
gasto
se se
mide
el el
cambio
en
laella
participación
loslos
medicamentos
i deb
un cambio porcentual equivalente en el gasto total de medicamentos, mantenienCon la bido
elasticidad
gasto se mide el cambio en la participación de los medicamentos i debido
adoun
cambio
porcentual
equivalente
gasto
total
de
medicamentos,
manteniendo
to
todo
lo demás
constante.
El
coeficiente
puede
ser
positivo
indicando que
el
bien
a un
cambio
porcentual
equivalente
enen
elel
gasto
total
de
medicamentos,
manteniendo
todo
demás
constante.
El
coeficiente
i puede ser positivo indicando que el bien es
a un cambio
porcentual
equivalente
en
el
gasto
total
de
medicamentos,
manteniendo
todo
lo
es de lujo, cuando la elasticidad gasto ηi es negativa el bien es inferior. La elasticidad
puede
demás
constante.
coeficiente
ser
positivo
indicando
que
bien
de
l
demás
constante.
ElEl
coeficiente
positivo
que
el el
bien
es es
demide
lujo
i puede
negativo
indicando
que
el i bien
es ser
inferior.
La indicando
elasticidad
precio
propio
propioElmide
el cambio 
porcentual
en lapositivo
participación
del grupo
deelmedicamendemás precio
constante.
coeficiente
puede
ser
indicando
que
bien
es
de
lujo,
o
i
tos i debido
a un cambio
equivalente
en
suelasticidad
nivel de precio;
resultados
porcentual
enque
laque
participación
del
grupo
de
medicamentos
ilospropio
debido
a un
cambio
negativo
indicando
el
bien
inferior.
La
precio
propio
mide
ca
negativo
indicando
elporcentual
bien
es es
inferior.
La
elasticidad
precio
mide
el el
cam
negativo
indicando
que
el
bien
es
inferior.
La
elasticidad
precio
propio
mide
el
cambio
mayores a 1 indican que la demanda es elástica y los menores a la unidad reflejan una
equivalente
en su niveldel
de
precio;
los
resultados mayores
aa 1un
que
la d
porcentual
participación
del
grupo
medicamentos
i debido
a indican
un
cambio
porce
porcentual
enen
la la
participación
grupo
dede
medicamentos
i debido
cambio
porcent
demanda
sensible a ladel
variación
precios. La elasticidad
precio
porcentual
en lapoco
participación
grupo en
delos
medicamentos
i debido
a uncruzada
cambiomide
porcentual
elástica
y los
menores
a la unidad
reflejan
una
demanda
sensible
lademan
varia
equivalente
su
nivel
de
precio;
resultados
mayores
1poco
indican
que
equivalente
enen
su
nivel
departicipación
precio;
loslos
resultados
mayores
a 1ai debido
indican
que
la ala
demanda
el cambio
porcentual
en la
del
grupo
de medicamentos
a un
camequivalente en su nivel de precio; los resultados mayores a 1 indican que la demanda es
bio enprecios.
del elasticidad
grupo
medicamentos
j;una
resultados
positivos
indican
quea los
bieLa
precio
cruzada
mide
el
cambio
porcentual
envariación
la partici
elástica
yprecio
los
menores
adela
unidad
reflejan
una
demanda
poco
sensible
a la
elástica
yellos
menores
a la
unidad
reflejan
demanda
poco
sensible
la
variación
en
elásticanes
y los
reflejan
unaque
demanda
sensible los
a labienes
variación
sonmenores
sustitutosayla
losunidad
negativos
reflejarían
para lospoco
consumidores
son en los
grupo
de
medicamentos
i cruzada
debidomide
amide
unelcambio
enporcentual
el
precio en
delen
de medic
precios.
elasticidad
precio
el
cambio
porcentual
la
participació
precios.
LaLa
elasticidad
precio
cruzada
cambio
lagrupo
participación
16
El modelo
EC AIDSmide
es estimado
usando
el método en
Iterate
seemingly
precios.complementarios.
La elasticidad precio
cruzada
el cambio
porcentual
la participación
del
resultados
positivos
los
bienes
sustitutos
y losdenegativos
refle
grupo
de
medicamentos
i indican
debido
aque
un
cambio
en
el
grupo
de
medicamen
grupo
de
medicamentos
i debido
a &un
cambio
enJudge
elson
precio
deldel
grupo
medicamento
unrelated
regression
—ISUR—
(Berndt
Savin,
1975;
etprecio
al., 1980).
grupo de medicamentos i debido a un cambio en el precio del grupo
de
medicamentos
j;
parapositivos
los
consumidores
los
bienes
sonson
complementarios.
El
modelo reflejarían
EC
AIDS e
resultados
positivos
indican
que
los
bienes
son
sustitutos
y 16los
negativos
reflejaría
resultados
indican
que
los
bienes
sustitutos
y los
negativos
Finalmente,
paraindican
el caso de
demanda
de son
medicamentos
que los consuresultados
positivos
quela los
bienes
sustitutossey16considera
los
16 negativos reflejarían que
usando
el
método
Iterate
seemingly
unrelated
regression
—ISUR—
para
los
consumidores
los
bienes
son
complementarios.
El
modelo
AIDS
es
esti
para
los
consumidores
los
bienes
son
complementarios.
El
modelo
ECEC
AIDS
es(Berndt
estim
midores asignan su presupuesto en dos etapas: la primera etapa o nivel, corresponde
para los consumidores los bienes son complementarios.16 El modelo EC AIDS es estimado
a la asignación
de gasto
distintas clases
terapéuticas
disponibles
para el(Berndt
trata1975;
Judge
et Iterate
al.,entre
1980).
usando
método
seemingly
unrelated
regression
—ISUR—
(Berndt& &Sav
S
usando
el elmétodo
Iterate
seemingly
unrelated
regression
—ISUR—
usando el método Iterate seemingly unrelated regression —ISUR— (Berndt & Savin,
1975;
Judge
1980).
1975;
Judge
et et
al.,al.,
1980).
1975; Judge
1980).
Paraet
la al.,
derivación
de las elasticidades en el modelo AIDS véase Green y Alston (1990) y para la estimaFinalmente,
para
el caso véase
de Attfield
la demanda
de medicamentos se consider
ción
de un modelo AIDS
bajo cointegración
(1997).
16
consumidores
asignan
sudepresupuesto
ende
dos
etapas:
la primera
etapa
o nivel,que
cor
Finalmente,
parael el
casode
demanda
demedicamentos
medicamentos
considera
qu
Finalmente,
para
caso
la lademanda
se se
considera
Finalmente, para el caso de la demanda de medicamentos se considera que los
la asignación
desugasto
entre distintas
clases
terapéuticas
disponibles
para
el trat
consumidores
asignan
su
presupuesto
etapas:
primera
etapa
o nivel,
correspo
consumidores
asignan
presupuesto
enen
dosdos
etapas:
la la
primera
etapa
o nivel,
correspond
162
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
miento de una de las patologías elegidas, y el segundo nivel, a la asignación de gasto
entre medicamentos de marca y genéricos, bien sean de origen nacional o extranjero.
Así, el modelo permite hallar las elasticidades precio de la demanda y los patrones de
sustitución entre medicamentos de marca y genéricos y por clase terapéutica al interior
de cada patología. En este caso se cumple el supuesto de separabilidad.
5. Resultados
5.1. Análisis de estadística descriptiva
El total de medicamentos estudiados fue de 83; de ellos se logró modelar estadísticamente información para 62, que en su totalidad se comercializan en el mercado privado;
13 de los medicamentos corresponden a marcas producidas por empresas innovadoras de origen extranjero, 32 por empresas no innovadoras nacionales y 6 de origen
extranjero. El total de los genéricos (11) son producidos por empresas nacionales no
innovadoras. De la información disponible se construyó el índice de concentración de
mercado Herfindahl-Hirschman, encontrando que independientemente del número de
laboratorios que elaboran el medicamento, la concentración es alta para el 98% de los
medicamentos estudiados, con relación al volumen de ventas por laboratorios en comparación al total.
De los 11 ingredientes activos considerados, el 36,36% no está incluido en el POS, y de
los estudiados solo hay un componente por patología listado en los medicamentos a los
que tienen derecho los colombianos afiliados al Sistema General de Seguridad Social
en Salud.
5.2. Resultados de la estimación
Inicialmente se indagó por las propiedades de series de tiempo, con el fin de especificar
la forma dinámica más apropiada del modelo y encontrar las posibles relaciones de
demanda a largo plazo en la ecuación (1). Si todas las variables son integradas de orden
1, la ecuación (1) es adecuada, en caso contrario se debería utilizar el modelo AIDS tradicional. Para esto se utilizó el test de Dickey y Fuller aumentado (ADF), el de Kwiatowski,
Phillips, Schmit y Shin (KPSS) y el de Phillips y Perron (PP). Los resultados son presentados en la tabla 2. El no rechazo de la hipótesis nula en el contraste de raíz unitaria de
163
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
Dickey
y Fuller,
Phillips ynula
Perron,
rechazode
deraíz
la hipótesis
nulaDickey
de estacionalidad
no rechazo
de yladehipótesis
en ely el
contraste
unitaria de
y Fuller, y de
no elrechazo
de la
hipótesis
nula endeelcada
contraste
delas
raíz
unitaria confirma
de Dickey
y estas
Fuller,son
y de
en
contraste
KPSS
al
logaritmo
una
de
variables,
que
no rechazo
de la yhipótesis
nula
el contraste
unitaria de en
Dickey
y Fuller,
y de
Phillips
y Perron,
el rechazo
de en
la hipótesis
nuladederaíz
estacionalidad
el contraste
KPSS
al
no rechazo
de la yhipótesis
nula
el contraste
unitaria de en
Dickey
y Fuller,
y de
Phillips
Perron,
rechazo
de en
la hipótesis
nuladederaíz
estacionalidad
el contraste
KPSS
al
I(1),
en lay mayoría
deellos
casos.
Phillips y Perron,
el rechazo
de la hipótesis
nula de
el la
contraste
al
logaritmo
de cadayuna
de las variables,
confirma
queestacionalidad
estas son I(1),enen
mayoríaKPSS
de los
Phillips y Perron,
el rechazo
de la hipótesis
nula de
el la
contraste
al
logaritmo
de cadayuna
de las variables,
confirma
queestacionalidad
estas son I(1),enen
mayoríaKPSS
de los
logaritmo de cada una de las variables, confirma que estas son I(1), en la mayoría de los
casos.
Tabla
2.
logaritmo de cada una de las variables, confirma que estas son I(1), en la mayoría de los
casos.
casos.
Resultados de las pruebas de raíz unitaria* en la demanda de medicamentos
casos.
Tabla 2. Resultados de las pruebas de raíz unitaria* en la demanda de medicamentos
Tabla 2. Resultados de las pruebas de raíz unitaria** en la demanda de medicamentos
Hiperlipidemia
Hiperlipidemia
Tabla 2. Resultados
de
las pruebas de raíz unitaria* Diabetes
en la demanda de
medicamentos
Hipertensión
esencial esencial
Diabetes
Hipertensión
Hiperlipidemia
Tabla
2
.
Resultados
de
las pruebas
Modelo
Grupo I
Grupode
II raíz unitaria en la demanda de medicamentos
Modelo
Modelo
Modelo
Modelo
Grupo I
Grupo I
Hiperlipidemia Grupo II
Grupo II
Diabetes
Hipertensión esencial
Diabetes
Hipertensión
esencial
Hiperlipidemia
ADF
PP
DF
PP
KPSS KPSS
ADF ADF
PP
KPSS
ADF Grupo
PP I KPSS
KPSS
DF
PP KPSS
PP
PP esencial
KPSS
Grupo
II KPSSDF DFPP Diabetes
Hipertensión
ADF Grupo
PP I KPSS
DF
PP
KPSS
DF
PP
KPSS
ADF
PP
KPSS
Grupo II
1,0916
2,0638
0,8915
0,15
0,15
0,8915
2,0638
1,0916
ADF 0,55
PP 0,9046
KPSS
DF -2,02
PP0,81870,8187
KPSS
DF
PP
KPSS
ADF
PP
KPSS
-0,01
0,6322
0,5395
0,55
0,9046
1,08 1,08
0,5395
-0,01
-2,02
0,15 0,6322
2,0638
1,0916
(0,89)
(0,25)
(0,99)
ADF
PP
KPSS (0,25)
DF
PP
KPSS
DF
PP
KPSS
ADF
PP
KPSS
-0,01
0,6322
1,08
0,5395
0,8187
0,55
0,9046
(0,99)
(0,89)0,8915
(0,96) (0,96)
-2,02
w
wmm
0,15
(0,89)
(0,25)
(0,99)
-0,01 0,6322
1,08 0,5395 (0,96)
0,8187 0,8915
0,55 0,9046 2,0638
wmP 1,0916
-2,02
log
-1,79
0,15
0,8915
2,0638
1,0916
-1,30231,3023
-1,79 (0,96)
(0,89)
(0,25)
(0,99)
-2,04
-1,58
0,4768
-1,56
-0,01 0,6761
0,6322
1,08 0,6948
0,5395
0,8187
0,55 0,6138
0,9046 -1,4714
wmPg -2,7995
2,7995
1,4714
-2,08
-2,02
log
-1,79
-1,58
0,6138
-2,08
0,4768
-1,56
0,6948
-2,04
0,6761
g
-1,58 0,6138 1,4714
0,4768 1,3023
-1,56 0,6948 (0,69)
(0,96) -2,04 0,6761
(0,89)
(0,25)
(0,99)
2,7995
-2,08
(0,06)
(0,54)
(0,54)
(0,61) (0,61)
(0,69) (0,69)
log Pg (0,06)
-1,79
-2,04 0,6761
-1,58 0,6138 1,4714
0,4768 1,3023
-1,56 0,6948
-2,08
(0,06)
(0,54)
(0,61)
---log P
Pg 2,7995
-1,79
log
-2,04
0,6761
-1,58 0,8936
0,6138 1,4714
0,4768 1,3023
-1,56 0,6579
0,6948 (0,69)
-1,07
m
2,7995
-2,08
0,9301
-1,51
4,53
0,8999
-0,98
(0,06)
(0,54)
(0,61)
3,0808
1,2414
2,2405
1,58
log Pm -1,2414
(0,69)
-1,07
0,9301
-1,51 0,6579
4,53
0,8999
-0,98 0,8936 -2,2405
-3,08083,0808
-1,07 (0,72)
(0,06)
(0,54)
(0,61)
1,2414
2,2405
1,58
(0,12)
(0,89)
(0,45)
log Pm
-0,98
1,58 0,93010,9301
-1,51 -1,51
0,6579 0,6579 (0,72)
4,53 0,8999
-1,07
4,53
0,8999
-0,98 0,8936
0,8936 (0,45)
1,2414
2,2405
1,58
(0,12)
(0,89)
(0,45)
(0,12) 3,0808
(0,72) -1,07
---log
Pmt (0,89)
log G
0,9301 3,0808
-1,51 0,5149
0,6579 (0,72)
4,53
0,8999
-0,98 0,9036
0,8936 2,2405
-1,96
1,2414
1,58
-0,33
0,5119
-0,98
0,9001
-2,26
(0,12)
(0,89)
(0,45)
0,9792
3,75
2,4961
log Gt 1,5777
(0,72)
-1,96
-0,98 0,9036 0,9792
0,9001 2,4961
-2,26 0,5149 (0,60) -0,33 0,5119
(0,12)
(0,89)
(0,45)
1,5777
3,75
(0,79)
(0,93)
(0,32)
log Gt -1,5777
-1,96
-2,49612,4961
-1,96 (0,60)
-0,33 0,5119
-0,98 0,9036 -0,9792
0,9001
-2,26 0,5149
- los respectivos
- son los3,75
1,5777
0,9792
(0,79)
(0,93)
(0,32)
*log
LosGvalores
de
estadísticos
se reportan
p-valor0,5149
se reporta(0,60)
en paréntesis
-0,98
3,75 que0,9001
-2,26 El-2,26
0,5149
-0,33
0,5119
-1,96
t
-0,33 en la
0,5119
-0,98 0,9036
0,9036
0,9001 en la tabla.
1,5777
0,9792
2,4961
(0,79)
(0,93)
(0,32)
*tabla.
Los Los
valores
de los
respectivos
son los3,75
quedel
se5%
reportan
en
tabla.
El p-valor
se
en paréntesis en la
(0,79)
(0,32)
(0,60)
valores
críticos
para unestadísticos
nivel(0,93)
de
significancia
de los
testla
PP
y KPSS
son -3.43
yreporta
0.46, (0,60)
respectivamente.
(0,79)
(0,93)
(0,32)
* Los Los
valores
de los
respectivos
son los quedelse5%
reportan
tabla.
El p-valor
se yreporta
en paréntesis en la
tabla.
valores
críticos
para unestadísticos
nivel de
significancia
de los en
testla
PP
y KPSS
son -3.43
0.46, respectivamente.
Los Los
valores
de de
los
respectivos
son los quedel
se5%
reportan
en
laPPtabla.
El p-valor
se ytabla.
reporta
en
en la
valores
críticos
para unestadísticos
nivel deestadísticos
significancia
de los
testse
y KPSS
sonen
-3.43
0.46, respectivamente.
**tabla.
Los
valores
los
respectivos
son
los
que
reportan
la
El paréntesis
p-valor se
tabla. Los valores críticos para un nivel de significancia del 5% de los test PP y KPSS son -3.43 y 0.46, respectivamente.
reporta
en paréntesis
en la tabla.
Los valores
para
un nivel
de significancia
del 5%
de los
Adicionalmente,
se realizó
un análisis
paracríticos
detectar
datos
atípicos
o influenciares
para
cada
Adicionalmente,
realizó
un respectivamente.
análisis para detectar datos atípicos o influenciares para cada
test
PP y KPSS sonse
-3.43
y 0.46,
Adicionalmente,
se realizó
un análisis
para detectar
atípicos
o influenciares
cada
modelo;
los resultados
muestran
la presencia
de estedatos
tipo de
observaciones,
por lo para
que estas
Adicionalmente,
se realizó
un análisis
para detectar
atípicos
o influenciares
cada
modelo;
los resultados
muestran
la presencia
de estedatos
tipo de
observaciones,
por lo para
que estas
modelo;incluidas
los resultados
muestran
la presencia
de
este
tipo
de observaciones,
por uno
lo que
estas
fueron
como
variables
dummies
en
la
especificación
de
cada
de
los
Adicionalmente,
secomo
realizó
un análisis
para detectar
datos
odeinfluenciares
para
modelo;incluidas
los resultados
muestran
la presencia
de
de atípicos
observaciones,
por uno
lo que
fueron
variables
dummies
eneste
la tipo
especificación
cada
deestas
los
17
fueron
incluidas
como
variables
dummies
en
especificación
de
cada
uno del
de
los
modelos.
el procedimiento
propuesto
porlaEngle
y Granger
(1987)
a través
test
cada
modelo;
los resultados
muestran
la presencia
de
este
tipo de(1987)
observaciones,
portest
17 Usando
fueron
incluidas
como
variables
dummies
en
especificación
de
cada
uno del
de
los
modelos.
Usando
el procedimiento
propuesto
porlaEngle
y Granger
a través
17
modelos.
Usando
procedimiento
propuesto
por
Engle yen
Granger
(1987) a través
del test
lo
que
estas
fueronel
incluidas
como
variables
dummies
especificación
de cada
de
Dickey
aumentado,
se verificó
la estacionalidad
delalos
residuales
estimados
en
17 y Fuller
modelos.
procedimiento
propuesto
por Engle y Granger
(1987) a través
del test
de
Dickey yUsando
Fuller el
aumentado,
se verificó
la estacionalidad
de los residuales
estimados
en
17
uno
deuno
los de
modelos.
Usando
procedimiento
propuesto
Engle
y Granger
(1987)
aen
de Dickey
y Fuller
aumentado,
verificó laindican
estacionalidad
de
los residuales
estimados
cada
los modelos.
Loselseresultados
que lospor
residuales
estimados
en cada
de Dickey
y Fuller
aumentado,
seresultados
verificó laindican
estacionalidad
de
los residuales
estimados
en
cada
uno
de
los
modelos.
Los
que
los
residuales
estimados
en
cada
través
del test
de Dickey
y Fuller aumentado,
se verificó
lalos
estacionalidad
de los residuacada uno
de I(0),
los
modelos.
resultados
indican
quevariables
residuales
estimados
en cada
modelo
son
lo cual Los
implica
que aunque
las
no son
individualmente
cada
unoson
de I(0),
los
resultados
indican
quevariables
los residuales
estimados
en cada
modelo
lo cual
implica
que aunque
las
no que
son
individualmente
les
estimados
en modelos.
cada
uno Los
de
los
modelos.
Los resultados
indican
los
residuales
modelo son su
I(0),
lo cual implica
que aunque
las variables
no al
sonparecer
individualmente
estacionarias
combinación
lineal resultó
estacionaria,
por lo que
existe una
modelo son
I(0),
lo
cual implica
que
aunque
las que
variables
nolasal
son
individualmente
estimados
ensu
cada
modelo
son
I(0),resultó
lo cual
implica
aunque
variables
no son
estacionarias
combinación
lineal
estacionaria,
por
lo que
parecer
existe
una
estacionarias
su combinación
lineal
resultó en
estacionaria,
por resultados
lo que al parecer
existeenuna
relación
de
largo
plazo
entre
las
variables
cuestión.
Los
se
muestran
la
individualmente
su combinación
lineal resultó
loexiste
queen
al
estacionarias
su estacionarias
combinación
lineal
resultó en
estacionaria,
por estacionaria,
lo que al parecer
una
relación
de largo
plazo entre las
variables
cuestión.
Los
resultados
se por
muestran
la
relación
de
largo
plazo
variables
en cuestión.
Los resultados
se muestran
en la
tabla
3 eexiste
incluyen
testentre
PPde
y las
KPSS
. plazo entre
parecer
unalos
relación
largo
las variables
en cuestión.
Los resultarelación
largo
plazo
variables
en cuestión.
Los resultados
se muestran
en la
tabla
3 e de
incluyen
los
testentre
PP y las
KPSS
.
tablase3 muestran
e incluyenen
loslatest
PP 3
y KPSS
.
dos
tabla
e incluyen
los test PP y KPSS.
tabla 3 e incluyen los test PP y KPSS.
17
Se incluyeron una variable dummy en el modelo de diabetes igual a 1 en la observación 29 y cero en otros casos. En el modelo de
SeSeincluyeron
incluyeron
una
variable
en
modelo
deigual
diabetes
igual
a 1;
1 en
29
y cero
en
otrosuna
variable
en elvalor
modelo
diabetes
a371 en
en el
la
observación
29
y cero2en
casos.
En dummies,
el modelo
de
hiperlipidemia
seuna
incluyó
una
dummydummy
con
deel
1 de
en
la observación
grupo
y enla
elobservación
grupo
se otros
incluyeron
dos
17
hiperlipidemia
seel
incluyó
una de
dummy
con
valor
de 1 se
en diabetes
la
observación
en
ella grupo
1;
y en de
el grupo
seobservación
incluyeron
conSecasos.
valor
de 1En
en
la
observación
43hiperlipidemia
y otra
en
la observación
53, yigual
cero
casos.
incluyeron
una
variable
dummy
en el
modelo
de
a37
1los
enotros
observación
29
y1cero
en
otros
casos.dos
En dummies,
el modelo
de
modelo
incluyó
unaen
dummy
con
valor
en2la
37
en eluna
17
con
valor
de
1
en
la
observación
43
y
otra
en
la
observación
53,
y
cero
en
los
otros
casos.
hiperlipidemia
incluyó
una dummy
con
de dos
1 de
en diabetes
la
observación
grupo
1;
el grupo
2en
se otros
incluyeron
dummies,
Segrupo
incluyeron
una
en elvalor
modelo
igualuna
a371 en
en el
lavalor
observación
29
y cero
casos.
el modelo
de
1; yseen
elvariable
grupo
2 se incluyeron
dummies,
con
dey1enen
la
observación
43dos
yEnotra
en launa
con valor de 1 en
observación
43 y otra
la observación
53, y cero en
casos.
hiperlipidemia
se la
incluyó
una dummy
con en
valor
de 1 en la observación
37los
en otros
el grupo
1; y en el grupo 2 se incluyeron dos dummies, una
observación
53,
y
cero
en
los
otros
casos.
—en los otros casos.
con valor de 1 en la observación 43 y otra en la observación —
53, y19
cero
17
17
— 19 —
— 19 —
— 19 —
164
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
Tabla 3.
Resultados de las pruebas de raíz unitaria sobre los residuales del modelo EC AIDS no
restringido en la demanda de medicamentos*
Test
Hiperlipidemia
Diabetes
Hipertensión
esencial
Grupo I
Grupo II
ADF
-7,61 (0,00)
-7,94 (0,00)
-6,24 (0,00)
-3,28 (0,00)
PP
-7,62 (0,00)
-7,95 (0,00)
-6,23 (0,00)
-3,22 (0,00)
KPSS
0,2983
0,1086
0,1526
0,1560
* Los valores de los respectivos estadísticos son los que se reportan en la tabla. El p-valor se
reporta en paréntesis. El valor crítico para un nivel de significancia del 1% del test KPSS es 0,739.
En cuanto a las restricciones de homogeneidad y simetría, se consideran supuestos
importantes en la teoría de demanda, y consistentes con un comportamiento de maximización de utilidad por parte del consumidor. En la tabla 4 se muestran los resultados
del test de Wald que se realizó para probar la hipótesis nula de homogeneidad, simetría,
y homogeneidad y asimetría conjuntamente.18 Los resultados indican que en la mayoría
de los casos las restricciones no son rechazadas a un nivel de significancia del 5%, con
excepción del grupo II de hiperlipidemia, lo cual podría ser explicado debido a que en
este caso el índice de precios elegido no muestra patrones y hábitos de consumo para
esta población. Sin embargo, siguiendo a Parkin (1998), dichas restricciones no siempre
son tratadas como restricciones verificables, sino que se asumen como ciertas y, por
ende, se imponen en el sistema de demanda, de ahí que, basándose en este argumento, el modelo se estimó imponiendo dichas restricciones.
En la Tabla 5 se presentan los resultados de los modelos estimados que tuvieron un
buen ajuste, los cuales envuelven las restricciones de homogeneidad y simetría. Para
asegurar la no singularidad de la matriz de covarianza del error se estimó, en todos los
casos, la ecuación de demanda para los medicamentos de marca. Los coeficientes para
la ecuación de demanda de los genéricos se obtuvieron usando las restricciones teóricas del modelo, a partir de los coeficientes estimados.
18
En el caso de hipertensión esencial, los grupos II y III fueron descartados debido a un pobre ajuste de los
modelos.
165
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
Tabla 4.
Contrastes de homogeneidad, simetría y aditividad en la demanda de medicamentos
y
En la
la Tabla 5
5 se presentan
presentan
los resultados
resultados
de los
los modelos Simetría
estimados que
queHomogeneidad
tuvieron un
un buen
buen
En
de
Modelo los
Homogeneidad
En la Tabla
Tabla 5 se
se presentan
los resultados
de los modelos
modelos estimados
estimados que tuvieron
tuvieron
simetríaun buen
ajuste, los
los cuales
cuales envuelven
envuelven las
las restricciones
restricciones de
de homogeneidad
homogeneidad y
y simetría.
simetría. Para asegurar
asegurar la
la
ajuste,
I
1,21 (0,27)
1,52 (0,22)
7,93 (0,01)
ajuste, losHiperlipidemia
cuales envuelven
las restricciones
de homogeneidad
y simetría. Para
Para
asegurar la
no
singularidad
de
la IImatriz
de covarianza
del
error se
estimó,
todos
los
casos,
la
Hiperlipidemia
0,03 (0,84)
(0,51) en
1,15
no
de
del
estimó,
en
los
casos,
no singularidad
singularidad
de la
la matriz
matriz de
de covarianza
covarianza
del error
error se
se0,42
estimó,
en todos
todos
los(0,56)
casos, la
la
Diabetes
0,64 (0,42)
(0,04)
5,13 la
(0,07)
ecuación de
demanda para los medicamentos
de marca. 5,12
Los coeficientes
para
ecuación
ecuación de
demanda para los medicamentos
de marca. 1,69
Los coeficientes
para
la ecuación
Hipertensión esencial
0,82 (0,37)
(0,18)
6,64 (0,04)
de demanda
demanda de
de los
los genéricos
genéricos se
se obtuvieron
obtuvieron usando
usando las
las restricciones
restricciones teóricas
teóricas del
del modelo,
modelo, a
de
de demanda
de los genéricos se obtuvieron usando las restricciones teóricas del modelo, aa
Fuente: elaboración propia (2009). El p-valor se indica entre paréntesis.
partir
de los
coeficientes estimados.
partir
partir de
de los
los coeficientes
coeficientes estimados.
estimados.
Tabla 5.
Tabla 5
5. Parámetros
estimadosestimados
en los
los modelos
AIDS EC
restringidos
para la
la demanda
demanda de
de
Parámetros
en los EC
modelos
AIDS restringidos
Tabla
AIDS
restringidos
para
Tabla 5.. Parámetros
Parámetros estimados
estimados en
en los modelos
modelos EC
EC AIDS restringidos para la demanda de
para lamedicamentos*
demanda de medicamentos*
medicamentos*
medicamentos*
Hiperlipidemia
Hipertensión
Hiperlipidemia
Hipertensión
Diabetes Diabetes
Hiperlipidemia
Hipertensión
esencial esencial
Grupo
Grupo II
IIGrupo II Diabetes
Grupo
I Grupo
esencial
Grupo
II
Parámetros
Diabetes
esencial
Grupo I
Grupo II
-0,26
 mj
-0,23-0,23
(-2,09)
-0,18 (-1,65)
0,11 (1,28)0,11 (1,28)
-0,26 (-2,21)
(-2,21)
(-2,09)
-0,18
(-1,65)
-0,26 (-2,21)
mj
 mj
-0,23 (-2,09)
-0,18 (-1,65)
0,11 (1,28)
-0,26 (-2,21)
0,04
(2,58)
0,05
(1,06)
0,06
(2,13)
0,03
(1,47)
 mj
0,05 (1,06)
0,040,04
(2,58)(2,58) 0,05 (1,06)
0,06 (2,13)0,06 (2,13)
0,03 (1,47) 0,03 (1,47)
 mj
0,04 (2,58)
0,05 (1,06)
0,06 (2,13)
0,03 (1,47)
mj
0,005
(1,9)
-0,008
(-1,36)
0,01
(0,84)
-0,06
(-3,75)

0,005
(1,9)-0,008 (-1,36)
-0,008 (-1,36)
0,01 (0,84)
-0,06 (-3,75)
0,005
(1,9)
0,01
(0,84)
-0,06
(-3,75)

m
0,005 (1,9)
-0,008 (-1,36)
0,01 (0,84)
-0,06 (-3,75)
 mm
-0,13
(-1,68)
-0,32
(-2,79)
-0,40
(-2,8)
-0,22
(-2,66)

-0,13 (-1,68)
-0,32 (-2,79)
-0,40 (-2,8)
-0,22 (-2,66)

-0,13 (-1,68)
-0,32 (-2,79)
-0,40 (-2,8)
-0,22 (-2,66)

-0,02-0,02
(-2,37)
-0,039 (-3,69)
-0,02 (-2,7)-0,02 (-2,7) –
(-2,37)
-0,039
(-3,69)
–
 outliers
-0,02 –(-2,37)
-0,039 (-3,69)
-0,02–(-2,7)
––
-0,035
–
-0,035 (-3,18)
(-3,18)
–
–
 outliers
outliers
–
-0,035
(-3,18)
–
–
-0,035 (-3,18)
–
–
R2
0,3700 –
0,5610
0,4721
0,3639
R2
0,3700
0,5610
0,4721
0,3639
R2
0,3700
0,5610
0,4721
0,3639
–
0,68
{0,51}
0,26
{0,77}
0,72
{0,49}
1,92
{0,15}
R2Breusch
0,3700
0,5610
0,4721
0,3639
0,68 {0,51}
0,26 {0,77}
0,72 {0,49}
1,92 {0,15}
Breusch
Goodfrey–
Goodfrey
0,68 {0,51}
0,26 {0,77}
0,72 {0,49}
1,92 {0,15}
Goodfrey
Breusch
0,26 {0,77}
White – Goodfrey 0,65 0,68
{0,11}{0,51}0,72 {0,73}
0,53 {0,83}0,72 {0,49}
0,71 {0,70}1,92 {0,15}
White
0,65 {0,25}
{0,11}
0,72 {0,73}
0,53 {0,40}
{0,83}
0,71 {0,68}
{0,70}
Jarque-Bera
2,72
1,80
0,76
White
0,65
{0,11}0,56 {0,55}
0,72 {0,73}
Jarque-Bera
2,72
{0,25}
{0,40}0,53 {0,83}
0,76 {0,68}0,71 {0,70}
Los
t-estadísticos aparecen
aparecen
entre
paréntesis0,56
y los
los{0,55}
p-valor entre
entre1,80
llaves.
** Los
t-estadísticos
entre
paréntesis
y
p-valor
llaves.
*Jarque-Bera
Los t-estadísticos aparecen entre
paréntesis
entre llaves. 1,80 {0,40}
2,72
{0,25} y los p-valor
0,56 {0,55}
0,76 {0,68}
Parámetros
Parámetros
Parámetros
* Los t-estadísticos aparecen entre paréntesis y los p-valor entre llaves.
En todos
todos los casos
casos el parámetro
parámetro λ es negativo
negativo y estadísticamente
estadísticamente significativo, por
por lo que
que
En
En todos los
los casos el
el parámetro λλ es
es negativo y
y estadísticamente significativo,
significativo, por lo
lo que
las
desviaciones
aa partir
largo
plazo,
debidas
aa la
no estacionalidad
de
las
las
del
equilibrio
de
largo
plazo,
de
En todos los
casosdel
el equilibrio
parámetrode
λ es
negativo
estadísticamente
significativo, por
lo
las desviaciones
desviaciones
a partir
partir
del
equilibrio
de
largo
plazo,y debidas
debidas
a la
la no
no estacionalidad
estacionalidad
de las
las
queson
las corregidas
desviaciones
del equilibrio
plazo,que
debidas
a la de
no estacionalidad
variables,
enaelpartir
siguiente
periododeylargo
significa
la curva
demanda tiene
variables, son corregidas en el siguiente periodo y significa que la curva de demanda tiene
de las
variables,
son corregidas
en el siguiente
periodo
y significa
que la curva
dependiente
negativa
y garantiza
garantiza
la concavidad
concavidad
en precios.
precios.
Según
los resultados
resultados
y el
eldesigno
signo
pendiente
negativa
y
la
en
Según
los
y
pendiente
negativa
y
garantiza
la
concavidad
en
precios.
Según
los
resultados
y
el
signo
manda tiene pendiente negativa y garantiza la concavidad en precios. Según los resulobtenido para
para 
, se
se contó
contó con
con dos
dos medicamentos
medicamentos de
de lujo,
lujo, hiperlipidemia
hiperlipidemia grupo
grupo II y
y diabetes,
obtenido
tados
obtenido
para
β, se contó con
medicamentos
de grupo
lujo, hiperlipidemia
obtenido
paray el,, signo
se contó
con dos
medicamentos
dedos
lujo,
hiperlipidemia
I y diabetes,
diabetes,
dos grupo
necesarios,
hiperlipidemia
grupo hiperlipidemia
II ee hipertensión
hipertensión
esencial.
Por otro
otro
lado, Por
las
yyy dos
necesarios,
hiperlipidemia
grupo
II
esencial.
Por
lado,
I
y
diabetes,
y
dos
necesarios,
grupo
II
e
hipertensión
esencial.
dos necesarios, hiperlipidemia grupo II e hipertensión esencial. Por otro lado, las
las
otrodummies
lado, las correspondientes
variables dummiesa correspondientes
a observaciones
resultaron
variables
observaciones atípicas
resultaronatípicas
estadísticamente
variables dummies correspondientes a observaciones atípicas resultaron estadísticamente
significativas en los modelos en las que fueron incluidas. Por su parte, las pruebas de
significativas en los modelos en las que fueron incluidas. Por su parte, las pruebas de
166
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
yy
bondad
de
ajuste
muestran
que
no
problemas
de
autocorrelación
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
yy
estadísticamente
los parecen
modelos existir
en las que
fueron incluidas.
Por su parte,y
bondad
de ajuste
ajuste significativas
muestran que
queenno
no
parecen
existir
problemas
de autocorrelación
autocorrelación
bondad
de
muestran
parecen
existir
problemas
de
y
heterocedastidad,
yy
se
cumple
con
el
supuesto
de
normalidad.
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
yy
heterocedastidad,
se
cumple
con
el
supuesto
de
normalidad.
las
pruebas
de
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocobondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
heterocedastidad,
y
se
cumple
con
el
supuesto
de
normalidad.
bondad de
de ajustey
muestran
queel
no
parecen
existir problemas
problemas de autocorrelación
autocorrelación y
heterocedastidad,
se
cumple
con
supuesto
de
normalidad.
heterocedastidad,
se
cumple con
con
elno
supuesto
de normalidad.
normalidad.
bondad
muestran
que
parecen
existir
bondad de ajuste
ajusteyyy se
muestran
queel
no
parecen
existir problemas de
de autocorrelación yy
heterocedastidad,
cumple
supuesto
de
heterocedastidad,
se
cumple
con
el
supuesto
de
normalidad.
rrelación
y
heterocedastidad,
y
se
cumple
con
el
supuesto
de
normalidad.
heterocedastidad,
y
se
cumple
con
el
supuesto
de
normalidad.
heterocedastidad,
cumple
el
de
heterocedastidad, yy
y se
se cumple
cumple con
con el
el supuesto
supuesto de
de normalidad.
normalidad.
heterocedastidad,
heterocedastidad, y se
se cumple con
con el supuesto
supuesto de normalidad.
normalidad.
En
cuanto
a
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
En
cuanto
aa las
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
En
cuanto
a
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
En
cuanto
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
EnEncuanto
cuanto
a
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
En
a
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
cuantoaen
a
las
elasticidades
para
cada
uno
de modelos,
los modelos,
estas
fueron
halladas
seecuaciones
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
En
cuanto
las
elasticidades
para
cada
uno
estas
fueron
halladas
según
las
En
cuanto
a
las
elasticidades
para
cada
uno
modelos,
estas
fueron
halladas
según
las
ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
En
cuanto
a
las
elasticidades
para
cada
uno
modelos,
estas
fueron
halladas
según
las
ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
En
cuanto
a
las
elasticidades
para
cada
uno
modelos,
estas
fueron
halladas
según
las
ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
En
cuanto
a
las
elasticidades
para
cada
uno
modelos,
estas
fueron
halladas
según
las
gún
las
ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
19
Entabla
cuanto
aen
las(3)
elasticidades
para
cadamedio
uno de
dey los
los
modelos,
estas fueron
halladas
según las
19
ecuaciones
aa partir
de
los
resultados
modelos
mostrados,
que
se
presentan
en
19
19en
la
6.
En
ella
se
indica
el
valor
mediano,
la
moda,
el
rango
yyy la
desviación
ecuaciones
(3)
de
los
resultados
de
modelos
mostrados,
que
se
presentan
en
19
la
tabla
6.
En
ella
se
indica
el
valor
medio
yyy los
mediano,
la
moda,
el
rango
la
desviación
ecuaciones
(3)
aaa partir
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
la
tabla
6.
En
ella
se
indica
el
valor
medio
mediano,
la
moda,
el
rango
la
desviación
19
19
19en
ecuaciones
en
(3)
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
la
tabla
6.
En
ella
se
indica
el
valor
medio
mediano,
la
moda,
el
rango
y
la
desviación
presentan
en
la
tabla
6.
En
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
ecuaciones
en
(3)
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
la
tabla
6.
En
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
la
desviación
19
19
ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
la
tabla
6.
En
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
la
desviación
19
19 En
19
estándar
para
cada
una
de
las
elasticidades
calculadas.
la
tabla
6.
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
la
desviación
19
estándar
para
cada
una
de
las
elasticidades
calculadas.
19
la
tabla
6.
En
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
la
desviación
estándar
cada
las
elasticidades
19
desviación
estándar
para
una
decalculadas.
las
elasticidades
calculadas.
lalatabla
tabla
6.para
En
ellauna
se de
indica
elcada
valor
medio
mediano, la
la moda,
el rango
rango y la desviación
desviación
estándar
para
cada
una
de
las
elasticidades
calculadas.
19 En
estándar
para
cada
una
de
las elasticidades
elasticidades
calculadas.
la
ella
se
indica
el
yyy mediano,
la tabla 6.
6.
En
ellauna
se de
indica
el valor
valor medio
medio
mediano, la moda,
moda, el
el rango yy la
la desviación
estándar
para
cada
las
calculadas.
estándar
para
cada
una
de
las
elasticidades
calculadas.
estándar
para
cada
una
de
las
elasticidades
calculadas.
estándar
para
cada
una
de
las
calculadas.
estándar para
para cada
cada una
una de
de las
las elasticidades
elasticidades calculadas.
calculadas.
estándar
estándar para
cada 6una
de las elasticidades
elasticidades
calculadas.
Tabla
6.elasticidades
Tabla
.
Estadística
descriptiva
de
las
en
cada
modelo
Tabla
66... Estadística
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Tabla
6
descriptiva
de
las
elasticidades
en
cada
modelo
Tabla
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Tabla 66.. Estadística
Estadística descriptiva
descriptiva de
de las
las elasticidades
elasticidades en
en cada
cada modelo
modelo
Tabla
Estadística
descriptiva
de las
elasticidades
en
cada
modelo
Desviación
t
–Tabla
6
.
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Desviación
tt –Tabla
6
.
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Desviación
–Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo Mínimo
Mínimo
25
75
Tabla
6
.
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Desviación
t
–25
75
Tabla
6
.
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Desviación
t
–Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
25
75
estándar
estadístico
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Desviación
t –- modelo
25
75
Tabla
66.. Estadística
descriptiva
de
las
elasticidades
en
cada
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
25
75
Tabla
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
estándar
estadístico
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Desviación
t
–25
75
estándar
estadístico
Modelos
Elasticidades Media Mediana Q25
Q75 Moda Desviación
Máximo Mínimo
t –estándar estadístico
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
25
75
estándar estadístico
estadístico
Desviación
tt –25
75
Hiperlipidemia
Desviación
–25
75
Hiperlipidemia
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
25
75
Desviación
–Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Hiperlipidemia
25
75
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Desviación
–estándar
estadístico
Hiperlipidemia
Desviación
ttttt–-esta25
75
Desviación
–Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
Hiperlipidemia
25
75
Desviación
–estándar
estadístico
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Hiperlipidemia
25
75
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
Modelos Elasticidades
Media
Mediana
Q25
Q75
Moda
Máximo
Mínimo
25
75

Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
Hiperlipidemia
25
75
estándar
estadístico
m
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

estándar
dístico
m
estándar
estadístico
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
Hiperlipidemia
m
Hiperlipidemia
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

m
Hiperlipidemia
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

m
Hiperlipidemia
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
m
Hiperlipidemia
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
m
Hiperlipidemia

m
Hiperlipidemia
Hiperlipidemia
m
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

2,17
2,13
2,10
2,25 1,06
2,10
0,08
27,1
2,35
2,06
ggg
m
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
m

m
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
g
m
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
g

2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
1,06
1,06
1,06
1,06
1,06
0,040,04
26,5
1,07
1,05

1,06
1,06
1,06
1,06
1,06
26,5
1,07
1,05
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
mmmmmggggggm
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20

2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
m
g
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20

2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
mmmmgggg
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
-0,09
-0,07
0,05
-1,8
-0,02
2,17
2,13 -0,15
2,10 -0,05
2,25 -0,05
2,10 0,08
27,1
2,35 -0,20
2,06
2,17
2,13
2,10
2,25
2,10
0,080,08
27,1
2,35
2,06
2,17
2,13
2,10
2,25
2,10
27,1
2,35
2,06
2,17
2,13
2,10 -0,05
2,25 -0,05
2,10
0,08
27,1
2,35
2,06
-0,09
-0,07
-0,15
0,05
-1,8
-0,02
-0,20
mmmmmgggg
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
mmmmggggg
-0,50
-0,51
-7,1
-0,28
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,09
-0,07 -0,57
-0,15 -0,45
-0,05 -0,58
-0,05 0,07
-1,8
-0,02 -0,58
-0,20
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
-0,09
-0,07
-0,15
-0,05
-0,05
0,050,05
-1,8
-0,02
-0,20
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
Grupo II
ggm
gm
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
Grupo
gm
-0,50
-0,51
-0,57
0,07
-7,1
-0,28
-0,58
0,50
0,51
0,45 -0,45
0,57 -0,58
0,58
7,1
0,58
0,28
Grupo
II
gg
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
gm
-0,50
-0,51
-0,57
-0,45
-0,58
-7,1
-0,28
-0,58
Grupo
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
-0,50
-0,51
-0,57
-0,45
-0,58
-7,1
-0,28
-0,58
gm
Grupo
I
g
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
-0,50
-0,51
-0,57
-0,45
-0,58
-7,1
-0,28
-0,58
gm


g
Grupo I
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
-0,50
-0,51
-0,57
-0,45
-0,58
-7,1
-0,28
-0,58
gm
0,50
0,51
0,45 -0,45
0,57 -0,58
0,58
0,07
7,1
0,58
0,28
gm
-0,50
-0,51
-0,57
-0,45
-0,58
-7,1
-0,28
-0,58
ggg
Grupo
II
-0,50
-0,51
-0,57
0,07
-7,1
-0,28
-0,58
gm
gm
mg
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
Grupo
-0,50
-0,51
-0,57
0,07
-7,1
-0,28
-0,58
mg
gm
0,09
0,07
0,05 -0,45
0,15 -0,58
0,05
0,05
1,8
0,20
0,02
Grupo
II
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
gm
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
gm
Grupo
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28

mg
Grupo
I
gm
Grupo
I
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
mg
mg
gm
Grupo II
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
Grupo
gm
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
gm

Grupo I
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28

mg
gm
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
mg
gg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
-3,77
-4,19
-4,1
-2,13
0,09
0,07 -4,57
0,05 -2,78
0,15 -4,64
0,05 0,91
0,05
1,8
0,20 -4,67
0,02
gg
mg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67

0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
gg
mg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
gg

mg
-3,77
-4,19
-4,57
0,91
-4,1
-2,13
-4,67
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
gg
mg

-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
0,09
0,07
0,05 -2,78
0,15 -4,64
0,05
0,05
1,8
0,20
0,02
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02

gg
mg
gg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mm
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
gg

-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
mm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
gg
mm
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28

-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
mm
gg
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67

mm
gg
-0,11
-0,08
-0,19
0,007
-15,7
-0,02
-0,28
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
mm
gg
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mm
-3,77
-4,19
-4,57 -0,05
-2,78 -0,05
-4,64
0,91
-4,1
-2,13
-4,67
mm
gg

 mg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
mm
gg gm
mg 
gm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28

0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mm



mg
gm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28

mm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30

-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mg
gm
mm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mg
gm




mm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mg
gm
mm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg
gm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28




mm
-0,11
-0,08
-15,7
-0,02
mg
gm
0,60
0,59 -0,19
0,50 -0,05
0,73 -0,05
0,77 0,007
5,0
0,77 -0,28
0,30
mg
mm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28

m gm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
0,98
0,98
0,98
0,98
0,98
0,000,12
2450
0,99
0,99
mg
gm
m
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
mg
gm

0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg
gm
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99

0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg
gm
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30

mg
mmmmm 
 gm
mg
gm
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg
gm
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
m
mgm
gm
0,60
0,59
0,50 0,98
0,73 0,98
0,77
0,12
5,0
0,77
0,30
0,98
0,98
0,98
0,00
2450
0,99
0,99
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
ggg
m
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
m
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99

m
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
g
m
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
g

m
2,31
2,30
2,26
46,2
2,44
2,18
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99

2,31
2,30
2,26 2,34
2,34 2,29
2,29 0,05
46,2
2,44
2,18
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
0,98
0,98
0,98
0,98
0,98
0,000,05
2450
0,99
0,99

0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
mmmmmgggggggm
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
0,98
0,98
0,98 -0,14
0,98 -0,15
0,98
0,00
2450
0,99
0,99

-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,16
-0,16
-0,18
0,02
-8,0
-0,08
0,22

2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22

2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
m
g
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
-0,16
-0,16
-0,18
-8,0
-0,08
-0,16
-0,16
-0,18 -0,14
-0,14 -0,15
-0,15 0,02
-8,0
-0,08 0,22
0,22
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
2,31
2,30
2,26
2,34
2,29
0,050,02
46,2
2,44
2,18
mmmmmmgggggg
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
2,31
2,30
2,26 -0,54
2,34 -0,55
2,29
0,05
46,2
2,44
2,18
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,54
-0,55
-0,54
0,01
-54,0
-0,50
-0,54
m

g
m
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
g
Grupo
II

m
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
Grupo
II
-0,54
-0,55
-0,54
0,01
-54,0
-0,50
-0,54
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
Grupo
 mmmgggggm
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
-0,16
-0,16
-0,18 -0,54
-0,14 -0,55
-0,15
0,02
-8,0
-0,08
0,22
Grupo II
II
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
Grupo
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
gm
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
Grupo II
II
gm
0,54
0,55
0,54
0,54
0,55
54,0
0,54
0,50
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
ggg
0,54
0,55
0,54
0,54
0,55
54,0
0,54
0,50
gm
Grupo
II
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
Grupo
II
-0,54
-0,55
-0,54
-0,54
-0,55
-54,0
-0,50
-0,54
gm
g
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
-0,54
-0,55
-0,54
-0,54
-0,55
-54,0
-0,50
-0,54
gm

g
Grupo
II
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
-0,54
-0,55
-0,54
-0,54
-0,55
-54,0
-0,50
-0,54

gm
Grupo
II
g
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
-0,54
-0,55
-0,54
-0,54
-0,55
-54,0
-0,50
-0,54

g
Grupo
II

-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
gm
Grupo II
II
g
gm

-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
mg
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
Grupo
gm

0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg
Grupo
gm
0,16
0,16
0,14 0,18
0,18 0,15
0,15 0,02
0,02
8,0
0,22
0,08
0,16
0,16
0,14
8,0
0,22
0,08
 mg
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
Grupo II
II
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
mg
gm
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
mg
gm
0,16
0,16
0,14
0,02
8,0
0,22
0,08
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
mg
gm
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg
0,54
0,55
0,54 0,18
0,54 0,15
0,55
0,01
54,0
0,54
0,50
mg
gm

0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
mg
gm

0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50

gg
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
mg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
 mg
gg
0,16
0,16
0,14
0,18
0,15
0,02
0,22
0,08
Desviación
t8,0
–mg
-2,43
-2,41
-2,65
-2,49
0,33
-7,4
-1,74
-3,39
0,16 Mediana
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
gg
mg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
gg

Modelos
Elasticidades
Media
Q25 -2,19
Q75 Moda
Máximo
Mínimo
mg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
gg
mg

-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
gg
0,16
0,16
0,14
0,18
0,15
0,020,04 estadístico
8,0
0,22
0,08
mg
estándar
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
gg
mg
-0,21
-0,20
-0,23
-0,17
-0,20
-5,3
-0,10
-0,32
gg

-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08

mm
-0,21
-0,20
-0,23 -0,17
-0,17 -0,20
-0,20
0,04
-5,3
-0,10
-0,32
gg

mm
-0,21
-0,20
-0,23
0,04
-5,3
-0,10
-0,32
gg

-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
mm
gg
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32

-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
mm
gg
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39

mm
gg
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
mm
mm
gg
 mg

-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
mm
-2,43
-2,41
-2,65
-2,19
-2,49
0,330,03
-7,4
-1,74
-3,39
gg
0,70
0,71 -0,23
0,68 -0,17
0,75 -0,20
0,72 0,03
23,3 -0,10
0,75 -0,32
0,59
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
0,70
0,71
0,68
0,75
0,72
23,3
0,75
0,59
gg gm
-0,21
-0,20
0,04
-5,3

mm
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
mm
para
19
mm
-0,21
-0,20
-0,23
-0,17
0,04
-5,3
-0,32
19
mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
Los errores
errores estándar
estándarpara
las elasticidades
elasticidades
fueron
calculados
través
del -0,20
método delta,
delta,
encontrándose
que todas
todas-0,10
las elasticidades
elasticidades
son
19 Los
mm
las
fueron
calculados
aaa través
del
método
encontrándose
que
las
son
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
19
mm
errores
estándar
para
las
elasticidades
fueron
calculados
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
Diabetes
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32

19 Los
mm
Los errores
errores estándar
estándarpara
para
las elasticidades
elasticidades
fueron
calculados
través
del -0,20
método delta,
delta,
encontrándose
que todas
todas-0,10
las elasticidades
elasticidades
son
-0,21 fueron
-0,20calculados
-0,23 aa través
-0,17del
-0,20
0,04
-5,3
-0,10
-0,32 son
mm
19
significativas.
-0,21
-0,20
-0,23
-0,17
0,04
-5,3
-0,32
método
encontrándose
que
las
19 Los
significativas.
mm las
-0,21 fueron
-0,20calculados
-0,23aa través
-0,17del
-0,20
0,04
-5,3
-0,10
-0,32 son
Los
errores
estándar
para
las
elasticidades
método
delta,
encontrándose
que
todas
las
elasticidades
son
19
significativas.
Los
errores
estándar
para
las
elasticidades
fueron
calculados
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
19
significativas.
19
Los
estándar
las
elasticidades
fueron
calculados
a través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
19
Los errores
errores
estándar
para
las
elasticidades
fueron
calculados
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
para
19 Los
significativas.
errores
estándar
para
elasticidades
método
delta,
encontrándose
que
todas
las
elasticidades
significativas.
19
m las
errores
estándar
para
las
elasticidades
fueron
calculados
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
1,01 fueron
1,01calculados
1,01 aaaa través
1,01 del
1,01
0,00
252,5
1,02
1,01 son
19 Los
Los
errores
estándar
para
las
elasticidades
fueron
calculados
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
19
Los
errores
estándar
para
las
elasticidades
fueron
calculados
a
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
19 Los
significativas.
19 errores
estándarestándar
para las
las elasticidades
fueron calculados
calculados
a22través
través
del método
método a
delta,
encontrándose
que delta,
todas las
las
elasticidades son
son
significativas.
19 Los
estándar
para
fueron
a22
del
delta,
encontrándose
que
todas
elasticidades
errores
Los
errores
para las elasticidades
fueron
calculados
través
del método
encontrándose
significativas.
Los
errores
estándar
para las elasticidades
elasticidades
fueron calculados
a
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
—
—
significativas.
—
22
—
significativas.
g
—
significativas.
22
—
2,29 son significativas.
2,28
2,25
2,31
2,25
0,04
57,3
2,45
2,20
—
22
—
significativas.
que todas las elasticidades
—
22
—
—
22
—
—
22
—
m
—
22
—
-0,14
-0,14
-0,16
-0,13
0,02
-7,0
-0,10
-0,22
—
22
—
— 22
22
— -0,13
22 —
—
—
22 —
g
-0,50
-0,50
-0,50 -0,49 -0,50
0,01
-83,3
-0,47
-0,50
Grupo
ecuaciones
en
(3)
a partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
ecuaciones
en
(3)
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
ecuaciones19en
en (3)
(3) aaa partir
partir de
de los
los resultados
resultados de
de los
los modelos
modelos mostrados,
mostrados, que
que se
se presentan
presentan en
en
ecuaciones
19
ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
19
la
tabla
6.
En
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
la
desviación
19
19
la
tabla
6.
En
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
la
desviación
19
19 En
la
tabla
6.
ella
se
indica
el
valor
medio
mediano,
la
moda,
el
rango
la
desviación
19
la
tabla
6.
En
ella
se
indica
el
valor
medio
mediano,
la
moda,
el
rango
la
desviación
la tabla
tabla 6.
6.19
En ella
ella se
se indica
indica el
el valor
valor medio
medio yyyy mediano,
mediano, la
la moda,
moda, el
el rango
rango yyyy la
la desviación
desviación
la
En
estándar
para
cada
una
de
las
elasticidades
calculadas.
estándar
para
cada
una
de
las
elasticidades
calculadas.
estándar
para
cada
una
de
las
elasticidades
calculadas.
estándar
para
cada
una
de
las
elasticidades
calculadas.
estándar para
para cada
cada una
una de
de las
las elasticidades
elasticidades calculadas.
calculadas.
167
estándar
estándar
para cada
una de
las elasticidades
calculadas.
Ecos de Economía
Tabla
66.. Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Universidad EAFIT
Tabla
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
bondad
de
ajuste
que
no
parecen
existir
problemas
de
autocorrelación
Tabla
6
...muestran
Estadística
descriptiva
de
las
elasticidades
en
modelo
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
yy
Nº 36
-cada
Año
17
/ enero-junio 2013 y
Tabla
6
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
Tabla
6
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
yy
bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
de
autocorrelación
Tabla
6
.
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
Desviación
ttde
–bondad
de
ajuste
muestran
que
no
parecen
existir
problemas
autocorrelación
Desviación
–Modelos
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
bondad
de Elasticidades
ajusteyy se
muestran
queel
no
parecen
existir
problemas
autocorrelación
yy
Desviación
ttde
–25
75
heterocedastidad,
cumple
con
supuesto
de
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Desviación
–25
75 normalidad.
estándar
estadístico
25
75
heterocedastidad,
se
cumple
con
el
supuesto
de
normalidad.
Desviación
t
–Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
25
75
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Desviación
t ––25
75
heterocedastidad,
y
con
normalidad.
Desviación
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
25
75
heterocedastidad,
y se
se cumple
cumple
con el
el supuesto
supuesto
de
tt –estándar
estadístico
Modelos
Elasticidades
Media Mediana
Mediana
Q25
Qde
Moda Desviación
Máximo Mínimo
Mínimo
25
75 normalidad.
heterocedastidad,
se
cumple
con
el
supuesto
de
normalidad.
Modelos
Elasticidades
Media
Q
Q
Moda
Máximo
estándar
estadístico
75
Modelos
Elasticidades
Media
Mediana
Q
Q
Moda
Mínimo
estándar estadístico
estadístico Máximo
25
75
heterocedastidad,
yy se
cumple
con
el
supuesto
de
normalidad.
Hiperlipidemia
estándar
estándar
estadístico
Hiperlipidemia

Hiperlipidemia
Hiperlipidemia
Hiperlipidemia
Hiperlipidemia
Hiperlipidemia
Hiperlipidemia

Diabetes
m
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
m
En
cuanto
aa las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las

1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
m
m
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
En
cuanto
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las

m
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
m
En
cuanto
a
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

m
En
cuanto
aa las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

m
1,01
1,01
1,01
1,01
1,01
0,00
252,5
1,02
1,01
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
En
cuanto
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
gg
m
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
En
cuanto
a
las
elasticidades
para
cada
uno
de
los
modelos,
estas
fueron
halladas
según
las
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
g
ecuaciones
en
(3)
aa partir
de
los
resultados
modelos
mostrados,
que
se
presentan
en
g
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06

g
ecuaciones
en
(3)
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
en
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
g
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06

ecuaciones
en
(3)
a
partir
de
los
resultados
de
los
modelos
mostrados,
que
se
presentan
2,29
2,28
2,25 de
2,31
2,25 0,08
0,04
57,3
2,45
2,20en
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06

ecuaciones19en
en (3)
(3)
partir
de los
los-0,07
resultados
los -0,05
modelos
mostrados,
que se
se-0,02
presentan
en
 mmggg aa partir
2,17
2,13
2,10
2,25
2,10
27,1
2,35
2,06
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
-0,09
-0,15
-0,05
0,05
-1,8
-0,20
ecuaciones
de
resultados
de
los
modelos
mostrados,
que
presentan
en
19
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
ecuaciones
en
(3)
a partir
de los
resultados
de
modelos
mostrados,
que se
presentan
en
19
m
la
tabla
6.
En
se
indica
el
valor
medio
yy los
mediano,
la
moda,
el
rango
yy-0,02
la
desviación
ella
19
m
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,20
la
tabla
6.
En
ella
se
indica
el
valor
medio
mediano,
la
moda,
el
rango
la
desviación
19
m
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
19
m
la
tabla
6.
En
ella
se
indica
el
valor
medio
y
mediano,
la
moda,
el
rango
y
la
desviación
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,14
-0,14
-0,16
-0,13
-0,13
0,02
-7,0
-0,10
-0,22
19 En
m
la
tabla
6.
ella
se
indica
valor
medio
yy mediano,
la
moda,
el
rango
la
desviación
-0,09 el
-0,07
-0,15 -0,05
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
19
m
la tabla
tabla 6.
6.19
En ella
ella
se indica
indica
el-0,51
valor medio
medio
mediano,
la0,07
moda, el
el-1,8
rango yyy-0,28
la desviación
desviación
-0,09
-0,07
-0,15
-0,05
0,05
-1,8
-0,02
-0,20
gg
m
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-0,02
-0,20
-0,50
-0,57
-0,45
-0,58
-0,58
la
En
se
el
valor
mediano,
la
moda,
rango
la
gg una
la
tabla 6.
En
se
indica
el
valor
medio
yy-0,49
mediano,
la
moda,
el-7,1
rango
y-0,28
la
desviación
ella
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,58
estándar
para
cada
de
las
elasticidades
calculadas.
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
gg una
-0,50
-0,50
-0,50
-0,50
0,01
-83,3
-0,47
-0,50
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
estándar
para
cada
de
las
elasticidades
calculadas.
-0,50
-0,51
-0,57 calculadas.
-0,45 -0,58
-0,58
0,07
-7,1
-0,28
-0,58
-0,50
-0,51
-0,57
-0,45
0,07
-7,1
-0,28
-0,58
gg una
estándar
cada
de
las
elasticidades
gm
Grupo
II para
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
estándar
para
cada
una
de
las
elasticidades
calculadas.
g
-0,50
-0,51
-0,57
-0,45
-0,58
-7,1
-0,28
-0,58
Grupo
estándar
para
cada
una
de
las
elasticidades
calculadas.
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
Grupo
gm
Grupo
II para cada
gm

0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
gm
estándar
una
de
las
elasticidades
calculadas.
Grupo
0,49
0,49
0,50 0,57
0,49 0,58
0,50 0,07
81,7
0,50
0,47
0,50
0,51
0,45
0,57
0,58
0,070,01
7,1
0,58
0,28
gm
Grupo
I
0,50
0,51
0,45
7,1
0,58
0,28
 gm
gm
Grupo
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
Grupo
gm
únicoIII
0,50
0,51
0,45 0,57
0,57 0,58
0,58
0,07
7,1
0,58
0,28
Grupo
0,50
0,51
0,45
0,07
7,1
0,58
0,28
gm
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
mg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
mg
0,14
0,14
0,16
0,13
0,13
0,02
7,0
0,22
0,10
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
Tabla
6. Estadística
descriptiva
de
las
elasticidades
en cada
modelo
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
Tabla
descriptiva
las
elasticidades
cada
mg 6. Estadística
0,09
0,07
0,05 de
0,15
0,05
0,05 en
1,8 modelo
0,20
0,02
 mg
mg

0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
Tabla
6
... Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
gg
Tabla
6
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02

-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
-2,18
-2,17
-2,33
-2,02
-2,34
0,20
-10,9
-1,52
-2,64
Tabla
6
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
 gg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
Tabla
6
.
Estadística
descriptiva
de
las
elasticidades
en
cada
modelo
gg
Desviación
t
–-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67

Desviación
t
–gg
Modelos
Elasticidades
Media
Q25
Q75 Moda
Máximo
Mínimo
-3,77 Mediana
-4,19
-4,57
-2,78
-4,64 Desviación
0,91
-4,1
-2,13
-4,67
t – gg
Modelos
Modelos
Modelos
Modelos
Modelos
Modelos
Modelos
Elasticidades
gg

Elasticidades
mm
Elasticidades
mm
 mm
Elasticidades
mm
mm
Elasticidades
Elasticidades
mm

Elasticidades
mm

mm
-3,77 Mediana
-4,19
-4,57
-2,78
-4,64
0,910,03 estadístico
-4,1
-2,13
-4,67
Desviación
tt –25
75
Media
Q
Q
Moda
estándar
25
75
-0,19
-0,19 -0,19
-0,21
-0,16
-0,17Desviación
-6,3 Máximo
-0,12 Mínimo
-0,33
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
-0,11
-0,08
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
Desviación
–Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
25
75
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
Desviación
t ––25
75
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
25
75
Desviación
tt –estándar
estadístico
Media
Mediana
Q25
Q75
Moda
Máximo
Mínimo
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
25
75
Media
Mediana
Q
Q
Moda
Máximo
Mínimo
estándar
estadístico
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
Media
Mediana
Q0,62
Q0,66
Moda
Máximo
Mínimo
estándar
estadístico
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
25
75
Hiperlipidemia
estándar
estadístico
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
0,64
0,64
0,67
0,02
32,0
0,71
0,57
Hiperlipidemia
estándar
estadístico
mm gm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28

0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg 
gm
Hiperlipidemia
mg
Hiperlipidemia
 mg

 gm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg
gm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
Hiperlipidemia

mg
gm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
Hiperlipidemia
mg
gm
Hiperlipidemia
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30



mg
gm
Hiperlipidemia
0,60
0,59 Hipertensión
0,50
0,73esencial
0,77
0,12
5,0
0,77
0,30
 mg
mg
m  gm
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99

1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
mmmmmm gm 0,98
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05

0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99

m
1,07
1,07 2,10
1,07 2,25
1,07 2,10
1,07 0,08
26,8
1,07
1,4
1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
0,98
0,98
0,98
0,98
0,98
0,000,04
2450
0,99
0,99
g
m

1,06
1,06
1,06
1,06
1,06
0,04
26,5
1,07
1,05
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
2,17
2,13
27,1
2,35
2,06
gg
m
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99

2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
gg
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06

2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
g
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06

2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
g
0,69
0,68
0,66
0,73
0,66
0,04
17,3
0,78
0,61
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06

2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
 mggg
2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
2,31
2,30
2,26 -0,05
2,34 -0,05
2,29
0,05
46,2
2,44
2,18

2,17
2,13
2,10
2,25
2,10
0,08
27,1
2,35
2,06
-0,09
-0,07
-0,15
-1,8
-0,02
-0,20
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
2,31
2,30
2,26
2,34
2,29
46,2
2,44
2,18
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
mmmm
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-1,02
-1,02
-1
-1
-1,02
0,04
-25,5
-1,01
-1,02
 mmmmg
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,16
-0,16
-0,18 -0,45
-0,14 -0,58
-0,15
0,02
-8,0
-0,08
0,22
 mgg
-0,09
-0,07
-0,15
-0,05
-0,05
0,05
-1,8
-0,02
-0,20
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,50
-0,51
-0,57
0,07
-7,1
-0,28
-0,58
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
gg
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58

-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
-0,78
-0,77 -0,54
-0,8 -0,54
-0,8 -0,55
-0,77 0,01
0,02
-39,0 -0,50
-0,73 -0,54
-0,82
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
Grupo
II
-0,54
-0,55
-54,0
-0,50
-0,51
-0,57
-0,45
-0,58
0,07
-7,1
-0,28
-0,58
Grupo
II
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
-0,50
-0,51
-0,57 -0,45
-0,45 -0,58
-0,58
0,07
-7,1
-0,28
-0,58
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
gmggggg
Grupo
II
II
-0,50
-0,51
-0,57
0,07
-7,1
-0,28
-0,58
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
Grupo
II
-0,50
-0,51
-0,57
-0,45
-0,58
-7,1
-0,28
-0,58
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
Grupo
Grupo
II
gm
Grupo
II
-0,54
-0,55
-0,54
-0,54
-0,55
-54,0
-0,50
-0,54
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
Grupo
II

0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
gm
Grupo
Grupo
II
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
0,08
0,09
0,07
0,1
0,11
0,02
4,0
0,12
0,04
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
Grupo
I
Grupo
 gm
gm
Grupo
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
Grupo IIIII
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
Grupo
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
gm
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
 mg
Grupo
I
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
gm
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
0,50
0,51
0,45
0,57
0,58
0,07
7,1
0,58
0,28
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
gm
0,54
0,55
0,54
0,54
0,55
0,01
0,54
0,50
 mg
0,16
0,16
8,0
0,22
0,08
0,05
0,05 0,14
0,05 0,18
0,05 0,15
0,05 0,02
0,006 54,0
8,0
0,05
0,07
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
mg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
mg
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg
0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
 mg
mg
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08

0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
gg

0,09
0,07
0,05
0,15
0,05
0,05
1,8
0,20
0,02
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
mg
-0,17
-0,16
-0,2 -2,19
-0,1 -2,49
-0,14 0,33
0,05
-3,4
-0,08 -3,39
-0,31
gg
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08

-2,43
-2,41
-2,65
-7,4
-1,74
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67

-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
gg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
 gg
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
gg
-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67

gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39

-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39

mm
-2,79
-2,92
-3,2
-2,3
-3,16
0,48
-5,8
-1,8
-3,57

-3,77
-4,19
-4,57
-2,78
-4,64
0,91
-4,1
-2,13
-4,67
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
-2,43
-2,41
-2,65 -0,17
-2,19 -0,20
-2,49
0,33
-7,4
-1,74
-3,39
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
-0,21
-0,20
-0,23
0,04
-5,3
-0,10
-0,32

-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mm
 mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
mm

-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
mm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32

mm
mm gm
-0,11
-0,08
-0,19
-0,05
-0,05
0,007
-15,7
-0,02
-0,28
0,65
0,65 -0,19
0,6 -0,05
0,71 -0,05
0,72 0,007
10,8 -0,02
0,74
0,49
-0,21
-0,20
-0,23
-0,17
-0,20
0,040,06
-5,3
-0,10
-0,32
-0,11
-0,08
-15,7
-0,28


-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg
gm
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mg
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
 mg

lasgm
mg
gm
19
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
mm
mg
gm
19 Los errores estándar
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
para
elasticidades
fueron
calculados
aa través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
mg
gm
19
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30


Los
errores
estándar
para
las
elasticidades
fueron
calculados
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
19 Los
mg
gm
errores
estándar
para
las
elasticidades
fueron
calculados
a
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
0,60 fueron
0,59 calculados
0,50 aa través
0,73 del
0,77
0,12
5,0que
0,77
0,30 son
 mg
m las
19
mg
gmelasticidades
errores
estándar
para
método
delta,
encontrándose
todas
las
elasticidades
son
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
19 Los
gm
errores
estándar
para
elasticidades
fueron
calculados
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
0,60
0,59
0,50
0,73
0,77
0,12
5,0
0,77
0,30
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
19 Los
Los
errores
estándar
para
las
elasticidades
fueron
calculados
aa través
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
m las
0,98
0,98
0,98
0,98
0,00
2450
0,99
19
significativas.
m
Los errores
errores estándar
estándar
para
las elasticidades
elasticidades
fueron
calculados
través
del 0,98
método delta,
delta,
encontrándose
que todas
todas 0,99
las elasticidades
elasticidades
son

significativas.
19
m
Los
para
las
fueron
calculados
a
través
del
método
encontrándose
que
las
son
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
significativas.
m
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
Los errores estándar
para
las elasticidades
fueron
calculados
a través
del 0,98
método delta,
encontrándose
que todas 0,99
las elasticidades
son
significativas.
m
0,98
0,98
0,98
0,98
0,00
2450
0,99
significativas.
m
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
De
los
resultados
de
elasticidad
se
tiene
que
la
elasticidad
gasto
demanda
de
medica
significativas.
m
0,98
0,98
0,98
0,98
0,98
0,00
2450
0,99
0,99
significativas.
gg
m
0,98
0,98
0,98 2,34
0,98 2,29
0,98
0,00
2450
0,99
0,99

2,31
2,30
2,26
0,05
46,2
2,44
2,18
g
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
 ggg
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
—
22
—
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
—
22
—

2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
mentos de genéricos
es
que la
unidad,
con
moda de
2,29
22
2,31mayor
2,30
2,26
2,34
2,29valores
0,05 para la
46,2
2,442,10,2,18
2,18

 mmggg
—
22
—
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
—
22
—
2,31
2,30
2,26
2,34
2,29
0,05
46,2
2,44
2,18
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
—
22
—
m
22
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22

m
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
—
22
—
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
 mmmm
para hiperlipidemia
y 2,25
para
diabetes,
por
lo
que
podría
decirse
que
con
relación
-0,16
-0,16
-0,18
-0,14
-0,15
0,02
-8,0
-0,08
0,22
-0,16
-0,16
-0,18 -0,14
-0,14 -0,15
-0,15
0,02
-8,0
-0,08
0,22 al
-0,16
-0,16
-0,18
0,02
-8,0
-0,08
0,22
-0,16
-0,16
-0,18
-0,14 -0,55
-0,15
0,02
-8,0
-0,08
0,22
 mgggg
-0,54
-0,55
-0,54
-0,54
0,01
-54,0
-0,50
-0,54
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
Grupo
II
-0,54
-0,55 genéricos
-0,54 -0,54
-0,54se -0,55
-0,55
0,01 como-54,0
-54,0
-0,50
-0,54
g
gasto
realizado
los medicamentos
comportan
bienes de
lujo, excep-0,54
-0,55
-0,54
0,01
-0,50
-0,54
g
Grupo
II
-0,54
-0,55
-0,54
-0,54
-0,55
0,01
-54,0
-0,50
-0,54
Grupo
II
g
-0,54
-0,55
-0,54 -0,54
-0,54 -0,55
-0,55
0,01
-54,0
-0,50
-0,54
Grupo
II
gm
-0,54
-0,55
-0,54
0,01
-54,0
-0,50
-0,54
Grupo
II
gg
-0,54
-0,55
-0,54
-0,54
-0,55
-54,0
-0,50
-0,54
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
Grupo II
II
gm
Grupo
gm

0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
Grupo
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
to
en IIel casode
hipertensión
esencial,
donde
el
resultado
obtenido
—0,66—
evidencia
gm
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
 mg
gm
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
gm
0,54
0,55
0,54
0,54
0,55
0,01
54,0
0,54
0,50
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg

0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg
 mg
que los medicamentos
para
esta
patología
son
considerados
como
bienes
necesarios.
mg
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg
0,16
0,16
0,14
0,18
0,15
0,02
8,0
0,22
0,08
mg
0,16
0,16
0,14 0,18
0,18 0,15
0,15
0,02
8,0
0,22
0,08
 mg
mg

0,16
0,16
0,14
0,02
8,0
0,22
0,08
0,16
0,16
0,14
0,18 -2,49
0,15
0,02
8,0
0,22
0,08

-2,43
-2,41
-2,19
0,33
-3,39
gg
En cuanto a la
elasticidad
gasto
de -2,65
los
medicamentos
de
marca-7,4
en tres -1,74
de los cuatro
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
gg
 gg
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39

gg
-2,43
-2,41
-2,65 -2,19
-2,19 -2,49
-2,49
0,33
-7,4
-1,74
-3,39
mm
gg

-2,43
-2,41
-2,65
0,33
-7,4
-1,74
-3,39
gg
-2,43
-2,41
-2,65
-2,19
-2,49
0,33
-7,4
-1,74
-3,39
-0,23
-0,20
0,04
-5,3
-0,10
-0,32

grupos estudiados
es -0,21
igual
o -0,20
superior
a la -0,17
unidad,
por tanto
los resultados
encontrados
mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
mm

mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32

mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04es decir,
-5,3son bienes
-0,10 de
-0,32
 mm
mm
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
son
equivalentes
a
los
del
parámetro
β
de
la
estimación,
lujo.
-0,21
-0,20
-0,23
-0,17
-0,20
0,04
-5,3
-0,10
-0,32
19
19 Los errores estándar para las elasticidades fueron calculados a través del método delta, encontrándose que todas las elasticidades son
19
Los errores
errores
estándar
para
las
elasticidades
fueron
calculados
través del
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
19 Los
estándar
para
las
elasticidades
fueron
calculados
aaa través
método
delta,
encontrándose
que
todas
las
elasticidades
son
19
errores
estándar
para
las
elasticidades
fueron
calculados
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
19 Los
errores
estándar
para
las
elasticidades
fueron
calculados
a través
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
19 Los
Para
el caso
II de hiperlipidemia,
los del
resultados
concluir
Los
errores
estándar
para
las
elasticidades
fueron
calculados
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
19
significativas.
Los
errores
estándardel
paragrupo
las elasticidades
elasticidades
fueron calculados
calculados aaa través
través
del método
método delta,
delta,encontrados
encontrándose que
que permiten
todas las
las elasticidades
elasticidades
son
significativas.
19
Los
errores
estándar
para
las
fueron
encontrándose
todas
son
significativas.
Los
errores
estándar
para
las
elasticidades
fueron
calculados
a
través
del
método
delta,
encontrándose
que
todas
las
elasticidades
son
significativas.
significativas.
significativas.
significativas.
que estos son considerados como necesarios.
—
22
—
—
22
—
22
—
22
—
—
22
—
—
22
—
22 —
— 22
En cuanto a la elasticidad precio de la demanda hicksiana de los genéricos y los de marca, el resultado fue menor a 1 en valor absoluto en casi todos los casos, por lo que se
168
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
puede concluir que la demanda es poco sensible a la variación en los precios; y dados
los resultados parecen ser más inelásticos los medicamentos marca en comparación
con los genéricos, al ser su moda más cercana a cero, es decir, responden menos a las
variaciones en los precios. En el caso de los medicamentos para hipertensión arterial
de marca la demanda es elástica, esto es, que la variación de 1% en los precios genera
una variación superior al 1% en la demanda.
Finalmente, en cuanto a la elasticidad precio cruzada, los resultados en todos los casos
arrojaron signo positivo, tal como se espera para el caso de bienes sustitutos. Sin embargo, el grado de sustitución parece ser elevado al evaluar la respuesta de la demanda
por medicamentos genéricos ante variaciones en el precio de los medicamentos de
marca en comparación con la respuesta de la demanda por medicamentos de marca
ante variaciones en el precio de los medicamentos genéricos. En el caso de las elasticidades de sustitución se obtuvieron valores para la moda de 0,77 y 0,72 para hiperlipidemia, 0,67 para diabetes y 0,72 para hipertensión, en todos los casos, valores positivos
y mayores a cero, por lo cual se puede concluir que los bienes pueden ser considerados
como sustitutos, lo que evidencia la posibilidad de sustitución intramolecular entre medicamentos de marca y genéricos.
6. Conclusiones y discusión
Aunque en el país existe información sobre prescripción para el mercado institucional,
esta es de carácter privado y no pudo ser utilizada.
Si bien el análisis realizado en esta investigación incluyó únicamente medicamentos
comercializados en el mercado privado, debido a las restricciones de acceso a la información sobre prescripción para el mercado institucional, las políticas y comportamientos del mercado en este segmento es de gran importancia a nivel mundial debido a que
son estos los que mayor impacto generan en la inversión en investigación y desarrollo a
largo plazo. Dado que el gasto se obtiene por el volumen de ventas multiplicado por el
precio en ventas a minoristas, este podría considerarse como proxy del gasto de bolsillo
de los consumidores, y en este sentido, el resultado obtenido en la elasticidad gasto y
por ende la clasificación de los productos como bienes de lujo, podría obedecer posiblemente a la falta de oportunidad en la entrega de medicamentos por parte de las EPS
169
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
o porque las cuotas moderadoras y copagos dentro del sistema de salud pueden estar
superando el costo de ellos.
En cuanto a la elasticidad gasto, se tiene que la variación en la demanda y en el gasto
es positiva, siendo la primera superior a la segunda; esto, en otras palabras, significa
que la demanda por dicho tipo de medicamentos en el mercado privado avanza de una
manera más rápida que el nivel de gasto generado; así podría pensarse que un cambio
en el gasto total puede tener mayor impacto en el consumo cuando el acceso al sistema
de salud nacional es bajo y cuando el acceso a consultas y compras particulares es alto
(Alexander, Flynn & Linkins, 1994).
Ahora, dado el resultado de las elasticidades precio propio y precio cruzadas, es importante señalar que una demanda inelástica es diferente a una demanda totalmente
inelástica, esto para efectos de los actores del mercado significa que una variación en
los precios de los medicamentos sí genera impacto en la demanda, pero esta variación
es inferior a la experimentada por los precios. En cuanto a la elasticidad cruzada se podría pensar que los consumidores no están respondiendo al incremento de los precios
de los medicamentos genéricos reduciendo su demanda de medicamentos de marca y
aumentando el consumo de sustitutos. Esto puede deberse a la percepción de mayor
calidad que tienen los agentes de los medicamentos de marca frente a los genéricos, a
la fidelidad a la marca que se genera durante la vigencia de la patente y al impacto de
la publicidad en el consumidor.
Finalmente, es importante resaltar que con los esfuerzos realizados en el actual sistema de salud colombiano, al adjuntar un listado de medicamentos esenciales y genéricos
al plan de beneficios se buscaba promover la competencia entre productores de moléculas iguales20 y se procuraba que el médico fuera un agente cada vez más perfecto
del paciente al eliminar los incentivos monetarios en la prescripción. Sin embargo, y
dadas las estadísticas nacionales con relación al acceso a medicamentos y lo encontrado en esta investigación, la concentración de mercado sigue siendo alta, posibilitando
el ejercicio de poder del mercado, y además se están generando pérdidas de equidad
dentro del sistema al trasladarse el consumo del mercado institucional al privado, dicha
situación es común a toda política pública que transfiere recursos entre sectores de
20
Esto debido a que la protección de patentes comenzó a regir a partir de 1993.
170
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
población sin que se establezcan acciones que permitan disminuir al máximo dichas
pérdidas.
Referencias
Akbulutgiller, K. (2008). Application of Almost Ideal Demand System for a Pharmaceutical. Recuperado de: http://dalea.du.se/theses/archive/4fb131bd-8534-4a139ba0-e966521263dd/df15f24f-9815-493d-8bb8-b4166b3fa391.pdf
Alexander, D. L.; Flynn, J. E. & Linkins, L. A. (1994, agosto). Estimates of the demand for
ethical pharmaceutical drugs across countries and time. Applied Economics, 26(8),
821-826.
Anderson, G. J. & Blundell, R. W. (1982). Estimation and hypothesis testing in dynamic
singular equation systems. Econométrica, 50, 1559-1571.
___. (1983). Testing restrictions in a flexible demand system: An application to consumers´ expenditure in Canada”. Review of Economic Studies, 50, 397-410.
Archila, E. J. et al. (2005, junio). Estudio sobre la propiedad intelectual en el sector farmacéutico colombiano. Informe de Investigación. Fedesarrollo y Fundación Santa
Fe de Bogotá. Recuperado de: ftp://ftp.fedesarrollo.org.co/pub/documentos/2005/
dc01-2005.PDF
Attfield, C. L. (1997, enero). Estimating a Cointegrating Demand System. European Economic Review, 41(1), 61-73.
Caves, R. E. & Williamson, P. J. (1985, diciembre). ¿What is Products Differentiation, Really? The Journal of Industrial Economics, 34(2), 113-132.
Caves, R. E. & Whinston, M. D. (1991). Patent Expiration, Entry and Competition in the U.S.
Pharmaceutical Industry. Brooking Papers on Economics Activity. Microeconomics,
1-66.
Chaudhuri, S.; Golberg, P. K. & Jia, P. (2003, diciembre). Estimating the Effects of Global
Patent Protection in Pharmaceuticals: A Case Study of Quinolones in India. National
Bureau of Economic Research, Working paper, 10159.
171
Ecos de Economía
Universidad EAFIT
Nº 36 - Año 17 / enero-junio 2013
Crawford, G. & Shum, M. (2005, julio). Uncertainty and Learning in Pharmaceutical Demand. Econometrica, 73(4), 1137-1173.
Deaton, A. S. & Muellbauer, J. (1980, junio). An Almost Ideal Demand System. American
Economic Review, 70(3), 312-326.
Ellison, S. F. et al. (1997, agosto). Characteristics of Demand for Pharmaceutical Products: An Examination of Four Cephalosporin’s. The RAND Journal of Economics,
28(3), 426-446.
Engle, R. F. & Granger, C. (1987, marzo). Cointegration and Error-Correction: Representation, Estimation, and Testing. Econometrica, 55, pp. 251-276.
Grabowski, H. G. & Vernon, J. M. (1987, agosto). Pioneers, imitators and generics-a simulation model of Schumpeterian competition. The Quarterly Journal of Economics,
102(3), 491-526.
Green, R. & Alston, J. M. (1990, mayo). Elasticities in AIDS Models. American Journal of
Agriculture Economic, 72(2), 442-445.
Hellerstein, J. K. (1994, verano). The Importance the Physicians in the Generic versus
Trade-name Prescription Decision. The RAND Journal of Economics, 29(1), 108-136.
Jaramillo, H.; Restrepo, J. M. & L atorre, C. (2003, agosto). Mercado de medicamentos,
regulación y políticas públicas. Borradores de Investigación. Serie Documentos en
Economía, 004328. Recuperado de: http://economia.urosario.edu.co/ investigacion/bi/bi38.pdf
Koukouritakis, M. (2003). Eu Accession Effects on Imports of Manufactures: the Case
of Greece. Department of Economics, University of Cyprus. Discussion paper, 02.
Recuperado de: http://www.econ.ucy.ac.cy/papers/2-2003.pdf
Mejía, R. S. et al. (2002, julio-agosto). La política farmacéutica nacional en Colombia y la
reforma de la seguridad social: acceso y uso racional de medicamentos. Cad. Saúde
Pública, 18(4), 1025-1039.
Merino, A. (2003). Demand for Pharmaceutical Drugs: a Choice Modelling Experiment.
(Tesis Ph.D). Departamento de Economía y Empresa, Universidad Pompeu Fabra.
Recuperado de: http://www.econ.upf.edu/docs/papers/downloads/704.pdf
172
Elasticidad de la demanda por medicamentos en el mercado farmacéutico privado en Colombia
JOHANNA VÁSQUEZ VELÁSQUEZ, KAROLL GÓMEZ PORTILLA
ELKIN CASTAÑO VÉLEZ, JOSÉ VICENTE CADAVID HERRERA,
ANDRÉS RAMÍREZ HASSAN
Mortimer, O. R. (1998, noviembre). Demand for Prescription Drugs: The Effects of Managed Care Pharmacy Benefits. Abstr Book Assoc Health Serv Res Meet, 15, 113-114.
Pashardes, P. (1993, julio). Bias in estimating the almost ideal demand system with the
Stone index approximation. The Economic Journal, 103(419), 908-915.
Santerre, R. E., Stephen, P. (2000). The pharmaceutical industry. Health Economics: Theories, Insights, and Industry Studies. The Dryden Press, 508-553.
Stern, S. (1996, diciembre). Market Definition and the Returns to Innovation: Substitution Patterns in Pharmaceutical Markets. MIT Sloan School & NBER, working paper,
36-46. Recuperado de: http://www.kellogg.northwestern.edu/faculty/sstern/htm/
NEW researchpage/Publications/Stern%20RX%20Demand.pdf
Zuleta, L. A. & Junca, J. C. (2001, abril). Efectos económicos y sociales de la regulación
sobre la industria farmacéutica colombiana: el caso de los estudios de bioequivalencia y biodisponibilidad, de los secretos empresariales y las buenas prácticas de
manufactura. Fedesarrollo-Misión Social. Recuperado de: http://www.misionsalud.
org/mision/estudio2.pdf
Zuleta, L. A.; Parra, M. L. (1999, julio). Incidencia del régimen de patentes de la industria
farmacéutica sobre la economía colombiana. Informe Final. Fedesarrollo. Recuperado de: http://www.misionsalud.org/mision/estudio1.pdf