funciones
Anuncio
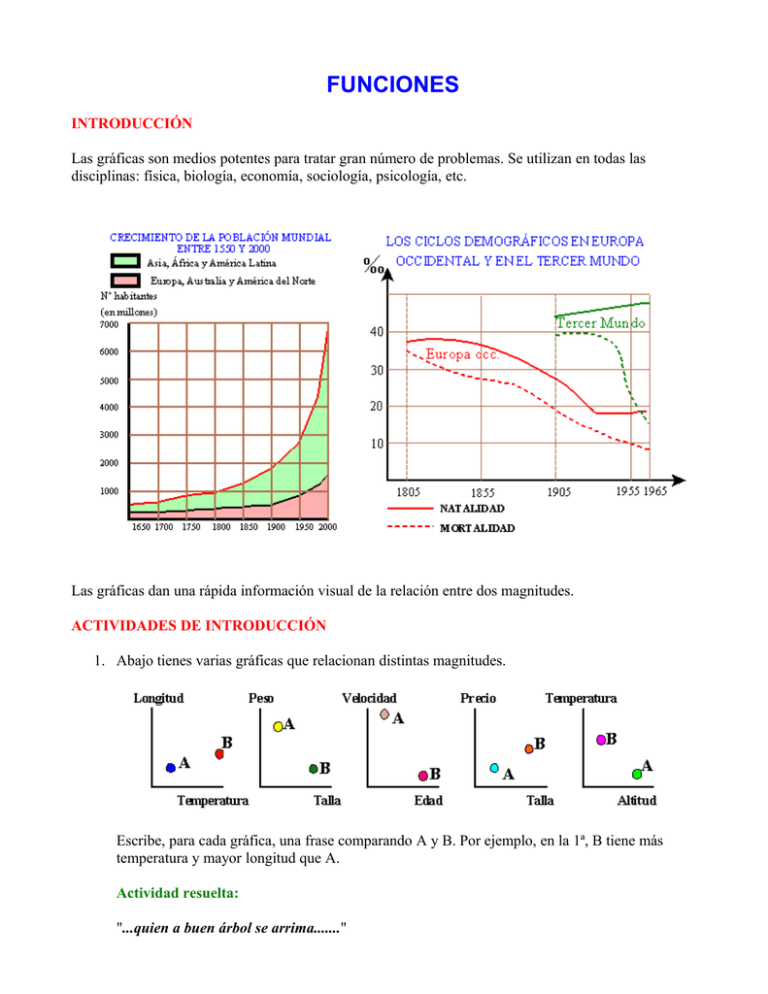
FUNCIONES INTRODUCCIÓN Las gráficas son medios potentes para tratar gran número de problemas. Se utilizan en todas las disciplinas: física, biología, economía, sociología, psicología, etc. Las gráficas dan una rápida información visual de la relación entre dos magnitudes. ACTIVIDADES DE INTRODUCCIÓN 1. Abajo tienes varias gráficas que relacionan distintas magnitudes. Escribe, para cada gráfica, una frase comparando A y B. Por ejemplo, en la 1ª, B tiene más temperatura y mayor longitud que A. Actividad resuelta: "...quien a buen árbol se arrima......." Desde las 9 de la mañana hemos ido anotando la longitud de sombra de un poste vertical. Éstos son los resultados: La hora del día y la longitud de la sombra son magnitudes que están relacionadas. Además, a cada hora del día le corresponde una única longitud de sombra. Podemos resumir escribiendo que la longitud de la sombra depende o es función de la hora del día. Si representas los pares de valores (hora del día, longitud de sombra): (9,21), (10,15'5), ........., etc. recogidos en la tabla, en unos ejes de coordenadas obtienes la gráfica: Como observas en ella, la longitud de la sombra disminuye o decrece hasta las 13 horas y comienza a aumentar o crecer a partir de dicha hora. Diremos que la función es decreciente desde t = 9 hasta t = 13, y creciente a partir de t = 13. Además, la mínima longitud de sombra (6 m.) se alcanza a las 13 horas. En ese punto, (13,6), la función presenta un mínimo. 2. ¡Cuidado con los medicamentos! En las instrucciones de un medicamento, que hay que administrar a un diabético, se establece que la dosis del mismo, expresada en mg, está en función del peso del paciente según la gráfica: Observa que a una persona de 50 Kg le corresponde una dosis de 20 mg. Diremos que 20 es la imagen de 50 o que 50 es un original de 20 y escribiremos 50 Kg → 20 mg. a. ¿Cuál es la imagen de 75?, es decir, ¿qué dosis hay que suministrar a una persona de 75Kg? b. ¿Se puede administrar a bebés?¿Y a personas obesas?. c. ¿Qué peso tenía una persona a la que suministraron 40 mg? d. ¿Para qué peso la dosis es máxima? Diremos que la variable dosis depende (o es función) de la variable peso: Peso → Dosis INTERPRETACIÓN DE FUNCIONES La relación entre dos magnitudes o variables puede expresarse mediante una gráfica, una tabla o una fórmula. Mediante gráficas A continuación proponemos unas actividades para que se realicen en grupo y sean discutidas en el aula. 3. Después de bañarse en su casa, Ana dibuja un esbozo de gráfica que muestra lo que ocurre con el volumen de agua de su baño en función del tiempo transcurrido. a. Si ambos grifos (caliente y frío) se abrieron al principio, ¿qué puede haber ocurrido en A? (Hay más de una respuesta). b. Cuando el baño se está vaciando, Ana pone el pie en el agujero del desagüe. ¿Qué parte de la gráfica muestra esto? c. ¿Cuándo aumenta el volumen del agua? ¿Cuándo disminuye? d. ¿Cuándo se alcanza el volumen máximo de agua? ¿Y el mínimo? Como observarás, es la forma de la gráfica la que nos muestra si el volumen de agua aumenta más o menos rápidamente (la mayor o menor inclinación de la gráfica). 4. Vamos de Benalmádena a unas clases en Alhaurín de la Torre. La distancia aproximada es de unos 10 Km. La clase comienza a las 8:15 y salimos de casa a las 7:30. Las siguientes gráficas muestran cómo las cosas son bastante distintas para Antonio, Bernabé, Carlos y Delicia. Antonio: Salgo con calma. En el camino comienzo a pedalear más fuerte. Bernabé: Acababa de salir cuando me di cuenta de que olvidé las zapatillas y tuve que volver. Carlos: Fui en moto, pero por el camino me quedé sin gasolina. Así que pie al suelo y andando. a. ¿A quién corresponde cada gráfica? b. ¿Qué diría Delicia? Si precisamos la gráfica de Antonio, podremos responder a varias cuestiones de manera más precisa. c. ¿Cuántos Km lleva recorrido Antonio a las 7:45?,¿qué ocurre a las 7:55?¿Cuánto tiempo empleó en la primera mitad del trayecto? d. Cuántos Km pedaleó entre las 8 menos cuarto y las ocho? e. ¿Cómo se puede saber que Antonio ha ido a la misma velocidad en los primeros 20 minutos? f. Si Antonio hubiera seguido con la misma velocidad, ¿habría llegado a tiempo al colegio?;¿ con cuánto adelanto/atraso?. g. ¿Entre qué horas fue menor la velocidad de Antonio?, ¿cómo se puede saber? h. Sandra sale al mismo tiempo que Antonio. Después de 20 minutos va exactamente 1 Km detrás de Antonio, y llega 5 minutos después que él al colegio. ¿Cómo se puede estar seguro de que Sandra no ha pedaleado siempre a la misma velocidad? Dibuja la gráfica de Sandra. i. Roberto sale de Benalmádena 5 minutos después que Antonio y llega 5 minutos antes. Dibuja la gráfica de Roberto en los mismos ejes que la de Antonio, sabiendo que ha pedaleado a velocidad constante. ¿Por qué tu gráfica y las de tus compañeros ha de ser exactamente igual? 5. Alicia va al colegio en autobús. El médico le ha prohibido ir en bici. Siempre coge el autobús de las 8 menos 25 y para en el colegio a las 8. Aquí ves la gráfica de Antonio y la de Alicia en el autobús: a. ¿Iba hoy el autobús puntual? b. El autobús ha parado varias veces por el camino. ¿Cómo lo puedes ver en la gráfica? c. ¿A qué hora y a qué distancia de Benalmádena adelantó el autobús a Antonio?.¿Cómo sería si el autobús fuese puntual? d. ¿Cómo puedes ver en las gráficas que Alicia estaba antes en la mitad del camino?.¿Cuántos minutos antes? e. ¿Cuántos Km le quedaban a Antonio cuando Alicia llegó al cole? f. ¿A qué hora aproximadamente llevaba más ventaja Alicia? g. Explica por qué ha tenido que haber un momento en el cual la ventaja de Alicia era exactamente de un kilómetro. 6. Dos monos subieron por un poste. El 1º subió lentamente al principio y después aumentó la velocidad gradualmente. ¿Cuál es la gráfica de este mono? a. Describe con palabras el ascenso del otro mono. b. ¿Qué separación había entre los monos después de 1 minuto, 2 minutos,....? c. ¿Qué tiempo emplearon en llegar a la mitad del poste? d. Completa la gráfica sabiendo que el mono B se quedó arriba y el mono A bajó a velocidad constante. 7. ¿Cuál de los tres perfiles de la derecha se corresponde con el de la carretera recorrida por un ciclista, si su gráfica es la de la izquierda? Como hemos comprobado, la observación de una gráfica permite analizar características como el crecimiento o decrecimiento y la existencia de valores máximos y mínimos. También se pueden observar fácilmente otras propiedades. Periodicidad Cuando un fenómeno se reproduce a intervalos regulares, en una serie de ciclos idénticos encadenados los unos a los otros, se le califica de periódico, teniendo en cuenta que el período equivale a la duración de un ciclo. En la gráfica de abajo tienes una curva que estima, con bastante exactitud, la temperatura media del aire en Fairbanks, Alaska (expresada en grados Fahrenheit): Observa cómo partes de la gráfica se repiten cada cierto intervalo. Este intervalo mínimo de repetición (el más pequeño posible) se llama periodo, en nuestro caso es de un año; y a este tipo de funciones les llamaremos periódicas. Hay numerosas situaciones reales que se traducen en funciones periódicas: ciclos lunares, mareas, estaciones, órbitas, ciclo menstrual, biorritmos, etc. Actividad (Biorritmos) 8. Según ciertas personas existen tres ciclos que ejercen influencia sobre las personas: el ciclo corporal (fuerza, vitalidad, resistencia a las enfermedades) de periodo 24 días; el ciclo de los sentimientos con un periodo de 28 días (creatividad, tristeza, alegría); y por último el ciclo intelectual con un periodo de 33 días. El día del nacimiento comienzan los tres ciclos en el punto cero y desde allí comienzan a subir. a. ¿Después de cuántos años llega el ciclo a un punto como el del nacimiento? b. ¿Cuántas veces en la vida alcanzamos el día total, es decir los tres ciclos en su máximo? c. Los días críticos son aquéllos en que una de las tres curvas alcanza su punto cero. Determina tus días críticos. Mediante tablas Se juegan 8 partidos durante el invierno. Ésta fue la asistencia de público a cada partido: Partido 1 Asistentes 2800 2000 2600 2300 1500 600 1400 900 Su gráfica es: 2 3 4 5 6 7 8 La cantidad de asistentes no cambia gradualmente entre partidos: no pasó de 2.800 a 2.000 entre el partido 1 y el partido 2. No hubo ningún partido entre los ocho mostrados en la gráfica. Por tanto, desde un punto de vista estricto, los puntos no deberían ser unidos. La variable nº de asistentes no toma valores entre dos consecutivos, por ello decimos que es una variable discreta. El gráfico anterior es más fácil de interpretar si los puntos se enlazan mediante líneas rectas. Ha de quedar claro que estas líneas no tienen un significado real. !No tendría sentido usar el gráfico para estimar cuánta gente va al partido número 3'5!. Ruptura de un eje En ciertas ocasiones hay que elegir con cuidado las escalas de los ejes para que la gráfica asociada a una tabla se lea adecuadamente. Lee los siguientes ejemplos: José está enfermo. La tabla nos muestra su temperatura corporal, tomada por su madre cada hora. Hora 8 9 10 11 12 13 14 15 16 17 Temperatura 37'1 37'1 37'2 37'4 37'6 38'7 38'1 38'4 38'6 38'3 Y éste es el gráfico de temperaturas: Cuando una persona está enferma, cada pequeño cambio en su temperatura puede ser importante y debería ser convenientemente reflejado por la gráfica. En el gráfico superior hay demasiado espacio malgastado y no acentúa convenientemente la variación de la temperatura. Sería mucho mejor numerar el eje de temperaturas de los 37º C hasta los 39ªC usando una línea quebrada para indicar que la escala no comienza en 0ªC. La variable Tiempo es una variable continua: tiene sentido preguntarse por la temperatura entre dos horas dadas. 9. La tabla no muestra la temperatura de José a las 9:30. ¿Podrías estimarla a partir de la gráfica? ¿Qué temperatura tenía a las 2 menos cuarto? Gráficas engañosas Esta tabla muestra los resultados en ventas de una empresa en los últimos 4 años: Año Ventas (en miles de €) Observa estas dos gráficas: 1999 2000 2000 3000 2001 7000 2002 12000 Representan exactamente la misma situación. Sin embargo, la segunda nos hace parecer que el volumen de ventas aumenta espectacularmente. Si variamos las escalas de los ejes podemos variar la perspectiva para una misma realidad. Mediante fórmulas Funciones lineales El grifo Un grifo vierte 15 litros por minuto. Es evidente que Tiempo y Volumen son en este caso dos magnitudes directamente proporcionales. Si construimos una tabla y dibujamos la gráfica obtendremos: Observa que la magnitud volumen V es igual a la magnitud tiempo t multiplicada por 15, que es la razón de proporcionalidad. Dos magnitudes X e Y directamente proporcionales de razón a dan lugar a gráficas del tipo anterior que son rectas que pasan por el origen de coordenadas, cuya ecuación es y = a · x. Al número a se le llama pendiente. 10. Representa en unos mismos ejes coordenados las siguientes funciones lineales: y = 2x; y = 3x, y = 0'4x, y = -x e y = -3x a. Estudia cómo varía la inclinación de la gráfica según la pendiente. b. ¿Qué cuadrantes del plano ocupa la gráfica si la pendiente es positiva?¿Y si es negativa? 11. Completa para cada gráfica la siguiente tabla: Halla en cada caso la fórmula que las define. 12. De una función lineal se conoce que, la imagen de 3 vale 12.¿Cuál es su fórmula?¿Cuál es la imagen del 5? 13. La siguiente gráfica indica cómo varía la altura del líquido en el vaso X a medida que se va llenando de forma continua. ************************************************************************************* ********** Los grados Fahrenheit se utilizan en Estados Unidos y otros países que no adoptaron el Sistema Internacional de Medidas. Para pasar de grados Fahrenheit a Centígrados se utiliza la fórmula: , siendo F el número de grados fahrenheit y C el resultado en grados centígrados. Actividades finales Interpretación de gráficas 1. En la siguiente gráfica tienes dibujada una vasija y, a su derecha, la gráfica correspondiente que relaciona la altura del agua con el tiempo de llenado: Completa las otras gráficas: NOTA: En muchos problemas similares es conveniente dividir la situación real en tramos homogéneos (como se ha hecho con las vasijas) y trasladar dichos tramos a los ejes coordenados. 2. Un circuito automovilístico tiene la siguiente forma: Dibuja la gráfica que relacione la velocidad con el tiempo. 3. Dada la gráfica siguiente busca su circuito correspondiente: 4. La montaña rusa Dibuja la gráfica que relacione la velocidad del coche con la distancia recorrida por la pista. 5. Se ha realizado una carrera de 400 metros lisos en la que han participado cuatro corredores. La versión del comentarista deportivo respecto de cada uno de ellos es: Corredor 1: Salió muy rápido pero poco a poco fue perdiendo fuerzas para llegar a la meta casi andando y llegó en terceras posición. Corredor 2: Mantuvo siempre la misma velocidad hasta los últimos 50 metros. A partir de ahí fue mucho más rápido. Corredor 3: Salió rápido pero a los 100 metros tropezó y cayó al suelo. Al cabo de unos segundos se levantó y continuó pero ya mucho más lento y llegó el último. Corredor 4: Salió lento pero conforme transcurría la prueba, aumentó la velocidad llegando el primero. Haz las gráficas espacio - tiempo y velocidad - tiempo de cada uno de los corredores. 6. Antonio sale de casa en dirección al polideportivo: Sale de casa, está un rato en el polideportivo y regresa. Sale de casa. A mitad de camino recuerda que no lleva zapatillas de deportes; vuelve a casa, regresa al polideportivo y vuelve a casa. Cuando vuelve a casa encuentra a una amiga a la que acompaña a su casa. Inmediatamente vuelve a la suya. Dibuja la gráfica distancia a su casa -tiempo empleado para cada una de las situaciones anteriores. 7. Un coche de un fugitivo huye a una velocidad constante de 160 Km/h por una autopista. Tras una curva observa con pavor, sin tener tiempo de parar, que el puente está derrumbado. Dibuja un esbozo de las gráficas velocidad -tiempo, espacio - tiempo y altura -tiempo. 8. Tiramos de la cadena del WC: ¿qué gráfica corresponde a esta situación? 9. ¿Qué gráfica corresponderá a la caída del paracaídas? 10. Esta pecera está siendo llenada por una manguera con caudal constante. Completa la gráfica: 11. El agua sale de este estanque con velocidad constante. Completa la gráfica: 12. Aquí hay 5 bocetos de gráficas y 5 descripciones de un estanque vaciándose. ¿Qué gráfica corresponde a cada descripción? Todas estas gráficas son decrecientes, pero con distinto aspecto. A: El nivel del agua desciende con la misma velocidad todo el tiempo. B: El nivel del agua desciende lentamente al principio y cada vez más y más rápido mientras el estanque se vacía. C: El nivel del agua desciende rápidamente al principio, y cada vez más y más lentamente mientras el estanque se vacía. D: El nivel del agua comenzó descendiendo rápidamente, y por un atasco del desagüe, el nivel dejó de bajar. Cuando se desatascó volvió a descender con rapidez. E: El nivel del agua cayó lentamente al principio. Después cada vez más rápido y después cada vez más despacio hasta que el estanque dejó de tener agua. 13. Aquí tienes 6 frascos y 9 gráficas. Elige la gráfica correcta para cada frasco. Dibuja cómo deberían de ser los frascos que corresponden a las dos gráficas restantes 14. Una mosca recorre, a velocidad constante, la trayectoria indicada desde la pared hasta la tarta. Dibuja la gráfica que relacione la altura con el tiempo empleado. 15. Una canica se deja caer desde el aire en un medio viscoso, por ejemplo aceite. ¿Cuál será gráfica de la velocidad en función del tiempo? Dibuja la gráfica espacio recorrido-tiempo. ¿Cuál sería la gráfica velocidad-tiempo si el medio viscoso fuera por ejemplo agua?¿Qué diferencias destacarías respecto de la del aceite? 16. Un monje budista se va a retirar a hacer profundas meditaciones a la cima de un monte. Para ello sale del pie del monte a las 12 del mediodía y llega a la cima a las doce de la noche. Tras estar dos días y medio de meditaciones, decide bajar del monte a las 12 del mediodía y llega al pie a las 12 de la noche (tardó el mismo tiempo en bajar porque se sintió varias veces indispuesto del vientre). Después de tanto tiempo de meditación no tuvo problemas para hacerse la siguiente pregunta: ¿existirá algún punto por el que yo pasara a la misma hora al subir y al bajar? Medita tú también y ayúdale a contestar a esta pregunta. 17. Una escalera de 10 metros está apoyada sobre una pared. Dibuja la gráfica altura del punto medio M en función de la distancia del pie de la escalera a la pared. 18. ¿Conoces el cuento de la liebre y de la tortuga? "Érase una vez una liebre a la que le gustaba fanfarronear ante todos los animales sobre su gran velocidad. Harta de su alardes la lenta tortuga la retó a una carrera y ...." Utiliza la siguiente gráfica y continua el cuento: 19. Entre la gráficas siguientes, indica la que corresponde la situación: "Un paseante sale de su domicilio, camina durante 3 horas, se para durante una hora, y retorna a su casa en autobús." En todas las gráficas, en el eje vertical se representa la distancia al punto de partida (en Km) y en el eje horizontal la duración (en horas). Dar , cuando sea posible , una interpretación de las otras gráficas. Sabiendo que el paseante camina a 3 Km/h de media, indicar sobra la gráfica elegida en la cuestión a), La graduación del eje vertical. Las coordenadas de los puntos destacables. 20. La distancia que separa a Málaga de Granada es de 120 Km. Antonio deja Málaga a las 11:00 y se dirige a Granada con una velocidad de 80 Km/h.. 30 minutos después José Mª sale de Granada a Málaga con una velocidad de 90 Km/h. Utiliza estos ejes y muestra el progreso de ambos motoristas. Usa la gráfica para indicar a qué distancia de Granada se cruzan los dos motoristas. Halla el tiempo que emplean en llegar a sus destinos. 21. Dos ciclistas salen a la misma hora al encuentro: Desde A hasta B con V = 30 Km/h y el de B hasta A a 20 Km/h. (d(A,B) =100 Km).Estima gráficamente cuándo se encontrarán. ¿A qué distancia de A? ¿Y de B?. 22. Un coche inicia un viaje a una velocidad constante de 90 Km/h. En el kilómetro 45 encuentra un camión y reduce su velocidad a 60 Km/h. Permanece detrás 15 minutos y cuando lo adelanta lo hace a 80 Km/h, velocidad que mantiene durante 1 hora hasta llegar a una cuesta abajo, en la que su velocidad aumenta a 100 Km/h. Si los Km de subida coinciden con los de bajada: ¿Cuándo encontró al camión? ¿A qué distancia y en qué momento adelanta al camión? ¿En qué kilómetro se inicia la cuesta? Calcula la duración del viaje y el tiempo empleado Periodicidad 23. La noria La noria de un parque de atracciones da una vuelta cada 10 segundos . En unos mismos ejes dibuja dos gráficas que muestren cómo cambia la altura del coche A y la del B durante un minuto 24. Carrusel La gráfica muestra la velocidad que alcanza el carrusel de una feria a lo largo de diferentes viajes que realiza. ¿Cuánto dura cada parada? ¿A qué velocidad va el carrusel? ¿Cuánto dura cada viaje? ¿En qué espacios de tiempo acelera? ¿En cuáles frena? ¿Cada cuánto tiempo se repite el movimiento del carrusel? ¿qué hará el carrusel a las dos horas de ponerlo en marcha? 25. Éstas son las órbitas de dos cometas alrededor del Sol: Esta es la gráfica que relaciona distancia al Sol con el tiempo en años. El cometa Encke tarda 3'3 años en dar una vuelta completa y el cometa Tempel2, tarda 5'3 años. Si el 1 de enero de 1996 coinciden en sus distancias mínimas al Sol, ¿cuándo volverá a repetirse? 26. Un elefante en un zoo está indispuesto y un veterinario toma su temperatura cada hora. Éstas son: ¿Cuándo tiene la temperatura más baja? ¿Y más alta? Dibuja una gráfica que muestre cómo cambia su temperatura. Elige un punto de comienzo conveniente para el eje de temperaturas. 27. La capacidad de un depósito es de 300 litros. Dispone de dos grifos de vaciado, de caudales respectivos 10 l/min y 15 l/min. Escribir todas las informaciones que sugiere esta gráfica. 28. Los seis recipientes tienen la misma altura 80 cm y la misma capacidad de 100 litros. Los llenamos sucesivamente utilizando un grifo que vierte 1/3 de litro por segundo. Las gráficas representan, para cada uno de los recipientes, la altura de la columna de agua en el recipiente en función del tiempo empleado en su llenado, Encontrar la curva correspondiente a cada recipiente. 29. Dado el perfil de esta carretera, dibuja una gráfica que relaciones velocidad - tiempo para un ciclista normal. 30. Un ciclista efectúa un circuito. La gráfica de su posición respecto del punto de partida en función del tiempo es: El ciclista corre a 25 Km/h en plano, a menor velocidad en subida y más rápido en descenso. ¿Cuál es la longitud del recorrido.? ¿A que distancia se inicia la subida y en qué minuto? ¿Cuándo y a qué distancia se inicia el descenso? 31. El self - service Abre a las 14h y cierra a las 15h. La cadena sirve a 10 personas por minuto. ¿Cuántas personas llegan entre las 14h 10' y las 14h 20'? ¿Qué ocurre a las 14h 5'? ¿A qué hora estará servida una persona que llegue a las 14h 20'? ¿A qué hora llegó una persona servida a las 14h 45'? ¿Cuántas personas han sido servidas entre las 14h y las 14h 50'? ¿Cuántas personas han llegado entre las 14h 45' y las 14h 50'? ¿Qué se puede decir del número de personas llegadas entre las 14h 50' y las 15h? 32. A partir de estas dos gráficas obtener el gasto medio por turista y año. 33. Unos montañeros han hecho el recorrido entre los puntos A, B, C, D y E del plano y quieren saber la distancia real que han andado. También se pide el perfil del terreno del recorrido de los montañeros. 34. Un tornero de tenis dura 10 días. Aquí tienes el número de asistentes cada día: Dibuja una gráfica que ilustre los resultados 35. Un paracaidista se lanza de un avión desde una altura de 3000 metros. Controlamos su altura cada 20 segundos: Dibuja la gráfica que relacione la altitud con el tiempo. Obtener aproximadamente su altitud a los 50 seg. ¿Al cabo de cuántos segundos la altitud será de 1.800 metros? ¿A partir de qué altitud y a partir de cuántos segundos la velocidad del paracaídas es constante? 36. Sabemos que el alcohol es el responsable del 33% de los accidentes de carretera. La curva siguiente representa el coeficiente c de riesgo de accidente en función de la tasa t de alcoholemia (en g/l de sangre) Por cuánto está multiplicado el riesgo de accidente para un conductor si tiene 1 g por litro de alcohol en sangre? Cuál es el valor de la tasa t para el coeficiente c = 40? Comenta el aspecto de la gráfica. El riesgo de accidente, ¿es proporcional a t? 37. El pie es una medida de longitud que mide 0'3048 metros. Obtener la medida en metros de una longitud en función de su medida en pies. Funciones lineales 38. Con una cuerda anudada de 30 cm. formamos rectángulos Completa la tabla: ¿Qué relación hay entre base y altura? Dibuja la gráfica. 39. Elabora una tabla y dibuja la gráfica: y = 1/x y = 2x y = x2 + 1 40. Los precios se disparan en el Supermercado Mastodonte. El supermercado Mastodonte aumenta los precios de los artículos de la sección "Zapatos" un 6%. Designamos por x el precio de un artículo antes del aumento y por y el precio del mismo artículo después de la subida. Completar la tabla: En unos ejes, dibujar los puntos cuyas coordenadas x e y están indicadas en la tabla anterior. Obtener y en función de x. 41. ! Brontosaurio baja precios! Después de este aumento, su rival Supermercado Brontosaurio decide una bajada del 20 % sobre el precio de los zapatos. Llamamos x al precio antes de la bajada e y al de después. Obtener la función que los relaciona. 42. La dilatación de una barra metálica es proporcional al aumento de temperatura que ella soporta. Su longitud es 76'4 cm a 20º C y 76'55 cm a 100º C.¿cuál es su longitud a -15º C? 43. Si toda la producción se vende, completa la gráfica de abajo. 44. Aquí tienes una jeringuilla sin marcas: Calcula el volumen a partir de la altura h. Haz una tabla que relacione el volumen con la altura y dibuja su gráfica. Pon las marcas en la jeringa de 5 cm3 y de 1.000 cm3. Definición de funciones afines Actividad de introducción Un estanque tiene un grifo que vierte 5 litros por minuto. Consideremos los siguientes casos: a. Si el volumen inicial del estanque fuera 0 litros: Tiempo (min.) 0 1 4 6 t Volumen (lit.) 0 5 20 30 5·t La fórmula que expresa la relación entre el Volumen y el tiempo es: V = 5·t b. Si el volumen inicial fuera de 20 litros. Tiempo min. 0 1 4 6 Volumen lit. 20 25 40 50 t 5·t+20 La fórmula que expresa la relación entre el volumen y el tiempo será V = 5·t + 20. Si el volumen inicial fuera de 5 litros obtendríamos una recta paralela a las anteriores que pasaría por (0,5) y cuya ecuación sería V = 5·t + 5. ¿Qué fórmula correspondería a esta situación gráfica? Las gráficas de las funciones lineales eran rectas que pasaban por el origen de coordenadas, su ecuación era y = a·x. Como acabamos de ver las gráficas de ecuación y = a·x+b son rectas paralelas a la de y = a·x que atraviesan al eje de ordenadas a altura b. Estas funciones se denominan funciones afines. En consecuencia sólo se precisan un par de valores para obtener su gráfica. Una función afín es la que tiene por ecuación y = a · x + b. Al coeficiente a se le llama pendiente y al b ordenada en el origen. Su gráfica es una línea recta. Determinación de una función afín a partir de una tabla. De una función afín, cuya fórmula desconocemos, sólo sabemos las imágenes de los valores 1, 5, 7 y 10: Si consideramos aisladamente la tabla de los incrementos de x y de y: )x )y 4 6 6 3 3 4'5 observamos que se corresponde con una relación de proporcionalidad directa de razón . Demostraremos que la fórmula que expresa la función tiene por pendiente 1'5, es decir, y = 1'5·x + b. Como f(1) = 3'5, será 3'5 = 1'5·1 + b, de donde b = 2 y la fórmula buscada sería y = 1'5 x + 2 Veamos que, en efecto, el coeficiente a es la pendiente: Consideramos dos valores cualesquiera x0 y x1, y sus respectivas imágenes mediante la función y = a x + b Se tiene que La pendiente es el cociente entre el incremento de y y de x para dos valores cualesquiera. Si la pendiente es positiva, la recta sube y si es negativa baja. Actividades 1. Determina la fórmula de la función afín que corresponde a cada caso: a. x 2 5 y -1 8 b. c. Servicios de grúa 2. Algunas veces se estropea el coche donde menos lo esperas. Si dispones de algún seguro de asistencia las cosas resultan más fáciles. No es nuestro caso, por lo que recurrimos a este servicio de grúas que se anuncia en un periódico: Elabora una tabla, dibuja la gráfica y obtén la ecuación que relaciona el precio según el nº de km para cada caso: a. Turismo fuera de Málaga capital en día laboral. b. Turismo fuera de Málaga capital de noche o en día festivo. c. Efectúa de nuevo los apartados a y b, pero para una furgoneta. Electricidad 3. A partir de una experiencia realizado con un aparato eléctrico se obtiene una tabla de valores donde V designa la tensión e I la intensidad de la corriente eléctrica: I 1 2 3 5 11 15 16 V 193 186 179 165 123 95 88 4. Comprueba si V es función afín de I, y en tal caso expresar la fórmula que los relaciona. 5. La caída 6. En una experiencia de mecánica se obtiene la tabla de valores siguiente, donde t indica el tiempo (en segundos) de la caída de un objeto y d la distancia (en metros) recorrida durante un tiempo t: t 0'1 0'2 0'5 0'7 1 1'2 1'3 d 0'05 0'2 1'25 2'45 5 7'2 8'45 7. ¿La función t v d es afín? 8. 9. Dada la siguiente gráfica: a. ¿Son (50,101) y (33,65) puntos de la gráfica? b. ¿Cuáles son las coordenadas de A y B?, es decir, ¿qué punto de la gráfica tiene de abscisa 3, y qué punto tiene de ordenada 3? c. ¿Qué punto de la gráfica tiene abscisa 25?, ¿qué punto tiene de ordenada 33? d. ¿Cuáles son las coordenadas de C y D? e. El punto (4,9) está en la gráfica puesto que 9 = 2· 4 + 1. Indica cuáles de los siguientes puntos están por debajo o por encima de la gráfica: (2,0), (2,27) y (2,1391). f. Indica qué puntos están a la izquierda o a la derecha de la gráfica: (0,5) (-33,5) (12,5). g. Indica la situación abajo-arriba, izquierda-derecha de los puntos: (323,259) y (-82,141). h. Dado el punto (4,2), señala el punto de la gráfica que está en su misma vertical. ¿Cuál está en la misma horizontal?. i. ¿Qué punto está en la vertical del 0?; ¿y en la horizontal?. Tiene relación con el lugar en el que la gráfica corta a los ejes? ¿Por qué? 10. A partir de los datos de la figura, obtener la fórmula que define esta gráfica: 11. Averiguar las coordenadas de A, B, C y D observando la figura. ¿Qué se puede decir de las funciones del tipo y = 0'5x + b, con b un número cualquiera? 12. Halla la función representada por la recta roja: 13. Ordena de mayor a menor los coeficientes a y b de la gráfica de la figura: Intersección de gráficas Curvas de oferta y demanda Un mercado de un producto está formado por vendedores y compradores. Cuando el precio de un producto es alto y deja ganancias es lógico que se tienda a producir más cantidad de producto (hay más oferta); si el precio es menor y se gana menos, la producción del artículo también será menor (hay menos oferta). De otro lado, a más precio menos cantidades comprará el consumidor (hay menos demanda), y a menor precio más cantidades se venderán (hay mayor demanda). Los economistas saben que la relación entre precio y oferta, y entre precio y demanda sigue en muchas ocasiones una formulación matemática. Supongamos que, tras un análisis de mercado, se llega a la conclusión de que las curvas de oferta y demanda de unos disquetes viene dada de la siguiente forma: OFERTA: , donde y es el precio en € y x el número de cajas de disquetes ofertadas. DEMANDA: , donde y es el precio en € y x el número de cajas que se demandan. El punto de equilibrio, que se corresponde con el corte de ambas gráficas, es el término en el que coinciden compradores y vendedores. Veamos cómo hallarlo: P es un punto de la línea de oferta, en consecuencia sus coordenadas verifican su ecuación: ; análogamente, por ser P de la gráfica de demanda también se cumple que . Es decir, las coordenadas de P son la solución del sistema determinado por las ecuaciones de ambas gráficas: . Procediendo por el método de igualación se obtiene P = (200,9) El mercado estará estable a un precio de 9 €. 14. Halla el punto donde se cortan las gráficas: a. b. Actividades de construcción y determinación de funciones afines 15. Un motorista parte de Málaga a Granada (120 Km) en el instante t = 0 con una velocidad constante. Sea d(t) la distancia (en Km) que separa al motorista de Granada en el instante t. (t está medido en horas). Se sabe que la función d: t d(t) es una función afín con d(0) = 120 y que d(2) = 60. a. Representar gráficamente d(t) en función de t. b. Determinar los números a y b tales que d(t) = at + b. c. Calcular gráfica y analíticamente el tiempo empleado por el motorista en llegar a Granada. 16. Rally automovilístico Tres coches A, B y C participan en un rally: El coche A empieza en el instante t = 0 h con una velocidad media de 120 Km/h. El coche B parte en el instante t = 1 h con velocidad media de 100 Km/h. El coche C parte en el instante t = 2 h con velocidad media de 120 Km/h. Designamos por dA, dB y dC las distancias recorridas por los coches A, B y C desde el comienzo de la etapa. a. Representar gráficamente sobre un mismo dibujo las funciones t dC(t) (2 cm por 1 hora y 1 cm para 40 Km). b. Obtener dA, dB y dC en función del tiempo t. c. Determinar gráficamente y por procedimientos de cálculo: d. El instante en que C coge a A. e. El instante en que C coge a B. f. El instante en que B coge a A. h. El instante en que C se sitúa a la misma distancia de A y B. 17. Peso ideal dA(t); t dB(t) y t Si x es la altura de una persona en cm, el peso teórico, en Kg, está dado por la fórmula a. Calcular el peso teórico de un alumno que mide 1'50 m. b. Calcular el peso teórico de un jugador de baloncesto de 2'10. c. Cuál será la talla de una persona cuyo peso teórico es de 65 Kg d. Obtener una tabla y representar gráficamente: 1 cm por cada 10 cm de talla y 1 cm por cada 10 Kg de peso. e. ¿Qué tipo de función es? f. Si fuera afín p(x) = ax + b. ¿Cuánto valen a y b? Tienes dos opciones: Usa la gráfica y determina a y b, o simplifica el segundo miembro de la fórmula inicial. g. El peso ideal es inferior un 15% al peso teórico: Calcula el peso ideal de una persona de peso teórico 70 Kg. h. Calcula el peso ideal de una persona de talla 1'60. Actividades finales Problemas sobre la función afín 1. Representar gráficamente las funciones: a. d. b. f(x) = 2x + 3 e. c. f. 2. Indicar pendiente y ordenada en el origen de las funciones afines siguientes: a. f(x) = 2 - 3x b. g(x) = 2(3x-4) c. h(x) = 3/5(x - 1) 3. ¿Pertenece el punto A(3,4) a la gráfica de la función f(x) = x + 1? ¿Y B(-5,-4)?; ¿Y C(-1,1)?. 4. Sean los puntos A(-1,-1), B(2,2) y C(-1,2). Determinar la función afín cuya representación gráfica pasa por A y B. ¿Pertenece C a esta representación? 5. f es una función afín definida por f(x) = ax + b . Calcular a, b y obtener la expresión de f(x) si: a. f(2) = 3 y f(1) = 2 b. f(3) = 4 y f(-1) = 2 c. f(1) = 11/6 y f(2) = 10/3 6. Indicar, en cada uno de los casos siguientes, si son funciones afines o no. Si la respuesta es afirmativa, precisar los valores de a y b tales que f(x) = ax + b. a. c. e. b. d. f. 7. Para estos ejercicios, decir si representan funciones afines. Si la respuesta es afirmativa obtener la fórmula que las define de entre las indicadas: 8. Halla la fórmula que define a estas funciones afines: 9. Obtener una función afín tal que: sea paralela a g(x) = 3x y pase por el punto A(2/3,1). 10. He aquí dos tablas incompletas de valores de dos funciones afines. Complétalas: 11. Explica por qué no existen funciones afines que respondan a estas tablas: 12. Representar en un mismo dibujo las funciones f y g definidas por f(x) = 2x - 1 y g(x) = -x + 5. Resolver mediante las gráficas y mediante cálculo, la ecuación f(x) = g(x). 13. Repetir el mismo ejercicio con las dos funciones f(x) = -2x + 1 y g(x) = 2x + 5. 14. La gráfica siguiente representa una función afín. De estas 4 fórmulas, ¿cuál es la que la define? f(x) = 5x; f(x) = -3x + 4; f(x) = 3/4x + 3; f(x) = - 3/4x + 3. Dibujar también en los ejes anteriores la gráfica de f(x) = 2x-3. Determinar gráficamente el punto M de intersección de las dos rectas anteriores. Calcular las coordenadas exactas de M. 15. Sea f(x) = 2x - 1 y g(x) = -x + 3 a. Dibuja ambas funciones en unos mismos ejes. b. Observa la gráfica y obtén el número m que tiene la misma imagen por f y por g. c. Encuentra el valor exacto de m (por cálculo). 16. Juan el taxista En su taxi Juan cobra las siguientes tarifas: 50 cts. por bajada de bandera y 40 cts. por Km. recorrido. Obtener el precio p del viaje en función del número x de kilómetros recorridos. 17. Los precios se disparan El supermercado MASTODONTE aumenta los precios de los artículos de la sección "ZAPATOS" un 6%.Designamos por x el precio de un artículo antes del aumento y por y el precio del mismo artículo después de la subida. Completar la tabla: En unos ejes, dibujar los puntos cuyas coordenadas x e y están indicadas en la tabla anterior. Obtener y en función de x. 18. ! BRONTOSAURIO baja precios! Después de este aumento, su rival Supermercado Brontosaurio decide una bajada del 20 % sobre el precio de los zapatos. Llamamos x al precio antes de la bajada e y al de después. Obtener la función que los relaciona. 19. El concierto Para invitar a un concierto a sus amigos, Juan tiene dos posibilidades: A: Hacerse socio del club organizador del concierto por un valor de 18 euros y pagar las entradas a 7 euros cada una. B: Pagar cada entrada a 10 euros. Sea n el número de invitados de Juan: Obtener en función de n el precio a pagar en los dos casos. Finalmente, Juan se presenta al concierto con 7 amigos. ¿Qué solución habría debido adoptar? 20. El director de un espectáculo de variedades sabe que si fija el precio de la entrada en 9 euros, podrá contar con 1000 espectadores. Por otro lado, cada descuento de 0,6 euros sobre el precio de la entrada repercutiría en 100 espectadores más. Sea x el número de descuentos de 0,6 euros. a. Obtener en función de x el precio P de una entrada, el número E de espectadores esperados y la recaudación esperada. b. ¿Cuál debe ser el precio de una entrada para que la recaudación sea máxima? 21. Un artesano debe entregar sus productos en un radio de 350 Km alrededor de su casa. Recibe las ofertas de dos transportistas en las siguientes condiciones: Transportista A: 60 cts de euro por Km. Transportista B: 45 euros de entrada y 50 cts. por Km. Dibujar en unos mismos ejes las gráficas de coste para x Km en los dos casos. ¿Qué transportista es más barato para 20 Km? ¿Y para 460 Km? ¿En qué caso cobran lo mismo? 22. Préstamos de libros La biblioteca municipal propone tres fórmulas de préstamo a sus lectores: A: 40 cts. por libro prestado. B: Abono anual de 2 euros. y de 30 cts. por libro. C: Abono de 5 euros y 15 cts. por libro prestado. a. Determinar según la opción de préstamo el precio por x libros prestados. Escribe A(x), B(x) y C(x). b. Representa las funciones A, B y C. c. Determinar gráficamente la fórmula más ventajosa según el número de libros prestados 23. El pie es una medida de longitud que mide 0'3048 metros. Obtener la medida en metros de una longitud en función de su medida en pies. 24. ¡ Qué calor! Una temperatura puede ser medida en grados CELSIUS o centígrados (como en España); en grados FAHRENHEIT (en países anglosajones) o en grados KELVIN (unidad utilizada por los científicos). Los cambios de unidades se hacen por mediación de funciones afines. Por ejemplo K = C + 273 donde K y C indican, respectivamente, una misma temperatura en grados Celsius o en grados Kelvin. Así, "20o C" representa la misma temperatura que "293o K". La siguiente tabla indica la temperatura de fusión de ciertos cuerpos. Obtener F en función de C y después en función de K. completar la tabla. 25. La longitud L de una barra de hierro varía con la temperatura t: A cada temperatura t corresponde una longitud determinada. Esta barra de hierro tiene una longitud de 20 metros cuando la temperatura es de 0ºC. Los físicos saben que esa longitud L (en metros) a temperatura t (en ºC) está dada por : L = at + 20 con a = 20·1'2·10-5. a. ¿Por qué la longitud L es función afín de la temperatura t? b. Calcular la longitud de esta barra de hierro cuando la temperatura sea de -50ºC, 100ºC y 500ºC. c. Calcular la longitud de la barra cuando la temperatura sea de 2000ºC. Has de saber que el hierro funde a los 1500ºC por lo que la longitud hallada anteriormente no es real. d. Representar gráficamente esta función afín cuando t varía entre -500ºC y 1500ºC. 26. Consumo de gasolina D. Ramón vive en Málaga y D. Salvador en S. Roque (Cádiz). La distancia que separa ambas ciudades es de 120 Km. Se van a encontrar en un punto M de la carretera que une las ciudades. El coche de D. Ramón consume 6 litros por Km y el D. Salvador 9 litros por Km. El problema consiste en calcular la distancia x en kilómetros entre Málaga y el punto M, para que los coches consuman la misma cantidad de gasolina. a. Explica por qué la cantidad de gasolina consumida por el coche de D. Ramón para ir de Málaga al punto M es una función afín b. Ídem con D. Salvador. c. Representar ambas funciones en unos mismos ejes (1 cm por cada 20 Km y 1cm por cada 2 litros). d. Obtener gráficamente el valor de x para el que los dos coches consumen la misma cantidad de gasolina. ¿Cuanto es esa cantidad? e. Obtener los resultados mediante cálculo. 27. Un ciclomotor, una moto y un coche efectúan el mismo trayecto desde A hasta B, distantes 100 Km. Llamamos c(t), m(t) y a(t) a las distancias (en Km) recorridas por el ciclomotor, la moto y el coche en el tiempo t (en horas). a. Obtener c(t), m(t) y a(t) en función de t. b. Dibujar en unos mismos ejes las funciones anteriores. c. ¿A qué hora la moto doblará al ciclo? (Comprobar con cálculo) d. En qué intervalo de tiempo el coche estará entre el ciclo y la moto. 28. De áreas Obtener el área sombreada A en función de x. 29. Llenado de una piscina Una piscina de fondo plano tiene forma de un rectángulo. Sus dimensiones son: 1'60 de alto por 5 m de largo por 10 metros de ancho. Durante el invierno, el agua es conservada con productos especiales a una altura de 1'10 metros. En el mes de junio, la llenamos con la ayuda de una manguera cuyo caudal es de 1200 litros por hora. Llamamos f(x) a la altura total del agua al cabo de x horas de llenado. a. Obtener f(x) en función x y comprobar que es afín b. ¿En cuánto tiempo llenarás la piscina? c. Dibujar la función f. Explicar cómo se puede encontrar gráficamente un valor aproximado al resultado anterior. 30. Una sala de fiestas tiene la forma indicada en este plano: Una pared móvil representada por el segmento MN, permite reducir la superficie de la sala . Las rectas MN y AB son paralelas. 1) Decoración mural. A fin de decorar las paredes de la sala , el organizador desea conocer el perímetro del polígono MNCEFGHD. La unidad de longitud es un metro. Notamos por x la longitud AM (con perímetro. ) y por f(x) este a. Calcula f(0) y f(50) b. Obtener f(x) en función de x y comprobar que es una función afín. c. Leer aproximadamente un valor del perímetro f(x) cuando M esté en la mitad del segmento AD. 2) Calefacción de la sala. El organizador desea conocer el volumen de la sala, para calentarla mejor. El techo está a una altura de 3 metros. Notamos g(x) al volumen de la sal en m3. d. Obtener g(x) en función de x y comprobar que es una función afín. e. Dibujar en unos ejes la función g (1cm por cada 5 metros en abscisas y 1 cm por 500 m3 en ordenadas) f. El organizador decide alquilar material de calefacción suplementario cuando el volumen de la sala sea superior a 3000 m3. Utilizando la gráfica anterior, encontrar aproximadamente los valores de x para los que el material de calefacción suplementario será necesario. 31. ABCD es un trapecio rectángulo (A= 90° y D = 90°). Además AB = 4, CD = 6 y AD = 5. M es un punto del segmento AD. Llamamos x = AM en cm. a. ¿Cuáles son los valores posibles de x? b. ¿Por qué el área ABM es una función afín de x? c. Ídem con MCD. d. Ídem con BMC. e. En unos mismos ejes representar las tres funciones. f. Obtener gráficamente para cada caso el valor de x tal que: 1. Los triángulos ABM y MCD tienen el mismo área. 2. Los triángulos BMC y MCD tienen el mismo área. 3. ¿Es posible que ABM y BMC tengan el mismo área? g. Obtener los resultados por cálculo. 32. El radio del círculo exterior es de 1 cm. a. Obtener el área A(x) de la parte coloreada en función de x. b. Representa gráficamente A(x) c. Determina gráficamente para qué valor de x, el área A(x) es igual a la cuarta parte del área del circulo exterior. 33. El espacio muerto de un coche o camión es la distancia entre la base del coche o camión y el suelo. Hay una fórmula para el espacio muerto. Esta es: e = 40 - (w : 10) donde e es el espacio muerto, en cm y. w es el peso del vehículo, en Kg. a. Completa la tabla: b. Dibuja en unos ejes los valores de w y e de la tabla. Dibuja una recta que una estos puntos. c. Usa la gráfica para buscar e cuando w = 180. d. ¿Cuánto vale e si w = 360? e. ¿Cuál es le valor de w cuando e = 0? ¿Qué le ocurre al coche entonces? f. Cuando el espacio muerto es de 12cm, ¿qué peso soporta el coche? 34. Para esta furgoneta, la fórmula del espacio muerto es: Dibuja la gráfica y responde con ella a las preguntas: a. Busca e cuando w = 200. b. Ídem con w = 360 c. ¿Cuál es el espacio cuando la carga soportada es de 600 Kg? d. Si la furgoneta lleva un peso de 500 Kg, ¿podrá descargar sobre una acera de 15 cm de altura? e. ¿Qué sucede si la furgoneta se carga con 1000 Kg? 35. El dibujo de la derecha muestra un gato para levantar coches. La altura h del gato (en cm) depende del número n de vueltas con el mango. La fórmula es Dibuja la gráfica y responde con ella a las preguntas: a. Busca h cuando n = 20. b. Ídem para n = 30, n = 25, n = 15, n = 0 y n = 1. 36. A nivel del suelo, el agua hierve a 100ºC. La temperatura a la que el agua hierve se llama "punto de ebullición". Si tú subes a una montaña, el punto de ebullición cambia. La fórmula para el punto de ebullición es ebullición (en ºC) y h es la altura (en pies). , donde p es el punto de a. Obtén una tabla y dibuja la gráfica (una recta) b. Cuál es el punto de ebullición cuando h = 2000 c. ¿Y si fueran 10.000 pies? d. El monte Everest tiene cerca de 30.000 pies de altura. ¿A qué temperatura hervirá allí el agua? 37. Si tú profundizas en el interior de la tierra la temperatura aumenta. La temperatura en las profundidades está dada por la fórmula: profundidad en metros desde la superficie , donde t es la temperatura en ºC y p es la a. Obtén una tabla y dibuja la gráfica. b. ¿Cuánto es t si p = 600? c. ¿Cuál es la temperatura a 1000 m de profundidad? d. ¿Cuál es la temperatura a 2000 m de la superficie? e. La profundidad de una mina es de 3500 m. ¿Qué temperatura tendrá? 38. El valor de uno de los ángulos de un polígono regular depende del número de caras que tenga el polígono. La fórmula para el ángulo es a es el ángulo en grados y n el número de lados. a. Usa la fórmula para buscar a cuando n = 6. b. ¿Cuánto vale a si n = 10? c. Obtén una tabla, dibuja la gráfica y responde con ella a las preguntas anteriores. d. ¿Cuál es la amplitud de cada ángulo en un polígono regular de 20 lados? 39. La dilatación de una barra metálica es proporcional al aumento de temperatura que ella soporta. Su longitud es 76'4 cm a 20ºC y 76'55 cm a 100ºC.¿cuál es su longitud a -15ºC? 40. Cuando un químico añade hidróxido de sodio (o sosa cáustica) al agua, ésta se calienta. La fórmula para obtener la temperatura del agua es t = 24 + 8m. t es la temperatura en grados ºC; m es la cantidad de sosa añadida, en Kg. a. Completa esta tabla: m 0 1 2 3 4 5 6 7 t 24 b. Dibuja unos ejes, m en el eje vertical desde 0 hasta 10, y t en el horizontal desde 0 hasta 100. Dibuja los puntos de tu tabla, y únelos. c. Usa la gráfica para hallar el valor de t cuando m = 2'5. d. ¿Cuánto hidróxido de sodio es necesario para llevar la temperatura del agua a 76ºC? e. ¿Cuál será la temperatura resultante de añadir 1'5 Kg de sosa cáustica? f. Usa una regla para prolongar la recta. ¿Cuánto vale t si m = 8'5? g. ¿Cuál es el valor utilizando la gráfica? ¿Y la fórmula? h. ¿ Por qué no es necesario extender el gráfico cuando t = 100ºC? 41. Buscar entre las figuras siguientes aquellas cuya área sea una función afín de a o una función lineal de a. 42. Un paseante vuelve a su casa a 1 Km de distancia a una velocidad de 6 Km/h. Su perro corre delante de él a 18 Km/h. llega a la casa y vuelve hacia sus amo, y comienza de nuevo su va y viene, hasta que el amo llega a la casa.. Representar gráficamente la distancia entre paseante y su casa en función del tiempo, y la distancia entre el perro y la casa. ¿cuál es la distancia recorrida por el perro? 43. En pruebas de una dieta experimental para gallinas, se determinó que el peso medio P (en gramos) de una gallina fue, según las estadísticas, una función lineal del número de días d después de que se inició la dieta, donde . Supongamos que el peso medio de una gallina al inicio de la dieta fue de 40 gramos y 25 días después fue de 675 gramos. a. Determinar P como una función lineal de d. b. Determinar el peso medio de una gallina cuando d = 10. 44. Dos ciudades A y B distan 90 Km. A las 10h, Vicente sale de A en su bicicleta para B a una velocidad media de 24 Km/h. Luis efectúa el mismo trayecto, pero sale a las 11'30h en moto a una velocidad media de 45 Km/h. Finalmente Marta deja B a las 10h 20' y, al volante de su coche, se dirige hacia A a una velocidad de 90 Km/h. a. Representa gráficamente las funciones que, para cada uno de ellos, relaciona distancia de B a A con el número de horas. b. ¿Se cruzan Marta y Luis? c. ¿A qué distancia y a qué hora alcanzará Luis a Vicente? d. ¿A qué distancia y a qué hora alcanzará Marta a Vicente.? 45. Un paciente con cáncer recibirá terapias mediante fármacos y radiación. Cada centímetro cúbico de medicamento que se usará contiene 200 unidades curativas, y cada minuto de exposición a la radiación proporciona 300 unidades curativas. El paciente requiere 2400 unidades curativas. Si se administran d centímetros cúbicos de la droga y r minutos de radiación, determinar una ecuación que relacione d y r. 46. Para regular su temperatura en relación con el calor ambiental, las ovejas aumentan su ritmo respiratorio r (por minuto) cuando la longitud de la lana l (en cm) disminuye. Una oveja con una longitud de lana de 2 cm, tiene un ritmo respiratorio de 160, y otra, con una longitud de lana de 4 cm, tiene un ritmo de 125. Si la relación de r y l es lineal. a. Determina una ecuación que relacione r con l. b. Determina el ritmo respiratorio de una oveja con una longitud de lana de 1 cm. 47. Unos biólogos americanos han encontrado que el número de chirridos por minuto hecho por los grillos de cierta especie está relacionados con la temperatura. La relación es casi lineal. A 68ºF, los chirridos de los grillos son casi 124 por minuto, mientras que a 80ºF son alrededor de 172 por minuto. a. Determina una ecuación que de la temperatura Fahrenheit t en función del número c de chirridos por minuto. b. Si se cuenta los chirridos en sólo 15 segundos, ¿cómo puede estimarse rápidamente la temperatura? 48. Cuando la temperatura T (en grados Celsius) de un gato es reducida, la frecuencia cardiaca del gato r (en latidos por minuto) disminuye. Bajo condiciones de laboratorio, un gato a una temperatura de 37ºC tuvo una frecuencia cardiaca de 220, y a una temperatura de 32ºC una frecuencia cardiaca de 150. Si r está relacionada linealmente con T, en donde T está entre 26 y 238, a. Determina una ecuación para r en función de T b. Determina la frecuencia cardiaca a una temperatura de 28ºC. REVISTA Aquiles y la tortuga El griego Zenón de Elea pensaba que el formidable guerrero Aquiles no podría jamás atrapar a una tortuga que estuviera a una cierta distancia de él. Zenón lo justificaba así: Supongamos que la tortuga se encuentra a 900 metros de Aquiles y recorre 20 metros por minuto mientras que Aquiles recorre 300 metros por minuto. € Cuando Aquiles avance 900 metros la tortuga habrá avanzado 60 metros. € Cuando él avance 60 metros, ella habrá recorrido 4 metros. € Cuando él avance 4 metros, ella habrá recorrido 27 cm. € Cuando él avance 27 cm., ella habrá recorrido 1'8 cm. € Y así sucesivamente. Puesto que cuando Aquiles avanza, la tortuga también, Zenón concluía que ¡Aquiles jamás atraparía a la tortuga. ! Con la ayuda de funciones afines vamos a terminar con este misterio. La relación existente entre la distancia d (en metros) recorrida por Aquiles y el tiempo t (en minutos) pasado desde su partida será: d = 300t. La relación entre la distancia que separa a la tortuga del punto de partida de Aquiles y el tiempo transcurrido será: d = 900 + 20t. Si representamos estas dos funciones en los mismos ejes: Queremos saber a qué distancia y al cabo de cuánto tiempo Aquiles atrapará a la tortuga. Cuando la atrape, la distancia a la que estarán la tortuga y Aquiles del punto de partida, será la misma. Por tanto, se verificará: 300t = 900 + 20t que nos da un valor para t de 3'21 min. En consecuencia, Aquiles y la tortuga se encontrarán a 964,28 m del punto de partida de Aquiles. Un hijo más viejo que su padre El físico Albert Einstein probó en 1920 que le tiempo no pasaba siempre de forma idéntica. Unos astronautas que viajaran en una nave espacial con una velocidad próxima a la de la luz, digamos 250.000 Km. envejecerían menos rápido con respecto a sus amigos que quedaron en la Tierra. Si A es su edad al partir, si t es el tiempo que pasa en la Tierra y si Av es la edad de los viajeros, se tiene la relación Av = 0'3t + A. Uno de ellos parte en el año 2000, con una edad de 20 años. ¿Qué edad tendrá en el 2010 en 2020? ¿En qué fecha tendrá 25 años? Ha dejado un hijo recién nacido. ¿Qué edad tendrá el hijo cuando el padre alcance los 30 años?