Movimiento rectilíneo uniforme (MRU)

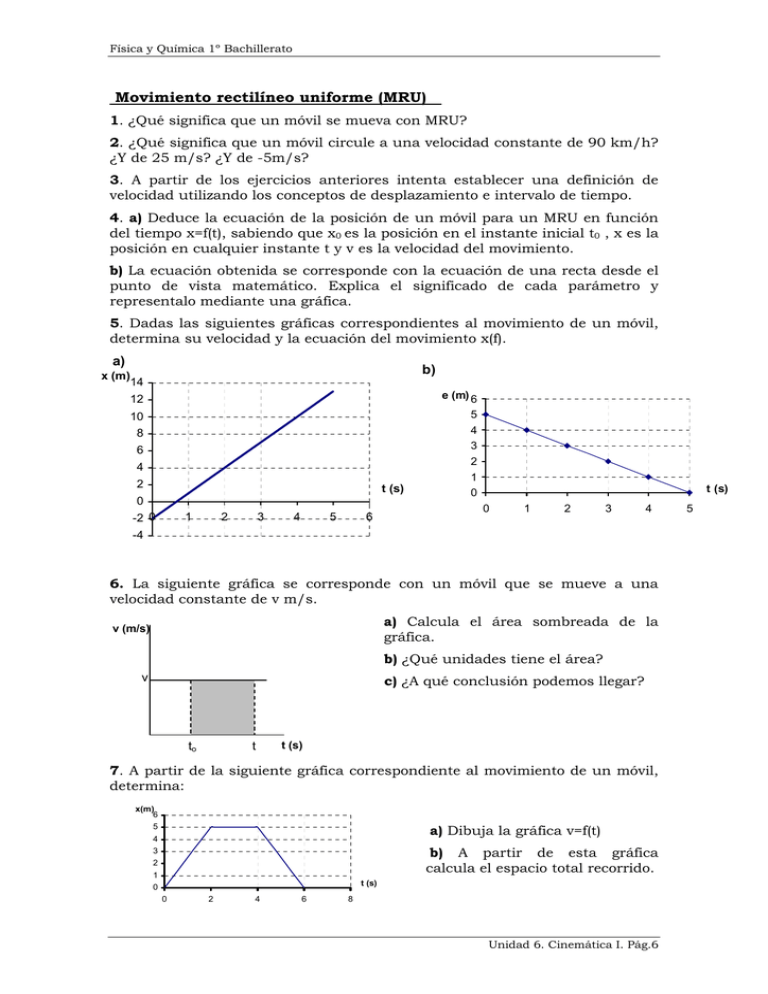
Física y Química 1º Bachillerato
Movimiento rectilíneo uniforme (MRU)
1. ¿Qué significa que un móvil se mueva con MRU?
2. ¿Qué significa que un móvil circule a una velocidad constante de 90 km/h?
¿Y de 25 m/s? ¿Y de -5m/s?
3. A partir de los ejercicios anteriores intenta establecer una definición de
velocidad utilizando los conceptos de desplazamiento e intervalo de tiempo.
4. a) Deduce la ecuación de la posición de un móvil para un MRU en función
del tiempo x=f(t), sabiendo que x0 es la posición en el instante inicial t0 , x es la
posición en cualquier instante t y v es la velocidad del movimiento.
b) La ecuación obtenida se corresponde con la ecuación de una recta desde el
punto de vista matemático. Explica el significado de cada parámetro y
representalo mediante una gráfica.
5. Dadas las siguientes gráficas correspondientes al movimiento de un móvil,
determina su velocidad y la ecuación del movimiento x(f).
a)
b)
x (m)
14
12
e (m) 6
10
5
4
3
2
1
0
8
6
4
2
t (s)
0
-2 0
1
2
3
4
5
6
t (s)
0
1
2
3
4
-4
6. La siguiente gráfica se corresponde con un móvil que se mueve a una
velocidad constante de v m/s.
a) Calcula el área sombreada de la
gráfica.
v (m/s)
b) ¿Qué unidades tiene el área?
v
c) ¿A qué conclusión podemos llegar?
to
t
t (s)
7. A partir de la siguiente gráfica correspondiente al movimiento de un móvil,
determina:
x(m)
6
5
a) Dibuja la gráfica v=f(t)
4
3
2
b) A partir de esta gráfica
calcula el espacio total recorrido.
1
t (s)
0
0
2
4
6
8
Unidad 6. Cinemática I. Pág.6
5
Física y Química 1º Bachillerato
Curso 2007-08
8. Un coche se mueve a una velocidad de 20 m/s. Sabiendo que su posición
inicial respecto al sistema de referencia es de 20 m. ¿Cuál es su posición en el
instante 1 minuto?. ¿Cuánto tiempo tarda en alcanzar la posición 1250 m?
Sol: 1220 m ; 61,5 s
9. De un cuerpo que posee un MRU conocemos los siguientes datos: en los
instantes 5 s y 13 s, se encuentra en las posiciones 112 m y 280 m,
respectivamente. ¿Cuál es su velocidad?. ¿Cuál es su posición en el instante
inicial?. ¿Y en el instante 1 minuto? Sol: 21 m/s; 7 m ; 1267 m
10. Dos trenes salen de la misma estación con una diferencia de 30 minutos y
con velocidades de 120 km/h y 45 m/s. Suponiendo que realizan un MRU,
indica la posición y el instante en que uno dará alcanzará al otro.
Sol: 230,54 km ; 6923,1 s
11. Dos automóviles se encuentran separados una distancia de 5 km. Los dos
se mueven en sentidos contrario con velocidades de 80 km/h y 20 m/s.
Calcular el instante y la posición en la que se encontrarán.
Sol: 2628,5 m ; 118,4 s
12. Un móvil A se encuentra una posición adelantada de 200 m respecto a
otro B y comienzan a moverse en el mismo sentido con velocidades de 100
km/h y 35 m/s. Indicar la posición y el instante en el que el móvil B
encuentra
al
A,
suponiendo
que
el
movimiento
es
rectilíneo.
Sol: 973 m ; 27,8 s
13. Dos móviles salen de la misma posición pero el segundo sale media hora
después que el primero. Sabiendo que las velocidades son 80 km/h y 40 m/s.
a) Calcular el instante y la posición en la que el segundo dará alcance al
primero. b) Calcular el tiempo y la distancia recorrida por cada móvil.
Sol: a) 89799 m ; 4045 s ; b) A : 4045 s y 89799 m B: 2245 s y 89799 m
14. Dos automóviles que marchan en el mismo sentido, se encuentran a una
distancia de 126 Km. Si el más lento va a 42 Km/h, calcular la velocidad del
más rápido, sabiendo que le alcanza en seis horas. Sol.: v = 63 km/h
15. Un deportista sale de su casa en bici a las seis de la mañana. Al llegar a
un cierto lugar, se le estropea la bici y ha de volver andando. Calcular a qué
distancia ocurrió el percance sabiendo que las velocidades de desplazamiento
han sido de 30 Km/h en bici y 6 Km/h andando y que llegó a su casa a la una
del mediodía. Sol.: 30 km
16. Un deportista recorre una distancia de 1.000 km, parte en moto y parte en
bici. Sabiendo que las velocidades han sido de 120 Km/h en la moto y 20
Km/h en bici, y que el tiempo empleado ha sido de 15 horas calcular los
recorridos hechos en moto y en bici.
17. Un ladrón roba una bicicleta y huye con ella a 20 km/h. Un ciclista que lo
ve, sale detrás del mismo tres minutos más tarde a 22 Km/h. ¿Al cabo de
cuánto tiempo lo alcanzará? Sol.: 30 minutos.
18. Calcular la longitud de un tren cuya velocidad es de 72 Km/h y que ha
pasado por un puente de 720 m de largo, si desde que penetró la máquina
hasta que salió el último vagón han pasado ¾ de minuto. Sol.: 180 metros.
Unidad 6. Cinemática I. Pág.7
Física y Química 1º Bachillerato
Movimiento rectilíneo uniformemente acelerado (MRUA)
1. ¿Qué significa que un móvil se mueva con MRUA?
2. ¿Qué significa que un móvil circule con una aceleración constante de
5 m/s2? ¿Y de -2 m/s2?
3. A partir de los ejercicios anteriores intenta establecer una definición de
aceleración utilizando los conceptos de incremento de velocidad e intervalo de
tiempo.
4. a) Deduce la ecuación de la velocidad de un móvil para un MRUA en
función del tiempo v=f(t), sabiendo que v0 es la velocidad en el
instante inicial t0, v es la velocidad en cualquier instante t y a es la aceleración
del movimiento.
b) La ecuación obtenida se corresponde con la ecuación de una recta desde el
punto de vista matemático. Explica el significado de cada parámetro y
representalo mediante una gráfica.
5. Dadas las siguientes gráficas correspondiente al movimiento de un móvil,
determina su aceleración y la ecuación v=f(t).
6
v (m/s)
6
v (m/s)
5
4
4
2
3
2
0
0
1
0
-1
t
0
1
2
3
4
5
1
2
3
4
6 t (s
5
-2
6
-4
-2
6
-3
6. La siguiente gráfica se corresponde con un móvil que se mueve a una
aceleración constante de a m/s2.
a) Calcula el área sombreada de la
gráfica.
a (m/s2)
b) ¿Qué unidades tiene el área?
a
c) ¿A qué conclusión podemos llegar?
to
t
t (s)
7. La siguiente gráfica nos muestra la v=f(t) de un MRUA:
a) Calcula el área
sombreadas.
v(m/s)
v
de
cada
una
de
las
zona
b) Calcula las unidades de cada área.
c) Calcula el área total.
v0
t0
d) ¿A qué conclusión podemos llegar?
t
e) Si suponemos que el desplamiento se ha producido
en el eje X (∆x), ¿podrías deducir la ecuación de la
posición
en función del tiempo x=f(t)?
t(s)
8. A partir de la siguiente gráfica correspondiente a v=f(t) de un móvil, calcula:
Unidad 6. Cinemática I. Pág.8
Física y Química 1º Bachillerato
a) La gráfica a=f(t)
b) El espacio total recorrido.
c) La velocidad del móvil en el
instante t=5s.
9. ¿Con qué ecuación matemática se corresponde la función x=f(t) para un
MRUA? Realiza un dibujo.
10. Deduce la siguiente ecuación: v 2 − v 02 = 2 a ∆x , que nos relaciona la
velocidad final, e inicial, la aceleración y el desplazamiento; a partir de las
ecuaciones x=f(t) y v= f(t).
11. Un coche circula a una velocidad de 50 km/h. En 10 s, su velocidad pasa
a ser 80 km/h. ¿Cuál ha sido su aceleración? Sol: 0,83 m/s2
12. Un coche tiene una aceleración de 3 m/s2. Si inicialmente tiene una
velocidad de 15 m/s. ¿Cuánto tiempo tarda en alcanzar 120 km/h? Sol: 6,1 s
13. Un coche circula por una ciudad a una velocidad de 50 km/h, y el
conductor ve como un peatón cruza la calle y en ese momento pisa el freno,
tardando en frenar 7 segundos. ¿Cuál ha sido su aceleración? ¿Qué distancia
ha recorrido? Sol: -1,98 m/s2 ; 48,8 m
14. Un automóvil puede alcanzar la velocidad de 100 km/h, partiendo del
reposo en 10'5 segundos.
Suponiendo el movimiento uniformemente
acelerado, calcular la aceleración, la velocidad y la posición en ese instante.
Sol: 2,6 m/s2 ; 27,3 m/s ; 434,2 m
15. En otra prueba del mismo automóvil, partiendo del reposo, recorre 1 km
en 31,8 segundos. Suponiendo que el movimiento es uniformemente
acelerado, calcular la aceleración y la velocidad final. Sol: 1,98 m/s ; 63 m/s
16. Un móvil posee una aceleración constante de -3 m/s2. Calcular su
velocidad en el instante 5 segundos, si en el instante 1 segundo vale 20 m/s.
Sol: 8 m/s
17. Un móvil cuya rapidez inicial es de 20 m/s se detiene tras recorrer 50 m.
Calcular la aceleración y el tiempo en que tardará en pararse. Sol:-4 m/s2 ; 5s
18. Un automóvil y un camión se encuentran separados por una distancia de
50 m. El camión se está moviendo con velocidad constante de 54 km/h. El
automóvil, que se encuentra parado, arranca con una aceleración de 1,6 m/s2
que se mantiene constante. Calcular el instante y la posición en el que el
automóvil alcanza al camión. Hacerlo analíticamente y gráficamente. ¿Qué
velocidad lleva el automóvil en el momento del encuentro? Sol: 21,6 s ; 373,3
m y 17,3 m/s
19. Desde dos puntos A y B que distan entre sí 200 m salen simultáneamente
dos móviles. El que sale de A tiene una velocidad inicial de 5 m/s y se dirige
hacia B con una aceleración constante de 1 m/s2. El que sale de B va hacía A
con movimiento uniforme, siendo su rapidez de 12 m/s. Indicar la posición y
el instante en el que se cruzaran. Sol: 89,6 m y 9,2 s
Unidad 6. Cinemática I. Pág.9
Física y Química 1º Bachillerato
Movimiento de caída libre y lanzamiento vertical
Galileo Galilei fue el primero en demostrar experimentalmente que, si se
desprecia la resistencia del aire, todos lo cuerpos, independientemente de cuál
sea su masa, caen a la tierra con la misma aceleración, la de la gravedad,
cuyo módulo es g=9,8 m/s2, su dirección perpendicular a la superficie de la
Tierra y sentido hacia su centro.
Este movimiento de caída libre es un movimiento uniformente acelerado
análogo al anterior. La única diferencia es el valor de la aceleración.
1. a) Cuando dejamos caer un objeto desde una cierta altura, ¿cuál es su
velocidad inicial?
b) Cuando lanzamos un cuerpo verticalmente, ¿cuál es su velocidad final al
alcanzar la altura máxima?
c) Anteriormente hemos dicho que el módulo de la aceleración de la gravedad
vale 9,8 m/s2, ¿qué valor debemos asignar a la gravedad teniendo en cuenta
su dirección y sentido? Este valor tiene que explicar que cuando lancemos un
objeto verticalmente hacia arriba este se pare al cabo de un cierto tiempo,
cuando alcance la altura máxima.
d) Indica cuál de las siguientes afirmaciones es verdadera explicando el
porqué:
1) Cuando dejamos caer un cuerpo desde una cierta altura llega al suelo con
velocidad cero.
2) Cuando dejamos caer un cuerpo desde una cierta altura llega al suelo con
velocidad negativa.
2. ¿Cuánto tiempo tardará en caer al suelo un cuerpo que se deja caer sin
velocidad inicial desde una altura de 10 m? Sol: 1,43 s
3. Se lanza verticalmente hacia arriba un cuerpo con una velocidad inicial de
90 km/h. Despreciando la resistencia del aire, calcular que altura alcanzará y
cuanto tiempo tardará en llegar al punto de partida. Sol: 2,55 s ; 31,9 m
4. ¿Con qué velocidad inicial se ha de lanzar verticalmente hacia abajo una
piedra desde la boca de un pozo de 50 m de profundidad para que llegue al
fondo en 2 segundos? ¿Con qué velocidad llegará al suelo?
Sol: -15,2 m/s ; -34,8 m/s
5. Si dejamos caer una piedra desde 50 m de altura, ¿cuál sería su posición,
la distancia recorrida y velocidad a los 3 segundos de haberla soltado?
¿Cuánto tardará en llegar al suelo? ¿Con qué velocidad llega?.
Sol: a) 15,8 m; 44,1 m; -28,4 m/s; b) 3,2 s ; -31,4 m/s
6. Se lanza verticalmente hacia arriba un cuerpo con una velocidad de 30
m/s. Determina:
a) Posición que ocupa y velocidad al cabo de un segundo. Sol: 25,1 m ; 20,2 m/s
b) Altura máxima que alcanza y tiempo empleado. Sol: 3,06 s; 45,9 m
c) Velocidad cuando llega al suelo y tiempo total empleado. Sol: -30 m/s ; 6,12 s
7. Una pelota es arrojada verticalmente hacia arriba desde la azotea de un
edificio de 10 metros de altura con una velocidad de 4,8 m/s. Calcular:
Unidad 6. Cinemática I. Pág.10
Física y Química 1º Bachillerato
a) Altura máxima que alcanza la pelota sobre el suelo de la calle. Sol: 11,17 m
b) El tiempo que tarda la pelota en llegar al suelo de la calle. Sol: 2 s
c) La velocidad con la que llega al suelo. Sol: -19,6 m/s
8. Se deja caer libremente un cuerpo desde una cierta altura tardando
10 segundos en llegar al suelo. Calcular:
a) La altura desde la que se dejó caer y la velocidad con la que llega al suelo.
Sol: 490 m ; -98 m/s
b) Su posición y velocidad transcurridos 4 segundos. Sol: 411,6 m ; -39,2 s
9. Desde un globo, a una altura de 175 m sobre el suelo y ascendiendo con
una velocidad de 8 m/s, se suelta un objeto. Calcular:
a) La máxima altura alcanzada por éste. Sol: 178,3 m
b) La posición y la velocidad del objeto al cabo de 5 s. Sol: 92,5 m ; -41 m/s
c) el tiempo que tardará en llegar al suelo. Sol: 7,72 s
10. Un hombre está frente a una ventana de 2 m de altura ve pasar un objeto
que cae desde arriba, siendo 0,3 s el tiempo que tarda el objeto en recorrer la
altura de la ventana. Calcula:
a) ¿Desde qué altura se dejó caer el objeto medidad desde la parte inferior de
la ventana? Sol: 3,38 m
b) ¿Qué velocidad tendrá el objeto al pasar por la parte inferior de la ventana?
Sol: 8,13 m/s
11.¿Qué velocidad inicial hay que comunicar a una piedra para que,
lanzándola verticalmente hacia arriba, alcance una altura máxima de 20 m?
¿Cuánto tiempo tardará en alcanzar dicha altura? Sol: 19,8 m/s ; 2,02 s
12. A una altura h del suelo se lanzan simultáneamente dos bolas con la
misma velocidad, una verticalmente hacia arriba y la otra verticalmente hacia
abajo. La primera bola llega al suelo 5 s más tarde que la segunda. ¿Con qué
velocidad fueron lanzadas las bolas? Sol: 24,5 m/s
13. Una persona situada a 60 m sobre el suelo ve subir, pasando delante de
él, un cuerpo lanzado desde abajo. Ocho segundos después lo ve bajar. ¿Con
qué velocidad fue lanzado el cuerpo? Sol: 52 m/s
14. Dos proyectiles se lanzan verticalmente hacia arriba con 2 segundos de
intervalo, el primero con velocidad inicial de 50 m/s y el segundo con
velocidad inicial de 80 m/s. Calcula:
a) ¿Cuál será el tiempo transcurrido hasta que las dos se encuentren a la
misma altura? Sol: 2,6 s para el primer móvil y 1,6 s para el segundo.
b) ¿A qué altura sucederá? Sol: 115,2 m
c) ¿Qué velocidad tendrá cada uno en ese momento? Sol: 14 m/s el primero y
64 m/s el segundo.
Unidad 6. Cinemática I. Pág.11