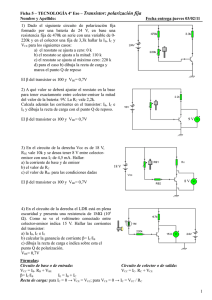
EL TRANSISTOR BIPOLAR

Autor principal
Dr. Alberto Lastres Capote
Autoras:
MSc. Adelaida Torres Colón
Dra. Agnes Nagy
E-mail: [email protected]
E-mail: [email protected]
[email protected]
E-mail: [email protected]
INDICE
2
2.1
MONOGRAFIA
EL TRANSISTOR BIPOLAR
EL TRANSISTOR BIPOLAR
Pagina
1
2
3
2.1.1
Principio de operación del transistor bipolar
Modos de operación del BJT
2.2
Modelo de gran señal de ebers-moll del BJT
4
2.2.1
2.2.2
Obtención de los parámetros del modelo básico.
Mejoras del modelo básico.
5
6
2.3
Modos de conexión del BJT
7
2.3.1
2.3.2
Configuración base-común
Configuración emisor-común
7
9
2.4
Parametros del transistor bipolar
11
2.4.1
Variación de los parámetros del BJT con la temperatura y el punto
de operación
12
2.5
Polarizacion de los transistores bipolares
13
2.5.1
2.5.2
2.5.2.1
2.5.2.2
2.5.2.3
2.5.2.4
Factor de inestabilidad del punto de operación
Polarizacion de los BJT en los circuitos integrados
Fuente de corriente polarizada a diodos o espejo de corriente
Fuente de corriente polarizada por resistencia
Fuente de corriente logarítmica o de Widlar.
Fuente de corriente estabilizada por diodos.
14
15
16
17
18
18
2.6
El BJT como interruptor
18
2.6.1
Tiempos de conmutación de los BJT
20
2.7
El BTJ como amplifificador de pequeña señal.
22
2.7.1
2.7.2
Índices de los amplificadores lineales
Línea de carga dinámica.
22
23
2.8
Modelo de pequeña señal del BJT
25
2.8.1
2.8.1.1
2.8.2
2.8.2.1
Modelo π- híbrido
Modelo π- híbrido simplificado
Modelo híbrido del BJT
Modelo híbrido simplificado
25
26
27
28
2.9
Análisis lineal de etapas simples con bjt a frecuencias
medias.
28
2.9.1
2.9.1.1
2.9.1.2
2.9.1.3
2.9.1.4
2.9.2
2.9.3
2.9.4
2.9.5
Análisis lineal del emisor-común sin resistor de emisor.
Cálculo de las ganancias de corriente:
Resistencia de entrada.
Ganancia de voltaje.
Resistencia de salida (Ro).
Análisis lineal de la configuración colector común
Análisis lineal de la configuración emisor común con RE
El amplificador en configuración base común
Comparación entre las diferentes configuraciones de amplificadores
29
29
30
30
30
31
32
33
33
2.10
2.11
Regulador de voltaje serie con diodo Zener de referencia
Ejercicios
Bibliografia
34
MONOGRAFIA
EL TRANSISTOR BIPOLAR
2. EL TRANSISTOR BIPOLAR
El término transistor que proviene de las palabras inglesas “transfer resistor” y se aplicó por primera
vez en 1948 a un dispositivo semiconductor controlado por corriente por Shockley de la Bell
Telephone. El transistor revolucionó la industria electrónica y superó en muchos aspectos a las
válvulas electrónicas. Entre sus principales ventajas están el menor tamaño, peso, costo y consumo
de potencia así como su mayor fiabilidad.
El transistor bipolar, tambien llamado transistor bipolar de unión (BJT) consta de tres terminales
(emisor, base y colector), según se muestra en la figura 2.1 y está formado por dos uniones p-n que
comparten una zona s/c común (base), pudiendo ser PNP ó NPN. En su símbolo la flecha en el
emisor indica la dirección de la corriente cuando se polariza en directa la unión base-emisor. Se
fabrican por diferentes tecnologías: planar-epitaxial, difusión, aleación y otras.
a)
b)
Figura 2.1 Símbolo del transistor bipolar a) Transistor PNP b) transistor NPN
Desde el punto de vista estructural, el ancho de la base WB debe ser muy pequeño para disminuir la
recombinación de los portadores minoritarios que transiten por ella. En general, el área del emisor
es mucho menor que la del colector, pues este último disipa mayor potencia. El emisor está más
dopado que la base y que el colector, para mejorar su eficiencia de inyección de las cargas móviles.
En la figura 2.2 se muestra la sección transversal de un transistor NPN.
Figura 2.2 Estructura del transistor bipolar NPN
Para un transistor NPN, cuando la unión B-E se polariza en directa, el emisor inyecta electrones a
la base en donde se convierten en portadores minoritarios y se mueven por difusión hacia el
colector. Al polarizar en inversa la unión B-C, los electrones como portadores minoritarios en base
son barridos por el campo hacia el colector, formando la principal componente de corriente de
colector. El colector no tiene que aportar electrones, por lo que su dopaje no tiene que ser alto,
aunque a menor sea mayor será su resistencia parásita en serie como se verá posteriormente. En el
1
A.Lastres, A. Torres, A. Nagy
colector se adiciona una zona n+ para mejorar el contacto óhmico. La región base para los
transistores bipolares planares, está dopada a un nivel intermedio entre el emisor y el colector pero
siempre debe cumplirse que la concentración de impurezas del emisor es mucho mayor que el de la
base (Nemisor >> Nbase). Por la explicado anteriormente se desprende que en la operación del
transistor bipolar aparecen los mecanismos de inyección, difusión, colección y recombinación.
2.1 Principio de operación del transistor bipolar.
A continuación se presenta el circuito de la figura 2.3 que será utilizado para analizar el principio de
operación del transistor PNP y destacar sus principales componentes de corriente. La unión B-E
está polarizada en directa (VEB>0) y la unión B-C en inversa (VCB<0). Recordar que en el análisis
de la unión p-n se planteó que el campo eléctrico aparece fundamentalmente en la ZCE y que se
considera cero en el cuerpo del s/c. Como el potencial es constante en el emisor, la base y el
colector, no circulará corriente de deriva a través del dispositivo. De aquí que las componentes de
corriente de un transistor bipolar son todas de difusión.
Figura 2.3 Amplificador BC en activa
En la figura 2.4 se señalan las diversas componentes de corrientes de un transistor PNP polarizados
en correspondencia con la figura 2.3. Al polarizar la unión E-B en directa se reduce la barrera de
potencial, por lo que aparece una inyección de huecos del emisor a la base en donde se convierten
en portadores minoritarios. También ocurre una inyección en el sentido inverso de electrones de la
base al emisor, pero que es despreciable si se cumple que Pemisor >> Nbase, lo que incrementa la
eficiencia de inyección del emisor. Como la base se hace muy estrecha, menor de 1 m (Lp <<
WB), los huecos inyectados en esta se difunden hacia la unión B-C. Un pequeño numero de estos
se recombinan con los electrones de la base y desaparecen. Para mantener neutra la región de base,
la fuente de polarización le entrega electrones para reponer los que se perdieron por recombinación,
lo que corresponde con la corriente de base.
Figura 2.4 Flujo de portadores en un transistor PNP
2
Los huecos que alcanzan la unión B-C, son halados hacia el colector debido a la polarización
inversa de ésta que incrementa su barrera de potencial y el campo eléctrico. Esta fracción de la
corriente de emisor que atraviesa la base y llega al colector se denota por FIE que será mayor
mientras menor sea WB, pues se reduce la recombinación en base.
Sin embargo, existe otra pequeña contribución a la corriente de colector dada por los portadores
minoritarios generados térmicamente dentro de la ZCE de la unión B-C polarizada inversamente.
Producto del campo aplicado, los huecos generados en el lado N de la ZCE atraviesan la unión
hacia el colector. De la misma forma los electrones generados en su lado P se mueven hacia la base.
Estas dos componentes de corriente constituyen la corriente de saturación inversa de la unión B-C
denotada por ICO que es del orden de los nA para el silicio y de A para germanio. De aquí se
concluye que la corriente de colector tiene dos componentes: una debida a la inyección de huecos a
través de la unión E-B polarizada en directa y otra debida a los portadores minoritarios generados
térmicamente dentro de la ZCE.
Estos transistores (PNP o NPN) se denominan bipolares pues su operación
movimiento de portadores mayoritarios y minoritarios al mismo tiempo.
se basa en el
Mientras menor sea el ancho de la base menor será la recombinación de los portadores minoritarios
que se difunden por esta, lo que incrementa el valor de F (típicamente entre 0.9 y 0.998). Si IE se
mantiene constante por ser VEB constante y el ancho de la base se disminuye producto del aumento
de VCB, el coeficiente F debe crecer. Este fenómeno de estrechamiento del ancho efectivo de la
base con la polarización VCB se le conoce como efecto Early.
La corriente de colector y la del emisor se expresan por:
IC = FIE + ICO
IE = IB + IC
de donde:
F
= (IC – ICO) / IE
donde F es la ganancia de corriente de gran señal en la configuración base común, que no es
constante pues varía con IE, VCB y la temperatura. Su valor se define durante el proceso de
fabricación, controlando las concentraciones de emisor, de base y el ancho de la base.
Se debe destacar que el BJT está formado por dos uniones, separadas por una región de base muy
estrecha que por ser común a ambas uniones provoca una interacción eléctrica entre ambas, lo que
se conoce como acción transistor. A pesar de esto, dos diodos conectados en serie para formar un
transistor no provocan la acción transistor pues no se cumple que WB sea muy estrecha.
Con relación a la propiedad del transistor de amplificación de voltaje, si se considera que todos los
portadores que inyecta el emisor alcanzan por difusión al colector o sea que (IE = IC), si la unión
E-B está polarizada en directa presentando una resistencia equivalente baja y la unión B-C está en
inversa presentando una resistencia alta, al dividir la caída de potencial a la salida entre la de la
entrada da un valor de AV mucho mayor que uno.
2.1.1 Modos de operación del BJT
En el transistor, cada una de sus dos uniones puede polarizarse en sentido directo o inverso en
forma independiente. De aquí que existan cuatro modos posibles de operación:
Modo
unión E-B
unión B-C
Activa en sentido directo
directa
inversa
Corte
inversa
inversa
Saturación
directa
directa
Activa en sentido inverso
inversa
directa
3
En activa en sentido directo que es la utilizada en los circuitos analógicos, el transistor opera como
se explicó anteriormente y se comporta como una fuente controlada de corriente en que para
voltajes de unión E-B de algunas décimas de V se cumple que IC = FIE + ICO .
Si ambas uniones se polarizan en inversa el transistor se corta, siendo IE e IC del orden de la
corriente de saturación inversa ICO. Si ambas uniones se polarizan en directa (saturación), circulará
una corriente apreciable inyectada por el colector a la base y solo aparece un pequeño voltaje a
través de las uniones. Es por este motivo que la operación del transistor entre corte y saturación
corresponde con una acción de interruptor.
El modo de activa en sentido inverso, cambia el papel del emisor y del colector, lo que provoca una
reducción brusca en el valor de la ganancia de corriente que limita su empleo en los amplificadores
( R << F). No obstante, este modo de operación se estudia en las compuertas digitales TTL como
se verá más adelante.
2.2 Modelo de gran señal de ebers-moll del BJT.
En el análisis de los circuitos con transistores bipolares es conveniente sustituir los elementos
activos por modelos equivalentes cuyo comportamiento simule el del dispositivo en cuestión. Estos
modelos se representan por un esquema equivalente formado por elementos circuitales básicos,
cuyas ecuaciones resultantes describen con buen grado de aproximación el comportamiento del
circuito real. Si el circuito equivalente resulta del comportamiento terminal del dispositivo en
cuestión, se le conoce como modelo terminal; si toma en cuenta los procesos físicos internos se
obtiene un modelo físico.
El modelo no lineal básico del BJT fue descrito por Ebers y Moll en el año 1954. Es un modelo
terminal de corriente directa en el cual no se toman en cuenta la carga almacenada en el
dispositivo. Es válido para todas las regiones de operación del transistor.
El circuito equivalente del modelo de E-M se basa en la interpretación del comportamiento externo
del transistor bipolar como dos uniones p-n que interactúan . Los dos diodos conectados en serie en
forma invertida, no representan completamente al transistor, pues la región base que es común a
ambas uniones por ser muy estrecha realiza un acoplamiento entre ellas que provoca una interacción
eléctrica significativa referida como acción transistor. Este acoplamiento es modelado por dos
fuentes de corriente dependientes.
Existen dos versiones del modelo de gran señal de E-M: la versión de inyección y la de transporte.
Matemáticamente, ambas versiones son equivalentes aunque la última es la más usada. La versión
de inyección escoge como referencia las corrientes por los diodos mientras que la de transporte, las
que circulan por las fuentes de corrientes.
El circuito equivalente de la versión de inyección para un transistor PNP se muestra en la figura 2.5.
Figura 2.5 Modelo de Ebers-Moll versión de inyección
4
El comportamiento de cada unión depende de la polaridad de la misma y de la corriente que le llega
de la otra. Se considera que todo el voltaje aparece aplicado a través de las dos ZCE. Las corrientes
de referencia son IEF e ICR que son las que circulan a través de los diodos y se expresan como:
IEF = IES[ eVBE/VT – 1]
ICR = ICS[ eVCB/VT – 1]
Los diodos en este modelo representan las uniones E-B y B-C del BJT. IEF es la corriente que fluye
a través de la unión para una diferencia de potencial dada si la región de colector es reemplazada
por un contacto óhmico sin afectar la base. IES es la corriente de saturación inversa de esta unión. La
corriente ICR describe la unión C-B al reemplazar al emisor por un contacto óhmico. ICS representa
la corriente de saturación inversa de esta unión.
Aplicando la Ley de Kirchoff de las corrientes en los nodos correspondientes, se pueden obtener las
expresiones de las tres corrientes IE, IC e IB. Las ecuaciones de E-M para un transistor NPN son
similares a estas, invirtiendo las direcciones de todas las componentes de corrientes y de voltajes de
unión. Los cuatros parámetros que describen este modelo son: IES, ICS, F y R. Estas magnitudes
no son independientes y entre ellas se cumple la relación de reciprocidad dada por:
F IES
=
RICS
= IS
donde F y R representan las ganancias de corriente de gran señal en base-común en activa para el
modo de operación normal e inverso respectivamente. IS es la corriente de saturación inversa común
a ambas uniones. Con esta relación el número de parámetros se reduce a tres: IS, F y R. Sus
valores típicos para un transistor integrado pequeño son:
0.98 <
F
< 0.998
0.4 <
R.
< 0.8
IES e ICS del orden de 10-15ª
El circuito equivalente para la versión de transporte se muestra en la figura 2.6. Las corrientes de
referencia son ICC e IEC que representan aquellas corrientes que son recolectadas o transportadas a
través de la base. Las corrientes por los diodos se expresan en función de estas dos.
Figura 2.6 Modelo de Ebers-Moll versión de transporte.
Al comparar esta versión con la de inyección, se tiene que:
ICC =
VBE/VT
F IES[e
– 1] = IS[eVBE/VT – 1]
Similarmente:
IEC = IS[eVCB/VT – 1]
Es a partir de esta versión de transporte que con determinadas transformaciones se obtiene el
modelo de pequeña señal -híbrido como se verá posteriormente.
2.2.1 Obtención de los parámetros del modelo básico.
Como ya se dijo, los tres parámetros necesarios para la utilización del modelo básico son IS, F y
R. Como la configuración emisor-común es la mas empleada, se acostumbra a trabajar con las
5
ganancias de corriente F (entre 50 y 250) y R (entre 1 y 5) que tienen el mismo significado que
tenía la para el base común. La relación entre ellas es:
F
=
F/(1- F)
La determinación de la corriente IS se basa en la expresión de la corriente de colector en activa,
dada por:
IC = IS[eVBE/VT – 1] IS eVBE/VT
Si VBE>>VT
De la medición de IC en función de VBE con VCB=0, al graficarse los resultados en escala semilogarítmica se obtiene una línea recta, como se muestra en la figura 2.7. El intercepto de la
prolongación de esta curva permite determinar la IS.
Figura 2.7. Determinación de Is.
Si a la vez se hacen mediciones de IB vs VBE y se representan en el mismo gráfico, se podrá obtener
el parámetro F de la relación IC/IB. Mediciones similares realizadas para el modo inverso de
operación permiten la medición de R.
2.2.2 Mejoras del modelo básico.
Entre las limitaciones que tiene el modelo básico de E-M presentado, se encuentran que considera a
los parámetros fundamentales como constantes, que no contempla los efectos resistivos ni
capacitivos parásitos. Es por esto que a este modelo estático, se le han introducido mejoras para ser
utilizado en el programa de simulación eléctrica SPICE.
Efectos resistivos. Se adicionan al modelo básico, según se muestra en la figura 2.8, en serie con
cada terminal, los resistencias óhmicas que se encuentran distribuidas en las regiones activas del
transistor.
Figura 2.8 Inclusión de los efectos
resisitivos al modelo básico
Efectos capacitivos. Los efectos de almacenamiento de cargas en el BJT son modelados a
través de dos capacitores de unión no lineales CjE y CjC (capacidades de transición) y dos
capacitores de difusión no lineales CDE y CDC como se muestra en la figura 2.9
6
Figura 2.9 Inclusión de los efectos resistivos
y capacitivos- al modelo básico
Las capacidades de transición que predominan en las uniones polarizadas en inversa, vienen dadas
por:
CjE(VBE) = CjEO/(1 – VBE/VoE)MJE
CjC(VCB) = CjCO/(1 – VCB/VoC)MJC
Donde CjEO y CjCO son los valores de las capacidades de las uniones para VBE=0 y VCB=0
respectivamente; VoE y VoC son las barreras de potencial en equilibrio de las uniones E-B y C-B
respectivamente; MjE y MjC son los coeficientes de gradiente de concentración de cada unión,
siendo sus valores de 0.5 para uniones abruptas (E-B) y 0.33 para uniones linealmente graduadas
(B-C).
Las capacidades de difusión se obtienen de la carga almacenada en la base (QB = TFICC para B-E) y
se expresan de la forma siguiente:
CDE = TFICC/VBE = TF gmF
CDC = TRIEC/VCB = TR gmR
Donde TF y TR son los tiempos de transito directo (modo normal de operación) e inverso (modo
inverso de operación y gm es la transconductancia del BJT que será definida posteriormente. En las
expresiones anteriores se usó el tiempo de transito en vez del tiempo de vida pues no se recombinan
la mayoría de los portadores minoritarios que atraviesan la base.
2.3 Modos de conexión del BJT.
El BJT es un dispositivo de tres terminales y tiene tres posibles formas de conexión de acuerdo con
el terminal que se escoja común desde el punto de vista de CA, tanto para el circuito de entrada
como para el de salida. Las tres configuraciones posibles son la base-común, la emisor-común y la
colector común.
2.3.1 Configuración base-común.
Se representa como se muestra en la figura 2.10, con la base común a la entrada y a la salida, en este
caso se representa el circuito con un transistor PNP. Para el transistor NPN la conducción
fundamental es debida al flujo de electrones del emisor al colector, las polaridades de corrientes y
tensiones son contrarias a las del transistor PNP, por lo que la corriente IE debe ser en el sentido de
la flecha del emisor cuando opera en activa.
Figura 2.10 Configuración base común.
7
Solamente para operación en activa, la corriente de colector es casi independiente de VCB por lo que
se considera como constante para un valor dado de IE, de acuerdo con la expresión:
IC =
FIE
+ ICO
donde F es la ganancia de corriente de gran señal en B-C e ICO es la corriente de saturación
inversa de la unión B-C, pero que en forma general y cambiando el signo con relación a la
referencia del diodo, se puede expresar por:
IR = ICO(1 - eVCB/VT).
Por tanto para el BJT se puede escribir como:
IC =
FIE
+ ICO(1 - eVCB/VT)
Esta ecuación permite sacar la gráfica IC vs VCB del base-común tomando como parámetro la
corriente IE. Esta colección de curvas que se muestra en la figura 2.11 se denomina característica
estática de salida La característica de entrada presenta a IE vs VBE para varios valores de VCB. Ya
que el circuito de entrada no es más que la unión B-E, esta característica es similar a la de un diodo
en directa. Se observa al variar VCB no ocurren cambios significativos sobre todo por encima de 1V.
Ojo valores de VCB grafico b
a)
b)
Figura 2.11 Características del transistor en BC a) salida b) entrada
En la característica de salida se observa que cuando VCB<0 y en el orden de 0.6V para silicio, la
corriente de colector puede tener un valor relativamente alto por estar operando el transistor en
saturación con ambas uniones polarizadas en directa.
Por otro lado, si se polarizan en inversa ambas uniones, el transistor se corta por lo que cuando IE =
0, IC = -IB = ICO. Para este caso en un transistor real, si se abre el emisor circulará una corriente ICBO
que es varios ordenes mayores que ICO, debido a dos factores: por un lado existe una corriente de
fuga superficial que es proporcional al voltaje de inversa de la unión B-C y por otro debido al efecto
de multiplicación de avalancha se generan nuevos portadores en la ZCE. Esto provoca que para
transistores pequeños de silicio a 25ºC, ICBO es del orden de nA y para germanio del orden de A.
La dependencia de ICBO con la temperatura es la misma que la de IS del diodo, en que dobla su valor
aproximadamente por cada incremento de 10ºC.. No obstante, debido al valor bajo de ICBO, en
transistores de silicio la temperatura de unión puede alcanzar alrededor de 200ºC mientras que los
de germanio se limitan a 100ºC.
Idealmente las variaciones de VCB influyen muy poco en el valor de IC y prácticamente es IE la que
la fija. En la práctica un aumento de VCB conlleva a una reducción del ancho efectivo de la base
8
WB, por lo que mayor cantidad de los portadores minoritarios que atraviesan la base pueden
alcanzar el borde de la ZCE de la unión B-C y ser absorbidos por el campo interno. Esto hace que IC
aumente ligeramente con el aumento de VCB y aparezca una ligera inclinación en la característica de
salida para el modo de operación de activa.. La variación de WB con VCB es conocido como efecto
Early o de modulación del ancho de la base y tiene tres consecuencias fundamentales:
Al hacerse WB menor, se reduce la posibilidad de recombinación de los portadores minoritarios
en la base, provocando que F se incremente al crecer VCB.
El gradiente de la concentración de los portadores minoritarios en la base se incrementa y como
la corriente de difusión es proporcional a este gradiente, IE se incrementa con VCB. Esto provoca
un traslado hacia arriba en la característica de entrada y que aparezca una ligera inclinación en
la característica de salida para la región activa cuya pendiente representa el inverso de la
resistencia de salida del transistor ro. Si no se considera el efecto Early, el valor de ro es infinito.
Para valores muy alto de VCB, WB puede reducirse a cero, provocando la ruptura conocida por
punch-through, en que la corriente IC crece violentamente y puede destruir al dispositivo.
2.3.2 Configuración emisor-común.
La mayoría de los circuitos con BJT emplean este tipo de conexión, que tiene como corriente de
control a la pequeña corriente de base en lugar que la del emisor como en el caso anterior. Para el
emisor-común, IB y VCE son las variables independientes mientras que VBE e IC son variables
dependientes, en la figura 2.12 se presenta un transistor NPN en la configuración emisor común.
VCE = VBE + VCB
IE = IB + IC
IC = FIE + ICO que al simultanear se tiene que:
IC = F/(1- F)IB + ICO/(1- F) = FIB + (1+ F)ICO.
F = F/(1- F)
F + 1 = 1/(1- F)
Figura 2.12 Configuración Emisor común
Donde F = F/(1- F) se define como ganancia de corriente de gran señal para la configuración
emisor-común y también se denota por hFE. Como normalmente IB >> ICO y F >> 1, se utiliza la
aproximación:
IC = F IB
Debido al efecto Early al incrementarse VCB aumenta F, lo que trae como consecuencia que F
aumente más sensiblemente, por lo que la variación de IC con VCE en activa es mayor que para basecomún como se observa en la característica de salida de la figura 2.13a. La característica de entrada
sigue siendo la de una unión p-n polarizada directamente donde el voltaje VCE influye relativamente
poco sobre esta. Es razonable esperar que la variación con la temperatura de V BE en directa sea la
misma que la del diodo, o sea de –2.5 mV/ oC. En la figura 2.13b se muestran las características de
entrada para la configuración EC.
9
a)
b)
Fig. 2.13 Características del transistor en configuración emisor común a) salida , b) entrada
En la característica estática de salida de la configuración emisor común (EC) aparecen al igual que
para base-común, las cuatro regiones de operación: activa, corte, saturación y ruptura. Cuando la
unión B-E está en directa y la B-C en inversa, el transistor opera en activa donde trabaja como
amplificador lineal y se cumple que:
IC =
FIB
+ (1+ F)ICO
Cuando las dos uniones se polarizan en directa, el transistor opera en saturación y no se cumple la
relación anterior, pues IC se mantiene prácticamente constante independientemente del valor de IB
que tendrá un calor superior a IC/ F. En esta región de operación el voltaje VCE es muy pequeño, del
orden de 200mV.
Al polarizar en inversa ambas uniones, opera en corte. Cuando la base está abierta en que IB = 0, por
la malla de salida entre colector y emisor circula la corriente conocida por ICEO, expresada como:
ICEO = (1+ F)ICO
Esta corriente ICEO es aproximadamente igual a ICO pues como se verá posteriormente
cero a bajos niveles de corriente IC.
F
tiende a
Por último, cuando VCE alcanza valores altos, el transistor opera en la región de ruptura no
permisible, donde la corriente IC crece fuertemente, que si no se controla lo destruye .
La influencia del efecto de la modulación de WB debido a VCB sobre las características de salida en
emisor comun, se modela para el BJT a través del voltaje de Early VA, con valores típicos entre 50V
y 100V en dependencia del tipo de transistor, lo cual se muestra en la figura 2.14. La pendiente de
la característica de salida en la región activa es el recíproco de la resistencia de salida r o del
transistor.
10
Figura 2.14 Características de salida en EC usando VBE como parámetro
El parámetro F aparece en los manuales de los fabricantes de BJT y se demuestra que varía con la
corriente de polarización o de reposo. Al graficar F normalizado vs log IC, se observa que a
corrientes medias alcanza un valor máximo, que decrece a niveles bajos y altos de IC, lo cual se
muestra en la figura 2.15. Se conoce que F se reduce a niveles bajos de corriente por la
recombinación que ocurre en la superficie producto de los defectos cristalinos. La reducción de F
en niveles altos de corriente se debe al efecto de amontonamiento de emisor, donde solo aparece
como emisor de portadores efectivo la periferia de este que se encuentra frente al contacto de base.
Figura 2.15 Variación de Beta normalizada con IC
Los valores típicos de los voltajes de cada unión para un BJT tipo NPN a 25oC son:
Material
Si
Ge
VCE sat
0.2V
0.1V
VBE act
0.7V
0.2V
VBE sat
0.8V
0.3V
VBE corte
0
-0.1V
VBE inic
0.5V
0.1V
Los valores de corrientes y voltajes obtenidos por cálculos aproximados a mano empleando los
datos antes expuestos para VBE y VCE, se correlacionan bien con los valores medidos
experimentalmente. Si se desea una exactitud mayor se acude a la simulación eléctrica con PSPICE.
2.4 Parámetros del transistor bipolar.
En la utilización de los BTJ deben respetarse las limitaciones impuestas por los fabricantes con
relación a los niveles de corriente, voltaje y potencia permitidos. Un transistor puede destruirse si la
unión B-C se somete a una disipación de potencia excesiva, digamos por encima de 500mW a 25ºC
para el BC-548. Esta potencia máxima permisible a la temperatura ambiente comienza a disminuir
a una velocidad dado por el parámetro resistencia térmica ja = 250 oC /W, como se muestra. En la
figura 2.16.
11
Figura 2.16 Disipación de potencia máxima admisible para el
transistor BC-548 contra temperatura
Aún cuando no se disipe la potencia permisible por el transistor, existen valores de voltaje y de
corriente que de sobrepasarse lo destruyen también. BVCBO, BVCEO y BVEBO son los máximos
voltajes de inversa entre los dos terminales señalados con el otro abierto y que para el BC-548 son
de 30V, 30V y 5V respectivamente. IC, ICM e IBM representan las corrientes máximas permisibles de
colector y de base que para el BC-548 son de 100mA (CD), 200mA (pico) y 200mA (pico)
respectivamente.
Otros parámetros de interés son la temperatura máxima de la unión B-C que para silicio es de 150ºC
y la resistencia térmica ja expresada en oC/W. Los parámetros que caracterizan su comportamiento
en régimen dinámico y transitorio se estudiarán posteriormente.
2.4.1 Variación de los parámetros del BJT con la temperatura y el punto de operación.
Los parámetros del BJT que varían con la temperatura son ICO, F o F y VBE.
La componente ICO de la corriente de colector depende de la concentración de portadores
minoritarios en la ZCE de la unión B-C y del área de esta. ICO es proporcional a ni2 que se
incrementa con el aumento de T; la influencia es mayor en los BJT de germanio que de silicio. ICO
dobla aproximadamente su valor por cada incremento de 10ºC de acuerdo con:
ICO(T) = ICO(TA) 2(T-TA)/10
En el caso de F, su dependencia con la temperatura aparece a través del ancho efectivo de base
(WB) que está relacionado con la altura de la barrera de de potencial (Vo) que a su vez es función de
la temperatura y por el incremento de la longitud de difusión LnB que crece con T:
F
= 1 – WB2/2LnB2
Este aumento de F provoca un incremento aún mayor en F, que en las características estáticas de
salida provoca una separación mayor entre curvas. La relación se expresa por:
F(T)
=
XTB
F(TA)(T/TA)
donde T y TA se expresan en valores absolutos y el parámetro que define dicha variación X TB varía
entre 1 y 2 de acuerdo con el tipo de transistor.
Las variaciones de VBE con T son similares a las del diodo por estar la unión E-B polarizada en
directa, o sea de aproximadamente VBE / T = –2mV/oC.
VBE(T) = VBE(TA) - ( VBE / T)(T – TA)
12
2.5 Polarización de los transistores bipolares.
En los circuitos con BJT, el punto de operación y la línea de carga estática tienen el mismo
significado que se explicó en el análisis de circuitos con diodos. Como método de análisis para
circuitos con transistores, se analiza primero la polaridad de las uniones E-B y B-C para definir su
posible modo de operación (activa, saturación o corte). De la selección de una de ellas, digamos
para activa, se realizan todos los cálculos correspondientes y del análisis de los resultados se
confirma o no la suposición realizada. De no ser afirmativa, se repiten los cálculos para otro modo
de operación.
Los circuitos con BJT de acuerdo con su aplicación, requieren de una polarización adecuada de las
uniones E-B y B-C para fijar el punto de operación en la característica de salida. El punto de
operación Q [VCEQ, ICQ, VBEQ, IBQ], indica los valores de corrientes y de voltajes de polarización
del transistor en reposo. Al seleccionar el circuito de polarización a emplear de acuerdo con la
aplicación, es importante tener presente lo relativo a la estabilidad de la polarización frente a
cambios paramétricos del transistor o de la temperatura. El circuito de polarización más simple con
una sola batería es el conocido como de polarización fija, el que se muestra en la figura 2.17. Si se
considera que el transistor opera en activa con VCEQ>VCEsat:
IEQ = IBQ + ICQ ICQ
(si F>>1)
IBQ = (VCC-VBEQ)/Rb VCC/Rb (casi constante
para VCC>>VBEQ)
ICQ = FIB + (1+ F)ICO
VCEQ = VCC - ICQRC (línea de carga estática)
VCEQ = VBEQ + VCBQ
Figura 2.17 Circuito de polarización fija
Al incrementarse la temperatura, tanto ICO como F aumentan, por lo que ICQ se incrementa. En la
característica de salida del transistor esto se refleja con un desplazamiento hacia arriba de cada
curva. Como IB es aproximadamente constante para este circuito, el punto de operación también se
desplaza a lo largo de la línea de carga estática desde la posición Q a Q´, lo que se muestra en la
figura 2.18. Este mismo efecto ocurre a temperatura ambiente si el transistor se reemplaza por otro
del mismo tipo, debido a la dispersión que sufren los parámetros y características del BJT en su
fabricación ( F puede variar de 2 a 3 veces de su valor nominal). Es por este motivo que el circuito
de polarización fija con IB constante, tiene aplicaciones muy limitadas por ser mala la estabilidad
del punto de operación Q frente a cambios de temperatura, envejecimiento o por dispersión
paramétricas que pueden hacer variar el modo de operación del transistor.
Figura 2.18 Desplazamiento del punto de operación para
aumento de la temperatura.
13
Si se invierte la polaridad de la batería VCC, el transistor opera en corte al tener la unión B-E en
inversa. En estas condiciones por la unión B-C circula una corriente (1+ F)ICO que sale de la base.
Por otro lado la polarización para un transistor PNP se realiza en forma similar a la del NPN pero
invirtiendo la polaridad de VCC.
Al superponer a la entrada la fuente de señal variable en el tiempo vs(t), aparecerá un movimiento
del punto de operación a lo largo de la línea de carga dinámica que toma en cuenta el efecto de la
carga. . No obstante, aunque en la operación del circuito existen simultáneamente las componentes
de CD y de CA, es conveniente analizarlas por separado pues son creadas por fuentes diferentes y
cumplen distintas funciones. Esto será visto más adelante.
Otro circuito muy utilizado para polarizar el transistor, es el circuito autopolarizado mostrado en la
figura 2.19, logra una mejoría considerable en la estabilidad del punto de operación al añadir el
resistor RE en el emisor que provoque una caída de potencial IEQRE mayor que VBEQ. Para su
análisis estático, es conveniente aplicar el Teorema de Thevenin a la entrada entre los puntos A y B
al desactivar el transistor.
VTH =VCCR2/(R1+R2)
Rb = R1llR2
VTH = IBQRb + VBEQ + IEQRE
IEQ = IBQ + ICQ ICQ (si F>>1)
ICQ = FIB + (1+ F)ICO
FIB
para Silicio a Tamb
IBQ = (VTH – VBEQ) / [Rb + (1+ F)RE]
VCEQ = VCC - ICQ(RE + RC)
Figura 2.19
a) Circuito autopolarizado, b) equivalente de Thevenin
Para analizar la estabilidad del circuito se observa que al crecer T se incrementan ICO y
disminuye VBEQ. De la ecuación de la malla de entrada se tiene que:
F
pero
IBQ = [VTH – VBEQ + 1+ F)ICORE] / [Rb + (1+ F)RE]
Al aumentar ICO y F y disminuir VBEQ, la corriente IBQ tiene que disminuir. Esto trae como
resultado que al incrementarse la temperatura la corriente ICQ tiende a subir pues crecen ICO y F a
la vez que se reduce VBE, lo que incrementa la caída IEQRE que automáticamente de acuerdo con la
ecuación de la malla de entrada provoca que IBQ e ICQ decrezcan. Esto limita el desplazamiento del
punto de operación a diferencia del de polarización fija. Este proceso regenerativo es producto del
lazo de realimentación negativa que aparece por la presencia de RE en el circuito.
2.5.1 Factor de inestabilidad del punto de operación.
Ya se conoce que el circuito autopolarizado estabiliza adecuadamente a ICQ frente a cambios de
temperatura, por dispersión paramétricas o envejecimiento. Dicha estabilización será mejor o peor
en dependencia de los valores relativos de R1, R2 y RE. El factor de inestabilidad relativa del punto
de operación da una medida del corrimiento de Q frente a variaciones de los valores de los
parámetros del transistor y se define como:
ICQ/ICQmin (%) = 100(ICQmax-ICQmin)/ICQmin
14
Este factor se calcula en % y no como la variación ICQ, pues no significa lo mismo un cambio de
1mA para ICQ =1mA (variación de100%) que para ICQ =10mA (variación de10%).
El método general de cálculo de este factor consiste en encontrar para un circuito de polarización
dado, la expresión de ICQ que la relaciona con los demás parámetros, voltajes y resistores del
mismo. Se evalúa la expresión de ICQ para las condiciones extremas que provoquen la ICQmin y la
ICQmax y con estos se calcula el factor de inestabilidad relativa del punto de operación. Para cada
circuito se puede encontrar una expresión particular para el cálculo de dicho factor que como se
verá posteriormente puede ser útil en su diseño.
Para el circuito autopolarizado se obtiene la siguiente expresión, al suponer que todos los
parámetros del transistor varían en forma independiente y sumar sus efectos individuales sobre ICQ:
ICQ/ICQmin = (1 + Rb/RE)(M2
donde:
F/ Fmax Fmin)
= Fmax- Fmin
ICO = ICOmax - ICqmin
VBE = VBEmax - VBEmin
F
+ (1 + Rb/RE)(M1 ICO/ICQmin) - M1 VBE/ICQminRE
M = 1/[(1 + Rb)/(1 + F)RE]
M1 evaluada para Fmin
M2 evaluada para Fmax
Tanto F como ICO aumentan cuando se eleva la temperatura mientras que VBE disminuye, por lo
que se deben establecer las siguientes correlaciones para el caso peor:
ICQmax se calcula con Fmax, ICQmax y VBEmin
ICQmin se calcula con Fmin, ICQmin y VBemax
La expresión anterior de la inestabilidad del punto de operación del circuito autopolarizado, tiene
tres términos a la derecha en que cada uno representa la variación con relación a uno de los
parámetros que varían. El último término tiene signo negativo por ser VBE negativo.
Para mejorar el factor de inestabilidad, de la expresión anterior salen las siguientes conclusiones:
La relación Rb/RE debe ser lo menor posible.
La caída ICQRE debe ser mucho mayor que VBE. Criterio: ICQRE = 5VBE (entre 1V y 3V
típico).
Si
F es elevada, se deben utilizar transistores con F lo mas alta posible.
Para reducir los efectos sobre el punto de operación de las variaciones de la fuente no regulada
VCC, se debe escoger el valor de R1 lo mayor posible para un valor dado de Rb.
En el caso de los transistores de silicio, el término relacionado con ICO puede despreciarse, por lo
que la mayor contribución la dan los relacionados con F y con VBE. En el caso del germanio, el
término relacionado con VBE influye poco y la mayor contribución lo aporta el de ICO.
2.5.2 Polarización de los BJT en los circuitos integrados.
En la electrónica discreta, las redes R-C dan la posibilidad de seleccionar la polarización de una
etapa independientemente de las otras sin afectar la señal a transmitir. En los CI se usa
acoplamiento directo por no ser posible fabricar capacitores de valores altos, por lo que se emplea el
acoplamiento directo. En los amplificadores de acoplamiento directo, los voltajes de CD de las
diferentes etapas interaccionan y se requiere del empleo de la realimentación negativa para
estabilizar el punto de operación. También se necesita compensar la temperatura pues existen
parámetros que dependen de ésta.
Es por este motivo que la polarización de las diferentes etapas de un CI es un problema que no es
posible resolver usando las técnicas de la electrónica discreta. Esto se debe principalmente a que se
15
necesitan resistores y capacitores de valores altos que no son posible de fabricar en los
microcircuitos. La filosofía que se sigue con vistas a polarizar el CI es emplear el mínimo posible
de componentes pasivas y de valores pequeños. Se emplean para lograr esto, una serie de bloques
típicos como son las fuentes de corriente y de voltaje. Estas a pesar de tener un número dado de
transistores, son más económicas y garantizan una polarización con menor sensibilidad a las
variaciones de VCC y de la temperatura. A continuación se verán algunos ejemplos.
2.5.2.1 Fuente de corriente polarizada a diodos o espejo de corriente. Las fuentes de corriente
logran la polarización estable y precisa de una etapa amplificadora reproduciendo en una rama del
circuito la corriente de referencia que circula por otra rama independientemente de los valores
absolutos de los parámetros de los dispositivos. El circuito más simple es el mostrado en la figura
2.20 que es diseñado para mantener a IC1 constante. El transistor Q2 (opera en activa) está conectado
como diodo al unirse base con colector.
IREF = IC2 = (VCC – VBE2) / R1
.
Q1 y Q2 cercanos dentro del mismo chip
Figura 2.20 Circuito de polarización espejo de corriente
Como Q1 y Q2 operan en activa con el mismo VBE, sus corrientes IE tienen que ser iguales. Si
F>>1, las corrientes de colector se expresan al despreciar el efecto Early como:
IC1 =
FIES
e(VBE1/VT)
IC2 =
FIES
e(VBE2/VT)
Donde IES = AE depende de LB, NE, NB y del área del emisor (AE). Dividiendo una entre la otra:
IC1/IC2 = AE1/AE2
La relación IC1/IC2 se limita a 5 por problemas tecnológicos. Si ambos transistores son idénticos con
AE1 = AE2, se obtiene que IC1 = IC2. Luego el transistor Q1 reproduce como una imagen la corriente
de referencia IREF, independientemente de los parámetros del transistor siempre que trabaje en
activa. Para VCE1 > VCEsat, la corriente imagen IC1 se mantiene casi constante como se muestra en la
figura 2.21.
ro1 = (VA + VCEQ1) / ICQ1
Figura 2.21 Característica de tensión corriente
circuito de fuente de corriente
16
El incremento ligero en IC1 es debido al efecto Early, donde la pendiente en esta región es el
recíproco de la resistencia de salida de la fuente de corriente (Ro), que para este caso es la ro del
transistor Q1. En este circuito, el valor de Ro no es muy grande como se desea para una fuente de
corriente ideal, por lo que se le introducen modificaciones al circuito introduciendo realimentación
negativa.
La rama de Q2 del espejo de corriente puede usarse como referencia de varias fuentes de corriente
para polarizar simultáneamente varias etapas. Esto se conoce como repetidores de corriente y se
muestra en la figura 2.22.
Si AE1 = AE2 = AE3 =....= AEN
IC1 = IC2 = IC3=.....= IREF
Figura 2.22 Circuito repetidor de
corriente
2.5.2.2 Fuente de corriente polarizada por resistencia. La resistencia de salida de la fuente
anterior se puede incrementar adicionando resistores en los emisores de los transistores como se
muestra en la figura 2.23.
IREF = IC2 = (VCC – VBE2) / (R1 + RE2) (si F>>1
IC1RE1 + VBE1 = IC2RE2 + VBE2
VBE = VBE1 - VBE2 = VT ln (IC1/IC2)
(si AE1 = AE2)
IC1/IC2 = RE1/RE2 [1 - VBE/IC2RE2 ]
Figura 2.23 Circuito fuente de corriente
polarizada por resistencia
Normalmente VBE << IC2RE2, de donde:
IC1/IC2 = RE1/RE2 .
La relación IC1/IC2 se controla por la razón entre los valores de resistores y se limita a 10 para evitar
un consumo de área excesivo. Con este tipo de polarización también se pueden implementar los
repetidores de corriente, en forma similar a la fuente anterior.
El resistor RE1 introduce realimentación negativa a Q1, lo que provoca un incremento de la
resistencia de salida de la fuente (Ro) respecto a la anterior. De un análisis aproximado empleando
modelos de pequeña señal como se verá posteriormente, se puede demostrar que Ro hfero/3 donde
hfe es de valor elevado y representa la ganancia de corriente en pequeña señal del emisor común.
17
2.5.2.3 Fuente de corriente logarítmica o de Widlar. Se emplea para obtener corrientes muy
pequeñas (del orden de A) con valores relativamente grande de corriente de referencia (mA), lo
cual se logra al hacer a RE2 = 0 para la fuente anterior con Q1 y Q2 idénticoslo cual se muestra en la
figura 2.24.
IREF = IC2 = (VCC – VBE2)/R1
V1 = IC1RE1 = VBE2 - VBE1 = VBE = VT ln IC2/IC1
IC1 = VBE/RE1 = (VT/RE1) ln (IC2/IC1)
Figura 2.24 Fuente de corriente de Widlar
La corriente IC1 puede ser muy pequeña sin que RE1 tenga un valor elevado. Por ser una ecuación
trascendental, se resuelve por medio de iteraciones sucesivas partiendo de un valor inicial de
(0.1V/RE1). Su principal desventaja como fuente de corriente es la dependencia de IC1 con la
temperatura a través del parámetro VT. La resistencia de salida de esta fuente es también elevada
pues la presencia de RE1 introduce realimentación negativa. La expresión de la Ro es similar a la del
caso anterior.
2.5.2.4 Fuente de corriente estabilizada por diodos.
En la figura 2.25 se muestra una fuente de corriente estabilizada por diodos. Se caracteriza por su
compensación térmica a través del uso de cadenas de diodos. Para N = 2 (N es la cantidad de
diodos)
I = (VEE – NVBE)/(R1 + R2)
(despreciando IB si F>>1)
VAB = IR2 + NVBE
Io = (VAB–VBE)/R3=(VEE – NVBE)R2/(R1+R2)RE+ (N-1)VBE/R3
Figura 2.25 Fuente de corriente estabilizada por diodos
De la expresión de Io hallada, se demuestra que el coeficiente de temperatura de la corriente de la
fuente es nulo (dIo/dT = 0) si se cumple que el número de diodos conectados es N = (1 + R 2/R1).
Para el caso de ser R1 = R2, se emplean dos diodos. De nuevo la Ro de la fuente es elevada por la
presencia de RE = R3.
2.6 El BJT como interruptor
Ya se estudió al BJT en régimen estático de operación, en que el punto de operación Q se localizaba
en el centro de la región activa. A este tipo de polarización en que el transistor siempre conduce
cuando se le aplica una señal pequeña, se le conoce come clase A. Sin señal aplicada el posible
movimiento de Q se debía a variaciones de la temperatura de unión por autocalentamiento, por
18
variaciones de TA o por la dispersión que desde el punto de vista de fabricación poseen los
elementos del circuito incluyendo al propio transistor y su envejecimiento.
La ubicación inicial del punto de operación tiene una gran importancia en el funcionamiento
dinámico del transistor, pues si se encuentra en la región activa es posible considerar al dispositivo
dentro de determinados límites como lineal. La gran mayoría de las aplicaciones del transistor están
asociadas a regímenes dinámicos de operación donde el BJT por efectos de una señal variable
externa aplicada en su circuito de entrada, provoca que el punto de operación se desplace sobre una
línea de carga Siempre que este desplazamiento de Q se circunscriba a la región activa, el BJT
opera como un elemento cuasi-lineal. Si en ese movimiento el punto de operación alcanza tanto la
zona de saturación como la de corte, entonces se dice que trabaja en régimen de conmutación o en
régimen de gran señal.
En este análisis se empleará la configuración emisor-común para representar un interruptor simple
al cual se le aplicara una señal en forma de pulso, según se muestra en la figura 2.26a.
a)
b)
Figura 2.26 a) Interruptor BTJ, b) desplazamiento del punto de operación sobre
la línea de carga
En condiciones estáticas siempre que vs 0, al no existir corriente por el circuito de entrada IB = 0
e IC = (1 + F)ICO 0. Como la caída en RC es cero, VCE VCC. En esta situación el transistor está
cortado y su punto de operación se denota por Q1 en la característica de salida mostrada en la figura
2.26b. El transistor simula un interruptor abierto y la potencia disipada en la unión B-C es casi nula.
Al cambiar vs de –V1 a V2 en t = T1, si V2 posee suficiente amplitud para provocar que el punto de
operación se desplace a la posición Q3, la corriente por el transistor alcanza el valor máximo
correspondiente a saturación y su voltaje VCE se mantiene casi constante a un valor pequeño igual a
VCEsat, que para silicio vale 0.2V. La corriente por el transistor cuando opera en saturación se
calcula de:
ICsat = (VCC – VCE sat)/RC
VCC/RC
si VCC >> VCE sat
IEsat = IBsat + ICsat donde la IBsat no siempre es despreciable frente a ICsat.
Como el voltaje VCE alcanza el valor mínimo (casi cero) para esta línea de carga, el circuito simula
un interruptor cerrado. Aunque la corriente que circula es máxima cuando está saturado el
transistor, VCEsut es mínimo por lo que la potencia disipada también será pequeña para este estado.
19
Para la electrónica digital estos dos estados de conducción son codificados atendiendo al álgebra de
Boole; se denominan estado”1” para interruptor abierto y estado “0” para interruptor cerrado.
Por otro lado, si la amplitud de la señal vs no es grande de forma que el punto de operación se
desplace de Q1 a Q2 (sin entrar en la región de saturación), el transistor trabajaría entre corte y la
región activa, por lo que en conducción disiparía una potencia relativamente alta con respecto al
caso anterior. En los circuitos digitales se emplean los dos casos de operación.
En todas las aplicaciones es conveniente que el cambio de un estado a otro se desarrolle lo más
rápidamente posible, por lo que a continuación se analizan los fenómenos que limitan la velocidad
de respuesta de los BJT.
2.6.1 Tiempos de conmutación de los BJT.
Las dos uniones del transistor tienen asociadas capacidades parásitas (CD para uniones en directa y
CT para uniones en inversa). Las cargas almacenadas en las ZCE y en las regiones neutrales del
transistor, son funciones no lineales de los voltajes de las uniones. Ellas tienen una influencia muy
fuerte sobre la velocidad de conmutación en las redes digitales y en la respuesta de frecuencia de los
amplificadores. A continuación se analiza que sucede en el transistor al tratar de pasarlo de corte a
saturación.
Al cambiar el pulso aplicado a la base del transistor a través de Rb en el circuito anterior, de –V1 a
V2, la corriente iC no responde inmediatamente a la señal de entrada. Para que el punto de operación
pase de la posición Q1 a Q3, es necesario suministrarle cargas a la base para establecer el exceso de
portadores minoritarios que proporcione la corriente ICsat. Este proceso requiere de determinado
tiempo. Por otra parte, el transistor no responde inmediatamente al cambio del pulso de voltaje de
entrada en t = T1, por lo que aparece determinada demora pues los portadores minoritarios deben
atravesar la base y alcanzar el colector. Esto se toma como el tiempo transcurrido desde que se
aplica V2 en t = T1 hasta que la corriente de colector alcance el 10% de ICsat que es su máximo valor.
A este intervalo se le conoce como tiempo de demora td. En la figura 2.27 se representa
esquemáticamente la variación del voltaje Vo y de la corriente del colector del transistor.
Figura 2.27 Formas de ondas de Vo e Ic mostrando los tiempos de conmutación
20
De igual forma, en su paso desde corte a saturación se va estableciendo la concentración de
portadores minoritarios del lado de la base y va creciendo la corriente. El tiempo en que i C se
incrementa desde el 10% al 90% de su valor final se conoce como tiempo de subida tr. Este es el
tiempo requerido para que el punto de operación atraviese la región activa. El tiempo total de
encendido tON es la suma de ambos:
tON = td + tr
Al alcanzar la región de saturación, la unión B-C se polariza en directa y se produce un incremento
notable de la concentración de portadores minoritarios a ambos lados de su ZCE, sobre todo en la
base.
En t = T2 en que vs retorna al valor –V1, para llevar al transistor a corte se produce de nuevo un
retardo en la conmutación inversa debido al tiempo requerido para suprimir el exceso de cargas en
ambas uniones. A este tiempo se le conoce como tiempo de almacenamiento ts y se mide como el
tiempo transcurrido desde t = T2 en que vs cambia, hasta el tiempo en que iC cae al 90% de ICsat. El
tiempo que transcurre durante la disminución de iC desde el 90% al 10% de ICsat se le conoce como
tiempo de caída tf. El tiempo total de desconectado tOFF se calcula de :
tOFF = ts + tf
La justificación de los tiempos de conmutación puede explicarse también a partir de la carga y
descarga de los capacitores parásitos de las uniones que tienen asociados siempre una constante de
tiempo de carga y otra de descarga. El fallo en la respuesta del BJT al ser excitado con un pulso de
entrada rápido resulta del hecho que el transistor saturado tiene portadores minoritarios en exceso
almacenados en base. El transistor no responde hasta que esta carga en exceso sea removida. El
tiempo de almacenamiento ts puede ser varias veces mayor que tr y ts requeridos para atravesar la
región activa. Evidentemente, el transistor requiere mas tiempo en pasar de saturación a corte que a
la inversa (tOFF > tON). Para el 2N2222A con VCC = 30V, IC = 150mA e IB = 15mA, tOFF = 285ns y
tON = 35ns.
Para incrementar la velocidad de conmutación se debe reducir ts, lo cual se logra conectando en
paralelo con la unión B-C un pequeño diodo Schottky como se hace en la familia lógica digital
Schottky TTL. En la figura 2.28 se muestran los símbolos del diodo y del transistor Schottky
Figura 2.28 Transistor Schottky
El diodo Schottky se obtiene al realizar un contacto metal-semiconductor tipo N y en directa posee
una característica similar a la del diodo de unión pero con V = 0.3V. Al conectar este diodo
polarizado directamente en paralelo con la unión B-C, se impide que esta unión se polarice
fuertemente en directa, evitando que el transistor se sature fuertemente. Por tanto, el paso de
saturación a corte será mucho más rápido por lo que se incrementa la velocidad de conmutación del
dispositivo.
21
2.7 El BJT como amplifificador de pequeña señal.
Un rasgo fundamental del transistor es su habilidad para amplificar señales variables en el tiempo,
es decir, entregar en su circuito de salida una señal cuya magnitud sea varias veces mayor que la
magnitud de la señal de entrada. A este modo de trabajo del BJT se le conoce como régimen
dinámico. Por otro lado, se considera que el amplificador es de pequeña señal cuando el
movimiento del punto de operación a lo largo de la línea de carga dinámica es limitado. Bajo estas
condiciones se considerará un comportamiento casi lineal de los transistores producto de que las
señales que procesan son de muy pequeña amplitud.
Un amplificador es un circuito capaz de entregar una respuesta de salida que tenga mayor nivel de
potencia que la del estímulo aplicado. Se requiere que la respuesta del amplificador tenga la misma
forma de onda que el estímulo, para que se reproduzca la información de forma análoga. Este
estímulo es generalmente un voltaje o una corriente variable, cuyo régimen de variación contiene
los elementos de la información. Estos circuitos pueden diseñarse para amplificar voltaje, corriente
o potencia, pero es común a todos la amplificación de potencia. Se debe tener claro que un
transformador no es un amplificador, pues aunque puede elevar el nivel de voltaje o de corriente, es
incapaz de incrementar la potencia. En la figura 2.29 se representa un esquema simbólico del
amplificador.
Figura 2.29 Esquema simbólico del amplificador
2.7.1 Índices de los amplificadores lineales. Cualquier amplificador se puede caracterizar a partir
de sus índices fundamentales, los cuales son las ganancias de voltaje (AV), de corriente (AI) o de
potencia (AP); la resistencia de entrada (Ri´) y la resistencia de salida (Ro´). En el esquema
simbólico de la figura 2.30 se representan las corrientes y los voltajes de entrada y salida, asi como
la fuente de señal.
Figura 2.30 Esquema simbólico del amplificador y algunos de sus parámetros
El índice de ganancia (A) es el más importante y se define como la relación respuesta/estímulo
referida a un punto en particular. Para la ganancia de voltaje referida a la entrada del amplificador
se calcula como AV = Vo/Vi, pero referida a la señal de entrada se calcula como A VS = Vo/Vs. Lo
mismo ocurre para la ganancia de corriente ( AI = IL/Ii o AIS = IL/IS) y de potencia (AP = Po/Pi). La
22
resistencia de entrada (Ri´) se define como la impedancia de Thevenin equivalente que posee el
amplificador entre sus terminales de entrada y que ve la fuente de excitación. Todo el amplificador
puede ser sustituido por su resistencia de entrada. La resistencia de salida (Ro´) es la impedancia
equivalente de Thevenin que se ve desde la carga mirando hacia el amplificador. En la figura 2.31
se muesta el equivalente de Thevenin de la entrada y la salida del amplificador.
a) entrada
b)salida
Figura 2.31 Circuito equivalente de thevenin a) de la entrada b) de la salida
Otras características importantes del amplificador son la estabilidad estática y dinámica, la
disipación de potencia, la distorsión, el ruido y el ancho de banda entre otros.
La notación que se empleará es la siguiente: variable en minúscula y subíndice en minúscula
representa valores instantáneos (ic y vce); variable en minúscula y subíndice en mayúscula
representa valores instantáneos totales (iC y vCE); variable en mayúscula y subíndice en minúscula
representa valores picos o efectivos (Ic y Vce); variable en mayúscula y subíndice en mayúscula
representa valores de CD (ICQ y VCEQ), en la figura 2.32 se muestra la notación que se empleara.
iC = ICQ + ic
vCE = VCEQ + vce
Figura 2.32 Notación para las corrientes
y voltajes
2.7.2 Línea de carga dinámica. Los circuitos con acoplamiento R-C, emplean los capacitores Ca1 y
Ca2 para desacoplar los voltaje y corriente de CD de la fuente de señal y la carga respectivamente,
según se muestra en la figura 2.33. Esto simplifica considerablemente el análisis estático del
amplificador.
= (VCC - VBE) / Rb
ICQ = FIB Si ICO = 0
VCEQ = VCC - ICQRC (línea de carga estática)
Vce = -ic(RC RL) (línea de carga dinámica
Alrededor de Q)
IB
Figura 2.33 Etapa amplificadora EC con
capacitares de desacoplo
23
Para operación dinámica con señal variable en el tiempo a la entrada y a frecuencias medias en que
las reactancias XCa1 y XCa2 tengan valores despreciables frente a RS y RL respectivamente, al aplicar
a vs el punto de operación instantáneo se moverá alrededor de Q siempre a lo largo de la línea de
carga dinámica de pendiente [-1/(RCllRL). En la figura 2.34 se muestra el movimiento del punto de
operación sobre la línea de carga dinámica. De la relación de fase entre iB y vCE se observa que
ocurre una inversión de fase entre la señal de entrada y la de salida, típica de la configuración
emisor-común.
Figura 2.34 Características de salida en EC mostrando las rectas de carga y la
componente sinusoidal de la señal
Si la amplitud de la señal de entrada es grande, al moverse el punto de operación sobre la lcd se
debe asegurar que este no llegue a la región de corte ni a la de saturación. En el diseño de los
amplificadores es por tanto muy importante realizar una adecuada selección de la posición del punto
de operación para lo cual se debe tomar en cuenta lo siguiente:
Se encuentre situado entre los límites tolerables del transistor (ICM, VCEO y PCM).
Permita que el recorrido de la señal no provoque que Q salga de la región activa (clase A)
Posibilite que el recorrido de Q sobre la línea de carga dinámica se efectúe en una región
razonablemente lineal de la región activa del transistor.
Reduzca el consumo innecesario de potencia en reposo.
La respuesta de frecuencia de un amplificador tiene tres rangos bien diferenciados, mostrado en la
figura 2.35: el de frecuencias bajas que lo determinan los efectos introducidos por los capacitores de
acoplamiento y de derivación de emisor de valores elevados (decenas y cientos de F), cuyo valor
maximo es la frecuencia de corte a las bajas y se denomina como fb; el rango de frecuencias
medias, en que las reactancias tienen valores despreciables y la gananancia del amplificador es
máxima y en el caso de ganancia de voltaje se denomina Avo . Por último, el rango de frecuencias
altas que está determinado por el efecto de los capacitores interelectródicos del transistor de algunos
pF, en este rango, la frecuencia frecuencia mínima se denomina frecuencia de corte a las altas fa.
Las frecuencias de corte se determinan para el valor de gananancia Avo/√2.
24
Figura 2.35 Respuesta de frecuencia de los amplificadores
2.8 Modelo de pequeña señal del BJT.
Cuando se limita el funcionamiento del transistor a la condición de señales pequeñas, el transistor
puede considerarse como un circuito lineal de tres terminales. Para el análisis del régimen dinámico
de estos, se utilizan modelos equivalentes de pequeña señal que describen el comportamiento del
transistor y que relacionan los cambios en voltaje y corriente alrededor del punto de operación. Por
tal motivo cada elemento del modelo es función de la polarización establecida.
2.8.1 Modelo Pi híbrido del BJT
El circuito equivalente de pequeña señal del BJT desarrollado a partir del modelo de Ebers-Moll es
el modelo -híbrido. Si en la versión de transporte del modelo de gran señal de E-M, se sustituyen
las dos fuentes de corriente por una sola conectada entre emisor y colector de valor ICT = ICC – IEC y
se considera que el transistor opera siempre en la región activa, se obtiene al realizar determinadas
transformaciones el modelo de pequeña señal -híbrido. Los elementos que integran este circuito
equivalente relacionan los cambios en voltajes y corrientes alrededor del punto de operación por lo
que sus parámetros dependen de este. En la figura 2.36 se muestra la estructura de este modelo de
pequeña señal para la configuración emisor-común, el cual es valido solamente para la región
activa.
Figura 2.36 Circuito equivalente -híbrido de pequeña señal
Este modelo fue propuesto por Giacoleto en donde se relaciona el comportamiento externo del
transistor bipolar con los procesos físicos internos del mismo. Tiene la ventaja de ser relativamente
sencillo y proporcionar una precisión aceptable en los resultados que se obtienen para toda la gama
de frecuencias de trabajo del transistor. Aunque los parámetros del modelo dependen de la
temperatura y del punto de operación, los mismos son independientes de la frecuencia.
25
La unión E-B polarizada en directa se modela con su resistencia incremental r y su capacidad de
difusión C . Recordar que debido al mecanismo de inyección del emisor, ocurre un incremento de la
concentración de portadores minoritarios en el borde de la ZCE en la base que provoca un
incremento de la recombinación y por ende la variación de la conductividad de esta región.
C representa la capacidad de transición de la unión B-C polarizada en inversa y la resistencia
incremental r de esta unión toma en cuenta la modulación del ancho de la base introduciendo una
realimentación positiva perjudicial de la salida a la entrada. Por suerte su valor es muy elevado del
orden de decenas de M y normalmente se desprecia.
El efecto transistor debido al acoplamiento entre las dos uniones p-n está modelado por la fuente de
corriente controlada (gmV ) que en el rango de frecuencias medias es proporcional a Ib pues al
considerarse infinito el valor de r se tiene que V = Ibr . Por definición, la transconductancia gm
que también depende de la temperatura y del punto de operación, se calcula de:
gm = [diC/dvBE]Q = ICQ/VT por ser iC = Is eVBE/VT en la región activa.
La resistencia de salida ro que es también resultado del efecto Early, como se conoce su valor se
calcula del recíproco de la pendiente de la característica de salida del transistor para su punto de
operación en la región activa, de acuerdo con:
ro = (VA + VCEQ)/ICQ (decenas a cientos de K )
La resistencia de acceso a la base rb toma en cuenta la caída de voltaje entre el contacto de base y la
región activa bajo el emisor. La misma decrece con el nivel de corriente y tiene valores entre 40 y
400 .
2.8.1.1 Modelo Pi híbrido simplificado del BJT
El modelo -híbrido simplificado mostrado en la figura 2.37, es válido solo para frecuencias
medias y bajas en que los efectos capacitivos del BJT son despreciables y se consideran como
circuitos abiertos (C es del orden de decenas de pF y C de varios pF).
Figura 2.37 Circuito equivalente -híbrido simplificado
De la figura se observa que para esta condición v = ibr . Si se cortocircuita el colector con el
emisor para la señal variable en el tiempo (vce = 0), no circula corriente alterna por ro, de donde:
ic = gmv = gmibr
Se define el parámetro incremental hfe como la ganancia de corriente del emisor-común con
cortocircuito a la salida para la región activa en el sentido directo de operación. De donde:
hfe = [ ic/ ib]VCEQ = [ic/ib]vce=0 = gmr
26
Este parámetro hfe se calcula en la característica de salida con los incrementos de ic y de ib a través
del punto de operación para un valor fijo de VCEQ..
Para el transistor BC-548B en un punto de operación de ICQ = 2mA y VCEQ = 5V, los valores típicos
de los parámetros del modelo son:
rb = 210
r = 4.3K
r = 14.3M
ro = 145.7K
C = 3pF
C = 69pF
gm = 76.9mA/V
2.8.2 Modelo híbrido del BJT
Este modelo de pequeña señal (válido para transistores NPN o PNP trabajando en bajas y medias
frecuencias) se obtiene a partir de la teoría de cuadripolos para la configuración emisor-común,
eligiendo como variables independientes a Ib y a Vce. Los parámetros así obtenidos pueden ser
dimensionalmente diferentes, por lo que se conocen como híbridos. En la figura 2.38 se muestra el
modelo.
Vbe = hieIb + hreVce
Ic = hfeIb + hoeVce
Figura 2.38 Modelo hibrido del transistor bipolar
Donde cada parámetro se define para la configuración emisor común como:
- hie =Vbe/Ib]vce=0
resistencia de entrada con salida en cortocircuito. [ ]
- hre = Vbe/Vce]Ib=0
coeficiente de transferencia inversa de voltaje con la entrada abierta.
- hfe = Ic/Ib]vce=0
ganancia de corriente con salida en cortocircuito.
- hoe = Ic/Vce]Ib=0
conductancia de salida con la entrada abierta. [A/V]
Los parámetros “h” son ofrecidos por la mayoría de los fabricantes en los datos de cada transistor.
Estos parámetros varían con el punto de operación, la temperatura y sufren una dispersión
paramétrica debido al proceso de fabricación. Por otro lado, independientemente que el cuadripolo
que representa al transistor es válido para cada configuración (E-C, B-C y C-C), los valores de los
parámetros “h” son diferentes para cada caso.
En general, los fabricantes ofrecen los valores de los parámetros “h” para un punto de operación y
temperatura dado, acompañado de curvas que permiten realizar correcciones para otros Q y T. Para
el transistor BC-548B los valores de los parámetros y de sus variaciones relativas referidas a un
punto de operación de (2mA, 5V) son:
min
tip
max
hie (K)
3.2
4.5
8.5
-4
hre
2x10
hfe.
240 330 500
hoe ( A/V)
30
60
27
2.8.2.1 Modelo híbrido simplificado del BJT
Una simplificación del modelo de los parámetros h se logra al despreciar el generador del circuito
de entrada hreVce por tener muy bajo valor el parámetro hre y cumplirse que hoeRcarga < 0.1, dicho
modelo se conoce como modelo híbrido simplificado, el que se muestra en la figura 2.39.
Figura 2.39 Modelo híbrido simplificado
Si se compara este modelo híbrido simplificado con el modelo -híbrido simplificado válido solo
para frecuencias medias y bajas, se obtienen algunas expresiones de interés como son:
hie = rb + r
r = hfe/gm = hfeVT/ICQ por ser IC = gmV = hfeIb
r = r /hre
1/ro = hoe – (1 + hfe)/r
Se concluye que si son conocidos los parámetros “h” que dan los fabricantes para un punto de
operación y temperatura, se pueden determinar los correspondientes parámetros del modelo
-híbrido.
2.9 Análisis lineal de etapas simples con BJT a frecuencias medias.
A continuación se analizará la respuesta de una etapa amplificadora cuando es excitada por una
señal de entrada sinusoidal de pequeña amplitud (algunos mV) para considerar que el transistor se
comporta linealmente. Bajo estas condiciones de pequeña señal, las componentes variables de la
respuesta se obtiene empleando el circuito equivalente incremental del BJT (híbrido ó -híbrido).
Dicho análisis se realizará en el rango de frecuencias medias, o sea, a frecuencias de señal de
entrada en que todas las reactancias presentes en el amplificador sean despreciables. En este rango
de frecuencias medias, las ganancias y demás índices del amplificador son números reales y las
impedancias son resistivas puras. Debido a que los parámetros del modelo de pequeña señal
dependen del punto de operación, como primer paso de este estudio se debe realizar el análisis
estático (en reposo con vs = 0).
La determinación analítica del comportamiento lineal de pequeña señal se realizará con el siguiente
método:
anular las fuentes de CD (cortocircuitar las de voltaje y abrir las de corriente)
reemplazar cada transistor por su modelo equivalente.
conectar las componentes restantes.
resolver el circuito lineal resultante con los métodos de análisis circuital.
Este método de análisis es válido tanto para transistores bipolares (NPN y PNP) como para
transistores de efecto de campo (MOS y JFET). La restricción básica de que los voltajes y los
corrientes sean suficientemente pequeños es para que el circuito opere linealmente y los parámetros
del modelo se mantengan aproximadamente constantes.
28
2.9.1 Análisis lineal del emisor-común sin resistor de emisor.
Se realizará este análisis empleando el modelo de pequeña señal -híbrido, con una señal de entrada
sinusoidal vs de algunos mV y en el rango de frecuencias medias, donde los capacitores de
acoplamiento (Ca) y de derivación de emisor (CE ) se comportan como cortocircuito para CA. En la
figura 2.40a se muestra un amplificador emisor comun en el cual la resistencia de emisor tiene
conectada en paralelo el capacitor CE y en la figura 2.40b en circuito equivalente para frecuencias
medias
b)
Rb = R1llR2
r = hfeVT/ICQ
ro = (VA + VCEQ)/ICQ
gm = ICQ/VT
Se simplifica si ro>>RC
a)
Figura 2.40 a) etapa amplificadora EC, b) su circuito equivalente de pequeña señal a
frecuencias medias
Para el caso del BJT es aconsejable calcular todos los índices del amplificador siguiendo el
siguiente orden: AI, Ri, AV y Ro.
2.9.1.1 Cálculo de las ganancias de corriente:
AI = Io/Ib
Sustituyendo:
siendo
Io = -gmV ro/(ro + RC)
y
V = Ibr
AI = Io/Ib = -gm r ro/(ro + RC) = -hfe ro/(ro + RC) pues hfe = gm r .
Para el modelo -híbrido simplificado, si se cumple que ro >> RC la Ai será máxima:
AI = Io/Ib = -hfe (ganancia de corriente del E-C con cortocircuito a la salida, independiente de RC).
Otros índices de ganancia de corriente son:
AI´ = Io/Ib = (Io/Ib )(Ib/Ii) = AI [Rb/(Rb +rb + r )] = AI [Rb/(Rb + hie)]
Para calcular AIS = Io/Is se debe transformar el circuito a la entrada, en la figura 2.41 se muestra la
transformación de la fuente de voltaje en fuente de corriente.
AIS = Io/Is = (Io/Ii)(Ii/Is) = AI´[RS/(RS + Rbllhie)] < AI
Figura 2.41 Transformación de la fuente de voltaje VS
en fuente de corriente IS
29
Por otro lado, si no se tiene calculado AI:
AIS = Io/Is = (Io/Ib)(Ib/Is) = AI [RSllRb/(RSllRb + hie)]
El signo (-) en AI sale como consecuencia del sentido tomado como referencia para Io, que garantiza
que la salida del amplificador sea una subida de voltaje respecto a tierra. Debe quedar claro que en
la configuración E-C, la AV tiene que ser negativa pues invierte fase.
2.9.1.2 Resistencia de entrada.
Ri = Vi/Ib = Ib(rb + r ) / Ib = hie (propia de E-C, relativamente baja)
Ri´ = Vi/Ii = Rb ll hie
(resistencia de entrada que ve la fuente)
Notar que Ri es independiente de la resistencia de carga RL y es igual a hie definida en el modelo
híbrido como resistencia de entrada con cortocircuito a la salida.
2.9.1.3 Ganancia de voltaje.
AV = Vo/Vi = IoRC/IbRi = AI RC/Ri = -hfe [ro/(ro + RC)](RC/hie)
Aparece el signo menos pues existe inversión de fase entre la señal de entrada y la de salida. Su
valor es alto. Es conveniente calcular cada nuevo índice con los resultados previamente calculado.
AVS = Vo/Vs = (Vo/Vi)(ViVs) = AV (Ri´/(Ri´ + RS)
También como:
AVS = Vo/Vs = IoRC/IsRs = AIS RC/Rs
De no ser necesario el cálculo del índice de ganancia de corriente, AV se encuentra como:
AV = Vo/Vi = -gmV (rollRC) / Ibhie = -hfe (rollRC)/hie = AI (rollRC)/Ri pues V = Ibr
Note que si se cumple que: ro >> RC y r >> rb,
AV = -gmRL.
Por otro lado, se puede ver que AV no puede ser incrementada arbitrariamente con valores elevados
de RC, pues para RC >> ro y r >> rb, ocurre que:
AV = - gm ro = -ICQ/VT[(VA + VCEQ)/ICQ = - (VA + VCEQ)/VT
- VA/VT si es VA >> VCEQ
Este sería el valor límite máximo posible a obtener en una etapa. Esta idea se emplea en los
amplificadores integrados y se conoce como carga activa donde se usa una fuente de corriente con
valor elevado de resistencia de salida, como elemento de carga en lugar del resistor RC. Para un
caso típico con VA = 100V y VT = 25 mV, AV = - 4000.
2.9.1.4 Resistencia de salida (Ro).
Para este ejemplo, es la resistencia equivalente de Thevenin vista por RC hacia atrás y el método de
cálculo es el siguiente: se cortocircuita la fuente independiente vs, se desconecta la RC y se aplica
una fuente V de valor arbitrario entre los terminales de salida que entrega una corriente I. El valor
de Ro se calcula de la relación V/I. Para el circuito bajo análisis queda el mostrado en la figura
2.42.
30
Con vs = 0, Ib = 0 y gmV = 0
Ro = V/I = ro
Se define también a: RC´ = Ro ll RC = ro ll RC
Si ro = . Ro´ = RC
Figura 2.42 Circuito eqivalente de Thevenin para el
cálculo de la resistencia de salida
Hasta aquí el análisis de la configuración E-C sin resistor RE. En general, se recomienda realizar los
cálculos en el siguiente orden: AI (AIS), Ri (Ri´), AV (AVS) y Ro (Ro´). En cada caso evaluar los
índices empleando los previamente calculados.
2.9.2 Análisis lineal de la configuración colector común ó seguidor de emisor.
Se conoce como seguidor emisor pues debido a que su AV 1 y por no invertir la fase entre el
voltaje de entrada y el de salida, un cambio en Vi aparece como un cambio idéntico en la salida a
través del resistor de carga conectado entre el emisor y tierra. Entre sus principales características
esta que su Ri es muy alta y que su Ro es muy baja, comparadas con la del emisor común.
Su uso más común es como etapa de acoplamiento ya que realiza la función de transformación de
los niveles de resistencia sobre un rango de frecuencia amplio con AV 1. Además incrementa los
niveles de potencia de la señal pues incorpora ganancia de potencia al tener una A I >> 1. En la
figura 2.43 se muestra su diagrama circuital y su circuito equivalente de pequeña señal a frecuencias
medias con el modelo híbrido simplificado pues por ser RE de valor pequeño (típico de esta
configuración), se considerará que: ( hoe RE < 0.1).
b)
a)
c)
Figura 2.43 a) Etapa amplificadora CC, b) su circuito equivalente de pequeña señal a
frecuencias medias, c) Transformación de la fuente de voltaje en fuente de
corriente IS
31
De acuerdo con el método propuesto para el cálculo de los índices en etapas amplificadoras con
BJT:
AI = Io/Ib = (1 + hfe)Ib / Ib = 1 + hfe (alta)
AIS = Io/Is = (Io/Ib)(Ib/Is) = (1 + hfe)[RSllRb/(RSllRb + Ri)] donde Rb = R1 ll R2
Ri = Vi/Ib = [Ib(hie) + (1 + hfe)IbRE ]/ Ib = hie + (1 + hfe)RE
Ri´ = Vi/Ii = Rb ll Ri
(muy alta)
(resistencia de entrada que ve la fuente)
AV = Vo/Vi = (1 + hfe)RE / Ri = AI RE/Ri
AV = (Ri - hie)/Ri = 1 - hie/Ri < 1
pero si se sustituye: AI = (Ri - hie)/RE
(destacar que si Ri >> hie la AV = 1)
AVS = Vo/Vs = IoRE/IsRS = AIS RE/RS
Para obtener la expresión de Ro y de Ro´ se aplica el método general de Thevenin, lo coal se muestra
en la figura 2.44
Ro = V/I = - Ib(RS ll Rb + hie)/[- (1+ hfe)Ib ]= (RS ll Rb+hie)/(1+ hfe)
Ro´ = Ro ll RE
(muy baja)
Figura 2.44 Circuito eqivalente de Thevenin para el cálculo de la resistencia de salida
2.9.3 Análisis lineal de la configuración emisor común con RE.
En la figura 2.45 se muestra una etapa amplificadora emisor común con RE. Para el análisis se
empleará el modelo híbrido simplificado si se cumple la condición de validez, que para este caso se
demuestra que es: hoe (RE + RC ll RL) < 0.1.
Rb = R1 ll R2
RL´ = RC ll RL
RS´ = RS ll Rb
AI = IL/Ib = (IL/Io) (Io/Ib ) = -hfe [RC / (RC + RL)]
a)
b)
Figura 2.45 a) Etapa amplificadora EC con RE, b) su circuito equivalente de
pequeña señal a frecuencias medias
32
AIS = IL/IS = (IL/Ib) (Ib/IS) = AI [RS´/ (RS´ + Ri)]
Ri = Vi/Ib = hie + (1 + hfe)RE
(expresión solo válida para el modelo simplificado)
Ri = hie + (1 + hfe)RE / [1 + hoe(RE + RL´)] (válida para el modelo completo)
Ri´ = Vi/Ii = Rb ll Ri
AV = Vo/Vi = ILRL /Ib Ri = AI RL/Ri
AVS = Vo/Vs = ILRL /IsRS = AIS RL /RS
(menor que la del E-C sin RE pues Ri >> RL)
También se puede obtener como:
AVS = Vo/VS = (Vo/Vi) (Vi/VS) = AV [Ri´/(Ri´+ RS)]
El resistor RE introduce realimentación negativa que incrementa la estabilidad del punto de
operación en reposo y de la ganancia de voltaje de pequeña señal a costa de reducir su valor.
Para encontrar a Ro en este ejemplo con hoe = 0, si se cortocircuita a vs la Ib = 0 por lo que la fuente
de corriente dependiente se abre (hfeIb = 0). De donde: Ro =
y Ro´ = Ro ll RC 0 RC.
2.9.4 El amplificador en configuración base común.
Su esquema circuital y el circuito equivalente de pequeña señal se muestran a continuación.
a)
b)
Figura 2.46 a) Etapa amplificadora BC, b) su circuito equivalente de
pequeña señal a frecuencias medias
El análisis de los diferentes índices de este amplificador, se realiza en forma similar a los ejemplos
antes analizados. En amplificadores de pequeña señal de audio no es muy utilizado, pues como se
verá posteriormente presenta problemas de carga. Como características generales presenta una
ganancia de corriente menor que la unidad, su AV es mucho mayor que uno, con muy baja
resistencia de entrada y muy alta resistencia de salida.
2.9.5 Comparación entre las diferentes configuraciones de amplificadores.
La configuración E-C proporciona una AV alta y una AI también alta, por lo que presenta la mayor
ganancia de potencia y da los mejores resultados para un amplificador de propósito general
por lo que es el más utilizado. La configuración C-C proporciona una AI elevada pero su AV es
menor de la unidad. Se utiliza como medio para acoplar un resistor de valor bajo con una fuente de
33
señal de resistencia interna alta, por tener una Ri muy alta y una Ro muy baja. La configuración B-C
proporciona una AV alta pero su AI es menor que la unidad. Es la menos utilizada en los
amplificadores pues su Ri extremadamente baja tiende a cargar a la etapa precedente, reduciendole
bruscamente su ganancia de voltaje. Puede servir en cambio para acoplar una carga de valor elevado
con fuentes de resistencia interna baja. Analizar la tabla 10.4 del texto.
2.10 Regulador de voltaje serie con diodo Zener de referencia.
Una fuente de voltaje regulada ideal es un circuito electrónico diseñado para entregar un
predeterminado voltaje de CD (VO) que es independiente de la corriente de carga (IL), de la
temperatura y también de cualquier variación del voltaje de línea. El regulador de voltaje paralelo
ya estudiado es el circuito de este tipo más sencillo; presenta como deficiencia la de ser baja la
corriente y la potencia que puede entregar en su salida, limitado por la capacidad del zener
empleado.
El regulador de voltaje serie mostrado en la figura 2.47 mejora esta deficiencia, pues el transistor
conectado en serie con la carga es el encargado de entregar la corriente de salida.
ICQ = (VZ - VBE)/RL
IBQ = ICQ/ F para ICEO = 0
VO = VZ - VBE
VCEQ = VNR - ICQRL
IRA = (VNR - VZ)/RA para rZ = 0
IZ = IRA - IBQ
Figura 2.47 Regulador de voltaje serie
Si se abre la carga se hace IL = 0, pero la corriente por el zener no crece bruscamente como ocurre
con el regulador paralelo. Esto se debe a que el transistor opera en la región activa, por lo que su
IB = IL/ F. Como F >> 1, aún para caso peor en que se esté entregando la máxima corriente a la
carga, la IB será relativamente baja. Desde el punto de vista del diseño, esto provoca que la
disipación de potencia máxima en el zener sea baja y no sea una limitante como lo es para el caso
del regulador paralelo.
El principio de operación de este regulador serie se basa en la utilización de un zener como
referencia interna con un voltaje VZ que es independiente de las variaciones de VNR y de IL. Si se
analizan estas dos variaciones en forma independiente, veamos el caso en que RL sea constante y se
varía VNR. Se observa de las expresiones anteriores, que ICQ e IBQ se mantienen casi constantes,
pero al crecer VNR aumentan IRA e IZ. La línea de carga se desplaza hacia la derecha con la misma
pendiente, por lo que VCEQ crece y contrarresta la posible variación de VNR manteniendo a VO casi
constante.
En la figura 2.48 se muestra el circuito equivalente del regulador serie.
34
Figura 2.48 Circuito equivalente del regulador serie
Analicemos el caso en que VNR se mantenga constante y se varíe a RL; si RL decrece , ICQ e IBQ
aumentan pero IZ disminuye. En la característica de salida del transistor, la línea de carga
incrementa su pendiente pero mantiene el intercepto en VNR que no cambia. El valor de VCEQ se
mantiene casi constante pues VO apenas varía.
Para el diseño se empleará la siguiente expresión que garantiza que por la carga circule la I L
máxima requerida y que la disipación de potencia en el zener sea la mínima posible sin que deje de
regular:
RAmax = (VNRmin - VZ) / (IZK + IBmax / F)
para rZ = 0
Al seleccionar el tipo de transistor a emplear, se tiene que tener en cuenta que su ICM especificada
por el fabricante debe de ser mayor que IL máxima y que su VCEO sea mayor que el VNR máximo.
En la figura 2.49 se muestra la habilidad de regulación de este circuito; se destaca que el % de
regulación de voltaje es muy bueno para todas las corrientes de carga hasta 350 mA y de 2 % para
IL = 400 mA.
Figura 2.49 Curva de regulación del voltaje de salida
La impedancia de salida de este regulador es muy baja pues utiliza al transistor en configuración
seguidor emisor y depende de la frecuencia y de la corriente de carga. De un análisis con el modelo
de pequeña señal a frecuencias medias, la Ro se puede obtener partiendo del circuito de la figura
2.50:
35
Ro = (rZ ll RA + hie) / ( 1 + hfe)
Ro = hie) / ( 1 + hfe)
pues rZ
0
Figura 2.50 Circuito equivalente de Thevenin para el
cálculo de la resistencia de salida
36
EJERCICIOS
MONOGRAFIA
EL TRANSISTOR BIPOLAR
POLARIZACIÓN DEL TRANSISTOR BIPOLAR
Ejercicio No. 1
En el circuito mostrado en la figura 1. Calcule: a) El punto de operación del transistor. Represente
la línea de carga estática en la característica de salida. b) El valor máximo de RC con el cual
permanece en activa. c) Analice, que ocurre si aumenta la temperatura o si se cambia el transistor
por otro de mayor?
DATOS: hFE = =150; VBE = 0.7V; VBE sat = 0.8V; VCE sat = 0.2V; ICO = 0.
Respuesta: a) ICQ = 1.5 mA y VCEQ = 2.25V; b) RC max = 6.36K.
Ejercicio No. 2
En el circuito mostrado en la figura 2, calcule R1 para que IE = 2 mA.
DATOS: hFE = = 50; VBE = 0.7V; VBE sat = 0.8V; VCE sat = 0.2V; ICO = 0.
Respuesta: R1 = 63.4K
Ejercicio No. 3.
En el regulador de voltaje serie de la figura 3, calcule: a) El punto de operación del transistor;
b) Las potencias disipadas en el Zener y en el colector del transistor; c) La potencia entregada por la
batería. Datos: Q: hFE = 100; VBE = 0.7V; VBE sat = 0.8V; VCE sat = 0.2V; ICO = 0.
DZ: VZ = 5.7V; IZK = 2 mA; rZ = 0.
Respuesta: a) ICQ = 100 mA, VCEQ = 5V; b) PZ = 43.3 mW, PC = 0.5 W; c) PVCC = 1086 mW
Ejercicio No. 4.
En el circuito de la figura 4, calcule el punto de operación y la potencia disipada en colector en
reposo. Datos: hFE = 100; VBE = 0.7V; VCEsat = 0.1V; ICO = 0.
Respuesta: ICQ = 2.75 mA, VCEQ = 3.5V, PC = 9.6 mW
Ejercicio No. 5.
En el circuito de la figura 5, calcule el punto de operación y la potencia disipada en colector en
reposo. Datos: hFE = 200; VEB = 0.6V; VEC sat = 0.1V; ICO = 0.
Respuesta: ICQ = 2.87 mA, VCE Q = 6.39V, PC = 18.34 mW
Ejercicio No. 6.
En los circuitos de la figura 6a y 6b, calcule el punto de operación y la potencia disipada en colector
en reposo. Datos: hFE = 260; VBE = 0.6V; VCE sat = 0.1V; ICO = 0.
Respuesta: a) ICQ = 1 mA, VCE Q = 4.9V, IBQ = 4 µA, PC = 4.9 mW
b) ICQ = 1 mA, VCE Q = 10V, IBQ = 4 µA, PC = 10 mW
37
A. Lastres, A. Torres, A. Nagy
Figura 5
Figura 6a
figura 6b
38
BIBLIOGRAFIA
MONOGRAFIA
EL TRANSISTOR BIPOLAR
Microelectronics. Millman and Halkias
A. Lastres, A. Torres, A. Nagy 39
DATASHEET
MONOGRAFIA
EL TRANSISTOR BIPOLAR
A. Lastres, A. Torres, A. Nagy 40