e - IES Antonio Serna Serna

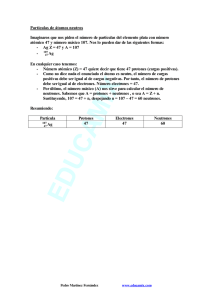
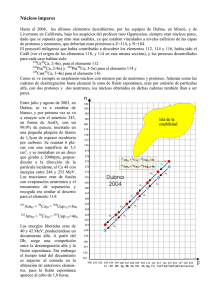
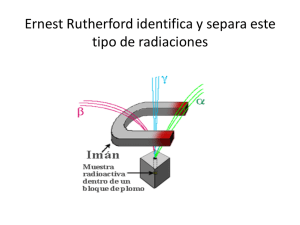
BLOQUE 5.2
FÍSICA NUCLEAR
1-EL
NÚCLEO ATÓMICO
El núcleo de los átomos se acepta universalmente que está formado por PROTONES y NEUTRONES (llamados
genéricamente NUCLEONES), en una cantidad que varía de unos núcleos a otros. La carga nuclear viene
determinada por el número de protones existentes, el cual tiene que ser igual al número de electrones
orbitales, para que el átomo sea eléctricamente neutro.
El NÚMERO ATÓMICO ( Z ), se define como el número de protones del núcleo. Indica la identidad química del
átomo y fija el lugar que le corresponde en la tabla periódica, así como su símbolo químico.
El NÚMERO MÁSICO (A), como la suma de los protones (Z) y neutrones (N) del núcleo.
Z
Los núcleos se representan como A
X
donde X es el símbolo del elemento y pueden ser:
• ISÓTOPOS :si tienen igual Z y distinto N ,
(
12
6
)
C , 146C , es decir, se diferencian en el número de
neutrones. Sin embargo, puesto que las propiedades químicas de los átomos vienen determinadas por
sus configuraciones electrónicas, y estas son iguales para todos ellos, podemos afirmar que todos
los isótopos de un mismo elemento presentan idénticas propiedades físicas
A principios del siglo XX, con el descubrimiento del protón y el neutrón, el problema del núcleo atómico
parecía resuelto. Sin embargo, aun quedaban por resolver algunas incógnitas:¿cómo se explica que puedan
coexistir protones en el núcleo, venciendo las intensas fuerzas de repulsión electrostática?
VOLUMEN
Y MASA DEL NÚCLEO
Mediante experiencias de dispersión de partículas α y difracción de electrones se ha comprobado que la
mayoría de los núcleos son aproximadamente esféricos. Su radio depende del número másico A:
1
R = 1,2 ⋅ 10 −15 ⋅ A 3 . Por tanto, el volumen del núcleo ( V = 4 ⋅ π ⋅ R 3 ) es proporcional al número másico,
3
es decir, al número de nucleones que contiene. Su volumen es minúsculo y representa tan sólo una fracción
muy pequeña del volumen total del átomo, pero en él se encuentra casi toda la masa, por lo que su densidad
es muy elevada. Se ha comprobado que los núcleos de todos los átomos tienen una
densidad de,
2,4x1014g/cm3; es decir, que 1 cm3 de materia nuclear tendría una masa de 240 millones de toneladas.
Como la masa del átomo es tan pequeña, las unidades ordinarias de masa son demasiado grandes, por ello,
para medirla se emplea la llamada unidad de masa atómica, que se representa con la letra u, y se define
como la doceava parte de la masa del átomo de carbono-12.
Con todo lo que acabamos de ver, está claro que no es posible explicar la estabilidad del núcleo
recurriendo a las fuerzas que hemos estudiado hasta el momento (gravitatorias y eléctricas)
2.- ESTABILIDAD
DE LOS NÚCLEOS.
ENERGÍA
DE ENLACE
Los nucleones se agrupan de modo que la distancia entre ellos es del orden de 10-15m. A esta distancia tan
pequeña, la fuerza eléctrica de repulsión entre los protones viene dada por la ley de Coulomb y es muy
grande. La fuerza gravitatoria atractiva entre los mismos protones es
despreciable frente a la fuerza eléctrica, pues es unas 1036veces más
pequeña. En consecuencia, para que los núcleos sean estables debe existir una
tercera fuerza, muy intensa, de corto alcance y atractiva que supere a las
fuerzas eléctricas de repulsión y mantenga unido al núcleo. Se denomina
INTERACCIÓN NUCLEAR FUERTE. Es una fuerza que sólo se manifiesta en el
interior del núcleo y su valor parece ser el mismo, entre dos protones, dos
neutrones, y un protón y un neutrón.
DEFECTO
DE MASA Y ENERGÍA DE ENLACE
Al determinar con precisión las masas de los núcleos de los átomos con un aparato denominado
espectrógrafo de masas, se obtuvo un resultado sorprendente. El valor obtenido era siempre inferior a la
suma de las masas de los nucleones que lo forman. Es decir, la masa real del núcleo es inferior a la suma
de las masa de sus protones y sus neutrones. A esta diferencia se la denomina DEFECTO DE MASA
(∆m ) y
se calcula mediante la expresión de la derecha:
Siendo mp la masa del protón; mn la masa del
neutrón y M la masa real del núcleo
obtenida experimentalmente.
En su TEORÍA DE LA RELATIVIDAD, EINSTEIN ya había establecido una equivalencia entre masa y energía
(E = m ⋅ c ) . Por lo tanto, de acuerdo con la fórmula anterior, la energía equivalente a este defecto de
2
masa es:
NÚCLEO
(E
Enlace
= ∆m ⋅ c 2
)
. Esta energía se denomina ENERGÍA DE ENLACE O ENERGÍA DE LIGADURA DEL
y es la energía que se libera al formarse el núcleo a partir de los nucleones que lo
constituyen. Coincide con la energía que hay que proporcionarle para separar los nucleones que lo forman.
Las energías de enlace de los núcleos son enormemente grandes.
Un dato importante acerca de la estabilidad del núcleo es la ENERGÍA DE ENLACE POR NUCLEÓN, que se
obtienen de la siguiente forma:
⇒ E Enlace por =
nucleón
2
E Enlace
nº de nucleones
Cuanto
mayor
estable
será
sea
el
ésta,más
núcleo.
Los
mayores valores se presentan para
números
másicos
comprendidos
entre 40 y 100 aproximadamente.
El núcleo más estable es el del
hierro-56, al que corresponde una
energía de enlace por nucleón de
8,8 Mev/nucleón
Si un núcleo pesado de divide en otros dos más ligeros
(FISIÓN NUCLEAR), o si dos núcleos ligeros se unen para
formar otros dos más pesados (FUSIÓN NUCLEAR) se
obtienen núcleos más estables, con mayor energía de
enlace por nucleón, y por lo tanto se libera energía.
Esta es la clave de la producción de energía en el
universo. En la figura puede observarse que, en
proporción, se libera mucha más energía al fusionarse
dos núcleos que al fisionarse uno, puesto que la fusión
tiene una pendiente mucho mayor.
3.-NÚCLEOS
INESTABLES: LA RADIACTIVIDAD NATURAL
Aunque la interacción fuerte es la responsable de la formación y estabilidad
de los núcleos, es también necesaria la existencia de neutrones en su
composición, ya que si el núcleo sólo estuviese compuesto de protones, la
creciente repulsión electrostática acabaría por desintegrarlo. El papel de
los neutrones es el de aportar interacción fuerte sin proporcionar
repulsión electrostática. En los núcleos pequeños, el número de protones y
neutrones en el núcleo coincide, sin embargo, a medida que aumenta el
número de protones, la creciente repulsión exige un número cada vez mayor
de neutrones presentes ( el nº de neutrones en el núcleo será mayor que el
de protones) tal y como se observa en la gráfica.
3
Pero el aumento de neutrones en el núcleo conlleva un problema añadido ya que los neutrones son partículas
inestables y cuando su número aumenta pierden su estabilidad y comienzan a desintegrarse.
Los núcleos son inestables a partir del elemento de número atómico 83 (Bismuto), cuyo nº de
neutrones es ya suficientemente elevado y para estabilizarse se transforman espontáneamente en
otros emitiendo radiaciones. Decimos que son elementos radiactivos. La Radiactividad fue descubierta de
forma casual por Bequerel en 1896 en el Uranio. Dos años más tarde, los esposos Curie descubrieron el
polonio y el radio, dos elementos también radiactivos.
3.1 TIPOS
DE RADIACTIVIDAD
La emisión radiactiva se divide en tres radiaciones de características distintas: Radiación
β,
γ
y Radiación
α
. Radiación
. Su poder de penetración en los
materiales es muy diferente. Así, la
una cartulina , la radiación
β
α
es frenada por
atraviesa el papel pero es
retenida por una lámina de Aluminio y por último, la
γ
es
capaz de atravesar varios cm de plomo u otros materiales
pesados.
RADIACIÓN
α
: Las partículas
α
son NÚCLEOS DE HELIO
(
4
2
)
He , están formadas por dos protones
y dos neutrones y su carga será +2. Suelen emitirlas los núcleos demasiado grandes para ser estables,
como los de Uranio, Torio, Radio y Plutonio.
RADIACIÓN β
−
y β + : La emisión β − sucede en aquellos núcleos que poseen exceso de neutrones.
En ellos los neutrones se desintegran
(
1
0
n → 11p +
La emisión
0
−1
transformándose en protones y emitiendo electrones.
e + ν e ) donde ν e es una partícula sin carga y sin masa llamada antineutrino.
β+
sucede en los núcleos con deficiencia de neutrones. La ganancia del número de
neutrones se consigue mediante la transformación
positrón y un neutrino. Globalmente se escribe:
RADIACIÓN
γ
A
Z
( p→
1
1
X→
A
Z −1
n+
1
0
e + ν e ) en la cual se emite un
0
+1
Y + β + +ν
: Es de naturaleza electromagnética de elevada energía. Se emiten cuando un núcleo
que se encuentra excitado vuelve a su estado fundamental. La emisión acompaña normalmente a las
α
4
y
β.
A
Z
X ∗ → ZAX + γ
3.2 LEYES
DE
SODDY
DE LA DESINTEGRACIÓN RADIACTIVA
1ª LEY: Cuando un núcleo radiactivo emite una partícula alfa se emiten dos protones y dos neutrones de
modo que el núcleo resultante tiene dos protones menos y su masa ha disminuído en 4 unidades.
A
Z
X →
A− 4
Z −2
Y + 42 α
2ª LEY: Cuando un núcleo radiactivo emite una radiación beta negativa un neutrón se transforma en un
protón y el núcleo resultante tendrá un protón más y la misma masa.
A
Z
X→
A
Z +1
Y+
0
−1
e
En la desintegración beta positiva ocurre lo contrario, un protón se convierte en un neutrón y el núcleo
A
resultante tendrá un protón menos y la misma masa. Z
X→
A
Z −1
Y+
0
+1
e
3ª LEY: Cuando un núcleo radiactivo emite radiación gamma no altera ni su masa ni su carga.
3.3 SERIES
O FAMILIAS RADIACTIVAS
Cuando un núcleo se va desintegrando, emite radiación y da lugar a otro núcleo distinto también radiactivo,
que emite nuevas radiaciones. El proceso continuará hasta que aparezca un núcleo estable, no radiactivo.
Todos los núcleos que proceden del inicial(núcleo padre) forman una serie o cadena radiactiva. Se conocen
cuatro series , tres de las cuales existen en la naturaleza y son la del Th-232, U-238 y Ac-227.
4.- MAGNITUDES
CARACTERÍSTICAS DE LA DESINTEGRACIÓN RADIACTIVA
Los fenómenos radiactivos son espontáneos y no se sabe en qué momento se va a desintegrar un núcleo. Sin
embargo sí es posible su estudio estadístico. Si una muestra contiene N núcleos sin desintegrar en un
instante inicial, según avance el tiempo el número de núcleos presentes irá disminuyendo puesto que se irán
desintegrando y por tanto desapareciendo. Como resultado del estudio estadístico se obtiene la siguiente
expresión que nos permite calcular el nº de núcleos radiactivos que quedan sin desintegrar en cada
instante y es la ECUACIÓN FUNDAMENTAL DE LA RADIACTIVIDAD:
Donde : NO
⇒ Número
λ ⇒ Constante
es s-1 y t
de núcleos de la muestra inicial, N
= 0 ⋅ e − λ ⋅t
⇒ Número
de núcleos que quedan sin desintegrar,
de desintegración radiactiva (su valor es carácterístico de cada núcleo) y sus unidades en el SI
⇒ Tiempo
transcurrido
Se llama ACTIVIDAD o VELOCIDAD DE DESINTEGRACIÓN (A) de una sustancia al nºde desintegraciones que se
producen por unidad de tiempo: .
A=λ⋅
. Su unidad en el SI es el becquerel (Bq).
5
Se define el PERÍODO DE SEMIDESINTEGRACIÓN ( T o t1/2 ) como el tiempo que ha de transcurrir para que
el número de núcleos presentes en una muestra se reduzca a la mitad. Si t=t1/2 entonces
sustituyendo en la ecuación fundamental de la radiactividad:
La VIDA MEDIA
O
= O ⋅ e −λ ⋅t1 / 2 ⇒
2
(τ ) de un núcleo, es el tiempo que, por término medio,
Su valor coincide con la inversa de la constante de desintegración:
5.- REACCIONES
NUCLEARES.
FISIÓN
Y
FUSIÓN
τ=
t1 =
2
=
O
2
y
ln 2
λ
tardará un núcleo en desintegrarse.
1
λ
(s )
NUCLEAR
Las reacciones nucleares son reacciones en las que intervienen núcleos atómicos. Generalmente, se
producen al bombardear un núcleo con otros de menor tamaño a gran velocidad o con partículas
subatómicas. El uso de partículas
α
y protones como proyectiles para bombardear los núcleos presenta la
desventaja de su repulsión electrostática. Los neutrones, en cambio, pueden entrar fácilmente en el núcleo
al no tener carga eléctrica. En estas reacciones se conserva el número atómico y el número másico. A
continuación se indican algunos ejemplos
FISIÓN NUCLEAR
Consiste en la división de un núcleo pesado en otros dos más ligeros que son más estables, ya que tienen
mayores energías de enlace por nucleón. La
reacción se inicia bombardeando el núcleo con un
neutrón. La energía liberada se debe a la
diferencia de masas entre los productos iniciales
y finales. Además se liberan varios neutrones que
hacen posible la fisión de nuevos núcleos iniciando
así una reacción en cadena
FUSIÓN NUCLEAR
Consiste en la unión de núcleos ligeros para formar núcleos más pesados, con
mayor energía de enlace por nucleón (más estables). Se más enrgía
que la
liberada en los procesos de fisión. Son muy difíciles de conseguir con la
tecnología actual, ya que para unirlos hay que vencer las fuerzas repulsivas que
existen entre los protones.
Son reacciones de fusión:
6
EJERCICIOS
124
1. El
Cs
tiene una vida media de 30,8 s. Si se parte de 6,2 µg, se pide:
a. ¿Cuántos núcleos hay en ese instante?
b. ¿Cuántos núcleos habrá 2 minutos después? ¿Cuál será la actividad en ese momento?
Dato: NA= 6,023x1023 mol-1
(Septiembre 2000)
55
2. En una excavación arqueológica se ha encontrado una estatua de madera cuyo contenido de 14 C es el de
58% del que poseen las maderas actuales de la zona. Sabiendo que el periodo de semidesintegración del
14
C es de 5570 años, determinar la antigüedad de la estatua encontrada. (Junio 2001)
3. Cuando un núcleo de
235
92
U captura un neutrón se produce un isótopo del Ba con número másico 141, y otro
del Kr, cuyo número másico es 36 y tres neutrones. Calcular Z del Ba y A del isótopo del Kr.
2002)
(Junio
4. La erradicación parcial de la glándula tiroides en pacientes que sufren hipertiroidismo se consigue
131
gracias a un compuesto que contiene el nucleido radiactivo del yodo I . Este compuesto se inyecta en
el cuerpo del paciente y se concentra en la glándula tiroides destruyendo sus células. Determina
cuántos gramos del nucleido deben ser inyectados en un paciente para conseguir una actividad
131
de3,7x109 Bq (desintegraciones/s). El tiempo de vida medio del I es 8,04 días. Dato: u=1,66x1027 Kg (Septiembre 2002)
5. Las masas atómicas del
14
7
y del
15
7
son 13,99922 u y 15,000109 u, respectivamente. Determina la
energía de enlace de ambos, en eV. ¿Cuál es el más estable? Datos: Masas atómicas: neutrón:
1,008665 u; protón: 1,007276 u; c=3x108 m/s; u=1,66x10-27kg; e=1,6x10-19C
(Septiembre
2002)
6. El 146 C es un isótopo radiactivo utilizado para determinar la antigüedad de objetos. Calcula la energía de
ligadura media por nucleón, en MeV, de un núcleo de
1
1
H :1.0073u;
14
6
C : 14,0032u;
14
6
carga protón=1,6x10
C.
Datos: Masas at:
-19
8
1
0
n :1,0087u;
C, c=3x10 m/s; mproton=1,66x10-27kg
(Junio 2003)
7. Un dispositivo usado en medicina para combatir, mediante radioterapia, ciertos tipos de tumor contiene
60
una muestra de 0,50 g de 27 Co . Su periodo de semidesintegración es 5,27 años. Determina la
actividad, en desintegraciones por segundo, de la muestra de material radiactivo. Dato: u=1,66x10-27
(Junio 2003)
131
131
8. El I tiene un periodo de semidesintegración T=8,04 días. ¿Cuántos átomos de I quedarán en una
muestra que inicialmente tiene N0 átomos al cabo de 16,08 días? Considera los casos N0=1012átomos y
N0=2 átomos. Comenta los resultados (Septiembre 2003)
9. Si un núcleo de Li, de número atómico 3 y número másico 6, reacciona con un núcleo de un elemento X se
producen dos partículas α . Escribe la reacción y determina Z y A del elemento X (Junio 2004)
10. Se preparan 250 g de una sustancia radiactiva y al cabo de 24 horas se ha desintegrado el 15%. Se
pide:
a. La constante de desintegración de la sustancia
b. El periodo de semidesintegración de la sustancia, así como su vida media y periodo
c. La masa que quedará sin desintegrar al cabo de 10 dias. (Septiembre 2004)
7
11. Completa las siguientes reacciones nucleares, determinando el número atómico y el número másico de X:
a.
14
6
C α X + e+ ν
b. 12 H + 13H α X + 01n
(Septiembre 2004)
12. El periodo de semidesintegración de una muestra de polonio es 3minutos. Calcula el porcentaje de una
cierta masa inicial de la muestra que quedará al cabo de 9 minutos. (Septiembre 2004)
17
13. Cuando el nitrógeno absorbe una partícula α se produce el isótopo 8 O y un protón. A partir de estos
datos determinar los números atómicos y másicos del nitrógeno y escribir la reacción ajustada (Junio
2005)
14. Calcula el periodo de semidesintegración de un núcleo radiactivo cuya actividad disminuye a la cuarta
parte al cabo de 48 horas. (Septiembre 2005)
15. Calcula la actividad de una muestra radiactiva de masa 5g que tiene una constante radiactiva
λ = 3x10 −9 s −1
y cuya masa atómica es 200 u. ¿Cuántos años deberíamos esperar para que la masa
radiactiva de la muestra se reduzca a la décima parte?
(Junio 2006)
Dato: NA= 6,023x1023
-1
mol
16. La fisión de un núcleo de
235
92
U se desencadena al absorber un neutrón produciéndose un isótopo de Xe
con número atómico 54, un isótopo de Sr con número másico 94 y 2c neutrones. Escribe la reacción
ajustada
(Junio 2006)
17. Un núcleo de
115
49
In absorbe un neutrón y se transforma en el isótopo
116
50
Sn conjuntamente con una
partícula adicional. Indica de qué partícula se trata y escribe la reacción ajustada (Septiembre 2006)
18. Si se fusionan dos átomos de hidrógeno, ¿se libera energía en la reacción? ¿y si se fisiona un átomo de
uranio? Razona tu respuesta (Junio 2001)
19. ¿Es la masa de una partícula
qué? (Septiembre 2001)
α
igual a la suma de las masas de dos protones y dos neutrones? ¿Por
20.Concepto de isótopo y sus aplicaciones (Septiembre 2002)
21. Define los conceptos de constante radiactiva, vida media o periodo de semidesintegración (Junio 2005)
22. Explica por qué la masa de un núcleo atómico es menor que la suma de las masas de las partículas que
lo constituyen (Junio 2006)
23. Explica el fenómeno de fisión nuclear del uranio e indica de dónde se obtiene la energía liberada
(Septiembre 2006)
24. En una excavación se ha encontrado una herramienta de madera de roble. Sometida a la prueba del
14
C se observa que se desintegran 100 átomos cada hora, mientras que una muestra de madera de
roble actual presenta una tasa de desintegración de 600 átomos/hora.Sabiendo que el periodo de
semidesintegración del
14
C es de 5570 años, calcula la antigüedad de la herramienta (Junio 2007)
25. ¿Qué es una serie o familia radiactiva? Cita un ejemplo. (Junio 2007)
8
26. Hallar el número atómico y el número másico del elemento producido a partir del
emitir 4 partículas
α
y dos
β
−
218
84
Po después de
. (Septiembre 2007)
9