Regiones circulares

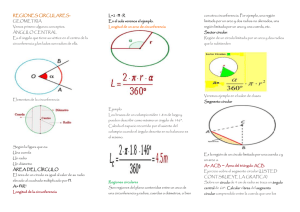
REGIONES CIRCULARES
Son regiones del plano contenidas entre un
arco de una circunferencia y radios, cuerdas
o diámetros, o bien con otra circunferencia.
Por ejemplo, una región limitada por un arco
y dos radios no alienados, una región
limitada por un arco y una cuerda, etc.
Área. Consideremos un círculo de radio r,
seleccionemos de él un sector circular de
radio r con ángulo central variable.
Si = 0 , el sector se reduce a un segmento,
el radio de la circunferencia, el sector de área
A = 0; si = radianes, el sector es medio
círculo y su área es
, si
= 2 radianes, el sector se transforma en un
círculo y su área es
.
Perímetro. Está constituida por la cuerda y
del arco que lo limitan, así P = c + s,
Donde se mide en radianes.
Área. Si la flecha es menor que el radio se
puede calcular por la resta de áreas: Área del
sector circular conformado por el arco del
segmento menos el área del triángulo
conformado por dos radios y la cuerda del
segmento,
Segmento Circular
Sector Circular
Consideremos una circunferencia de radio r
> 0, rotemos en el plano el segmento OA = r
alrededor del punto O, cierto ángulo , con 0
< < 2 o 0º < <360º. La región barrida
por de dicho segmento se llama sector
circular, región de un círculo limitada por un
arco y dos radios que lo subtienden.
Perímetro. Está constituida por los dos
radios y el arco que lo limitan, por lo que su
perímetro depende del radio r del círculo y
ángulo central
(en radianes) entre los
radios.
Es la región de un círculo limitada por una
cuerda c y un arco s. El segmento
perpendicular h a la cuerda que une el punto
medio de la cuerda con el punto medio del
arco se llama flecha del segmento circular,
ella puede ser menor o mayor que el radio
del círculo. Al segmento circular se le asocia
también un ángulo central que subtiende a la
cuerda.
Anillo O Corona Circular
Imagine hacer crecer concéntricamente una
circunferencia a partir de cierto valor de su
radio r hasta que el mismo tome el valor R >
r. La región barrida por la circunferencia al
crecer, de la manera indicada, se llama anillo
o corona circular. Región limitada entre dos
circunferencias concéntricas (que comparten
el mismo centro),
Perímetro. Está constituida por la
circunferencia interior y la circunferencia
exterior,
Área. Se puede calcular restando las áreas de
dos sectores circulares,
(Con
Área. Se calcula restando, el área del círculo
exterior menos el área del círculo interior,
en radianes)
Faja Circular
Es la región de un círculo entre dos cuerdas
paralelas,
Trapecio Circular
Es la región que tiene en común un anillo
circular y un sector circular de la
circunferencia de radio mayor,
Perímetro. Está constituida por dos cuerdas
y dos arcos.
Área. Se puede calcular restando las áreas de
dos segmentos circulares.
Perímetro. Está constituido por dos
segmentos de igual longitud y dos arcos,
(Con
en radianes)
Regiones
Circulares