blog de 3 corte - Tecnológico Comfenalco

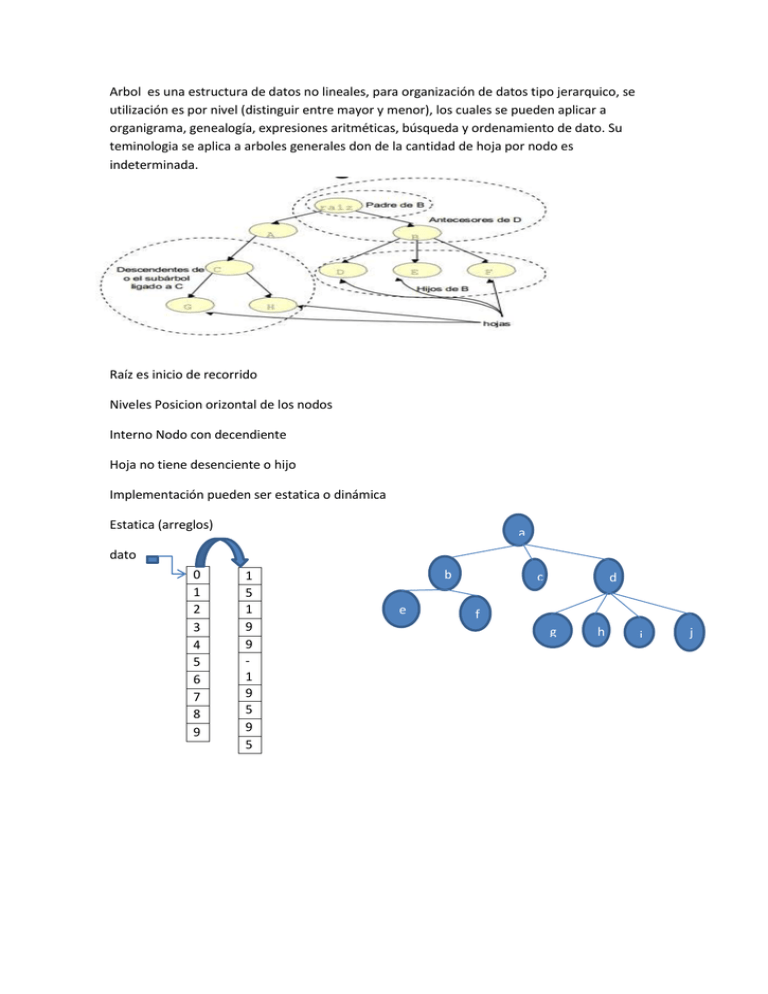
Arbol es una estructura de datos no lineales, para organización de datos tipo jerarquico, se
utilización es por nivel (distinguir entre mayor y menor), los cuales se pueden aplicar a
organigrama, genealogía, expresiones aritméticas, búsqueda y ordenamiento de dato. Su
teminologia se aplica a arboles generales don de la cantidad de hoja por nodo es
indeterminada.
Raíz es inicio de recorrido
Niveles Posicion orizontal de los nodos
Interno Nodo con decendiente
Hoja no tiene desenciente o hijo
Implementación pueden ser estatica o dinámica
Estatica (arreglos)
a
dato
0
1
2
3
4
5
6
7
8
9
1
5
1
9
9
1
9
5
9
5
b
e
c
d
f
g
h
i
j
Dinámica (nodo)
En ciencias de la computación, un árbol binario es una estructura de datos en la cual cada
nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de
ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena
ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado
un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda,
los montículos binarios y Codificación de Huffman.
Definición de teoría de grafos
Representación grafica
Un árbol binario sencillo de tamaño 9, 4 niveles y altura 3 (altura = máximo nivel - 1), con un
nodo raíz cuyo valor es 2.
En teoría de grafos, se usa la siguiente definición: «Un árbol binario es un grafo conexo,
acíclico y no dirigido tal que el grado de cada vértice no es mayor a 3». De esta forma sólo
existe un camino entre un par de nodos.
Un árbol binario con enraizado es como un grafo que tiene uno de sus vértices, llamado raíz,
de grado no mayor a 2. Con la raíz escogida, cada vértice tendrá un único padre, y nunca más
de dos hijos. Si rehusamos el requerimiento de la conectividad, permitiendo múltiples
componentes conectados en el grafo, llamaremos a esta última estructura un bosque.
Tipos de árboles binarios
Un árbol binario es un árbol con raíz en el que cada nodo tiene como máximo dos hijos.
Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos hijos.
Un árbol binario perfecto es un árbol binario lleno en el que todas las hojas (vértices con cero
hijos) están a la misma profundidad (distancia desde la raíz, también llamada altura).
A veces un árbol binario perfecto es denominado árbol binario completo. Otros definen un
árbol binario completo como un árbol binario lleno en el que todas las hojas están a
profundidad no n-1, para alguna n.
Un árbol binario es un árbol en el que ningún nodo puede tener más de dos subárboles. En un
árbol binario cada nodo puede tener cero, uno o dos hijos (subárboles). Se conoce el nodo de
la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho.
Implementación
Un árbol binario puede declararse de varias maneras. Algunas de ellas son:
Estructura con manejo de memoria dinámica, siendo el puntero que apunta al árbol, pueden
utilizarse un sencillo arreglo de enteros con tantas posiciones como nodos deba tener el árbol.
La información de la ubicación del nodo en el árbol es implícita a cada posición del arreglo. Así,
si un nodo está en la posición i, sus hijos se encuentran en las posiciones 2i+1 y 2i+2, mientras
que su padre (si tiene), se encuentra en la posición truncamiento((i-1)/2) (suponiendo que la
raíz está en la posición cero). Este método se beneficia de un almacenamiento más compacto y
una mejor localidad de referencia, particularmente durante un recorrido en preorden. La
estructura para este caso sería por tanto:
int árbol[NUMERO_DE_NODOS];
Recorridos sobre árboles binarios
Recorridos en profundidad
Método de este recorrido es tratar de encontrar de la cabecera a la raíz en nodo de unidad
binaria. Ahora pasamos a ver la implementación de los distintos recorridos:
Recorrido en preorden
En este tipo de recorrido se realiza cierta acción (quizás simplemente imprimir por pantalla el
valor de la clave de ese nodo) sobre el nodo actual y posteriormente se trata el subárbol
izquierdo y cuando se haya concluido, el subárbol derecho. Otra forma para entender el
recorrido con este metodo seria seguir el orden: nodo raíz, nodo izquierda, nodo derecha.
En el árbol de la figura el recorrido en preorden sería: 2, 7, 2, 6, 5, 11, 5, 9 y 4.
void preorden(tArbol *a)
{
if (a != NULL) {
tratar(a);
//Realiza una operación en nodo
preorden(a->hIzquierdo);
preorden(a->hDerecho);
}
}
Recorrido en postorden
En este caso se trata primero el subárbol izquierdo, después el derecho y por último el nodo
actual. Otra forma para entender el recorrido con este metodo seria seguir el orden: nodo
izquierda, nodo derecha, nodo raíz. En el árbol de la figura el recorrido en postorden sería: 2,
5, 11, 6, 7, 4, 9, 5 y 2.
void postorden(tArbol *a)
{
if (a != NULL) {
postorden(a->hIzquiedo);
postorden(a->hDerecho);
tratar(a);
//Realiza una operación en nodo
}
}
Recorrido en enorden
En este caso se trata primero el subárbol izquierdo, después el nodo actual y por último el
subárbol derecho. En un ABB este recorrido daría los valores de clave ordenados de menor a
mayor. Otra forma para entender el recorrido con este metodo seria seguir el orden: nodo
izquierda,nodo raíz,nodo derecha.
Recorridos por niveles
En este caso el recorrido se realiza en orden por los distintos niveles del árbol. Así, se
comenzaría tratando el nivel 1, que sólo contiene el nodo raíz, seguidamente el nivel 2, el 3 y
así sucesivamente. En el árbol de la figura el recorrido en amplitud sería: 2, 7, 5, 2, 6, 9, 5, 11 y
4.
Al contrario que en los métodos de recorrido en profundidad, el recorrido por niveles no es de
naturaleza recursiva. Por ello, se debe utilizar una cola para recordar los subárboles izquierdos
y derecho de cada nodo.
El esquema algoritmo para implementar un recorrido por niveles es exactamente el mismo
que el utilizado en la versión iterativa del recorrido en preorden pero cambiando la estructura
de datos que almacena los nodos por una cola.
Creación de árboles a partir de los recorridos
Para poder dibujar un árbol binario en base a los recorridos, se necesitan por lo menos dos de
los recorridos de profundidad (en caso de que no se repitan los nodos, ya que si se repiten los
nodos es recomendable tener los tres recorridos), ya sean inorden y preorden o inorden y
postorden, la única diferencia entre usar el recorrido en preorden o postorden es que en
preorden se usa el primer nodo para encontrar la raíz y en postorden se usa el último nodo.
El método consiste en ir dividiendo los recorridos del árbol en pequeños subárboles, se va
encontrando la raíz con el preorden o postorden y se divide en dos subárboles basándonos en
el recorrido en inorden. En el caso de que los nodos se repitan es conveniente tener los 3
recorridos para identificar más fácilmente cuál de los nodos es la raíz actual.
Para el árbol de la figura corresponden los siguientes recorridos:
Preorden
Inorden
Postorden
Para encontrar la raíz es necesario tener el recorrido preorden o postorden, ya que la raíz es el
primer nodo o el último nodo respectivamente. En este caso la raíz es el .
Una vez encontrada la raíz, es necesario saber su posición en el recorrido inorden, del paso
anterior se tiene el nodo , pero existen 2 nodos con ese valor, el primero y el de en medio. Si
el primer dos es la raíz, entonces no existe ninguna rama del lado izquierdo, en ese caso la
siguiente raíz de acuerdo con el recorrido en postorden es y de acuerdo con preorden es ,
lo cual es una incongruencia, de esa forma sabemos que el otro es la raíz.
Entonces marcamos la raíz en el recorrido inorden:
Preorden
Inorden
Postorden
El recorrido inorden, es un recorrido de los árboles binarios en los que se empieza desde el
nodo que se encuentra más a la izquierda de todos, sigue con la raíz y termina con los nodos
del lado derecho, entonces, como en el recorrido inorden ya encontramos la raíz, la parte
izquierda representa el subárbol izquierdo y la parte derecha representa el subárbol derecho.
En los recorridos tenemos 5 nodos a la izquierda del y a la derecha se encuentran 3 valores,
entonces podemos crear los recorridos para el subárbol izquierdo y el subárbol derecho
Subárbol derecho
Subárbol derecho
Preorden
Preorden
Inorden
Inorden
Postorden
Postorden
Se sigue repitiendo el proceso hasta encontrar todos los nodos del árbol, en este punto la
siguiente raíz izquierda es el y la raíz derecha el .
Cuando se llegan a nodos en los que únicamente cuentan con una rama es necesario saber que
rama es la derecha y cuál es la izquierda (para algunos árboles con balanceo como los AVL),
por ejemplo siguiendo la rama de la derecha partiendo de que el es la raíz el recorrido
inorden es
entonces el siguiente nodo va a la derecha, no hay nodo a la izquierda,
después, los recorridos para el subárbol son:
Preorden
Inorden
Postorden
Finalmente el siguiente nodo se coloca a la izquierda del .
Este método es 100% efectivo cuando no existen nodos repetidos, cuando los nodos se repiten
la complejidad aumenta para poder descubrir cuál es el nodo raíz en el recorrido inorden.
Métodos para almacenar árboles binarios[editar · editar código]
Los árboles binarios pueden ser construidos a partir de lenguajes de programación de varias
formas. En un lenguaje con registros y referencias, los árboles binarios son construidos
típicamente con una estructura de nodos y punteros en la cual se almacenan datos, cada uno
de estos nodos tiene una referencia o puntero a un nodo izquierdo y a un nodo derecho
denominados hijos. En ocasiones, también contiene un puntero a un único nodo. Si un nodo
tiene menos de dos hijos, algunos de los punteros de los hijos pueden ser definidos como
nulos para indicar que no dispone de dicho nodo. En la figura adjunta se puede observar la
estructura de dicha implementación.
Los árboles binarios también pueden ser almacenados como una estructura de datos
implícita en vectores, y si el árbol es un árbol binario completo, este método no desaprovecha
el espacio en memoria. Tomaremos como notación la siguiente: si un nodo tiene un índice i,
sus hijos se encuentran en índices 2i + 1 y 2i + 2, mientras que sus padres (si los tiene) se
encuentra en el índice
(partiendo de que la raíz tenga índice cero). Este método
tiene como ventajas el tener almacenados los datos de forma más compacta y por tener una
forma más rápida y eficiente de localizar los datos en particular durante un preoden
transversal. Sin embargo, desperdicia mucho espacio en memoria.
Árbol de expresiones
Es un árbol binario completo para representar y calcular expresiones aritméticas en este los
hojas son los operando y el resto de nodo los operadores
Expresión: a+b*c
+
a
*
b
c
Árbol binario de búsqueda(abb)
Este es un árbol que se puede implementar a algoritmo que permite crearuna estructura que
odena y aumenta la eficiencia de en el proceso de búsqueda en compañía con estructura
como vectores y lista enlazadas.
Tiene un mayor eficacia, mnor numero de comparaciones al buscar
v
12 7
40 4
24 70
L
Recorrido inOrden 4,7,12,24,40,70; por cada comparación salta un promedio del 50% de los
elemento que ya no se tiene en cuenta
Opraciones
BUUQUEDAD: Iniciando en la raíz se compara si el elemento es igual que el que fue
encontrado, si el elemento e mayor se salta a la derecha, sino a la izquierda,se repite el
proceso nuevamente tomando el nodo actual como la nueva raíz hasata que se llegue a null
o sean iguales los datos comparados.
INSERTAR: se busca el datos (clave) en le árbol y sino existe se crea un dodo y se inserta en el
extremo de la rama recorrida, si es mayor a la derecha , si es menor a la izquierda
ELEMINAR: se debe buscar la clave, si existe pueden darse 3 casos.
Caso 1: si es una hoja, simplemente se suprime
Caso 2: si tiene un solo subArbol, se reemplaza por su decendiente inmediato
Caso 3: si tiene dos subArbol , se reemplaza por el nodo mas a la izquierda del
subArbolDerecho o se reemplaza por el nodo mas a la derecha del subArbolizquierdo
Ejemplo:
Crear un abb a partir de la siguiente clave 33, 44, 22, 12, 2, 53, 40, 8, 4.
33
44
22
12
53
40
2
3
8
4
7
Eliminar los nodos con clave 4, 22, 44, 33 en el abb anterior
33
44
22
12
53
40
2
3
8
4
7
paso 1
33
7
44
22
12
53
40
2
3
8
paso 2
33
12
44
2
3
53
40
8
Paso 3
33
12
3
40
8
53
Paso 4
12
40
2
3
53
8
Arboles binario de búsqueda balancioados(AVL)
Debido a las operaciones los arboles abb pueden tener una tendencia degenerada, lo que
hace que se pierda, por lo que el algoritmo de avl propone un algoritmo mejorado de que
restructura el árbol cunado pierde balance y asi recuperar la efiencia
Balance
FE o
subizq FE 1
niveles FE 0
FE subder
FE
Factor de equilibrio(FE) ------ FE=hsi-hsd
Para que un árbol sea avl en todo los nodos debe cumplirse lo siguiente si (FE>2 &FE<2) es un
árbol balanceado. Las operaciones de este árbol son las siguiente:
Insertar: inicialmente se aplica la misma regla abb, adicionalmente se calcula el FE en todo los
nodos de rama de la inserción, comenzando por el nodo insertado, no hay problema si
después de la hoja el FE es 0 o lleguamos a la raíz si que el FE salga del rango de balance, en
caso de que el FE salga del rango de balance se restructura el árbol en un proceso llamado
rotación que puede ser de vario casos.
Caso 1 (II) Izquierdo- Izquierdo
Insertar c, b, a
2
0
b
c
1
0
b
0
c
a
0
a
Caso 2(ID) Izquierdo- Derecha
Insertar c, b, a
-2
0
b
c
-1
0
b
0
a
0
a
c
Caso 3(DD)Derecha-Derecha
Insertar c, b, a
-2
0
b
c
-1
0
0
c
a
b
0
a
Caso 4 (DI)Derecha-Izquierda
Insertar c, b, a
-2
0
b
a
1
c
0
0
a
c
0
b
Método de ordenamiento por inserción binaria
Es método consiste en realizar una búsqueda dicotómica lo que indica que debe dividir en dos
al momento de realizar una inserción, el procedimiento de este método es prácticamente
tomando la posición de la variable del inicio y la del final del vector, luego se debe sumar las
posiciones y se procede a dividir en dos de esta manera tenemos el centro del vector
Ejemplo:
El centro se encuentra ubicado en la posición 2.
Una forma de realizar este método es comparando el elemento central con el elemento que se
desee insertar, pero se debe cumplir una condición la cual es si el numero central es <= que el
que esta dela parte derecha ò si es el caso contrario, nos quedamos con la parte izquierda
incluyendo la parte central.
Ejemplo:
Se repite el procedimiento sobre el área con la que nos
quedamos, hasta que dicha área sean nula
Cuando el área se nula, tendremos a posición inserción
Método de inserción directa
Este método parte de un vector aleatoriamente ordenando y se
marca por el primer elemento como parte ordenada y el resto será
parte desordenada, luego se toma el primer elemento de la parte no ordenada y se almacena
en una
variable temporal
2
Después se empieza comparando hasta que se encuentra un elemento menor
Se desplaza una posición a la derecha todos los elementos que resulten mayores que el que
se desea insertar y la variable temporal se coloca en el lugar encontrado
Alguna delas comparación que podemos encontrar en estos dos métodos es la siguiente:
Directa
La búsqueda secuencial se aplica para
localizar una clave un vector no ordenado.
Pierde mucho tiempo en saber dónde tiene
que insertar la variable temporal
Binaria
Para aplicar el árbol de búsqueda binaria la
lista o el vector donde se busca debe de
estar ordenado
Realiza numerosas comparaciones
Requerimiento de mínimos de memoria
El algoritmo de este método es el siguiente:
Public int [] InsercionBinaria(){
Int longitud = num.length;
Int [] arreglo = new int [ongitud];
Int aux, I, izq, der, medio, n_arreglo=1;
Copiar (num, arreglo);
For(i=1; i< longitud; ++1){
Iqz=0;
Der= n_arreglo -1;
While(iqz<=der){
Medio=(iqz+der)/2;
If (num[i] > arreglo[medio]){
Iqz=medio+1;
}
Else{
Der=medio-1;
}
}
While(iqz<n_arreglo){
Aux=arreglo(iqz);
Arreglo(iqz)-arreglo(n_arreglo);
Arreglo(n-arreglo)=aux;
++iqz;
}
++n_arreglo;
Búsqueda eficiente
Toma su nombre debido a la simulación de
los arboles binarios
}
Return arreglo;
}
}
Este algoritmo de ordenación rápida, o QuickSort, se implementa a través de un
procedimiento recursivo que implementa tres pasos:
Selecciona un elemento de referencia o pivote, con base en el cual se reorganizará el arreglo a
ordenar
Reorganiza el arreglo de tal manera que a la izquierda del pivote se sitúen todos los elementos
menores a él y a la derecha los mayores.
Se invoca recursivamente el método de ordenación tanto para el subconjunto de elementos de
la izquierda como para el de la derecha.
En la siguiente implementación en JAVA, el proceso de ordenación está implementado en el
método quickSort, mientras que el método ordenacionRapida sirve para presentar al usuario
final un mismo estilo de invocación del algoritmo.
// Ordenacion rapida: Quick Sort
public static void ordenacionRapida(int[] v) {
final int N = v.length;
quickSort(v,0,N-1);
}
public static void quickSort(int[] v, int inicio, int fin) {
if(inicio>=fin) return ;
int pivote = v[inicio];
int izq = inicio+1;
int der = fin;
While(izq<=der) {
while(izq<=fin && v[izq]< pivote) izq++;
while(der>inicio && v[der]>=pivote) der--;
if(izq<der) {
int tmp = v[izq];
v[izq] = v[der];
v[der] = tmp;
}
}
if(der>inicio) {
int tmp = v[inicio];
v[inicio]= v[der];
v[der] = tmp;
}
quickSort(v,inicio, der-1);
quickSort(v, der+1, fin);
}
Ordenación Shell
Este algoritmo de ordenación Shell Sort se base en el algoritmo de ordenación por inserción,
el cuál tiene un muy buen desempeño si el vector está relativamente ordenado. Entonces,
teniendo esto como premisa, el Shell Sort, ordena por inserción subconjuntos del vector que
están separados entre sí por distancias relativamente mayores (empezando con distancias
iguales a la mitad del tamaño del vector), la cuales se van reduciendo rápidamente.
El siguiente código escrito en el lenguaje JAVA recibe como parámetro el conjunto de
elementos representado en un arreglo de números enteros y define inicialmente el
incremento como la mitad del tamaño del vector, entonces se ordenan por inserción los
elementos de las posiciones v[0] y v[n/2], luego los de las posiciones v[1] y v[n/2] +1, y así
sucesivamente. Cuando termina este proceso, se divide por dos el tamaño del incremento y se
repite el proceso hasta que el incremento sea igual a 1, en cuyo caso su comportamiento sería
exactamente el del algoritmo de ordenación por inserción.
// Algoritmo de ordenacion ShellSort
public static void ordenacionShell(int[] v) {
final int N = v.length;
int incremento = N;
do {
incremento=incremento/2;
for(int k=0; k<incremento;k++) {
for(int i=incremento+k; i<N; i+=incremento) {
int j=i;
while(j-incremento>=0 && v[j]<v[j-incremento] ){
int tmp = v[j];
v[j] = v[j-incremento];
v[j-incremento] = tmp;
j-=incremento;
}
}
}
} while(incremento > 1);
}
En cuanto a la complejidad del algoritmo, ésta tiende a ser O(n log n), teniendo en cuenta que
este método se basa en la ordenación por inserción la cual tiende a ser O(n) en el mejor de los
casos (es decir, cuando el vector está casi ordenado), y que el proceso de ordenación por
inserción se repite tantas veces como tarde la variable incremento en llegar al valor de 1, que
es aproximadamente el logaritmo en base 2 del tamaño del vector.
Ordenación Shaker
El algoritmo de ordenación por el método Shaker, también conocido como "Cocktail" o
"Sacudida" es una mejora del método de la burbuja en la cual el proceso se realiza tanto desde
la primera posición a la última del arreglo como en sentido inverso, evitando así que los
elementos más pequeños tarden un mayor tiempo en "ascender" a las posiciones superiores.
La implementación de este algoritmo en lenguaje JAVA es la siguiente:
// Algoritmo de ordenacion Shaker Sort
public static void ordenacionShaker(int[] v) {
final int N = v.length;
int limInferior = 0;
int limSuperior = N-1;
while(limInferior <= limSuperior) {
for(int j=limInferior; j<limSuperior; j++) {
if(v[j]>v[j+1]) {
int tmp = v[j];
v[j] = v[j+1];
v[j+1] = tmp;
}
}
limSuperior--;
for(int j=limSuperior;j>limInferior; j--) {
if(v[j]<v[j-1]) {
int tmp = v[j];
v[j] = v[j-1];
v[j-1] = tmp;
}
}
limInferior++;
}
}
La complejidad del algoritmo es cuadrática, puesto que si bien mejora un poco el rendimiento
del método de la burbuja, no cambia el hecho de recorrer el arreglo una vez por cada cada
elemento que se quiere dejar en su posición correcta. Se puede probar con la ecuación de
recurrencias T(n) = k n + T(n-1) con la tecnología del motor de cálculo WolframAlpha.
Ordenación por Inserción
Este algoritmo de ordenación por inserción toma cada elemento a partir del segundo y recorre
el vector en sentido inverso ubicando el elemento en su posición correcta haciendo los
intercambios necesarios. Cuando termina de ubicar un elemento en su posición correcta,
continúa con el siguiente elemento hasta hacer este proceso con todos los elementos del
arreglo.
La implementación de este algoritmo en lenguaje JAVA es la siguiente:
// Algoritmo de ordenacion por insercion
public static void ordenacionInsercion(int[] v) {
final int N = v.length;
for(int i=1; i<N; i++) {
int j=i;
while(j>0 && v[j]<v[j-1] ){
int tmp = v[j];
v[j] = v[j-1];
v[j-1] = tmp;
j--;
}
}
}
Ordenación por Burbuja - BubbleSort
Este algoritmo de ordenación por el método de la burbuja, o Bubble Sort recorre todo el
arreglo comparando cada uno de los elementos con el elemento siguiente e intercambiándolos
de ser necesario. Al finalizar este proceso, el elemento mayor queda ubicado en la última
posición de arreglo, mientras que todos los elementos menores han "ascendido" una posición.
El proceso se continúa repitiendo nuevamente desde la posición inicial del arreglo hasta que
cada elemento "caiga" a su posición correcta.
La implementación de este algoritmo en lenguaje JAVA es la siguiente:
// Algoritmo de ordenacion por Burbuja
public static void ordenacionBurbuja(int[] v) {
final int N = v.length;
for(int i=N-1; i>0; i--) {
for(int j=0; j<i; j++) {
if(v[j]>v[j+1]) {
int tmp = v[j];
v[j] = v[j+1];
v[j+1] = tmp;
}
}
}
}
La complejidad del algoritmo es cuadrática, puesto que cada para lograr llevar un elemento a
la última posición del arreglo se deben recorrer todos los elementos del mismo, y este proceso
se repite para todos los demás elementos. Se puede probar con la ecuación de recurrencias
T(n) = k n + T(n-1) con la tecnología del motor de cálculo WolframAlpha.
Metodo de ordemaniento directo
Es un método de ordemaniento simple en el cual la lista se va ordenando con una entrada a la
vez hacia la izquierda,los datos a clasificar son considerado uno a la vez, cada elemento se
inserta en la posición apropiada con respecto al resto de los valores ya ordenados.
Ejemplo: Supóngase que se desea ordenar los siguientes claves del arreglo A utilizando el
método de inserción directa el cual consiste en insertar un elemento del arreglo en la parte
izquierda del mismo que ya se encuentra ordenada.
A= 15, 67, 08, 16, 44, 27, 12, 35
Comparaciones realizadas:
1ª pasada A[2] < A[1] 67 < 15 No hay intercambio
A= 15, 67, 08, 16, 44, 27, 12, 35
2ª pasada A[3] < A[2] 08 < 67 Si hay intercambio
A= 15, 08, 67, 16, 44, 27, 12, 35
3ª pasada A[4] < A[3] 08 < 15 Si hay intercambio
A= 08, 15, 67, 16, 44, 27, 12, 35
4ª A= 08,15,16,44,67,27,12,35
5 ª A= 08,15,16,27,44,67,12,35
6 ª A= 08,12,15,16,27,44,67,35
7 ª A= 08,12,15,16,27,35,44,67
La característica de este método es el que generalmente utilizan los jugadores de carta
cuándo ordenan estas, de ahí que también se conozca con el nombre de método de la baraja.
La idea central de este algoritmo consiste en insertar un elemento de arreglo en la parte
izquierda del mismo, ya que se encuentra ordenada.
El código de este método es :
Public class insercionDirecta{
Public static void main(String[]args){
Int I;
Int a[]={8,14,5,9,3,23,17};
System.out.print(“ insercion directa”);
System.out.print(“ valor ante de la ordenacion”);
For(i=0; i<a.length; i++)
System.out.print(“ a[i]+”);
insertarDirecta(a,a.length);
System.out.print(“ valores ordenados”);
For(i=0; ia.length; i++);
System.out.print(“ a[i]+”);
}
Puclic static void insertarDirecto(int a[], int n){
For (int i=1; i<n; i++){
Int k=I;
Int aux=a[i];
While((k>0)&&(a[k-1]>aux)){
A[k]=a[k-1];
k--;
}
A[k]=aux;
}
}
}
Ordenación por Montículos
El algoritmo de ordenación por montículos o Heap Sort recorre el conjunto de elementos
desde la posición de la mitad hasta la primera organizando el montículo correspondiente a
dicho elemento. Una vez terminado este proceso, se inicia el proceso de ordenación
intercambiando el primer elemento por el último del arreglo y reorganizando el montículo a
partir de la primera posición.
// Ordenacion por monticulos – HeapSort
public static void ordenacionMonticulos(int[] v) {
final int N = v.length;
for(int nodo = N/2; nodo>=0; nodo--) hacerMonticulo(v, nodo, N-1);
for(int nodo = N-1; nodo>=0; nodo--) {
int tmp = v[0];
v[0] = v[nodo];
v[nodo] = tmp;
hacerMonticulo(v, 0, nodo-1);
}
}
public static void hacerMonticulo(int[] v, int nodo, int fin) {
int izq = 2*nodo+1;
int der = izq+1;
int may;
if(izq>fin) return;
if(der>fin) may=izq;
else may= v[izq]>v[der]?izq:der;
if(v[nodo] < v[may]) {
int tmp = v[nodo];
v[nodo] = v[may];
v[may] = tmp;
hacerMonticulo(v, may, fin);
}
}
Metodo de ordenamiento heapsort
De los método de ordenamiento interno este es uno de los más eficaces debido a que la
mayoría de los método de ordenamiento utilizan comparaciones este también los utiliza esta
técnica y el tiempo que utiliza es relativamente corto.
El método de ordenamiento interno se aplica para ordenar conjuntos pequeños de datos.
Este método consiste en ingresar todos los elementos en un arreglo a ordenar en un heap o
montículo luego se extrae el nodo que queda como raíz después de repetitivas comparaciones
de esta manera obteniendo el conjunto ordenado.
Heap (Montículo) + Sort (Ordenar) = Ordenar por Montículo
Montículo: Es un árbol binario completo, que permite implementar una cola con prioridad, y
donde los elementos se almacenan de izquierda a derecha cumpliendo la propiedad de que la
clave de un nodo siempre es mayor que el valor de cualquiera de sus hijos. Lo que nos asegura
que la raíz del árbol, en un montículo, siempre es el elemento mayor de la estructura.
Inserción
Se crea el árbol con los datos del arreglo, la regla a tener en cuenta es padre debe ser mayor
que el hijo y si el Hijo >padre se debe reorganizar el árbol, este proceso también se realiza en
el vector
3
3
2
4
1
4
2
4
4
2
3
1
3
2
Después de la reorganización así queda el árbol y el arreglo, y mediatamente se continúa con
el proceso de inserción de nodos en el árbol
4
4
2
3
2
3
1
1
Luego de la creación del arbol se procede a el ordenamiento haciendo uso del método
heapsort, empezando desde debajo de la derecha a izquieda hasta llegar a la raíz
4
3
2
1
Se extrae el valor del nodo riaz y el ultimo nodo del ultimo nivel del arbol, luego esto valores se
intercambian en el vector, luego se sobre escribe el valor del nodo raizpor el valor del ultimo
nodo y el ultimo nodo se elimina
4
4
2
2
3
1
3
1
Asi que da después del proceso, recuerde la regla: Padre> hijo, asi que como 1 es menor que
los hijos, se procede a reorganizar el arbol
1
2
3
1
3
2
Posterior al proceso, asi queda la reorganización, este paso se realizaran hasta que terminar
con la eliminación de todos los nodos del arbol, por ende con el ordenamiento.
3
3
2
1
1
2
1
3
2
1
3
2
1
1
2
2
2
1
2
1
1
1
2
1
1
Ventajas
Más rápido que algunos de los algoritmos de ordenamiento existente
Mejor desempeño
Funcionamiento efectivamente con datos en desorden
Desventaja
Bastante complejo de programar, requiere destreza y habilidad del programador
No es estable, es eficaz con datos del mismo valor
Ordenación por Selección - SelectSort
Este algoritmo de ordenación por selección recorre todo el arreglo desde la primera posición
buscando el menor elemento de todos. Cuando termina, lo reemplazar por el elemento de la
primera posición y repite todo el proceso con el segundo elemento y así sucesivamente.
La implementación de este algoritmo en lenguaje JAVA es la siguiente:
// Algoritm de ordenacion por seleccion.
public static void ordenacionSeleccion(int[] v) {
final int N = v.length;
for(int i=0; i<N; i++) {
5
int posMenor = i;
for(int j=i+1; j<N; j++) {
if(v[j]<v[posMenor]) posMenor=j;
}
if(posMenor!=i) {
int tmp
v[i]
= v[i];
= v[posMenor];
v[posMenor] = tmp;
}
}
}
Metodo Radix sort y addres calculation sort
Radix sort es un método que ordena enteros procesando sus dígitos de forma indivial.como
lo enteros pueden representar cadenas de caracteres como: Fecha, nombre. No está solo
limitado a entero.
Este método funciona de la siguiente manera
Su pongamos la siguiente lista de numero entero: 31,41,81,54,23,33,64,98,93,88
Haremos diversos montones de ficha caracterizados por contener el mismo digito(leyendo el
numero derecha a izquierda)
0
1
31
41
81
2
3
23
33
93
4
54
64
5
6
El siguiente código pertenece a este código
public static void ordenacionResiduos(int[] v) {
int max = 1;
int nbytes = 4;
// cantidad de repeticiones
// numero de bytes a desplazar
int nColas = (int) Math.pow(2,nbytes) ;
// Creación e inicialización del arreglo de colas
Queue<Integer>[] cola = new LinkedList[nColas];
for(int i=0; i<nColas; i++) cola[i]=new LinkedList<Integer>();
7
8
88
98
9
int
div
= 0;
// posición a comparar
for(int i=0; i<max; i++) {
// parte 1: recorrer el vector para guardar cada elemento
// en la cola correspondiente
for(int numero: v) {
// buscar el mayor número del vector
if(i==0) if(numero>max) max=numero;
// calcular en qué cola debe ir cada número
int numCola = (numero>>div) & 0xf;
cola[numCola].add(numero);
}
div = div+nbytes;
// parte 2: recorrer las colas en orden para poner cada
// elemento en el vector;
int j=0;
for(Queue<Integer> c: cola) {
while(!c.isEmpty()) v[j++]=c.remove();
}
// la primera vez se actualiza el número de veces que se
// debe ejecutar el proceso
if(i==0) { max = (int) (Math.log(max)/Math.log(nColas)) + 1; }
}
}
Este algoritmo recorre el arreglo trasladando cada elemento a una cola determinada por el
residuo, o dígito menos significativo del número. Cuando todos los elementos han sido
trasladados a las colas, se recorren todas las colas en orden trasladando ahora los elementos al
vector. El proceso se repite ahora para los demás dígitos de los elementos del vector.
Si bien se habla de dígitos (unidades, decenas, centenas, etc), para un computador es más
eficiente hacer las operaciones a nivel de bit, con desplazamientos, que las operaciones de
división y residuo. Por tal motivo, la implementación que se presenta a continuación utiliza
corrimientos de 4 bits, que se pueden representar como dígitos hexadecimales
Addres-calculation sort
En este momento una función fn(), se aplica a cada tecla y el resultado de esta función
determia en cuál de los sub-Archivo el registro se va a colocar. La simple inserción se utiliza a
menudo después de todo los elementos del archivo originales han colocado en sub-Archivos,
los sub-archivo se utilizan para conectar el resultado ordenado.
Ejemplo:
Merge sort utiliza la técnica divide y vencerás para ordenar un arreglo de registros a[1], a[2],
…, a[n]. El arreglo es dividido en dos subarreglos de tamaño similar a[1], a[2], …, a[n/2] y
a[n/2+1], a[n/2+2], …, a[n], lo que contrasta con la partición que hace quick sort. A
continuación, se ordena recursivamente cada uno de los subarreglos por separado. Las
llamadas recursivas se detienen en cuanto el tamaño del subarreglo es 1 y es precisamente
cuando el subarreglo está ordenado. Posteriormente, para reconstruir el arreglo original de
tamaño n, se fusionan los dos subarreglos ordenados.
Las regla a tener en cuenta es: Si la longitud de la lista es 0 ó 1, entonces ya está ordenada. En
otro caso: Dividir la lista desordenada en dos sublistas de aproximadamente la mitad del
tamaño. Ordenar cada sublista recursivamente aplicando el ordenamiento por mezcla. Mezclar
las dos sublistas en una sola lista ordenada.
public static void mergesort(int[ ] matrix, int init, int n)
{
int n1;
int n2;
if (n > 1)
{
n1 = n / 2;
n2 = n - n1;
mergesort(matrix, init, n1);
mergesort(matrix, init + n1, n2);
merge(matrix, init, n1, n2);
}
}