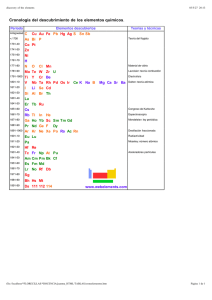
Curso de Química de coordinación

Curso de Química de
coordinación
Comportamiento espectroscópico
Espectroscopía de los
compuestos de
coordinación
Rafael Moreno Esparza
(2009-2)
31 mayo 09
Espectroscopía
0
Propiedades espectroscópicas del H
Este patrón de líneas oscuras es característico de
cada elemento.
Y se le conoce como espectro de absorción atómica
Por otro lado, si calentamos ese mismo gas,
empieza a brillar
Y si enfocamos la luz que emite, se observan
únicamente líneas brillantes de ciertas longitudes
de onda
Este patrón de líneas brillantes, también es
característico de cada elemento.
Y se le conoce como espectro de emisión atómica
Entonces, tenemos que cualquier elemento en fase
gas, produce dos clases de espectros
31 mayo 09
Espectroscopía
2
En el año de 1900, Max Planck demuestra que los
átomos de un sólido caliente, tienen energías que
son un múltiplo de una cantidad fija.
A esta cantidad de energía la llamó quantum o
paquete de energía.
energía.
Desde antes, se sabía que los gases absorbían o
emitían energía en paquetes, es decir estaba
cuantizada
En tanto que la luz que se producía por medio de un
foco, era continua.
Sin embargo si interponemos hidrógeno (o cualquier
otro elemento) entre el foco y el prisma, la luz
resultante no era continua.
El espectro observado muestra una serie de líneas
obscuras muy angostas, que se conocen como líneas
espectrales donde faltanEspectroscopía
ciertos colores específicos 1
31 mayo 09
Propiedades espectroscópicas
Es decir este comportamiento depende de la
manera que lo hagamos interactuar con la
radiación electromagnética
Si hacemos que la luz pase por donde está el gas
obtenemos el espectro de absorción
En cambio si le damos suficiente energía,
obtendremos el espectro de emisión
31 mayo 09
Espectroscopía
3
1
Propiedades espectroscópicas
¿Pero a qué se debe este fenómeno?
Lo podemos atribuir a que los átomos que
componen al gas, absorben la luz
¿Y por qué absorben la luz?
Sabemos que la radiación es causada por la
vibración de las cargas y la rapidez de la
vibración determina la longitud de onda.
Esto significa que, si solamente ciertas
longitudes de onda pueden ser absorbidas o
emitidas por el átomo, sus electrones vibran
solamente a ciertas frecuencias
Los resultados obtenidos del estudio de los
espectros de líneas de los elementos no podían
explicarse empleando la física clásica.
31 mayo 09
Espectroscopía
4
Modelo del átomo
Si consideramos el modelo del átomo propuesto por
Rutherford,
Rutherford, que era muy popular al principio del
siglo XX, al electrón se le consideraba como si
estuviera dando vueltas alrededor del núcleo
De tal manera que la fuerza centrífuga estuviera
balanceada respecto a la atracción coulómbica
Entonces, un átomo así debería de ser capaz de
absorber o emitir cualquier cantidad de energía
De manera que el cambio en su energía meramente
alteraría el radio de la órbita
Así, los físicos de la época se vieron forzados a
considerar desechar por completo este modelo (a
pesar de estar tan bien sostenido por la evidencia
experimental)
O hacerle algunas modificaciones difíciles de digerir
31 mayo 09
El modelo de Bohr
Es claro que, sería estúpido proponer que el átomo
pudiera contener cualquier energía (tal como lo
dicta el modelo planetario)
Y a pesar de ello absorber o emitir energía en
cantidades especiales y medidas
¿Pero entonces como es un átomo?
Pues la alternativa era postular que los electrones
en el átomo podían tener solamente ciertos valores
de energía
Esto implicaba automáticamente, que el átomo
podría absorber o emitir únicamente ciertas
energías
Es decir que al principio del siglo XX, este era un
verdadero rompecabezas para los científicos
31 mayo 09
Espectroscopía
Espectroscopía
5
El modelo de Bohr
Una teoría o un modelo raramente se abandona por
completo, a menos que no haya alternativa
De hecho el modelo planetario no se abandonará
sino hasta que finalmente se desarrolla el modelo
cuántico
El más simple y sensato de los modelos del átomo
basado en el de Rutherford es el de Bohr
Afortunadamente, (Niels
(Niels Bohr)
Bohr) un físico danés,
sugiere un cambio en el modelo muy radical
Lo radical del modelo, reside en que Bohr propone
que para explicar las líneas espectrales, los
electrones deben seguir una regla medio mafufa
6
31 mayo 09
Espectroscopía
7
2
El modelo de Bohr
Esta regla es que los electrones solo pueden estar
en ciertas órbitas especiales y todas las otras órbitas
están prohibidas
Por lo tanto, los electrones pueden saltar de una
órbita a otra y al hacerlo vibran
Consecuentemente producen radiación
Bohr,
Bohr, descubrió que se podía explicar el espectro del
hidrógeno cuantitativamente si se consideraba que
en el átomo de hidrógeno los electrones se movían
en aquellas órbitas especiales donde el momento
angular del electrón era un múltiplo de h/2π
/2π
Es decir que la energía del electrón estaba
cuantizada
31 mayo 09
Espectroscopía
8
El modelo de Bohr
Esta propuesta tan arbitraria y mafufa en su tiempo,
se hace aceptable en parte, ya que consigue salvar el
modelo planetario del átomo al menos por un
tiempo
La evidencia espectroscópica de la estructura en
capas de los electrones puede verse en los espectros
de líneas
Así, en el caso del átomo de hidrógeno, la energía de
cada uno de los niveles cuánticos se puede obtener
usando esta ecuación:
E =−
31 mayo 09
El modelo de Bohr
Y para determinar la diferencia de energía entre
cualesquiera dos niveles es: 

Momento angular de los estados del átomo de
hidrógeno: Estado p= n(h/2π
/2π), n es un entero
31 mayo 09
1(h/2π
/2π)
2(h/2π
/2π)
2(h/2π
/2π)
3(h/2π
/2π)
3(h/2π
/2π)
3(h/2π
/2π)
Espectroscopía
n2
Espectroscopía
9
El modelo de Bohr
De esta manera, este modelo puede racionalizar el
comportamiento químico de los elementos, al
arreglar a los electrones en capas
Es decir, al cuantizar las energías de los electrones
en capas discretas (llamadas K, L, M, N, O, etc.
etc.),
explica las propiedades químicas de los elementos
De esta manera tenemos que cuando un átomo se
encuentra en su estado basal y lo excitamos usando
un haz de luz, solamente ciertas de las longitudes de
onda tendrán la energía suficiente para hacer que el
electrón pueda pasar a otra órbita
Y cuando dejamos de excitarlo, los electrones que se
pasaron a una órbita de mayor energía al regresar a
su órbita original emiten energía
1
1
E 2 − E1 = hν = hZ 2  2 − 2 
 n1 n2 
1s
2s
2p
3s
3p
3d
kZ 2
10
31 mayo 09
Espectroscopía
11
3
El modelo de Bohr
Espectroscopía
12
El modelo de Bohr
Transiciones del hidrógeno (emisión):
En n
∞
31 mayo 09
UltravioletaEspectroscopía
Energía (kJ/mol
(kJ/mol)
Visible
184
246
276
293
1
984
-1312.0
0
1167
6
5
4
3
2
1230
0
-36.4
-52.3
-82.0
-145.6
-328.0
-1312
14
En n
∞
UltravioletaEspectroscopía
Energía (kJ/mol
(kJ/mol)
Visible
184
246
1
31 mayo 09
276
-1312.0
0
293
6
5
4
3
2
984
0
-36.4
-52.3
-82.0
-145.6
-328.0
1167
Núcleo
Capa K, n=1, r=0.529
r=0.529 Å
Capa L, n=2, r=2.116
r=2.116 Å
Capa M, n=3, r=4.761
r=4.761 Å
Capa N, n=4, r=8.464
r=8.464 Å
Capa O, n=5, r=13.225
r=13.225 Å
1230
Órbitas de Bohr del hidrógeno
31 mayo 09
El modelo de Bohr
Transiciones del hidrógeno (absorción):
-1312
13
El modelo de Bohr
Conviene aquí
aquí comentar que la propuesta de Bohr le
abre el camino a la mecánica cuántica,
independientemente del hecho de que es incorrecta
casi en todos sus detalles
Sin embargo es una herramienta que nos permite
visualizar mecánicamente
mecánicamente el fenómeno
espectroscópico
Particularmente, porque el modelo no nos da
ninguna pista del origen de el enlace químico
Además no da ninguna base para entender por que
ocurre la cuantización de la energía del electrón
Ni tampoco explica la razón por la cual un electrón
no irradia energía al estar en movimiento
31 mayo 09
Espectroscopía
15
4
El modelo de Bohr
A pesar de este funesto historial, el coraje de
reconocer la necesidad de una desviación de la física
clásica, le ganó a Bohr un lugar en la historia
Todavía hoy, a los estados permitidos, se conocen
como estados estacionarios, como los bautizó Bohr
A estos estados estacionarios, se les caracteriza por
medio del uso de los números cuánticos.
Que explican el patrón característico del átomo de H
Hasta este momento hemos hablado de los
electrones y de las otras partículas subatómicas
como si fueran pedacitos de materia duros (¡tienen
masa!) como bolas de billar
Que además tienen niveles energéticos claramente
cuantizados
31 mayo 09
Espectroscopía
16
¿Partículas u ondas?
Así, algunos metales (los alcalinos) pueden emitir
electrones si la luz incidente es visible, en cambio
otros solo emiten electrones con luz ultravioleta
Es decir, cada metal tiene una frecuencia umbral,
por debajo de la cual no se produce la emisión de
electrones
Además
Además se ha demostrado experimentalmente que:
Que la energía de los electrones emitidos es
independiente de la intensidad del haz incidente
Que la energía de los electrones emitidos es
proporcional a la frecuencia de la radiación
incidente
Que el número de electrones emitidos por unidad
de tiempo es proporcional a la intensidad de la
radiación incidente
31 mayo 09
Espectroscopía
18
¿Partículas u ondas?
Los cuales, pueden medirse de manera muy precisa,
usando los espectros de emisión y absorción de los
elementos
Sin embargo, a menudo tienen un comportamiento
que no se puede explicar con este modelo
Por otro lado, la radiación electromagnética, que
tradicionalmente se había percibido como un
fenómeno ondulatorio, tiene propiedades que se
pueden asociar al comportamiento de las partículas
Y además decimos que tiene momento efectivo y
que está cuantizada en paquetes llamados fotones
Cuando la luz incide en una superficie metálica, se
puede producir emisión de electrones
A este fenómeno se le conoce con el nombre de
efecto fotoeléctrico
31 mayo 09
Espectroscopía
17
¿Partículas u ondas?
Este fenómeno, no puede deducirse de la teoría
electromagnética clásica pues según esta, la energía
de los electrones debe variar con la intensidad y ser
independiente de la frecuencia
En 1905, Albert Einstein,
Einstein, demuestra que se podían
resolver estas dificultades si se aplicaban los
postulados de Plank a este fenómeno
Para ello, sugiere que en vez de pensar en la luz
incidente como un fenómeno ondulatorio, debe
considerarse como una corriente de corpúsculos a
los que llamó fotones.
Cada uno de estos fotones tiene una energía
determinada
31 mayo 09
Espectroscopía
19
5
¿Partículas u ondas?
La cantidad de energía de cada fotón está dada
según Einstein por esta expresión:
E fotón = hν
Cuando los fotones golpean la superficie metálica
estos, pueden ceder su energía a un electrón del
metal
Y parte de esta energía la emplea para arrancarlo de
la superficie del metal dándole energía cinética.
Si la frecuencia es inferior a la umbral, el efecto no
se produce
Ahora bien, matemáticamente, ya sea que
consideremos que los electrones (o la luz) como
partículas o como ondas, depende esencialmente de
la observación que pretendemos describir
31 mayo 09
Espectroscopía
20
¿Partículas u ondas?
Esta es una propiedad que típicamente se percibe
asociada con el comportamiento de las ondas
Esto desde el punto de vista de la mecánica clásica,
es claramente una contradicción
Esta dualidad partícula-onda de las propiedades de
los electrones fue expresada por Louis de Broglie
De Broglie,
Broglie, postula que la materia posee
características de onda y de partícula al mismo
tiempo
Y expresa esta dualidad en una ecuación que ya es
muy famosa y se considera muy profunda
En esta, la longitud de onda se expresa como una
función de la masa y de la velocidad
h
λ=
31 mayo 09
Espectroscopía
mv
22
¿Partículas u ondas?
Así, algunas veces una representación será más útil
que la otra, en tanto que en otras ocurrirá lo
opuesto
Conviene recordar entonces, que cualquiera que sea
el modelo matemático empleado, el resultado es
una descripción de las propiedades de las
propiedades y no de la naturaleza de los electrones o
la luz
Considerando que es posible pesar a los electrones,
lo cual es tradicionalmente una propiedad de las
partículas.
Resulta muy desconcertante saber que los
electrones también pueden hacer cosas (como por
ejemplo difractarse) de manera muy similar a la
radiación visible o a los Rayos X.
31 mayo 09
Espectroscopía
21
¿Partículas u ondas?
Esto nos sugiere, que las observaciones de
comportamiento ondulatorio o de partícula,
simplemente se relacionan a diferentes atributos
de la materia o de la luz
Evidentemente, esto es una idea que genera mucha
confusión
Para los humanos, todos los días, la experiencia nos
sugiere que las cosas son, o bien partículas o bien
ondas, nunca ambas
¡Una pelota es una partícula y el sonido es una
onda¡
En la práctica por tanto, la dualidad partícula-onda
es significativa para entidades muy, muy pequeñas
Como por ejemplo, los átomos y las moléculas
31 mayo 09
Espectroscopía
23
6
¿Partículas u ondas?
El obstáculo que se nos presenta para entender su
naturaleza se debe a que es difícil relacionar nuestra
experiencia cotidiana con la luz y la materia, con la
aparente naturaleza conflictiva de las partículas que
son tan pequeñas
Así, parece ridículo sugerir que la materia que
manipulamos cotidianamente puede tener
propiedades ondulatorias, pero no lo es
El problema descansa en la magnitud de la longitud
de onda
Para cualquier objeto visible, el tamaño de la
longitud de onda es tan pequeño que no puede
percibirse
Así
Así, es posible concluir que longitud de onda
efectiva de una partícula es importante únicamente
cuando la partícula es muy pero muy pequeña
31 mayo 09
Espectroscopía
24
De órbitas a orbitales de Schröedinger
Si en el modelo de Bohr,
Bohr, los electrones dan vueltas
alrededor del núcleo en órbitas cuantizadas,
cuantizadas, el
modelo cuántico ya no lo considera así.
Antes de discutir este modelo, debemos considerar
que: las dos de las piezas de información
información más
importantes que debemos conocer acerca de un
objeto cualquiera son:
la posición por una parte y
la velocidad (o mas bien el momento) por otra
Pero resulta que, no es posible determinar con
precisión la posición y el momento de un electrón al
mismo tiempo
A este fenómeno, se le conoce como principio de
incertidumbre de Heisenberg
31 mayo 09
Espectroscopía
26
¿Partículas u ondas?
Consideremos una pelota de baseball, cuya masa es
de 150 g y que se mueve a 160 km/h (45 m/s).
m/s).
Al sustituir esto en la ecuación
de
de
Broglie:
:
Broglie
h
6.63 " 10#34
#35
!=
=
% 9.81 " 10
mv
0.15 $ 45
Esto ¡es muy pequeño!
Por otro lado, un electrón que se moviera a la
misma velocidad, cuya masa en estado estacionario
es de 9.10939 x 10-30 kg tendría una longitud de
onda asociada de:
−34
λ=
h
6.63×10
=
≈ 1.6×10−6
−30
mv
9.10939×10 ⋅ 45
La cual es una longitud de onda mucho más
observable experimentalmente
31 mayo 09
Espectroscopía
25
De órbitas a orbitales
Esto puede ilustrarse como sigue:
Para definir la posición de un electrón, es
necesario ver donde está.
Para poder ver un objeto, es necesario que la luz
que lo ilumine tenga una longitud de onda
menor que el tamaño del objeto
Como los átomos son mucho menores que la
longitud de onda de la luz visible, será necesario
emplear radiación con longitud de onda del tamaño
de un átomo
Estas longitudes de onda están asociadas a
radiación electromagnética de gran energía
Como la radiación electromagnética tiene también
asociado un momento efectivo, al chocar con los
electrones, les transferirán parte de ese momento
31 mayo 09
Espectroscopía
27
7
De órbitas a orbitales
De manera que el momento original del electrón
cambia
Así, aunque hemos visto al electrón, al mismo
tiempo le hemos cambiado su momento, es decir,
nuestra observación hace que las propiedades del
objeto cambien
Un análisis riguroso de este fenómeno y otros
relacionados, muestra que:
Al conocer con mayor precisión la posición de un
electrón, se conocerá con menor precisión su
momento y viceversa
Hay un límite con el cual se pueden conocer la
posición y el momento de un objeto cualquiera al
mismo tiempo y se determina con esta ecuación:
h
Donde:
∆x ⋅ ∆p ≥
31 mayo 09
∆x = incertidumbre en la posición
∆p = incertidumbre en el momento
Espectroscopía
4π
28
De órbitas a orbitales
De tal manera, que podemos decir que la
probabilidad de encontrar al electrón en un sitio
particular es lo mismo que hablar de la densidad
electrónica de ese punto
Entonces, la densidad electrónica o densidad de
probabilidad son formas de representar a los
electrones en los átomos
Y describen a los electrones localizados en una
región específica del espacio con una densidad
particular en cada punto del espacio
Para que el modelo de Bohr funcione, es necesario
postular la cuantización de la energía de manera
aparentemente arbitraria para que el modelo se
ajuste a las observaciones
31 mayo 09
Espectroscopía
De órbitas a orbitales
Este hecho que pudiera parecer desastroso a
primera vista, no lo es
Pero si nos obliga a emplear un tratamiento
diferente para analizar las propiedades del electrón.
Así, en vez de hablar de la posición o de la velocidad
de un electrón, hablaremos de la probabilidad de
que se encuentre en un lugar en un tiempo
determinado
Aunque la posición de un electrón no puede
definirse exactamente, la probabilidad de
encontrarlo si puede calcularse
Además, si la probabilidad de encontrar al electrón
en un sitio es grande, la densidad electrónica de ese
sitio será grande
31 mayo 09
Espectroscopía
La ecuación de Schröedinger
Es decir, este modelo no explica por que hay niveles
energéticos cuantizados
Erwin Schröedinger en 1925, propone que la
manera más directa de explicar esto era enfatizar la
naturaleza ondulatoria del electrón por medio de
ecuaciones que describieran las propiedades
ondulatorias de los electrones en los átomos
Con esto, y mucha intuición, sugiere que un sistema
atómico puede tratarse con una ecuación como la
siguiente:
2
∇ ψ+
30
29
31 mayo 09
8π 2me
h2
(E −V ) ψ = 0
Espectroscopía
31
8
La ecuación de Schröedinger
Es decir, usó un método llamado mecánica
ondulatoria para describir las propiedades de los
electrones y sus niveles energéticos (orbitales)
empleando ecuaciones de onda
Además de los sistemas atómicos, hay muchos
otros sistemas mucho más familiares que se
describen satisfactoriamente con las ecuaciones de
onda
Entre estos fenómenos se encuentra el de una
cuerda de guitarra que al fijarse en dos extremos,
produce únicamente notas de cierta frecuencia (la
fundamental y sus harmónicos)
Es decir, las vibraciones de una cuerda fija en sus
dos extremos, están cuantizadas
31 mayo 09
Espectroscopía
32
La ecuación de Schröedinger
Esto, es una consecuencia perfectamente natural,
del hecho de ambos extremos de la cuerda estén
fijos
Por cierto el fijar los extremos de la cuerda
constituye lo que llamamos condición a la frontera
de la ecuación de onda que describe las notas
La ecuación de onda empleada para describir el
comportamiento de los electrones en un átomo,
requiere de manera similar, la imposición de ciertas
condiciones a la frontera perfectamente naturales
Esta ecuación de onda que ha causado problemas a
muchas generaciones de estudiantes, y seguramente
continuará haciéndolo, pero las matemáticas no las
vamos a resolver en nuestro curso
31 mayo 09
Las unidades de energía
energía (breviario)
La energía
energía puede expresarse de muchas maneras y
existen dos expresiones que nos permiten
transformarla de unas unidades a otras libremente.
La primera de estas relaciones es:
c = νλ
Donde c es la velocidad de la luz en el vacío, λ la
longitud de onda y ν la frecuencia
La segunda de estas relaciones es:
E = hν
Donde E es la energía de la radiación, h la constante
de Plank y ν la frecuencia
Y por tanto, la frecuencia y la energía
energía son
inversamente proporcionales a la longitud de onda.
31 mayo 09
Espectroscopía
34
Espectroscopía
33
Las unidades de energía
energía (breviario)
Una tabla con las unidades de energía
energía más comunes
se presenta a continuación:
1.Joule
1.Joule por mol (J/mol):
J/mol): Un Joule es la unidad de
energía
energía del SI definida como: kg•
kg•m 2/s2. Dado que
las energías asociadas a una sola molécula son
extraordinariamente pequeñas usualmente
discutimos la energía empleada por una mol de
sustancia.
2.N
2.Número de onda (cm
(cm-1): También se conoce
como centímetros a la menos uno (o recíproco de
cm).
cm). Estas unidades se obtienen cuando la
frecuencia se expresa en hertz (1/s)
1/s) y la velocidad
de la luz se expresa en cm/s,
cm/s, típicamente se
emplea en las diferentes espectroscopias.
31 mayo 09
Espectroscopía
35
9
Comportamiento espectroscópico
Las unidades de energía
energía (breviario)
3. Caloría por mol (cal/mol):
cal/mol): La caloría
caloría se define
originalmente como la cantidad de energía
necesaria para calentar un gramo de agua un
grado centígrado.
4. Electrón volt (eV):
eV): Se define como la energía
obtendrá in electrón al acelerarlo por una
diferencia de potencial de in volt.
volt. Esta cantidad
se emplea preferentemente en las áreas de
fisicoquímica y electroquímica.
5. Litros atmósfera (L-atm
): Es una unidad que
(L-atm):
relaciona presión y trabajo.
31 mayo 09
Espectroscopía
36
Para apreciar la magnitud y como se puede medir el
valor de Δο o 10Dq
10Dq;; examinemos un caso sencillo
El [Ti(H2O)6]3+, un complejo que en disolución
acuosa presenta un color púrpura muy notable
Esta propiedad además de caracterizar al complejo
cualitativamente, puede hacerlo también
cuantitativamente, para ello es necesario medir el
espectro de absorción de la disolución
El espectro de este en la región del visible, presenta
una banda centrada en 499.3 nm, lo cual
corresponde a una frecuencia de 20029 cm-1 que a
su vez puede transformarse en 239.58 kJ / mol
31 mayo 09
Comportamiento espectroscópico
 Espectro del [Ti(H2O)6]3+, en agua:
31 mayo 09
Espectroscopía
Espectroscopía
37
Comportamiento espectroscópico
Para poder explicar este espectro, recurrimos a la
teoría del campo cristalino
La cual, nos indica que en la configuración d 1 en su
estado basal, el electrón ocupará uno de los
orbitales degenerados t2g
Y que al adquirir energía procedente del haz de luz
incidente, empleará esta energía para subir a un
estado excitado de energía superior, es decir alguno
de los orbitales eg
Entonces el color púrpura es el resultado de la
absorción de la luz de cierta frecuencia la cual se
emplea en la promoción del electrón de un orbital
t2g a uno eg
38
31 mayo 09
Espectroscopía
39
10
Comportamiento espectroscópico
 Interacción luz-electrón, (dependencia del campo):
31 mayo 09
Espectroscopía
40
Comportamiento espectroscópico
Esta transición se puede representar así:
t2g0 eg1 ← t2g1 eg0
Esta es la más sencilla de las transiciones
observables en los elementos de transición, pues
dicha transición refleja directamente la diferencia
de energía entre los dos estados (basal y
excitado) del sistema
Cuando el sistema estudiado tiene otras
interacciones, por ejemplo entre los electrones
que cohabitan en el mismo nivel energético (d
(d2 en
adelante) , dichas interacciones deberán tomarse
en cuenta
Hablaremos de ellas más adelante
31 mayo 09
Distorsión tetragonal y espectro
Si dos ligantes trans de un octaedro se alejan o se
acercan del ion metálico a lo largo de un eje, ocurre
una distorsión
Tales distorsiones no se ven favorecidas puesto que
ordinariamente ello conlleva una pérdida en la
energía de enlace
Sin embargo, en ciertas situaciones se presenta un
efecto que favorece tales distorsiones
Se le conoce con el nombre de efecto de Jan-Teller,
y está basado en el teorema que dice:
una molécula no lineal en un estado electrónico
degenerado, debe distorsionarse para disminuir
su simetría
de manera que pierda la degeneración y
disminuya su energía
31 mayo 09
Espectroscopía
42
Espectroscopía
41
Distorsión tetragonal y espectro
Este teorema no predice el tipo de distorsión que
ocurrirá
Una representación intuitiva de este problema, que
es quizá más aceptable que el teorema abstracto,
surge del hecho de que las configuraciones
electrónicas susceptibles a la distorsión (d
(d 1 por
ejemplo), no son esféricamente simétricas
En el caso de una estructura octaédrica, el electrón,
presente en uno de los orbitales (d
(d z2), repelerá a los
ligantes en esa dirección
O de otra manera, la electronegatividad del ion
metálico respecto a los ligantes será menor en la
dirección z que en cualquiera de las direcciones x o y
31 mayo 09
Espectroscopía
43
11
Distorsión tetragonal y espectro
A este fenómeno físico se le llama:
anisotropía
La anisotropía dará como resultado en enlaces más
repulsivos en la dirección z y menos repulsivos en
las otras
Así, los enlaces en el primer caso serán más largos
que los demás
demás
Si el electrón hubiese estado en el orbital dx2-y2 la
anisotropía actuaría de manera opuesta, y el
acortamiento se presentará en el eje z
Esta representación tiene la ventaja de ser fácil de
visualizar
Aunque no es capaz de darnos los resultados
cuantitativos que se obtienen empleando el
teorema
31 mayo 09
Espectroscopía
44
Distorsión tetragonal y espectro
Así, en el caso de un ion como el [Ti(H2O)6]+3, en un
campo octaédrico
Con una configuración t2g1 (triplemente
degenerada), estará sujeto a la distorsión de JanTeller
Dado que según el teorema la triple degeneración
está prohibida, se presentará una distorsión
Al presentarse la distorsión, el electrón podrá
ocupar un nivel energético de menor energía
A pesar de que el teorema no indica la dirección en
que ocurrirá la distorsión, en este caso es factible
ver que la estabilización del electrón es
aproximadamente dos veces mayor si hay una
compresión que si hay una descompresión
Es decir, la EECC será mayor en D4h que en O h
31 mayo 09
Distorsión tetragonal y espectro
Cambios en la energía
energía de los orbitales debido a una
distorsión tetragonal:
Espectroscopía
45
Distorsión tetragonal y espectro
Por tanto, el espectro de este ion deberá mostrar
dos señales (bandas) en vez de una sola
En todo caso esta distorsión
distorsión provoca que se
presente una transición adicional
31 mayo 09
Espectroscopía
46
31 mayo 09
Espectroscopía
47
12
Distorsión tetragonal y espectro
La mejor evidencia de la presencia de este efecto
viene del estudio estructural de sólidos de Cu(II)
Este elemento tiene la configuración d9, en este
caso el noveno electrón podrá
podrá ocupar tanto el
orbital dz2 como el d x2-y2 , haciendo que el sistema
esté
esté degenerado obligando al complejo a
distorsionarse
Otra manera de ver este problema es empleando el
formalismo del agujero, que describe a este sistema
como un d 10 pero con un agujero
Este se comporta exactamente como un electrón,
excepto que en vez de ocupar el orbital de menor
energía flotará hacia el de mayor energía
¡Por cierto! esta descripción permite describir
todos los sistemas dn como d 10-n inversos
31 mayo 09
Espectroscopía
48
Distorsión tetragonal y espectro
Así el espectro de los complejos tetragonales de
Cu(II) puede considerarse como el los de Ti(III) pero
invertido
31 mayo 09
Estados atómicos y términos
Los estados energéticos de un ion libre:
Antes de entrar a la siguiente etapa en el estudio
del efecto de los ligantes sobre los iones
metálicos, es necesario que examinemos un poco
la teoría que se encuentra detrás de los niveles
energéticos de un ion en ausencia de los ligantes
Para ello es necesario establecer claramente el
significado de dos cantidades que serán parte de
nuestra discusión a partir de este momento
El primero de ellos es la configuración:
Es la asignación de un número determinado de
electrones a un conjunto de orbitales
Así, cuando hay dos electrones en los orbitales d,
tendremos la configuración d 2
Que se extiende a cualquier conjunto de orbitales
31 mayo 09
Espectroscopía
50
Espectroscopía
49
Estados atómicos y términos
Y el segundo es el Término espectroscópico
espectroscópico::
Es un nivel energético de un sistema atómico
El cual debe especificarse por su configuración
Cada configuración da a lugar a un número de
niveles energéticos y por tanto a un número igual
de términos
La energía de cada una de las transiciones
espectrales del átomo de hidrógeno se puede
determinar usando la fórmula de Rydberg:
Rydberg:
 1
1 

ν = 109737cm −1  − 
 n 2 n 2 
1
2
para n2 > n1, siempre y cuando sean enteros
31 mayo 09
Espectroscopía
51
13
Una pequeña desviación histórica
Esta ecuación consta de dos términos,
Es práctica común entre los espectroscopistas
aplicar esta palabra a las energías asociadas a los
estados de un átomo que presenta una transición
espectroscópica
Entonces, los términos espectroscópicos son en
esencia, una descripción abreviada de la energía, el
momento angular y la multiplicidad del espín de un
átomo en un estado particular
De esta manera es conveniente que seamos capaces
de especificar
la energía,
el momento angular y
la multiplicidad
Con una representación simbólica
31 mayo 09
Espectroscopía
52
Estados atómicos y términos
Se puede demostrar, que entre los electrones de una
capa semillena ( de valencia) y los de una capa llena
(del kernel) no hay otras interacciones además del
apantallamiento de la carga nuclear efectiva que
estos últimos ejercen sobre los primeros
En tanto que, los electrones dentro de una capa
semillena en un ion libre, están sujetos a dos
perturbaciones: Primeramente está la repulsión
interelectrónica
La energía de la configuración depende de la
manera en que los electrones ocupan los orbitales
de la capa (es decir de su simetría
simetría))
La repulsión interelectrónica separa a los niveles
degenerados
31 mayo 09
Espectroscopía
54
Una pequeña desviación histórica
Aunque los términos espectroscópicos se derivan
de los orbitales atómicos, el proceso histórico
ocurrió al revés
Es decir, primero se observaron los estados
espectroscópicos S, P, D y F; y se nombraron por
las características de las líneas espectrales
(S → P) = sharp,
(P → S) = principal,
(D → P) = diffuse y
(F → D) = fundamental
Y no fue sino hasta más tarde, que los símbolos s,
p, d y f se emplearon para designar los orbitales
atómicos
31 mayo 09
Espectroscopía
53
Estados atómicos y términos
Además, existe la interacción de los momentos de
espín y orbital a través del mecanismo de
acoplamiento espín-orbital
Este separa a su vez a los estados de diferente
ocupación
Esto puede representarse con el siguiente esquema:
31 mayo 09
Espectroscopía
55
14
Estados atómicos y términos
La separación de una configuración se presenta
entonces con diferentes términos cada uno con una
energía característica
Esta, está
está determinada por dos factores:
La repulsión
repulsión interelectrónica
Las interacciones espín-orbital
La separación energética debida a la repulsión
repulsión
electrónica en los iones libres es del orden de los
10000 cm-1
En tanto que las interacciones espín
espín orbital son del
orden de 1000 cm-1
Dado que la energía
energía debida a la repulsión
repulsión
interelectrónica es un orden de magnitud mayor
que las energías de acoplamiento espín-orbital,
enfocaremos nuestra atención al primer fenómeno
31 mayo 09
Espectroscopía
56
Estados atómicos y términos
Podemos definir un número cuántico L que tiene la
misma relación al estado atómico, como la que l
tiene a un orbital atómico (L=2
(L=2 describe un estado
D) y se determina así:
L = l1 −l2 ,l1 −l2 −1,…,l1 −l2 − 2, l1 −l2
De la misma manera que la componente Z del
momento orbital de un electrón lz se especifica por
el número cuántico ml, la componente Z del
momento orbital total Lz se especifica por el
número cuántico ML
Y también podemos definir entonces la componente
Z del momento angular total como:
Estados atómicos y términos
Para ello debemos recordar las siguientes
definiciones:
Un término es un nivel energético que surge de una
configuración y se caracteriza por:
su momento angular orbital total, L , que puede
ser cero, o entero positivo y es equivalente a la l
del caso monoelectrónico
su momento angular de espín total, S, que puede
ser cero, entero positivo o semientero,
equivalente a la s del caso mono-electrónico.
Así tenemos que los átomos que tienen estados S,
P, D o F, tienen el mismo momento angular de un
electrón en un orbital s, p, d o f en el átomo de
hidrógeno
31 mayo 09
Espectroscopía
El número posible de valores de ML está dado por:
ML =
∑m
li
= ml + ml + ml + ! + ml
1
2
3
n
De la misma manera podemos definir un número
cuántico de espín que represente el espín atómico
total:
S=
∑s
i
Así para un valor dado de S, habrá 2S+1 estados de
espín caracterizados por MS,
O
M S = S,S −1,S − 2,!,−S
M S = ms + ms + ms + ! + ms
1
58
57
Estados atómicos y términos
M L = L,L −1,L − 2,!, 0,!,−L
31 mayo 09
Espectroscopía
31 mayo 09
2
Espectroscopía
3
n
59
15
Estados atómicos y términos
Ahora bien, el momento angular total de un
electrón cualquiera, es la resultante de dos
contribuciones:
El vector de momento angular orbital
Y el vector de momento angular de espín
Dado que ambos están cuantizados, podemos definir
un nuevo número cuántico j así:
j = l +s
en virtud de que s = ± ½,
½, es obvio que cualquier
valor de l tendrá dos valores de j los cuales serán
iguales a l+½ y l−½
31 mayo 09
Espectroscopía
60
Estados atómicos y términos
Ahora, usando este nuevo número cuántico para los
estados atómicos, podemos acoplar el momento
total angular orbital (L
(L) con el momento total de
espín (S
(S), y obtendremos un número cuántico total
atómico (J
(J ) así:
J = L + S,L + S −1,L + S − 2,!, 0,!, L − S
El origen de los valores de J puede concebirse como
la resultante de la suma vectorial de las dos
contribuciones
El número de valores que J puede adquirir cuando
L>S será igual a 2 S+1
Un término se etiqueta empleando sus valores de L
S y J usando el siguiente esquema: (2S+1)X J
31 mayo 09
Estados atómicos y términos
En donde X se etiqueta usando una letra de acuerdo
a su valor, así:
L=
0
1
2
3
4
5
6
X=
S
P
D
F
G
H
I
La cantidad 2S+1 se conoce con el nombre de
multiplicidad del término y es igual al número de
electrones desapareados más uno
Los términos se nombran según el valor de S así:
S
0
½
1
1½
2
2½
singulete doblete triplete cuarteto quinteto sexteto
Finalmente el valor de J se pone como subíndice a la
derecha del término
31 mayo 09
Espectroscopía
62
Espectroscopía
61
Estados atómicos y términos
Regresemos momentáneamente al mundo real y a
los espectros que generaron esta nomenclatura
Consideremos las transiciones de un orbital 1s a uno
2p en el hidrógeno
Los términos de estas transiciones son:
2S
1/2
2S
1/2
→ 2P1/2
→ 2P3/2
Debido a que el término 2P1/2 tiene un poco más de
energía que el 2P3/2, la línea espectral se divide en
dos, es decir se genera un doblete, este, es el origen
del uso de la palabrita
31 mayo 09
Espectroscopía
63
16
Asignación de los términos
Asignación de los términos
Ahora bien, para el B, las subcapas 1s2 y 2s2 tienen
L=0,
L=0, S=0 y J=0 y por tanto no contribuyen, sin
embargo el electrón en 2p1, tiene L=1 y S=½ y
J=1 ± ½
Esto nos da los siguientes términos: 2P1/2 y 2P3/2
Hemos visto que el término con que se representa el
estado basal del hidrógeno es 2S1/2
Para el átomo de helio, L=0 y S=0 y J=0 entonces
el término del estado basal del He será: 1S0
Para el caso del Li y el Be,
Be, aprovechamos el hecho de
que las capas y subcapas cerradas no contribuyen al
término (tal como en el caso del He)
He)
entonces el Li tiene un estado basal igual al del H
(2S1/2)
Y como en el Be,
Be, L=0 y S=0 y J=0,
=0, entonces su
estado basal será igual al del He (1S0)
31 mayo 09
Espectroscopía
64
Nótese, que una vez que lleguemos al Ne,
Ne,
tendremos nuevamente que su estado basal se
podrá representar con el término 1S0 (el mismo
que el del He)
He)
Y claro el Na tendrá el mismo que el del Li (2S
(2S1/2)
Y el Mg el mismo estado basal que el Be (1S
1S
( 0) y así
sucesivamente
31 mayo 09
Espectroscopía
Asignación de los términos
Configuraciones permitidas (Principio de Pauli)
Pauli)
Para encontrarlas construimos una tabla que
muestra todos los posibles arreglos que pueden
tener los electrones en los orbitales escogidos
En la tabla cada columna contiene al conjunto de
orbitales deseados
Cada celda puede contener únicamente 0, 1(↑
1(↑) o
2 (↑↓
(↑↓)) electrones, si son dos deben aparearse
Cada columna representa un microestado, cada
microestado es una combinación de ML y MS
El valor de ML para cada arreglo se encuentra
sumando ml y el de MS sumando ms
(Ojo: se asigna el valor de +½ a las flechas
hacia arriba y – ½ a las flechas hacia abajo)
31 mayo 09
Espectroscopía
66
65
Asignación de los términos
Como ejemplo veamos la configuración
configuración del C en su
estado basal (C=1s
(C=1s22s22p2) es decir, p2
Se hace una tabla con todos los arreglos que pueden
tener 2 electrones en los orbitales disponibles
Como tenemos 3 orbitales p, ml vale+1,
vale+1, 0 y -1
ml
+1 ↑↓
0
↑↓
-1
↑
↑
↑↓
↑
↑
↑
↑
↓ ↓
↓
↓
↓ ↓
↑ ↑
↓
↓
↑ ↑
↓ ↓
↓
↑
↓
↑
Se obtiene MS = ∑ms
MS 0 0 0 +1 +1 +1 -1 -1 -1 0 0 0 0 0 0
y ML = ∑ m l
ML +2 0 -2 +1 0 -1 +1 0 -1 +1 0 -1 +1 0 -1
31 mayo 09
Espectroscopía
67
17
Asignación de los términos
Después
Después contamos los microestados
ML +2 0 -2 +1 0 -1 +1 0 -1 +1 0 -1 +1 0 -1
MS 0 0 0 +1 +1 +1 -1 -1 -1 0 0 0 0 0 0
y los clasificamos en otra tabla de ML x MS estados,
según los valores de obtenidos en la tabla anterior
En esta, el microestado de la primera columna,
tiene ML=+2 y MS=0 y lo
MS
colocamos en el lugar
+1
0
-1
correspondiente, se
hace lo mismo
-2
para cada
-1
microestado
ML
0
y de esta
manera
+1
construímos
+2
la nueva tabla
31 mayo 09
Espectroscopía
68
Asignación de los términos
Después, separamos de la tabla de microestados los
estados atómicos apropiados:
Los estados se deben construir tomando en
cuenta que el arreglo de microestados debe tener
los valores valores apropiados de ML y MS del
estado que forman
Para ello consideramos que cada estado atómico
forma un arreglo de microestados que tiene
2S+1 columnas y 2L+1 renglones
Por ejemplo,
ejemplo, un estado 3P requerirá
requerirá de un
arreglo de 3x3 microestados
Uno 1D, de una columna de 5 microestados y
Un 1S de un solo microestado y así
así en cada caso
31 mayo 09
Espectroscopía
70
Asignación de los términos
Para asegurar que todos los microestados se han
escrito, se recurre a la fórmula siguiente:
N =
Nl !
x ! (N l − x )!
Donde N es el número de microestados asociados a
una configuración lx que tiene x electrones en un
conjunto de orbitales con un número cuántico
azimutal l, donde Nl = 2(
2(2l+1)
2l+1)
Es decir el número de combinaciones de ml y ms
para un solo electrón en el conjunto de orbitales
31 mayo 09
Espectroscopía
69
Asignación de los términos
Entonces de la tabla vemos que hay :
+1
ML
MS
0
-1
-2
-1
0
+1
+2
3 microestados con ML=0 y MS=0,
=0, uno es 1S
5 microestados con ML de +2 a -2,
-2, de 1D
Resta una matriz de 3x3 es decir un estado 3P
Entonces los estados de la configuración
configuración p2 son:
son:
1S, 1D y 3 P
31 mayo 09
Espectroscopía
71
18
Asignación de los términos
¿Pero y cómo
cómo los ordenamos energéticamente?
Pues para eso nos acordamos que las interacciones
de repulsión separan a los tripletes (sistemas con
electrones desapareados) de los singuletes
(sistemas con electrones apareados (en el mismo
orbital) alrededor de 10000 cm-1
En tanto que el acoplamiento espín-orbital
espín-orbital separa
un orden de magnitud menos
Los términos degenerados 3P se separarán aun más
en presencia de un campo magnético
A este método se le conoce como acoplamiento de
Russel-Saunders y puede emplearse para átomos
con mayor número de electrones que el del caso
anterior
31 mayo 09
Espectroscopía
72
Asignación de los términos
Pero a nosotros lo que nos interesa es lo que les
ocurre a los electrones que están
están en orbitales d,
entonces revisaremos los resultados que se
obtienen empleando este método para la serie dn :
d 1: ya hemos visto que en este caso hay 10
maneras de poner a un electrón en los cinco
orbitales d,
por tanto esta configuración únicamente tiene
un término 2D
Es decir, esta configuración genera un solo
término d1 → 2D
ML máxima es 2
31 mayo 09
Espectroscopía
74
Asignación de los términos
El resultado de este relajo se puede presentar
empleando un diagrama como el que se muestra a
continuación en lo que llamamos un diagrama de
Russell-Saunders:
31 mayo 09
Espectroscopía
73
Asignación de los términos
En el caso siguiente las cosas se complican un poco:
d 2: hay 45 maneras de poner dos electrones en
cinco orbitales, los valores de M L de estos
arreglos ocurren el siguiente número de veces:
ML = ±4 ssd 1 vez
= ±3 ssd 4 veces
= ±2 ssd 5 veces
= ±1 ssd 8 veces
= 0 ssd 9 veces
total =
ssd 45 veces
Después
Después de expurgar,
expurgar, esta configuración
genera:
d 2 → 1G(9),
(9), 1D(5),
(5), 1S(1),
(1), 3F(21),
(21), 3P(9)
31 mayo 09
Espectroscopía
75
19
Asignación de los términos
Asignación de los términos
¿Pero y las demás
demás configuraciones es decir, que
pasa cuando tenemos las configuraciones d 3 a d 9 ,
El argumento empleado para asignar los
términos de las configuraciones superiores es
similar al empleado hasta ahora
Aunque evidentemente resulta ser, que entre
más electrones tengamos, el problema de la
asignación puede convertirse en algo
asquerosamente laborioso
Espectroscopía
76
Regla de Hund
En todo caso, una vez que se han encontrado los
términos que surgen de una configuración, se
requiere saber algo acerca del orden energético
que tienen
Para conseguir esto, debemos tomar en cuenta las
siguientes reglas:
El término más importante será el que tiene la
menor energía (estado basal del sistema), esto
se decide aplicando las reglas de Hund,
Hund, que
plantean lo siguiente:
El término que tiene la mayor multiplicidad
tiende a ser el de menor energía
De los términos con igual multiplicidad el de
mayor L será el que tenga la menor energía
31 mayo 09
Espectroscopía
Configuración Términos
s2, p6 y d10
p1 y p 5
p2 y p 4
p3
d1 y d 9
d2 y d 8
d3 y d 7
d4 y d 6
d5
A continuación se presentan los términos
encontrados para cada configuración
electrónica
31 mayo 09
Términos de las capas llenas y semillenas
78
31 mayo 09
1S
2P
3P, 1D, 1S
4S, 2D, 2P
2D
3F, 3P, 1G, 1D, 1S
4F, 4P, 2H, 2G, 2D, 2F, 2D, 2P
5D, 3H, 3G, 3F, 3F’, 3D, 3P, 3P’, 1I, 1G, 1F, 1D,
1D’ , 1S, 1S ’
6S, 4G, 4F, 4D, 4P, 2I, 2H, 2G, 2G’, 2F, 2F’ , 2D,
2D’ , 2D”, 2P, 2S
Espectroscopía
77
Regla de Hund
Así es fácil aunque muy laborioso en ocasiones
obtener el estado basal de cada configuración
Las energías relativas de los demás estados se
pueden calcular empleando argumentos empíricos
equivalentes
Aunque hemos indicado que para conocer los
valores de energía exactos de los desdoblamientos
del campo cristalino, debemos considerar las
interacciones electrón-electrón, si hay más de uno
Hasta este momento, únicamente hemos
considerado el llamado caso mono-electrónico aun
cuando fuesen muchos los electrones d de los que
hablábamos
En tanto que hablemos cualitativamente del
problema, esto no presenta problemas serios
31 mayo 09
Espectroscopía
79
20
Espectroscopia, un poco más
Sin embargo la interpretación cuantitativa
requiere de mayor cuidado
Examinemos ahora que ocurre con el momento
angular total de los diferentes orbitales ocupados
por un solo electrón en presencia de un campo:
Configuración ML Espín; Multiplicidad Estado
s 1:
L=0
S=½ ; (2x½+1)=2 ⇒
2S
p1 :
L=1 S= ½ ; (2x½+1)=2 ⇒
2P
d1 :
L=2 S= ½ ; (2x½+1)=2 ⇒
2D
f 1:
L=3 S= ½ ; (2x½+1)=2 ⇒
2F
31 mayo 09
Espectroscopía
80
Espectroscopia, un poco más
Al acercar ligantes (Oh por ejemplo), en cada caso
tendremos:
s1 (2S):
S): es esféricamente simétrico y no se verá
afectado por el campo, genera un solo estado
p1 (2P):
P): si el campo es octaédrico, genera un estado
triplemente degenerado,si el campo es de menor
simetría puede desdoblarse en varios estados
d1 (2D):
D): en ausencia de fuerzas externas, el
conjunto de cinco orbitales es degenerado y su
estado basal es 2D (el electrón puede estar en
cualquiera de los cinco orbitales con espín α o β),
en presencia de un campo octaédrico, los orbitales
degenerados se desdoblan en un triplete y un
doblete de mayor energía
f1 (2F):
F): en un campo octaédrico tendremos dos
tripletes
y un singuleteEspectroscopía
con diferente energía
energía
31 mayo 09
81
Espectroscopia, un poco más
Entonces los orbitales mencionados se transforman
así:
Término
Campo octaédrico
Estados
2S
→
(A1g)
Espectroscopia, un poco más
Otros términos
términos y la influencia del campo octaédrico
Término Ion →Oh Componentes (estados en Oh)
S
→ A1g
2P
→
(T1u)
P
→ T1u
2D
→
(T2g ) (E
(Eg)
D
→ Eg+T2g
F
→ A2g+T1g+T2g
G
→ A1g+ Eg+T1g+T2g
H
→ Eg+T1g+T1g+ T2g
I
→ A1g+A2g+Eg+T1g+T2g+ T2g
2F
→
(T1g ) (T2g) (A2g)
Es claro que las transformaciones en otros campos
serán diferentes,
Pero los términos que tienen la misma L, tendrán
transformaciones equivalentes
Y serán independientes de la multiplicidad
31 mayo 09
Espectroscopía
82
31 mayo 09
Espectroscopía
83
21
Espectroscopia, un poco más
Regresamos al problema de las configuraciones dn,
en particular al caso d2
En ausencia de un campo, esta configuración
presenta dos estados con la misma multiplicidad, 3F
y 3P; los demás estados tienen menor multiplicidad
y por tanto se encuentran a mayor energía
El estado basal debe ser aquel que tiene a los dos
electrones en diferentes orbitales
Si se aplica un campo octaédrico, estos orbitales
deben ser dos de los orbitales t2g
Al excitar uno de estos electrones para promoverlo
a los orbitales eg, encontramos que existen dos
posibilidades
31 mayo 09
Espectroscopía
84
Espectroscopia, un poco más
Es decir que el sistema tiene tres transiciones
posibles:
del estado basal a [(xy
[(xy))1(z 2) 1]
del estado basal a [(xy
[(xy))1(x2-y2)1]
y finalmente del estado basal a [eg2]
Si regresamos al asunto del desdoblamiento en
presencia de un campo octaédrico
octaédrico,, recordamos que
los orbitales p no cambian ante este, pero los f sí
sí
Si recordamos que los dos términos
términos que surgen de
la configuración d2, son F y P, y que estos términos
términos
se comportan exactamente igual que los estados f y
p que surgen de las configuraciones f1 y p1,
31 mayo 09
Espectroscopía
86
Espectroscopia, un poco más
La primera puede ser, que el electrón promovido
provenga de los orbitales xz o yz,
yz, puede pasar:
al orbital z2
o al orbital x 2-y 2
Nótese que las dos configuraciones resultantes
[(xy
[(xy))1( x2-y2)1] y [(xy
[(xy))1(z 2) 1] tienen diferente energía,
debido a la repulsión ínterelectrónica
Pues la primera obliga a los electrones a estar en la
misma vecindad (el plano xy)
xy)
Evidentemente si el electrón procede del orbital xy
se puede argüir similarmente que las dos
configuraciones resultantes tienen diferentes
energía
Cuando ambos electrones se promueven
(configuración [eg2]), se obtiene un estado
energético adicional
31 mayo 09
Espectroscopía
85
Espectroscopia, un poco más
De esta manera, el estado F se desdoblará en tres
estados [( 3T1g ), ( 3T2g ), ( 3A2g )]
En tanto que el P permanecerá como un solo
estado, [( 3T1g )]
El desdoblamiento de los
estados de menor energía
de las configuraciones
d1 y d2 se muestra a
continuación
31 mayo 09
Espectroscopía
87
22
Espectroscopia, un poco más
¿Pero y las demás
demás configuraciones?
Pues ya hemos visto que los estados de las demás
configuraciones serán:
d3 (4F, 4P), d4 (5D) y d5 (6S)
Si ahora empleamos el formalismo del agujero,
donde cada configuración d10-n se trata como si
fuera dn invertida debido a que los agujeros tienden
a flotar hacia el estado de mayor energía
Y dado que los estados de las configuraciones
restantes son:
d8( 3F, 3P), d7( 4F, 4P) y d6(5D)
Notamos de inmediato que los estados de menor
energía son todos S, P, D o F; para cualquiera de
las configuraciones dn
31 mayo 09
Espectroscopía
88
Espectroscopia, un poco más
Por tanto el desdoblamiento de los estados ante un
campo octaédrico de los estados de cada
configuración, ocurre como se indica a
continuación:
continuación:
las configuraciones d1 y d4 se desdoblan como se
muestra en la figura (a
(a), en tanto que las
configuraciones d6 y d9 como la figura (a
(a) pero
invertida
Las configuraciones d2 y d3 como la figura (b
(b),
mientras que las configuraciones d8 y d7 como la
figura (b
(b) pero invertida
Finalmente las configuraciones d 0, d 5 y d 10 no se
desdoblan pues todas son S
31 mayo 09
Espectroscopia, un poco más
Las transiciones posibles de las configuraciones d1 y
d2 :
31 mayo 09
Espectroscopía
90
Espectroscopía
89
Espectroscopia, un poco más
Ion libre Estado basal
2D
d1
3F
d2
4F
d3
5D
d4
6S
d5
5D
d6
4F
d7
3F
d8
2D
d9
1S
d10
31 mayo 09
Complejo
Diagrama
(t2g)1
a
(t2g)2
b
(t2g)3
b invertido
(t2g)3 (eg)1
a invertido
(t2g)3
(eg)2
Sin desdoblamiento
(t2g)4 (eg)2
a
(t2g)5
(e
(eg)2
b
(t2g)6
(eg)3
b invertido
(t2g)6
(eg)4
a invertido
(t2g)6
(eg)5
Sin desdoblamiento
Espectroscopía
91
23
Espectroscopia, un poco más
Espectroscopia, un poco más
31 mayo 09
Espectroscopía
92
Las reglas de selección
Como hemos visto, la estimación de las diferencias
de energía entre los varios estados es relativamente
simple de hacer
Sin embargo, no hemos indicado algo fundamental,
esto es, si las transiciones ocurren o no
Experimentalmente hemos visto que en muchos de
los sistemas electrónicos, el número de estados que
encontramos es mucho mayor que el que se
requieren para explicar nuestros espectros
Para poder entender esto, es necesario conocer las
de las reglas que gobiernan estas transiciones
Sabemos que la materia puede absorber energía
energía
siempre y cuando la energía de la radiación sea
igual a la diferencia entre los niveles cuantizados de
diferentes estados de la sustancia
31 mayo 09
Espectroscopía
94
31 mayo 09
Espectroscopía
93
Las reglas de selección
Pero para que ocurra una transición,
transición, es decir, para
que el componente del campo eléctrico de la
radiación se absorba o emita, hay un requisito
adicional
Este es que la transición energética en la molécula
debe estar acompañado por un cambio en su centro
eléctrico para que se pueda hacer trabajo eléctrico
por el campo electromagnético de la radiación
Únicamente si se satisface esta condición, la
transición ocurrirá
Los requisitos para que ocurran estas transiciones
están resumidos en un conjunto de reglas que
conocemos como reglas de selección
Las cuales, reflejan las restricciones que tienen los
átomos o las moléculas en sus cambios de estado
31 mayo 09
Espectroscopía
95
24
Las reglas de selección
Entonces, aquellas transiciones que son posibles de
acuerdo a estas reglas, las conocemos como
transiciones permitidas
De hecho, cualquier transición no cumple con estas
reglas, se dice que está prohibida
Aunque claro, como en la vida, en realidad lo que
tenemos es que hay unas transiciones más
prohibidas que otras
Debe notarse sin embargo que el término
término
prohibidas se refiere a si se cumplen un conjunto de
reglas impuestas por un modelo simple
Y aunque este es un buen modelo, pueden ocurrir
transiciones a través de mecanismos no
considerados en el mismo
31 mayo 09
Espectroscopía
96
Las reglas de selección
Primera regla de selección
Esta regla indica que para que una transición
transición sea
permitida debe haber un cambio de 1 en el número
cuántico azimutal l,
l, es decir D l=±1
Esto significa que, las únicas transiciones
permitidas son aquellas donde hay un entre
orbitales de diferente subcapa
Es decir, si la transición ocurre de orbital s a
uno p o de uno p a uno d o de uno d a uno f, la
transición está permitida,
Cualquier otra combinación
combinación está prohibida,
esto significa claro que las transiciones entre
orbitales d están formalmente prohibidas
Aquellas transiciones prohibidas por esta regla se
les llama prohibidas por espín
espín
31 mayo 09
Espectroscopía
98
Las reglas de selección
La intensidad de la absorción
absorción o la emisión que
acompaña una transición está relacionada a la
probabilidad con que ocurre dicha transición
Es decir entre más probable sea una transición, más
intensa será la emisión o la absorción que la
acompaña
De esta manera, las transiciones permitidas valores
de probabilidad grandes y por tanto tienen
asociadas absorciones de mayor intensidad
En tanto que las transiciones prohibidas tienen
valores de probabilidad pequeños y por tanto dan
absorciones de poca intensidad
Hay tres reglas de selección relevantes en
espectroscopia electrónica
31 mayo 09
Espectroscopía
97
Las reglas de selección
Segunda regla de selección (multiplicidad de espín
espín))
Esta regla indica que para que una transición
transición ocurra
el estado final y el inicial deben tener la misma
multiplicidad de espín
Esto significa que, las únicas transiciones
permitidas son aquellas el espín
espín total del sistema
no cambia, además tal cambio se refiere no
solamente a la transición en sí, sino al cambio de
espín del propio electrón
Es decir, las transiciones permitidas son
aquellas que ocurren entre dos estados con la
misma multiplicidad
Cualquier otra combinación
combinación está prohibida
31 mayo 09
Espectroscopía
99
25
Las reglas de selección
Tercera regla de selección (de Laporte o de paridad):
Esta regla prohíbe las transiciones entre estados con
la misma simetría
simetría (o paridad) respecto al centro de
inversión
Esto significa que, las únicas transiciones
permitidas son aquellas donde hay un cambio en
la paridad
Es decir, si la transición ocurre de un estado
gerade a uno ungerade o viceversa, la transición
está permitida,
Pero las transiciones de un estado gerade a uno
gerade están prohibidas
también lo están las ungerade-ungerade
31 mayo 09
Espectroscopía
100
Las reglas de selección
Sin embargo, la espectroscopia óptica no solamente
es posible, sino que como hemos visto, es una de las
fuentes experimentales que soportan a las teorías de
enlace de los complejos
El elemento fundamental que permite explicar lo
anterior, descansa en el hecho de que las reglas de
selección se relajan a través de varios mecanismos,
permitiendo así que dichas transiciones ocurran
Uno de los mecanismos de relajación de algunas
transiciones, se presenta por medio de aquellos
movimientos vibracionales que pueden eliminar el
centro de simetría de una molécula
Y que permiten que las transiciones que de otra
manera serian prohibidas sean observables
31 mayo 09
Espectroscopía
102
Las reglas de selección
Dado que todos los orbitales d en los complejos
centrosimétricos tienen simetría gerade,
gerade, esto
significa que las transiciones d-d en todas las
moléculas octaédricas, están formalmente
prohibidas
Siendo esto cierto, parece extraño que estemos
hablando de la espectroscopia de los compuestos
de coordinación,
coordinación, pues
pues pareciera que esta no es
posible
Dada esta restricción, pudiera parecer que la
espectroscopia UV y visible de los complejos de
los metales de transición en entornos octaédricos
octaédricos
es inexistente
Puesto que las transiciones d-d no deberían verse
¿Pero y el color?
31 mayo 09
Espectroscopía
101
Las reglas de selección
Una manera en que funciona esto, tiene que ver con
los ligantes que rodean al átomo central, si no son
idénticos la molécula pierde el centro de inversión y
por tanto absorbe
O bien porque debido a que la molécula vibra
(recuerden que entre mayor sea la temperatura de
la disolución mayor energía cinética tendrán las
moléculas) de manera que el centro de simetría
simetría se
elimina temporalmente
La interacción
interacción entre los modos vibracionales y los
electrónicos se llama acoplamiento vibrionico
(vibracional-electr
ónico))
vibracional-electrónico
31 mayo 09
Espectroscopía
103
26
Las reglas de selección
Las reglas de selección
Estas transiciones son observables pero débiles,
pues el número de moléculas que tienen la
conformación asimétrica será una fracción del total
Una disolución de la misma concentración de
benceno (el
(el cual tiene únicamente transiciones
permitidas),
permitidas), dará
dará un espectro fuera de la escala
Es decir, en un instante dado, el número de
moléculas que han perdido el centro de simetría es
mucho menor que el total, típicamente, los
complejos octaédricos tienen coeficientes de
extinción que van de 1 a 100 dm3/mol cm
Como los complejos tetraédricos no tienen centro de
simetría, la regla de Laporte se relaja y las
transiciones de estos complejos son
aproximadamente 100 veces mayores que las de los
complejos octaédricos
Esto significa que si preparamos una disolución 0.1
de un complejo ML6 su espectro en la región del
visible será observable
Es decir que sus coeficientes de extinción molar
están en un intervalo de 100 a 1000 dm3/mol cm
31 mayo 09
Espectroscopía
104
Ancho de banda
Otro factor de importancia que define la
espectroscopia electrónica,
electrónica, tiene que ver con el
ancho de la banda de una transición
En general todos los espectros de los compuestos de
transición muestran bandas muy anchas
Esto también
también ocurre porque los complejos vibran,
esta vibración, hace que los ligantes se acerquen y se
alejen del metal y al hacerlo, provocan que la
energía de los orbitales involucrados en la transición
cambie
Al alejarse, la energía disminuirá y al acercarse
crecerá
Este efecto es más notable en disolución, pues hay
más choques
31 mayo 09
Espectroscopía
106
31 mayo 09
Espectroscopía
105
Espectroscopia, un poco más
A continuación
continuación los espectros electrónicos de sales de
los metales de la primera serie de transición, Titanio
(III): d1
31 mayo 09
Espectroscopía
107
27
Espectroscopia, un poco más
Vanadio (III) =d
=d2
31 mayo 09
Cromo (II) =d
=d4
31 mayo 09
Espectroscopía
108
Espectroscopia, un poco más
Espectroscopía
110
Espectroscopia, un poco más
Cromo (III) =d
=d3
31 mayo 09
Hierro (II) =d
=d6
31 mayo 09
Espectroscopía
109
Espectroscopia, un poco más
Espectroscopía
111
28
Espectroscopia, un poco más
Cobalto (II) =d
=d7
31 mayo 09
Cobre (II) =d
=d9
31 mayo 09
Espectroscopía
112
Espectroscopia, un poco más
Espectroscopía
114
Espectroscopia, un poco más
Niquel (III) =d
=d8
31 mayo 09
Espectroscopía
113
Espectroscopia, un poco más
Comparación
Comparación de las sales con configuración tipo a:
d1 , d4 , d 6 y d 9
31 mayo 09
Espectroscopía
115
29
Espectroscopia, un poco más
Comparación
Comparación de las sales con configuración tipo b:
d2 , d3 , d 7 y d 8
31 mayo 09
Espectroscopía
116
Espectroscopia, un poco más
¿Y la configuración d5?
31 mayo 09
¡Otra vez las reglas de selección!
Vale la pena aquí notar que en el caso de los
complejos d5 cuyo estado basal es el único que es
un sextuplete,
sextuplete,
De manera que todas sus transiciones no
solamente estarán prohibidas por Laporte, sino
también por espín
Las transiciones que están doblemente prohibidas
serán entonces extremadamente débiles
La regla de selección de espín se relaja como
resultado del acoplamiento de los momentos de
espín y angular de los orbitales dando absorciones
observables (2a y 3a serie)
31 mayo 09
Espectroscopía
118
Espectroscopía
117
Espectroscopia, un poco más
Tetraédricos, el caso d7
31 mayo 09
Espectroscopía
119
30
Espectroscopia, un poco más
Tetraédricos, el caso
31 mayo 09
d8
Espectros de transferencia de carga
Ocurren como resultado de un proceso de afinidad
electrónica-energía de ionización opuesto al de la
formación del enlace
Es como si en el NaCl,
NaCl, tratásemos de ionizar un
electrón del Cl− (-AE) y se lo diésemos al Na+ (-PI)
La energía de este proceso es tan grande que
solamente se obtiene empleando un fotón de alta
energía (región de UV), por eso el NaCl es blanco.
Si ahora pensamos en un compuesto que tenga un
metal para el que la energía de ionización es
mayor, el proceso de regresar el electrón al metal
se verá favorecido energéticamente y se requerirán
fotones de menor energía
Espectroscopía
120
31 mayo 09
Espectros de transferencia de carga
Un ejemplo de esto es el MnO4-, que no tiene
electrones en d y por tanto no puede tener
transiciones tipo d-d
Sin embargo, nótese que el estado de oxidación del
Mn es de +7, puede decirse que la reacción de
oxidación interna (pasar un electrón del O al metal)
ocurrirá con un fotón de poca energía, este también
es el caso del CrO42Si la terminología iónica nos la tomamos con
precaución, rápidamente entendemos que la
transferencia ocurre en realidad entre un orbital
cuyo carácter es principalmente del ligante y un
orbital que tiene carácter metálico
31 mayo 09
Espectroscopía
122
Espectroscopía
121
Espectros de transferencia de carga
Espectros del KMnO4 y el K2Cr2O7
31 mayo 09
Espectroscopía
123
31
Espectros de transferencia de carga
Y aunque es conveniente etiquetar a la transición
en términos de la predominancia de los orbitales,
no debemos perder de vista que estos orbitales
son combinaciones lineales de los orbitales de
ambos el metal y el ligante
Las transiciones observadas en este caso, dado que
no están prohibidas por ninguna de las reglas, son
las más intensas
Sus coeficientes de extinción están en el intervalo
de 10000 a 30000 dm3/mol cm
Entre estas están: las de no enlace del ligante a
enlace del metal
(eL→ eM), (t
(t2 → e) y (e
(eM → t2*).
31 mayo 09
Espectroscopía
124
Espectros de transferencia de carga
Un ejemplo de los espectros de transferencia de
carga lo tenemos en los complejos de piridina que
presentamos aquí,
aquí, además de las bandas de la
piridina aparece una banda muy intensa adicional
en 290 y 310 nm
[Ir(OH)(NH3)3(py)2]2+
[IrCl2(py)4]+
Piridina
31 mayo 09
Las reglas de selección
A continuación, un resumen de lo anterior:
ε
Tipo de
Clase de
transición
(dm3/mol cm)
Complejos
cm)
complejos d5
Prohibidas por
10-3 a 1
espín y por
bajo espín
Laporte
Prohibidas por
complejos
1 a 10
Laporte
octaédricos
Permitidas por
complejos
10 a 100
espín
cuadrados
Permitidas por
complejos
100 a 1000
espín Permitidas
tetraédricos
por Laporte
bandas de
100 a 1000000
transferencia
de carga
31 mayo 09
Espectroscopía
126
Espectroscopía
125
Diagramas de Orgel
Es muy conveniente contar con una representación
pictórica de la información con el efecto de la
fuerza del campo
Los diagramas de Orgel nos dan un medio muy
conveniente de predecir el número de bandas de un
compuesto de coordinación
Estos diagramas muestran el comportamiento de la
energía de los estados en función de la fuerza del
campo y son muy sencillos, pues omitimos los
estados que tienen multiplicidades diferentes a la
del estado basal
Y únicamente se consideran los casos de campo
débil y dejaremos a los de campo fuerte para
después
después
31 mayo 09
Espectroscopía
127
32
Diagramas de Orgel
31 mayo 09
Espectroscopía
Dq (cm-1)
128
Diagramas de Orgel
Y no solamente eso, también es factible presentar
los campos tetraédrico y octaédrico de la misma
configuración
Energía (cm-1)
15000
d1 y d 6 tetraédrico
d9 y d 4 octaédrico
d1 y d 6 octaédrico
d9 y d 4 tetraédrico
10000
5000
2E
2T
2
0
2T
-5000
-10000
2E
-2000
31 mayo 09
-1000
0
Dq (cm-1)
1000
Espectroscopía
2
2000
130
Diagramas de Orgel
Otra característica de estos diagramas es que
pueden mostrar tanto el comportamiento de una
configuración dn como la de la configuración d10-n
al mismo
tiempo
15000
d9 octaédrico
Energía (cm-1)
Energía (cm-1)
A continuación el diagrama para una configuración
d1, la más sencilla para comprender su
funcionamiento
Cl−<dtp−<F−<<H 2O<NH3<NH2CH2CH2NH2
En este
diagrama
15000
se ve que los
diferentes
10000
ligantes
separarán
5000
2E
a los dos
g
estados,
0
más, o menos,
2T
2g
dependiendo
-5000
de su posición
en la serie
espectroquímica -10000 0
500
1000
1500
2000
2500
d1 octaédrico
10000
5000
2T
g
2T
2g
2g
0
-5000
2E
-10000
g
-2000
31 mayo 09
2E
-1000
0
Dq (cm-1)
1000
Espectroscopía
2000
129
Diagramas de Orgel
De esta manera, tenemos un método
método gráfico que
nos presenta cualitativa y cuantitativamente el
comportamiento de cada configuración electrónica
ante los campos con las dos simetrías que más se
presentan
Adicionalmente tendremos que si conocemos el
valor de ΔO o Δ T de un nuevo compejo, podemos
instantaneamente situar al ligante en la serie
espectroquímica
Desafortunadamente estos diagramas únicamente
funcionarán para los compuestos de campo débil y
tendremos que emplear diagramas más
complicados para los demás
A continuación otros diagramas de Orgel
31 mayo 09
Espectroscopía
131
33
El diagrama del Co2+ (d
(d7)
4T
1
Diagramas de Orgel
=(e g)2(t2g)5
4A
Energía (cm-1)
20000
4T
4P
10000 4
T
2=(e g)
3(t
2g)
4
1g
4T
4F
2g
2g
Diagramas de Orgel
Notamos que el desdoblamiento tetraédrico, es
exactamente el inverso al del octaédrico
En este se presenta el desdoblamiento de los
términos del Co2+, (4F y 4P )
Nótese que aquí también se muestra
explícitamente el comportamiento de los estados
4T (F ) y 4T ( P) con mezcla (línea sólida) y sin
1g
1g
mezcla (línea punteada)
Esto se debe a que como los términos 4T1g tienen
la misma simetría, no pueden cruzarse
Al aproximarse se mezclan modificando su energía,
entre más se aproximen, más se mezclarán
=(t2g)4(e g)3
=(t2g)4(e g)3
=(t2g)4(e g)3
0
-10000
4T
2=(e g)
3(t
2g)
4
4T
1g=(t2g)
5(e
2
g)
-20000
4A
2=(eg )
3(t )4
2g
-1500 -1000
31 mayo 09
-500
0
500
Dq (cm-1)
1000 1500
Espectroscopía
132
31 mayo 09
Diagramas de Orgel
31 mayo 09
Espectroscopía
134
El diagrama del Ni2+ (d
(d8)
1G
Energía (cm-1)
Al centrar nuestra atención en los términos T1 se
puede notar además que debido a que estos dos
estados se encuentran más próximos que en el
caso octaédrico, se mezclan más
Así, las líneas de estos estados tienen mayor
curvatura en el caso tetraédrico que en el
octaédrico
Dado que los diagramas de Orgel,
Orgel, solo pueden
aplicarse al caso de los complejos de campo débil
(alto espín), el estado 2G no se muestra
Si añadiéramos al diagrama los estados de bajo
espín, veríamos entonces claramente, que al
aumentar la fuerza del campo, las configuraciones
d4, d 5, d 6 y d7; pueden cambiar de alto espín a
bajo espín, como se ha visto cualitativamente
Espectroscopía
20000
3P
10000
1D
3F 0
Diagramas de Orgel
3T
1g
=(t2g)4(eg)4
3T
2g
=(t2g)5(eg)3
3T
5
3
1g =(t2g) (eg)
1E =(t )6(e )2
g
2g
g
-10000
-20000
3A
500
31 mayo 09
133
1000
Dq (cm-1)
2g
=(t2g)6(eg)2
1500
Espectroscopía
135
34
Diagramas de Orgel
Un diagrama más general para los complejos O h y
Td de campo débil
31 mayo 09
Espectroscopía
136
Diagramas de Tanabe-Sugano
Además
Además para hacerlos generales habremos de
incluir algunos otros parámetros
Tomando en cuenta que la repulsión electrónica es
la responsable de las diferencias energéticas entre
los estados espectroscópicos
espectroscópicos (Términos),
(Términos), es
necesario expresarla por medio de algunos
parámetros
parámetros que hablen de ella
Estos no son más que combinaciones lineales de
algunas integrales de coulomb y de intercambio, y
se les conoce como los parámetros de Racah B y C
Estos, a pesar de poder obtenerse numéricamente,
en general se evalúan empíricamente a partir de los
espectros de los iones libres
31 mayo 09
Espectroscopía
138
Diagramas de Tanabe-Sugano
Los diagramas de Tanabe y Sugano están
relacionados con los de Orgel,
Orgel, pero incluyen tanto
los términos de alto como los de bajo espín
Estos diagramas se emplean para tratar el problema
de la interpretación del espectro incluyendo ambos
campos (fuerte y débil)
Pero ahora en vez de graficar la separación
separación de los
estados directamente en términos de la energía, se
considera que el estado basal es el cero y la energía
de cada uno de los otros estados se grafica relativa
al estado basal
Dado que estos diagramas consideran, la correlación
que existe entre los estados de alto y bajo espín, es
necesario incluir todos los estados del sistema
31 mayo 09
Espectroscopía
137
Diagramas de Tanabe-Sugano
Aquí
Aquí se presenta una tabla con los valores de B y
C para un grupo de metales de transición
Carga→
Carga→
0
Elemento↓
B
Elemento↓
560
Ti
V
580
Cr
790
460
Mo
370
W
720
Mn
850
Re
Fe
805
Ru
600
Co
780
Ni
1025
Pd
Cu
31 mayo 09
+1
+2
+3
B/C
B
B/C
B
B/C
B
B/C
3.3 680 3.7 720 3.7
3.9 660 4.2 765 3.9 860 4.8
3.2 710 3.9 830 4.1 917 4.5
3.9 440 4.5
5.1
4.3 870 3.8 960 3.5 680
1.4 470 4.0
1140 3.2
4.4 870 4.2 1060 4.1
5.4 670 3.5 620 6.5
5.3 880 4.4 1120 3.9
4.1 1040 4.2 1080 4.5
830 3.2
1220 4.0 1240 3.8
Espectroscopía
+4
B
B/C
1040
4.1
139
35
31 mayo 09
Espectroscopía
140
Diagramas de Tanabe-Sugano
Para el caso del compuesto de campo débil,
débil, según el
diagrama de Orgel, esperaríamos
esperaríamos que el estado basal
del ion libre 5D, se desdoblara en un estado basal
5T y un estado excitado 5E al incrementar el
2g
g
campo octaédrico
Y que por tanto observaríamos
observaríamos una sola transición
(banda) en el espectro
Recordemos que las transiciones observadas serán
únicamente aquellas cuya multiplicidad no cambia
Entonces, el diagrama de Tanabe y Sugano que
mostremos debe tener una sección
sección que contemple
esto para el [CoF6]3-, a continuación
continuación el diagrama:
31 mayo 09
Espectroscopía
142
Diagramas de Tanabe-Sugano
De lo anterior, puede estimarse que B ~1000 cm-1 y
C~4B para la mayoría de los metales de transición
Ahora bien con objeto de emplear correctamente
estos diagramas, estudiaremos un ejemplo en donde
presentaremos el diagrama y lo analizaremos
En este diagrama solo mostramos unos cuantos
términos, los más importantes
Nuestro ejemplo serán
serán dos complejos de Co3+ el
cual tiene la configuración
configuración (d 6)
Hemos visto que en esta configuración
configuración pueden
existir complejos tanto de alto como de bajo espín
De manera que elegiremos dos ligantes, uno de
campo débil (el Fluor)
Fluor) y otro de campo fuerte (la
etilendiamina)
etilendiamina)
31 mayo 09
Espectroscopía
141
Diagramas de Tanabe-Sugano
Diagrama de Tanabe y Sugano para la configuración
configuración
d6 :
E/B (cm
(cm-1)
Diagramas de Tanabe-Sugano
Para obtener las diferencias de energía entre
estados de diferente multiplicidad, se requieren
ambos parámetros B y C (p ej.
ej. la diferencia entre
las energías entre el 4F y el 2G es 4B+3C)
4B+3C)
Y para caracterizar los estados de la misma
multiplicidad, el parámetro B basta
Entonces, los diagramas de Tanabe y Sugano se
se
presentan como gráficas
gráficas de la energía de separación
separación
en términos de 10Dq, pero expresados en unidades
de E/B y 10Dq/B respectivamente
Además para representar exactamente los valores
de energía debemos conocer el valor de B/C
Al emplear estos diagramas se puede caracterizar
espectroscópicamente ahora si, tanto los complejos
de alto como los de bajo espín
1H
3F
3G
5D
[CoF6]310Dq/B (cm
(cm-1)
31 mayo 09
Espectroscopía
143
36
Diagramas de Tanabe-Sugano
Claramente, esta primera parte del diagrama
muestra que para los complejos de campo débil
débil
únicamente observaremos una transición
Ahora, como resultado del incremento en el
campo, el singulete 1I, que tiene mucha mayor
energía en el ion libre, se va desdoblando en varios
términos uno de los cuales, el 1A1g se estabiliza
disminuyendo su energía muy rápidamente
Cuando el valor de 10Dq/B llega a 18.5, el estado
1A
1
1g procedente del singulete I se convierte en el
estado basal, pues a partir de ese valor es el
término que tiene menor energía
31 mayo 09
Espectroscopía
144
Diagramas de Tanabe-Sugano
En este lugar el apareamiento electrónico ocurre y
se presenta una discontinuidad en el diagrama
A partir de este punto, el término 1A1g es el nuevo
estado basal en tanto que los términos 5T2g y 5Eg
continúan divergiendo al aumentar el campo,
incrementando su energía
Entonces, dado que la etilendiamina es un ligante
de campo fuerte y el complejo de cobalto es
diamagnético,
diamagnético, el estado basal del complejo de
etilendiamina [Co(en)
Co(en)3]3+ se encontrará
encontrará en el lado
derecho del diagrama, esto lo veremos a
continuación:
31 mayo 09
Diagramas de Tanabe-Sugano
E/B (cm
(cm-1)
Diagrama de Tanabe y Sugano para la configuración
configuración
d6 :
1H
Diagramas de Tanabe-Sugano
Queda entonces claro que para los complejos de
alto espín como es el caso del [CoF6]3- los estados
que tendrá importancia serán solamente los del
quintuplete y por lo tanto solo se verá la transición
5T → 5E
2g
g
En tanto que para los complejos de bajo espín
como es el caso del [Co(en)
Co(en)3]3+ , debemos esperar
dos transiciones,
1A
1
1
1
1g → T 1g y A 1g → T 2g
[Co(en)
Co(en)3]3+
[CoF6]310Dq/B (cm
(cm-1)
31 mayo 09
145
En realidad se observan un pico y un hombro,
debido al efecto de Jahn-Teller, que también es
aplicable en este caso
3F
3G
5D
Espectroscopía
Espectroscopía
146
31 mayo 09
Espectroscopía
147
37
Diagramas de Tanabe-Sugano
Incluso, es posible observar además que al
incrementar el campo, ambas transiciones
incrementen su energía, aunque la segunda lo hará
más rápidamente
Ajustar el espectro observado de un complejo al
diagrama correspondiente de Tanabe Sugano,
nos permite obtener los valores de Δ del complejo
Además es posible evaluar el parámetro de
repulsión electrónica B
El valor aparente de este parámetro en los
complejos, al cual llamaremos B’, siempre es
menor que el del ion libre
31 mayo 09
Espectroscopía
148
Efecto nefelauxético
nefelauxético
Esto es el resultado de un fenómeno conocido
como efecto nefelauxético (expansión de la nube)
y que se atribuye a la deslocalización de los
electrones en los orbitales moleculares formados
por los orbitales del metal y los del ligante
Como consecuencia de esta deslocalización,
deslocalización, la
repulsión electrónica disminuye haciendo que B’
siempre sea menor que B
Jørgensen sugiere que este efecto puede calcularse
empleando dos parámetros, uno para el metal y
otro para el ligante (serie nefelauxética)
El efecto total en el complejo es proporcional al
producto de ambos parámetros: 1-β
1-β=hL x k M
31 mayo 09
Efecto nefelauxético
nefelauxético
149
Espectroscopia, un poco más
A continuación un ejemplo numérico, tres
complejos de Cr3+:
Valores del efecto:
Ligante L
hL
Metal M
kM
F-
0.8
Mn(II)
0.07
H2O
1.0
V(III)
0.10
NH3
1.4
Ni(II)
0.12
ox2-
1.5
Cr(III)
0.20
en
1.5
Fe(III)
0.24
CN-
2.1
Co(III)
0.33
31 mayo 09
Espectroscopía
Espectroscopía
150
31 mayo 09
Espectroscopía
151
38
Espectroscopia, un poco más
Estos espectros muestran dos bandas bien
definidas y en algunos se detecta la presencia de
una tercera
Esta banda muy a menudo estará oscurecida por
la presencia de lo que se conoce como banda de
transferencia de carga, que corresponde a la
transferencia de un electrón desde un orbital del
ligante a uno del metal
Esto se racionaliza pensando que esta banda
corresponde a la ionización del ligante y significa
que el metal se reduce, esto ocurre a energías
menores cuando el metal está en un estado de
oxidación mayor y cuando el ligante es más
fácilmente oxidable
31 mayo 09
Espectroscopía
152
Espectroscopia, un poco más
Para asignar entonces cada una de las bandas a una
transición particular,
recordamos que el
Cr3+ (d
(d3), es un 4F,
Al estar en un campo
octaédrico, se desdoblará
en un estado basal 4A2g,
y dos estados excitados,
4T
4
2g y T 1g
Además, tendremos un tercer
estado con la misma multiplicidad
4P, 4T
1g
En la figura vemos cada transición
transición y
su costo energético:
energético:
31 mayo 09
Espectroscopia, un poco más
Las transiciones observadas serán,
ν1 = 4A2g → 4T2g;
ν2 = 4A2g →4T1g
ν3 = 4A2g → 4T1g(4P)
4P)
Ya que las demás están prohibidas
A continuación los valores experimentales de ν1, ν2
y ν3 en kk o 1000 x cm-1
Ligante
ν1
ν2
ν3
Fluor
14.9
22.7
34.4
oxalato
17.5
23.9
?
etilendiamina
21.8
28.5
?
31 mayo 09
Espectroscopía
154
Espectroscopía
153
Espectroscopia, un poco más
Si regresamos al diagrama tenemos que la primera
transición según el diagrama es:
ν 1 = 10Dq es decir Δ
Crece al pasar de F a en,
en,
como se esperaba según
la serie electroquímica
La segunda transición es:
ν 2 = 18Dq,
Y la tercera transición
según la figura debe ser
ν 3 = 12Dq + 15B
31 mayo 09
Espectroscopía
155
39
Espectroscopia, un poco más
El valor observado de la primera transición, será
10Dq o sea Δ
Sin embargo para el caso de F el valor de ν2
debería ser 80% mayor que la de ν1, es decir
26.8kk
Por otra parte el de ν3 debería ser 12Dq + 15B, es
decir 31.7kk
Una vista a la tabla indica que algo anda mal
Ligante
ν1
ν2
ν3
Fluor
14.9
22.7
34.4
oxalato
17.5
23.9
?
etilendiamina
21.8
28.5
?
31 mayo 09
Espectroscopía
156
Espectroscopia, un poco más
La primera transición (de menor energía) tiene una
energía igual a 10Dq,
10Dq,
La segunda
debería
tener una
energía de
18Dq si no
fuera por
que los
estados 4T1g
procedente
del 4F y el 4T1g
que viene del 4P
tienen la misma simetría
y ello hace que se mezclen
31 mayo 09
Espectroscopia, un poco más
Esta mezcla será inversamente proporcional a la
diferencia de energía entre los estados F y P
Como resultado de la mezcla de los estados, el
estado 4T1g(4F), tendrá menor energía en tanto
que el estado 4T1g(4P), tendrá mayor energía que la
que debiera tener si no hubiese ocurrido esta mezcla
En el caso del Cr3+, el valor exacto de B es de 918 y
C de 4133 cm-1 para el ion libre
Usando estos parámetros, podemos comparar los
resultados calculados con los obtenidos
experimentalmente
31 mayo 09
Espectroscopía
158
Espectroscopía
157
Espectroscopia, un poco más
Para mejorar la interpretación debemos hacer dos
correcciones, la primera es la mezcla de los estados
Y la segunda tiene que ver con que el valor de B
para el ion libre, que no es el mismo que de sus
complejos debido al efecto nefelauxético
Si se conocen las tres transiciones, el valor de B’ se
obtiene directamente así:
15B′ = ν3 + ν2 − 3ν1
Así para el caso del F,
B′ =
31 mayo 09
34400 + 22700 − 3 ( 14900 )
15
Espectroscopía
= 827cm−1
159
40
Espectroscopia, un poco más
Si se desconoce una de las transiciones, todavía
podemos obtener el valor de Β’
Para ello empleamos la ecuación que define la razón
nefelauxética así,
B'
β =
ν1 = A2g → T2g = 10Dq = ∆o
2
2
ν3 = A2g
Por tanto β=0.7 y B’=0.7x918=642
Una vez que se conocen los valores de D y B’ es
posible estimar todas las frecuencias de las
transiciones de un complejo
31 mayo 09
Espectroscopía
2
1g
2
1
2
Con estas ecuaciones hemos caracterizado por
completo nuestro sistema:
160
Espectroscopia, un poco más
Exp
34.4
22.7
14.9
I
33.4 + x
26.8 - x
14.9
22.4
14.9
Exp
*
23.9
17.5
I
34.8 + x
31.5 - x
17.5
II
38.1
24.0
17.5
Δ=17.5
B’=642
Exp
*
28.5
21.8
I
40.0 + x
39.3 - x
21.8
II
46.5
28.7
21.8
Δ=21.8
B’=642
Espectroscopía
1
2
(
)
→ T (P) = 7.5B '+ 1.5∆ + ( 225B ' + ( ∆ ) − 18B ' ∆ )
ν2 = A2g → T1g (F) = 7.5B '+ 1.5∆ − 1 225B '2 + ( ∆ ) − 18B ' ∆
1 − β = hL ⋅ kM = 1.5 × 0.2 = 0.3
[CrF6]3Predicción
12Dq + 15B + x
18Dq-x
10Dq
[Cr(
Cr(ox)
ox)3]3Predicción
12Dq + 15B +x
18Dq-x
10Dq
[Cr(en)
Cr(en)3]3+
Predicción
12Dq+15B+x
18Dq-x
10Dq
Las ecuaciones apropiadas para los complejos
octaédricos d3 y d8 que nos permiten calcular las
tres frecuencias ν (II en la tabla) son:
B
Para estimar el valor de β recurrimos a la serie
nefelauxética usando los valores apropiados en la
ecuación:
31 mayo 09
Espectroscopia, un poco más
II
Δ=14.9
B’=827
162
31 mayo 09
Espectroscopía
161
Errores del modelo del campo cristalino
Aunque la serie espectroquímica racionaliza las
diferencias energéticas,
energéticas, espectroscópicas y
magnéticas de los compuestos de coordinación,
Y puede incluso tener cierta capacidad de predicción
Presenta dificultades de interpretación muy serias
Si el desdoblamiento de los orbitales d , procede
únicamente del efecto de las cargas puntuales
(iones o dipolos), debería esperarse que los aniones
ejercieran el mayor efecto
Por lo contrario, los ligantes aniónicos están en el
lado bajo de la serie
31 mayo 09
Espectroscopía
163
41
Errores del modelo del campo cristalino
Diagramas de Tanabe-Sugano
Aún peor, el OH- esta por debajo del H2O a pesar de
su carga
En tanto que el NH3 que tiene un momento dipolo
de µ=4.90x10-30Cm, tiene un mayor efecto que el
agua que tiene un momento dipolo de µ=6.17x1030Cm,
Es decir el efecto sobre el campo es mayor en el
amoniaco a pesar de que sus momentos dipolo están
en el orden inverso
Esta debilidad de la TCC, sugiere que la suposición
de que los ligantes y metales interactuaban de
manera puramente electrostática, es cuando menos
incompleta
31 mayo 09
Espectroscopía
164
31 mayo 09
Espectroscopía
Diagramas de Tanabe-Sugano
Diagramas de Tanabe-Sugano
La configuración
configuración d2 (transiciones)
(completa)
E/B (cm
(cm-1)
E/B (cm
(cm-1)
La configuración
configuración
d2
1S
UV
1S
1G
3P
1D
1G
3P
Visible
3F
IR
1D
3F
10Dq/B
31 mayo 09
165
(cm
(cm-1)
Espectroscopía
10Dq/B (cm
(cm-1)
166
31 mayo 09
Espectroscopía
167
42
Diagramas de Tanabe-Sugano
2D
2F
E/B (cm
(cm-1)
2D
Diagramas de Tanabe-Sugano
La configuración
configuración d3 (transiciones)
(completa)
E/B (cm
(cm-1)
La configuración
configuración
d3
UV
2F
2D
2H
3G
4P
2D
2H
3G
Visible
4F
IR
4P
4F
10Dq/B (cm
(cm-1)
10Dq/B (cm
(cm-1)
31 mayo 09
Espectroscopía
168
31 mayo 09
Diagramas de Tanabe-Sugano
Diagramas de Tanabe-Sugano
3G
3F
3G
3G
E/B (cm
(cm-1)
1I
1I
UV
Visible
3F
3G
3H
3H
5D
IR
5D
10Dq/B (cm
(cm-1)
10Dq/B (cm
(cm-1)
31 mayo 09
169
La configuración
configuración d4 (transiciones)
(completa)
E/B (cm
(cm-1)
La configuración
configuración
d4
Espectroscopía
Espectroscopía
170
31 mayo 09
Espectroscopía
171
43
Diagramas de Tanabe-Sugano
La configuración
configuración d5 (transiciones)
(completa)
2H
4D
4F
E/B (cm
(cm-1)
2H
4D
4F
2I
4F
4P
Diagramas de Tanabe-Sugano
2I
E/B (cm
(cm-1)
La configuración
configuración
d5
UV
4F
4P
Visible
4H
4H
6S
IR
6S
10Dq/B (cm
(cm-1)
31 mayo 09
Espectroscopía
10Dq/B (cm
(cm-1)
172
31 mayo 09
Diagramas de Tanabe-Sugano
31 mayo 09
Diagramas de Tanabe-Sugano
E/B (cm
(cm-1)
3D
1S
1G
1I
3D
1S
1G
1I
3F
3P
3H
5D
173
La configuración
configuración d6 (completa)
(completa)
E/B (cm
(cm-1)
La configuración
configuración
d6
Espectroscopía
UV
Visible
3F
3P
3H
10Dq/B (cm
(cm-1)
Espectroscopía
IR
5D
10Dq/B (cm
(cm-1)
174
31 mayo 09
Espectroscopía
175
44
Diagramas de Tanabe-Sugano
De esta manera, si tenemos por ejemplo un
complejo de Fe(II) y los ligantes que lo rodean
tienen un campo cercano a la región
región del círculo y
cambiamos la temperatura observaremos un cambio
de color y además un cambio en el comportamiento
magnético del complejo.
En nuestro grupo hemos sintetizado complejos que
tienen este comportamiento.
Uno de ellos muestra este comportamiento con un
cambio de espín al enfriar
El otro muestra dos cambios de espín al enfriar
El primero es el [Fe(Tpen
)] y el otro es un dímero
[Fe(Tpen)]
31 mayo 09
Espectroscopía
176
Diagramas de Tanabe-Sugano
Comportamiento del [Fe(Tpen
)] al enfriar:
[Fe(Tpen)]
[Fe(Tpen
)](ClO
ClO4)2
[Fe(Tpen)](
31 mayo 09
Diagramas de Tanabe-Sugano
El dímero
dímero tiene un ligante similar al Tpen,
Tpen, con un
benceno en vez de una piridina, esto es:
Espectroscopía
177
Diagramas de Tanabe-Sugano
El complejo tiene esta estructura y se comporta así
así:
[(Bztpen)Fe-NC-N-CN-Fe(Bztpen)](PF6) 3
Además también tiene como puente entre dos Fe
una dicianamida:
dicianamida:
31 mayo 09
Espectroscopía
178
31 mayo 09
Espectroscopía
179
45
Diagramas de Tanabe-Sugano
3P
3P
2D
E/B (cm
(cm-1)
3P
Diagramas de Tanabe-Sugano
La configuración
configuración d7 (transiciones)
(completa)
E/B (cm
(cm-1)
La configuración
configuración
d7
2H
3P
2D
Visible
2G
2H
3P
2G
3P
4F
Espectroscopía
IR
4F
10Dq/B (cm
(cm-1)
31 mayo 09
180
10Dq/B (cm
(cm-1)
31 mayo 09
Diagramas de Tanabe-Sugano
Espectroscopía
La configuración
configuración d8 (transiciones)
(completa)
1S
1S
1D
1D
1G
3P
UV
Visible
1G
3P
3F
IR
3F
10Dq/B (cm
(cm-1)
Espectroscopía
181
Diagramas de Tanabe-Sugano
E/B (cm
(cm-1)
d8
E/B (cm
(cm-1)
La configuración
configuración
31 mayo 09
UV
10Dq/B (cm
(cm-1)
182
31 mayo 09
Espectroscopía
183
46