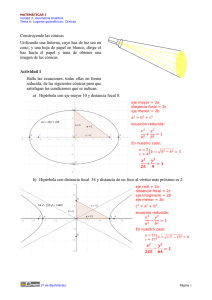
La elipse

Carlos María Rodríguez
La elipse en la Sala Capitular de la Catedral de Sevilla,
¿algo más que belleza?
Un estudio de la elipse y sus propiedades de reflexión
Número de alumno: Dpt261
Número de palabras: 3984
Índice:
1. Evolución histórica y definiciones de las cónicas
1.1) El periodo clásico..............................................................pág.4
1.2) Grandes avances tras la Edad Media................................pág.7
1.3) Las cónicas en la actualidad..............................................pág.8
2. ¿Por qué una elipse en la Catedral de Sevilla?
2.1) La Catedral de Sevilla y la Sala Capitular.......................pág.10
2.2) Definición y propiedades básicas de la elipse.................pág.10
2.3) Las propiedades de reflexión de las cónicas....................pág.14
2.4) La propiedad de reflexión de la elipse.............................pág.15
2.5) ¿Dónde aparecen estas propiedades?...............................pág.17
3. La elipse en la Sala Capitular
3.1) La elipse de la planta de la Sala Capitular.......................pág.18
3.2) La elipse de la bóveda de la Sala Capitular.....................pág.21
4. Conclusión
4.1) Respondiendo a la pregunta inicial.................................pág.23
4.2) Objetivos alcanzados........................................................pág.23
4.3) Ampliaciones del tema.....................................................pág.23
5. Bibliografía....................................................................................pág.24
6. Anexos............................................................................................pág.26
2
Resumen:
Las Matemáticas están a nuestro alrededor en todo momento, pero a veces
olvidamos lo importantes que son, aunque estén ahí. Y la Arquitectura es sin duda uno
de los reflejos más importantes de ella en la vida real. Las Matemáticas no sólo le dan
una misteriosa belleza, sino que confieren a los edificios propiedades asombrosas.
Por otro lado, es por todos sabido que uno de los atractivos más importantes de
España son sus importantes raíces culturales. Por la Península han pasado numerosas
civilizaciones; y la Arquitectura es un perfecto ejemplo, pues está fuertemente
impregnada por las culturas del momento.
Esto, unido a mi fuerte interés por las Matemáticas, da lugar a este trabajo. Cuando
descubrí que la Catedral de Sevilla fue la primera construcción de toda la Península que
contenía a la elipse, decidí que esta investigación matemática y en parte histórica
coincidía con mis apetencias. ¿Eligieron los arquitectos de la Catedral la elipse
simplemente por la belleza arquitectónica, o existen otras razones?
Pretendo ir desarrollando conocimientos sobre las cónicas en todos los aspectos, ya
que la elipse es una de ellas. Veremos que las cónicas poseen unas propiedades de
reflexión interesantísimas que estudiaremos, justificando su presencia en edificios. Me
centraré en algunos de sus usos en otras áreas, para aportar mayor riqueza; y finalmente
estudiaré su uso en la Catedral de Sevilla.
Adicionalmente me propuse investigar por mí mismo todo lo relativo a matrices e
integración que uso a lo largo de este trabajo, antes de que fuese desarrollado en el aula,
demostrando todas las propiedades y resultados que fuese precisando. Paralelamente
explorar herramientas matemáticas como Geogebra y de representación para construir
las diferentes figuras que ilustran el trabajo. Conseguiré así desarrollar conocimientos
en muchos ámbitos. Recomiendo al lector leer la nota en el anexo para comprender
correctamente esto.
3
1. Evolución histórica y definiciones de las cónicas
1.1 El período clásico
Para poder estudiar las propiedades físicas de las cónicas y sus aplicaciones en la
vida real, primero debemos estudiar cómo surgieron y qué son. Fue el matemático
griego Menecmo (350 A.C.) quien descubrió estas curvas, pero tuvieron que pasar casi
100 años para que Apolonio las estudiase en profundidad1, dando la primera definición
de cónicas2:
1ª definición: Las curvas que resultan al cortar una superficie cónica
por un plano se llaman, siguiendo la tradición clásica, cónicas.
Apolonio (262-190 A.C) clasificó las cónicas y encontró la propiedad plana que las
definía. Esta definición se ve más clara en la figura 13:
4i
Fig. 1: El cono y sus cortes
Como dato interesante, fue Apolonio quién dio nombre a estas curvas: “ellipsis”
(deficiencia) “hypérbola” (exceso) y “parábola” (equilibrio); los pitagóricos los usaron
al referirse a los casos posibles que se plantean en la resolución de la ecuación
cuadrática, tema unido a éste. También definió la circunferencia como un caso
particular de la elipse. Sus tratados sobre cónicas sólo pudieron ser conservados gracias
a Thābit ibn Qurra, que los tradujo.
1
PEREZ SANZ, Antonio. Curvas con historia; y VARIOS; Secciones Cónicas, una mirada desde la
derivación implícita.
2
RÍO SÁNCHEZ, J. Lugares Geométricos, Cónicas.
3
VALLE SIERRA, Jesús. SECCIONES CÓNICAS, editado con Microsoft Paint.
4
Para diferenciar cada cónica en el cono, debemos considerar los elementos
siguientes (ver fig.25):
 El vértice del cono V
 El eje del cono, z
 Las generatrices del cono, L
 El plano de corte P
 El ángulo , formado entre L y z
 El ángulo , formado entre z y P
De esta forma podemos estudiar la formación de cada
cónica:
Fig.2: Doble cono desde el perfil
 Si
, se tratará de una elipse.
 Si
, se tratará de una circunferencia.
 Si
, se tratará de una hipérbola, tendrá una rama en cada cono.
 Si
, se tratará de una parábola, el plano será paralelo a las generatrices.
Antes de esto debemos decir que existen unos casos particulares, llamados cónicas
degeneradas, en los que V está contenido en P:
 Si
, la cónica será sólo un punto, V, ya que P no cortará a ninguno de los
dos conos.
 Si
, la cónica será una recta, la generatriz L, pues L estará contenida en P.
 Si
, la cónica será una doble recta, pues el plano cortará por dos sitios
diferentes al cono.
Poco después, los griegos estudiaron una importante propiedad de las cónicas, la
excentricidad, dando lugar a la segunda definición de cónicas6. Se denota por la leta
griega épsilon (ε) y varía según cada cónica.
2ª definición: Se define cónica como el lugar geométrico de los puntos de un
plano cuya razón de distancias a un punto fijo (foco), y a una recta fija
(directriz), es constante, la excentricidad.
Para calcularla, además de un método independiente para algunas de las cónicas,
existe una fórmula general, que obtenemos a partir de su gráfica, como ahora veremos.
Es posible definir también la excentricidad como “el grado de desviación de una sección
cónica respecto a la circunferencia”.
5
6
Hecha por mí con GeoGebra y Microsoft Paint
RÍO SÁNCHEZ, J. Lugares Geométricos, Cónicas.
5
Esto se aprecia en la figura 37:
Fig.3: Elipse, parábola e hipérbola
con sus respectivas directrices
La segunda definición es:
 Para la parábola:

Para la hipérbola:

Para la elipse:
Hipatia, la famosa matemática, estudió el trabajo de Apolonio, y realizó varios
estudios sobre ello, algo muy importante, pues fue la última en tratar las cónicas en
varios siglos.
1.2 Grandes avances tras la Edad Media
Hasta el siglo XVI, las cónicas no volvieron a investigarse, cuando el astrónomo
alemán Kepler (1570-1630) descubrió que las órbitas de los planetas alrededor del sol
son elipses, siendo el Sol uno de los focos. Más tarde Newton (1642-1727) demostró
7
Hecha por mí con GeoGebra y Microsoft Paint
6
que la órbita de un cuerpo alrededor de una fuerza de tipo gravitatorio es siempre una
cónica.
Cuando los matemáticos de los siglos XVI y XVII estudiaron los trabajos griegos,
observaron una falta de generalidad de los métodos de demostraciones, por lo que llevó
sustituyeron la visión puramente geométrica de las secciones cónicas por otra que
incorporaba coordenadas y distancia; las cónicas pasaron a definirse como lugares
geométricas que cumplían unas propiedades. En el siglo XVI, Descartes (1596-1650)
desarrolló un método para relacionar las curvas con ecuaciones, con variables. Jan de
Wit (1629-1672) descubrió que todas las ecuaciones de segundo grado con dos
variables son cónicas. Esto lo estudiaremos posteriormente8.
Con el Teorema de Dandelin, en el siglo XVIII, se obtiene una tercera definición
para la elipse y la hipérbola9:
3ª definición: Una elipse es el lugar geométrico de los puntos del plano cuya
suma de distancias a otros dos fijos, llamados focos, es constante. Una
hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de
distancias a otros dos fijos, llamados focos, es constante.
Estas propiedades las veremos en bastante más profundidad más tarde, y dado que
pensamos centrarnos en la elipse, probaremos esta definición. En la figura 410 vemos
una línea de tiempo resumiendo este recorrido histórico:
355/370-415/416: Hipatia
350AC: Menecmo
1625-1672: Johan de Witt
826-901: Thābit ibn Qurra
262-190AC: Apolonio
1642-1727: Newton
1571-1630: Kepler
1596-1650: Descartes
1794-1847: Dandelin
Fig.4: Línea de tiempo de los matemáticos relacionados con las cónicas.
8
REY PASTOR, J. Geometría Analítica.
RÍO SÁNCHEZ, J. Lugares Geométricos, Cónicas.
10
Hecho por mí, utilizando el motor de búsqueda de google para hallar las imágenes
9
7
1.3 Las cónicas en la actualidad
Hoy en día se consideran las cónicas como ecuaciones de segundo grado con dos
incógnitas. A continuación estudiaremos la ecuación y la matriz correspondiente a cada
una. Para esto, debemos hallar en primer lugar la forma matricial de la ecuación
completa, y después mostraremos todas las posibilidades. Este es uno de los temas que
investigué por mi cuenta, pues necesito saber trabajar con matrices para convertir estas
ecuaciones en matrices.
Debemos pasar la siguiente ecuación a un producto de matrices:
Para hacer esto, realicé el siguiente razonamiento: En forma matricial, tendría una
estructura de 1x1. Por lo tanto, la primera matriz tendrá 1 fila, y la última 1 columna;
esto se debe a las propiedades del producto de matrices. “Si multiplicamos una matriz
de
por otra de
, la matriz resultante será de
”11. Por otro lado, sabemos
que la matriz resultante tendrá 9 sumandos, como vemos en la ecuación anterior (hay 6
términos, pero 3 están siendo multiplicados por 2). Sabiendo esto, averigüé que la
matriz buscada es:
De esta forma, sustituyendo valores en la matriz, hallamos todas las cónicas
posibles, que se encuentran en la siguiente página12. Hay más información sobre esto en
el anexo 1.
11
12
Sociedad Matemática Thales. Propiedades del producto de matrices.
Hecha por mí con Microsoft Word, recopilando lo estudiado.
8
Matriz
Ecuación
Cónica
Elipse real
Elipse imaginaria
Hipérbola real
Hipérbola imaginaria
Parábola en el eje
horizontal
Parábola en el eje vertical
Par rectas imaginarias
(elipse degenerada)
Par rectas
(hipérbola degenerada)
Par de rectas paralelas al
eje x
Par de rectas imaginarias
paralelas al eje x
Par de rectas superpuestas
en el eje x
Par de rectas paralelas al
eje y
Par de rectas imaginarias
paralelas al eje y
Par de rectas superpuestas
en el eje y
9
2. ¿Por qué una elipse en la Catedral de Sevilla?
2. 1 La Catedral de Sevilla y la Sala Capitular
La Catedral de Sevilla es la catedral gótica más grande de todo el mundo13. Es
Patrimonio de la humanidad, además de Bien de Valor Universal desde 2010. Se
considera que su construcción comenzó el 1401, pero no existen registros de esto hasta
el 1433. En teoría, fue acabada en octubre de 1506, cuando se colocó la piedra en su
parte más alta, pero realmente se realizaron trabajos ininterrumpidos en la Catedral
durante varios siglos14. La última gran obra fue realizada en 2008, donde se sustituyeron
una gran cantidad de materiales por otros más resistentes al demostrarse que cada día el
edificio sufría oscilaciones de hasta
por culpa de la dilatación y contracción de las
paredes.
En general, la Sala Capitular de una Catedral, o algún edificio de esta índole, es una
sala bastante amplia, en la que todos los monjes se reunían para tratar los distintos
temas que les afectasen. Es una de las salas más importante, muy decorada, y
generalmente se empezaba a construir por esta sala.
Fue Hernán Ruiz II el encargado de comenzar la
Sala Capitular, pero fue acabada por Asensio de Maeda
en 1592. Esto hace que acabe teniendo un toque
renacentista, incorporando así una planta elíptica
innovadora que fue usada anteriormente por Miguel
Ángel para la plaza del Capitolio.15. Se sabe que fue la
primera construcción de la Península Ibérica en incluir
Fig.5. El exterior de la
la elipse en un edificio, haciendo que sea especialmente
Catedral de Sevilla
importante en la historia de la arquitectura16. La figura
517 nos muestra la Catedral.
2.2 Definición y propiedades básicas de la elipse
Pasemos ya a centrarnos en la elipse. La elipse está compuesta de dos ejes
perpendiculares, AB y CD; eje mayor y eje menor, respectivamente. La circunferencia
es un tipo de elipse concreto, donde ambos focos coinciden en el centro, y por lo tanto
ambos ejes son iguales. Durante todo el trabajo usaremos la misma notación, El eje
mayor será 2a, el menor 2b, y la distancia del centro a un foco es c (ver fig.618).
13
VARIOS. La Catedral de Sevilla. Ediciones Guadalquivir. 1ªed. 1985
Íbid
15
Íbid
16
Íbid
17
VARIOS. La Catedral de Sevilla nombrada Patrimonio de la Humanidad.
18
Hecha por mí con GeoGebra y Microsoft Paint
14
10
La excentricidad de una elipse es equivalente al cociente entre su “semidistancia
focal” (c) y la mitad de su eje mayor. Este valor se encuentra entre 0 y 1. Considerando
lo dicho previamente:
Fig.6: Segmentos importantes
de la elipse.
Cuánto más se acerque e a 0, más parecida será la
elipse a una circunferencia, es decir, ambos semiejes
tenderán a tener longitudes similares. En cambio, si
se acerca a 1, la elipse tendrá una diferencia mucho
mayor entre los semiejes, resultando en una elipse
más “aplastada”. En las siguientes elipses podemos
apreciar esto (fig.719):
Como ejemplo real, podemos ver a
continuación una tabla con la excentricidad de
las órbitas de los planetas del Sistema Solar
(fig.720 y fig.821). Dado que estas órbitas son
prácticamente circulares, las excentricidades
son cercanas a 0. La de Mercurio es la más
grande, ya que parece más una elipse.
Fig.8: Excentricidades de los
planetas del sistema solar.
Fig.7: Elipses con diferentes
excentricidades.
Fig.9: Órbita de los planetas del sistema
solar (además de Plutón y Eris).
La tercera definición de elipse (la de Dandelin) nos dice que la suma de las
distancias entre los focos y un punto cualquiera es constante. Probar esto no es muy
complejo, y con algo de geometría se puede hacer. Antes de ponernos a ello, debemos
ver un par de puntos. En primer lugar, simplemente decir que esta constante es 2a. Para
19
Hecha por mí con GeoGebra y Microsoft Paint
Hecho por mí, con información de: PÉREZ, T. y ARRATIA, O.; Cónicas. En: Varios, Invitación a las
Matemáticas.
21
Imagen de EL PAÍS, obtenida del Jet Propulsion Laboratory
20
11
ver esto, estudiamos lo que ocurre a la suma de estas distancias cuando
en el extremo derecho de la elipse (aquí lo llamamos ):
, es decir,
 Distancia
 Distancia
 Suma:
La segunda tarea que debemos hacer es probar que
, algo muy
importante para proceder. Para ello, aunque hay varias formas, probaremos que la
distancia entre los puntos
y
es , pudiendo así aplicar Pitágoras.
Para entender lo que hice, veamos primero nuestra elipse, en la figura 1022:
Lo que pretendo hacer en los próximos pasos es probar
que una circunferencia de radio
con centro
y otra de radio y de centro
son tangentes.,
pues lo serán en la recta
. Esto lo vemos en la
23
figura 11 .
Fig.10
Para probar esto, hallaremos
los puntos de corte entre
ambas circunferencias en forma de función, pero existe un
paso previo que podemos realizar para simplificar
problemas, y es colocar la recta
horizontal, como
24
se muestra en la fig. 12 :
Fig.12
Fig.11
Una vez tengamos este segmento horizontal, recolocamos el origen de coordenadas
en el segundo foco25. Nos quedan dos circunferencias:


22
Hecha por mí con Geogebra y Microsoft Paint
Íbid
24
Íbid
25
Es importante que este paso no es realmente una transformación de la elipse, sino tan sólo un recurso
geométrico para simplificar el problema.
23
12
Para hallar estas ecuaciones utilizamos las distintas herramientas para la
transformación de funciones y la ecuación genérica de la circunferencia, la cual
comento en el anexo 2. Pasamos a resolver ahora este sistema:
Sustituimos la primera en la segunda:
En efecto, existe un único punto de corte (sólo hay constantes). Podemos establecer
que
. De hecho, si sustituimos ahora esto en el punto de corte:
Esto es lo que esperábamos del dibujo, y así queda mucho más simple.
Volvamos a la tercera definición. Desarrollamos la ecuación simplificada y
centrada en el origen de la elipse:
Sustituimos b2 por (a2-c2):
Añadimos
a cada lado para poder simplificar a un producto notable:
Utilizando Pitágoras se ve claramente que cada radiovector, la distancia entre un
punto y cada foco, es
término:
 Distancia

Distancia
Su suma será:
13
por lo que cada uno medirá la raíz del primer
En el anexo 3 el lector encontrará otra forma de probar que
esta última propiedad.
utilizando
2.3 Las propiedades de reflexión de las cónicas
Una de las cosas que hacen más importantes las cónicas son sus propiedades de
reflexión. Aunque nos centraremos en la de la elipse, primero mencionaremos las de la
hipérbola y la parábola:
 La hipérbola: En la hipérbola, la tangente por un punto será la bisectriz entre
ambos radiovectores. Ocurre de forma similar a la elipse, sólo que aquí la
bisectriz es la tangente en lugar de la normal, como ahora veremos.
 La parábola: En la parábola, todo rayo que llegue paralelo a su eje de simetrías
se reflejará en la curva y pasará por el foco. Debido a esto se construyen las
antenas con forma de paraboloide (la figura generada al hacer girar una parábola
sobre su eje de simetría); las señales, al llegar paralelas al eje de simetría, se
reflejarán en la antena y llegarán al receptor, que estará en el foco. Todo esto se
puede ver en la siguiente figura (Fig.1326):
Fig.13: Esquema de las propiedades de reflexión de las cónicas.
26
DORIS HINESTROZA, G. Propiedades de reflexión de las cónicas. Editado.
14
2.4 Las propiedades de reflexión de las elipses
La propiedad de reflexión de la elipse consiste en que la normal en cualquier punto
será la bisectriz de los dos radiovectores. En consecuencia, todo rayo que salga del foco
F1, se reflejará pasando por el segundo foco F2 (ver fig.1427).
Fig.14: Reflexión en la elipse. Es
importante fijarse en los ángulos
.
Para probarlo, desarrollaremos una expresión que será correcta si esta propiedad lo
es, hasta hallar una igualdad segura, probando así que nuestra teoría es correcta. Esto no
es más que un recurso para hacer más fácil el desarrollo, empezando por el final para ir
volviendo atrás y ver si es correcto. Si se cumple la propiedad de reflexión, los dos
ángulos formados entre la normal y los radiovectores serán iguales. En primer lugar,
utilizando la propiedad de los triángulos de que la suma de los ángulos es 180º en los
dos triángulos del dibujo anterior, obtenemos las siguientes expresiones:


Igualamos:
Recordemos que esta es la hipótesis que realizamos, si la normal es la bisectriz
entonces ambos ángulos serán iguales (
y
). Para poder continuar con las
operaciones, tomaremos tangentes, algo complejo, por lo que debemos considerar una
serie de cosas antes. En primer lugar, recordemos que es el ángulo formado entre el
semieje mayor y la normal. Por lo tanto, será:
El opuesto de la inversa de la derivada en cada punto es la pendiente de la normal
en . Cuando tomamos la arcotangente, estamos hallando el ángulo que forma la normal
con la horizontal.
Para poder operar debemos sustituir la derivada, la cual hallamos derivando
implícitamente la expresión original:
27
Hecho por mí con Geogebra
15
Sustituimos:
Al mismo tiempo, y sabiendo que las coordenadas de F1 son
podemos determinar que las tangentes de y son:
y de F2
;


Tomamos tangentes en nuestra hipótesis:
Utilizamos las fórmulas correspondientes a la suma de ángulos y los ángulos
dobles:
Sustituimos lo deducido anteriormente:
16
2.5 ¿Dónde aparecen estas propiedades?
Esta propiedad tiene aplicaciones muy interesantes en nuestra vida, otorgando unas
prestaciones increíbles.
Podemos empezar, por ejemplo, con un objeto
que ni sospecharíamos que podría utilizar las
elipses, los “cascos”, como los de la figura 1528.
Este tema es realmente extenso, pero intentaremos
verlo de la forma más concisa y eficaz posible. En
teoría, si creamos un auricular cuyo fondo sea un
elipsoide, podemos concentrar todo el sonido en un
punto para así maximizar la calidad del sonido,
Fig.15. Unos cascos
pero esto no es lo único posible.
Centrémonos en un sólo auricular. Un foco de este elipsoide se encuentra en la
fuente del sonido. El otro, en la cabeza del usuario, donde todo el sonido se concentrará,
dando lugar a un sonido envolvente y de alta calidad. Si el sonido está grabado
convenientemente, nos transmite la sensación de que el sonido viene de diferentes
sitios, dando sensación de 3D, algo que hoy en día está muy de moda, al ser la última
tecnología. Además, dado que el sonido siempre recorrerá la misma distancia, se
minimizan las interferencias, pues la suma de los radiovectores es constante.
El inconveniente de esta tecnología es que los materiales de las auriculares deben
ser de la mejor calidad. Por ejemplo, para permitir una buena reflexión del sonido, se
utilizan aleaciones de neodimio. Esto hace que estos auriculares sólo estén al alcance de
los consumidores más exigentes, y a pesar de que cada vez más utilizan la elipse, para
sacarle el máximo rendimiento es necesario una importante inversión29.
He escogido este ejemplo por ser cercano a nosotros, pero la elipse es utilizada en
muchos otros lugares. Desde hace muchísimo más tiempo la bóveda de los teatros de
ópera30 o de las salas de conciertos también tiene forma elipsoidal, para que el público
escuche mejor, como se ve en la figura 1631. También las antiguas conchas de los
apuntadores de teatro se basaban en este principio, su voz quedaba en escena sin que los
espectadores pudieran oírles32.
Fig. 16: Reflexión del sonido en un teatro.
28
EFECTO FUTURA. Auriculares de lujo.
Información de EFECTO FUTURA. Auriculares de lujo; principalmente.
30
EDUCARED. Reflexión del sonido.
31
Íbid.
32
Íbid.
29
17
3. La elipse de la Sala Capitular
3.1 La elipse de la planta de la Sala Capitular
En la fig. 17 vemos una foto de la planta de la Sala Capitular33:
Fig. 17: Planta de la Sala Capitular
Podemos obtener esta imagen de la página
oficial de la Catedral de Sevilla, donde se puede
acceder a un paseo virtual. La escala de la imagen
es 1:300 aproximadamente. He utilizado este
programa para hallar una foto realizada desde
arriba, de otra forma sería imposible.
En primer lugar dibujaremos la elipse
correspondiente. Para ello utilizamos el software
gratuito GeoGebra, utilizando la herramienta
“Cónica dados cinco de sus puntos”. Marcamos
cinco puntos incluidos en la elipse, y obtendremos
ésta.
Debemos
asegurarnos
de
marcar
correctamente las paredes y el suelo para evitar
errores. Lo vemos en la figura 1834.
Fig. 18: La elipse ya colocada
En la figura 1935 vemos la elipse resultante.
Esta será la que analizaremos, hallando su
ecuación o su área, entre otras cosas. Lo primero
que hemos hecho es averiguar la posición de los
focos usando
. Usando esto
podemos averiguar además la excentricidad:
Fig. 19: La elipse por sí sola
Esta alta excentricidad es comprensible, pues c es bastante grande, y está
considerablemente “aplastada”.
Dado que, por ejemplo, la integral de la elipse puede encontrarse en cualquier sitio
con letras para representar la longitud de cada eje, aquí sustituiré desde el principio los
valores reales, a pesar de que no hacerlo suele ser más útil a la par que elegante36.
Para hallar la ecuación de la elipse utilizamos GeoGebra, o medir el tamaño de cada
eje, calcular la proporción y escribir la expresión. Finalmente, nos queda que:
33
Todas las imágenes obtenidas con el tour 3D de la Sala Capitular, para ser capaz de obtener imágenes
fidedignas desde la cúpula.
34
La fig.13 editada
35
La elipse por sí sola, hecha con Geogebra.
36
Aún así, en el anexo 1 se encuentra la versión sin sustituir valores de lo que ahora estudiaremos
18
Esta era tan sólo la versión simplificada de la ecuación, siendo los valores reales
m y
m aproximadamente, pues es difícil medir estos valores
exactamente.
Para medir la superficie de la planta de la sala capitular integraremos la ecuación
con a y b sustituidos:
Fig. 20: La elipse dividida en
cuatro secciones iguales
Para entender porqué estamos calculando cuatro
veces la integral entre 0 y
, podemos utilizar el
aspecto de la función, que vemos en la fig.2037.
La zona marcada en rojo es la que calcularíamos
si no multiplicáramos por cuatro al calcular la
integral entre 0 y
quedándonos con el valor
positivo de la raíz.
Para poder continuar, debemos realizar un cambio de variable. Ésta consistirá en
sustituir por
, y desarrollamos la cadena de igualdades:
Para integrar el coseno cuadrado debemos realizar una operación. Sabemos que:


37
Hecha por mí con Geogebra y Paint
19
Sumamos:

Por lo tanto, ahora mismo tenemos que la integral que buscamos será:
A continuación procederemos a hallar el resultado final sustituyendo los valores en
t.
Finalmente tenemos la fórmula general para hallar el área de cualquier elipse, y el
área de la nuestra38. Como dato interesante, diremos que de aquí también podemos
deducir la fórmula del área de la circunferencia. Ambos ejes son iguales, y, por lo tanto,
el área es
Pasemos ahora a la bóveda.
38
Este dato es tan sólo una aproximación, así como los hechos durante el proceso, tan sólo he mantenido
una cifra decimal, pues no tendría sentido utilizar más dado el inevitable error de las medidas.
20
3.2 La elipse de la bóveda de la Sala Capitular
La figura 2139 corresponde a la
bóveda de la sala capitular, obtenida
cómo en el apartado anterior.
Fig. 21: La bóveda de la Sala
Capitular
En la fig. 2240 vemos la elipse
obtenida. La elipse se sale de la imagen,
pero esto no afecta a su exactitud, pues al
tener que marcar cinco puntos cualesquiera,
estos se encuentran en las zonas visibles.
Fig. 22: La elipse en su lugar en la Bóveda
La figura 2341 es la elipse, que procederemos a
analizar. Como antes, hemos hallado c, y en este caso
la excentricidad es:
Fig. 23: De nuevo, la elipse sola
Es muy similar a la anterior, y es que el
arquitecto intentaría que la planta y la bóveda fueran
lo más proporcionales posible, para que fuera más
bello.
Ya que ya hemos visto cómo hallar el área, veamos ahora algo diferente. En este
caso hallaremos el volumen de la cúpula. Algo importante es que la altura de la cúpula
en sí es igual al semieje menor; si no fuese así no podríamos aplicar simplemente la
fórmula del área de un volumen de revolución como vamos a hacer.
El volumen de la cúpula será la mitad de la del elipsoide completo formado al rotar
la elipse por el eje horizontal. Veamos primero la fórmula de la elipse (hecha igual que
antes):
39
Utilizando el Tour 3D, al igual que antes
La figura 17 editada con GeoGebra
41
Elipse trazada con GeoGebra
40
21
El volumen del elipsoide completo será:
Este es el volumen del elipsoide completo (el 2 se encuentra ahí por la misma razón
que en el área, sólo que en este caso es 2 para no “barrer” dos veces lo mismo al hacerlo
rotar). El que buscamos será la mitad, sólo queremos medio elipsoide:
Sustituimos:
Ya podemos hallar el volumen buscado, a lo que ahora procederemos. Destacaré de
nuevo que si
, es decir, si es una circunferencia, obtenemos la fórmula del
volumen de la esfera (en este caso la semiesfera). Los valores de a y b reales son
y
. Sustituyendo obtenemos que:
Es increíble como con tan sólo un par de valores, literalmente, hemos sido capaces
de hallar tantísimas cosas de esta sala. Sabemos dónde están los focos, todas las
distancias, el área de la planta y el volumen de la cúpula.
22
4. Conclusión
4.1 Respondiendo a la pregunta inicial
Tras este largo estudio, podemos dar una respuesta a nuestra pregunta inicial; la
elipse fue utilizada por algo más que su belleza, fue usada por sus propiedades físicas,
teníamos razón. Se podría pensar que es casualidad, pero esto es extremadamente
improbable. De la propia naturaleza de la Sala Capitular deducimos que el sonido es
importante, pues se destinaba a las reuniones. No es casual que fuera esta sala la
elíptica, y no otra cualquiera; fue diseñada con esta forma con un objetivo. El
Renacimiento propició el uso de nuevas formas, y dio lugar a grandes obras como ésta.
No es especialmente complejo probar esta propiedad, y es perfectamente comprensible
que se utilizasen en esta época de experimentación y avances.
Existen muchos otros edificios que a lo largo de la historia han ido adaptando la
elipse a su estructura, pero que sería imposible incluir en este trabajo debido a las
limitaciones impuestas. Entre otros, la arquitectura de Dalí estuvo compuesta en una
sorprendente medida por las cónicas, por lo que en casi todas sus obras podemos
encontrarlas.
4.2 Objetivos alcanzados
Sin duda alguna uno de los mayores beneficios de este trabajo fue la gran cantidad
de temas abordados. No sólo hemos tocado la gran mayoría de los temas que he
estudiado hasta ahora, sino que he ampliado conocimientos en todos los sentidos, no
sólo en Matemáticas. He tratado matrices, álgebra, geometría, integrales, derivadas, y
por supuesto las cónicas. Por otro lado, he estudiado la historia de uno de los edificios
más emblemáticos de Andalucía, además de Arquitectura, Tecnología y mucho más.
4.3 Ampliaciones del tema
Algo increíble es que aún tendríamos tres cónicas más para estudiar, a cada cual más
prodigiosa e interesante, siendo las propiedades de reflexión la punta del iceberg. La
cantidad de estudios realizables de temática cercana a éste es virtualmente infinito.
En cuanto a este trabajo en sí, existen algunos detalles que podrían haberse incluido
pero que simplemente no cabían. Algo que sin duda sería interesantísimo sería medir la
eficiencia de la reflexión. Con un micrófono lo suficientemente preciso, colocándolo en
posiciones estratégicas en torno al foco y con algunos simples programas informáticos
podríamos obtener datos cualitativos que utilizar.
Para terminar, nada mejor que mostrar dos frases de grandes personalidades
separadas por dos mil años pero que aún así simbolizan perfectamente este trabajo:
“La geometría es una ciencia del conocimiento del ser, pero no de lo que está sujeto a la
generación y a la muerte. La geometría es una ciencia de lo que siempre es.”
Platón
“Para que un objeto sea altamente bello es preciso que su forma no tenga nada de
superfluo, sino las condiciones que lo hacen útil, teniendo en cuenta el material y los
usos a prestar. Cuando las formas son más perfectas exigen menos ornamentación”.
Salvador Dalí
23
Bibliografía:

BESCÓS i ESCRUELA, E; PENA i TERRÉN, Z. Matemáticas 1ºBachillerato.
Oxford educación, 2008, 1ºedición.

BOYER, Carl. Historia de la matemática. Alianza Universal Textos, 2ª edición,
1987.

BRONSHTEIN, I.; SEMENDIAEV, K. Manual de Matemáticas para
Ingenieros y Estudiantes.

CARO MERCHANTE, Antonio. “Introducción a las curvas cónicas”. En:
DESCARTES (Ministerio de educación). “Cónicas”. Actualizado en 2000.
[Consultada en julio de 2011]. Disponible en:
http://descartes.cnice.mec.es/Descartes1/4a_eso/Propiedades_de_las_conicas_re
presentacion/cohistoria.html

DORIS HINESTROZA, G. “Propiedades de reflexión de las cónicas”. En:
Universidad del Valle, Facultad de Ciencias, Departamento de Matemáticas.
Proyecto 2. Sin fecha. [Consultado en enero y febrero de 2012]. Disponible en:
http://www.univalle.edu.co/~dohin/calculo-III/PROYECTO2.pdf

EDUCARED. “Reflexión y refracción del sonido”. En: Educared. Actualizada
en 2011. [Consultada el 29 de junio de 2011]. Disponible en:
http://portales.educared.net/wikiEducared/index.php?title=Reflexi%C3%B3n_y
_refracci%C3%B3n_del_sonido

FUNDACIÓN TELEFÓNICA. “Catedral de Sevilla, visita virtual 3D”. En:
FUNDACIÓN TELEFÓNICA. Catedral D Sevilla. Actualizada en 2011.
[Consultada el 29 de junio de 2011]. Disponible en:
http://www.catedraldesevilla.es/

IBÁÑEZ TORRES, Raúl. “El vientre de un arquitecto”. Sin fecha de
actualización. [Consultado en diciembre y enero de 2011-12]. Disponible en:
http://webpages.ull.es/users/imarrero/sctm04/modulo1/10/ribanez.pdf

MARÍN TEJERIZO, J. A. Matemáticas para Técnicos. Sociedad anónima
española de traductores y autores, 1ª edición, 1958.

RECIO MIR, Álvaro. “Sacrum Senatum, Las Estancias Capitulares de la
Catedral de Sevilla”. Universidad de Sevilla, 2008, primera edición.
24

REY PASTOR, J. Geometría Analítica. Sociedad anónima española de
traductores y autores

REY PASTOR, J; CASTRO BRZEZICKI, A. Elementos de las Matemáticas
Editorial Saeta, 1972, sexta edición.

RÍO SÁNCHEZ, J. Lugares Geométricos. Cónicas. Editorial Síntesis, 2ªedición,
noviembre 1996.

SEVILLA 360. “La Catedral de Sevilla: Sala Capitular”. En: SEVILLA 360.
Sevilla 360. Actualizada el 11 de noviembre de 2010 [Consultada el 29 de junio
de 2011]. Disponible en:
http://www.sevillaen360.es/index.php/blogsevilla/1854-la-catedral-de-sevillasala-capitular

VARIOS. La Catedral de Sevilla. Ediciones Guadalquivir. 1ªed. 1985.

VARIOS. Secciones cónicas, una mirada desde la derivación implícita. Textos
académicos, 1ª edición noviembre 2008.

VITUTOR. “Cónicas”. En: Vitutor. Actualizada en 2010. [Consultada el 1 de
julio de 2011]. Disponible en:
http://www.vitutor.com/geo/coni/f_1.html
25
Anexo 1:
Para estudiar las matrices vamos sustituyendo valores en cada término de la matriz,
y los que ye elegido tan sólo están ahí para simplificar la expresión resultante o para dar
la ecuación más conocida para la cónica en cuestión. Por ejemplo, para la elipse he
elegido
,
y 1 para dejarla en la forma
, la más común.
De hecho, la ecuación de segundo grado puede no tener 2h, 2g o 2f, pero si los
usamos el resultado será más simple, lo he colocado para dejar claro que en realidad se
trata de una suma de dos elementos con la misma parte literal. Además, esto nos permite
hacer que la matriz sea simétrica, aún más fácil. Si no lo fuera, no habría problemas,
salvo que habría que sacar factor común para dar lugar a coeficientes del tipo
.
Anexo 2:
Aquí sólo pretendo comentar rápidamente la ecuación de la circunferencia, pues no
es de gran importancia en este trabajo y es un tema muy extenso. Se deriva de la elipse,
y con un mínimo de comprensión de ésta se deduce que es:
Al ser ambos ejes iguales, se saca factor común de los denominadores, que pasan a
multiplicar al 1, quedando la expresión anterior.
En cuanto al resto de las transformaciones mencionadas en las páginas 12 y 13, tan
sólo hemos trasladado a la izquierda una de las circunferencias añadiendo la distancia
trasladada a la x, uno de los recursos básicos de la transformación de funciones.
Anexo 3:
Sabiendo que la suma de los radiovectores es siempre 2a, podemos hallar una
forma más simple de probar que
. Si consideramos que x valga 0,
será
, siendo
la ecuación de la elipse. En esta situación, ambos radiovectores (la
distancia entre un punto cualquiera y un foco) serán iguales, y dado que la suma es
ambos medirán a. Así se forman dos triángulos rectángulos con catetos b y c e
hipotenusa a. Por lo tanto, basándonos en el Teorema de Pitágoras, podemos determinar
que
.
Anexo 4:
Se trata del proceso para hallar la integral de la elipse utilizando tan sólo letras.
Correspondería a lo dicho en las páginas 18 y19. Llegamos a lo mismo, sólo que esto es
aplicable a cualquier elipse.
26
Nota al lector:
Aquí sólo pretendo definir cuál ha sido mi papel en cada sección, para evitar
conflictos. Cualquier desarrollo matemático presente en este trabajo ha sido realizado
por mí, sin obtener ayuda exterior y sin basarme en fuentes o similares. Incluso aunque
un desarrollo matemático no esté expresamente escrito, lo he hecho yo por mi cuenta, a
menos que sea algo tan básico como las definiciones, que considero mi punto de
partida. Esto incluye también la gran mayoría de las imágenes, excepto una imagen y las
fotografías. La mayoría han sido creadas y editadas por mí para desarrollar lo ya
expresado y obtener figuras claras y que sirvieran exactamente para lo que yo quería.
La historia, las definiciones y parte de las aplicaciones son un compendio de
información realizado a partir de libros, páginas web y otros documentos citados en la
bibliografía. A pesar de ello, existen algunos documentos de los que no he utilizado
información y por lo tanto no he citado, pero que he usado como información
suplementaria para establecer las bases o que contenían información sobre temas que
realmente no trataban el tema que yo estudiaba.
27
28
29