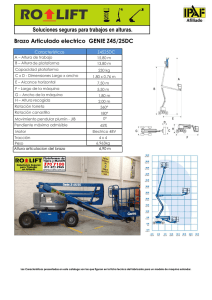
FISICA 2º BACHILLERATO A) CAMPO ELÉCTRICO Cuando en el

FISICA 2º BACHILLERATO
CAMPO ELECTRICO
A) CAMPO ELÉCTRICO
Cuando en el espacio vacío se introduce una partícula cargada, ésta lo perturba, modifica,
haciendo cambiar su geometría, de modo que otra partícula cargada que se sitúa en él,
estará sometida a una acción debida a la deformación producida por la primera.
El Campo electrico es un campo vectorial de fuerzas cuya magnitud activa es la
carga.
B) Concepto de carga eléctrica
Es una magnitud escalar. En los problemas de interacción electrostática suponemos que
la carga de un cuerpo está concentrada en el centro de éste, por lo que hablaremos de
cargas puntuales. La unidad de carga es el Culombio [C] y como es una unidad muy
grande se suelen utilizar submúltiplos.
C) Ley de Coulomb
“La ley de Coulomb, nos indica que la fuerza de atracción o repulsión entre dos
cargas puntuales Q1 y Q2 separadas una distancia r, es directamente proporcional al
producto de sus cargas e inversamente proporcional al cuadrado de la distancia
que las separa”.
Esta fuerza es un vector que tiene como dirección la recta que une el centro de cada una
de las cargas y se calcula mediante la expresión:
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
Fe = k Q1 Q2 r
r2
(1)
Donde el vector r es un vector unitario en la dirección de la recta que une las dos cargas,
y k es una constante que depende del medio eléctrico interpuesto entre las cargas,
soliendo expresarse de la siguiente forma:
k=
(2)
Con lo que la Ley de Coulomb queda:
Ɛ0 es la constante dieléctrica del vacío y se verifica que su valor es: Ɛ0 = 8.85 x 10-12
C2m-2N-1 y la constante k valdrá: k = 9.0 x 109 C-2 m2 N.
Sustituyendo este valor en la expresión general de Coulomb (1), tendremos:
Fe = 9 109 Q1 Q2 r
r2
El signo de la fuerza, depende del signo de las cargas eléctricas. Si las cargas son del
mismo signo la fuerza es positiva (repulsiva) y si tienen signos opuestos es negativa
(atractiva).
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
-
Campo eléctrico creado por una carga puntual en un punto.
El campo eléctrico creado por una carga puntual en un punto es la fuerza que actuaría
sobre una unidad de carga situada en ese punto. Por tanto el campo eléctrico es
directamente proporcional a la carga eléctrica que crea el campo e inversamente
proporcional al cuadrado de la distancia que separa el centro de la carga del punto donde
se calcula el campo eléctrico. Es una magnitud vectorial que se mide en [N/C] y se calcula
mediante la expresión:
El campo eléctrico es un vector que tiene como dirección la recta que une el centro de la
carga con el punto donde se calcula y el sentido depende del signo de la carga que crea
el campo; si ésta es positiva el sentido del campo se aleja de la carga y si ésta es
negativa va dirigida hacia la carga.
La fuerza eléctrica que actúa sobre una carga situada en un punto en el que la intensidad
de campo eléctrico es E, se expresa como:
-
Campo eléctrico creado por una distribución de cargas. (Principio de
superposición).
Al igual que ocurría en el campo gravitatorio, cuando el campo eléctrico en un punto se
debe a un conjunto de cargas, el campo total en dicho punto se obtiene sumando
vectorialmente las intensidades de los campos creados individualmente por cada carga
por separado.


E =  Ei
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
-
Líneas de fuerza eléctrica
Son líneas imaginarias que sirven para representar los campos eléctricos. Estas líneas
coinciden con las trayectorias que sigue una carga abandonada en reposo en el interior
del campo El vector campo eléctrico es tangente a las líneas de fuerza en cada punto.
Como existen infinitos puntos en el campo, tan sólo se dibujan algunas líneas que tienen
las siguientes propiedades:
a) Las líneas de fuerza salen de las cargas positivas y entran en las cargas negativas
b) El número de líneas que entran o salen de una carga puntual es proporcional al
valor de la carga.
c) Las líneas de fuerza no pueden cortarse. De lo contrario, en el punto de corte
existirían dos vectores de campo eléctrico distintos.
d) En el caso de las cargas eléctricas positivas, el sentido del vector campo eléctrico
va en sentido de los potenciales decrecientes.
e) En el caso de las cargas eléctricas negativas, el sentido del vector campo eléctrico
va en sentido de los potenciales crecientes.
-
Superficies equipotenciales
Otro modo de representar gráficamente el campo es mediante las superficies
equipotenciales, que son aquellas superficies que contienen puntos con el mismo
potencial. A partir de esta definición se pueden deducir las siguientes conclusiones:


Cuando una carga se mueve sobre una superficie equipotencial no se realiza
trabajo, ya que la diferencia de potencial es cero.
Las líneas de fuerza son perpendiculares a las superficies equipotenciales. Es
decir que la intensidad de campo en un punto es perpendicular a la superficie
equipotencial que pasa por dicho punto. En efecto, si el trabajo realizado
al mover una
 
carga sobre la superficie equipotencial vale cero,
significa
que
y
son
dr
F


perpendiculares, por lo que también lo son E y dr .
FISICA 2º BACHILLERATO
CAMPO ELECTRICO

Dos superficies equipotenciales nunca pueden cortarse. Si lo hicieran, en todos
los puntos de la línea de corte habría dos vectores campo eléctrico, cada uno
perpendicular a una de las superficies, lo cual no es posible.
-
Diferencia de energía potencial eléctrica
El campo eléctrico es un campo de fuerzas conservativos, al igual que el campo
gravitatorio, por esta razón es posible describir los fenómenos electrostáticos en función
de una magnitud escalar llamada energía potencial eléctrica, que varía con la posición.
Si un campo de fuerzas es conservativo, el trabajo realizado por las fuerzas del campo es
independiente del camino seguido y sólo depende de la posición inicial y final.
Se define la diferencia de energía potencial eléctrica entre dos puntos A y B, de un
campo eléctrico, como el trabajo realizado por las fuerzas del campo para trasladar una
carga q entre esos puntos.
 
W   F  dr  ( E PB  E PA )   E P
B
B
A
A
Donde:
Como origen de energías potenciales se toma el infinito al que se le asigna el valor cero:
EP (  ) = 0.
Según esto la energía potencial eléctrica en un punto de un campo eléctrico se puede
definir como el trabajo realizado por las fuerzas del campo para trasladar una carga q
desde dicho punto al infinito.
WA  E P  ( E P( )  E P( A) )  E P( A)
Al igual que en el campo gravitatorio, siempre que el trabajo lo realice el campo ,
podremos decir que el proceso ocurre de forma espontánea , lo que ocurre es que en el
caso del campo eléctrico tenderá a aumentar la energía potencial si la carga que se
desplaza es negativa o tenderá a disminuir la energía potencial si la carga que se
desplaza es positiva; y en cualquiera de los dos casos el trabajo será positivo.
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
-
Diferencia de potencial y potencial eléctrico
Se define diferencia de potencial eléctrico entre dos puntos A y B de un campo
eléctrico como el trabajo realizado por las fuerzas del campo para trasladar la unidad de
carga positiva entre dichos puntos.
Si el campo eléctrico es debido a una carga Q, la diferencia de potencial será:
W AB
=
q
=
Donde V(r) =
  B
B
B
  B
F  dr
Q
A q  A E  dr  A E  dr  cos0  A E  dr  A K r 2  dr 
B
KQ KQ
= (VB-VA)

rB
rA
K Q
r
es el potencial eléctrico en un punto a una distancia r de la carga Q.
Como origen de potenciales se toma el infinito al que se le asigna el valor cero: V( r= ) = 0
El potencial eléctrico en un punto se puede definir como el trabajo realizado por las
fuerzas del campo para trasladar la unidad de carga positiva desde ese punto al
infinito.
Características del potencial: V  K
Q
r
a) El potencial es una magnitud escalar que sirve para caracterizar un campo
eléctrico, ya que el valor del mismo sólo depende de la carga que crea el campo y
de la distancia del punto a la carga.
b) En el caso de una carga puntual el potencial es el mismo en todos los puntos que
equidistan de la carga que lo crea.
c) El signo del potencial coincide con el signo de la carga que lo crea, es decir
positivo si la carga es positiva y negativo si la carga es negativa.
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
d) El potencial en un punto es la energía potencial que posee la unidad de carga
positiva colocada en ese punto. V( A) 
E P ( A)
q
 EP ( A)  V( A)  q
La unidad de potencial en el S.I. es J/C = V (voltio).
e) Conocida la diferencia de potencial eléctrica entre dos puntos de un campo
eléctrico, se puede calcular el trabajo realizado por las fuerzas del campo para
trasladar una carga q entre eso dos puntos:
WAB  EP  ( EP ( B )  EP ( A) )  (qV( B )  qV( A) )  qV
WAB = q ( VA – VB )
1) Si la carga q es positiva el trabajo será realizado por las fuerzas del campo
(espontaneo y positivo) si la carga se desplaza de potenciales mayores a
potenciales menores ( VA > VB ) justo en sentido contrario que en el campo
gravitatorio.
2) Si la carga q es negativa el trabajo será realizado por las fuerzas del campo
(espontaneo y positivo) si la carga se desplaza de potenciales menores a
potenciales mayores ( VA < VB ) justo en el mismo sentido que en el campo
gravitatorio.
f) Al ser el potencial una magnitud escalar, el potencial total en un punto debido a un
conjunto de cargas será la suma algebraica de los potenciales creados por cada carga
en ese punto.
n
n
i 1
i 1
VT  Vi  K 
qi
ri
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
D) Campo eléctrico uniforme
Se llama así a un campo que tiene el mismo módulo, dirección y sentido en todos sus
puntos. Sus líneas de fuerza son líneas rectas, cuyo sentido señalan hacia potenciales
decrecientes. Sus superficies equipotenciales son planos perpendiculares a la dirección
del campo.
Un campo eléctrico uniforme es el que existe en la región comprendida entre dos láminas
conductoras paralelas, con cargas iguales de signo opuesto (condensador plano)
La relación entre la intensidad de campo y el potencial viene dada por la expresión:
 
B 

V
V    E  dr ; Si E  Cte  V   E  dr   E  d ; E 
; siendo d la
d
A
A
B
distancia entre las placas.
Expresión que indica que, en un campo eléctrico uniforme, la diferencia potencial varía
linealmente con la distancia, decreciendo en el sentido del campo: VB  V A   E  d
E) Movimiento de una carga en un campo eléctrico uniforme
1) Partícula en reposo o en movimiento con una velocidad inicial, v0 en un
campo eléctrico uniforme
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
Sea una partícula de masa m y carga q positiva en reposo o en movimiento con una

velocidad inicial en un campo eléctrico uniforme con una intensidad E que actúa
verticalmente: Sobre la carga actuará debido al campo eléctrico una fuerza constante:




 F qE
en la misma
F  q  E que le comunicará un MRUA con una aceleración a  
m
m
dirección que el campo eléctrico; para ello conviene recordar las ecuaciones:
(1) d = d0 + v0 t + ½ at2; (2) v2 = v02 + 2 a d; (3) v = v0 + a t.
En el caso de que la partícula de masa m y carga q sea negativa en las mismas
condiciones, dicha partícula experimentará un MRUR con la misma aceleración


 F qE
y en la misma dirección que el campo eléctrico; utilizaremos las mismas
a 
m
m
ecuaciones (1), (2) y (3) pero con signo negativo.
2) MOVIMIENTO DE UNA CARGA QUE SE MUEVE CON VELOCIDAD CONSTANTE
EN UNA DIRECCIÓN PERPENDICULAR AL CAMPO ELÉCTRICO.
Al entrar en el campo eléctrico, la partícula se encuentra sometida simultáneamente a la
acción de dos movimientos: un movimiento rectilíneo y uniforme a lo largo del eje X
debido a la velocidad inicial, y a otro movimiento uniformemente acelerado debido a la
fuerza que ejerce el campo eléctrico.
Como resultado de la composición de estos dos movimientos, que actúan a la vez, se
obtiene una trayectoria parabólica:
La ecuación de cada parábola se obtendrá teniendo en cuenta las siguientes ecuaciones:
En el eje X: ax = 0; vx = v0 ; x = v0 t


 F qE

(1) En el eje Y: v0y = 0; ay = a 
; vy = v0 + q E t / m (2); y = + ½ a t2 (3)
m
m
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
La ecuación de la trayectoria de la parábola se obtiene al despejar el tiempo t en (1) y
sustituirlo en (3): y = ½ (q E / m v02) x2 (4)
F) Ley de Gauss: Concepto de Flujo eléctrico y aplicaciones
-
ᶲ:
Flujo eléctrico,
El flujo eléctrico a través de una superficie es una magnitud
escalar que mide el número de líneas de campo que atraviesan dicha superficie. El
flujo eléctrico se calcula como el producto escalar del vector intensidad de campo
eléctrico E y el vector superficie S.
ᶲ = E S = E S cos α
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
-
Ley de Gauss : Hasta ahora hemos considerado los cuerpos cargados como si
fueran cargas puntuales, sin embargo en la realidad eso no es así. “El flujo
eléctrico a través de una superficie cerrada S es directamente proporcional a
la carga neta Q que encierra la superficie”. La superficie cerrada empleada
para calcular el flujo del campo eléctrico se denomina superficie Gaussiana.
Demostración: Supongamos una carga eléctrica puntual positiva Q de radio R
que se encuentra encerrada en una superficie, S tal y como muestra la figura:
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
-
Aplicaciones de la Ley de Gauss
a) Campo creado por un placa conductora.
El campo eléctrico creado por una placa conductora puede ser calculado
utilizando la ley de Gauss. En la siguiente figura se ha representado un plano
infinito cargado con una densidad superficial de carga σ (= q/S) uniforme y
positiva. Las líneas de campo siempre salen de las cargas positivas, por lo que
el campo creado por el plano será uniforme (ya que la densidad de carga lo es)
y sus líneas irán hacia afuera de ambos lados del plano.
El flujo del campo eléctrico a través de cualquier superficie cerrada es siempre
el mismo (ley de Gauss); en este caso, por simplicidad de cálculo, se ha
elegido una superficie Gaussiana cilíndrica (representada en rojo en la figura).
El flujo a través de la superficie lateral del cilindro es nulo (ninguna línea de
campo la atraviesa). Las únicas contribuciones no nulas al flujo son las que se
producen a través de sus dos bases. El flujo del campo eléctrico a través del
cilindro es entonces:
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
Como las dos bases del cilindro son iguales y el módulo del campo es el mismo en todos
los puntos de su superficie, la integral anterior se simplifica, quedando:
El valor del flujo viene dado por la ley de Gauss:
Y q /S es la densidad superficial de carga σ:
b) Campo creado por un conductor esférico.
El campo eléctrico creado por un conductor esférico puede ser calculado
utilizando la ley de Gauss. En este caso, por simplicidad de cálculo, se ha
elegido una superficie Gaussiana esférica, SG (representada en verde en la
figura).
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
En consecuencia, el campo eléctrico creado por un conductor esférico en un punto
exterior es el mismo que crearía una carga puntual Q situada en el centro de la esfera.
c) Campo creado por un hilo conductor.
Imagina un hilo uniformemente cargado cuya densidad lineal de carga es λ (λ=Q/L). Si
utilizamos la ley de Gauss para determinar el valor de E, es común seguir los siguientes
pasos:
1. Se escoge una superficie cerrada que envuelva al objeto que crea el campo eléctrico.
Dicha superficie denominada superficie gaussiana debe poseer un área fácil de obtener y
debe ser perpendicular a dicho campo eléctrico. En nuestro caso, parece evidente que la
superficie gaussiana debería ser el cilindro "virtual".
2. Se aplica la expresión general del flujo eléctrico para cualquier tipo de superficie. Aquí
tendremos en cuenta que el flujo total que atraviesa el cilindro es la suma de los flujos que
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
atraviesan todas sus caras. Sin embargo, dado que las líneas de campo solo atraviesan
los laterales, el flujo eléctrico por las bases es nulo.
ΦE = ΦB + ΦL + ΦB ⇒ ΦB = 0 ⇒ ΦE = ΦL
En nuestro caso como en el el lateral
son paralelos, su producto escalar
Teniendo en cuenta que la superficie lateral de un cilindro es SL =2·π·R·h
3. El valor obtenido en el punto anterior se iguala a la expresión del teorema de Gauss. En
nuestro caso, tendremos en cuenta que λ=Q/L.
FISICA 2º BACHILLERATO
CAMPO ELECTRICO
Por tanto, si consideramos que d es la distancia al punto donde medimos la intensidad del
campo eléctrico d = R: