Analisis de Sistemas Combinacionales

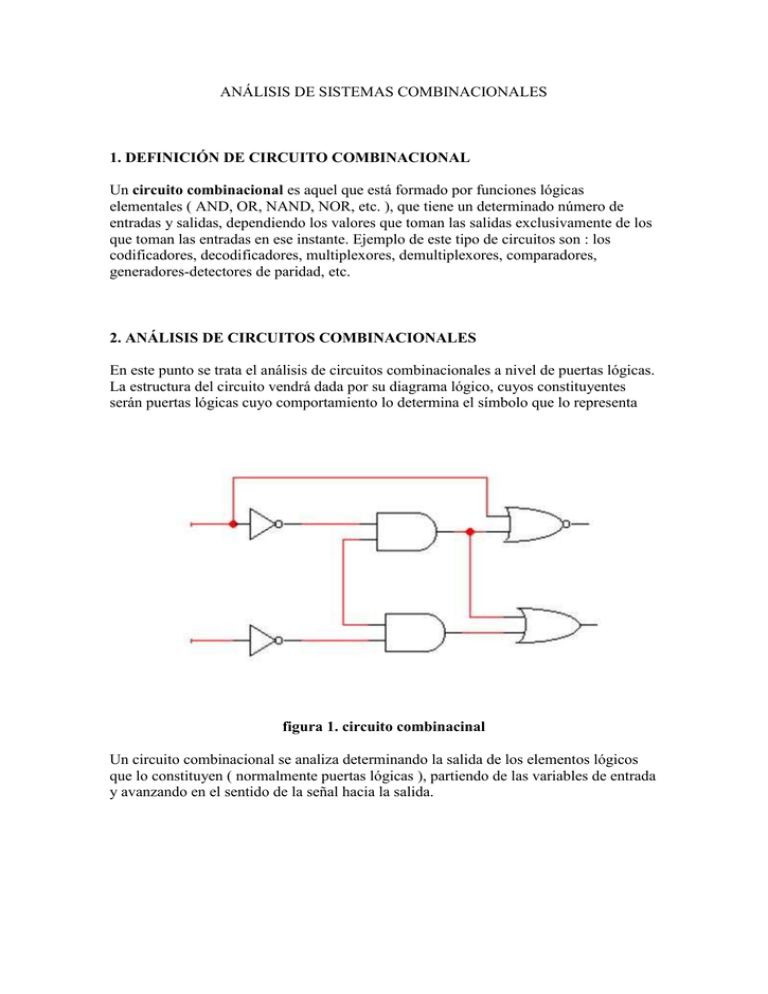
ANÁLISIS DE SISTEMAS COMBINACIONALES
1. DEFINICIÓN DE CIRCUITO COMBINACIONAL
Un circuito combinacional es aquel que está formado por funciones lógicas
elementales ( AND, OR, NAND, NOR, etc. ), que tiene un determinado número de
entradas y salidas, dependiendo los valores que toman las salidas exclusivamente de los
que toman las entradas en ese instante. Ejemplo de este tipo de circuitos son : los
codificadores, decodificadores, multiplexores, demultiplexores, comparadores,
generadores-detectores de paridad, etc.
2. ANÁLISIS DE CIRCUITOS COMBINACIONALES
En este punto se trata el análisis de circuitos combinacionales a nivel de puertas lógicas.
La estructura del circuito vendrá dada por su diagrama lógico, cuyos constituyentes
serán puertas lógicas cuyo comportamiento lo determina el símbolo que lo representa
figura 1. circuito combinacinal
Un circuito combinacional se analiza determinando la salida de los elementos lógicos
que lo constituyen ( normalmente puertas lógicas ), partiendo de las variables de entrada
y avanzando en el sentido de la señal hacia la salida.
3. SÍNTESIS Y DISEÑO DE CIRCUITOS COMBINACIONALES
A continuación se intentan exponer las fases que se siguen en el proceso de síntesis y
diseño de circuitos combinacionales :





Definición de la función a realizar y especificación de las entradas y salidas.
Tabla de la verdad.
Ecuaciones lógicas de las salidas.
Simplificación de las ecuaciones.
Realización o implementación de las ecuaciones simplificadas mediante puertas
lógicas.
3.1.Implementación con puertas AND,OR,NOT
La implementación con puertas AND, OR y NOT se realiza en el último paso del
apartado anterior, sustituyendo las operaciones básicas que aparecen en la expresión
lógica de mi circuito digital, de suma lógica, producto lógico y complementación. Estas
operaciones se sustituyen por su representación simbólica obteniendo la realización del
circuito mediante puertas lógicas.
Un ejemplo: Una vez realizado mi diseño he obtenido la siguiente función
, siendo F la salida del circuito, y A,B,C las entradas.
figura 3. Implementación con puertas AND, OR Y NOT
Ahora solamente queda interconexionar los términos anteriores con la entrada B,
mediante sumas ( OR ).Luego el circuito completo queda :
figura 4. Implementación total del circuito con puertas AND, OR Y NOT
3.2.Implementación con puertas NAND y NOR
Para implementar circuitos digitales solamente con puertas NAND o NOR debo conocer
como implemento las operaciones básicas AND, OR y NOT, mediante el uso exclusivo
de NAND o NOR.
La puerta NOT se puede obtener o es equivalente mediante NAND o NOR ( se
justifica con las tablas de verdad ), conectando ambas entradas :
Síntesis con NAND :
Síntesis con NOR :
Si quisiéramos implementar el circuito de la figura 1, por ejemplo, con puertas
NOR/NAND sustituiríamos cada puerta AND, OR y NOT por su equivalencia según
hemos visto anteriormente, eliminando posteriormente las situaciones redundantes.
4. CODIFICADORES
Son sistemas combinacionales con m £ 2n entradas y n salidas que se encargan de
transformar una serie de señales sin codificar en un conjunto que responda a un código.
4.1. Codificadores sin prioridad
Su cometido es la generación de un número binario sobre sus n salidas que identifique
cuál de las entradas está activadas ( ver siguiente figura 7).
figura 7. codificador
Como no hay nada que impida el que se activen simultáneamente varias líneas de
entrada de un codificador, los circuitos codificadores se diseñan normalmente para que
respondan a una sola señal de entrada activa, dando lugar a los codificadores con
prioridad.
El codificador de la figura 7 corresponde a un codificador de octal a binario sin
prioridad , cuya tabla de verdad es la siguiente:
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
1
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
1
0
0
1
0
1
0
0
0
0
0
0
1
0
1
1
0
0
0
0
0
0
0
0
1
1
1
1
Las funciones lógicas para las salidas, a partir de la tabla de verdad anterior y entrada
ENABLE ( E ) para activar la entrada cuando vale 1 o inhibirla cuando vale 0, quedan:
A2 = ( B4 +B5 + B6 + B7 ) E
A1 = ( B2 +B3 + B6 + B7 ) E
A0 = ( B1 +B3 + B5 + B7 ) E
Siendo la función lógica : F = ( B0 + B1 + B2 +B3 + B4 + B5+ B6 + B7 ) E , una señal de
salida especial que se activa cuando todas las señales de entrada son nulas y E=1.
4.2. Codificadores con prioridad
Para obtener codificadores que respondan a una sola señal de entrada activa, se le asigna
valores fijos de prioridad a las líneas de entrada, de forma que en cada instante sólo se
genera el código de salida de la entrada activa que tenga la máxima prioridad.
figura 8 . símbolo de un codificador 74148 con prioridad de 8 líneas a 3 líneas
figura 9 . TABLA DE VERDAD del codificador con prioridad
Por tanto, en la salida del codificador aparecerá el mayor número i, tal que Bi esté
activada ( si hemos impuesto en el diseño el criterio de prioridad a la entrada más alta ).
La EI (negada) es la señal ENABLE, las Ii (negadas) entradas, Ai (negadas) salidas, EO
(negada) señal de salida especial que se activa cuando todas las señales de entrada son
nulas y GS (negada) señal de grupo que se activa cuando EI (negada ) = L y hay
petición de servicio.
El codificador 74148 se trata de un codificador con prioridad cuyas entradas y salidas
son activas a nivel bajo. Esto significa que las entradas se activan con ceros lógicos y
las salidas aparecen complementadas. Una entrada o salida activa a nivel bajo se
simboliza en los diagramas lógicos ( figura 8 ), en lógica positiva, insertando un
pequeño circulo . También se suele indicar que la línea es activa a nivel bajo poniendo
la correspondiente negada ( ver siguiente figura 11 ).
figura 11. Ejemplo de indicación de líneas a nivel bajo
5. DECODIFICADORES
Un decodificador es un circuito combinacional con n entradas y m 2n salidas. Para cada
una de las 2n posibles configuraciones binarias que se pueden presentarse en su entrada,
el sistema pone a 1 una y sólo una de las salidas, de acuerdo con la siguiente regla: si la
configuración binaria presente en las entradas forma el número binario i, entonces se
activa la salida i-ésima.
Según esto el funcionamiento de un decodificador es el opuesto al de un codificador.
5.1. Decodificadores BCD-DECIMAL y Excitador BCD-7 segmentos
En el decodificador BCD-DECIMAL, n=4 y m=10 ( ver figura 12 siguiente)
Obteniendo las expresiones lógicas de la tabla de verdad anterior, podremos realizar la
síntesis del circuito combinacional mediante puertas lógicas ( ver figura 13 ):
figura 13 . síntesis mediante puertas del decodificador BCD-DECIMAL
CD4028BC
En el Excitador BCD-7 segmentos es un tipo de decodificador que me da la
posibilidad de conectarlo a un display numérico digital de 7 segmentos a, b, c, d, e, f y g
( figura 14 ), y obtener la visualización del código binario BCD:
figura 13 . display numérico digital de 7 segmentos
Todas las posibilidades de salida por el display son las siguientes :
figura 14 . salidas posibles del display numérico digital de 7 segmentos
Si identificamos cada segmento cuando debe estar activo o no podemos obtener la tabla
de verdad :
figura 15 .tabla de verdad del Excitador BCD-7 segmentos
Nota : para interpretar la tabla anterior no tener en cuenta las entradas LE, BI y LT
(negadas) cuya función es otra y no aporta nada a lo que estamos viendo ahora.
Ahora obtendría la expresiones lógicas mediante minterms/maxterms y las
implementaría con puertas lógicas.
5.2. Implemetación de funciones lógicas con decodificadores
Un decodificador genera en sus salidas, todos los minterms de un número de variables
igual al número de líneas de entrada. Por tanto, con un decodificador de n entradas-2n
salidas y puertas OR, se pueden implementar funciones lógicas de n variables ( también
podría tomar los ceros de la función y utilizaría puertas NOR ). Veamos un ejemplo :
figura 16 . implementación de función lógica con decodificador
Si el decodificador tuviera sus salidas activas a nivel bajo, se generan los minterms
negados luego en vez de puertas OR debo usar NAND.
6. MULTIPLEXORES Y DEMULTIPLEXORES
6.1. Multiplexores
Un multiplexor es un sistema digital que consta de varias entradas y una salida, y
mediante un mecanismo de selección, una determinada entrada se transfiere a la salida.
Figura 17. Multiplexor y su tabla de verdad
Una definición más formal de multiplexor sería la de un circuito combinacional con n
entradas de selección o control (a, b,.. ), 2n entradas de datos (K1 , K2 , ... ) y una salida
Z. Los datos de la se rutan desde la entrada de datos cuyo número de orden coincide con
el número binario puesto en la entrada de selección hacia la salida ( ver figura 18 )
Figura 18. Selección de la entrada de datos del multiplexor
La síntesis con puertas lógicas se realiza obteniendo la expresión lógica de la salida Z,
obteniendo :
Es importante reseñar que algunos multiplexores presentan entradas ENABLE o
STROBE para dar permiso de funcionamiento o no al multiplexor.
6.2. Demultiplexores
El funcionamiento es el contrario al del multiplexor, encauzando los datos desde una
fuente común de entrada hacia uno de 2n destinos de salida.
Por tanto, un demultiplexor es un circuito combinacional con una entrada J, n entradas
de selección y 2n salidas.
Es importante comentar que los demultiplexores pueden trabajar como decodificadores.
Vamos a explicar como se consigue esto con un ejemplo: supongamos que tenemos un
DEMUX 1:4 ( una J entrada a cuatro salidas ), si hago la entrada J=1 siempre activa,
transformo el funcionamiento a un DECODIFICADOR 2:4, actuando ahora las señales
de selección (a, b,... ) como entrada de código a decodificar y las salidas como salidas
del código decodificado.
Figura 20. Demux actuando como decodificador
La síntesis con puertas sería, partiendo de su tabla de verdad :
Figura 21. Síntesis con puertas de un demultipexor/decodificador
6.3. Implementación de funciones lógicas con multiplexores
Viendo un ejemplo, podremos ver como se realiza la síntesis, como voy a utilizar un
MUX 4:1 tengo 2 entradas de selección. Por tanto, elijo de la función lógica a
implementar 2 de las variables como señales de selección y determino cual debe ser las
entradas del multiplexor con la que me queda.
Figura 22 .Implementación de funciones lógicas con multiplexores
Si tuviera más de 3 variables lógicas para este caso de MUX 4:1 necesitaría usar más de
un multiplexor. Es importante decir que la elección de las variables que van a actuar de
señales de selección es indiferente y muchas se toman unas u otras simplemente por
motivo de diseño.