ω αθ ω ω

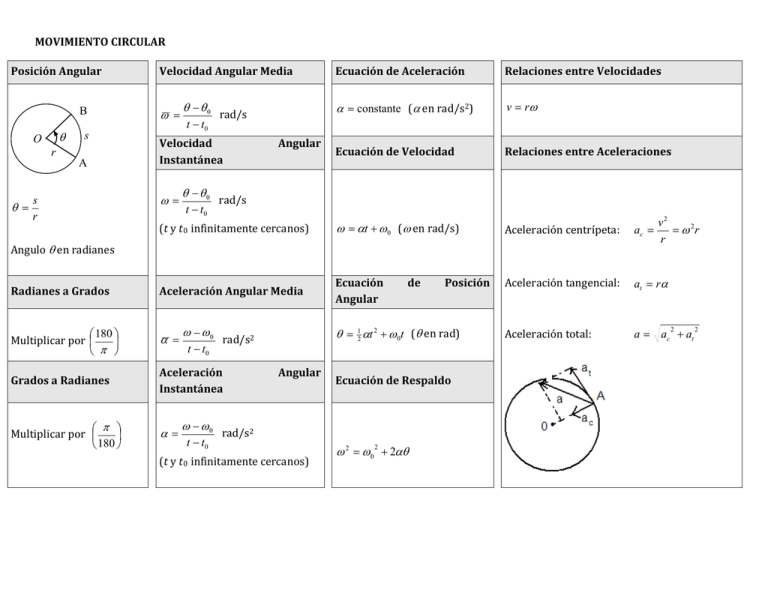
MOVIMIENTO CIRCULAR
Posición Angular
Ecuación de Aceleración
Relaciones entre Velocidades
α = constante (α en rad/s2)
v = rω
Ecuación de Velocidad
Relaciones entre Aceleraciones
(t y t 0 infinitamente cercanos)
ω = αt + ω 0 (ω en rad/s)
Aceleración centrípeta:
ac =
Radianes a Grados
Aceleración Angular Media
Ecuación
Angular
Aceleración tangencial:
at = rα
 180 
Multiplicar por 

 π 
α =
Aceleración total:
a = ac + at
B
θ
O
s
r
A
s
θ =
r
Angulo θ en radianes
Grados a Radianes
 π 
Multiplicar por 

 180 
Velocidad Angular Media
ω =
θ − θ0
t − t0
rad/s
Velocidad
Instantánea
ω=
θ − θ0
t − t0
ω − ω0
t − t0
rad/s
rad/s2
Aceleración
Instantánea
α=
ω − ω0
t − t0
Angular
rad/s2
Angular
(t y t 0 infinitamente cercanos)
de
Posición
θ = 12 αt 2 + ω 0t (θ en rad)
Ecuación de Respaldo
ω 2 = ω 0 2 + 2αθ
v2
= ω 2r
r
2
2
1. Un disco de 60 cm de diámetro gira 72 rpm. Calcular el período, la velocidad angular, la rapidez y la
aceleración normal en un puno de la periferia.
2. Hallar la velocidad angular, la velocidad lineal y la aceleración normal de un cuerpo en la Tierra
situado:
a) En punto del ecuador;
b) En un punto a 45º de latitud norte. Radio de la Tierra: 6366198 m
3. El diámetro de las ruedas delanteras de un carruaje es de 60 cm. y el de las ruedas traseras es de 1,10
m. La velocidad de giro de las ruedas delanteras cuando el carruaje se desplaza con velocidad constante
es de 160 rpm. Calcular:
a) La velocidad angular de las ruedas traseras;
b) La velocidad del carruaje;
c) Las vueltas que habrán dado las ruedas delanteras y traseras en un kilómetro de recorrido.
4. El plato de un tocadiscos, al ponerlo en marcha, adquiere una velocidad angular de 45 rpm después de
haber completado 4 vueltas. Calcular su aceleración angular.
5. Hallar la aceleración tangencial, la aceleración normal y el módulo de la aceleración de un punto de la
periferia de un disco de 30 cm. de diámetro colocado sobre el plato del tocadiscos del problema anterior
y al cabo de ¼ de vuelta de iniciado el movimiento
6. En el modelo Bohr del átomo de hidrógeno, un electrón gira alrededor de un protón en una órbita
circular de 5.29 x 10-11m de radio con una velocidad de 2.18 x 106 m/s ¿Cuál es la aceleración del electrón
en este modelo del átomo de hidrógeno.
7. Una rueda de feria Ferris tiene un radio de 15m y completa cinco vueltas sobre su eje horizontal a cada
minuto.
a) ¿Cuál es la aceleración, magnitud y dirección de una pasajero más alto?
b) ¿Cuál es la aceleración en el punto más bajo?
8. Un abanico que está girando completa 1200 revoluciones cada minuto. Consideremos un punto en la
punta de un aspa, la cual tiene un radio de 0.15m.
a) ¿A que distancia se mueve el punto en una revolución?
b) ¿Cuál es la velocidad del punto?
c) ¿Cuál es su aceleración?
9. Se cree que ciertas estrellas neutrón (estrellas extremadamente densas) giran alrededor de 1 rev/s. Si
una estrella tal tiene un radio de 20 km (valor típico) (a) ¿Cuál es la velocidad de un punto situado en el
ecuador de la estrella y (b) ¿Cuál es la aceleración centrípeta de este punto?
10. Un móvil con MCU describe 10 ciclos en 2 s . Calcula su período, frecuencia y rapidez angular.
Por Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M
Página 2
11. Un móvil con MCU gira a 360 rpm . Si el radio de la circunferencia mide 50 cm, calcula su rapidez
angular y tangencial.
12. Un móvil con MCU describe una circunferencia de 4 m de diámetro cada 2s . Calcula su aceleración
centrípeta.
13. En un movimiento circular uniforme, con centro en el origen de coordenadas, se observa que para
cierto instante la posición es r = 8 m i + 6 m j mientras que la velocidad angular tiene un valor de 2 seg-1.
Calcular y representar sobre un esquema de la trayectoria:
a) el vector velocidad para ese instante,
b) el vector aceleración en el mismo instante.
14. En un movimiento circular uniforme, con centro en el origen de
coordenadas, se observa que para cierto instante la posición es r = 8 m i + 6 m j
mientras que la velocidad angular tiene un valor de 2 seg-1. Calcular y
representar sobre un esquema de la trayectoria:
a) El vector velocidad para ese instante,
b) El vector aceleración en el mismo instante.
15. Calcular la rapidez tangencial y la aceleración centrípeta de la traslación terrestre alrededor del Sol.
AYUDA: la distancia media entre el Sol y la Tierra es d TS = 149.6 x 106 Km.
La Tierra completa una vuelta en torno al Sol en un año o 365.242199 días.
16. Un disco de 10 cm. de radio que gira a 30 rev/min tarda un minuto en detenerse cuando se lo frena.
Calcular:
a) su aceleración angular,
b) el número de revoluciones hasta detenerse,
c) la rapidez tangencial de un punto del borde del disco antes de empezar a frenar, d) la aceleración
centrípeta, tangencial y total para un punto del borde del disco.
Por Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M
Página 3