Problemas de cinemática

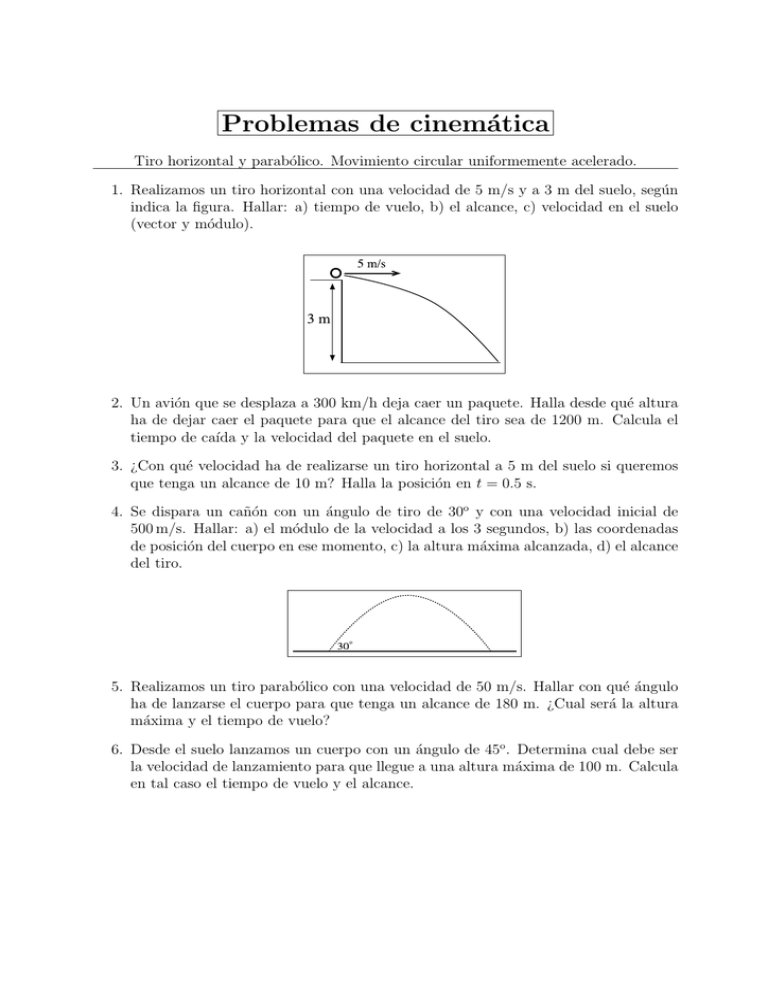
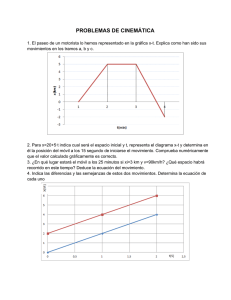
Problemas de cinemática
Tiro horizontal y parabólico. Movimiento circular uniformemente acelerado.
1. Realizamos un tiro horizontal con una velocidad de 5 m/s y a 3 m del suelo, según
indica la figura. Hallar: a) tiempo de vuelo, b) el alcance, c) velocidad en el suelo
(vector y módulo).
2. Un avión que se desplaza a 300 km/h deja caer un paquete. Halla desde qué altura
ha de dejar caer el paquete para que el alcance del tiro sea de 1200 m. Calcula el
tiempo de caı́da y la velocidad del paquete en el suelo.
3. ¿Con qué velocidad ha de realizarse un tiro horizontal a 5 m del suelo si queremos
que tenga un alcance de 10 m? Halla la posición en t = 0.5 s.
4. Se dispara un cañón con un ángulo de tiro de 30o y con una velocidad inicial de
500 m/s. Hallar: a) el módulo de la velocidad a los 3 segundos, b) las coordenadas
de posición del cuerpo en ese momento, c) la altura máxima alcanzada, d) el alcance
del tiro.
5. Realizamos un tiro parabólico con una velocidad de 50 m/s. Hallar con qué ángulo
ha de lanzarse el cuerpo para que tenga un alcance de 180 m. ¿Cual será la altura
máxima y el tiempo de vuelo?
6. Desde el suelo lanzamos un cuerpo con un ángulo de 45o . Determina cual debe ser
la velocidad de lanzamiento para que llegue a una altura máxima de 100 m. Calcula
en tal caso el tiempo de vuelo y el alcance.
7. El cauce de un barranco posee una anchura de 60 m. Si solo podemos lanzar objetos
con un ángulo de 60o , calcula cual es la velocidad mı́nima que podemos dar a los
objetos para que crucen el barranco.
8. Calcula la velocidad angular y la frecuencia de las manecillas de un reloj analógico.
9. Un tractor se mueve a una velocidad de 40 km/h. Si la rueda grande tiene un
diámetro de 1.20 m y la pequeña de 40 cm, calcula cuántas vueltas da cada rueda
en 15 minutos.
10. Un volante rotatorio posee una velocidad de 300 rpm y frena hasta detenerse tras
efectuar 100 revoluciones. Calcula: a) aceleración angular, b) tiempo empleado en
detenerse, c) aceleración tangencial y normal a los 4 segundos si el volante tiene un
radio de 50 cm.
11. Un disco que parte del reposo posee una aceleración angular α = 2 rad/s2 . Calcula
en qué instante su velocidad angular es de 100 rad/s y las vueltas que ha dado en el
proceso. Si el radio del disco es de 1 m calcula en qué instante la aceleración normal
es de 200 m/s2 .
Fórmulas moviminiento circular uniformemente acelerado
ω=
∆ϕ
,
∆t
T =
ϕ = ϕo + ωo t +
2π
,
ω
1 2
αt ,
2
ω = 2πf,
v = ω R,
ω = ωo + α t,
at = α R,
an = ω 2 R =
v2
R
ω 2 = ωo 2 + 2 α (ϕ − ϕo )
Fórmulas tiro horizontal
x = vo t,
y = ho −
1 2
gt ,
2
%v = (vo , −g t),
g = 9, 8m/s2
Fórmulas tiro parabólico
(x, y) = (v0 cos α t, vo sin α t −
1 2
g t ) (Posición),
2
vo2 sin2 α
2g
g = 9, 8m/s2
X=
vo2 sin 2α
g
(Alcance) H =
Tv =
2vo sin α
g
(Tiempo de vuelo) %v = (vo cos α, vo sin α − g t) (Velocidad)
2
(Altura máxima)
Soluciones
1. a) Tv = 0.782 s, b) X = 3.912 m, c) %v = (5, −7.66), |%v | = 9.147 m/s
2. ho = 1016 m. Tv = 14.4 s. %v = (83.3, −141, 12), |%v | = 163.87 m/s
3. vo = 9.89 m/s. (x, y) = (4.94, 3.76) m
4. a) |%v | = 485.96 m/s. b) (x, y) = (1299.03, 705.9) m. c) Hm = 3188.77 m. d)
X = 22092.4 m
5. α = 22.44o , Hm = 18.58 m, Tv = 3.89 s.
6. vo = 62.6 m/s, Tv = 9.03 s, X = 399.87 m
7. vo = 26.1 m/s
8. Ω =
1
π
1
π
rad/s, F =
Hz, ω =
rad/s, f =
Hz.
1800
3600
30
60
9. 1326.29 vueltas la grande, 3978.87 vueltas la pequeña.
10. a) α = −
π
= −0.785 rad/s2 , b) t = 40 s, c) at = −0.392 m/s2 , an = 399.72 m/s2 .
4
11. t = 50 s, ϕ = 397.88 vueltas, t = 7.07 s
3