Práctica 5 ESTUDIO NUMÉRICO DE LA CINÉTICA DE UNA
Anuncio

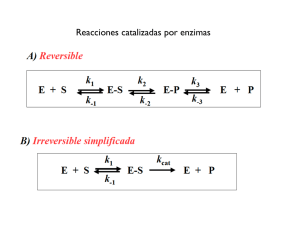
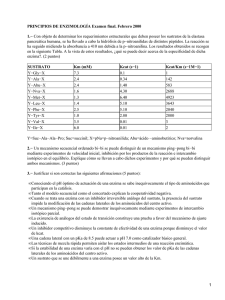
Termodinámica y Cinética Química Área de Química Física Práctica 5 ESTUDIO NUMÉRICO DE LA CINÉTICA DE UNA REACCIÓN ENZIMÁTICA 1. Objetivo Se empleará un programa informático de cálculo que permite obtener la variación de las concentraciones de reactivos, intermedios y productos de una reacción enzimática con el tiempo. A partir de esos datos se obtendrá la velocidad de reacción, se verificará la ecuación de Michaelis-Menten y se extraerá la correspondiente constante de Michaelis. 2. Fundamento teórico 2.1. Actividad enzimática Los enzimas son proteínas altamente especializadas que catalizan numerosas reacciones en los sistemas biológicos. Una propiedad importante es su especificidad a la hora de reaccionar con sustratos, acelerando determinadas reacciones químicas en disolución. En general, un enzima proporciona el ambiente en que una reacción determinada es, energéticamente, más favorable. El rasgo distintivo de una reacción catalizada enzimáticamente es que ocurre en un lugar específico del enzima, el sitio activo. La molécula fijada en el sitio activo y sobre la que actúa el enzima se denomina sustrato. El complejo enzima-sustrato formado es de vital importancia para definir el comportamiento cinético de las reacciones catalizadas. Una reacción enzimática sencilla puede formularse como sigue: k1 k2 E + S ES E + P [1] k-1 donde E, S y P representan enzima, sustrato y producto, respectivamente. ES y EP son complejos del enzima con el sustrato y con el producto. La función del catalizador es aumentar la velocidad de una reacción reduciendo la energía de activación de la misma, Ea. Los catalizadores no modifican los equilibrios de la reacción ni se consumen durante el proceso. 2.2. Velocidad de reacción. Mecanismo de Michaelis-Menten La velocidad de una reacción cualquiera viene determinada por la concentración de reactivo/s y por una constante de velocidad, k, y expresada por una ley de velocidad. Por ejemplo para una reacción unimolecular o de primer orden, S → P, la cantidad de S que ha reaccionado por unidad de tiempo viene dado por la siguiente expresión: Prácticas de Termodinámica y Cinética-2º curso Licenciatura de Biotecnología 1 Termodinámica y Cinética Química Área de Química Física V =− d [S ] d [P ] = = k [S ] dt dt [2] donde k, tiene unidades de s-1 y S de mol·l-1. Así pues, la concentración de sustrato, [S], afecta a la velocidad de una reacción catalizada por un enzima. No obstante, el estudio del efecto de [S] en una reacción enzimática no es simple. Este tipo de comportamiento cinético es explicado por la teoría de Michaelis y Menten, que postula que el enzima se combina con el sustrato en un paso reversible rápido, para dar el complejo ES, según se muestra en la reacción [4]. k1 k2 E + S ES → E + P [4] k-1 La reacción de esta forma alcanza rápidamente un estado estacionario en el que [ES] permanece aproximadamente constante con el tiempo. El complejo ES se descompone seguidamente en un segundo paso más lento que limita la velocidad de la reacción global dando el enzima libre E y el producto de reacción P. Por tanto la ley de velocidad para la reacción global viene determinada por la etapa más lenta, según indica la ecuación [5]: V = k 2 [ES ] [5] donde V se determina por la descomposición de ES. Bajo las condiciones de estado estacionario ([ES]=cte) la velocidad del proceso se mantiene constante en los primeros estadios de la reacción y coincide con la velocidad inicial, Vo. Experimentalmente Vo puede determinarse calculando la pendiente de la representación de [P] frente al tiempo (ecuación [2]). Además, a medida que la concentración inicial de S aumenta, desplazando el equilibrio hacia la formación de ES, también lo hace Vo hasta alcanzar un valor constante. Este valor final se denomina velocidad máxima, Vmax. Esto se observará cuando prácticamente todo el enzima esté formando complejo ES y la concentración de E libre sea extremadamente pequeña ([ES]=[Et], donde Et es la concentración total de enzima utilizada). En estas condiciones, el enzima está saturado por el sustrato, de forma que un aumento adicional en la [S] ya no tiene efecto sobre la velocidad inicial del proceso. De esta manera, se puede definir que Vmax = k2·[Et], la cual varía de un enzima a otro, y donde k2 se define de manera general como kcat, una constante de velocidad de primer orden que se denomina número de recambio. Utilizando la aproximación del estado estacionario, se obtiene la Ecuación de Michaelis-Menten: Vo = Vmax [ S ] Km + [S ] [6] donde Km = k −1 + k 2 k1 [7] Prácticas de Termodinámica y Cinética-2º curso Licenciatura de Biotecnología 2 Termodinámica y Cinética Química Área de Química Física es la constante de Michaelis. Esta constante depende de las velocidades relativas de las dos etapas en las que se divide el mecanismo de Michaelis-Mente. Valores pequeños de Km implican que el complejo enzima-sustrato es muy estable y no se disocia fácilmente para formar el producto final. La recolección de datos de velocidades iniciales frente a concentraciones variables de substrato permite extraer la velocidad máxima y la constante de Michaelis. Tradicionalmente esto se hace mediante una gráfica de Lineweaver-Burk, en el que se representan los inversos de las velocidades iniciales frente al inverso de la concentración de sustrato. Sin embargo, resulta más preciso utilizar una gráfica de EadieHofstee. Este análisis está basado en la siguiente ecuación1: V0 = − K m V0 +V [S ] max . [7] De esta forma, representando las velocidades iniciales frente al cociente de esas mismas velocidades obtiene una línea recta cuya pendiente es la constante de Michaelis cambiada de signo. Los parámetros cinéticos kcat y Km son útiles para el estudio y comparación de los diversos enzimas a través de su eficiencia catalítica. La eficiencia catalítica se define como la relación entre ambos (kcat/Km). 3. Procedimiento de cálculo Para resolver la cinética de la reacción enzimática [1] y mecanismos afines, se empleará el programa Kintecus2. Este programa realiza una integración numérica de las ecuaciones de velocidad a partir de un determinado mecanismo de reacción. A partir de una serie de datos de entrada (concentraciones iniciales, constantes de velocidad, temperatura) obtiene las concentraciones de todas las especies involucradas en función del tiempo. 3.1. Ejecución del programa Kintecus Sigue los siguientes pasos (debes tener un ordenador en Windows con el programa Excel en condiciones de funcionamiento) 1) Descárgate de la página web de la asignatura el fichero comprimido ENZIMA.zip. Descomprímelo en una carpeta abierta al efecto. Comprueba que tienes dos ficheros: Kintecus.exe y CineticaEnzimatica.xls 2) Comprueba en la configuración regional de tu ordenador (Panel de control) que está seleccionado el “punto” como separador de decimales y la “coma” como separador de miles. 3) Abre el fichero de Excell CineticaEnzimatica.xls. Si pregunta por “¿habilitar macros?” contestar “SI”. Si no permite habilitar los macros por cuestiones de seguridad ve en el menú de Excell a “HerramientasMacros” y selecciona el nivel “bajo” de Seguridad. 4) Una vez está el fichero CineticaEnzimatica.xls abierto y con los macros habilitados dispones ya del banco de trabajo donde realizar tus cálculos. El fichero de Excell consta de las siguientes hojas de cálculo (comprueba en líneas generales lo que hay en ellas): • Una hoja o página de CONTROL desde donde se controla el programa y que es la primera que aparece. 1 Para obtener esta ecuación a partir de la fórmula de Michaelis-Menten [6], inviértela y multiplica por Vmax. Reordenando y despejando V0 llegas a [7] 2 Consulta la página www.kintecus.com Prácticas de Termodinámica y Cinética-2º curso Licenciatura de Biotecnología 3 Termodinámica y Cinética Química Área de Química Física • • • • Una hoja MODEL en el que se especifican todas las reacciones del mecanismo de tu reacción, incluyendo las constantes de velocidad. Una hoja SPECIES en el que se especifican las concentraciones iniciales de las especies químicas involucradas Una hoja PARM en el que se especifican parámetros numéricos del cálculo tales como el tiempo total del cálculo y el paso de tiempo. Una hoja HELP con instrucciones de ayuda. 5) Ve a la hoja CONTROL e introduce en la casilla correspondiente (Kintecus PATH) la dirección completa de la carpeta en la que te encuentras en tu ordenador (por ejemplo: C:\Documents and Settings\Administrador\Escritorio\Practica) 6) Ve a la hoja PARM y selecciona las unidades de concentración en Moles/litro y el tiempo total de simulación. 7) Ve a la hoja SPECIES y fija las concentraciones iniciales de todas las especies. 8) Ve a la hoja de CONTROL y presiona el botón RUN. Se abrirá entonces una pantalla de windows. Teclea entonces la tecla ENTER tres veces. El cálculo se ejecutará en unos pocos segundos. Si la ejecución ha sido exitosa, en la carpeta se habrán creado una serie de ficheros de los cuales el más importante es uno llamado CONC.TXT. Comprueba que este fichero se ha creado. 9) Para representar los resultados presiona en la hoja de control la tecla PLOT RESULTS. Se crearán entonces dos nuevas hojas: una hoja denominada CONC en el que están escritas todas las concentraciones en función del tiempo y una hoja denominada CONCENTRATIONS en el que se representan gráficamente dichas concentraciones. 3.2. Ejecución del programa para un ejemplo de referencia. Con la ayuda del profesor ejecuta el programa para los siguientes datos3 (ejemplo sin inhibidor) Mecanismo de reacción: (E= enzima, S= substrato, I=inhibidor, P=producto) Reacción Constantes de Velocidad Constantes de Equilibrio* E+S==>ES 5.00E+06 75 ES ==> E+S 66666.66667 E+I==>EI 8.50E+06 1000 EI==>E+I ES+I==>EIS 9.57E+06 1000 EIS==>ES+I EI+S==>EIS 5.53E+07 1000 EIS==>EI+S EI+P==>EIS 7.13E+06 1000 EIS==>EI+P ES==>E+P 1.14E+05 *Las constantes de equilibrio fijan la constante de velocidad de la reacción inversa (Keq = KD/KI) 3 Muchos de esos datos pueden aparecer ya por defecto en el fichero Excel que has descargado al inicio de la práctica. En ese caso no modifiques nada. Prácticas de Termodinámica y Cinética-2º curso Licenciatura de Biotecnología 4 Termodinámica y Cinética Química Área de Química Física Tiempo total de simulación: 30 minutos Concentraciones iniciales(moles/litro): E 4 10-9 EI e I 0 S 0.01 EIS 0 ES 0 P 0 Representa los resultados de las concentraciones y observa qué ocurre con cada una de las especies. ¿Cómo evoluciona la concentración de sustrato y producto? ¿Qué le pasa a la concentración de enzima y a la del complejo enzima-sustrato? ¿Es válida la aproximación de estado estacionario en la cual se sustenta la ecuación de Michaelis-Menten? 3.3. Verificación del mecanismo de Michaelis-Menten y extracción de la constante y de la velocidad máxima. Repite el ejemplo del punto 3.2 para las siguientes concentraciones de sustrato: 0.01M (ya la tienes), 0.02M, 0.05M, 0.1M, 0.15M, 0.2M, 0.5M, 1.0M, 1.5M y 2.0 M. Anota las velocidades iniciales de formación de producto a partir de las pendientes iniciales de las correspondiente concentración de producto en función del tiempo. Representa la velocidad inicial en función de la concentración de sustrato. ¿Qué observas? Elabora la correspondiente gráfica de Eadie-Hofstee, haz un ajuste lineal y extrae la constante de Michaelis, la velocidad máxima y el coeficiente de correlación. 3.4. Análisis del efecto de un inhibidor Repite los cálculos del punto 3.3 pero para una concentración inicial de inhibidor de 4 ×10-4 M. Representa conjuntamente los datos de velocidad sin y con inhibidor frente a la concentración de substrato. ¿Qué observas?. Elabora la gráfica de Eadie-Hofstee para el caso con inhibidor y extrae de nuevo la velocidad máxima y la constante de Michaelis. Representa conjuntamente los datos sin y con inhibidor y comenta los resultados. 3.4. Análisis del metabolismo del etanol en el hígado humano El etanol se metaboliza en el hígado a través de la enzima alcohol deshidrogenasa hepática (NADP+). Conforme a la base de datos BRENDA4, una enzima similar humana (con el etanol como sustrato) tiene una constante de Michaelis de 0.45 mM y un número de recambio de 30.7 s-1. Asumiendo la misma concentración de enzima que la que has tenido en cuenta hasta el momento, e ignorando el efecto de inhibidores, realiza simulaciones con Kintecus para estudiar este proceso. Elabora una gráfica en la que se muestre la destrucción de alcohol con el tiempo en el hígado. Estima cual sería el tiempo de duración de una “resaca” si suponemos que éste es el tiempo necesario para que la concentración de alcohol se reduzca a un 10% de su valor inicial. Extiende el tiempo de simulación si es necesario. Considera también otros valores alternativos de las constantes cinéticas también asumibles en este caso a partir de la base de datos BRENDA. 4 http://www.brenda.uni-koeln.de Prácticas de Termodinámica y Cinética-2º curso Licenciatura de Biotecnología 5