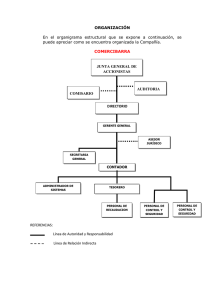
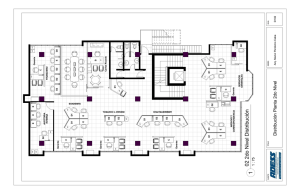
UNA REVISIÓN DEL MÉTODO CIENTÍFICO Introducción La

UNA REVISIÓN DEL MÉTODO CIENTÍFICO
José Manuel Perea Muñoz
Universidad de Córdoba. España. Departamento de Producción Animal. 14071 Campus Rabanales, Córdoba,
[email protected]
Introducción
La investigación podría definirse como la actividad mediante la cual se resuelven
problemas. Si la resolución de estos problemas es significativa para el conocimiento
científico, entonces estamos hablando de investigación científica. La segunda condición
que define al conocimiento científico es que éste se genera mediante la aplicación del
llamado método científico; sin embargo, no podemos delimitarlo como un conjunto de
reglas inviolables que demarcan lo que es científicamente aceptable y lo que no. Aquí
comienzan los problemas. El científico utiliza diferentes modos y técnicas para construir
conocimiento, y éstas están sujetas al paradigma del momento. Por tanto, lo que hoy es
aceptable puede que mañana no lo sea. Incluso algunos epistemólogos contemporáneos
como Feyerabend niegan que la ciencia sea metodológica en su teoría del anarquismo
epistemológico.
Una aproximación inicial al problema del método nos lleva a considerar que éste debe
generar conocimientos formalmente verdaderos y materialmente verdaderos. Para los
antiguos griegos la ciencia era “LA VERDAD”, y el modo de aproximarnos a ella era la
lógica. La conformidad del pensamiento consigo mismo era el método científico del
momento, y actualmente continúa formando parte del mismo, sea cual sea la corriente
de pensamiento que utilicemos para delimitarlo. Asegurar la verdad formal, al menos en
apariencia, es el sentido en el que se postulan las leyes y las teorías científicas; que no
son más que generalizaciones que explican, o intentan explicar, la realidad.
Los postulados generales emanan de las observaciones particulares que hacen los
científicos, y se basan en la inducción. A partir de las ideas de Galileo y Bacon, la
ciencia también está obligada a ser verdad material, por lo que el paso previo a la
consolidación de las leyes es la formulación de una hipótesis que debe ser
empíricamente demostrada. Esta es la esencia del método hipotético–deductivo de
Bacon (1620). Las observaciones particulares dan lugar a hipótesis que pueden ser
contrastadas, verificadas o falsadas, empíricamente. Cuando el experimento prueba la
1 hipótesis, de ésta surge entonces la teoría o ley general que explica la realidad. Aquí
aparecen otros dos fundamentos del método científico: la repetibilidad y la
refutabilidad. Una proposición científica es refutable si un experimento puede demostrar
su falsedad. Un experimento es repetible si se puede desarrollar en otro momento por
otros investigadores.
¿El experimento confirma la hipótesis?
Sólo en apariencia, dado que no se puede afirmar algo universal a partir de un conjunto
finito de datos u observaciones. Para entender mejor esta idea y su consecuencia para el
método científico, vamos a utilizar el clásico ejemplo del color de los cisnes, más
profundamente desarrollado por Taleb (2008). Supongamos que es usted un británico
del siglo XVIII que suele dar largos paseos al atardecer por la campiña inglesa, repleta
de cisnes. ¿De qué color es el primer cisne que ve? Es blanco. ¿Y el segundo? También
blanco. Todos los cisnes que contempla durante sus paseos son de color blanco.
Supongamos que usted observa una media de veinte cisnes en cada paseo, y sale cinco
tardes a la semana en promedio. Anualmente usted contempla en torno a 5.200 cisnes,
todos de color blanco. A lo largo de su vida ¿cuántos cisnes habrá tenido oportunidad de
admirar? Considerando una esperanza de vida de cincuenta años y asumiendo que
paseará regularmente toda su vida, podría contemplar algo más de 260.000 cisnes (y no
hay manera de descartar que el mismo cisne haya sido observado varias veces); por
supuesto, todos de color blanco. Después de observar que todos esos cisnes eran de
color blanco, usted podría formular la proposición “todos los cisnes son de color de
blanco”.
La creencia en la veracidad de su predicado no sólo es avalada por sus propias
observaciones. ¿Cuántos cisnes habrán sido observados a lo largo de la historia? Todos
blancos. Su predicado “todos los cisnes son de color blanco” recibe apoyo empírico
adicional cada que vez que alguien contempla un cisne y es de color blanco. Sin
embargo, unos años después de plantear su proposición, en el mismo sigo XVIII, el
hombre europeo observó el primer cisne de color negro. Lo hizo con el descubrimiento
de Australia, único continente donde habitan de modo natural cisnes negros.
2 El hecho de observar un solo cisne de color negro aporta evidencia suficiente para
rechazar su predicado “todos los cisnes son de color blanco”. El indefinido número de
cisnes observados a lo largo de la historia (todos de color blanco), no verifica la
hipótesis; sin embargo, una sola observación en contra demuestra su falsedad. Por tanto,
el experimento puede rechazar categóricamente cualquier hipótesis, pero sólo aporta
evidencias a favor de la verdad aparente de la misma. En consecuencia, el científico
puede estar seguro de lo que es falso, pero debe conformarse con lo aparentemente
verdadero.
Este problema es reconocido en lógica como la falacia del consecuente, y pone de
manifiesto los límites del método científico en la búsqueda de la verdad. Para el
positivismo primitivo de Bacon, el conocimiento científico (“LA VERDAD”), surge de
generalizaciones empíricamente contrastables que se desarrollan a partir de
observaciones sistemáticas particulares. Esta visión es verificacionista, es decir, acepta
que los contrastes experimentales aportan pruebas que verifican las hipótesis. Sin
embargo, ya hemos visto que las generalizaciones empíricas no pueden ser verificadas,
sólo refutadas. Por esta razón, Popper (1934) planteó el falsacionismo como el criterio
de demarcación científica: dado que las leyes científicas no pueden ser verificadas, la
ciencia progresa demostrando la falsedad de las hipótesis. Tanto falsacionismo como
verificacionismo aparecen por primera vez como parte del problema inductivo en el
pensamiento de Hume.
El falsacionismo no invalida la concepción positivista de Bacon, pero relativiza el
alcance de la ciencia. Al reconocer que las leyes científicas no son infalibles, aunque la
ciencia busque la verdad, debe conformarse con lo verosímil. En consecuencia, el
conocimiento científico se compone de sucesivas teorías que son demostradas falsas y
así, demostrando lo que es falso, se aproxima cada vez más a la verdad. Estas ideas
constituyen la base del programa de investigación científica desarrollado por Lakatos
(1978) que, con una visión muy pragmática de la ciencia, se centra en el progreso
científico y no en la verdad en sí misma. En esencia, su método defiende que el
progreso científico se basa en intentos sistemáticos de refutación de teorías formuladas
con base falsable; es decir, que pueden ser objeto de rechazo empírico. Los científicos
deben plantear conjuntamente una hipótesis y las posibles circunstancias donde se
demostraría su falsedad; y a continuación desarrollar intentos sistemáticos de refutación.
3 Si no se encuentran pruebas adversas, la hipótesis se refuerza inductivamente y
prevalece como teoría hasta que se demuestre su falsedad, y sea sustituida por una
nueva teoría capaz de explicar mejor los hechos y/o predecir otros que la teoría anterior
no alcanzaba a considerar.
Por tanto, el conocimiento científico es dinámico y evolutivo, pues se va
perfeccionando a medida que se sustituyen unas teorías por otras mejores. En
consecuencia, la velocidad de avance depende de la actitud crítica de la ciencia consigo
misma. Es decir, de los esfuerzos que los científicos desarrollen por falsar las teorías del
momento.
El valor de la prueba.
Si una sola prueba negativa refuta la hipótesis, e incontables pruebas positivas no la
verifican, entonces las mejores teorías científicas no son aquellas que siempre se
confirman empíricamente, sino aquellas que pueden ser sometidas a riesgo de falsación
y continúan sin ser falsadas. La prueba negativa tiene un valor absoluto dado que
conduce a la verdad. Pero la ciencia también se conforma con lo verosímil, por lo que
acumular pruebas positivas, aunque no conduzca a la verdad, sí nos lleva a lo
aparentemente verdadero. Por tanto, las pruebas positivas deben tener algún valor.
Veámoslo con un ejemplo.
Supongamos que usted gestiona una distribuidora de alimentos balanceados y está
preparando un envío de 10.000 kg de soja en sacos de 100 kg. Cuando tiene preparados
los 100 sacos, un empleado le informa de que la soja venía contaminada con maíz.
Usted en ese momento se alarma y baraja sus opciones. Si el cliente detecta el error en
el envío y usted no le ha informado del mismo, muy probablemente no le vuelva a
comprar más (además de que le puede denunciar a las autoridades por fraude). Pero si
usted determina el porcentaje de contaminación y aplica el correspondiente ajuste en el
precio de venta (el maíz es mucho más barato que la soja), puede que el cliente acepte el
envío y además, si lo hace, su honestidad quedará reforzada y el cliente, al confiar más
en usted, puede que le haga más pedidos. Usted se decanta por la segunda opción.
Ahora su objetivo es determinar el porcentaje de maíz que los sacos contienen mezclado
con la soja. Abre el primer saco, extrae en torno a 1 kg de grano y lo evalúa, llegando a
4 la conclusión de que hay un 5% de maíz. ¿Puede confiar entonces en que el porcentaje
de contaminación de todo el envío es del 5%? Ha evaluado 1 kg de 1 sólo saco, lo que
le parece poco en comparación con los 10.000 kg de envío. Confiar en que la verdadera
proporción es del 5%, conociendo sólo el 0,0001% de la realidad es muy arriesgado
para usted, por lo que se decide a abrir un segundo saco y evaluar un segundo kg. El
segundo saco arroja un porcentaje de contaminación del 10%, por lo que usted se
alarma un poco. Si con la primera muestra estimó un 5%, y con la segunda un 10%,
¿cuál es la verdadera proporción en todo el envío?
Probablemente ninguna de las dos muestras haya estimado correctamente la verdadera
proporción poblacional, pero pueden ser consideradas aproximaciones a la misma. El
problema podría expresarse del siguiente modo:
De modo que tanto en el primer muestreo como en el segundo, usted estima la
verdadera proporción poblacional, pero cometiendo un error. Ese error hace que a veces
subestime la verdadera proporción poblacional y otras veces la sobreestime.
Si usted pudiera cuantificar exactamente el error que comete en cada estimación, tendría
certeza de la verdadera proporción poblacional. Lamento informarle de que no es
posible, por lo que nunca tendrá certeza de la verdadera proporción (a no ser que
examine, uno por uno, todos los sacos hasta los 10.000 kg que completan el envío). La
buena noticia es que, aunque no pueda determinar el error que cometió en cada muestra
extraída, sí que puede tener una buena aproximación de su tamaño probable.
El riesgo, la incertidumbre, el azar y la imprecisión son elementos de la naturaleza de
cualquier proceso vital. No podemos huir de ellos, sólo tenemos que manejarlos del
modo adecuado. Estoy seguro de que usted usa normalmente el avión como medio de
transporte. Debe usted saber que la probabilidad de tener un accidente aéreo es muy
baja; si usted volara una vez al día, tendría un accidente aéreo una vez cada 3.800 años
(según la asociación internacional de transporte aéreo). Aunque la tasa de mortalidad en
accidentes aéreos es superior al 95%. Es decir, aproximadamente 1 de cada 20 pasajeros
sobreviven. Ahora que conoce esta información, ¿cambiará de medio de transporte?
Apuesto a que no, aunque probablemente siga sintiendo miedo cada vez que sube a un
avión si es una persona aprensiva. Parece que la lógica dice que si existe un riesgo lo
5 mejor es evitarlo (especialmente si usted es aprensivo). Este predicado no es del todo
cierto. Si existe un riesgo, lo mejor es evaluar el beneficio potencial de asumirlo. Esto
es lo que usted hace, consciente o inconscientemente, cada vez que viaja en avión: sube
si le compensa ahorrar tiempo o dinero a cambio de una pequeña probabilidad de
catástrofe.
Lo que realmente nos preocupa son los riesgos que no conocemos bien o de los que no
tenemos cierto control. Cuando el riesgo se hace cotidiano, tendemos a no evaluarlo
correctamente. Si no está de acuerdo con mi planteamiento, debe usted saber que morir
en un accidente de tráfico es 100 veces más probable que en uno de avión; y que tiene 1
posibilidad entre 150 de morir en un accidente doméstico. ¿Evitará ahora conducir o
limpiar su casa? ¿Tomará medidas de seguridad adicionales? También apuesto a que no.
El conocimiento científico no es ajeno a estos planteamientos. El papel de la ciencia
también es determinar cuántas observaciones positivas confirmarían una hipótesis y con
qué confianza.
Las evidencias se usan para actualizar la probabilidad de que una hipótesis pueda ser
cierta, asumiendo condiciones de incertidumbre e imprecisión. Si se admite un rango de
variación y la imposibilidad de conocer con certeza la verdad, el conocimiento
científico se entiende como un proceso de actualización de las medidas de verosimilitud
al conocerse nuevas evidencias. Esta idea sustenta al enfoque bayesiano, denominado
así por el uso recursivo del teorema de Bayes en los diferentes modelos de formulación.
Todos tienen en común la asignación de una probabilidad como medida de
verosimilitud y constituyen la base de razonamiento para el posterior desarrollo de los
contrastes de hipótesis. La aplicación de estos modelos de inferencia permite hacer
estimaciones precisas en la población a partir de un conjunto finito de evidencias
muestrales y, lo más importante, también informan de cuánta confianza podemos tener
en las estimaciones.
Sigamos con el problema de la contaminación del grano. El gerente no puede cuantificar
exactamente el error que comete en cada estimación, por lo que nunca tendrá certeza de
la verdadera proporción poblacional en base a evidencias muestrales. Pero mediante la
aplicación de modelos de inferencia puede calcular el tamaño probable de ese error, por
6 lo que puede corregir su estimación y obtener un intervalo donde conoce la probabilidad
de encontrar la verdadera proporción poblacional.
Esto se cumple si el azar ha intervenido en el proceso de muestreo y todos los granos
han tenido más o menos la misma probabilidad de formar parte de la muestra. Si la
muestra ha sido aleatoria, el error también lo es. Imaginemos las casi infinitas muestras
que el gerente puede extraer. Como en todas comete un error y éste es aleatorio, la
media de los errores tiende a 0.
En una única muestra no sabemos si el error ha sobreestimado o subestimado la
verdadera proporción poblacional, pero sí que podemos afirmar que la probabilidad de
subestimarlo es la misma que la de sobreestimarlo. Además podemos determinar la
probabilidad de ambos sucesos. Por el contrario, si de algún modo los granos de maíz
han tenido más o menos probabilidad de ser seleccionados que lo esperado por azar, el
error que estamos cometiendo en la estimación está sistemáticamente sobreestimando o
subestimando la verdadera proporción poblacional. En ese caso, la media de los errores
no es 0. En consecuencia, el intervalo que calculamos está sistemáticamente desplazado,
y la probabilidad de que la verdadera proporción poblacional quede dentro del intervalo
ya no es cuantificable. Por tanto, la confianza de que la estimación sea cierta se ve
alterada de un modo indetectable.
Volvamos al ejemplo. Si el gerente estimase la proporción poblacional utilizando la
información conjunta de ambas muestras, su seguridad crece porque procede de conocer
una evidencia mayor:
1
:
5%; 5%
1
:
10%; 10%
2
:
7,5%; 7,5%
Es más probable que la verdadera proporción poblacional se aproxime a 7,5% a que se
aproxime a 5% o a 10%, debido a que el tamaño probable del error de la estimación
conjunta es menor que en las estimaciones individuales. Es importante resaltar que es
posible que el error de la estimación conjunta sea mayor que el error de las estimaciones
individuales. No conocemos ninguno de ellos, sólo estamos hablando de su tamaño
probable.
7 Puede que el gerente siga sin confiar en que la contaminación real sea del 7,5%.
Después de todo, sólo conoce el 0,0002% de su envío. Al considerar que no tiene
seguridad suficiente, se decide por examinar 1 kg de todos los sacos. Ahora conocerá el
0,01% de la realidad. El gerente se sorprende de que, en cada nuevo saco que abre,
obtiene una estimación diferente de la anterior. En algunos sacos incluso obtiene
proporciones de maíz cercanas al 0%, mientras que en otros son superiores al 10%. Esto
se debe a que incrementando el número de observaciones aparecen por azar
desviaciones mayores. Pero lo importante no es la estimación individual que arroja cada
kg de pienso, sino la estimación conjunta.
Cada kg adicional que examina incrementa la precisión de la estimación conjunta y
disminuye el tamaño probable del error. Esto se encuadra dentro de la ley de los grandes
números, que engloba varios teoremas, destacando el de Kolmogórov. El tamaño
probable del error disminuye con el incremento del tamaño muestral.
Supongamos que el gerente no se conforma con 1 kg de cada saco y añade 1 kg
adicional de cada uno. Las estimaciones que va calculando podrían expresarse del
siguiente modo:
1
:
5%; 5%
1
:
10%; 10%
2
:
7,5%; 7,5%
50
:
9,3%; 9,3%
100
:
7,9%; 7,9%
150
:
8,3%; 8,3%
200
:
8,6%; 8,6%
Para terminar de calcular el tamaño probable del error necesitamos recurrir a un modelo
teórico que proporcione la base de razonamiento. Estos modelos de inferencia han ido
desarrollándose a lo largo de los dos últimos siglos y permiten calcular el indicador de
verosimilitud (la probabilidad de estar en lo cierto), por tanto, el valor de las pruebas
positivas. Se trata de variables aleatorias que modelan la probabilidad de ocurrencia de
determinados sucesos en experimentos aleatorios estándares. Si el modo en que
8 extraemos evidencias se parece a uno de estos experimentos aleatorios, podemos
conocer la probabilidad de ocurrencia de determinados sucesos. Si el resultado del
experimento se parece a lo predicho por la variable aleatoria de referencia, entonces
tenemos apoyo empírico a favor de la verosimilitud poblacional del resultado
experimental. Y lo más importante, podemos calcular la probabilidad de estar
equivocados, lo que sustenta la confianza del científico en sus resultados.
El problema al que se enfrenta el gerente se parece a un modelo binominal, donde se
extraen aleatoriamente n granos de una población incontable de granos (N). En la
primera extracción, la probabilidad de obtener 1 grano de maíz puede definirse como p.
Por tanto, la probabilidad de obtener 1 grano de soja puede derivarse como 1–p. Dado
que tenemos un número incontable de granos, la probabilidad de obtener un grano de
maíz en la segunda, tercera o enésima extracción no se modifica sensiblemente por el
resultado de la primera, segunda o n–1 extracciones, por lo que sigue siendo p. De este
modo, la proporción muestral se centra en p. Si el muestreo ha sido aleatorio, lo más
probable es que la estimación muestral coincida con la verdadera proporción
poblacional (p). Y si no coindice se debe a que, por azar, hemos extraído más granos de
soja (x) que lo esperable según la expresión x = n(1–p); dado que en los sacos sólo hay
granos de maíz y de soja. Si se extraen menos granos de soja, entonces es que se han
extraído más granos de maíz, y al revés. En consecuencia, el tamaño probable del error
también depende del valor de p, según la expresión p(1–p). Teniendo en cuenta todo lo
anterior, el tamaño probable del error se determina del siguiente modo y se denomina
error estándar.
á
1
El gerente puede ahora determinar el error estándar de cada estimación (Tabla 1). Con
un sólo kg, el tamaño probable del error es entre 4 y 5 veces superior a la estimación
(primera y segunda fila de la Tabla 1). Esto significa que la proporción poblacional
probablemente se encuentre en un intervalo entre el 0% y el 26,8% si se considera la
primera muestra, y entre el 0% y el 40% si se considera la segunda muestra. Ambas
9 estimaciones son poco útiles para resolver el problema, pues los intervalos son muy
amplios.
A medida que se incrementa el tamaño muestral, podemos observar cómo el tamaño
probable del error cada vez es más pequeño. Esto sucede porque se incrementa la
evidencia en que se basa la estimación de la proporción poblacional, con dos
repercusiones prácticas. Por una parte, el valor estimado de p cada vez es más preciso
con cada nueva observación. Por otra parte, el tamaño probable del error es cada vez
menor con cada nueva observación.
Tabla 1. Estimaciones de la proporción poblacional a partir de diferentes muestras
aleatorias.
n (kg)
1
1
2
50
100
150
200
2.000
pmuestral
0,05
0,10
0,075
0,093
0,079
0,083
0,086
0,085
1–pmuestral
0,95
0,90
0,925
0,907
0,921
0,917
0,914
0,915
Pmuestral(1–pmuestral)
0,048
0,090
0,069
0,084
0,073
0,076
0,079
0,078
Error estándar
0,218
0,300
0,186
0,041
0,027
0,023
0,020
0,006
Estimación
5,0% + 21,8%
10,0% + 30,0%
7,5% + 18,6%
9,3% + 4,1%
7,9% + 2,7%
8,3% + 2,3%
8,6% + 2,0%
8,5% + 0,6%
Puede que el gerente decida pasar toda la noche examinando grano para conocer 2.000
kg del envío (última fila de la tabla anterior). Ahora conoce el 20% de la población y
puede estimar que probablemente la verdadera proporción esté entre el 7,9% y el 9,1%.
Este rango de variación le parece suficiente para que su cliente acepte el envío, así que
decide no hacer más estimaciones. Después de todo, a no ser que abra todos los sacos y
evalué todo el envío, no va a conseguir certeza absoluta.
El gerente es buen observador y si usted también lo es, se habrá dado cuenta de que el
valor de la prueba positiva cambia con el tamaño muestral. A medida que se incrementa
el tamaño muestral, una evidencia extra aporta cada vez una menor parte de certeza.
Esto es similar a lo que en economía se conoce como ley de los rendimientos
decrecientes.
10 Para ilustrar esto, vamos a considerar las variaciones en el error estándar expresadas en
tanto por ciento y la contribución de cada unidad muestral a la reducción del mismo. En
la segunda muestra, el error estándar fue del 30%. Incrementar en una unidad el tamaño
muestral (n=3), reduce el error estándar a casi la mitad (18,6%). La contribución a la
certeza de un kg de balanceado adicional, fue del 11,37%, cuando pasamos de n=1 a
n=2. En la cuarta muestra (n=50), con 48 unidades muestrales adicionales, el error
estándar cae al 4,1%. La contribución individual de cada unidad muestral es ahora del
0,30%, cuando pasamos de n=2 a n=50. Siguiendo el razonamiento anterior, con n=100
la contribución a la certeza de cada unidad muestral adicional es del 0,028%. Con
n=150, el valor unitario es de 0,009%, y con n=200 cae hasta el 0,005%. Si
calculásemos la contribución a la certeza de la última unidad muestral que completa la
población, su contribución sería prácticamente 0.
¿Podemos confiar en la estimación?
Con una muestra del 20% (n=2.000 kg) el gerente ha estimado una proporción
poblacional del 8,5%. Teniendo en cuenta el error estándar, sabe que es muy probable
que la verdadera proporción se encuentre en el intervalo de 7,9% a 9,1%. Pero esto
todavía no es suficiente. Sin una medida de verosimilitud, la expresión “muy probable”
carece de sentido. La resolución de este problema requiere que volvamos a considerar
un modelo teórico de inferencia. Conociendo el tamaño probable del error y
considerando que el modo en que extraemos evidencias se parece a un experimento
aleatorio cuyas probabilidades de referencia son conocidas, podemos conocer la
probabilidad de ocurrencia de determinados sucesos. En base a esta variable aleatoria,
podemos determinar la confianza que el gerente puede tener en sus intervalos.
El modelo teórico de inferencia que vamos a utilizar es la distribución normal estándar,
variable aleatoria continua que también se conoce como distribución de Gauss. La
distribución normal estándar constituye la base de la inferencia moderna y ha permitido
modelar numerosos fenómenos en todos los campos científicos. También se denomina
campana de Gauss debido a su forma acampanada y su errónea atribución al matemático
alemán Karl Gauss. El primero que la desarrolló fue el matemático francés Abraham de
Moivre, en un contexto de aproximación de la distribución binomial a la normal; sin
11 embargo su uso es tan crucial en la obra de Gauss que se le suele atribuir su
descubrimiento.
La variable normal estándar es simétrica respecto al centro, que es cero (media y
mediana coinciden), y su desviación típica es 1. A una distancia de la desviación típica
respecto a la media, entre -1 y 1, se concentra en torno al 68,3% de los valores que
puede tomar la variable. A dos veces esta distancia se encuentra aproximadamente el
95,4% y a tres veces el 99,7%. Es decir, a medida que nos alejamos del centro cada vez
es más improbable encontrar un valor.
Si el experimento aleatorio que estamos considerando es gaussiano, entonces esperamos
que la distribución de sus posibles resultados siga las probabilidades determinadas por
la función normal estándar. Por tanto, estandarizando la variable podemos conocer la
probabilidad de ocurrencia de cualquiera de sus posibles resultados.
; ~
,
,
~
0,1
El experimento aleatorio que estamos considerando no es gaussiano, sino binomial.
Pero sabemos por el teorema central del límite que los experimentos binomiales son
aproximadamente normales cuando n y p no son demasiado pequeños. Por tanto, los
posibles resultados del experimento aleatorio al que se enfrenta el gerente siguen una
distribución normal aproximada con los siguientes parámetros:
~
,
;
; 1
El gerente no conoce el valor poblacional de p ni de np(1–p), pero puede utilizar sus
estimaciones muestrales. Si a una desviación típica de p están el 68,3% de los posibles
resultados del experimento aleatorio, entonces la probabilidad de que la proporción
poblacional quede en el intervalo definido por el error estándar es la misma.
La última estimación que hizo el gerente se basó en 2.000 kg de grano (n=2.000) y
obtuvo una proporción del 8,5%, con un error estándar del 0,6%. Por tanto, la
probabilidad de que la verdadera proporción poblacional se encuentre entre 7,9% y
9,1% es del 68,3%. Si quiere calcular un intervalo en el que la probabilidad de encontrar
la proporción poblacional sea 95,4%, simplemente debe multiplicar por 2 el error
estándar.
12 Ahora el gerente sabe que en el intervalo 7,3%–9,7% hay una probabilidad del 95,4%
de contener a la verdadera proporción poblacional. Ahora el gerente, además de una
estimación bastante precisa, dispone de un indicador de verosimilitud. Este indicador
define el nivel de confianza o credibilidad que el gerente puede darle al intervalo.
Parsimonia verosímil.
El primer paso del progreso científico consiste en establecer una hipótesis, es decir, un
conjunto de circunstancias y las consecuencias observables que necesariamente
ocurrirán si fuera verdadera. La hipótesis, por tanto, es deductiva; se predicen las
consecuencias necesarias de la veracidad de la misma. Sin embargo el experimento es
inductivo; genera una prueba empírica que da apoyo a la verosimilitud de la hipótesis, si
se cumplen las consecuencias necesarias; o demuestra que la hipótesis es falsa, si no se
cumplen las consecuencias pronosticadas. Utilizando experimentos o estudios
observaciones cuyos posibles resultados pueden modelarse según variables aleatorias
estándares, las generalizaciones empíricas se someten a contraste. Aquellas que no se
rechacen con una probabilidad inferior al 5%, pasan a considerarse leyes probabilísticas.
De este modo se construye el conocimiento científico.
En este momento podemos considerar un nuevo problema de la inducción puesto de
manifiesto por el filósofo norteamericano Nelson Goodman, conocido como la paradoja
de Goodman. Esta idea relativiza aún más el modo en que la ciencia construye el
conocimiento. Goodman lo planteó más o menos del siguiente modo. Consideremos el
color de las esmeraldas. Todas las esmeraldas que el ser humano ha encontrado hasta el
momento son de color verde, por lo que se concluye que “las esmeraldas son de color
verde”. Sin embargo, también es posible que algunas esmeraldas no sean verdes, sino
verdules; entendiendo como verdul que la esmeralda es de color verde hasta cierto
tiempo (pongamos, hasta el 24 de mayo de 2120), y a partir de ese momento, la
esmeralda cambia de color, de verde a azul. El problema para la ciencia que introduce la
paradoja de Goodman es que la evidencia que sustenta la conclusión “las esmeraldas
son verdes” es exactamente la misma que sustenta la conclusión “las esmeraldas son
verdules”. Así que la próxima esmeralda verde que se encuentre en el mundo da apoyo
inductivo simultáneo a ambas hipótesis.
13 Las observaciones pueden dar lugar a un número casi infinito de generalizaciones, pero
la ciencia sólo considera algunas de ellas como válidas (verde frente a verdul, verjo,
vergris, etc.). Si el modo de generalizar se encuadra en la ortodoxia académica del
momento, entonces es válida. No debemos confundir validez con verosimilitud. Las
generalizaciones no consideradas válidas también pueden ser verosímiles; simplemente
se descartan porque no son compatibles con alguna de las normas generales aceptadas
por la ortodoxia. Desde este punto de vista, sólo son aceptables las hipótesis que
generen inferencias que no infrinjan las normas generales aceptadas.
Una visión parcial del problema nos lleva a considerar el principio de parsimonia de
Ockham, fraile franciscano y filósofo aristotélico inglés del siglo XIV. Su regla también
se conoce como “navaja de Ockham” y se suele formular del siguiente modo: cuando
dos hipótesis tienen las mismas consecuencias y están en las mismas condiciones, la
hipótesis más simple tiene más probabilidades de ser cierta. En un sentido práctico, el
principio de parsimonia sirve de ayuda para el desarrollo de teorías, hipótesis e
inferencias, aunque no es irrefutable.
Un análisis más profundo nos lleva a considerar la validez de las normas, dado que
emanan de las propias inferencias. Kuhn, filósofo estadounidense del siglo XX, acuñó el
significado actual de paradigma, encuadrándolo como el conjunto de prácticas
aceptadas por la ciencia del momento. El paradigma es el hilo conductor del científico,
pues delimita cómo se puede observar, qué preguntas debe plantearse, qué hipótesis son
aceptables, cómo se buscan las evidencias, etc. El paradigma representa el equilibrio
entre las normas válidas del momento y las inferencias aceptables, y está
constantemente en revisión, de modo que normas e inferencias van reajustándose unas
con otras. Cuando el equilibro se rompe, se produce un cambio de paradigma que hace
que inferencias e hipótesis inaceptables en el pasado, ahora tengan sentido.
La dictadura de los mediocres.
Todo lo anterior lo podemos ejemplificar con el físico alemán Albert Einstein. Parecía
que quedaba muy poco por descubrir en física después de la mecánica de Newton. De
hecho, la física ha sido uno de los campos más estables desde el siglo XVII hasta la
publicación de la teoría de la relatividad. Su publicación ha cambiado por completo las
14 reglas en el área de la física, relegando a la mecánica cuántica de Newton a una simple
aproximación en velocidades lentas. El cambio de paradigma no sólo ha supuesto un
gran avance para el conocimiento científico, sino que ha modificado sustancialmente el
modo en que se generan hipótesis e inferencias en el área.
Einstein formuló hipótesis y generalizaciones muy heterodoxas para el paradigma de su
momento. Probablemente si las hubiera formulado ahora, muy pocas revistas de
investigación las hubiesen publicado. En nuestro contexto actual, la ciencia se encuentra
totalmente institucionalizada y se rige por los denominados “índices de impacto”. El
único (casi exclusivo) indicador de calidad de la obra de un científico, de un grupo de
investigación o de una institución consiste en el número de veces que sus manuscritos
son citados por otros artículos académicos durante un corto periodo de tiempo tras cada
publicación. El científico tiene una imperiosa necesidad de generar manuscritos y de
recibir citas, pues los fondos que recibe para seguir investigando dependen del impacto
de su obra. Las revistas de investigación también son categorizadas según las citas que
reciben, por lo que los editores intentan publicar artículos que potencialmente reciban
mientras más citas y en menos tiempo mejor. En este sentido, los artículos heterodoxos
no son bien recibidos por las revistas de investigación, dado que están muy alejados de
las tendencias actuales y, en consecuencia, potencialmente serán menos citados o
citados más tarde.
Sólo hay que revisar la historia de la ciencia para comprender que progresa más y a más
velocidad si cambiamos el modo en que se enfoca la realidad; es decir, bajo postulados
heterodoxos. Sin embargo, en el paradigma actual se prima la investigación ortodoxa,
pues el sistema de recompensas para el científico y su institución se basa en el impacto
de la obra; y son las publicaciones que aparecen en el momento preciso las que más
citas recibirán. Es más eficiente para el científico producir generalizaciones que maticen
o mejoren la precisión de alguna teoría ortodoxa, que trabajar para encontrar una teoría
que explique mejor o desde otro punto de vista la realidad.
Por este motivo, entre otros que no tocan exponer aquí, algunos se han atrevido a
denominar este periodo como “la dictadura de los mediocres”, pues el sistema tiende a
excluir las ideas heterodoxas.
15 Diseño de experimentos.
En el ejemplo de la distribuidora de alimentos balanceados han ido apareciendo las
reglas básicas que rigen el diseño de experimentos; aunque no se trataba de un
experimento, sino de un estudio observacional. La diferencia entre estudios
observacionales y experimentales es que en los primeros no se pueden aislar las
unidades experimentales de las condiciones donde están insertas. Entonces, los efectos
causales sólo pueden ser asociados a las respuestas de las unidades de observación y
siempre teniendo en cuenta el efecto de las circunstancias particulares del entorno.
Por el contrario, en los estudios experimentales es posible establecer las relaciones
causales entre las respuestas y los tratamientos. El experimento se diseña con esa
finalidad. Los tratamientos emanan directamente de la hipótesis y se definen como las
circunstancias que, si la hipótesis fuera cierta, deberían causar variaciones (efectos) en
las variables de respuesta medidas sobre las unidades experimentales. Cuando los
estudios son comparativos se establecen dos o más tratamientos y se comparan sus
efectos sobre las unidades experimentales. Un factor de variación podría ser la dieta, la
temperatura o la raza. Se tienen tantos tratamientos como niveles tenga el factor de
variación. Así, si se quieren comparar tres dietas, tendremos tres tratamientos, o si se
quieren evaluar dos razas, tendremos dos tratamientos.
A veces también vamos a necesitar tratamientos de control, positivo o negativo,
dependiendo de la naturaleza del problema que estamos evaluando. Un tratamiento de
control negativo aplicado a un grupo de unidades experimentales genera las respuestas
necesarias para conocer el efecto base. Se trata de someter a las mismas condiciones del
experimento (manipulación, manejo, registro de variables, etc.) pero sin recibir
tratamiento alguno. De este modo podemos obtener los niveles basales, necesarios para
comparar o evaluar los resultados de los tratamientos.
Ronald Fisher, quien trabajó en agronomía a principios del siglo XX, es considerado el
padre del diseño experimental. Hasta ese momento, los diseños experimentales
comúnmente utilizados y considerados más efectivos eran los que evaluaban un solo
factor cada vez. Fisher consideraba que era mejor utilizar diseños con múltiples
factores, dado que en los sistemas naturales la influencia de unos factores se asocia con
las respuestas de otros. Esta visión supuso una mejora sustancial de la inferencia, dado
16 que evaluando simultáneamente el efecto de varios factores y sus interacciones, se
ponen de manifiesto nuevas relaciones causales que en diseños con un solo factor nunca
se habrían conocido.
Supongamos que usted sigue siendo el gerente de la distribuidora de alimentos
balanceados (después de todo, el cliente quedó satisfecho con el envío). Usted
reflexiona ahora sobre las posibles causas de la contaminación del grano para encontrar
un modo de evitarlo en el futuro. Observa que algunos de sus empleados oyen la radio
mientras lo descargan. Si prestan atención a la radio puede que se despisten e inicien la
descarga sobre el silo equivocado, y aunque lo corrijan rápidamente, van quedando
restos que, equivocación tras equivocación, disminuyen la calidad del balanceado. En
base a este razonamiento usted formula la siguiente hipótesis: “trabajar oyendo la radio
incrementa los errores en la descarga”. Antes de prohibir el uso de auriculares durante el
trabajo, usted decide obtener evidencia empírica suficiente. No puede ir restringiendo
los derechos de sus trabajadores sin una base sólida.
De su hipótesis emana un único factor de variación, el uso de auriculares, con dos
niveles: “auriculares” frente a “sin auriculares”. Las unidades experimentales serían los
trabajadores que descargan granos y, como variable de respuesta, se decide a evaluar el
número de errores diarios de cada trabajador. Si su hipótesis es correcta y tras observar
un número suficiente de descargas, los trabajadores con auriculares deberían haber
cometido más errores que los trabajadores que no oían la radio.
No quitar ojo de las descargas durante dos meses, momento en que decide hacer una
evaluación de sus evidencias. Debe plantear un modelo de contraste de hipótesis. De
nuevo, Ronald Fisher fue quien sentó las bases. Se trata de una regla de decisión que
rechaza o no la verosimilitud poblacional de su hipótesis en base a las evidencias
muestrales disponibles. En primer lugar, debe plantear su hipótesis en términos
adecuados para la regla de decisión.
Si su hipótesis “trabajar oyendo la radio incrementa los errores en la descarga” es cierta,
significa que los errores de los trabajadores que oyen la radio son, en promedio,
superiores a los errores cometidos por los trabajadores que no usan auriculares; por
tanto, su diferencia debería ser mayor que cero. Esta es la primera hipótesis que plantea
y se denomina hipótesis alternativa (H1).
17 La hipótesis alternativa se acepta necesariamente cuando la hipótesis nula (H0) se
rechaza, y su formulación delimita la región de aceptación del contraste. Sin embargo,
la regla de decisión se aplica sobre la hipótesis nula, que es la segunda hipótesis que
plantea. En este caso, la hipótesis nula sería que la media de los errores procedentes de
trabajadores con auriculares es la misma que la media de los errores procedentes de
trabajadores sin auriculares; es decir, su diferencia sería cero, si fuera cierta.
:
;
0
:
;
0
A través de la regla de decisión se comprueba si la distribución de sus observaciones es
compatible con lo pronosticado por la variable aleatoria de referencia que modela el
experimento, si la hipótesis nula fuera cierta, y con una probabilidad de equivocarse
determinada.
Actualmente se han desarrollado múltiples modelos de contraste de hipótesis. Cada uno
de ellos funciona bajo sus condiciones particulares, requieren que los datos cumplan usa
seria de premisas y tienen ventajas e inconvenientes. Inicialmente los modelos de
contraste de hipótesis se pueden clasificar el paramétricos y no paramétricos,
dependiendo de si la regla de decisión se basa en parámetros (media, varianza, etc.) o en
rangos u otras transformaciones de las observaciones. Los contrastes no paramétricos
son menos poderosos que los paramétricos, pero tienen la ventaja de no necesitar
determinadas condiciones muestrales o poblacionales que, a veces, o no tienen sentido o
simplemente no se pueden garantizar.
Todos los contrastes requieren de una variable aleatoria que modela la distribución de
los resultados del experimento. Si la hipótesis nula fuera cierta, los resultados del
experimento deberían ser compatibles con lo predicho por la variable aleatoria teórica.
Si los resultados del experimento se alejan mucho de lo predicho, entonces tenemos
evidencias que apoyan la falsedad de la hipótesis nula y, como consecuencia necesaria,
se acepta la hipótesis alternativa. Si por el contrario los resultados experimentales son
compatibles con lo predicho por la variable aleatoria, entonces no hay evidencia para
rechazar la hipótesis nula, que prevalece sobre la alternativa.
18 Que los resultados sean compatibles con lo predicho, significa que se acepta cierto
alejamiento. Este alejamiento corresponde al error experimental y se utiliza para obtener
el indicador de verosimilitud. Mientras más alejamiento se tolere, con más seguridad se
rechazará la hipótesis nula. La ciencia acepta como alejamiento mínimo aquel que
contenga el 95% de los posibles resultados del experimento. Es decir, que la hipótesis
nula se rechace con una probabilidad de haber tomado la decisión equivocada sólo del
5%. El resultado de aplicar la regla de decisión es dicotómico, o se acepta la hipótesis
nula o se rechaza. Del mismo modo, la hipótesis nula puede ser cierta o falsa. Por tanto,
la decisión que tomemos se enmarca en alguno de los siguientes cuadros:
Contraste
No Rechazar Ho
Rechazar Ho
Realidad
Ho cierta
Ho falsa
Decisión correcta
Error Tipo II
p=1–α
p=β
Error Tipo I
Decisión correcta
p=α
p=1–β
El contraste nos induce a tomar la decisión correcta cuando la regla de decisión no
rechaza la hipótesis nula y ésta es cierta, y cuando la regla de decisión rechaza la
hipótesis nula y ésta es falsa. Aunque nunca vamos a saber si hemos acertado, sólo
sabemos si el contraste nos induce a rechazar o no la hipótesis nula y la probabilidad de
habernos equivocado, bien por error tipo I (α) o bien por error tipo II (β).
Cometemos error tipo I cuando rechazamos algo que es cierto, con una probabilidad de
α. Esto es a lo que se llama “nivel de significación”. Para que la comunidad científica
acepte generalizaciones empíricas como leyes probabilísticas, el nivel de significación
de las evidencias que lo apoyan debe ser inferior al 5%.
Cometemos error tipo II cuando no rechazamos algo que es falso, con una probabilidad
de β; aunque paradójicamente, en la mayoría de los contrastes no se puede calcular.
Esto se debe al modo en que se formula la hipótesis alternativa. Mientras que la
hipótesis nula es una afirmación concreta, la hipótesis alternativa suele ser global y
contiene un amplio abanico de posibilidades.
Volvamos al ejemplo de la distribuidora de alimentos balanceados. El contraste que el
gerente quiere aplicar se denomina comúnmente contraste para la diferencia de medias
con muestras independientes. El contraste parte de la formulación de una conjetura
19 poblacional, que se verifica a partir de dos muestras independientes y aleatoriamente
extraídas. La regla de decisión requiere además que la variable de respuesta siga una
distribución normal poblacional y que las varianzas poblacionales sean conocidas. Si los
tamaños muestrales son grandes se pueden utilizar las varianzas muestrales, y la
normalidad de las distribuciones poblacionales no es tan importante. Se trata de un
contraste paramétrico, dado que el indicador utilizado para el contraste (Z) se basa en la
media y en la varianza, y además sigue una distribución normal.
̅
:
~
0,1
El gerente ha observado a sus empleados durante 60 días, obteniendo los siguientes
datos:
38; ̅
5,6;
44; ̅
:
:
1,2
1,6;
0,5
Al aplicar el contraste se obtiene que:
̅
;
5,6
1,2
38
1,6
0,5
44
:
; 19,16
Las observaciones experimentales del gerente han generado un valor de Z, indicador de
contraste, de 19,16 (Figura 1). Dado que la variable aleatoria que modela el
experimento es la normal estándar (Z), debemos comparar 19,16 con el valor de Z de la
distribución normal estándar que deja a su derecha un área del 100·α %. Supongamos
que el gerente quiere una significación del 5%, por lo que asigna un valor a α del 0,05.
20 Entonces, el valor de Zα es de 1,645. Si la hipótesis nula fuera cierta (es decir, no hay
diferencias entre ambos grupos de trabajadores), el indicador obtenido debería haber
alcanzado un valor de cero. Si no fuera cero, aceptamos que por azar el indicador
hubiera alcanzado como máximo un valor de 1,645, es decir, estamos dando una
confianza del 95%. Por tanto, la hipótesis nula será rechazada si el indicador
experimental queda a la derecha del valor de Z que deja a su derecha un área del 5%
(Z=1,645).
0,4
100 ∙ (1–α) = 95%
fZ(z)
0,3
0,2
100 ∙ α = 5%
0,1
0
-5
-3
-1
1
Z
3
5
Zα=1,645 Figura 1. Regiones de aceptación y rechazo del contraste de hipótesis basado en la
normal estándar, cuando la significación es del 5%.
Rechazando la hipótesis nula bajo estas condiciones, sólo nos equivocaremos el 5% de
las veces, dado que la probabilidad de obtener un valor superior a 1,645 es del 5%.
Como se cumple que 19,16>1,645, el gerente puede rechazar la hipótesis nula y aceptar
la alternativa (que los empleados con auriculares cometen más errores) con una
probabilidad de haber cometido error tipo I del 5%.
Como ya habrá percibido, la evidencia empírica que contrasta la hipótesis del gerente no
procede de la experimentación, sino de la observación. No puede establecer relación
causal, sino asociación. La consecuencia práctica para el gerente es mínima
(probablemente habrá prohibido el uso de auriculares en el trabajo), pero, si
estuviéramos ante un caso científico, el gerente tendría graves problemas para sostener
21 la generalización “trabajar oyendo la radio incrementa los errores en la descarga”. Por
ejemplo, no sabemos si los trabajadores que usan auriculares siempre los usan, son
siempre los mismos, los usan siempre o a veces los usan unos y otras otros. En
definitiva, no podemos saber si el mayor número de errores responde al uso de
auriculares o intervienen otros factores como la mala pericia de los trabajadores que
oyen la radio (puede ser que oír la radio sea más frecuente en los trabajadores menos
hábiles).
Para obtener respuestas claras a los factores, las unidades experimentales deben
mantenerse en las mismas condiciones y estar sometidas a la menor cantidad posible de
fuentes de variación. Lo ideal sería que los tratamientos fueran la única fuente de
variación. En los contrastes basados en estudios observacionales no es posible controlar
todas las variables que inciden en las unidades de observación; por tanto, es esperable
que las respuestas a los factores no sean tan nítidas como en diseños experimentales.
Cuando no es posible evitar alguna fuente de variación ajena al tratamiento, existen
técnicas como la bloquización o la medición de covariables que minimizan su efecto.
Ejemplos típicos de estas variables podrían ser el uso de animales no homogéneos, las
condiciones climáticas o las diferentes salinidades del suelo en experimentos
agronómicos. El problema de estas variables es que incrementan el error experimental y
causan sesgos. Cuando no se puede evitar su incidencia, se deben establecer
mecanismos de control que aseguren que su efecto sea aleatorio, es decir, que afecten a
las variables de respuesta incrementando la varianza en todos los tratamientos. La
consecuencia es que el error experimental es mayor y, por tanto, es necesario un mayor
número de unidades muestrales.
Si no se establecen mecanismos de control, existe la posibilidad de que algunos
tratamientos sean sistemáticamente favorecidos y otros sistemáticamente perjudicados.
Esto no sólo incrementa el error, sino que los hace sistemáticos positivos y/o negativos
que ponen en peligro todo el experimento, pues no hay forma de solucionar el problema
a posteriori. Hay que tener en cuenta que cualquier tipo de proximidad o sistema es
causa de sesgo, por lo que los mejores diseños son los totalmente aleatorios. La
ejecución del experimento también debería ser aleatoria. Es decir, que las mediciones se
tomen de modo aleatorio, que los tratamientos sean administrados de modo aleatorio,
22 etc. La intervención del azar en todas las operaciones tiende a mejorar la nitidez de los
resultados.
La belleza de lo aleatorio.
Cuando se habla de lo aleatorio rápidamente resuena en nuestra mente la distribución
normal. La mayoría de los modelos de inferencia la utilizan como variable aleatoria de
referencia, y si además incluimos las distribuciones que derivan de la normal o que se
pueden aproximar a ella, estamos considerando prácticamente todos los modelos de
inferencia. Si los fenómenos que estamos intentando explicar se comportan como
gaussianos, entonces podemos hacer estimaciones válidas de su verosimilitud. La buena
noticia es que la mayoría de los fenómenos y de las variables que los describen tienden
a comportarse de modo gaussiano; o mejor dicho, no tenemos evidencias de que no lo
sean.
Pensemos en alguna de las variables que como científicos en agronomía nos pueden
interesar, por ejemplo, el rendimiento lechero (kg/lactación). Si estudiásemos el
rendimiento lechero en su país, probablemente consideraríamos que la variable debe
comportarse de modo gaussiano. Es decir, la mayoría de las vacas tendrían una
producción por lactación cercana a la media, y a medida que el rendimiento se aleja del
centro de la distribución, la probabilidad de encontrar un individuo es cada vez menor.
Supongamos que el rendimiento medio es de 8.000 kg/lactación con una desviación
típica de 1.000 kg/lactación. Si la variable fuera gaussiana, ya sabemos que el 68,3% de
la población tendría una producción entre los 7.000 y los 9.000 kg/lactación; y el 95,4%
estarían en el intervalo 6.000–10.000 kg/lactación. Si de esta población extraemos una
muestra aleatoria lo suficientemente grande (500 vacas, por ejemplo) y desarrollamos
un contraste que ponga a prueba la verosimilitud de que el rendimiento lechero sigue
una distribución normal, muy probablemente las evidencias no permitan rechazar la
normalidad de la distribución con una significación muy alta (casi cero).
Vamos a centrarnos en los extremos. Sólo 23 de cada 1.000 vacas superarían los 10.000
kg/lactación. Es decir, la probabilidad de encontrar un individuo que supere la
producción media en al menos un 25% es del 2,3%. Si consideramos ahora la
probabilidad de superar la media en al menos el 30% (10.400 kg/lactación), la
23 probabilidad disminuye a 8 de cada 1.000. Siguiendo con el razonamiento, la
probabilidad de encontrar una vaca con un rendimiento superior al 35% (10.800
kg/lactación) desciende a 2 de cada 1.000; superior al 40% (11.200 kg/lactación) vuelve
a descender hasta 6 de cada 10.000; superior al 50% (12.000 kg/lactación) baja a 3,6 de
cada 1.000.000; y sólo 6,7 de cada 10.000.000.000.000.000 vacas producirían el doble
que la media (16.000 kg).
Lo que acabamos de comprobar se cumple en todas las variables normales: cuando nos
alejamos de la media, la probabilidad de encontrar un valor disminuye cada vez a mayor
velocidad, y en los extremos, la velocidad de disminución se acelera exponencialmente.
Esto es de interés para hacer inferencia con variables que tienen un techo biológico,
como la producción de leche. Los modelos explicativos y predictivos que trabajan bajo
la distribución normal funcionan muy bien con este tipo de fenómenos porque se
focalizan en lo probable, es decir, en la media y en los valores que quedan en torno a
ella, y dan muy poca importancia a los extremos. Después de todo, los valores extremos
son tan poco probables que pueden considerarse imposibles en sentido práctico, y
además tienen un valor explicativo o predictivo muy bajo en comparación con el centro
de la distribución.
Consideremos ahora la producción lechera anual de las granjas bovinas de su país. Esta
variable también es de interés para usted y para mí, que ambos trabajamos en
agronomía. En La Pampa (Argentina), la media anual en 2009 fue de 388.074 kg y su
desviación típica de 54.890 kg. Si la variable fuera gaussiana y siguiendo con el
ejemplo anterior, podemos calcular la probabilidad de diferentes sucesos (Tabla 2).
Tabla 2. Probabilidad de diferentes sucesos según la distribución normal con media
388.074 y desviación típica 54.890.
Producción anual (kg/año)
Sea superior a la media (388.074 kg/año)
20% superior a la media (465.689 kg/año)
40% superior a la media (543.304 kg/año)
60% superior a la media (620.918 kg/año)
80% superior a la media (698.533 kg/año)
Doble que la media (776.148 kg/año)
Probabilidad (%)
50,0 (1 de cada 2 granjas)
7,87 (1 de cada 13 granjas)
0,23 (1 de cada 500 granjas)
0,0011 (1 de cada 10.000 granjas)
0,00000078 (1 de cada 1.250.000 granjas)
0,000000000078 (1 de cada 12.500.000.000 granjas)
24 En 2009 en La Pampa no había más de 200 granjas lecheras. Si la variable fuera
gaussiana, resultaría prácticamente imposible que tan sólo una de esas 200 granjas
produjera el doble que la media (1 de cada 12.500.000.000 es un número bastante
pequeño). Sin embargo no sólo una, sino que fueron dos las explotaciones con una
producción anual muy superior al doble de la media.
La primera mala noticia es que el modelo gaussiano no explica convenientemente esta
realidad, pues asigna una verosimilitud teórica (1/12.500.000.000) que en absoluto es
compatible con la evidencia empírica (2/200). La segunda mala noticia es que si de esta
población (N≈200) extraemos una muestra aleatoria lo suficientemente grande (50
granjas, por ejemplo), la distribución muestral puede considerarse normal si así lo
confirman los test de normalidad. Esto va a suceder muy probablemente si por azar no
es seleccionada ninguna de estas dos granjas con producciones extremas. Pero también
la considerará normal si alguna de ellas formase parte de la muestra, porque lo más
probable es que usted siga las recomendaciones de la mayoría de los manuales de
estadística y las elimine del estudio al considerarla valores atípicos.
La consecuencia de la primera mala noticia es que utilizar modelos gaussianos para
explicar variables que no siguen la distribución normal puede generar inferencias
erróneas, especialmente en lo referente a la verosimilitud de fenómenos extremos. La
consecuencia de la segunda mala noticia es que no podemos confiar en la verosimilitud
de las inferencias generadas de este modo.
Hoy en día hay una peligrosa generalización de los modelos gaussianos. Se han
aplicado y se aplican con regularidad a variables y fenómenos de diverso ámbito como
económicos (beneficio de las empresas, trabajadores de las instituciones, movimiento de
divisas, etc.) sociales (número de hijos, años de educación formal, etc.) psicológicos,
etc. La mayor parte de estas variables no tienen un techo o límite biológico y no existe
ningún motivo para que tengan que comportarse como gaussianas, aunque en las
muestras sí que lo hagan. La potencia de la inferencia paramétrica gaussiana se ha
puesto de moda en casi todos los campos científicos, constituyendo una de las prácticas
aceptadas por la ciencia del momento. Es decir, los modelos gaussianos definen en su
conjunto una de las normas válidas del paradigma científico que todavía no estamos
dispuestos a cambiar. La consecuencia no sólo es que se están generando inferencias
25 potencialmente erróneas, sino que se está dando una verosimilitud a los acontecimientos
extremos muy inferior a la que realmente tienen.
Pavos inductivistas y cisnes negros.
En definitiva, aunque la ciencia se conforme con generalizaciones empíricas
aparentemente verdaderas, debe seguir manteniendo una postura crítica y escéptica;
pues la verosimilitud de las inferencias también depende de que los fenómenos
realmente se comporten del mismo modo que las variables aleatorias utilizadas de
referencia. Esto relativiza aún más la confianza en las generalizaciones probabilísticas,
especialmente cuando se trata de inferencias cuantitativas.
Los modelos probabilísticos de inferencia pueden explicar con bastante precisión el
comportamiento de algunos fenómenos sin ni siquiera conocer el diagrama causal de los
mismos. Se trata de fenómenos en los que la probabilidad de un evento raro es tan
pequeña que podemos descartar su ocurrencia a nivel práctico. Además, las
consecuencias del (casi imposible) evento raro no son más importantes que las
consecuencias de los eventos normales.
Sin embargo, existen fenómenos en los que la probabilidad de eventos raros suele ser
subestimada por las variables aleatorias estándares (considere de nuevo la producción
lechera en La Pampa). La inferencia paramétrica podría explicar y predecir con cierta
precisión el comportamiento de estos fenómenos, pero no así la ocurrencia de eventos
raros, que son sistemáticamente subestimados. El problema puede ser grave si además
las consecuencias de los eventos raros son más importantes que las consecuencias de los
eventos normales.
Para profundizar en este concepto vamos a utilizar el ejemplo del pavo inductivista de
Chamblers, quien adaptó el ejemplo originario de Bertrand Russell, filósofo y
matemático británico del siglo XX. Imagine que usted compra un pavo todos los meses
de enero con el objetivo de engordarlo y servirlo en la mesa el día de Navidad. Este año
lo compra el 14 de enero, lo coloca en el gallinero de su jardín, y todos los días le da
una buena ración de grano en torno a las 8:00 de la mañana, antes de irse al trabajo. Los
fines de semana le gusta levantarse temprano, así que repite la rutina junto a sus hijos.
26 Veámoslo desde el punto de vista del pavo. El día 15 de enero a las 8:00 recibe 200 g de
grano de buena calidad y pasa el día entretenido por el gallinero. El día 16 de enero
vuelve a recibir 200 g del mismo grano a las 8:00 de la mañana. Los siguientes días
hasta febrero ocurre exactamente lo mismo, así que el pavo analiza la situación. “A las
8:00 de la mañana durante 15 días he recibido una buena ración de granos, sin faltar ni
un día. Pero 15 días constituyen pocas observaciones para extraer conclusiones, así que
mejor esperar a tener más evidencias.” Transcurrió el tiempo hasta junio, y al pavo
nunca le faltó su ración de grano en torno a las 8:00 de la mañana. El pavo vuelve a
considerar las evidencias. “Veamos, he comido siempre a las 8:00 de la mañana y esto
ha sido independiente de la estación del año, de las condiciones climáticas e incluso del
estado de ánimo del criador. Fines de semana también incluidos.” A pesar de las
observaciones, el pavo considera que aún no tiene evidencias suficientes para formular
una conclusión, así que decide seguir observando. Llegamos a 23 de diciembre y el
pavo vuelve a hacer balance. “Veamos, he comido regularmente durante casi un año a
las 8:00 de la mañana. Esto ha sido así durante todas las estaciones del año y todos los
días de la semana. Ha dado igual que lloviera, hiciera frío o calentara el sol. No ha
importado el humor ni el estado de ánimo del criador. ¡Ahora sí!”.
Ahora el pavo considera que tiene evidencia suficiente para concluir “como todos los
días 200 g de grano a las 8:00 de la mañana”. Así que a las 7:50 del día siguiente el
pavo ya estaba nervioso. Ya había llegado a la conclusión de que siempre comía a las
8:00 y estaba ansioso esperando su ración diaria. Sin embargo ese día, 24 de diciembre,
no apareció usted con sus 200 g de grano, sino armado de un cuchillo con el que le cortó
el pescuezo al pavo.
El evento del día 24 de diciembre era totalmente predecible desde su perspectiva. Usted
compró el pavo con ese objetivo y conocía los verdaderos motivos de la administración
de grano. Pero desde la óptica del pavo, el evento del día 24 de diciembre era totalmente
improbable e impredecible. Además, las consecuencias para el pavo fueron
catastróficas. A esto es a lo que Taleb denominó “cisnes negros”: eventos altamente
improbables con consecuencias de gran magnitud. La observación por el hombre
occidental del primer cisne negro también puede considerarse un “cisne negro”.
27 Pues bien, los cisnes negros no sólo no son predecibles por los modelos clásicos de
inferencia, sino que además somos muy vulnerables a ellos precisamente porque no
entran dentro de las expectativas probables, y el paradigma actual nos empuja a no
focalizarnos en los eventos raros. Incluso muchos de ellos aún no tienen precedentes,
por lo que ni tan siquiera tenemos una mínima señal de su existencia. Pensemos en el
pavo, ¿qué señal tenía de que el día 24 le iban a cortar el pescuezo?
Este problema todavía no ha sido resuelto por la ciencia y, aunque existen otras
variables aleatorias que podrían ser de utilidad para predecir efectos improbables,
nuestras mejores opciones se enmarcan dentro de la robustez. De acuerdo con Taleb,
esto no significa que la ciencia deba conformarse con lo cualitativo, sino que debe
construir bases sólidas sobre las que asentar las inferencias y moderar las expectativas.
A nivel práctico, la teoría del cisne de negro de Taleb nos lleva a considerar que
debemos construir robustez para protegernos del impacto negativo de lo altamente
improbable y dejar espacio para su impacto positivo. Como usted sabe, Grecia está
sufriendo una de las crisis económicas más duras de su historia. La crisis comenzó a
forjarse hace casi diez años y actualmente tiene consecuencias importantes en toda la
zona euro. Si usted lee el periódico habrá visto alguno de los profundos análisis de la
crisis griega que hacen los economistas; incluso ya hay ensayos sobre ella. Sin embargo,
hace 10 años, los mismos economistas que hoy explican con meridiana claridad su
diagrama causal, no fueron capaces de predecirla. ¿Es que las evidencias de hoy eran
otras que las de hace 10 años? Lo que ocurre es que al analizar la crisis griega en
retrospectiva, las evidencias que hoy sirven para fundamentarla son las mismas que en
su día sirvieron para descartarla (o que pasaron inadvertidas).
Problemas, problemas y más problemas.
El gerente de la distribuidora de alimentos balanceados ha resuelto sus problemas
aplicando técnicas de inferencia del método científico. A partir de la observación ha
construido una hipótesis y diseñado un modo de someterla a contraste. Las evidencias
empíricas acumuladas le han servido para dar apoyo inductivo a su hipótesis, con una
significación del 5%. Por tanto, ha obtenido generalizaciones empíricas verosímiles. El
proceder del gerente no dista mucho de lo que usted puede leer en cualquier trabajo de
28 investigación, sin embargo, ninguna revista científica lo publicará. El problema está en
el problema.
El gerente ha resuelto un problema que sólo es de interés para él mismo y para su
empresa. Si el gerente hubiera resuelto un problema de interés para la comunidad
científica, entonces sí que podría publicar sus resultados en cualquier revista de
investigación. Si usted está considerando iniciar un proyecto de investigación, debe
saber que gran parte de su éxito como científico radica en el problema que va a resolver.
Si encuentra un problema que merezca la pena resolver, entonces está de enhorabuena;
su resolución será publicada casi con toda seguridad. Lo que diferencia a los buenos
investigadores es su capacidad para encontrar buenos problemas de investigación;
conjeturas que no sólo le interesen a ellos, sino que también sean de interés para sus
colegas.
Encontrar un buen problema de investigación requiere de paciencia y lectura. Si tiene
libertad para investigar lo que considere (lo que no es probable, pues son los
investigadores experimentados quienes delimitan las líneas de investigación), comience
por lo que sea de su interés. Seleccione un tema que le motive y haga un plan de lectura.
Su objetivo como investigador es publicar la resolución de problemas científicos en
revistas de investigación. Y las revistas de investigación contienen las fronteras del
conocimiento de cualquier tema considerado (pues en ella se publican las últimas
soluciones a los problemas significativos). Por tanto, un plan de lectura eficiente sólo
debería considerar revistas de investigación. Ocasionalmente puede acudir a otras
fuentes, pero debe tener en cuenta que la información contenida en ellas no tiene por
qué ser veraz y, sobre todo, puede que esté anticuada.
El proceso de revisión por pares diferencia a los medios de comunicación científica de
los demás y garantiza (al menos teóricamente) el rigor académico y metodológico de los
artículos publicados en ellos. Puede que encuentre información relevante en otras
fuentes, pero debe tomarla con cautela. Por ejemplo, la opinión de un experto, por muy
experto que sea, no es conocimiento científico.
Si utiliza un buscador académico y unas cuantas palabras clave, encontrará miles de
resultados de cualquier tema. No se agobie. No necesita leer todos los artículos, sólo los
más relevantes. No tiene que conocer una cantidad inmanejable de información, sólo
29 tiene que utilizar aquella que sea relevante. Un buen plan podría ser redefinir la
búsqueda con palabras clave hasta encontrar una cantidad manejable de información
(100–200 artículos). Restrinja la búsqueda a los últimos 5 años. Si un tema no ha sido
tratado por las revistas de su área en los últimos 5 años, puede que sea un tema cerrado.
Cambie de tema, pues le costará encontrar un buen problema que resolver.
Una vez que tenga una cantidad manejable de información, comience a leer y a tomar
notas. Las notas son importantes porque nos ayudan a recordar y, sobre todo, a recordar
en el sentido en que leímos. Con las notas evitamos errores y sirven para poner por
escrito nuestros propios argumentos. Inicialmente no lea completamente todos los
artículos, céntrese en los resúmenes. A partir del mismo, señale si merece la pena seguir
leyendo o no. Con la experiencia desarrollará la habilidad suficiente para discernir qué
puede ser clave para su investigación y qué puede pasar sin ser leído. Esa habilidad se
adquiere leyendo, así que no se preocupe por cometer errores tipo II y evite cometer
errores tipo I.
Cuando termine de evaluar todos los resúmenes, comience a leer aquellos artículos
marcados como relevantes. Comience de más a menos relevante. Recuerde que más vale
una fuente certera que docenas de fuentes mediocres. A medida que vaya leyendo tome
notas y reléalas cuando sea necesario. Las notas guiarán su lectura. Cuando encuentre
un artículo muy relevante, probablemente encontrará algunos argumentos apoyados en
citas que considere de interés. Sígales la pista y no se quede sólo con la cita. Este es un
buen modo de ir construyendo su tema de investigación.
Al principio los temas son muy amplios. A medida que los va dominando, va centrando
su interés en aspectos más concretos del mismo. Simultáneamente, la cantidad de
artículos relevantes va disminuyendo con el aumento de la especificidad del tema. Un
tema inicial podría ser la economía ganadera. Un tema específico podría ser la
construcción de fronteras paramétricas para el análisis de la eficiencia de sistemas
bovinos extensivos.
Hágase preguntas que guíen su búsqueda. Al principio encontrará fácilmente todas las
respuestas a las preguntas formuladas. A medida que vaya dominando el tema, irán
apareciendo preguntas de difícil respuesta, e incluso preguntas sin respuesta. Cuando
usted sea capaz de plantear las grandes preguntas que aún no han sido resultas en su
30 tema específico, puede considerar que tiene un dominio suficiente del mismo. Estas
preguntas son las que buscaba.
Ya se habrá dado cuenta de que no puede encontrar preguntas que merezcan la pena
responder si no domina su tema en profundidad. Pero eso no es suficiente. Puede que
usted trabaje duro y resuelva alguna de ellas, pero en absoluto tiene garantía de
publicación. La segunda cualidad que diferencia a los buenos investigadores es que,
además de encontrar preguntas que merezcan la pena resolver (primera cualidad), son
capaces de convencer a los científicos de su área de conocimiento de que necesitan las
respuestas de su pregunta.
Si analiza con detalle esos artículos que ha ido leyendo observará que en muy pocas de
las preguntas que resuelven (por no decir ninguna) resulta evidente su repercusión para
el área en cuestión. De hecho, si se limita a leer los objetivos de los artículos puede que
no advierta la importancia que tienen para el conocimiento científico (y eso que usted
también puede considerarse un experto en el área). No se alarme, a la mayoría de los
científicos de su área les ocurre lo mismo. Por eso, es necesario justificar muy bien por
qué se resuelve la pregunta que usted quiere abordar. Debe responder a la pregunte ¿por
qué?
Encontrar una buena pregunta y justificar el motivo por el cual debe ser respondida
todavía no es suficiente. Aún necesita que esa justificación sea significativa no sólo para
usted, sino para los demás científicos de su área. Debe responde a la pregunta ¿qué
cambia si resuelvo la pregunta?. Si encuentra una justificación significativa a su
pregunta, enhorabuena, ya tiene un problema de investigación. En los artículos
científicos, el objetivo del estudio suele aparecer como última frase de la introducción y
las justificaciones significativas suelen aparecer justo antes.
31