3 - IES Diego de Siloé

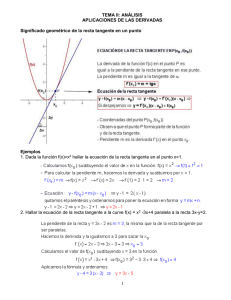
ESTUDIO Y GRAFICAS DE FUNCIONES
y = x3 − 3x 2 + 4
• Dominio de f =R
• Simetrías: No tiene
• Periodicidad: No tiene
• Monotonía. Extremos:
y ' = 3 x(x − 2 ) , y ' = 0
Intervalo
(−∞,0)
x=0
(0,2)
x=2
(2,∞)
Signo f '
+
0
−
0
+
f(x) es
creciente
máximo
decreciente
mínimo
creciente
• Concavidad. Puntos de inflexión
y ' ' = 6(x − 1) , y ' ' ' = 6
Intervalo
(−∞,1)
x=1
(1,∞)
Signo f ''
−
0
+
f(x) es
cóncava
punto inflex.
convexa
• Asíntotas: No tiene
• Puntos de corte con los ejes
P1=(0,4) máximo, P2=(-1,0), P3=(2,0) mínimo
P4=(1,2) punto de inflexión
• Signo de la función
Intervalo
(−∞,-1)
(-1,2)
(2,∞)
f(x) es
−
+
+
• Gráfica de la función
________________________________________________________________________________________________________________________
IES Diego de Siloé. Matemáticas. Ejercicios representación de funciones
1/7
y=
x2
x −1
• Dom f=R−{1}
• Simetrías: No tiene
• Periodicidad: No lo es
• Monotonía. Extremos:
x( x − 2)
y '=
(x − 1)2
Intervalos
(−∞,0)
x=0
(0,1)∪(1,2)
x=2
(2,∞)
Signo f '
+
0
−
0
+
f(x) es
creciente
máximo
decreciente
mínimo
creciente
• Concavidad. Puntos de inflexión
2
y ''=
(x − 1)3
Intervalo
(−∞,1)
Signo f ''
−
f(x) es
cóncava
x=1
(1,∞)
+
no existe
convexa
• Asíntotas
x=1
[Límites laterales]
y=x+1. [Posición de la curva respecto de la asíntota]
• Puntos de corte con los ejes. Puntos
P1=(0,0) máximo
P2=(2,4) mínimo
• Signo de la función
Intervalo
f(x) es
(−∞,0)
(0,1)
(1,∞)
−
−
+
• Gráfica
________________________________________________________________________________________________________________________
IES Diego de Siloé. Matemáticas. Ejercicios representación de funciones
2/7
y=
x2 + 1
x2 − 1
• Dom f=R−{±1}
• Simetrías: Es par
• Periodicidad: No es
• Monotonía. Extremos:
−4 x
y '=
2
2
x −1
(
)
Intervalos
(−∞,0)
x=0
(0,∞)
Signo f '
+
0
−
f(x) es
creciente
máximo
decreciente
Intervalo
(−∞,-1)
(-1,1)
(1,∞)
Signo f ''
+
−
+
f(x) es
convexa
cóncava
convexa
• Concavidad. Puntos de inflexión
y' ' =
12 x 2 + 4
(x − 1)
2
3
• Asíntotas
x=1, x=−1 (hallamos los límites laterales)
y=1 [Posición de la curva respecto de la asíntota]
• Puntos de corte con los ejes
P1=(0,-1) máximo
• Signo de la función
Intervalo
(−∞,-1)
(−1,0)
(0,1)
(1,∞)
f(x) es
+
−
−
+
• Gráfica
________________________________________________________________________________________________________________________
IES Diego de Siloé. Matemáticas. Ejercicios representación de funciones
3/7
y=
2 x 2 + 3x − 4
x2
• Dom f=R−{0}
• Simetrías: No tiene
• Periodicidad: No es
• Monotonía. Extremos.
−3 x + 8
y '=
x3
8
8
x=0
(0, )
Signo f '
−
∃/
+
0
−
f(x) es
decreciente
creciente
máximo
decreciente
• Concavidad. Puntos de inflexión
6 x − 24
6(− 3x + 16)
, y' ' ' =
y' ' =
4
x5
x
Intervalo
x=
8
(−∞,0)
Intervalos
3
( ,∞)
3
3
(−∞,4)−{0}
x=4
(4,∞)
Signo f ''
−
0
+
f(x) es
cóncava
punto inflexión
convexa
• Asíntotas
x=0 [Hallamos los límites laterales]
y=2 [Posición de la curva respecto de la asíntota]
• Puntos de corte con los ejes
P1=(-2'35...,0), P2=(0'85...,0)
5
8 41
P3=( , ) máximo; P4=(4, ) punto de inflexión
3 16
2
• Signo de la función
Intervalo
(−∞, -2'3..)
(−2'3.., 0'8..)
(0'8.., +∞)
f(x) es
+
−
+
• Gráfica
________________________________________________________________________________________________________________________
IES Diego de Siloé. Matemáticas. Ejercicios representación de funciones
4/7
y = x x(4 − x )
• Dom f=[0,4]
• Simetrías: No tiene
• Periodicidad: No es
• Monotonía. Extremos:
2 x(3 − x )
y' =
x(4 − x )
Intervalos
Signo f '
f(x) es
(−∞,0)
x=0
−
decreciente
mínimo
fuera del dominio
(0,3)
x=3
(3,∞)
x=4
+
0
creciente
máximo
−
decreciente
solo válido en (3,4]
La tangente es paralela
al eje de ordenadas
• Concavidad. Puntos de inflexión
y' ' =
2 x 3 − 12 x 2 + 12 x
(x(4 − x ))3 2
Intervalo
[0, 3 − 3 )
+
x= 3 − 3
0
( 3 − 3 ,4]
Signo f ''
f(x) es
convexa
punto inflexión
cóncava
−
• Asíntotas: No tiene
• Puntos de corte con los ejes. Otros puntos
P1=(0,0) mínimo; P2=(4,0) mínimo
P3=(3, 3 3 ) máximo, P4=( 3 − 3 ,( 3 − 3 ) 3 3 − 3 ) punto de inflexión
• Signo de la función
Intervalo
[0,4]
f(x) es
+
• Gráfica
________________________________________________________________________________________________________________________
IES Diego de Siloé. Matemáticas. Ejercicios representación de funciones
5/7
y=
x2 −1
x2 − 4
• Dom f=(−∞,-2) ∪(-2,-1]∪[1,2)∪(2,∞)
• Im f=R
• Simetrías: Par
• Periodicidad: No es
• Monotonía. Extremos:
(
− x x2 + 2
y '=
(
2
)
2
x −1 x − 4
)
2
Intervalos
(−∞,0) ∩ Dom (0,∞) ∩ Dom
Signo f '
+
−
f(x) es
creciente
decreciente
No existe la derivada en x=±1⇒ Tangente || OY
• Concavidad. Puntos de inflexión
y ''=
2 x 6 + 15 x 4 − 18 x 2 − 8
(x − 1) (x
2
32
2
−4
)
3
;
y''(1+)=+, y''(2−)=− ⇒ hay un punto de inflexión en (1,2), x=±1'162...
En (2,→), y''>0 ⇒ y es convexa
• Asíntotas
x=2, x=−2 [Hallamos los límites laterales]
y=0
[Posición de la curva respecto de la asíntota]
• Puntos de corte con los ejes
P1=(1,0) máximo, P2=(−1,0) máximo
• Signo de la función
Intervalo
(−∞,−2)
(−2,−1]
[1,2]
(2,∞)
f(x) es
+
−
−
+
• Gráfica
________________________________________________________________________________________________________________________
IES Diego de Siloé. Matemáticas. Ejercicios representación de funciones
6/7
y=e
x2
x 2 −1
• Dom f=R−{±1}
• Simetrías: Par
• Periodicidad: No lo es
• Monotonía. Extremos:
y '=
− 2x
(x − 1)
2
2
e
x2
x 2 −1
Intervalos
(−∞,−1)
Signo f '
+
f(x) es
creciente
(−1,0)
x=0
(0,1)
+
0
−
creciente
máximo
decreciente
x=−1
−
x=1
(1,∞)
−
−
decreciente
• Concavidad. Puntos de inflexión
y ''=
(
)
(x − 1)
4
2 3x − 1 e
2
x2
x 2 −1
4
Intervalo
[0, 4
1
)
x= 4
3
1
3
(4
1
,∞)
3
Signo f ''
−
0
+
f(x) es
cóncava
punto inflexión
convexa
• Asíntotas
+
x=±1 [Hallamos los límites laterales: x=1+ε, y→ +∞; x=1−ε, y→ 0 ]
y=e [Posición de la curva respecto de la asíntota]
• Puntos de corte con los ejes. Otros puntos
P1=(0,1) máximo
P2=(±0’759..., 0'25...) puntos de inflexión
• Signo de la función
Intervalo
Dominio
f(x) es
+
• Gráfica de la función
________________________________________________________________________________________________________________________
IES Diego de Siloé. Matemáticas. Ejercicios representación de funciones
7/7