Desarrollo de Estructuras Serie y Paralela para
Anuncio

Universidad de Concepción
Dirección de Postgrado
Facultad de Ingeniería - Programa de Doctorado en Ciencias de la Ingeniería con
Mención en Ingeniería Eléctrica
Desarrollo de Estructuras Serie y Paralela para
Compensación Dinámica de Sistemas Eléctricos
PABLO FERNANDO ACUÑA RIOS
CONCEPCIÓN-CHILE
2013
Profesor Guía: Luis Morán Tamayo
Dpto. de Ingeniería Eléctrica, Facultad de Ingeniería
Universidad de Concepción
UNIVERSIDAD DE CONCEPCIÓN
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA ELÉCTRICA
Profesor Patrocinante
Dr. Luis A. Morán T.
Tesis de Grado
Doctorado en Ciencias de la Ingenierı́a con mención en Ingenierı́a Eléctrica
Desarrollo de Estructuras Serie y Paralela para
Compensación Dinámica de Sistemas Eléctricos
Concepción, Junio de 2013
Pablo Fernando Acuña Rios
UNIVERSIDAD DE CONCEPCIÓN
Facultad de Ingenierı́a
Departamento de Ingenierı́a Eléctrica
Profesor Patrocinante:
Dr. Luis A. Morán T.
Desarrollo de Estructuras Serie y Paralela para
Compensación Dinámica de Sistemas Eléctricos
Pablo Fernando Acuña Rios
Tesis de Grado
Doctorado en Ciencias de la Ingenierı́a con mención en Ingenierı́a Eléctrica
Junio de 2013
Resumen
Los filtros activos son equipos que mejoran la calidad de suministro eléctrico compensando
dinámicamente las armónicas de corriente y la potencia reactiva. Habitualmente se considera
la aplicación de estos equipos en baja tensión (< 1kV), pues su aplicación en media tensión
está condicionada a las capacidades de bloqueo de los semiconductores o la utilización de un
transformador reductor de acoplamiento. Sin embargo, con adecuados esquemas de control y
estructuras de múltiples niveles es posible asegurar su operación en sistemas industriales de
potencia de media tensión. Esta tesis evalúa el desempeño dinámico de una alternativa de baja
tensión y además propone la utilización de topologı́as de convertidores de potencia de media
tensión que no han sido evaluadas como filtros activos. Se exploran configuraciones que sean
capaces de resolver los problemas de calidad de suministro, y además de operar en baja tensión,
puedan operar en niveles industriales de potencia entre 0.4 MW y 40 MW para media tensión
entre 4.16 kV y 15 kV. Las topologı́as presentadas en esta tesis son el filtro activo paralelo de
cuatro piernas para baja tensión, el filtro activo paralelo NPC monofásico en media tensión y
el filtro activo serie monofásico con enlace dc compartido en media tensión.
i
ii
“Confı́a en el Señor con todo tu corazón, y no te apoyes en tu propio entendimiento.”
Proverbios 3:5
iii
Agradecimientos
Primero y ante todo a Dios. A mis esposa Carla Figueroa por su apoyo, esfuerzo y compromiso durante los años del doctorado. A mis padres y hermanos por confiar en mı́. Al apoyo
incondicional de mis familiares, compañeros y amigos. En especial al grupo de trabajo encabezado por mi profesor guı́a, Luis Morán, y su apoyo durante el tiempo que le dediqué a este
trabajo.
Agradecer también el financiamiento otorgado por CONICYT, a través de la Beca de Doctorado, y el Proyecto Basal, CONICYT FBO-16.
Índice general
Índice de figuras
IX
Índice de tablas
X
1. Introducción
1
1.1. Introducción General . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.2. Aspectos Generales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2.1. Compensadores en Conexión Paralela . . . . . . . . . . . . . . . . . . . .
6
1.2.2. Compensadores en Conexión Serie . . . . . . . . . . . . . . . . . . . . . .
7
1.3. Revisión Bibliográfica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.3.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.3.2. Revisión y Discusión . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.4. Hipótesis de Trabajo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
1.5. Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
1.5.1. Objetivo General . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
1.5.2. Objetivos Especı́ficos . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
1.5.3. Aportes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
1.5.4. Publicaciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
1.6. Metodologı́a y Alcances
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
1.6.1. Metodologı́a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
1.6.2. Alcances . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
iv
ÍNDICE GENERAL
v
1.6.3. Recursos Disponibles . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
1.6.4. Recursos no Disponibles . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
2. FAP Usando un Convertidor de 4 piernas y 2 niveles
20
2.1. Nomenclatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
2.2. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
2.3. Modelo del Convertidor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.4. Control Predictivo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
2.5. Corriente de Referencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
2.5.1. Control voltaje dc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
2.6. Resultados de Simulación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
2.7. Resultados Experimentales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
2.8. Conclusión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
3. Filtro Activo Paralelo
45
3.1. Nomenclatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
3.2. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
3.3. Modelo del Convertidor NPC . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
3.4. Control Predictivo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
3.5. Generación de la Referencia de Corriente . . . . . . . . . . . . . . . . . . . . . .
53
3.5.1. Control del voltaje dc . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
3.6. Diseño del circuito de potencia . . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
3.6.1. Diseño del reactor de enlace . . . . . . . . . . . . . . . . . . . . . . . . .
57
3.6.2. Diseño de los condensadores dc . . . . . . . . . . . . . . . . . . . . . . .
58
3.7. Resultados de Simulación y Experimentales
. . . . . . . . . . . . . . . . . . . .
58
. . . . . . . . . . . . . . . . . . . . . . . . . .
59
3.7.2. Resultados Experimentales . . . . . . . . . . . . . . . . . . . . . . . . . .
60
3.8. Conclusión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
3.7.1. Resultados de Simulación
ÍNDICE GENERAL
vi
4. Filtro Activo Serie
67
4.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
4.2. Topologı́a y Principio de Operación . . . . . . . . . . . . . . . . . . . . . . . . .
70
4.3. Sistema de Control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
4.3.1. Generador de la señal de Referencia . . . . . . . . . . . . . . . . . . . . .
74
4.3.2. Generación de Señales de Disparo . . . . . . . . . . . . . . . . . . . . . .
76
4.3.3. Control del Voltaje dc . . . . . . . . . . . . . . . . . . . . . . . . . . . .
77
4.4. Diseño del Filtro Activo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
4.4.1. Condensador dc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
4.4.2. Filtro de Salida LC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
4.4.3. Potencia Aparente Nominal . . . . . . . . . . . . . . . . . . . . . . . . .
80
4.5. Desempeño del FAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
82
4.5.1. Simulaciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
82
4.5.2. Resultados Experimentales . . . . . . . . . . . . . . . . . . . . . . . . . .
83
4.6. Conclusión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
5. Conclusiones Generales
88
5.1. Conclusiones Generales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
5.2. Trabajo Futuro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
Índice de figuras
1.1. Tipos de conexión de filtros . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2. Módulo NPC monofásico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.3. Módulo VSI monofásico puente H. . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.1. Sistema Autónomo Hı́brido de Generación . . . . . . . . . . . . . . . . . . . . .
23
2.2. Diagrama equivalente trifásico del filtro activo propuesto. . . . . . . . . . . . . .
25
2.3. Topologı́a del VSI-PWM de cuatro piernas y dos niveles. . . . . . . . . . . . . .
25
2.4. Circuito equivalente del filtro activo propuesto.
. . . . . . . . . . . . . . . . . .
25
2.5. Circuito equivalente para el cálculo del voltaje de Thevenin. . . . . . . . . . . .
26
2.6. Circuito equivalente para el cálculo de la impedancia de Thevenin. . . . . . . . .
26
2.7. Circuito equivalente de Thevenin para el modelo matemático. . . . . . . . . . .
27
2.8. Diagrama Circuital para el modelo matemático. . . . . . . . . . . . . . . . . . .
27
2.9. Diagrama en bloques del control digital predictivo propuesto. . . . . . . . . . . .
28
2.10. Diagrama en bloques del generador de referencia. . . . . . . . . . . . . . . . . .
31
2.11. Relación entre desbalance de corriente de carga permisible. . . . . . . . . . . . .
34
2.12. Diagrama en bloques del control de voltaje dc . . . . . . . . . . . . . . . . . . .
35
2.13. Resultados de simulación. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
2.14. Resultados experimentales para transiente. . . . . . . . . . . . . . . . . . . . . .
43
2.15. Resultados experimentales para impacto de carga . . . . . . . . . . . . . . . . .
43
2.16. Resultados experimentales para desbalance. . . . . . . . . . . . . . . . . . . . .
44
vii
ÍNDICE DE FIGURAS
viii
3.1. Diagrama de conexión del filtro activo paralelo propuesto en un sistema eléctrico con apoyo d
3.2. Diagrama equivalente trifásico del filtro activo propuesto. . . . . . . . . . . . . .
49
3.3. Diagrama circuital del convertidor NPC monofásico (vC1 = vC2 = vdc ). . . . . .
49
3.4. Forma de onda del voltaje de cinco niveles en la salida del convertidor NPC monofásico. 50
3.5. Ejemplo de trayectorias permitidas en función del número de cambios de estado de los semico
3.6. Diagrama Circuital para el modelo matemático. . . . . . . . . . . . . . . . . . .
51
3.7. Diagrama en bloques del esquema de control predictivo propuesto. . . . . . . . .
52
3.8. Diagrama en bloques del Generador de Referencia de Corriente . . . . . . . . . .
53
3.9. Diagrama en bloques del control del voltaje dc. . . . . . . . . . . . . . . . . . .
55
3.10. Formas de onda simuladas para el esquema de compensación propuesto . . . . .
60
3.11. Formas de onda experimentales en régimen transiente . . . . . . . . . . . . . . .
62
3.12. Res. exp. para cambio escalón de carga. . . . . . . . . . . . . . . . . . . . . . . .
63
3.13. Res. exp. para conexión de carga motor. . . . . . . . . . . . . . . . . . . . . . .
63
3.14. Res. exp. bajo variación en el valor de la impedancia del sistema . . . . . . . . .
65
3.15. Relación entre el error de seguimiento de corriente (er ) y el T HD de is . . . . .
66
4.1. Diagrama Circuital del Sistema . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
4.2. Diagrama Circuital compensado . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
4.3. Circuito Equivalente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
4.4. Circuito equivalente monofásico . . . . . . . . . . . . . . . . . . . . . . . . . . .
72
4.5. Diagrama fasorial equivalente . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
4.6. Diagrama de control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
4.7. Diagrama en bloques del SOGI-PLL. . . . . . . . . . . . . . . . . . . . . . . . .
74
4.8. Diagrama de flujo del SOGI . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
4.9. Diagrama de Bloques del Generador de Señales de Disparo. . . . . . . . . . . . .
77
4.10. Diagrama del lazo de control del voltaje dc . . . . . . . . . . . . . . . . . . . . .
77
4.11. Circuito eq. rizado voltaje en la salida del convertidor . . . . . . . . . . . . . . .
79
4.12. Resultados de Simulación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
84
ÍNDICE DE FIGURAS
ix
4.13. Resultados de Simulación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85
4.14. Señales de control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
86
4.15. Resultados Experimentales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
86
4.16. Resultados Experimentales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
Índice de tablas
2.1. Especificación de Parámetros
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
3.1. Estados permitidos seleccionados para el NPC monofásico . . . . . . . . . . . .
50
4.1. Valores del Filtro LC (Vbase = 13.8 kV y Sbase = 10 MVA) . . . . . . . . . . . .
83
x
Capı́tulo 1
Introducción
1.1.
Introducción General
La calidad con que se suministra la energı́a eléctrica es producto de la estrecha relación que
existe entre los consumidores y los distribuidores. La responsabilidad de los distribuidores radica principalmente en mantener una buena continuidad en el servicio y garantizar una forma de
onda de voltaje sinusoidal y constante tanto en amplitud como en frecuencia. Por otro lado, los
consumidores deben mantener una forma de onda de corriente lo más sinusoidal posible, libre
de armónicas, y en fase con la correspondiente forma de onda de voltaje, es decir, sin consumo
de potencia reactiva. Para que esto sea posible, los filtros pasivos sintonizados son la solución
estándar utilizada industrialmente (ver Fig. 1.1a). Estos filtros atenúan individualmente la amplitud de las armónicas de corriente que circulan hacia el sistema y a su vez aportan la potencia
reactiva necesaria para corregir el factor de potencia. Sin embargo, presentan inconvenientes
como gran tamaño, influencia de la impedancia de la lı́nea en las caracterı́sticas de filtrado,
junto a la degradación y pérdida de sintonı́a asociada al paso del tiempo. Dado su naturaleza
pasiva, es decir, actúan sólo para una armónica especı́fica y en forma no controlada, presentan
problemas como resonancia y sobre-compensación. Ante un evento de resonancia se amplifican
las armónicas de corriente, distorsionando indirectamente el voltaje de la barra principal, mien-
1
CAPÍTULO 1. INTRODUCCIÓN
2
tras que ante un evento de sobre-compensación actúan las protecciones de sobre voltaje, debido
a que no todas las instalaciones cuentan con taps automáticos para ajustar el nivel de tensión.
Como respuesta a los filtros pasivos, se han propuesto diversas topologı́as de filtros activos de
potencia. El filtro activo está compuesto principalmente por un módulo convertidor estático de
potencia dc-ac, un elemento almacenador de energı́a y un filtro de salida. Estos filtros activos
son superiores a los pasivos en su capacidad de filtrado, son más pequeños en tamaño, no
presentan problemas de resonancia serie o paralela, y se adaptan a las condiciones de carga.
Existen filtros activos en conexión paralela y serie al sistema, y se conectan a él de acuerdo
al diagrama de la Fig. 1.1b y 1.1c, respectivamente. Comúnmente, los filtros activos paralelos
inyectan una corriente de compensación que anula la corriente armónica producida por la carga.
Los filtros activos serie operan generando un voltaje en serie a los voltajes de alimentación, el
cual es utilizado para compensar caı́das de tensión y filtrado de componentes armónicas en el
voltaje. Además, de manera no habitual, los filtros serie pueden operar generando un voltaje
en serie, proporcional a la corriente armónica, de manera de actuar como una alta impedancia
que impide la circulación de estas corrientes armónicas.
El lugar de interés para realizar la conexión de estos filtros activos corresponde al PCC (Punto de Común Acoplamiento). En sistemas de distribución industrial de media y alta tensión este
punto tiene tensiones que superan los 15 [kV], por lo tanto, es necesario contar con convertidores estáticos que toleren dichos niveles de tensión. Técnicamente, las restricciones eléctricas
impuestas por los semiconductores sólo permiten la aplicación directa (sin transformador) en
media tensión de filtros activos que usen topologı́as de dos niveles como el puente trifásico [1].
Además, los semiconductores disponibles en el mercado alcanzan tensiones de bloqueo por bajo
7 [kV], y pueden operar con reducida frecuencia de conmutación (<2kHz), limitando su uso a
convertidores PWM para 4.16 kV. A fin de superar esas limitaciones, convertidores multinivel
NPC y en cascada implementados con puentes H se han usado para alcanzar mayores niveles de
tensión y reducir la generación de bajas frecuencias de conmutación [2]- [3]. La mayorı́a de esas
aplicaciones se han desarrollado para accionamientos de motores AC, en donde la caracterı́stica
CAPÍTULO 1. INTRODUCCIÓN
3
de voltaje y corriente de operación sólo contiene términos fundamentales y balanceados debido
a la operación natural de los motores. Sin embargo, las aplicaciones de filtros activos se caracterizan por requerir compensar componentes desbalanceadas y con armónicas, las cuales hacen
propicio el uso de esquemas monofásicos que desacoplen el control en cada una de las fases. Esto
justifica la implementación de nuevas topologı́as monofásicas orientadas a la compensación en
media tensión, planteando nuevos objetivos como capacidad de compensación de armónicas de
corriente, pero considerando las limitaciones de los semiconductores disponibles en el mercado.
1.2.
Aspectos Generales
En las últimas décadas los sistemas de potencia se han enfrentado a nuevos desafı́os producto
del aumento permanente de la demanda eléctrica, conexión de cargas crı́ticas, y nuevas normas
de regulación para las lı́neas de transmisión y distribución de energı́a eléctrica. La sociedad
moderna, cada vez más dependiente de energı́a eléctrica, fuerza a los sistemas a operar con
elevada confiabilidad y casi 100 % de disponibilidad. En este complejo escenario, la calidad de
la energı́a se está convirtiendo en una importante preocupación entre los usuarios y empresas
eléctricas, forzando al desarrollo y aplicación de estrictos estándares debido a la conexión de
cargas más sensibles y sofisticadas por la electrónica que incluyen [4]. Estos requerimientos
han obligado a desarrollar nuevas tecnologı́as para mejorar la operación y controlabilidad de
los sistemas de potencia. Basados en esas nuevas tecnologı́as, se ha creado diferentes conceptos:
Flexible AC Transmission Systems (FACTS), Flexible Reliable and Intelligent Electrical Energy
Delivery System (FRIENDS), Custom Power Devices [5] y Smart Grids. En todos esos nuevos
conceptos, los equipos de compensación basados en convertidores estáticos conectados en serie
y/o en paralelo constituyen uno de los principales avances técnicos para abordar los nuevos
desafı́os de operación que presentan los actuales sistemas de distribución [6].
El concepto de FACTS fue originalmente creado en los ochenta para resolver problemas
de operación debidos a restricciones en la construcción de nuevas lı́neas de transmisión, para
4
CAPÍTULO 1. INTRODUCCIÓN
Etapas
de Filtros
Fuente
AC
vs
PCC
vL
Ls
is
il
5th
11th
7th
13th
(a)
Filtro Activo
Paralelo
Fuente
AC
vs
Cargas
PCC
vL
Ls
Cargas
is
il
if
u
v
w
Convertidor
dc-ac
(b)
Filtro Activo
Serie
Fuente
AC
vs
Ls
+ vSAF −
PCC
vL
Cargas
is
u
v
w
il
Convertidor
dc-ac
(c)
Figura 1.1: Tipos de conexión de Filtros (a) Filtro Pasivo Sintonizado Paralelo (b) Filtro Activo
Paralelo. (c) Filtro Activo Serie
mejorar los márgenes de estabilidad de los sistemas y facilitar el intercambio de energı́a entre
diferentes compañı́as generadoras y grandes usuarios. El concepto FRIENDS fue creado en los
noventa y propone una red de suministro eléctrico flexible y confiable, basada en la utilización
de una red de comunicación que permite al consumidor elegir arbitrariamente la calidad de la
CAPÍTULO 1. INTRODUCCIÓN
5
electricidad que desea recibir, optando por redes con o sin compensación e incluso suministro de
energı́a ininterrumpida. Custom Power Devices son aplicaciones especiales de FACTS, orientadas
a satisfacer requerimientos de calidad de la energı́a a nivel de distribución, como lo son sags
y swells [6]. Power custom devices tales como Distributed Static Compensator (DSTATCOM),
Dynamic Voltage Restorer (DVR), active power filters (APF), se han investigado extensamente
en la literatura técnica [7]. Aunque los Custom Power Devices están disponibles hace más de
una década, la adopción de su tecnologı́a por parte del mercado ha sido pobre, debido al alto
costo de venta y alto tiempo de reparación ante condiciones de falla [8]. Finalmente, Smart Grids
aparece recién el año 2005 en [9], y principalmente propone una distribución online de la energı́a
eléctrica, en vez del tradicional uso de la distribución programada. Al incorporar información,
comunicación y tecnologı́a en cada aspecto de la generación, distribución y consumo, los sistemas
son capaces de responder a un amplio rango de condiciones que se enfocan en:
Minimizar el impacto ambiental.
Ampliar el mercado.
Mejorar la confiabilidad y el servicio.
Reducir costos y mejorar la eficiencia.
En un futuro cercano, independiente del concepto que se aplique a las redes de distribución
eléctricas, se requerirán equipos que cumplan con los estrictos aspectos técnicos asociados a
la calidad de suministro. En esta tesis de grado, se desarrollarán Custom Power Devices para
compensación de voltaje, armónicas de corriente y potencia reactiva.
Tradicionalmente, la compensación paralela es usada para controlar el factor de potencia,
reducir la distorsión armónica de corriente, y para incrementar la potencia que puede ser distribuida, mientras la compensación serie es usada para cambiar la impedancia equivalente de una
lı́nea, la forma de onda del voltaje, y también es efectiva para la regulación de tensión, distorsión y desbalance de voltaje. A la vez, si es usada en lı́neas de transmisión, se puede obtener
fácilmente un control del flujo de potencia y estabilidad.
CAPÍTULO 1. INTRODUCCIÓN
6
La mayorı́a de los compensadores activos actúan sobre el flujo de potencia reactiva para
controlar el perfil de tensión y aumentar la eficiencia de los sistemas de potencia. El concepto
de compensación de VAR utilizando convertidores estáticos de potencia abarca un amplio y
diverso campo, tanto en problemas del sistemas de distribución como problemas de los clientes,
especialmente los relacionados con problemas de calidad de energı́a, ya que la mayorı́a de éstos
pueden atenuarse o resolverse con un adecuado control de potencia reactiva [10].
1.2.1.
Compensadores en Conexión Paralela
El principio de compensación paralela ha sido utilizado principalmente para compensar
corrientes armónicas y potencia reactiva de forma local, de acuerdo al nivel de tensión donde
se requiere la solución. Para aplicaciones industriales en baja tensión, es posible encontrar
soluciones industriales en base a convertidores de dos niveles, al igual como los que se utilizan
en variadores de frecuencia comerciales. En base a las caracterı́sticas de los compensadores de
dos niveles, esta tesis desarrolla una estrategia de control predictivo aplicada a la topologı́a de
cuatro piernas.
De igual manera que las topologı́as con inversores Neutral Point Clampled (NPC) PWM,
las topologı́as que usan convertidores trifásicos implementados con módulos monofásicos, ya
se presentan como alternativa para aplicaciones de accionamientos AC para motores de media
tensión. En base a ese conocimiento y tomando como inicio la topologı́a presentada en [11]
(ver Fig. 1.2), se desarrollará un procedimiento para compensación de armónicas de corriente
y potencia reactiva. La principal ventaja de esta topologı́a es el desacoplo del control en cada
fase y el alto número de niveles presente en los terminales de los convertidores, reduciendo el
estrés del voltaje aplicado en el punto de común acoplamiento. Para este tipo de aplicaciones
se propone un procedimiento para obtener las referencias de corriente y mantener constante el
voltaje dc en cada condensador. Se analizará el convertidores NPC monofásico de tres niveles.
Los inversores NPC de tres niveles monofásicos representan un equivalente al inversor de cinco
niveles NPC trifásico. Esto se presenta como una ventaja para la aplicación de los filtros activos
7
CAPÍTULO 1. INTRODUCCIÓN
propuestos.
P
+
vdc
−
NPC Monofásico
S1
S3
S2
S4
C1
x
+
vdc
−
iox
n
S1
S3
S2
S4
vf x
C2
N
u
v
w
Figura 1.2: Módulo NPC monofásico.
1.2.2.
Compensadores en Conexión Serie
El principio de compensación serie ha sido utilizado para compensar voltajes en sistemas de
distribución industrial. Sólo se han publicados pocos artı́culos que muestran la posibilidad de
compensar corrientes armónicas con ese esquema [12]. Con el objetivo de ampliar el campo de
operación de los filtros, esta tesis de grado propone un nuevo esquema de compensación serie
para corrientes armónicas (ver Fig. 1.3). La compensación de corrientes armónicas será obtenida distorsionando el voltaje aplicado a la carga. Para simplificar el control del voltaje dc, la
topologı́a a utilizar tiene la capacidad de conectar módulos de potencia monofásicos en serie
compartiendo un mismo enlace dc. Trabajos previos demuestran que para compartir el enlace
dc y sobrellevar los corto circuitos en el voltaje de salida, es posible usar un transformador de
acoplamiento en la salida de cada módulo.
8
CAPÍTULO 1. INTRODUCCIÓN
+
vSAF
u
v
w
np
ns
VSI
Cdc
bus dc
Figura 1.3: Módulo VSI monofásico puente H.
1.3.
1.3.1.
Revisión Bibliográfica
Introducción
La revisión bibliográfica que a continuación se presenta es esencial para la realización de la
Tesis de Grado, pues define el contexto y las bases del trabajo a realizar, ya que a partir de la
discusión que se genera de dicha revisión de las distintas publicaciones se define el tema que
finalmente será desarrollado. Se abordan temas tales como calidad de suministro, filtros activos,
configuraciones hı́bridas, estrategias de control, compensación armónica, etc.
1.3.2.
Revisión y Discusión
El número de publicaciones relacionada con compensación activa y Custom Power Devices
es bastante extensa. La literatura muestra un par de artı́culos que resumen el estado del arte
en este tipo de aplicaciones [8], [13]. Desde comienzos de los ochenta los investigadores han
estado trabajando en filtros activos para compensar dinámicamente potencia reactiva y eliminar
componentes de corrientes armónicas. Filtros activos en conexión paralela fueron propuestos
para satisfacer esos objetivos [8]. A principios de los noventa filtros activos en conexión serie
fueron introducidos con el objetivo de compensar regulación de voltaje, distorsión y desbalances
[14], [15]. Bajo el nombre de Dynamic Voltage Restorer, se han desarrollado distintas topologı́as
CAPÍTULO 1. INTRODUCCIÓN
9
de filtros activos serie. En combinación con filtros pasivos, ellos han sido propuestos como
aisladores de corrientes armónicas [16]. Desde entonces, las investigaciones y artı́culos se han
centralizado en describir los principios de operación, aspectos de control, y generación de señales
de referencia requeridas para que los equipos cumplan con el criterio online de compensación.
Finalmente, buscando alcanzar altos niveles de voltaje, se propuso la utilización de GTOs,
pero la compensación estuvo limitada a compensación de potencia reactiva [3]. Debido a esto,
el campo de aplicación de los filtros activos puede abrirse a sistemas de media tensión, si se
desarrollan topologı́as que usen semiconductores confiables como los IGBTs, y a su vez, puedan
en conjunto tolerar los niveles de bloqueo que deben soportar en media tensión.
Compensadores en Conexión Paralela
La mayorı́a de las referencias que analizan compensadores en conexión paralela han sido
publicadas en los noventa. Con la tecnologı́a en semiconductores de potencia que se tiene en
estos dı́as, la única posibilidad de implementar convertidores para media y alta tensión es
con la combinación en cascada de puentes H, convertidores con condensadores flotantes, o con
unidades multinivel. Hammond introduce la idea de celdas de potencia conectadas en cascada
para alcanzar la capacidad de operación en media tensión [17]. Cada celda de potencia compuesta
por inversores monofásicos opera a un voltaje no superior a 690 V. Sin embargo, con esta
estructura, el voltaje máximo alcanzado es 6.9 kV y ha sido desarrollado para aplicaciones de
accionamientos en AC. Siguiendo este enfoque, se han propuesto similares topologı́as, pero sólo
para mejorar el manejo de potencia reactiva [18], sin incluir la compensación de armónicas de
corriente. En este mismo contexto Akagi presenta un filtro activo paralelo implementado con
celdas trifásicas junto a un transformador que adecua el nivel de voltaje al soportado por los
semiconductores disponibles [19]. La compensación activa de potencia con ese esquema es posible
para sistemas de media tensión, sin embargo necesita de la construcción de un transformador
especial, lo que incrementa el costo y la complejidad. Peng propone un convertidor implementado
con módulos en cascada para aplicaciones de alto voltaje [20]. El convertidor está compuesto
CAPÍTULO 1. INTRODUCCIÓN
10
de inversores PWM monofásicos y está diseñado para aplicaciones en general. En [21] Peng
analiza la operación dinámica del convertidor estático implementado con su topologı́a. Los
resultados de simulación y experimentales muestran una mejor respuesta dinámica que sus
pares convencionales.
Un gran número de artı́culos analizando filtros activos en conexión paralela fueron publicados durante la última década. Nuevas referencias relacionadas se han generado recientemente,
pero están más orientadas en tratar de resolver problemas especı́ficos, tales como desbalance de
voltaje en el lado dc para el caso de convertidores multinivel, nuevas técnicas PWM, esquemas
de control para accionamientos y compensación de potencia reactiva [22]- [23]. Nuevas publicaciones, pero utilizando las mismas topologı́as en distintas aplicaciones o escenarios como por
ejemplo, usando generación distribuida, celdas fotovoltaicas y ultracapacitores como elementos
almacenadores de energı́a [24]- [25]. Además, se propone la conexión de convertidores en paralelo para incrementar los niveles de corriente [26]. Ese tipo de esquemas, aunque conectados en
paralelo al sistema de distribución, no están diseñados para operación en media tensión. Altos
niveles de voltaje pueden alcanzarse utilizando semiconductores en serie en esa topologı́a, lo cual
no es la mejor solución, debido a que no es posible asegurar distribución de corriente uniforme
a través de cada semiconductor.
Compensadores en Conexión Serie
Para la atenuación de los armónicos de corriente producidos por una carga no lineal, los
filtros activos paralelo presentan ventajas ya que operan como una fuente de corriente controlada
generando los armónicos de corriente necesarios, junto con compensar potencia reactiva [27].
No obstante, la tendencia a aprovechar las ventajas de la tecnologı́a activa y pasiva se instala
como opción de compensación mediante la utilización de filtros hı́bridos. Como por ejemplo
en [28], donde se utiliza un filtro activo serie en conjunto con filtros pasivos sintonizados. El
esquema trabaja como una fuente de corriente sinusoidal en fase con el voltaje del sistema, para
ası́ obtener un factor de potencia unitario y presentar una alta impedancia para las armónicas
CAPÍTULO 1. INTRODUCCIÓN
11
de corriente. Se destaca en este trabajo la obtención de regulación de tensión cercana al 0 %, que
se consigue manejando la amplitud de la corriente de componente fundamental. La obtención
de un factor de potencia unitario se logra inyectando un voltaje cuya magnitud es función del
voltaje de la lı́nea, mientras que la compensación de armónicos se hace por medio de filtros
pasivos. Como desventaja de este esquema de compensación está la dependencia de los filtros
pasivos para filtrar los armónicos de corriente, además de utilizar una pequeña fuente de voltaje
dc para alimentar la barra continua del filtro activo.
En [29] se presenta un filtro hı́brido paralelo para la compensación de corrientes armónicas.
Este esquema está compuesto por un filtro sintonizado LC para cada fase y por un filtro activo
de baja potencia, conectado en serie sin usar transformadores de acoplamiento. La funcionalidad
del filtro LC es absorber las corrientes armónicas producidas por una carga no lineal, mientras
que el filtro activo aumenta el ancho de banda del conjunto.
La idea de conectar un filtro activo directamente al sistema a compensar sin utilizar un
medio de transformación es propuesta en [30], donde se utiliza un filtro activo hı́brido en conexión
paralela caracterizado por la conexión en serie de un filtro LC por fase y un pequeño filtro activo
trifásico. El condensador del filtro LC impone una alta impedancia a la frecuencia fundamental,
esta caracterı́stica permite la conexión directa del filtro activo hı́brido al sistema de alta tensión,
en este caso 6.6 kV, sin usar un transformador. Esto contribuye a una reducción en costos,
tamaño y peso.
En [31], se propone un filtro activo serie, con un inversor trifásico PWM fuente de voltaje y
opera conectado con un filtro pasivo LC, siendo capaz de compensar los armónicos de corrientes
y simultáneamente las componentes de secuencia negativa y secuencia cero generados por una
fuente de tensión desbalanceada. Además, elimina la componente de secuencia cero de corrientes
que circulan por el neutro. Como desventaja de este esquema de compensación es la utilización
del filtro pasivo LC dedicado para la compensación de armónicas de corriente.
A pesar de que el filtro activo serie clásico opera como una fuente de tensión controlada, definiendo su uso para compensar voltaje en aplicaciones donde existan desbalances, mala
CAPÍTULO 1. INTRODUCCIÓN
12
regulación y distorsión [32], estos equipos también se han utilizado para la compensación de
corrientes armónicas. En [33], [34] y [35] han desarrollado un filtro activo serie diseñado para la
compensación de armónicos de corriente para un rectificador de 12 pulsos, en que los terminales
de la barra dc del filtro activo (constituido por un condensador) están directamente conectados
en paralelo al condensador electrolı́tico de la barra dc del rectificador, formando una barra dc
común. En [33], se muestra que el filtro activo es capaz de compensar armónicos de corriente,
manteniendo la regulación de tensión en la barra dc. En [34], se realiza un análisis de estabilidad con respecto a un primer esquema de control de corriente, luego al obtener problemas de
inestabilidad debido a retardos en la extracción de los armónicos de corriente, se propone una
segunda señal de referencia para este lazo, consiguiendo resultados satisfactorios. En [35] se hace
un exhaustivo estudio de la configuración de la barra dc común y se compara con una barra
dc independiente para cada inversor monofásico. Los resultados indican que la configuración
original es la mejor opción debido a que no se utiliza un valor de capacitancia grande, y además
se evitan sobre-tensiones en la barra dc del filtro activo.
Otro esquema de compensación se muestra en [36], donde el filtro está compuesto por transformadores de acoplamiento, un inversor fuente de voltaje trifásico, compartiendo el mismo
capacitor de la barra dc del rectificador de 12 pulsos. En este trabajo se propone un control
digital, y la referencia de corriente se obtiene midiendo los voltajes del sistema, y a partir de
estas señales se calcula la Transformada Discreta de Fourier (DFT), el resultado obtenido se
invierte para luego aplicar la transformada inversa de la DFT, luego las magnitudes de corriente
se controlan mediante el error entre el voltaje dc de la carga y una referencia. Los resultados
obtenidos son una corriente prácticamente sinusoidal, además de corregir factor de potencia y
regulación de voltaje dc de la carga.
Siguiendo con la lı́nea de filtros activos serie, en [37] se presenta un esquema de compensación
que, a diferencia de los anteriores, no posee una barra dc común entre la carga del rectificador y
el lado dc del filtro activo. El objetivo de este trabajo es mostrar que al eliminar los armónicos
de voltaje producidos por la generación de corrientes armónicas propias de la carga, es posible
CAPÍTULO 1. INTRODUCCIÓN
13
eliminarlas obteniendo una corriente sinusoidal, y además demuestra que el filtro es capaz de
sustentar por sı́ mismo el voltaje en la barra dc usando un control adecuado.
El esquema de compensación presentado en la última parte de la tesis se basa principalmente
en dos trabajos encontrados en la literatura técnica. En [38], se presenta una configuración para
un compensador, cuyo propósito es corregir dinámicamente los desbalances de tensión en un
sistema trifásico. La configuración topológica en un principio interviene solamente una fase de
un sistema trifásico, y si la carga a compensar es sensible a ciertas caracterı́sticas, se propone una
configuración que interviene sólo dos fases. Esta última caracterı́stica es aprovechada en [28],
donde se propone por primera vez un filtro activo serie capaz de compensar armónicos de
corriente en las tres fases. En ese trabajo sólo se muestra parte del diseño y la efectividad para
un rectificador no controlado de seis pulsos, cuya carga solamente es resistiva.
1.4.
Hipótesis de Trabajo
Las siguientes hipótesis de trabajo guiarán esta tesis:
No es restricción compensar dinámicamente en media tensión porque existen los esquemas
de control y topologı́as adecuadas.
Una estrategia de control predictivo para filtros activos de potencia puede ser aplicada a
diferentes topologı́as de convertidores sin necesidad de replantear el algoritmo predictivo.
Estructuras multinivel (tres y cinco niveles) implementadas con módulos monofásicos pueden ser usadas como filtros serie y paralelo, si se les aplica un adecuado esquema de control.
Los convertidores monofásicos que forman una topologı́a trifásica pueden ser controlados
mediante control predictivo independiente por fase.
Filtros activos serie pueden ser implementados para eliminar corrientes armónicas generadas por cargas no lineales.
CAPÍTULO 1. INTRODUCCIÓN
14
Se puede utilizar un solo enlace dc compartido para los convertidores estáticos monofásicos
que conforman el esquema de compensación serie trifásico.
1.5.
1.5.1.
Objetivos
Objetivo General
El objetivo general de esta tesis es desarrollar nuevas topologı́as de filtros activos para sistemas de potencia en baja y media tensión. El primer filtro propuesto considera la aplicación en
baja tensión. Los dos restantes serán implementados con módulos monofásicos que permiten la
operación independiente orientada a media tensión. Se investigarán caracterı́sticas no tradicionales de compensación, es decir, no solamente filtros paralelos compensarán potencia reactiva
y componentes de corrientes armónicas, o filtros serie compensarán perturbaciones de voltaje
(distorsión, sags, swells, desbalance). Cada topologı́a propuesta tendrá un adecuado esquema
de control que optimice su desempeño dinámico.
1.5.2.
Objetivos Especı́ficos
Cada uno de los siguientes objetivos es relacionado con cualquiera de las topologı́as que se
propondrán.
Probar la operación de la topologı́a para estado estacionario y transiente.
Implementar un prototipo de laboratorio que permita validar el procedimiento de diseño,
modelo matemático y diseño del esquema de control.
Adicionalmente, sobre la topologı́a serie propuesta el siguiente objetivo es considerado:
Probar que las componentes armónicas de la corriente del sistema pueden ser mitigadas aplicando un voltaje distorsionado a la carga no lineal, aún cuando ella es del tipo
inductiva.
CAPÍTULO 1. INTRODUCCIÓN
1.5.3.
15
Aportes
Se resumen a continuación los principales aportes de la tesis, dividiendo éstos en tres grupos: los relacionados con el control predictivo aplicado a filtros activos, los relacionados con la
compensación paralela y los relacionados con la compensación serie.
Compensación Paralela
En la tesis se desarrolla una estructura paralela, compuesta por módulos NPC monofásicos. Cómo contribución principal, se propone una topologı́a que usa semiconductores de baja
tensión, pero puede ser utilizada en sistemas de media tensión. Se realiza un estudio detallado
para analizar las caracterı́sticas dinámicas y estáticas del esquema de compensación propuesto,
concluyendo que esta topologı́a es una alternativa viable para ser usada en sistemas de media
tensión.
Compensación Serie
En la tesis se desarrolla una estructura serie, compuesta por módulos puente H monofásicos.
Como contribución principal, se propone un esquema de compensación serie para compensar
armónicas de corriente. La compensación serie propuesta permite operar con convertidores de
baja tensión, utilizando un voltaje de compensación que es equivalente a sólo una parte del valor
de tensión de la lı́nea de media tensión. Este voltaje es controlado y menor al soportado por los
semiconductores. Por otra parte, los módulos monofásicos pueden ser conectados en cascada,
permitiendo obtener mayores niveles de tensión, en caso de que la compensación de reactivos
imponga una condición de mayor tensión en los terminales de los convertidores.
Control Predictivo
Esta tesis propone un sistema de control predictivo que permite implementar distintas topologı́as de convertidores estáticos para filtros activos, tanto en baja como media tensión. Se
CAPÍTULO 1. INTRODUCCIÓN
16
obtiene un modelo generalizado, de fácil implementación, que permite la implementación de las
topologı́as sin recurrir a técnicas de control especı́ficas para cada una de ellas.
En otro orden de importancia, también existe una contribución secundaria que tiene relación
con la reducción del tiempo de desarrollo para cada topologı́a.
1.5.4.
Publicaciones
Las publicaciones generadas directa o indirectamente en el desarrollo de esta tesis se citan
a continuación:
Publicaciones en Revistas
Acuña, P.; Morán, L.; Dixon, J.; , “Current harmonics compensation for electrolytic processes using a series active scheme,” Power Electronics, IET , vol.5, no.8, pp.1254-1261,
September 2012.
Aceptada para publicación en TPEL 2013 (IEEE Transactions on Power Electronics):
Acuna, P.; Morán, L.; Rivera, M.; Dixon, J.; Rodriguez, J., “Improved Active Power
Filter Performance for Renewable Power Generation Systems,” Power Electronics, IEEE
Transactions on , vol.PP, no.99, pp.1,1, 0 doi: 10.1109/TPEL.2013.2257854
Actualmente en revisión para publicación en TPEL:
“An Active Power Filter using Single-Phase Three-Level NPC Converters and Predictive
Control for Medium Voltage Distribution Systems”.
Publicaciones en Conferencias
Acuña, P.F.; Morán, L.A.; Weishaupt, C.A.; Dixon, J.W.; , “An active power filter implemented with multilevel single-phase NPC converters,” IECON 2011 - 37th Annual
Conference on IEEE Industrial Electronics Society , vol., no., pp.4367-4372, 7-10 Nov.
2011.
CAPÍTULO 1. INTRODUCCIÓN
17
Acuña, P.; Morán, L.; Rivera, M.; Rodriguez, J.; Dixon, J.; , “Improved active power filter
performance for distribution systems with renewable generation,” IECON 2012 - 38th
Annual Conference on IEEE Industrial Electronics Society , vol., no., pp.1344-1349, 25-28
Oct. 2012.
Proyectos
Fondef VIU 110006 - Equipo para la corrección del factor de potencia en instalaciones
eléctricas en baja tensión, 2012. Cargo: Jefe de Proyecto.
1.6.
1.6.1.
Metodologı́a y Alcances
Metodologı́a
La metodologı́a a utilizar en esta tesis sigue los procedimientos que sigue la mayorı́a de los
desarrollos en electrónica de potencia:
Deducción del modelo teórico a utilizar.
Deducción de los criterios de diseño para cada componente del circuito de potencia.
Simulación para operación en lazo abierto y cerrado; estado transiente y estacionario.
Implementación del prototipo de laboratorio.
Test de laboratorio para distintas condiciones de operación.
Análisis de resultados y generación de publicaciones.
1.6.2.
Alcances
El análisis de los compensadores se realiza en primera instancia a través del modelo circuital.
CAPÍTULO 1. INTRODUCCIÓN
18
El diseño de los componentes se realizará en base a un punto de operación arbitrario del
equipo.
Los semiconductores utilizados en las simulaciones serán considerados ideales.
Las salidas de interés son el factor de potencia en el PCC, el contenido armónico de la
corriente de entrada, el voltaje en el enlace dc de los convertidores, y la corriente y voltaje
de salida de los convertidores.
Los algoritmos desarrollados serán validados en el prototipo diseñado en laboratorio, serán
programados en Matlab-Simulink y exportados a una plataforma dSPACE.
1.6.3.
Recursos Disponibles
A continuación se detallan los recursos que se utilizaron para el desarrollo de la Tesis.
En la UdeC
Servicio de Biblioteca Central y servicio online de IEEE para revisión de publicaciones en
conferencias y revistas.
En el L.C.S.E
Se contó con computadores con versiones de evaluación de MatLab para realizar las simulaciones.
Protoboards y componentes análogas/digitales para implementación de circuitos.
Osciloscopios digitales.
FPGA Nexys II con tarjetas de E/S análogas para la implementación del control en tiempo
real.
CAPÍTULO 1. INTRODUCCIÓN
1.6.4.
19
Recursos no Disponibles
Para suplir los recursos que no provienen de la universidad se contó con el apoyo de los
proyectos:
Proyecto Fondecyt Regular N◦ 108 0237, titulado “Development of Static Converter Topologies for Medium and High Voltage Power Systems Active Compensation”.
Proyecto Innova BioBı́o de Apoyo a la realización de Tesis, 11CH S2919 F11.
Además, se utilizó para la parte experimental una Real-Time Interface (RTI) dSPACE
DS1103 R&D facilitada por el Dr. Marco Rivera y el Prof. José Rodriguez de la UTFSM.
20
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
21
Capı́tulo 2
Filtro Activo Paralelo con Convertidor
de Cuatro Piernas
2.1.
Nomenclatura
AC
Corriente alterna
dc
Corriente continua
PWM
Modulación por ancho de pulso
PC
Control Predictivo
PLL
Phase-locked-loop
vdc
Voltaje dc
vs
Vector de voltaje del sistema [vsu vsv vsw ]T
is
Vector de la corriente del sistema [isu isv isw isn ]T
iL
Vector de la corriente de carga [iLu iLv iLw iLn ]T
vxn
Vector de voltaje de salida del VSI [vun vvn vwn ]T
io
Vector de la corriente de salida del VSI [iou iov iow ion ]T
i∗o
Vector de la corriente de referencia [i∗ou i∗ov i∗ow i∗on ]T
in
Corriente del neutro
Lf
Inductancia del filtro
Rf
Resistencia del filtro
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
2.2.
22
Introducción
La generación mediante energı́as renovables afecta la calidad de la energı́a debido a su naturaleza no predecible y/o variante en el tiempo según las condiciones ambientales o climáticas.
Las plantas de generación solar y los generadores eólicos deben estar conectados al sistema a
través de convertidores estáticos PWM de alta potencia [39]. Esta naturaleza no uniforme de
generación de potencia, junto a los requerimientos de reactivos de las máquinas de inducción
presentes en los sistemas de generación (sólo aplicaciones eólicas), crean distorsión de voltaje y
afectan directamente la regulación de voltaje en los sistemas de potencia eléctricos. Este nuevo
escenario de los sistemas de distribución requerirá de técnicas de compensación cada vez más
sofisticadas.
Aunque los filtros activos de potencia implementados con inversores fuente de voltaje de
cuatro piernas (4L-VSI) ya están presentes en la literatura técnica [40–44], la principal contribución de esta parte de la tesis es el diseño e implementación de un algoritmo de control
predictivo especı́fico para aplicaciones de filtros activos. Tradicionalmente, los filtros activos son
controlados usando controladores pre-ajustados, como PI o adaptivos, para el lazo de corriente
como para el lazo de voltaje dc [45, 46]. Los controladores PI deben ser diseñados en base al
circuito equivalente lineal, mientras que los controladores predictivos usan el modelo no-lineal, el
cual es más cercano a las condiciones de operación reales. Un modelo adecuado obtenido usando
control predictivo mejora el desempeño del filtro activo, especialmente durante condiciones de
operación transiente, porque el filtro es capaz de seguir rápidamente la referencia de corriente,
mientras mantiene un voltaje dc constante en los terminales del convertidor.
Hasta aquı́, la implementación de control predictivo en convertidores de potencia ha sido
usado principalmente en accionamientos de motores de inducción [47–54]. En aplicaciones como
los accionamientos de motores, el control predictivo representa un esquema de control intuitivo que maneja caracterı́sticas multivariable, simplifica el tratamiento de compensación por
tiempos de retardo, y permite el reemplazo de los moduladores PWM. Sin embargo, ese tipo
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
23
de aplicaciones presenta desventajas relacionadas a oscilaciones e inestabilidad que se crean a
partir de la exactitud dada a los parámetros del modelo [53]. Una de las ventajas del algoritmo
propuesto es que éste se adecua bien en aplicaciones de filtros activos, dado que los parámetros
de salida del convertidor de potencia son bien conocidos [55]. Estos parámetros de salida se
obtienen con el filtro de salida del convertidor y la impedancia equivalente del sistema. El filtro
de salida del convertidor es parte del diseño del filtro activo, y la impedancia del sistema se
obtiene a través de procedimientos estándares [56, 57]. En el caso de desconocer los parámetros
de impedancia del sistema, se podrı́a usar una estimación de ellos para determinar un modelo
del sistema equivalente R-L que sea adecuado para modelar el filtro [58].
Este capı́tulo presenta el modelo matemático del 4L-VSI y el principio de operación del
esquema de control predictivo propuesto. Se presenta una completa descripción del generador
de referencia de corriente implementado en el filtro activo. Finalmente, se muestra el desempeño
del filtro activo y la efectividad del esquema de control a través de simulaciones, validadas con
resultados experimentales en un setup de laboratorio de 2kVA.
Sub-estación
de Distribución
Generación
de Energı́a
Renovable 1
Generación
de Energı́a
Renovable 2
PCC
Convertidor estático
PWM AC/AC
Industriales
Convertidor estático
Filtro Activo PWM dc/AC
Paralelo
Residenciales
Figura 2.1: Sistema Autónomo Hı́brido de Generación con filtro activo de potencia paralelo.
2.3.
Modelo del Convertidor de Cuatro Piernas
La figura 2.1 muestra la configuración de un sistema de distribución tı́pico en base a generación por energı́as renovables. Este sistema consiste de varios tipos de unidades de generación y
diferentes tipos de cargas. Fuentes de generación de energı́a renovable, tales como solar y eólica,
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
24
se usan tı́picamente para generar electricidad para usuarios residenciales y pequeñas industrias.
Ambos tipos de generación de energı́a usan convertidores estáticos AC/AC y dc/dc para la
conversión de voltaje y bancos de baterı́as para almacenamiento de energı́a. Estos convertidores
se encargan de obtener el máximo de energı́a posible del sol y el viento. El comportamiento del
consumo de energı́a es aleatorio e impredecible, por lo tanto, puede ser monofásico, trifásico,
balanceado o desbalanceado, y lineal o no-lineal. Un filtro activo se conecta en paralelo al punto
de común acoplamiento (PCC) para compensar armónicas de corriente, desbalance de corriente
y potencia reactiva. Está compuesto de un condensador electrolı́tico, un convertidor de cuatro
piernas, y un filtro de salida de primer orden como lo muestra la Fig. 2.2. Este diagrama considera la impedancia equivalente del sistema Zs , representada como una inductancia de valor
Ls , la impedancia del filtro de salida Zf , representada por una resistencia de valor Rf y una
inductancia de valor Lf , y la impedancia de la carga ZL .
La topologı́a del convertidor de cuatro piernas se muestra en la Fig. 2.3. Cada estado de
conmutación de los semiconductores (Sx , x = u, v, w, n) puede tomar el valor 0 ó 1, de acuerdo
a si está apagado o encendido. Esta topologı́a de convertidor es similar al convertidor trifásico
puente completo convencional, pero adiciona una cuarta pierna conectada al neutro del sistema.
Al igual que las otras piernas, la cuarta pierna, está conectada al PCC a través de un filtro de
salida, cuya función es evitar cortocircuitos entre el voltaje dc del convertidor y el neutro del
sistema. La cuarta pierna incrementa los estados de conmutación de los semiconductores desde
8 (23 ) a 16 (24 ), aumentando la flexibilidad del control [59], junto con la caracterı́stica principal
que es permitir compensación de desbalances de corriente.
El voltaje de salida, vxn , medido entre el punto de salida x de cada pierna del convertidor y
el punto n, se expresa en términos de los estados de conmutación (Sx ) de acuerdo a lo siguiente:
vxn = vxN − vnN = Sx vdc − Sn vdc = (Sx − Sn ) vdc ,
x = u, v, w, n.
(2.1)
El modelo matemático del filtro, se obtiene a partir de un análisis del voltaje e impedancia
de Thevenin en los terminales de salida del convertidor. El objetivo es establecer un modelo
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
vs
is
Zs
25
iL
PCC
ZL
Ls
io
Sistema
Cargas
Lf
Zf
Rf
vdc
Filtro Activo
Paralelo
Figura 2.2: Diagrama equivalente trifásico del filtro activo propuesto.
Convertidor de
Cuatro Piernas
P
Su
+
vdc
−
Sv
Cdc u
Su
Sw
v
Sv
io
Sn
w
Sw
Sn
n
Zf
Rf Lf
N
Figura 2.3: Topologı́a del VSI-PWM de cuatro piernas y dos niveles.
equivalente representado por una fuente de tensión (veq ) y una impedancia en serie equivalente
(Zeq ). El circuito equivalente con impedancias del filtro activo se muestra en la Fig. 2.4. Es
importante mencionar que este circuito equivalente, se analiza en forma generalizada, es decir,
no se considera la topologı́a del convertidor de potencia y las impedancias de salida del filtro en
cada fase x, Zf x , pueden ser iguales o distintas a la impedancia de salida en el neutro del filtro,
Zf n .
Zf x
vxn
+
Zs
ZL
−
n
Zf n
+
−
vs
n,
Figura 2.4: Circuito equivalente del filtro activo propuesto.
Se calcula el voltaje de Thevenin de acuerdo a la Fig. 2.5. Para este modelo se asume que
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
Zf ,
26
Zs
+
+
veq
ZL
−
vs
−
Figura 2.5: Circuito equivalente para el cálculo del voltaje de Thevenin.
Zf ,
Zs
ZL
Figura 2.6: Circuito equivalente para el cálculo de la impedancia de Thevenin.
ZL >> Zs , la parte resistiva del equivalente del sistema se desprecia, impedancias iguales en
las salidas del convertidor (Zf , = Zf x + Zf n = 2Zf x ,
x = u, v, w, n) , y la reactancia serie
está en el rango de 3-7 % p.u., lo cual es una aproximación aceptable del sistema real. Luego:
veq = vZL = vZs + vs ≈ vs ,
(2.2)
donde vZL es el voltaje en la impedancia ZL y vZs es el voltaje en la impedancia Zs .
Para el cálculo de la impedancia equivalente, se usa la Fig. 2.6 y las mismas consideraciones
que en (2.2). Esta impedancia equivalente se determina por la conexión serie entre la impedancia
equivalente del filtro de salida Zf , y el arreglo paralelo entre la impedancia equivalente del
sistema Zs y la impedancia de la carga ZL (2.3):
Zeq =
Zs ZL
+ Zf , ≈ Zs + Zf , .
Zs + ZL
(2.3)
De esta forma, se obtiene el diagrama equivalente de la Fig. 2.7. Este diagrama establece
que la impedancia vista por el convertidor tendrá un valor dado por Ze q y un voltaje que se
aproxima a vs .
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
27
Zeq
io
vxn
+
+
−
−
vs
Figura 2.7: Circuito equivalente de Thevenin para el modelo matemático.
Finalmente, a partir de la Fig. 2.4 y la Fig. 2.7, se obtiene el diagrama circuital (ver Fig.
2.8) que permite obtener el modelo matemático del filtro.
Convertidor de
Cuatro Piernas
P
+
vdc
−
Sx
Cdc x
Sx
io
Sn
+ vxn −
Sn
N
n
Req Leq
+ v
− s
+
vnN
−
Figura 2.8: Diagrama Circuital para el modelo matemático.
A partir de la Fig. 2.8, se obtienen las ecuaciones del modelo matemático del filtro:
vxN = Req io + Leq
d io
+ vs + vnN .
dt
(2.4)
Considerando que vxN − vnN = vxn , (2.4) queda de la siguiente forma:
vs = vxn − Req io − Leq
d io
,
dt
(2.5)
donde Req y Leq corresponden a los valores de la resistencia e inductancia equivalentes, considerando la impedancia de Thevenin Zeq en los terminales de salida del convertidor (2.3). De la
misma forma, io es la corriente inyectada por el filtro activo. Finalmente, en la ecuación (2.5)
Req = 2Rf y Leq = Ls + 2Lf .
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
2.4.
28
Control Predictivo de Corriente
La Fig. 2.9 muestra el diagrama en bloques del esquema de control digital predictivo propuesto. Este esquema de control es básicamente un algoritmo de optimización digital y, por lo
tanto, puede ser implementado en un microprocesador. Consecuentemente, el análisis desarrollado debe ser usando matemática discreta la que permita considerar restricciones adicionales,
como tiempos de retardo y aproximaciones [48, 60–67]. La caracterı́stica principal del control
predictivo es el uso del modelo del sistema para predecir el comportamiento de las variables a
controlar. El controlador usa esa información para seleccionar el estado de conmutación óptimo
que será aplicado al convertidor de potencia, acorde a un criterio de optimización predefinido.
El algoritmo de control predictivo es fácil de implementar y entender. La Fig. 2.9 muestra las
partes principales que componen la implementación del algoritmo.
vs
iL
3
Generador
Corriente
Referencia
3
vdc
Modelo
Predictivo
io ∗
4
io k+1
Su
Función
de Costo
g k+1
io
Sv
Sw
Sn
3
Convertidor
4 Piernas
io
Figura 2.9: Diagrama en bloques del control digital predictivo propuesto.
Generador de Corriente de Referencia
Esta unidad se diseña para generar la referencia de corriente que se usa para compensar
componentes indeseables de corriente. En este caso, se miden los voltajes del sistema, las corrientes de carga y el voltaje dc del convertidor, mientras que la corriente por el neutro y la
corriente del neutro en la carga se generan directamente a través de esas señales (2.5).
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
29
Modelo Predictivo
Se usa el modelo del convertidor para predecir la corriente de salida del convertidor. Dado
que el controlador opera en tiempo discreto, tanto el controlador como el modelo del sistema
deben ser representados en el dominio discreto [60]. El modelo discreto consiste en una ecuación
matricial que representa la predicción del sistema. Esto significa que para un tiempo de muestreo
Ts , conociendo los estados del convertidor y las variables de control al instante kTs , se puede
predecir el siguiente estado en el instante [k + 1]Ts . Debido a la naturaleza de primer orden de
las ecuaciones de estado que describen el modelo en (2.1)-(2.5), una aproximación de la derivada
suficientemente adecuada se considera en esta tesis:
dx
x[k + 1] − x[k]
≈
.
dt
Ts
(2.6)
Los 16 valores de la predicción de la corriente de salida posibles pueden ser obtenidos usando
(2.5) y (2.6) como:
io [k + 1] =
Req Ts Ts vxn [k] − vs [k] + 1 −
io [k].
Leq
Leq
(2.7)
Como lo muestra (2.7), para predecir la corriente de salida (2.7) en el instante (k + 1), se
requieren los valores del voltaje del sistema vs y el voltaje de salida del convertidor vxn . El
algoritmo calcula los 16 posibles valores asociados con los posibles valores que las variables de
estado pueden alcanzar.
Optimización de la Función de Costo
El vector de corrientes de salida (io ) es igual a la referencia (i∗o ) cuando la función de costo g
es igual a cero. Entonces, el objetivo de optimización de la función de costo es alcanzar un valor
para g cercano a cero. Se elige el vector de voltaje vxn , dentro de los 16 posibles valores, tal que
minimiza la función de costo, y luego se aplica este voltaje al siguiente instante de muestreo
(k + 1), considerando un tiempo de muestreo fijo (Ts ). La función de costo dependerá de las
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
30
variables medidas, variables que se predicen y variables estimadas y/o calculadas a partir de las
demás variables. Especı́ficamente, en esta topologı́a de cuatro piernas, para predecir todas las
corrientes en el instante k + 1 sólo se predicen directamente las corrientes iou , iov e iow , tal como
se muestra en (2.8):
iox [k + 1] = iox [k] −
Req Ts
Ts
iox [k] +
(vxn [k] − vsn [k]) , x = u, v, w,
Leq
Leq
(2.8)
donde vxn está definido en (2.1).
Dado que la corriente por el neutro es una combinación lineal de las demás, ésta se predice
en función de las otras como (2.9):
ion [k + 1] = − (iou [k + 1] + iov [k + 1] + iow [k + 1]) ,
(2.9)
Para seleccionar el estado de conmutación óptimo que debe ser aplicado al convertidor de
potencia, se comparan los 16 valores de predicción obtenidos para el vector de corrientes io [k +1]
con el vector de referencias de corriente usando una función de costo g, definida a continuación:
g[k + 1] = (i∗ou [k + 1] − iou [k + 1])2
+ (i∗ov [k + 1] − iov [k + 1])2
+ (i∗ow [k + 1] − iow [k + 1])2
+ (i∗on [k + 1] − ion [k + 1])2
(2.10)
Finalmente, es posible observar que no existen factores de peso asociados al control de cada
una de las cuatro corrientes de salida del convertidor. Esto hace que la ponderación de una
corriente sobre otra sea la misma. La caracterı́stica tetra-filar permite inyectar una corriente
controlada a través de la cuarta pierna. En operación normal, es decir, sin desbalance de carga,
no existe inyección por la cuarta pierna. Sin embargo, en el caso de desbalances en las corrientes
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
31
de carga, la corriente inyectada por la cuarta pierna, se impone de tal forma que sea igual al
opuesto de corriente que circula por el neutro de la carga, permitiendo que hacia el sistema no
exista circulación por el neutro. Aquı́, el esquema de generación de referencia es clave, pues para
mantener la ley de corriente de Kirchhoff, la magnitud instantánea de la corriente inyectada por
la cuarta pierna, se resta equitativamente en las corrientes inyectadas por las tres fases restantes.
Ası́, en caso de desbalance de corriente en las fases de la carga, el filtro activo le resta a sus
referencias en cada fase la tercera parte de la corriente por el neutro, y el total de la corriente
por el neutro, es inyectado con signo negativo a través de la cuarta pierna. Luego, aplicando la
ley de corrientes, se obtiene que:
iou + iov + iow + ion =
ion ion ion
+
+
− ion = 0,
3
3
3
(2.11)
donde ion = iLu + iLv + iLw .
2.5.
Generación de la Corriente de Referencia
∗
vdc
i0
+
Controlador
PI
ie
vdc
iα
iL
Filtro
Pasa-Bajo
−
id
Filtro
Pasa-Bajo
αβ/
dq
uvw/
αβ0
iβ
iq
−1
sin (ωt)
vs
SRF
PLL
+
+
+
+
+
i∗d
− −ied
− ieq + iq
i∗q
i0
i∗α
αβ0/
uvw
dq/
αβ
i∗β
io ∗
cos (ωt)
Figura 2.10: Diagrama en bloques del generador de referencia de la corriente basado en transformación dq.
Para obtener las señales de las corrientes de referencia del filtro activo se usa un generador
de referencia de la corriente basado en transformación dq. Este esquema presenta una adecuada
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
32
capacidad de seguimiento. Este esquema evita las fluctuaciones de voltaje que deterioran la
señal de referencia de la corriente y que terminan por afectar el desempeño final del esquema de
compensación [68]. Las señales de referencia de las corrientes se obtienen a partir de las correspondientes corrientes de la carga como lo muestra la Fig. 2.10. Este módulo calcula las señales
de referencia de las corrientes necesarias para que el convertidor compense potencia reactiva,
armónicas de corriente, y desbalance de corriente. El factor de potencia por desplazamiento
(sin φ(L) ) y la distorsión armónica total máxima de la carga (T HD(L) definen las relaciones entre la potencia aparente requerida por el filtro activo, con respecto a la carga, como lo muestra
(2.12).
SAP F
SL
q
sin φ(L) + T HD(L) 2
q
=
1 + T HD(L) 2
(2.12)
donde el valor de T HD(L) incluye la máxima corriente armónica a compensar, definida como
el doble de la frecuencia fs . Es importante considerar que la máxima componente armónica
de corriente que puede ser compensada es igual la mitad de la frecuencia de conmutación del
convertidor.
El esquema dq opera en un marco de referencia rotatorio, entonces, las corrientes medidas
deben ser multiplicadas por las señales sin(wt) y cos(wt). Usando la transformación dq, la
componente d de la corriente se sincroniza con el correspondiente voltaje de fase del sistema
y la componente q de la corriente se invierte 90◦ . Las señales sin(wt) y cos(wt) se obtienen
a partir de un Synchronous Reference Frame (SRF) PLL [69]. El SRF-PLL genera una señal
sinusoidal pura, en fase con la componente de secuencia positiva del voltaje del sistema, aún
cuando este voltaje esté severamente distorsionado. Es importante mencionar que este tipo de
PLLs tienen la capacidad de entregar una señal sinusoidal pura, es decir, libre de distorsión,
siempre y cuando las armónicas presentes en los voltajes del sistema sean menores a 5 % y 3 %
en 5th y 7th respectivamente [70]. La ec. (2.13) muestras la relación entre las corrientes reales
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
33
iLx (t) (x = u, v, w) y las asociadas a las componentes dq, (id y iq ).
i
r
Lu
1
1
2 sin ωt cos ωt 1 − 2 − 2
id
√
=
√ iLv .
3
3
3
− cos ωt sin ωt
0 2 −2
iq
iLw
(2.13)
Un filtro pasa bajo (LPF) extrae la componente dc de las corrientes id para generar las componentes de referencia armónica −ied . Las componentes de referencia reactiva de las corrientes
se obtienen desfasando las correspondientes componentes AC y dc de iq en 180◦ . Para mantener
el voltaje dc constante, se debe modificar la amplitud de la corriente de referencia adicionando
una señal de referencia (ie ) a la componente activa d. Este lazo de control del voltaje dc se
explicará en extenso en el cap. 3.5.1. Las señales resultantes i∗d , y i∗q se transforman de vuelta al
sistema trifásico aplicando las transformadas inversas de Park y Clark, de acuerdo a (2.14). En
este capı́tulo se usa una frecuencia de corte del filtro pasa-bajo de 20 Hz.
∗
iou
√1
2
r
i∗ = 2 √1
ov
3
2
∗
√1
iow
2
1
0 1 0
0
i0
√
0 sin ωt − cos ωt i∗ .
− 12 23
d
√
− 12 − 23
0 cos ωt sin ωt
i∗q
(2.14)
La corriente que circula por el neutro de la carga se compensa inyectando el mismo valor
instantáneo obtenido de las corrientes, desfasado en 180◦ , como lo muestra (2.15).
i∗on = − (iLu + iLv + iLw ) .
(2.15)
Tal como se muestra en la Fig. 2.10, las señales del bloque de generación de referencias dq no
están solamente asociadas a corrientes de referencia que cumplen con los objetivos de compensación de corrientes armónicas y potencia reactiva, sino que también tienen asociada la función
de mantener constante el valor del voltaje dc. Como se verá más adelante, esta caracterı́stica
de las corrientes de referencia beneficia la implementación de un control predictivo libre de factores de peso. En la ausencia de factores de peso, el control predictivo actuará como seguidor
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
34
de corriente, independientemente que se esté controlando el voltaje dc con un controlador PI.
Sin embargo, una desventaja importante al utilizar el esquema dq para generar las corrientes
de referencia es la aparición de componentes armónicas no deseadas de tercer orden (3ra ) en las
corrientes de referencia. En una condición de desbalance en las corrientes de carga en el marco
abc, cuando se aplica la transformación desde abc a dq, se genera una componente armónica de
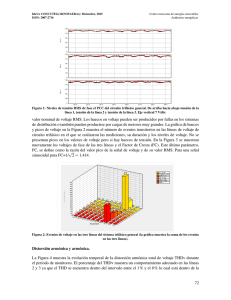
segundo orden en las componentes id e iq . La amplitud de esas armónicas depende del porcentaje de desbalance en la carga (expresado como la relación entre la componente de secuencia
negativa iL,2 y la componente de secuencia positiva iL,1 ). Debido a que el esquema de compensación de armónicas sólo extrae la componente continua en id , las componentes armónicas de
segundo orden que se generan no pueden ser removidas de id e iq . Luego, cuando se transforma
nuevamente al marco abc, se genera una componente armónica de tercer orden en la corriente
de referencia [71]. La Fig. 2.11 muestra el porcentaje de desbalance presente en la corriente
del sistema y el porcentaje de 3ra armónica presente en la corriente del sistema, en función
del porcentaje de desbalance presente en la carga. Entonces, en presencia de un porcentaje de
desbalance de corriente, a pesar de que en corriente de carga no exista 3ra armónica, el filtro
activo, debido a su sistema de generación de referencias, hará que circule un porcentaje de 3ra
armónica hacia el sistema.
4
#-#: % de 3ra armónica en is (
3
is,3th
)
is,1
i
[ %]
2-2: Desb. de corriente sist. ( is,2
)
s,1
2
1
0
0
5
10
15
20
i
25
30
L,2
) [ %]
Desbalance Corriente de carga ( iL,1
Figura 2.11: Relación entre desbalance de corriente de carga permisible, correspondiente contenido armónico de tercer orden, y desbalance de la corriente del sistema (con respecto a la
componente de secuencia positiva de la corriente del sistema, is,1 ).
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
2.5.1.
35
Control voltaje dc
El lazo de control del voltaje dc no requiere de la utilización de un algoritmo predictivo. En
este caso, se selecciona un controlador PI. Se diseñará el PI, para que su salida sea proporcional
a la potencia ac a frecuencia fundamental absorbida por el convertidor. Adicionalmente, se
considera que la respuesta rápida impuesta por la dinámica del inductor de salida no afecta
la respuesta lenta impuesta por la dinámica del condensador dc. De esta forma, las corrientes
de referencia que ingresan a la evaluación de la función de costo del bloque predictivo, tendrán
incorporada una componente fundamental, encargada de mantener constante el valor del voltaje
dc. Este es un importante punto en la evaluación, dado que la función de costo (2.10) se obtiene
usando sólo las corrientes de referencia. Esto permite evadir el uso de factores de peso en la
función de costo. Generalmente, los factores de peso se obtienen en forma experimental, y no
son bien definidos cuando se requieren diferentes condiciones de operación. Por esta razón, el
controlador PI representa una simple y efectiva alternativa para el control del voltaje dc.
√
El voltaje dc se mantiene constante (con un mı́nimo valor de 6 vs(rms) ) hasta que la potencia
activa absorbida por el convertidor, decrece a un nivel donde no es posible compensar sus
pérdidas. La potencia activa absorbida por el convertidor se controla ajustando la amplitud de
la señal de control (ie ), la cual está en fase con cada voltaje de fase. En el diagrama en bloques
se muestra en la Fig. 2.10, el voltaje dc se mide y luego se compara con un valor de referencia
constante (vdc ∗ ). El error (e) se procesa por el controlador PI, con dos ganancias, Kp y Ti .
Ambas ganancias se calculan de acuerdo a la respuesta dinámica requerida.
∗
vdc
e
+ −
C (s)
ie
G (s)
vdc
Figura 2.12: Diagrama en bloques del control de voltaje dc
La Fig. 2.12 muestra que la salida del controlador PI se ingresa a la función de transferencia
del voltaje dc G (s).
Para encontrar la función de transferencia G (s) se realiza un balance de potencias, igualando
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
36
la potencia del lado ac con la del lado dc en el convertidor. Como la corriente de control del
enlace dc se genera de manera que esté en fase con el voltaje ac, para que la transferencia de
potencia se produzca con factor de potencia unitario, podemos escribir la potencia activa a
frecuencia fundamental, Pac(f ) , que se transfiere entre el inversor y la red, vsx(f ) , como:
3
Pac(f ) = vsu(f ) iou(f ) + vsv(f ) iov(f ) + vsw(f ) iow(f ) = vs io(f ) .
2
(2.16)
Como se puede apreciar en la Fig. 2.10, la señal de compensación de voltaje del condensador,
ie , que sale del controlador PI pasa a través de las transformadas Clarke y Park inversas. Es
por esto que se debe determinar cómo se ve afectada dicha señal hasta llegar a la corriente de
referencia del convertidor. Para esto se considera nulo el efecto de id , iq e i0 , de modo que se
pueda observar el efecto producido por ie .
∗
iou
√1
2
r
i∗ = 2 √1
ov
3
2
√1
i∗ow
2
1
0 1 0
0
0
√
− 12 23
0 sin ωt − cos ωt ie .
√
3
1
−2 − 2
0 cos ωt sin ωt
0
(2.17)
Multiplicando y utilizando relaciones trigonométricas fundamentales obtenemos que:
sin (ωt)
r
2
i∗ =
sin ωt − 2 π
i
e
ov
3
3
2
∗
iow
sin ωt + 3 π
∗
iou
(2.18)
Se ha determinado que cada referencia de corriente fundamental se ve amplificada por la
q
ganancia del sistema de generación de referencias (Ke = 23 ). De esta forma la ecuación (2.16)
relaciona la potencia ac del convertidor, con la señal de compensación ie :
3
Pac(f ) = vs (t)Ke ie (t).
2
(2.19)
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
37
Luego, se debe encontrar una relación entre la señal de compensación ie y el voltaje dc vdc .
Para esto, se utiliza la ecuación de potencia del capacitor del enlace dc:
Pdc = Cdc vdc (t)
dvdc (t)
dt
(2.20)
Y por balance de potencia tenemos que:
3
dvdc (t)
vs Ke ie (t) = Cdc vdc (t)
2
dt
(2.21)
Para obtener la función de transferencia en el dominio de Laplace, se debe linealizar el sistema
en torno a un punto de operación para vdc (t) y ie (t). Luego, aplicando pequeñas perturbaciones
en torno a dicho punto de operación:
3
d(vdc0 + ∆vdc )
vs Ke (ie0 + ∆ie ) = Cdc (vdc0 + ∆vdc )
2
dt
(2.22)
Evaluando (2.21) en el punto de operación vdc (t) = vdc0 e ie (t) = ie0 :
3
dvdc0
vs Ke ie0 = Cdc vdc0
2
dt
Restando (2.23) y (2.22), y despejando
(2.23)
d∆vdc
:
dt
∆vdc dvdtdc0
d∆vdc
3
vs
=
∆ie −
.
dt
2 C (vdc0 + ∆vdc )
(vdc0 + ∆vdc )
Como vdc0 >> ∆vdc y vdc0 es constante en el punto de operación, es decir,
(2.24)
dvdc0
dt
= 0 , (2.24)
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
38
se reduce a:
d∆vdc
3 vs
=
∆ie
dt
2 C (vdc0 )
(2.25)
Ası́, la función de transferencia que representa la relación entre ∆vdc e ∆ie , queda representa
por el sistema de primer orden (2.26):
G (s) =
donde Ke =
q
2
3
3 1 Ke vs
∆vdc
=
,
∗
∆ie
2 s Cdc vdc
(2.26)
∗
y vdc
= vdc0 .
La función de transferencia en lazo cerrado equivalente del sistema con controlador PI (2.27)
se muestra en (2.28):
C(s) = Kp
1
1+
Ti · s
,
(2.27)
ωn
· (s + a)
vdc
= 2 a
.
ie
s + 2ζωn · s + ωn2
(2.28)
2
Debido a que el tiempo de respuesta del lazo de control del voltaje dc debe ser más lento
que el de corriente, un factor de amortiguamiento ζ = 1 y una frecuencia angular ωn = 2π · 100
rad/s, se usan para obtener una respuesta crı́ticamente amortiguada con un mı́nimo de oscilación
de voltaje. El correspondiente tiempo integral Ti = 1/a (2.28) y la ganancia proporcional Kp
pueden ser derivadas a partir de la ec. (2.29) y (2.30).
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
ζ=
s
ωn =
2.6.
8 Kp Ke vs Ti
,
∗
3 Cdc vdc
s
39
(2.29)
3 Kp Ke vs
.
∗
2 Cdc vdc
Ti
(2.30)
Resultados de Simulación
Se desarrolló un modelo de simulación del convertidor trifásico de cuatro piernas usando
MATLAB-Simulink y los parámetros que se indican en la Tabla 2.1. El objetivo es verificar la
efectividad de la compensación de corrientes armónicas bajo diferentes condiciones de operación.
Una carga puente rectificador trifásico de 6 pulsos se usó como carga no-lineal. El algoritmo
predictivo propuesto se programó usando un bloque de S-function que permite la simulación
del modelo discreto, el cual puede se puede implementar posteriormente de manera rápida
en una plataforma de control digital dSPACE DS1103 R&D. Las simulaciones se realizaron
considerando un tiempo de muestreo de 20 [µs].
Tabla 2.1: Especificación de Parámetros
a
Variable
Descripción
Valor
vs
f
vdc
Cdc
Lf
Rf
Ts
Te
Voltaje Fuente
Frecuencia sist.
Voltaje dc
Condensador dc
Inductor del Filtro
Resistencia interna de Lf
Tiempo de Muestreo
Tiempo de Cálculo
55 [V ]
50 [Hz]
162 [V ]
2200 [µF ] (2.0 pu)
5,0 [mH] (0.5 pu)
0,6 [Ω]
20 [µs]
16 [µs]
a
Note: Vbase = 55 V y Sbase = 1 kVA.
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
40
100
(a)
vsu
0
−100
5
(b)
iLu
0
−5
5
(c)
iou
0
−5
5
(d)
iLn
0
−5
5
(e)
isn
0
−5
5
(f) 0
is
−5
(g)
170
vdc
160
150
t1
t2
t3
t4
(50ms/div)
Figura 2.13: Resultados de simulación. (a) Voltaje de fase del sistema. (b) Corriente de carga.
(c) Corriente de salida del filtro activo. (d)Corriente del neutro de la carga (e) Corriente del
neutro del sistema. (f) Corrientes del sistema. (g) Voltaje dc del convertidor.
En los resultados de simulación se muestran en la Fig. 2.13, el filtro activo comienza a
compensar al tiempo t = t1 . En ese tiempo, el filtro activo inyecta una corriente de salida iou
para compensar componentes armónicas de corriente, desbalance de corriente, y corriente por el
neutro simultáneamente. Durante la compensación, las corrientes del sistema (is ) muestran una
forma sinusoidal, con una baja distorsión armónica total (T HD = 3,93 %). En t = t2 , se genera
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
41
un impacto de carga balanceado desde 0.6 a 1.0 p.u. Las corrientes del sistema permanecen
sinusoidales a pesar del cambio brusco en la amplitud de la corriente de carga. Finalmente, en
t = t3 , se introduce un cambio escalón en la fase u desde 1.0 a 1.3 p.u., el cual es equivalente
a un 11 % de desbalance de corriente. De acuerdo a lo esperado en el lado de la carga, existe
circulación de corriente por el neutro (iLn ), pero en el lado del sistema, no existe circulación de
corriente por el neutro (isn ). Los resultados de simulación muestran que el control propuesto
efectivamente elimina desbalance de corriente. Adicionalmente, la Fig. 2.13 muestra que el
voltaje dc permanece estable a través de todas las condiciones de operación del filtro activo.
2.7.
Resultados Experimentales
Se corrobora la efectividad de la compensación en un prototipo experimental de 2kVA.
Una carga puente rectificador trifásico se seleccionó como carga no-lineal con el objetivo de
verificar la efectividad del método de compensación para corrientes armónicas. Se aplicó un
escalón de carga para evaluar el desempeño del lazo de control del voltaje dc en términos de su
respuesta transitoria. Finalmente, se usó una carga desbalanceada para validar el desempeño de
la compensación de la corriente del neutro.
Debido a que la implementación experimental se desarrolló en una dSPACE I/O board,
todos los bloques de SIMULINK que se usaron en la simulación son 100 % compatibles con las
capacidades de la dSPACE. El lazo de control completo se ejecuta por el controlador cada 20
[µs], mientras que el siguiente estado de conmutación está disponible a los 16 [µs]. Se obtuvo
una frecuencia de conmutación de 4.64 kHz. La Fig. 2.14 muestra la respuesta transiente del
esquema de compensación. La Fig. 2.14a muestra que la corriente se hace sinusoidal cuando
el filtro activo empieza a operar, y el voltaje dc permanece constante en el valor seteado. Los
resultados experimentales mostrados en Fig. 2.14b indican que la distorsión armónica total de
la corriente del sistema (T HDi ) se reduce desde 27.09 % a 4.54 %. Esta es una consecuencia
de la buena caracterı́stica de seguimiento que presentan las corrientes de salida del convertidor
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
42
para sus respectivas corrientes de referencia, como lo muestra la Fig. 2.14d. En la Fig. 2.15 se
muestra la respuesta transiente para un impacto de carga. Las corrientes del sistema permanecen
sinusoidales y el voltaje dc retorna a su referencia describiendo una respuesta tı́pica de un
sistema de segundo orden sub-amortiguado (sobrepaso máximo de 5 % y 2 ciclos de tiempo de
asentamiento). En ese caso, se aplicó un impacto de carga desde 0.6 a 1.0 p.u. Finalmente, la
carga conectada a la fase u se incrementó bruscamente desde 1.0 a 1.3 p.u. Las correspondientes
formas de onda se muestran en Fig. 2.16. La Fig. 2.16a muestra cómo el filtro activo es capaz de
compensar la corriente del neutro presentando una rápida respuesta dinámica. Más aún, la Fig.
2.16b muestra que la corriente por el neutro del sistema ion se compensa y elimina efectivamente,
mientras que las corrientes del sistema permanecen balanceadas aún cuando se aplica un 11 %
de desbalance de carga.
2.8.
Conclusión
Se ha propuesto un esquema de compensación diseñado para mejorar la calidad de la corriente
de un sistema de distribución usando un filtro activo de cuatro piernas y dos niveles. Las ventajas
del sistema propuesto están relacionadas con su simplicidad, modelamiento e implementación.
El uso de un algoritmo de control predictivo para el lazo de corriente del convertidor ha probado
ser una efectiva solución para aplicaciones de filtros activos de potencia. Se ha demostrado que se
mejoran la capacidad de seguimiento de corriente y el tiempo de respuesta transiente. Resultados
de simulación y experimentales prueban que el algoritmo predictivo es una buena alternativa
a métodos clásicos de control lineal. Dada la robustez y estabilidad obtenida para el control
predictivo, se concluye que realizando modificaciones menores en el control implementado para
esta topologı́a de dos niveles, se puede implementar un control para una topologı́a de n-niveles,
tal y como se muestra en el siguiente capı́tulo.
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
43
iLu
30
iou
i Lu
i su
25
% of h1
isu
20
15
10
vdc
5
0
10
20
30
Harmonic Order h
(a)
40
50
(b)
vsu
isu
iou
i∗ou
isv
vsu
isw
isu
(d)
(c)
Figura 2.14: Resultados experimentales para transiente después de la conexión del PAF. (a)
Corriente de carga, iLu , corriente del filtro activo, iou , voltaje dc del convertidor, vdc , y corriente
del sistema isu . Espectro en frecuencia. (c) Voltaje y corriente del sistema, vsu y isu , isv , isw .
(d) Señales de referencia de corriente, i∗ou , y corriente del filtro activo, iou (caracterı́stica del
seguimiento).
iLu
iou
isu
vdc
Figura 2.15: Resultados experimentales para impacto de carga (0.6 a 1.0 p.u.). Corriente de
carga, iLu , corriente del filtro activo, iou , corriente del sistema, isu , y voltaje dc del convertidor,
vdc .
CAPÍTULO 2. FAP USANDO UN CONVERTIDOR DE 4 PIERNAS Y 2 NIVELES
iLu
44
isu
isv
iLn
isw
ion
isn
isn
(a)
(b)
Figura 2.16: Resultados experimentales para impacto de desbalance en la fase u de la carga (1.0
a 1.3 p.u.).(a) Corriente de carga, iLu , Corriente del neutro de carga, iLn , corriente del neutro
del filtro activo, ion , y corriente del neutro del sistema isn . (b) corrientes del sistema, isu , isv ,
isw , y isn .
Capı́tulo 3
Filtro Activo Paralelo NPC
3.1.
Nomenclatura
NPC
Neutral Point Clamped
AC
Corriente alterna
dc
Corriente continua
PWM
Modulación por ancho de pulso
PC
Control Predictivo
PLL
Phase-locked-loop
NPC
Neutral Point Clamped
vs
Vector de voltaje del sistema [vsu vsv vsw ]T
is
Vector de la corriente del sistema [isu isv isw ]T
iL
Vector de la corriente de carga [iLu iLv iLw ]T
vfx
Vector de voltaje de salida del VSI [vf u vf v vf w ]T
io
Vector de la corriente de salida del VSI [iou iov iow ]T
i∗o
Vector de la corriente de referencia [i∗ou i∗ov i∗ow ]T
Lf
Inductancia del filtro
Rf
Resistencia del filtro
45
CAPÍTULO 3. FILTRO ACTIVO PARALELO
VP N
voltaje en del enlace dc
VC1
voltaje en condensador superior del enlace dc
VC2
voltaje en condensador superior del enlace dc
vdc
Voltaje dc
3.2.
46
Introducción
Como alternativa a usar generadores de gran escala, las redes de distribución actuales tratan
de expandir su capacidad de generación integrando pequeñas fuentes de energı́a que provengan
principalmente de fuentes como el sol y el viento. Existe una necesidad de redes de distribución
que puedan transmitir efectivamente la potencia extraı́da desde estas fuentes de generación.
Una limitación principal de la transmisión usando este tipo de fuentes de energı́a es la debilidad
del sistema. El sistema completo debe responder con estabilidad ante problemas de calidad de
suministro como impactos de carga, corrientes desbalanceadas y consumo de potencia reactiva.
Sin embargo, la poca robustez produce perturbaciones en el punto de común acoplamiento
(PCC).
Soluciones de electrónica de potencia, tales como convertidores multinivel y filtros activos de
potencia, son capaces de integrar este tipo de fuentes de energı́a con un impacto mı́nimo en la
calidad de la energı́a. La introducción de convertidores multinivel al mercado crea un interesante
nicho para tecnologı́as de compensación activa en sistemas de alta tensión. Mientras soluciones
en electrónica de potencia, como por ejemplo FACTS, se han propuesto y presentado como una
buena alternativa para entregar la potencia reactiva en adelanto o en atraso a sistemas de baja
tensión, su aplicación en sistemas de media tensión no ha sido popular. Sin embargo, el rápido
desarrollo experimentado en el diseño y construcción de convertidores PWM de media tensión,
especialmente para aplicaciones de accionamiento de motores, ayudará a superar la falta de
confianza asociada a la operación de filtros activos de potencia más sofisticados y precisos.
Convertidores PWM para media tensión se han utilizado en aplicaciones industriales de ac-
CAPÍTULO 3. FILTRO ACTIVO PARALELO
47
cionamientos variables en motores desde los 90’s. Convertidores de diferentes topologı́as, tales
como NPC, fly-back, módulos de potencia monofásicos, ya han demostrado que son tecnologı́a
que es muy confiable y rentable para aplicaciones industriales [72–77]. Esas mismas topologı́as,
pero con un adecuado sistema de control pueden ser también usadas para implementación de
filtros activos de potencia [78]. El esquema propuesto en el Capı́tulo 2 es un buen ejemplo de
cómo operar con efectividad y robustez un filtro activo de potencia, aplicando una técnica de
control predictiva modificada. El filtro activo propuesto en este capı́tulo está dirigido a aplicaciones de compensación de potencia reactiva y armónicas corriente en sistemas de distribución
en media tensión. El uso de convertidores monofásicos beneficia el control independiente por
fase y aumenta la flexibilidad, permitiendo que puedan conectarse más de estos convertidores
en cascada, para ası́ alcanzar mayores niveles de tensión. Cada convertidor genera un voltaje
entre lı́neas de cinco niveles, reduciendo la generación de armónicas de baja frecuencia, en comparación a los convertidores trifásicos de 2 niveles convencionales. Además, esta caracterı́stica
monofásica permite operar con control independiente, beneficiando la compensación de corrientes desbalanceadas.
Este capı́tulo presenta el modelo matemático del convertidor NPC y el principio de operación
del control predictivo propuesto para la estrategia multinivel. Además, presenta el generador de
la referencia de corriente utilizado para la estrategia monofásica. Finalmente, el desempeño del
filtro activo y la efectividad del esquema de control se demuestran a través de simulaciones y
validados con resultados experimentales en un setup de laboratorio de 2kVA.
3.3.
Modelo del Convertidor NPC
La Fig. 3.1 muestra la conexión de un filtro activo propuesto conectado en un sistema de
distribución con apoyo de energı́as renovables no convencionales (ERNC). El consumo eléctrico
del sistema es aleatorio e impredecible, por lo tanto, puede ser monofásico o trifásico, balanceado
o desbalanceado, y lineal o no-lineal. Un filtro activo se conecta en paralelo en el punto de común
48
CAPÍTULO 3. FILTRO ACTIVO PARALELO
acoplamiento (PCC) para compensar corrientes armónicas, desbalance de corriente y potencia
reactiva. La Fig. 3.2 muestra el diagrama equivalente trifásico del filtro activo propuesto. Este
diagrama considera la impedancia equivalente del sistema Zs , la impedancia del filtro de salida
Zf y la impedancia de la carga ZL . En particular, este filtro activo está compuesto de un
condensador dc, tres convertidores NPC monofásicos, y un filtro de salida de primer orden.
Cada convertidor NPC monofásico tiene dos piernas de 4 IGBT, como lo muestra la Fig. 3.3.
Además de ser controlados en forma independiente, la ventaja de utilizar una topologı́a
monofásica es permitir la conexión de más unidades en cascada, lo que permite la operación
del filtro en sistemas de mayor voltaje, como se muestra en lı́nea punteada de la Fig. 3.1. Con
respecto a la calidad del voltaje, el voltaje del convertidor del filtro activo está compuesto de
cinco niveles (ver Fig. 3.4), lo que reduce el estrés de los semiconductores y la diferencia de
tensión instantánea en los terminales del filtro de salida. Cada voltaje de salida vf x (x = u, v,
w) se puede generar usando las 16 secuencias de estado que pueden generarse a partir de los
estados individuales de los 4 semiconductores disponibles (Sx ). Cada uno de estos estados es
representado como un 1, encendido, y un 0, apagado. Sin embargo, de los 16 estados permitidos
se seleccionaron 9 (ver Tabla 3.1). Se seleccionaron aquellos estados permitidos que limitan a
una transición encendido-apagado (0 − 1) de los semiconductores entre niveles consecutivos, y
dos, tres y cuatro transiciones en el caso de saltar entre niveles no consecutivos. Como ejemplo,
la Fig. 3.5 muestra algunas de las trayectorias permitidas en función del número de transiciones
asociadas a los semiconductores (S1 , S2 , S3 , S4 ).
El voltaje de salida vf x de cada convertidor monofásico, medido desde el punto (n), puede
expresarse en términos de los estados de conmutación como:
vf x = vC1 (S1 − S3 ) + vC2 (S2 − S4 ) ,
x = u, v, w,
(3.1)
donde la suma de cada capacitor es equivalente al voltaje entre los puntos P y N, definido
49
CAPÍTULO 3. FILTRO ACTIVO PARALELO
Fuente
Energı́a
Renovable
vs
Ls Rs
Transf.
de Baja
Filtro
Activo
is
Zs
Cargas
iL
io
Transf.
de Alta
Rf
Lf
+
vf 1
−
Zf
NPC
monofásico
ver Fig. 3.3
1
ZL
Conexión Serie
de m-unidades
+
vf m
−
m
Figura 3.1: Diagrama de conexión del filtro activo paralelo propuesto en un sistema eléctrico
con apoyo de ERNC.
vs
Zs
is
iL
PCC
ZL
Ls
Sistema
io
Cargas
Lf
Rf
Zf
NPC
monofásico
ver Fig. 3.3
Filtro Activo
Paralelo
Figura 3.2: Diagrama equivalente trifásico del filtro activo propuesto.
NPC monofásico
P
+
vC1
−
S1
S3
S2
S4
C1
Zf
Rf Lf
iox
x
+vf x − n
+
vC2
−
N
S1
S3
S2
S4
C2
u
v
w
Figura 3.3: Diagrama circuital del convertidor NPC monofásico (vC1 = vC2 = vdc ).
50
CAPÍTULO 3. FILTRO ACTIVO PARALELO
2vdc
[V]
vdc
0
vf x
−vdc
−2vdc
(5ms/div)
Figura 3.4: Forma de onda del voltaje de cinco niveles en la salida del convertidor NPC monofásico.
Tabla 3.1: Estados permitidos seleccionados para el NPC monofásico
S1
1
1
1
0
0
0
0
0
0
S2
1
1
1
1
1
1
0
0
0
S3
1
0
0
1
0
0
1
0
0
S4
1
1
0
1
1
0
1
1
0
1
1
1101
vf x
0
vC1 = vdc
vC1 + vC2 = 2vdc
−vC1 = −vdc
0
vC2 = vdc
−vC1 − vC2 = −2vdc
−vC2 = −vdc
0
1100
1
0100
4
3
1111
0101
0111
2
0000
0001
0011
Figura 3.5: Ejemplo de trayectorias permitidas en función del número de cambios de estado de
los semiconductores del convertidor NPC.
como:
vP N = vC1 + vC2 = 2vdc
(3.2)
51
CAPÍTULO 3. FILTRO ACTIVO PARALELO
NPC monofásico
P
+
vC1
−
S1
S3
S2
S4
C1
io
Req Leq
+
− vs
x
+ vf x − n
+
vC2
−
S1
S3
S2
S4
C2
N
Figura 3.6: Diagrama Circuital para el modelo matemático.
De la misma forma como se determinó el modelo matemático generalizado utilizado para
modelar el filtro activo de cuatro piernas, es decir, a partir de la impedancia equivalente de
Thevenin vista por el convertidor, se obtiene un modelo para la topologı́a NPC monofásica
propuesta. Las consideraciones para este modelo son: Req y Leq son los parámetros del modelo
del convertidor para Req = Rf y Leq = Ls + Lf , cuando no existe cable neutro (Zf n = 0),
dado que la conexión del filtro es en delta. Se asume, al igual que en el capı́tulo anterior, que
ZL >> Zs , que la parte resistiva de la impedancia del sistema es despreciable, y que la reactancia
serie del sistema está en el rango de un 3-7 % p.u. Ası́, el modelo matemático del filtro activo,
derivado del diagrama equivalente mostrado en la Fig. 3.6 , es:
vs = vf x − Req io − Leq
3.4.
d io
,
dt
(3.3)
Control Predictivo
El diagrama en bloques del esquema de control predictivo propuesto se muestra en la Fig.
3.7. Se demostrará que este esquema de control propuesto podrá ser aplicado a la topologı́a NPC
monofásica al igual que fue aplicado a la topologı́a de cuatro piernas, con la única diferencia,
que los estados del convertidor no son los mismos. Para implementarlo en una topologı́a NPC
52
CAPÍTULO 3. FILTRO ACTIVO PARALELO
monofásica se deben considerar los siguiente tres bloques principales, como lo muestra la Fig.
3.7.
vs
v
3
vPN
∗
u
u
3
iL
w
Gener.
Ref.
dq
v
w
u
Opt.
Func.
Costo
g k+1
io ∗
w
v
io
3
Sx
NPC
monofásico
3
io k+1
3
vPN
u
v
w
Modelo
Predictivo
Figura 3.7: Diagrama en bloques del esquema de control predictivo propuesto.
Generador de la corriente de referencia
Esta unidad es diseñada para generar la referencia de corriente que se usa para compensar
componentes armónicas de corriente. En este caso, cada fase trabaja en forma independiente,
por lo tanto, se propondrá un esquema de generación de referencias monofásico. Los voltajes
del sistema, las corrientes de carga y el voltaje dc del convertidor se miden.
Modelo Predictivo
Los 9 posibles valores de la corriente que generará el control predictivo se pueden obtener
de (3.1) y (3.3):
io [k + 1] =
Ts Req Ts vf x [k] − vs [k] + 1 −
io [k].
Leq
Leq
(3.4)
Como se muestra en (3.4), para predecir la corriente de salida io en el instante (k + 1), se
requieren tanto el valor del voltaje vs como el voltaje de salida vf x . El algoritmo calcula los 9
valores de io [k + 1], asociados a las combinaciones que pueden tomar las variables de estado.
53
CAPÍTULO 3. FILTRO ACTIVO PARALELO
Optimización de la función de costo
Para seleccionar el estado de conmutación óptimo que debe ser aplicado a cada convertidor
monofásico, se obtienen los 9 valores de la predicción io [k + 1], y luego son comparados con la
referencia usando una función de costo g, definida como:
g[k + 1] = (i∗ox [k + 1] − iox [k + 1])2
(3.5)
La corriente de salida (io ) es igual a su referencia (i∗o ) cuando g = 0. Entonces, el objetivo
de la optimización es alcanzar un valor de g cercano a cero. Se elige el vector de voltaje vf x que
minimice la función de costo y luego se aplica en el siguiente tiempo de muestreo.
3.5.
Generación de la Referencia de Corriente
vP∗ N
+
PI
vP N
2 sin (ωt)
iLx
×
×
2 cos (ωt)
sin (ωt)
iex
Filtro
Pasa-Bajo
Filtro
Pasa-Bajo
+
+
+
īd
īq
i∗d
×
i∗q
Control P. React
on/off
×
+ iox ∗
+
+
−
×
cos (ωt)
Figura 3.8: Diagrama en bloques del Generador de Referencia de Corriente basado en la transformada dq.
Cada señal de referencia de corriente (i∗ox ) se obtiene a partir de la corriente de carga usando
un esquema basado en la transformada dq monofásica, como se muestra en la Fig. 3.8. Este
bloque calcula la potencia activa requerida por el convertidor y entrega la referencia de co-
CAPÍTULO 3. FILTRO ACTIVO PARALELO
54
rriente a cada controlador predictivo de corriente. Este esquema de generación opera en ejes de
referencia sincrónicos rotatorios debido a la multiplicación de las señales medidas por sin(wt)
y cos(wt), donde la componente d está sincronizada con el voltaje fase neutro del sistema y la
componente q está desfasada en 90◦ . Las señales de sincronismo se obtienen desde un PLL del
tipo a Synchronous Reference Frame.
La ecuación (3.6) muestra la relación entre la corriente en ejes estacionarios iLx (t) y sus
componentes dq, (id e iq ), mientras que la ecuación (3.7) muestra la transformación desde ejes
estacionarios a ejes rotatorios.
iLx (t) = |iLx | sin (ωt + φ) = id sin (ωt + φ) +
(3.6)
iq cos (ωt + φ)
id
sin (ωt)
= 2
iLx (t)
iq
cos (ωt)
(3.7)
id |id | (1 − cos (2ωt)) cos (φ)
=
iq
|iq | (1 + cos (2ωt)) sin (φ)
(3.8)
Reemplazando (3.6) en (3.7), puede encontrarse la expresión matemática equivalente (3.8):
Para eliminar las componentes de frecuencia mayor a la fundamental de id e iq , se usa un filtro
pasa-bajo (LPF), con frecuencia de corte en 20 Hz. La expresión resultante (3.9) corresponde
a las componentes fundamentales dq de las señales de corriente. Para mantener controlado el
voltaje dc se debe modificar la amplitud de la señal de referencia de cada convertidor. Esto se
hace agregando una referencia (iex ) a la componente activa d, como se explicará en detalle en
la sección 3.5.1. Las expresiones resultantes i∗d e i∗q corresponden a las componentes dq de cada
señal de referencia de corriente. La misma transformación monofásica usada en (3.6) se aplica
para reconstruir la señal de referencia en ejes estacionarios, a partir de sus componentes dq,
55
CAPÍTULO 3. FILTRO ACTIVO PARALELO
como se muestra en (3.10).
3.5.1.
īd |id | cos (φ)
=
īq
|iq | sin (φ)
(3.9)
i∗ox = i∗d sin (ωt + φ) + i∗q cos (ωt + φ)
(3.10)
Control del voltaje dc
Como se explicó anteriormente, el control predictivo se enfoca sólo en realizar el control de
corriente, mientras que el voltaje dc se controla paralelamente en un lazo de control PI. De esta
forma, la función de costo del control predictivo queda libre de factores de peso, es decir, cada
corriente tendrá un factor de ponderación igual con las otras.
El voltaje dc permanece constante (con un valor mı́nimo de
√
2vs ) hasta que la potencia
activa absorbida por cada convertidor decrece hasta un nivel donde no se pueden compensar sus
pérdidas. La potencia activa absorbida por cada convertidor se controla ajustando la amplitud
de la señal de referencia de potencia activa (iex ), la cual está en fase con el voltaje de fase.
En el diagrama de bloques de la Fig. 3.8 se muestra que el voltaje dc vP N de cada módulo
se mide y luego se compara con una referencia constante vP∗ N . El error (ex ) se procesa en un
controlador PI, con dos ganancias, Kp y Ti . Ambas ganancias son calculadas de acuerdo a la
respuesta dinámica requerida.
vP∗ N
ex
+ −
C (s)
iex
G (s)
vP N
Figura 3.9: Diagrama en bloques del control del voltaje dc.
Al igual que el capı́tulo anterior, la función de transferencia entre vP N e iex se obtiene
con el método de balance de potencias, pero considerando que la potencia en cada módulo es
monofásica, y no ve afectada por la ganancia de la generación de referencias. A pesar de ser un
56
CAPÍTULO 3. FILTRO ACTIVO PARALELO
sistema que requiere un análisis por fase, se aproxima la potencia monofásica a un tercio de la
potencia total. En este caso, la potencia en el lado ac para cada fase es:
Pac(f )1φ =
1
(vs Ke ie ) .
2
(3.11)
De esta forma, la salida del controlador PI está relacionada con la entrada a la función de
transferencia G (s), la cual se representa por un sistema de primer orden (3.12):
G (s) =
vP N
1 1 Ke vs
=
ie
2 s Cdc vP∗ N
(3.12)
donde Ke = 1.
El equivalente de la función de transferencia en lazo cerrado del sistema junto al controlador
PI (3.13) se muestra en (3.14):
C(s) = Kp
1
1+
Ti · s
,
(3.13)
2
ωn
· (s + a)
vP N
= 2 a
.
ie
s + 2ζωn · s + ωn2
(3.14)
Para obtener una respuesta crı́ticamente amortiguada, con oscilación de voltaje mı́nima, se
usa un amortiguamiento ζ = 1 y una velocidad angular de ωn = 2π · 100 rad/s. Con esos valores
se asegura que respuesta en el tiempo del lazo de control del voltaje dc sea más lenta que la
de corriente. El correspondiente tiempo integral Ti = 1/a (3.14) y ganancia proporcional Kp
pueden calcularse usando (3.15) y (3.16):
CAPÍTULO 3. FILTRO ACTIVO PARALELO
3.6.
ζ=
s
ωn =
s
57
Kp Ke vs Ti
,
Cdc vP∗ N
(3.15)
1 Kp Ke vs
.
2 Cdc vP∗ N Ti
(3.16)
8
Diseño del circuito de potencia
Los principales componentes de la topologı́a de filtro activo son el reactor de enlace y los
condensadores dc. El reactor de enlace debe permitir el di/dt en la corriente de salida de cada
convertidor. Este di/dt se impone por la referencia de corriente que genera el control predictivo.
Ası́ también, el reactor de enlace debe atenuar las componentes de alta frecuencia generadas
por la conmutación de los semiconductores. Los condensadores dc deben permitir almacenar la
potencia activa requerida para mantener el voltaje dc constante ante condiciones de operación
transientes.
3.6.1.
Diseño del reactor de enlace
El criterio de diseño que se utiliza para calcular el valor de la inductancia del reactor de
enlace está basado en la pendiente δ de la corriente de salida de cada convertidor obtenida usando
(3.17). La amplitud de la pendiente está basada en el máximo error de corriente que se permite
entre la corriente de salida y su referencia en cada periodo de la frecuencia de conmutación fs :
∆if
2δ
=
∆T
1/2fs
La caı́da de voltaje a través del reactor de enlace es igual a:
(3.17)
58
CAPÍTULO 3. FILTRO ACTIVO PARALELO
Lf
∆if
= vf − vP CC
∆T
(3.18)
Reemplazando (3.17) en (3.18), el valor del reactor Lf puede obtenerse como:
Lf =
vf − vP CC
,
4δfs
(3.19)
donde vf y vP CC son los valores máximos instantáneos del voltaje de salida del convertidor y el
voltaje en el P CC, respectivamente.
3.6.2.
Diseño de los condensadores dc
El valor del condensador dc se obtiene usando (3.20). Con ese valor, cada condensador
dc puede almacenar suficiente energı́a para alimentar la potencia instantánea requerida por el
sistema durante medio ciclo, sin modificar el valor del voltaje dc en más de un 5 %.
Cdc ≥
T
vs máx iL
∗
4 (vP N 2 − vP2 N
mı́n )
,
(3.20)
donde vs máx es el valor peak del voltaje de fase del sistema, iL es el valor rms de la corriente
de carga, T es el periodo ac del sistema, vP∗ N es el valor de la referencia de voltaje dc y vP N
mı́n
es el valor mı́nimo de voltaje permitido en el lado dc.
3.7.
Resultados de Simulación y Experimentales
Con el objetivo de verificar la efectividad de compensación y viabilidad técnica de la implementación de la topologı́a propuesta, esta sección presenta los resultados de simulación y
CAPÍTULO 3. FILTRO ACTIVO PARALELO
59
experimentales para el filtro activo NPC monofásico. Dada la caracterı́stica monofásica de la
estrategia propuesta, la parte experimental sólo consideró la intervención de una de las fases
del sistema. Para asegurar que los resultados simulados y experimentales coinciden, se presentan distintas condiciones de operación para compensación de reactivos y corrientes armónicas.
Finalmente, se verifican las caracterı́sticas de compensación del método predictivo propuesto a
través de un set de resultados evaluados para la condición de desconocimiento de parámetros
de impedancia de carga y sistema.
3.7.1.
Resultados de Simulación
Los resultados de simulación se desarrollaron usando MATLAB-Simulink. El algoritmo de
control predictivo se programó en un bloque de funciones S-function, el cual permite simular el
modelo discreto para luego ser fácilmente implementado en una plataforma de control digital. En
las simulaciones se usó un tiempo de muestreo de 20 [µs]. El filtro activo propuesto se probó con
una carga no-lineal de 0.5 MVA y 4.16 kV. Los parámetros del filtro activo son: vP N =6100 V,
Cdc = 2200 µF, Rf = 0.02 Ω, Lf = 28 mH y fs = 6.35 kHz. Todos los voltajes y corrientes de las
figuras están en sistema por unidad (p.u.). En los resultados de simulación que se muestran en la
Fig. 3.10, el filtro activo comienza a compensar en t = t1 . En ese tiempo, el filtro activo inyecta
una corriente de salida io para compensar componentes de corrientes armónicas. Durante la
compensación, las corrientes del sistema (is ) muestran formas de onda sinusoidal, con una baja
distorsión armónica total (THD = 3.69 %). En t = t2 , se genera un impacto de carga trifásica
balanceada desde 1.0 a 1.3 p.u. Las corrientes del sistema se mantienen sinusoidales, a pesar
del cambio en la magnitud de la corriente. En t = t3 , se conecta un motor trifásico, el cual
introduce un factor de potencia por desplazamiento en atraso de 0,86. Finalmente, en t = t4 , se
enciende la señal de control de potencia reactiva del filtro activo. Los resultados de simulación
muestran que las corrientes del sistema tienen forma sinusoidal y en fase con el voltaje del
sistema. Adicionalmente, las Fig. 3.10 (e) y (f) muestran que el voltaje dc y el voltaje de salida
del convertidor se mantienen estables durante toda la operación el filtro activo.
60
CAPÍTULO 3. FILTRO ACTIVO PARALELO
2
(a)
vsu
0
−2
2
(b)
iLu
0
−2
2
(c)
iou
0
−2
2
(d)
isu
0
−2
1.1
(e)
vP N
1
0.9
2
(f)
vfn
0
−2
t1
t2
t3
t4
t5
(50ms/div)
Figura 3.10: Formas de onda simuladas para el esquema de compensación propuesto (a) Voltaje
de fase de alimentación (b) Corriente de carga (c) Corriente de salida del filtro activo (d)
Corriente (negro) y voltaje (gris) del sistema (e) voltaje dc de un convertidor (f) voltaje de
salida de un convertidor NPC.
3.7.2.
Resultados Experimentales
La efectividad de la compensación del filtro activo se corrobora en un setup experimental de
2kVA. Los parámetros del setup experimental son: inductor L = 3mH (0.2 pu); condensadores
Cdc = 2200 µF (3.3 pu); voltage del sistema = 55 V / 50 Hz; voltage dc del convertidor NPC vP N
= 80V. Se usaron un rectificador de seis pulsos y un motor de 0.37kW como cargas, de manera
de comprobar la efectividad de la compensación de armónicas y potencia reactiva respectiva-
CAPÍTULO 3. FILTRO ACTIVO PARALELO
61
mente. Sólo se compensó una fase del sistema trifásico, utilizando un módulo de potencia NPC
monofásico de 5 niveles. Se aplicó un escalón de carga para evaluar el desempeño del lazo de
control del voltaje dc en términos de su respuesta transitoria. Finalmente, se realizaron test de
variación de impedancia del sistema para estudiar la robustez de la implementación del control
predictivo propuesto para el filtro activo. Estos test se usaron para establecer el porcentaje de
incertidumbre máximo en el valor estimado de la impedancia del sistema, antes de exceder los
lı́mites de distorsión armónica en las corrientes del sistema.
El lazo completo de control se ejecuta por el controlador cada 20 [µs], mientras que cada
estado del convertidor está disponible a los 11 [µs]. Con lo anterior se obtiene una frecuencia
de media de conmutación de 6.28 kHz. Si bien es cierto, esta frecuencia no es adecuada para
semiconductores disponibles en media tensión, se propuso un procedimiento de diseño que puede ser aplicado para obtener una frecuencia de conmutación menor, con el costo de compensar
hasta las armónicas que están por bajo la mitad de la frecuencia de conmutación deseada. La
Fig. 3.11 muestra la respuesta transiente del esquema de compensación. La Fig. 3.11a muestra
que la corriente del sistema se hace sinusoidal cuando el filtro activo comienza a operar. De la
misma forma, se observa la forma de onda esperada de cinco niveles en el voltaje de salida del
NPC. Los resultados de la Fig. 3.11b indican que la distorsión armónica total de la corriente
del sistema se reduce desde 25.46 % a 3.76 %. Esta es consecuencia de la buena caracterı́stica
de seguimiento de las corrientes de referencia, como lo muestra la Fig. 3.11c. En la Fig. 3.12 se
muestra la respuesta transiente del filtro activo ante un cambio escalón de carga. Las corrientes
del sistema permanecen sinusoidales y el voltaje de los condensadores retorna a su referencia en
la forma esperada, es decir, con una tı́pica respuesta de un sistema de segundo orden crı́ticamente amortiguado (sin sobrepaso y en dos ciclos de asentamiento). En este caso, se aplicó un
cambio escalón de carga desde 1.0 a 1.3 p.u. Finalmente, se conecta la carga de motor, y sus
correspondientes formas de onda se muestran en la Fig. 3.13. Se observa en dicha figura que el
filtro responde rápidamente, es decir, en menos de un ciclo ante escalones de potencia reactiva.
62
CAPÍTULO 3. FILTRO ACTIVO PARALELO
i∗ou
iou
vf u
isu
isu = iLu
(a)
30
i Lu
i su
% of h1
25
20
15
10
5
0
10
20
30
Harmonic Order h
40
50
(b)
i∗ou
iou
er
(c)
Figura 3.11: Formas de onda experimentales en régimen transiente. (a) Corrientes de referencia,
i∗ou , y corrientes del filtro activo, iou ,voltaje de salida del NPC,vf u , y corriente del sistema isu .
(b) Espectro en frecuencia (T HD of iLu = 25.46 % y T HD de isu = 3.76 % ). (c) Error de
seguimiento ( valor medio < 1 %).
Efecto de Errores en los Parámetros del Modelo
Tomando como base que el modelo del convertidor en el control predictivo es discontinuo y
no-lineal, un análisis mediante root locus no es posible, y un análisis de la estabilidad en lazo
cerrado serı́a muy complejo. Por esta razón, se analizará la información que provee la variación
63
CAPÍTULO 3. FILTRO ACTIVO PARALELO
iLu
iou
isu
vP N
Figura 3.12: Resultados experimentales para cambio escalón de carga (1.0 a 1.3 p.u.). Corriente
de carga, iLu , corriente del filtro activo, iou , corriente del sistema, isu , y voltaje dc del convertidor,
vP N .
vsu
iLu
vsu
isu
Figura 3.13: Resultados experimentales para conexión de carga motor (compensación de potencia reactiva). Corriente de carga, iLu , voltaje del sistema vsu , corriente del sistema, isu , y voltaje
del sistema vsu .
del valor ingresado como impedancia del sistema en el algoritmo predictivo. Estos resultados
se usan para mostrar cómo se comporta la implementación del filtro activo propuesto ante
incertidumbre en ese parámetro.
El modelo predictivo (3.4) puede re-escribirse como:
io [k + 1] = Kv vf x [k] − vs [k] + Ki io [k] .
donde Kv =
Ts
Leq
y Ki = 1 −
Req Ts
Leq
(3.21)
.
La corriente que se predice tiene dos componentes claves: la componente que está en dirección de los nueve posibles valores de los vectores del voltaje de salida, y la otra en la misma
dirección que el vector de corriente actual. Debido a la naturaleza discreta del voltaje de salida,
CAPÍTULO 3. FILTRO ACTIVO PARALELO
64
(±2vdc , ±vdc y 0), la primera componente siempre tratará de minimizar la función de costo
g seleccionando el vector de voltaje más adecuado, aún cuando un error en Kv esté presente.
Por otro lado, hay una componente que está directamente relacionada con el valor actual de
las corrientes de salida. Esta componente tiene una componente fundamental relacionada con
el controlador PI, la cual absorbe el error del voltaje dc en estado estacionario, y componentes
armónicas que actúan para compensar distorsión armónica. Es posible graficar el efecto sobre
las corrientes que se predicen como función de la variación en el valor de impedancia del sistema
utilizado en el modelo predictivo.
Las figuras 3.14a, 3.14b y 3.14c se seleccionan como casos representativos particulares. Si
el controlador predictivo usa el valor real de la impedancia del sistema, entonces el error entre
la corriente de referencia y la corriente de salida es mı́nimo, como lo muestra la Fig. 3.14a. Si
el error (er ) crece, las corrientes del sistema se distorsionan severamente, como lo muestra la
Fig. 3.14b and 3.14c. La Fig. 3.15 muestra cuánto puede cambiar el valor de la impedancia del
sistema antes de que la corriente del sistema no satisfaga los requerimientos del estándar IEEE
519. (THD > 5 %).
La Fig. 3.15 muestra claramente que el THD de la corriente del sistema crece si el error
de seguimiento er se hace mayor, considerando valores de Zs desde 0,1 a 2 p.u. Si el valor
estimado y usado para Zs está entre 0,5 y 1,5 p.u., el filtro activo propuesto permite obtener
corrientes con un THD menor al 5 %. Una caracterı́stica importante del algoritmo del control
predictivo implementado es que el filtro activo permanece operando, aún si el valor estimado
de la impedancia del sistema no está dentro de la banda que asegura un THD permitido por el
estándar IEEE 519.
3.8.
Conclusión
En este capı́tulo se ha propuesto un filtro activo paralelo implementado con convertidores
multinivel NPC monofásicos. Una de las principales ventajas de la topologı́a propuesta tiene
65
CAPÍTULO 3. FILTRO ACTIVO PARALELO
i∗ou
iou
er
isu
(a)
i∗ou
iou
er
isu
(b)
i∗ou
iou
er
isu
(c)
Figura 3.14: Resultados experimentales bajo variación en el valor de la impedancia del sistema.
(a) sin variación en Zs . (b) 1,5Zs (c) 2Zs
relación con la flexibilidad introducida por los módulos monofásicos con control predictivo independiente. Al igual que en el capı́tulo anterior, el control predictivo demuestra ser una buena
alternativa a los controles lineales clásicos, debido a su simplicidad y buenos resultados de seguimiento de las señales de referencia. Además, la caracterı́stica de obtener un THD menor al
5 % se mantiene aún cuando el modelo incluye incertidumbre en el parámetro de impedancia
66
CAPÍTULO 3. FILTRO ACTIVO PARALELO
15
T HD of is
[ %]
10
er
5
5
0
0
0.5
1
Zs
Zsr
1.5
2
Figura 3.15: Relación entre el error de seguimiento de corriente (er ) y el T HD de la corriente
del sistema (is ) bajo variación de la impedancia nominal del sistema.
del sistema, especı́ficamente el valor entre 0,5 y 1,5 p.u. El uso combinado de control predictivo
y convertidores NPC monofásicos mejora la forma de onda del voltaje de salida de los convertidores, reduciendo las armónicas de baja frecuencia asociadas a la frecuencia de conmutación.
El filtro activo propuesto constituye una alternativa a los convencionales filtros activos implementados con VSI’s de 2 niveles, pues ofrece la posibilidad de ampliar el campo de aplicación
de los filtros a compensación de armónicas y potencia reactiva en sistemas de distribución en
media tensión.
Capı́tulo 4
Filtro Activo Serie como Compensador
de Armónicas
4.1.
Introducción
Los procesos de electro-obtención (EW) y electro-refinación (ER) usan rectificadores de
altas corrientes para tratar soluciones de cobre procesado. Comúnmente, se utilizan arreglos
multi-pulsos de puentes rectificadores de fase controlada. Ellos introducen distorsión armónica
al sistema y consumen elevada potencia reactiva. Estos arreglos se diseñan para obtener distorsión armónica de corriente consistente con el estándar IEEE 519 [79], aún cuando operen
sólo rectificadores de seis pulsos. Esto adiciona filtros de armónicas de bajo orden (menores a
11) a cualquier esquema de compensación. El uso de etapas de filtros pasivos secuencialmente
conectados es la opción preferida para la elevada demanda de potencia reactiva de los rectificadores [80–82]. Esta solución presenta desventajas como el alto número de componentes del
filtro, la introducción de resonancias al sistema, las cuales degradan la confiabilidad del mismo,
y la necesidad fı́sica de espacio adicional para la instalación de los filtros (5000 ft2 ) [83]. Por
ejemplo, una planta tı́pica de EW de 10MVA utiliza 3.5 MVAR de filtros distribuidos en etapas
individuales para las armónicas 3, 5 ,7 y 11 (ver Fig. 4.1 ).
67
68
CAPÍTULO 4. FILTRO ACTIVO SERIE
Etapa de
Filtros Pasivos
Fuente
AC
vs
Carga
Transformador Puente
Multipulso Rectificador 6-p EW–ER
PCC
vL
vR
6p
Ls
is
Io
6p
5th
7th
11th
Rdc +
Ldc Vo
Vce −
13th
Figura 4.1: Diagrama Circuital del Sistema de EW-ER compensado con Filtros Pasivos.
Fuente
AC
vs
Carga
Transformador Puente
MultipulsoRectificador 6-p EW–ER
SAF
vL
Ls
PCC
is
+ vSAF −
w
v
u
vR
6p
n1
n2
6p
VSI
Cdc
Io
Rdc +
Ldc Vo
Vce −
Bus dc
Figura 4.2: Diagrama Circuital del Sistema compensado con Filtro Activo Serie.
Configuraciones alternativas de rectificación PWM (pulse-width modulated) se han investigado en la literatura [83,84] con el objetivo de mejorar el desempeño eléctrico de las largamente
utilizadas configuraciones en base a tiristores. En [85] se presenta una evaluación extensa de la
operación, configuración y propiedades eléctricas de los rectificadores PWM y en base a tiristores. En ella se concluye que los rectificadores PWM deberán reemplazar a los rectificadores
a tiristores. Si bien es cierto, esto elimina la necesidad de compensación de potencia reactiva. Sin embargo, esta tendencia está condicionada por el desarrollo de semiconductores con
bajas pérdidas por conducción y módulos PEEB (Power Electronics Building Blocks) de elevada confiabilidad. A partir de la discusión previa, se puede concluir que esos factores niegan
la posibilidad de intervenir o cambiar la tecnologı́a de los rectificadores y abren una ventana
de oportunidades para compensación por medio de filtros activos en aplicaciones de altas corrientes. El interés en aplicaciones de filtros activos de potencia ha crecido considerablemente
debido al impacto que genera todo lo relacionado con calidad de energı́a [86]. Filtros en conexión paralela, serie e hı́brida se han presentado como una tecnologı́a que puede ser integrada al
rango de aplicaciones industriales de 1-10 MVA [87, 88]. Los filtros activos tienen el potencial
CAPÍTULO 4. FILTRO ACTIVO SERIE
69
de atenuar corrientes armónicas en el sistema y compensar potencia reactiva [30, 36, 80, 89, 90].
Aunque estos filtros activos estarı́an compuestos de los mismos convertidores de potencia que
encontramos en la industria, la adopción de esta tecnologı́a por parte del mercado ha sido baja,
debido a su alto costo y no comprobada confiabilidad.
Tı́picamente, la conexión serie se usa para compensar distorsión de voltaje, sags, swells y
desbalances, mientras la conexión paralela para distorsión armónica de corriente y corrección
del factor de potencia por desplazamiento [38, 91, 92]. Otra topologı́a es la hı́brida [93, 94], la
cual emplea una combinación de filtro activo y pasivo. Esta topologı́a se posiciona como la alternativa para aplicaciones de media tensión. Los filtros activos serie conocidos como Dynamic
Voltage Restore (DVR) se han utilizado solo para compensar regulación de voltaje, sags, swells y
desbalances. Estos equipos no son ni diseñados ni usados para compensar corrientes armónicas.
Sin embargo, filtros activos serie en combinación con filtros pasivos en paralelo han probado
ser una buena solución para compensación de corrientes armónicas [93]. En ese esquema, el
filtro activo serie opera como una fuente de tensión controlada a la frecuencia donde se necesita
atenuar la armónica de corriente. Comparado con los conocidos filtros activos paralelos, esta topologı́a se adecua más para compensación de rectificadores de fase controlada, dado los menores
requerimientos de potencia aparente del convertidor y el desempeño mostrado ante circulación
de corrientes armónicas. Más aún, se pueden implementar capacidades de regulación de voltaje
sólo con una simple modificación en el esquema de control, lo que permite que funcione como
DVR y como compensador de corrientes armónicas. En términos de eficiencia y pérdidas, este
esquema presenta mejor rendimiento que los esquemas tradicionales de filtros pasivos. Los filtros pasivos usados para compensar potencia reactiva y corrientes armónicas son normalmente
filtros pasa-alto tipo C, con una resistencia paralela al inductor. Dependiendo de la capacidad
en potencia del filtro, las pérdidas en ellos pueden alcanzar los cientos de kW [80]. Dado que la
topologı́a propuesta se implementa con convertidores PWM fuentes de voltaje, las pérdidas son
menores al 5 % de la potencia del convertidor.
Este capı́tulo propone un esquema de compensación serie para aplicaciones de EW y ER [28].
CAPÍTULO 4. FILTRO ACTIVO SERIE
70
El compensador propuesto se diseña para operar como alta impedancia para la circulación de
armónicas de corriente, eliminando la necesidad de filtros pasivos sintonizados. Esta forma no
tradicional de compensación armónica se logra inyectando un voltaje en contrafase y proporcional a las armónicas que se desea eliminar. Consecuentemente, el rectificador trabaja con un
voltaje de entrada distorsionado, que a la vez introduce distorsión de voltaje en el lado dc (direct current). Ası́, el voltaje de salida (Vo ) estará compuesto en parte de un voltaje promedio
controlable y un rizado adicional correspondiente a la distorsión. El rango de operación de la
carga electrolı́tica es del orden de los cientos para el voltaje y de los kilo para la corriente. En
las celdas electrolı́ticas, el voltaje de reacción (Vce ) toma lugar como una fuente de voltaje dc
constante con una demanda elevada de corriente. La cantidad de corriente dc se regula por la
diferencia entre el voltaje de reacción y el voltaje promedio de salida del rectificador. El voltaje
de diseño para el rectificador es ligeramente mayor a la suma de las celdas. Por esta razón, una
distorsión de voltaje a la salida o rizado no afecta la operación del proceso electrolı́tico.
Este capı́tulo final presenta un completo análisis del compensador serie propuesto, incluyendo
el principio de operación, sistema de control, y los parámetros claves para el diseño del filtro.
Resultados de simulación se obtienen usando una planta de 10MVA. A su vez, estos resultados
se contrastan con los obtenidos en un prototipo experimental de laboratorio de 2 kVA.
4.2.
Topologı́a y Principio de Operación
La Fig. 4.1 muestra la topologı́a del filtro activo serie propuesto, el cual se compone de
tres inversores monofásicos fuente de voltaje con filtro LC de salida. Tomando como ventaja
la implementación usando convertidores monofásicos, el filtro activo permite conexión de más
de una unidad monofásica en serie, tal como se muestra en lı́neas punteadas en la Fig. 4.1.
El filtro activo implementado con módulos monofásicos en cascada presenta ventajas en términos de flexibilidad de compensación (ej. corrientes desbalanceadas y simplicidad en el control).
Además, la conexión en cascada de unidades monofásicas permite la cancelación de componen-
71
CAPÍTULO 4. FILTRO ACTIVO SERIE
tes armónicas asociadas a la técnica de conmutación PWM utilizada [95]. Cada VSI comparte
el mismo bus dc (VC ), evitando incrementar el número de lazos de control de voltaje dc asociados con el control independientes de cada convertidor [96]. Un reducido número de lazos de
control representa una simplificación significativa en el diseño y operación del filtro activo. Otra
importante caracterı́stica de los convertidores monofásicos es que las armónicas predominantes
están asociadas con la frecuencia de conmutación propia del convertidor, por lo tanto, no existe
circulación de segunda armónica.
Los VSI’s están conectados en serie al sistema de distribución a través de transformadores
de acoplamiento. El la Fig. 4.3, vSAF representa la forma de onda del voltaje inyectado por el
filtro activo serie, vL el voltaje equivalente de la inductancia serie, (vs − vL ) el voltaje en el
PCC, y vR el voltaje en los terminales del rectificador de carga. El filtro activo serie presenta
una alta impedancia equivalente para las armónicas de corriente, actuando ası́ como fuente de
voltaje controlada para la circulación de esas armónicas. Como resultado, se modifica la forma
de onda del voltaje en los terminales del rectificador y se fuerza a que la corriente del sistema
is sea más sinusoidal. El circuito equivalente mostrado en la Fig. 4.4 explica el principio de
operación en el caso de frecuencia fundamental y componentes armónicas. Refiriéndose a la Fig.
4.4, si G ≫ jkXs , entonces las armónicas de corriente del sistema están dadas por (4.1):
isk =
vs
(vPCCk − vRk )
(vPCCk − vRk )
≈
jkXs + G
G
vL
Ls
vPCC+vSAF−
G
vR
(4.1)
EW–ER
is
Figura 4.3: Circuito equivalente monofásico del filtro serie propuesto.
Si la ganancia G es lo suficientemente grande (al menos 10 veces más grande que kXs ),
jkXs puede ser despreciado y las componentes de la corriente del sistema pueden ser atenuadas
significativamente. In ese caso, la impedancia equivalente se comporta como una fuente de
72
CAPÍTULO 4. FILTRO ACTIVO SERIE
voltaje controlada por corriente Gish (4.2).Entonces, corrientes con formas de onda cercana a
una sinusoidal circularán en el sistema.
∗
vSAF
= Gish + vSAF1
jXs G = 0
is vL
vs
vSAF1
vR
(4.2)
Gisk
jkXs
vL
isk
vSAFk
vRk
(b)
(a)
Figura 4.4: Circuito equivalente monofásico del filtro serie propuesto. (a) para componente
fundamental. (b) para componentes armónicas.
Una de las ventajas de los filtros activos es que se puede lograr simultáneamente la compensación de potencia reactiva y las corrientes armónicas. Sin embargo, ambas caracterı́sticas
pueden ser desacopladas y controladas independientemente. El filtro activo propuesto puede lograr ambas compensaciones simultáneamente o secuencialmente, dependiendo de la estructura
de control que se utilice. Si se requiere de las dos compensaciones, la potencia aparente del
convertidor debe crecer. Si se requiere compensación de potencia reactiva, la magnitud de la
componente fundamental del voltaje inyectado se controla manteniendo el voltaje en el PCC
en fase con la corriente del sistema, lo que permite operar con factor de potencia unitario. En
este sentido, la compensación de potencia reactiva se determina con el diagrama fasorial de
la Fig. 4.5, donde φ1 es el ángulo entre el voltaje y la corriente del sistema, y vSAF−Q es la
potencia reactiva que debe generar el filtro activo para subir el factor de potencia a la unidad.
La amplitud de la componente fundamental de vSAF−Q debe satisfacer (4.3):
vSAF−Q ≥ 2vs sin
φ1
2
(4.3)
73
CAPÍTULO 4. FILTRO ACTIVO SERIE
vL
vL
φ1
is
vs
vs
θ1
vL
vR
vSAF−Q
(a)
θ2
is
(vs − vL )
(vL + vSAF−Q )∗
φ2
vR
∗
(b)
Figura 4.5: Diagrama fasorial equivalente. (a) sistema no compensado. (b) sistema compensado.
Si el filtro activo serie propuesto se usa sólo para compensar armónica de corriente, el voltaje
a frecuencia fundamental inyectado por el convertidor PWM debe tener una pequeña amplitud,
la cual se ajusta variando la cantidad de potencia activa que absorbe el convertidor. Para cumplir
efectivamente la compensación de corrientes armónicas, el filtro activo serie debe ser capaz de
∗
generar un voltaje vSAF
cuya forma de onda se calcula a través del esquema de control de la
Fig. 4.6.
vs
vPCC
+ vSAF− vR
is
Carga
vo
SRF
PLL
sin(ωt)
Gen.
Ref.
G ish
x
+
vSAF1
PI
vC∗
vi
+
−
(4.3)
∗
vSAF
Gen.
Señal
Pulsos
Lazo voltaje dc
PWM
vC
Figura 4.6: Diagrama de control en bloques del filtro activo serie.
4.3.
Sistema de Control
La Fig. 4.6 muestra el diagrama del sistema de control propuesto. Está compuesto de un
lazo de control del voltaje dc, un generador de la señal de referencia, el cual provee la señal de
voltaje proporcional Gisk , y un generador de las señales de disparo para el convertidor PWM.
74
CAPÍTULO 4. FILTRO ACTIVO SERIE
4.3.1.
Generador de la señal de Referencia
Cada corriente se introduce en un bloque phase-locked-loop (PLL) como lo muestra la Fig.
(ver Fig. 4.7). Se implementó adicionalmente un PLL monofásico llamado Second Order Generalized Integrator (SOGI) [97] para extraer la componente fundamental de cada corriente (Fig.
4.7). Este método de extracción de la componente fundamental tiene la ventaja de ser rápido y
adecuado para seguimiento online, tiene pocos requerimientos de hardware (requiere el 50 % de
multiplicadores comparado con el synchronous reference frame PLL [98]), y puede ser fácilmente
implementado en una FPGA (ver Fig. 4.8). Tiene como salida una señal sinusoidal (o1 ). esta
forma de onda sinusoidal tiene la misma fase y magnitud que la componente fundamental de
corriente de entrada (i). Es importante mencionar que este método no introduce desfases que
puedan afectar la efectividad de la compensación. Se usan tiempos de cálculo en la FPGA del
orden de 2 µs, lo que se considera prácticamente instantáneo, comparado con los 20ms de cada
ciclo eléctrico de corriente y voltaje. La función de transferencia en lazo cerrado de la estructura
de la Fig. 4.7 es:
H (s) =
i
−
+
o1
ks ωs
= 2
i
s + ks ωs + ω
+
ks
x
−
1
s
(4.4)
o1
ω
1
s
x
Figura 4.7: Diagrama en bloques del SOGI-PLL.
Reemplazando s con la función de transferencia de un integrador de segundo orden (4.5) en
(4.4), se obtiene la función de transferencia en lazo cerrado (4.6):
75
CAPÍTULO 4. FILTRO ACTIVO SERIE
s2 =
Ts 3z −1 − z −2
2 1 − z −1
(4.5)
o1 = c1 ik−1 − c2 ik−2 + c3 ik−3 + c4 ok−1
−c5 ok−2 − c6 ok−3 − c7 ok−4
donde, c1 = 32 ks ωTs , c2 = − 43 c1 , c3 =
c1
,
3
(4.6)
c4 = 2 − c1 , c5 = −1 − c2 + 9c7 , c6 = −c3 − 83 c7
y c7 = − 14 ω 2Ts2 . Para una frecuencia de muestreo de 6103 Hz y ks = 1, se usan las siguientes
constantes: c1 = 0,0771, c2 = 0,1029, c3 = 0,0256, c4 = 1,9227, c5 = 0,9031, c6 = 0,0217, y
c7 = 0,0006.
El diagrama de flujo de las señales que se muestra en la Fig. 4.7 muestra cómo implementar
el SOGI-PLL en su forma discreta (4.6), de acuerdo a lo requerido para implementarlo en una
FPGA. El subı́ndice k − M representa el retardo asociado a M muestras por ciclo. Cómo el
tiempo de ejecución es igual a 2 µs, el cual no es mayor que la frecuencia de muestreo, el
SOGI-PLL se presenta como una buena solución para obtener la fundamental de la corriente
sin retardos asociados.
Finalmente, las corrientes del sistema y sus correspondientes fundamentales extraı́das de cada
fase se restan para obtener el contenido armónico que necesita ser compensado. Las componentes
∗
armónicas se amplifican por la ganancia G, y el resultado (vSAF
) se aplica al generador PWM
de las señales de disparo. La ganancia G depende de la efectividad requerida por el filtro activo,
y su valor depende de cuanta potencia activa es capaz de manejar el filtro, tal y como se explica
en el capı́tulo 4.4.3.
76
CAPÍTULO 4. FILTRO ACTIVO SERIE
Repetir en cada instante (k)
Calcular las sumas
o1 = ...
Guardar en variables auxiliares
aux ik−3 = aux ik−2
aux ik−2 = aux ik−1
aux ik−1 = ik
aux ok−4
aux ok−3
aux ok−2
aux ok−1
= aux ok−3
= aux ok−2
= aux ok−1
= ok
Calcular las multiplicaciones
Figura 4.8: Diagrama de flujo de las señales del SOGI-PLL para implementación digital.
4.3.2.
Generación de Señales de Disparo
Se genera una forma de onda triangular sincronizada con el voltaje del sistema. La frecuencia de la forma de onda triangular fija la frecuencia de conmutación de los semiconductores
del convertidor. Existen dos importantes variables que deben considerarse para especificar la
frecuencia de conmutación de los filtros activos de potencia. Se requieren altas frecuencias de
conmutación para filtrar armónicas de alta frecuencia, sin embargo, la capacidad en potencia
del semiconductor limita la frecuencia de conmutación máxima. En este caso, se selecciona una
frecuencia de 1.5 kHz para emular la operación de un convertidor comercialmente disponible.
Luego, se usa un Synchronous Reference Frame PLL trifásico para generar la onda diente de
sierra en fase con vsu que describe la frecuencia de la red (ωt). Esta onda diente de sierra se usa
para leer una triangular (tri) almacenada en una memoria ROM interna de la FPGA de 4096
x 12-bit. La exactitud de la triangular está limitada por el máximo número de periodos que
producen un mı́nimo de n puntos para cada triangular por ciclo. En este caso, el número de
puntos n de cada triangular es 18 y la frecuencia de la triangular es 1.5 kHz. Luego, el bloque
de generación de las señales de disparo produce una señal de conmutación unipolar para cada
∗
inversor monofásico comparando vSAF
y tri, como lo muestra la Fig. 4.9.
77
CAPÍTULO 4. FILTRO ACTIVO SERIE
vPCC
∗
vSAF
Generador S. Disp.
PWM
SRF–PLL
−
+
−1
−
+
ωt
Memoria
ROOM
4096 x 12
Switches
Figura 4.9: Diagrama de Bloques del Generador de Señales de Disparo.
4.3.3.
Control del Voltaje dc
El voltaje dc permanece constante hasta que que la potencia activa absorbida por cada inversor decrece al nivel donde no es capaz de suplir las pérdidas en el convertidor. La potencia
activa absorbida por cada inversor se controla ajustando la amplitud de la componente fundamental (vSAF1 ), la cual está en fase con cada corriente, y condicionada de acuerdo a la técnica
de modulación utilizada, es este caso, PWM unipolar con ganancia K = 0.613. Como los inversores comparten el condensador dc, se requiere sólo un controlador PI, como lo muestra la Fig.
4.10.
∆VC∗
+
∆e
−
∆vc
C(s)
Gs (s)
∆VC
KsV
Figura 4.10: Diagrama del lazo de control del voltaje dc
En el diagrama en bloques mostrado en la Fig. 4.10, el voltaje en el condensador VC se mide
usando un transductor KsV , para luego ser comparado con la referencia VC ∗ . El error se procesa
en un controlador PI, con dos ganancias: Kp y Ti . Ambas ganancias se calculan de acuerdo a
los requerimientos de respuesta dinámica. La salida del controlador PI ingresa a cada bloque
Gs (s), los cuales están representados como funciones de transferencia de primer orden (4.7).
3
∆VC
=
Gs (s) =
∆vc
2
√
2 · K · is · cos(φ)
s · Cdc · VC ∗
(4.7)
78
CAPÍTULO 4. FILTRO ACTIVO SERIE
Se añade una señal sinusoidal, extraı́da por el circuito generador de la referencia, a las formas
de onda proporcionales al contenido armónico de corriente. La amplitud de la señal sinusoidal
se modifica a través de la acción del controlador PI. La función de transferencia en lazo cerrado
del sistema con controlador PI (4.8) se muestra a continuación (4.9):
C(s) = Kp
1
1+
Ti · s
(4.8)
2
ωn
· (s + a)
∆VC
a
=
∗
∆VC
s2 + 2ζωn · s + ωn2
(4.9)
Añadiendo la señal sinusoidal a la entrada del generador de señales de disparo, la potencia
activa que fluye por los condensadores cambia, controlando ası́ el voltaje en el condensador.
El tiempo de respuesta del control del voltaje dc no necesita ser demasiado rápido, debido
a las dinámicas lentas que tiene el condensador electrolı́tico. Las ganancias proporcionales e
integrales deben sintonizarse para una respuesta crı́ticamente amortiguada. En este caso, se usa
un factor de amortiguamiento ζ = 1 y una frecuencia natural de oscilación ωn = 2π · 100 rad/s.
Los correspondientes tiempo integral Ti = 1/a (4.9) y ganancia proporcional Kp pueden ser
calculados a partir de (4.10) y (4.11).
√
4 ζ 2 2 · Cdc · VC ∗
Ti =
3 Kp · K · is · cos(φ)
(4.10)
√
2 ζωn 2 · Cdc · VC ∗
Kp =
3 K · is · cos(φ)
(4.11)
79
CAPÍTULO 4. FILTRO ACTIVO SERIE
4.4.
4.4.1.
Diseño del Filtro Activo
Condensador dc
El valor del condensador dc se obtiene usando (4.12). Con ese valor, el condensador es
apto para conservar suficiente energı́a durante la ausencia de medio ciclo de red, resultando en
variaciones de no más de 5 %.
Cdc ≥
T vsm iLm
,
2 VC∗2 − VC2
(4.12)
donde vsm es el peak del voltaje fase neutro, iLm es la corriente rms de la carga, T es el
perı́odo de la red, VC ∗ es la referencia de voltaje dc y VC es el mı́nimo voltaje permitido en el
bus dc.
4.4.2.
Filtro de Salida LC
El filtro LC de segundo orden conectado en los terminales de salida del convertidor, elimina
el voltaje generado por cada convertidor monofásico. Este filtro se diseña en base al máximo
rizado de voltaje armónico permitido en los terminales del transformador de acoplamiento, sin
afectar la ganancia a frecuencia fundamental. El filtro no debe atenuar el contenido armónico
de baja frecuencia requerido para compensar las corrientes armónicas que genera la carga.
Lf
Zsys
vo
Cf
v1
Figura 4.11: Circuito equivalente para el rizado de voltaje en los terminales de salida del convertidor.
A partir de la Fig. 4.11, para calcular Lf y Cf , es posible representar la impedancia equivalente a la frecuencia de conmutación del convertidor Zsys , reflejada en el secundario del trans-
CAPÍTULO 4. FILTRO ACTIVO SERIE
80
formador como:
Zsys(secundario) = (n2 /n1 )2 Zsys(primario)
(4.13)
A la frecuencia de conmutación, el siguiente criterio debe satisfacerse:
1. XCf << XLf , para asegurar que la mayor parte del voltaje a la frecuencia de conmutación
caiga en Lf .
2. XCf y XLf << Zsys , para asegurar una división del voltaje entre entre Lf y Cf .
En este ejemplo, Lf = 9,3mH y Cf = 3,6µF se obtienen considerando un transformador serie
con una razón de transformación 1:1, asumiendo XLf = 10XCf , y Ls = 2 %, con respecto a los
valores referenciados a la base Vbase = 13.8 kV y Sbase = 10 MVA. La razón de transformación del
transformador seleccionado limita la corriente de los IGBT’s a módulos IGBT que se encuentren
disponibles en el mercado. Ellos deben ser capaces de soportar altos niveles de voltaje de bloqueo
(ej. ABB - 5SNA 0750G650300 - 6.5kV). Para operar los IGBT’s a menor voltaje, se deberı́a
cambiar la razón de transformación del transformador, lo que hace crecer a corriente nominal
en el secundario, y por ende, la corriente que deben soportar lo semiconductor. En base a lo
anterior, se debe escoger la mejor combinación entre capacidad de voltaje y corriente disponible.
4.4.3.
Potencia Aparente Nominal
Debido a que el filtro activo serie puede ser usado para compensación de potencia reactiva
ası́ como para compensación de corrientes armónicas, la potencia aparente requerida por el
convertidor puede variar. Para compensar potencia reactiva, el voltaje rms requerido por el
convertidor será mayor, y puede ser obtenido a partir de (4.3). Si el filtro activo se usa sólo para
compensar corrientes armónicas, sólo se requiere una fracción de voltaje rms en los terminales
ac del convertidor. El voltaje nominal requerido en ese caso, será igual al voltaje rms de las
81
CAPÍTULO 4. FILTRO ACTIVO SERIE
componentes armónicas. Las componentes armónicas se calculan considerando una corriente
tı́pica de 12 pulsos circulando a través de las lı́neas de alimentación principal. De acuerdo a
(4.2), el filtro activo deberá generar componentes armónicas de orden 12p ± 1-th. Entonces, el
voltaje nominal de compensación se calcula como:
vSAF r
v
u N uX
G
=t
n=1
is
12n ± 1
2
+ vSAF 12
(4.14)
donde G es la ganancia de compensación, is es la corriente rms del sistema, y vSAF 1 es la
componente fundamental del voltaje inyectado para compensación de potencia reactiva. Ası́, los
VA requeridos por el filtro activo están dados por (4.17), y están compuestos de dos partes. Una
que representa la parte asociada a la circulación de corrientes armónicas del sistema, y otra que
representa el voltaje de compensación de potencia reactiva.
SSAF r =
√
3 vSAF r is
(4.15)
Las ecuaciones (4.14) y (4.17) demuestran que potencia del compensador depende de la
función de compensación, debido a que ésta determina la magnitud del voltaje inyectado. Considerando que un rectificador controlado tı́picamente opera con un ángulo de desplazamiento
α igual a 10◦ en aplicaciones de EW y ER, la potencia reactiva puede calcularse, y por ende,
el voltaje de compensación. Para el ejemplo de la planta cuya potencia nominal, Sr , sea de
10MVA, la potencia reactiva Qr serı́a:
Qr = Sr sin (α) = 5,00 MV Ar
(4.16)
El voltaje requerido sólo para compensar potencia reactiva se calcula usando (4.3). De esta
CAPÍTULO 4. FILTRO ACTIVO SERIE
82
forma, se obtiene vSAF −Q es igual a 2.4 kV, los cuales se usan finalmente para calcular la potencia
aparente necesaria por el convertidor:
SSAF = 3 vSAF −Q is = 3,03 MV A,
(4.17)
equivalente a un 30 % de la potencia nominal.
Ası́ también, puede calcularse la amplitud individual de las armónicas caracterı́sticas de la
carga, lo que entrega el aporte de las corriente armónicas al voltaje de compensación. Usando
(4.14), es decir, para una carga de 12 pulsos, la potencia aparente para compensar las armónicas
serı́a 2,10 MVA. Entonces, si el filtro activo se diseña para obtener ambos tipos de compensación,
la potencia aparente requerida se acerca a un 50 % de los 10 MVA de la carga. Sin embargo, si
sólo se compensan corrientes armónicas, entonces se reduce la amplitud del voltaje requerido,
y por ende la potencia aparente requerida por el convertidor se reduce a sólo un 20 % de los 10
MVA presentes en la carga.
4.5.
Desempeño de la Compensación del Filtro Activo
de Potencia
4.5.1.
Simulaciones
Se simuló un sistema de rectificación para una planta de electro-obtención de cobre de 10
MVA, con los siguientes parámetros dc: Rdc = 0.3Ω, Ldc = 5 mH, y Vce = 200 V. El filtro activo
serie fue testeado compensando un rectificador de 12-pulsos. Las simulaciones se realizaron
usando Matlab. La Tabla 4.1 muestra los valores de los parámetros del filtro LC en p.u., con
respecto a los 10MVA y 13.8kV bases. La ganancia del control G se setea en 10 p.u., lo cual
equivale a 190 Ω. Los kVA nominales del filtro activo serie son 36 % (360 kVA) de la potencia
nominal de la carga. En este caso, el filtro activo serie compensa corrientes armónicas y potencia
CAPÍTULO 4. FILTRO ACTIVO SERIE
83
reactiva.
Tabla 4.1: Valores del Filtro LC (Vbase = 13.8 kV y Sbase = 10 MVA)
valor
valor p.u.
Lf 9.3 mH
0.154
Cf
3.6 µF
0.022
Cdc 3300 µF
5.98
Las Fig. 4.12 y 4.13 muestran las formas de onda obtenidas a través de simulación antes y
después de que el filtro activo comience a operar. Antes de conectar el filtro activo, el THD de is
es 9.58 %, tal como lo muestra la Fig. 4.12a. Sin embargo, al estar compensada por el filtro activo
serie, el THD se reduce desde 9.58 % a 3.55 % (ver Fig. 4.12b). Más aún, se mejora el factor de
potencia desde 0.94 a 0.98. El filtro activo se comporta como una resistencia equivalente de 190
Ω. La Fig. 4.12c muestra un análisis del espectro y la reducción individual de las armónicas de
corriente en el sistema. La Fig. 4.13 demuestra que aún cuando se distorsiona el voltaje dc en
el rectificador con un rizado igual al 5.97 debido al efecto del filtro activo serie, la corriente dc
permanece constante y sin rizado.
4.5.2.
Resultados Experimentales
Con el objeto de validar el esquema de compensación propuesto, se implementó un prototipo
de 2 kVA usando IGBT. Cada inversor fue operado con una frecuencia de conmutación de
1.5kHz. Esta baja frecuencia de conmutación se selecciona para emular el sistema operando en
el rango de IGBT’s de alta potencia. La razón de transformación de los transformadores de
acoplamiento fue 1:3. El condensador del bus dc es de 2700 µF. La estrategia de control, la
modulación y la sincronización con la red se implementaron en una FPGA Nexys 2 de Digilent
Inc. Por simplicidad, se utilizó una carga R-L en vez de una R-L-V conectada a los terminales
de salida del rectificador. Se implementó la carga con un inductor de 6 mH y un arreglo de
resistencias variables en el rango de 0 a 150 Ω. El rectificador se conectó a los 380V 50 Hz. La
Fig. 4.14 muestra las señales de control del bloque de generación de referencias. La Fig. 4.14
muestra también la componente fundamental de la corriente ias 1 , obtenida usando el filtro SOGI,
84
CAPÍTULO 4. FILTRO ACTIVO SERIE
vsa →
1
[pu]
0.5
← ias
0
−0.5
−1
(10ms/div)
(a)
vsa →
1
[pu]
0.5
← ias
0
−0.5
−1
(10ms/div)
(b)
0
log { % of h1 }
10
is
i s (SAF )
−1
10
−2
10
0
10
20
30
Harmonic order h
40
50
(c)
Figura 4.12: Resultados de simulación (a) Voltaje del sistema y corriente del sistema antes de la
compensación (b) Voltaje del sistema y corriente del sistema con SAF (Vbase = 13.8 kV y Sbase
= 10 MVA). (c) Comparación en escala logarı́tmica entre los espectros armónicos de corriente,
expresados en términos de la fundamental de corriente. ( Para is , T HDi =9.58 % y para is (SAF ),
T HDi =3.55 % ).
y la forma de onda de sincronismo utilizando el SRF-PLL, ωt, la cual está en fase con el voltaje
del sistema vsu .
Los resultados experimentales en estado estacionario demuestran la factibilidad del esquema
de compensación propuesto y validan la efectividad del esquema de control implementado. Las
Fig. 4.15a y 4.15b muestran las corrientes de entrada antes y después de la compensación. La
85
CAPÍTULO 4. FILTRO ACTIVO SERIE
1
[pu]
0.8
տ
Vo
0.6
ւ
Io /2
0.4
0.2
0
(10ms/div)
(a)
1
[pu]
0.8
տ
Vo
0.6
Io /2
ւ
0.4
0.2
0
(10ms/div)
(b)
1
a
vSAF
ւ
[pu]
0.5
0
−0.5
−1
(10ms/div)
(c)
Figura 4.13: Resultados de Simulación. (a) voltaje dc del rectificador (T HDv = 2.63 %) y corriente dc del rectificador antes de la compensación (b) voltaje dc (T HDv = 5.87 %) y corriente
dc con compensación. (c) Voltaje ac de salida del filtro activo serie.
forma de onda de la corriente de entrada en la Fig. 4.15b se comporta de acuerdo a lo esperado,
es decir, la corriente del sistema se hace más sinusoidal, y el THD se reduce desde 10.10 %
a 4.90 %. Se muestra en la Fig. 4.15c el mismo análisis de espectros de las corrientes usado
en la parte de simulaciones. Este análisis muestra la reducción individual de las componentes
armónicas en la corriente del sistema. El voltaje en los terminales de salida de los VSI (Fig.
4.16) tiene la componente fundamental requerida para suplir las pérdidas en el convertidor y
los transformadores de acoplamiento.
86
CAPÍTULO 4. FILTRO ACTIVO SERIE
vsa
ias
ias 1
ωt
Figura 4.14: Señales de control. CH1 = ωt medida en el conversor DA, CH2 = ias 1 medida en el
conversor DA, CH3 = ias y CH4 = vsa .
ias
ibs
ics
ias
ibs
ics
vsa
ias h
(a)
(b)
0
log { % of h1 }
10
is
i s (SAF )
−1
10
−2
10
0
10
20
30
Harmonic order h
40
50
(c)
Figura 4.15: Resultados Experimentales. (a) Corriente del sistema y voltaje del sistema sin
compensación (CH1 = ias h medida en el conversor DA, CH2 = ics , CH3 = ias y CH4 = ibs ).
(b)Corriente del sistema y voltaje del sistema con compensación (CH1 = vsa , CH2 = ics , CH3
= ias y CH4 = ibs ). (c) Comparación en escala logarı́tmica entre los espectros armónicos de
corriente, expresados en términos de la fundamental de corriente. (Para is , T HDi = 10,10 %, y
para is (SAF ), T HDi = 4,90 %).
87
CAPÍTULO 4. FILTRO ACTIVO SERIE
a
vSAF
VC
Figura 4.16: Resultados Experimentales. Voltaje de salida del VSI y voltaje en el condensador
u
luego de la compensación, CH1 = vSAF
y CH2 = VC
4.6.
Conclusión
Se propuso un esquema de compensación serie capaz de compensar corrientes armónicas en
sistemas de rectificación de media tensión. El filtro activo serie propuesto se caracteriza por la
integración de convertidores VSI monofásicos conectados en serie, compartiendo el mismo bus
dc. Los resultados experimentales obtenidos en un prototipo de laboratorio de 2-kVA se han
usado para demostrar la factibilidad y efectividad del filtro activo propuesto para compensar
armónicas de corriente. La compensación de armónicas de corriente se logra distorsionando el
voltaje aplicado a los terminales ac del rectificador. Esto permite eliminar la necesidad de filtros
pasivos.
Capı́tulo 5
Conclusiones Generales
5.1.
Conclusiones Generales
En esta tesis se propusieron tres esquemas de compensación que permiten atenuar armónicas de corriente y reducir el flujo de potencia reactiva en sistemas de transmisión de energı́a
eléctrica. El análisis, diseño y evaluación de estos esquemas de compensación utilizó como criterios relevantes los ı́ndices de calidad de energı́a y desempeño de compensación dinámico. Los
resultados fueron simulados y comprobados con prototipos de laboratorio. Para el primer filtro
activo desarrollado con un inversor de cuatro piernas, se propuso una estrategia de control predictiva. Se determinó, en base al desarrollo teórico y práctico, que la estrategia propuesta puede
ser aplicada en diferentes topologı́as de filtros activos, sólo cambiando la función de estados de
conmutación del convertidor utilizado. Usando una estrategia de control predictivo de las corrientes de compensación, es posible aislar el bloque de generación de referencias del control del
convertidor, independiente de la topologı́a que se esté usando. Se tomó dicha caracterı́stica para
implementar el control independiente del segundo compensador propuesto, implementado con
convertidores NPC monofásicos. Con esa implementación se comprobó que dicha topologı́a es
una opción real para incluir filtros activos de potencia a sistemas de media tensión. Finalmente
se propuso una aplicación no convencional de filtrado de armónicas de corriente utilizando un
88
CAPÍTULO 5. CONCLUSIONES GENERALES
89
filtro activo serie en sistemas de media tensión.
5.2.
Trabajo Futuro
Sin duda la compensación en paralelo tiene ventajas que permiten asegurar que es una alternativa técnicamente factible de implementar en el corto plazo. Por ello, se considera que se
deben investigar técnicas de identificación de parámetros en lı́nea que permitan actualizar los
parámetros utilizados en el control predictivo. Esto permitirá darle la robustez necesaria a la
operación del filtro, para su futura adopción por parte del mercado de filtros activos de potencia. Además, se debe analizar la factibilidad de extender la aplicación del compensador NPC
monofásico a aplicaciones de alta tensión, considerando n-convertidores en serie por cada fase.
Por último, se considera como trabajo futuro el estudio de este tipo de aplicaciones orientado a
la calidad de la energı́a en aplicaciones de distribución a partir de energı́a solar.
Bibliografı́a
[1] L. Lorenz. Power semiconductors state-of-art and development trends. In Power Electronics, 2007. ICPE ’07. 7th Internatonal Conference on, pages 683–686, Oct. 2007.
[2] J. Rodriguez, Jih-Sheng Lai, and Fang Zheng Peng. Multilevel inverters: a survey of topologies, controls, and applications. Industrial Electronics, IEEE Transactions on, 49(4):724–
738, Aug 2002.
[3] D. Soto and T.C. Green. A comparison of high-power converter topologies for the implementation of facts controllers. Industrial Electronics, IEEE Transactions on, 49(5):1072–1080,
Oct 2002.
[4] A. Petersson R. Grünbaum and B. Thorvaldsson. Facts, improving the performance of
electrical grids. ABB Review, pages 11–18, mar. 2003.
[5] J.J. Shea. Understanding facts-concepts and technology of flexible ac transmission systems
[book review]. Electrical Insulation Magazine, IEEE, 18(1):46–46, Jan.-Feb. 1999.
[6] C.W. Taylor. Improving grid behaviour. Spectrum, IEEE, 36(6):40–45, Jun 1999.
[7] Bhim Singh, K. Al-Haddad, and A. Chandra. A review of active filters for power quality
improvement. Industrial Electronics, IEEE Transactions on, 46(5):960–971, Oct 1999.
[8] H. Akagi. The state-of-the-art of power electronics in japan. Power Electronics, IEEE
Transactions on, 13(2):345–356, Mar 1998.
90
91
BIBLIOGRAFÍA
[9] S.M. Amin and B.F. Wollenberg. Toward a smart grid: power delivery for the 21st century.
Power and Energy Magazine, IEEE, 3(5):34–41, Sept.-Oct. 2005.
[10] J.P. Bickford.
Reactive power control in electric systems.
Electronics and Power,
29(7.8):587–, July-August 1983.
[11] C.A. Weishaupt, L.A. Moran, J.R. Espinoza, L.W. Dixon, and G. Joos. A reactive power compensator topology based on multilevel single-phase npc converters. In Industrial
Technology (ICIT), 2010 IEEE International Conference on, pages 1339–1344, March 2010.
[12] A. Varschavsky, J. Dixon, M. Rotella, and L. Moran. Cascaded nine-level inverter for
hybrid-series active power filter, using industrial controller. Industrial Electronics, IEEE
Transactions on, 57(8):2761–2767, Aug. 2009.
[13] Bhim Singh, K. Al-Haddad, and A. Chandra. A review of active filters for power quality
improvement. Industrial Electronics, IEEE Transactions on, Oct 1999.
[14] A. Campos, G. Joos, P. Ziogas, and J. Lindsay. Analysis and design of a series voltage
compensator for three-phase unbalanced sources. Industrial Electronics, IEEE Transactions
on, 39(2):159–167, Apr 1992.
[15] F.-Z. Peng, H. Akagi, and A. Nabae. A new approach to harmonic compensation in power
systems. pages 874–880 vol.1, Oct. 1988.
[16] Fang Zheng Peng, H. Akagi, and A. Nabae. A new approach to harmonic compensation
in power systems-a combined system of shunt passive and series active filters. Industry
Applications, IEEE Transactions on, 26(6):983–990, Nov/Dec 1990.
[17] P.W. Hammond. A new approach to enhance power quality for medium voltage ac drives.
Industry Applications, IEEE Transactions on, 33(1):202–208, Jan/Feb 1997.
BIBLIOGRAFÍA
92
[18] M.D. Manjrekar, P.K. Steimer, and T.A. Lipo. Hybrid multilevel power conversion system: a
competitive solution for high-power applications. Industry Applications, IEEE Transactions
on, 36(3):834–841, May/Jun 2000.
[19] H. Akagi, A. Nabae, and Satoshi Atoh. Control strategy of active power filters using
multiple voltage-source pwm converters. Industry Applications, IEEE Transactions on,
IA-22(3):460–465, 1986.
[20] Fang Zheng Peng, Jih-Sheng Lai, J.W. McKeever, and J. VanCoevering. A multilevel
voltage-source inverter with separate dc sources for static var generation. Industry Applications, IEEE Transactions on, 32(5):1130–1138, Sep/Oct 1996.
[21] Fang Zheng Peng and Jih-Sheng Lai. Dynamic performance and control of a static var
generator using cascade multilevel inverters. Industry Applications, IEEE Transactions on,
33(3):748–755, May/Jun 1997.
[22] C.K. Lee, S.S.Y.R. Hui, and H.S.-H. Chung. A 31-level cascade inverter for power applications. Industrial Electronics, IEEE Transactions on, 49(3):613–617, Jun 2002.
[23] Chong Han, Z. Yang, Bin Chen, A.Q. Huang, Bin Zhang, M.R. Ingram, and A. Edris.
Evaluation of cascade-multilevel-converter-based statcom for arc furnace flicker mitigation.
Industry Applications, IEEE Transactions on, 43(2):378–385, March-april 2007.
[24] M.E. Ortuzar, R.E. Carmi, L.W. Dixon, and L. Moran. Voltage-source active power filter
based on multilevel converter and ultracapacitor dc link. Industrial Electronics, IEEE
Transactions on, 53(2):477–485, April 2006.
[25] F. Blaabjerg, Zhe Chen, and S.B. Kjaer. Power electronics as efficient interface in dispersed
power generation systems. Power Electronics, IEEE Transactions on, 19(5):1184–1194,
Sept. 2004.
[26] L. Asimmoaei, E. Aeloiza, J.H. Kim, P. Enjeti, F. Blaabjerg, L.T. Moran, and S.K. Sul. An
interleaved active power filter with reduced size of passive components. In Applied Power
BIBLIOGRAFÍA
93
Electronics Conference and Exposition, 2006. APEC ’06. Twenty-First Annual IEEE, pages
8 pp.–, March 2006.
[27] L. Moran, P.D. Ziogas, and G. Joos. A solid-state high-performance reactive-power compensator. Industry Applications, IEEE Transactions on, 29(5):969–978, Sep/Oct 1993.
[28] D. Figueroa, L. Moran, P. Ruminot, and J. Dixon. A series active power filter scheme for
current harmonic compensation. In Power Electronics Specialists Conference, 2008. PESC
2008. IEEE, pages 3587–3591, june 2008.
[29] S.G. Dan, D.D. Benjamin, R. Magureanu, L. Asiminoaei, R. Teodorescu, and F. Blaabjerg. Dsp control of line hybrid active filter. In Industrial Electronics, 2005. ISIE 2005.
Proceedings of the IEEE International Symposium on, volume 4, pages 1729–1734, 2005.
[30] R. Inzunza and H. Akagi. A 6.6-kv transformerless shunt hybrid active filter for installation
on a power distribution system. Power Electronics, IEEE Transactions on, 20(4):893–900,
july 2005.
[31] L. Moran, I. Pastorini, J. Dixon, and R. Wallace. Series active power filter compensates
current harmonics and voltage unbalance simultaneously. Generation, Transmission and
Distribution, IEE Proceedings-, 147(1):31–36, Jan 2000.
[32] H. Akagi. The state-of-the-art of active filters for power conditioning. In Power Electronics
and Applications, 2005 European Conference on, pages 15 pp.–P.15, 2005.
[33] H. Fujita and H. Akagi. An approach to harmonic current-free ac/dc power conversion
for large industrial loads: the integration of a series active filter with a double-series diode
rectifier. Industry Applications, IEEE Transactions on, 33(5):1233–1240, Sep/Oct 1997.
[34] S. Srianthumrong, H. Fujita, and H. Akagi. Stability analysis of a series active filter integrated with a double-series diode rectifier. Power Electronics, IEEE Transactions on,
17(1):117–124, Jan 2002.
BIBLIOGRAFÍA
94
[35] S. Srianthumrong and H. Akagi. A dc model for transient analysis of a series active filter
integrated with a double-series diode rectifier. Industry Applications, IEEE Transactions
on, 39(3):864–873, May-June 2002.
[36] A.D. le Roux, Hd.T. Mouton, and H. Akagi. Digital control of an integrated series active
filter and diode rectifier with voltage regulation. Industry Applications, IEEE Transactions
on, 39(6):1814–1820, nov.–dec. 2003.
[37] B. Singh and V. Verma. A new control scheme of series active filter for varying rectifier
loads. In Power Electronics and Drive Systems, 2003. PEDS 2003. The Fifth International
Conference on, volume 1, pages 554–559 Vol.1, Nov. 2003.
[38] V.B. Bhavaraju and P.N. Enjeti. An active line conditioner to balance voltages in a threephase system. Industry Applications, IEEE Transactions on, 32(2):287–292, mar/apr 1996.
[39] J. Rocabert, A. Luna, F. Blaabjerg, and P. Rodriguez. Control of power converters in ac
microgrids. Power Electronics, IEEE Transactions on, 27(11):4734–4749, nov. 2012.
[40] M. Aredes, J. Hafner, and K. Heumann. Three-phase four-wire shunt active filter control
strategies. Power Electronics, IEEE Transactions on, 12(2):311–318, March 1997.
[41] S.R. Naidu and D.A. Fernandes. Dynamic voltage restorer based on a four-leg voltage
source converter. Gener. Transm. Distrib., IET, 3(5):437–447, May 2009.
[42] N. Prabhakar and M.K. Mishra. Dynamic hysteresis current control to minimize switching
for three-phase four-leg vsi topology to compensate nonlinear load. Power Electronics,
IEEE Transactions on, 25(8):1935–1942, August 2010.
[43] V. Khadkikar, A. Chandra, and B. Singh. Digital signal processor implementation and
performance evaluation of split capacitor, four-leg and three h-bridge-based three-phase
four-wire shunt active filters. Power Electronics, IET, 4(4):463–470, April 2011.
BIBLIOGRAFÍA
95
[44] Fei Wang, J.L. Duarte, and M.A.M. Hendrix. Grid-interfacing converter systems with
enhanced voltage quality for microgrid application;concept and implementation. Power
Electronics, IEEE Transactions on, 26(12):3501–3513, dec. 2011.
[45] Xueliang Wei. Study on digital pi control of current loop in active power filter. Electrical
and Control Engineering (ICECE), 2010 International Conference on, pages 4287–4290,
June 2010.
[46] R.L. de Araujo Ribeiro, C.C. de Azevedo, and R.M. de Sousa. A robust adaptive control
strategy of active power filters for power-factor correction, harmonic compensation, and
balancing of nonlinear loads. Power Electronics, IEEE Transactions on, 27(2):718 –730,
feb. 2012.
[47] J. Rodriguez, J. Pontt, C. Silva, P. Correa, P. Lezana, P. Cortes, and U. Ammann. Predictive current control of a voltage source inverter. Trans. Ind. Electron., IEEE, 54(1):495–503,
February 2007.
[48] P. Cortes, G. Ortiz, J.I. Yuz, J. Rodriguez, S. Vazquez, and L.G. Franquelo. Model predictive control of an inverter with output LC filter for UPS applications. Trans. Ind. Electron.,
IEEE, 56(6):1875–1883, June 2009.
[49] R. Vargas, P. Cortes, U. Ammann, J. Rodriguez, and J. Pontt. Predictive control of a
three-phase neutral-point-clamped inverter. Trans. Ind. Electron., IEEE, 54(5):2697–2705,
October 2007.
[50] P. Cortes, A. Wilson, S. Kouro, J. Rodriguez, and H. Abu-Rub. Model predictive control
of multilevel cascaded H-bridge inverters. Trans. Ind. Electron., IEEE, 57(8):2691–2699,
August 2010.
[51] P. Lezana, R. Aguilera, and D.E. Quevedo. Model predictive control of an asymmetric
flying capacitor converter. Trans. Ind. Electron., IEEE, 56(6):1839–1846, June 2009.
BIBLIOGRAFÍA
96
[52] P. Correa, J. Rodriguez, I. Lizama, and D. Andler. A predictive control scheme for currentsource rectifiers. Trans. Ind. Electron., IEEE, 56(5):1813–1815, May 2009.
[53] M. Rivera, J. Rodriguez, B. Wu, J.R. Espinoza, and C. Rojas. Current control for an
indirect matrix converter with filter resonance mitigation. Trans. Ind. Electron., IEEE,
59(1):71–79, January 2012.
[54] P. Correa, M. Pacas, and J. Rodriguez. Predictive torque control for inverter-fed induction
machines. Trans. Ind. Electron., IEEE, 54(2):1073–1079, April 2007.
[55] M. Odavic, V. Biagini, P. Zanchetta, M. Sumner, and M. Degano. One-sample-periodahead predictive current control for high-performance active shunt power filters. Power
Electronics, IET, 4(4):414–423, April 2011.
[56] Ieee recommended practice for electric power distribution for industrial plants. IEEE Std
141-1993, page I, 1994.
[57] R.L. de Araujo Ribeiro, C.C. de Azevedo, and R.M. de Sousa. A robust adaptive control
strategy of active power filters for power-factor correction, harmonic compensation, and
balancing of nonlinear loads. Power Electronics, IEEE Transactions on, 27(2):718–730,
feb. 2012.
[58] M. Sumner, B. Palethorpe, D.W.P. Thomas, P. Zanchetta, and M.C. Di Piazza. A technique
for power supply harmonic impedance estimation using a controlled voltage disturbance.
Power Electronics, IEEE Transactions on, 17(2):207–215, March 2002.
[59] S.M. Ali and M.P. Kazmierkowski. Pwm voltage and current control of four-leg vsi. ISIE,
1:196–201, July 1998. Pretoria, South Africa.
[60] S. Kouro, P. Cortes, R. Vargas, U. Ammann, and J. Rodriguez. Model predictive control A simple and powerful method to control power converters. Trans. Ind. Electron., IEEE,
56(6):1826–1838, June 2009.
BIBLIOGRAFÍA
97
[61] D.E. Quevedo, R.P. Aguilera, M.A. Perez, P. Cortes, and R. Lizana. Model predictive
control of an afe rectifier with dynamic references. Power Electronics, IEEE Transactions
on, 27(7):3128 –3136, july 2012.
[62] Zhonghan Shen, Xuegui Chang, Weiwei Wang, Xi Tan, Na Yan, and Hao Min. Predictive
digital current control of single-inductor multiple-output converters in ccm with low cross
regulation. Power Electronics, IEEE Transactions on, 27(4):1917 –1925, april 2012.
[63] M. Rivera, C. Rojas, J. Rodriidguez, P. Wheeler, Bin Wu, and J.R. Espinoza. Predictive
current control with input filter resonance mitigation for a direct matrix converter. Power
Electronics, IEEE Transactions on, 26(10):2794 –2803, oct. 2011.
[64] M. Preindl and S. Bolognani. Model predictive direct speed control with finite control set
of pmsm drive systems. Power Electronics, IEEE Transactions on, PP(99):1, 2012.
[65] T. Geyer. Computationally efficient model predictive direct torque control. Power Electronics, IEEE Transactions on, 26(10):2804 –2816, oct. 2011.
[66] M. Rivera, V. Yaramasu, J. Rodriguez, and Bin Wu. Model predictive current control of
two-level four-leg inverters;part ii: Experimental implementation and validation. Power
Electronics, IEEE Transactions on, 28(7):3469–3478, July 2013.
[67] V. Yaramasu, M. Rivera, Bin Wu, and J. Rodriguez. Model predictive current control
of two-level four-leg inverters;part i: Concept, algorithm, and simulation analysis. Power
Electronics, IEEE Transactions on, 28(7):3459–3468, July 2013.
[68] M. I. M. Montero, E. R. Cadaval, and F. B. Gonzalez. Comparison of control strategies
for shunt active power filters in three-phase four-wire systems. Power Electronics, IEEE
Transactions on, 22(1):229–236, January 2007.
[69] Se-Kyo Chung. A phase tracking system for three phase utility interface inverters. Power
Electronics, IEEE Transactions on, 15(3):431 –438, May 2000.
98
BIBLIOGRAFÍA
[70] M. Karimi-Ghartemani, S.A. Khajehoddin, P.K. Jain, A. Bakhshai, and M. Mojiri. Addressing dc component in pll and notch filter algorithms. Power Electronics, IEEE Transactions
on, 27(1):78 –86, jan. 2012.
[71] L.S. Czarnecki. On some misinterpretations of the instantaneous reactive power p-q theory.
Power Electronics, IEEE Transactions on, 19(3):828 – 836, may 2004.
[72] N. Hatti, K. Hasegawa, and H. Akagi. A 6.6-kv transformerless motor drive using a five-level
diode-clamped pwm inverter for energy savings of pumps and blowers. Power Electronics,
IEEE Transactions on, 24(3):796 –803, march 2009.
[73] V.F. Corasaniti, M.B. Barbieri, P.L. Arnera, and M.I. Valla. Hybrid power filter to enhance
power quality in a medium-voltage distribution network. Industrial Electronics, IEEE
Transactions on, 56(8):2885 –2893, aug. 2009.
[74] V. Verma, B. Singh, A. Chandra, and K. Al-Haddad. Power conditioner for variablefrequency drives in offshore oil fields.
Industry Applications, IEEE Transactions on,
46(2):731 –739, march-april 2010.
[75] M. Malinowski, K. Gopakumar, J. Rodriguez, and M.A. Perez. A survey on cascaded
multilevel inverters. Industrial Electronics, IEEE Transactions on, 57(7):2197 –2206, july
2010.
[76] H. Abu-Rub, J. Holtz, J. Rodriguez, and Ge Baoming. Medium-voltage multilevel converters ;state of the art, challenges, and requirements in industrial applications. Industrial
Electronics, IEEE Transactions on, 57(8):2581 –2596, aug. 2010.
[77] J. Rodriguez, S. Bernet, P.K. Steimer, and I.E. Lizama. A survey on neutral-point-clamped
inverters. Industrial Electronics, IEEE Transactions on, 57(7):2219 –2230, july 2010.
[78] O. Vodyakho and C.C. Mi. Three-level inverter-based shunt active power filter in threephase three-wire and four-wire systems.
24(5):1350 –1363, may 2009.
Power Electronics, IEEE Transactions on,
BIBLIOGRAFÍA
99
[79] Ieee recommended practices and requirements for harmonic control in electrical power
systems. IEEE Std 519-1992, pages 0–1, 1993.
[80] P. Aravena, G. Vallebuona, L. Moran, J. Dixon, and O. Godoy. Passive filters for high power
cycloconverter grinding mill drives. In Industry Applications Society Annual Meeting, 2009.
IAS 2009. IEEE, pages 1–7, oct. 2009.
[81] E.P. Wiechmann, R.P. Burgos, and J. Holtz. Sequential connection and phase control
of a high-current rectifier optimized for copper electrowinning applications. Industrial
Electronics, IEEE Transactions on, 47(4):734–743, aug 2000.
[82] Po-Tai Cheng, S. Bhattacharya, and D.M. Divan. Application of dominant harmonic active filter system with 12 pulse nonlinear loads. Power Delivery, IEEE Transactions on,
14(2):642–647, apr 1999.
[83] E.P. Wiechmann, P. Aqueveque, A.S. Morales, P.F. Acuna, and R. Burgos. Multicell highcurrent rectifier. Industry Applications, IEEE Transactions on, 44(1):238–246, jan.-feb.
2008.
[84] P.S. Maniscalco, V. Scaini, and W.E. Veerkamp. Specifying dc chopper systems for electrochemical applications. Industry Applications, IEEE Transactions on, 37(3):941–948,
may/jun 2001.
[85] P.E. Aqueveque, E.P. Wiechmann, and R.P. Burgos. On the efficiency and reliability of
high-current rectifiers. In Power Electronics Specialists Conference, 2008. PESC 2008.
IEEE, pages 4509–4516, june 2008.
[86] Delince Francois Schipman Kurt. Power quality filters - actively improving quality. ABB
Power Quality Products, pages 51–55, 2011.
[87] A.D. le Roux, H. Mouton, and H. Akagi. Dft-based repetitive control of a series active
filter integrated with a 12-pulse diode rectifier. Power Electronics, IEEE Transactions on,
24(6):1515–1521, june 2009.
BIBLIOGRAFÍA
100
[88] L. Gyugyi N. Hingorani. Understanding facts, concepts and technology of flexible ac transmission systems. IEEE Press, pages 1–35, 2000.
[89] H. Fujita, T. Yamasaki, and H. Akagi. A hybrid active filter for damping of harmonic resonance in industrial power systems. Power Electronics, IEEE Transactions on, 15(2):215–
222, mar 2000.
[90] Zhiguo Pan, F.Z. Peng, and Suilin Wang. Power factor correction using a series active
filter. Power Electronics, IEEE Transactions on, 20(1):148–153, Jan. 2004.
[91] L.A. Moran, J.W. Dixon, and R.R. Wallace. A three-phase active power filter operating
with fixed switching frequency for reactive power and current harmonic compensation.
Industrial Electronics, IEEE Transactions on, 42(4):402–408, aug 1995.
[92] A. Varschavsky, J. Dixon, M. Rotella, and L. Moran. Cascaded nine-level inverter for
hybrid-series active power filter, using industrial controller. Industrial Electronics, IEEE
Transactions on, 57(8):2761–2767, aug. 2010.
[93] Sangsun Kim and P.N. Enjeti. A new hybrid active power filter (apf) topology. Power
Electronics, IEEE Transactions on, 17(1):48–54, jan 2002.
[94] V.F. Corasaniti, M.B. Barbieri, P.L. Arnera, and M.I. Valla. Hybrid power filter to enhance
power quality in a medium-voltage distribution network. Industrial Electronics, IEEE
Transactions on, 56(8):2885–2893, aug. 2009.
[95] J.A. Munoz, J.R. Espinoza, C.R. Baier, L.A. Moran, E.E. Espinosa, P.E. Melin, and D.G.
Sbarbaro. Design of a discrete-time linear control strategy for a multicell upqc. Industrial
Electronics, IEEE Transactions on, 59(10):3797–3807, oct. 2012.
[96] P. Flores, J. Dixon, M. Ortuzar, R. Carmi, P. Barriuso, and L. Moran. Static var compensator and active power filter with power injection capability, using 27-level inverters and
photovoltaic cells. Industrial Electronics, IEEE Transactions on, 56(1):130–138, jan. 2009.
BIBLIOGRAFÍA
101
[97] G. Fedele, C. Picardi, and D. Sgro. A power electrical signal tracking strategy based on the
modulating functions method. Industrial Electronics, IEEE Transactions on, 56(10):4079–
4087, oct. 2009.
[98] C.H. da Silva, R.R. Pereira, L.E.B. da Silva, G. Lambert-Torres, B.K. Bose, and S.U. Ahn.
A digital pll scheme for three-phase system using modified synchronous reference frame.
Industrial Electronics, IEEE Transactions on, 57(11):3814–3821, nov. 2010.