Conductividad Térmica en Líquidos

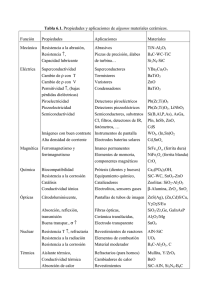
Conducción
Transporte Molecular de Energía
Fenómenos de Transporte
ILQ – 230 (II – 2011)
Prof. Alonso Jaques
Mecanismos de Transporte de Energía
• Conducción
Típicamente tiene lugar a través de sólidos, líquidos y gases.
• Convección
Transferencia de calor a través del movimiento de volumen de entidades
macroscópicas: flujo de fluidos.
• Radiación
No existe medio físico para este modo de transferencia de calor. (Ondas
Electromagnéticas)
• (Más las combinaciones de los modos anteriores)
Adaptado de Bird, Steward, Lightfoot 2ed, Ch 9.
Ley de Fourier de Transporte de Energía
Comúnmente se entiende que la
conducción de calor (difusión de
calor) siga el gradiente de
temperatura en un sistema, i.e., el
calor fluye debido a un gradiente
de temperatura, a una velocidad
(flujo) que es proporcional a la
magnitud del gradiente.
Este
comportamiento llamado Ley
Fourier En un sistema 1-D
(Cartesiano), esto viene descrito
por
𝑑𝑇
𝑞𝑦 = −𝑘
𝑑𝑦
Ley de Fourier y Conductividad Térmica
• La Ley de Fourier define la conductividad térmica, 𝑘 W/m ∙ K ,
• Combinando el transporte de energía entre las diferentes direcciones .
• Se puede expresar de forma vectorial como,
𝐪 = −𝑘 𝛻𝑇
• En de asimetría en la conductividad termica (𝑘𝑥 ≠ 𝑘𝑦 , 𝑘𝑧 ), se debe considerar el
tensor de conductividad térmica.
𝐪 = − 𝐤 ∙ 𝛻𝑇
Ley de Fourier y Conductividad Térmica
• Se define la difusividad térmica 𝛼 𝑚2 /𝑠 , (considerar como una medida de la
inercia en el transporte de energía).
𝛼=
𝑘
𝜌𝐶𝑝
• Notar que las unidades de 𝛼 son equivalentes a las unidades de viscosidad
cinemática, 𝜈.
• Se hace conveniente comparar el transporte de momentum y energía en un
mismo sistema. Definiendo el numero de Prandtl,
𝜈 𝐶𝑝 𝜇
𝑃𝑟 = =
𝛼
𝑘
Adaptado de Bird, Steward, Lightfoot 2ed, Ch 9.
• La pared de un congelador consiste en una placa de 10
cm de espesor de espuma de poliestireno como aislante.
La temperatura dentro del congelador es -5 C, mientras
que la temperatura exterior corresponde a la
“temperatura ambiente (25 C). La conductividad
térmica de la espuma es k = 0.032 W/m·K ¿Cuál es el
flujo de calor (en estado estacionario) a través de la
pared del congelador?
• Desarrolle una expresión que entregue la distribución
radial de temperatura en la pared de una cañería
cilíndrica, asumiendo estado estacionario y k constante.
Conductividad Térmica en Gases
Tal como se mostro que las propiedades de transporte de momentum (viscosidad)
puede ser estimada considerando las iteraciones entre las moléculas (Teoría Cinética
de Gases y Teoría de Champman-Enskog), similarmente se puede analizar la
conductividad térmica.
• La energía de traslación de una molécula es dada por:
1
3
2
𝑈 = 𝑚 𝑣 = 𝑘𝑏 𝑇
2
2
3
2
• Recordar para gas ideal,𝐶𝑃 − 𝐶𝑉 = 𝑅, gas ideal monoatómico 𝐶𝑉 = 𝑅 :
Conductividad Térmica en Gases (a bajas presiones)
Teoría Cinética
Realizando un balance de energía entre
con respecto a dos planos de referencia
se obtiene,
1
𝑘 = 𝜌𝐶𝑉 𝑣 𝜆𝑓
3
Sustituyendo los resultados obtenidos
para la trayectoria libre media y la
velocidad promedio se tiene,
𝑘=
𝑘 = 𝐶𝑉 𝜇
1
𝑑𝑝
2
𝑘𝑏 3 𝑇
𝜋 2𝑚
Pr = 1,67
∞
𝑣=
0
Adaptado de Bird, Steward, Lightfoot 2ed, Ch 9.
8𝑘𝑏 𝑇
𝑣𝑃𝑣 𝑣 𝑑𝑣 =
𝜋𝑚
𝑣
1
λ𝑓 =
=
𝑁
𝜔𝑐
2𝜋𝑑𝑝 2 𝑉
1 2
Conductividad Térmica en Gases (a bajas presiones)
Chapman-Enskog
• Incorporando el efecto de interacción entre las moléculas se deriva una expresión
similar para la conductividad térmica basada en la teoría de Chapman-Enskog,
𝑘 = 1,9891
× 10−4
𝑇/𝑀𝑤
𝜎𝑓 2 Ω𝑘
cal
cm ∙ s
𝜎𝑓 : Diámetro característico de la molécula; Ω𝑘 : Integral de colisión
La conductividad térmica y el numero de Prandlt:
5
𝑘 = 𝐶𝑉 𝜇
2
Pr = 0,67
Potencial de Lennard-Jones
Φ𝑢 𝑟 = 4𝜀𝑓
𝜎𝑓
𝑟
12
𝜎𝑓
−
𝑟
6
• El potencial de Lennard-Jones es
una aproximación matemática
entre dos átomos (o moléculas)
no enlazados basado en su grado
de separación.
- 𝜎𝑓 : Diámetro característico de la
molécula.
- 𝜀𝑓 : Energía característica de
interacción entre las molécula.
Adaptado de Bird, Steward, Lightfoot 2ed, Ch 9.
Conductividad Térmica de mezcla de gases
• En caso de mezclas gaseosas puede ser estimado por,
Conductividad Térmica en Líquidos
El mecanismo de transporte de energía en líquidos es similar al de los gases. No
obstante, la mayor densidad conduce a mayores velocidades de transferencia de
energía (i.e., conductividades mayores).
Observaciones empíricas nos dicen que las conductividades térmicas en líquidos
típicamente se escalan linealmente con la temperatura como:
klíquidos  a  bT
Donde T es la temperatura, y a, y b son constantes empíricas.
Note que tanto en gases como líquidos, estamos hablando acerca de movimiento
molecular escalado, y no de movimiento a macroescala visto en flujo
volumétricos de fluidos (transporte de moméntum).
Conductividad Térmica en Líquidos
La conductividad térmica en líquidos puede analizarse revistando la teoría cinética y
considerando la velocidad promedio de las partículas en función de la velocidad del
sonido.
• Velocidad promedio de partículas en el liquido:
𝑣𝑙𝑖𝑞
8𝐶𝑉
=
𝜋𝐶𝑃
1/2
𝑐𝜆𝑙
𝑐𝜆𝑙 : velocidad del sonido en el liquido. Distancia libre media en el liquido,
𝑀𝑤
λ𝑓 =
𝜌𝑁
1/3
• La conductividad térmica en liquido puede ser estimada como
𝑘=
𝜌𝑘𝑏 3 𝑁 2
𝑀𝑤
2
1/3
8𝐶𝑉
𝜋𝐶𝑃
1/2
𝑐𝜆𝑙
Conductividad Térmica en Solidos
El mecanismo de transporte de energía en sólidos es más complejo. Depende
extremadamente de la estructura cristalina y de electrones del material.
En breve, existen dos modos primarios de conducción en sólidos:
• Vibraciones de Red (fonones) (dominante en aisladores eléctricos,
dielectricos)
• Conducción de Electrones (dominante en conductores eléctricos)
Conductividad Térmica en Solidos Dieléctricos
Lo más simple es considerar el mecanismo de
conductividad térmica en sólidos cristalinos, como si se
pudiera expresar en términos de fonones, o vibraciones
de red (ondas) que permiten el transporte de energía a
través del sólido.
Nota: Los fonones pueden incluso ser considerados que
actúan como partículas discretas (dualidad de ondapartícula), lo que los hace más fáciles de entender para
algunos.
La conductividad térmica puede estimarse como,
1
𝑘 = 𝜌𝐶𝑉 λ𝑓 𝑐𝜆𝑠
3
http://en.wikipedia.org/wiki/Phonon
Conductividad Térmica en Solidos Metalicos
• En metales se puede descomponer la conductividad térmica en términos de
contribución por fonones y electrones: (𝑘 = 𝑘fonones + 𝑘electrones )
• Por lo general en metales 𝑘electrones ≫ 𝑘fonones
• La contribución por el transporte de electrones a la conductividad térmica
puede estimarse a partir de la ley de Weidmann-Franz ,
𝑘electrones = Lo 𝜎 𝑇
donde, Lo = 2,45 𝑊 Ω/𝐾 2 (constante de Lorenz), 𝜎: conductividad eléctrica.