FICHA 1G_definitiva Model (1)

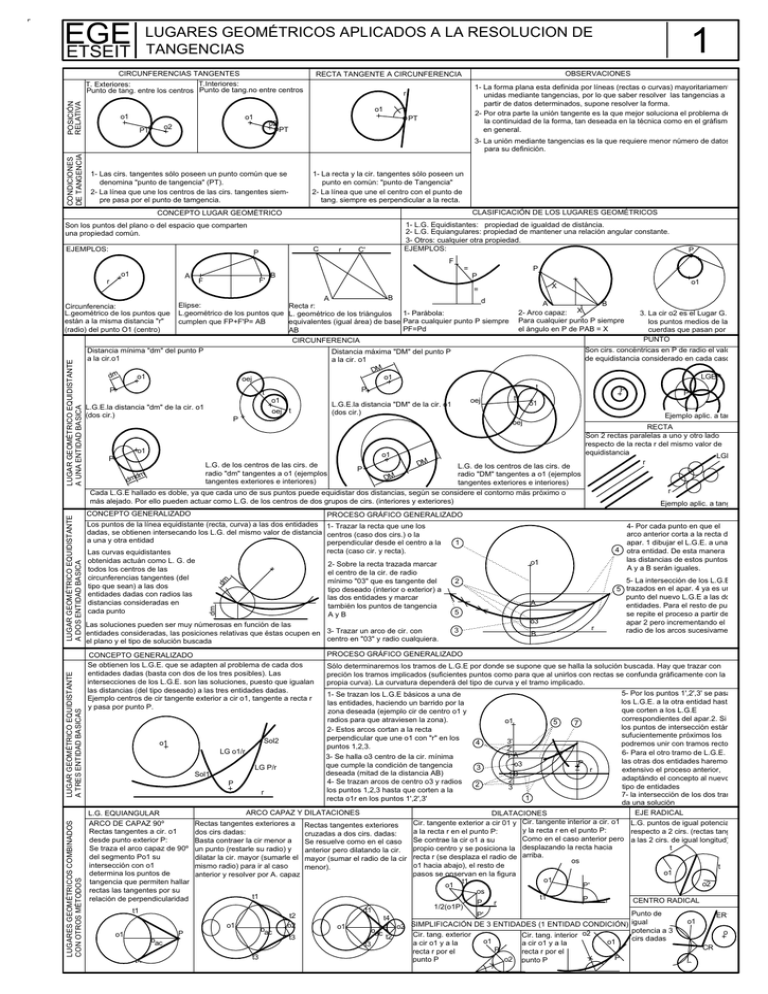
EGE
ETSEIT
LUGARES GEOMÉTRICOS APLICADOS A LA RESOLUCION DE
TANGENCIAS
POSICIÓN
RELATIVA
CIRCUNFERENCIAS TANGENTES
T.Interiores:
T. Exteriores:
Punto de tang. entre los centros Punto de tang.no entre centros
OBSERVACIONES
RECTA TANGENTE A CIRCUNFERENCIA
1- La forma plana esta definida por líneas (rectas o curvas) mayoritariamente
unidas mediante tangencias, por lo que saber resolver las tangencias a
partir de datos determinados, supone resolver la forma.
2- Por otra parte la unión tangente es la que mejor soluciona el problema de
la continuidad de la forma, tan deseada en la técnica como en el gráfismo
en general.
r
o1
o1
o1
PT
o2
o2
1
PT
PT
CONDICIONES
DE TANGENCIA
3- La unión mediante tangencias es la que requiere menor número de datos
para su definición.
1- Las cirs. tangentes sólo poseen un punto común que se
denomina "punto de tangencia" (PT).
2- La línea que une los centros de las cirs. tangentes siempre pasa por el punto de tamgencia.
1- La recta y la cir. tangentes sólo poseen un
punto en común: "punto de Tangencia"
2- La línea que une el centro con el punto de
tang. siempre es perpendicular a la recta.
CLASIFICACIÓN DE LOS LUGARES GEOMÉTRICOS
CONCEPTO LUGAR GEOMÉTRICO
1- L.G. Equidistantes: propiedad de igualdad de distáncia.
2- L.G. Equiangulares: propiedad de mantener una relación angular constante.
3- Otros: cualquier otra propiedad.
EJEMPLOS:
Son los puntos del plano o del espacio que comparten
una propiedad común.
EJEMPLOS:
C
P
r
C'
P
F
=
o1
A
r
F'
F
B
P
P
Circunferencia:
L.geométrico de los puntos que
están a la misma distancia "r"
(radio) del punto O1 (centro)
o1
X
=
B
A
d
Elipse:
Recta r:
L.geométrico de los puntos que L. geométrico de los triángulos 1- Parábola:
cumplen que FP+F'P= AB
equivalentes (igual área) de base Para cualquier punto P siempre
PF=Pd
AB
A
B
2- Arco capaz: X
Para cualquier punto P siempre
el ángulo en P de PAB = X
LUGAR GEOMÉTRICO EQUIDISTANTE
A UNA ENTIDAD BASICA
CIRCUNFERENCIA
Distancia mínima "dm" del punto P
a la cir.o1
dm
o1
o1
dm
dm
oej
L.G.E.la distancia "DM" de la cir. o1
(dos cir.)
oej t
t
o1
DM
P
DM
L.G. de los centros de las cirs. de
radio "DM" tangentes a o1 (ejemplos
tangentes exteriores e interiores)
RECTA
Son 2 rectas paralelas a uno y otro lado
respecto de la recta r del mismo valor de
equidistancia
LGEr
r
r
LUGARES GEOMÉTRICOS COMBINADOS
CON OTROS MÉTODOS
LUGAR GEOMÉTRICO EQUIDISTANTE
A TRES ENTIDAD BASICAS
dm
Las curvas equidistantes
obtenidas actuán como L. G. de
todos los centros de las
circunferencias tangentes (del
tipo que sean) a las dos
entidades dadas con radios las
distancias consideradas en
cada punto
dm
LUGAR GEOMÉTRICO EQUIDISTANTE
A DOS ENTIDAD BASICA
Cada L.G.E hallado es doble, ya que cada uno de sus puntos puede equidistar dos distancias, según se considere el contorno más próximo o
más alejado. Por ello pueden actuar como L.G. de los centros de dos grupos de cirs. (interiores y exteriores)
CONCEPTO GENERALIZADO
Los puntos de la línea equidistante (recta, curva) a las dos entidades
dadas, se obtienen intersecando los L.G. del mismo valor de distancia
a una y otra entidad
Ejemplo aplic. a tang.
PROCESO GRÁFICO GENERALIZADO
1- Trazar la recta que une los
centros (caso dos cirs.) o la
perpendicular desde el centro a la
recta (caso cir. y recta).
2- Sobre la recta trazada marcar
el centro de la cir. de radio
mínimo "03" que es tangente del
tipo deseado (interior o exterior) a
las dos entidades y marcar
también los puntos de tangencia
AyB
Las soluciones pueden ser muy númerosas en función de las
entidades consideradas, las posiciones relativas que éstas ocupen en 3- Trazar un arco de cir. con
centro en "03" y radio cualquiera.
el plano y el tipo de solución buscada
CONCEPTO GENERALIZADO
Se obtienen los L.G.E. que se adapten al problema de cada dos
entidades dadas (basta con dos de los tres posibles). Las
intersecciones de los L.G.E. son las soluciones, puesto que igualan
las distancias (del tipo deseado) a las tres entidades dadas.
Ejemplo centros de cir tangente exterior a cir o1, tangente a recta r
y pasa por punto P.
P
o1
oej
L.G. de los centros de las cirs. de
radio "dm" tangentes a o1 (ejemplos
tangentes exteriores e interiores)
P
Ejemplo aplic. a tang.
P
o1
P
LGEP
t
P
t
L.G.E.la distancia "dm" de la cir. o1
(dos cir.)
Son cirs. concéntricas en P de radio el valor
de equidistancia considerado en cada caso
Distancia máxima "DM" del punto P
a la cir. o1
DM
o1
oej
P
3. La cir o2 es el Lugar G. de
los puntos medios de las
cuerdas que pasan por P.
PUNTO
4- Por cada punto en que el
arco anterior corta a la recta del
apar. 1 dibujar el L.G.E. a una y
4 otra entidad. De esta manera
las distancias de estos puntos a
A y a B serán iguales.
1
o1
2
A
5
o3
3
B
r
5- La intersección de los L.G.E.
5 trazados en el apar. 4 ya es un
punto del nuevo L.G.E a las dos
entidades. Para el resto de punto
se repite el proceso a partir del
apar 2 pero incrementando el
radio de los arcos sucesivamente
PROCESO GRÁFICO GENERALIZADO
Sólo determinaremos los tramos de L.G.E por donde se supone que se halla la solución buscada. Hay que trazar con
preción los tramos implicados (suficientes puntos como para que al unirlos con rectas se confunda gráficamente con la
propia curva). La curvatura dependerá del tipo de curva y el tramo implicado.
5- Por los puntos 1',2',3' se pasan
los L.G.E. a la otra entidad hasta
que corten a los L.G.E
correspondientes del apar.2. Si
o1
5
7
los puntos de intersección están
sufucientemente próximos los
Sol2
3'
4
o1
podremos unir con tramos rectos
2'
LG o1/r
6- Para el otro tramo de L.G.E. a
1' A
las otras dos entidades haremos
P
o3
3
LG P/r
r
extensivo el proceso anterior,
Sol1
1B
adaptándo el concepto al nuevo
2
P
2
tipo de entidades
3
r
7la intersección de los dos tramos
1
da una solución
ARCO CAPAZ Y DILATACIONES
EJE RADICAL
DILATACIONES
L.G. EQUIANGULAR
Cir. tangente exterior a cir 01 y Cir. tangente interior a cir. o1 L.G. puntos de igual potencia
ARCO DE CAPAZ 90º
Rectas tangentes exteriores a Rectas tangentes exteriores
y la recta r en el punto P:
respecto a 2 cirs. (rectas tang.
a la recta r en el punto P:
Rectas tangentes a cir. o1
dos cirs dadas:
cruzadas a dos cirs. dadas:
Como en el caso anterior pero a las 2 cirs. de igual longitud)
desde punto exterior P:
Basta contraer la cir menor a
Se resuelve como en el caso Se contrae la cir o1 a su
t
propio centro y se posiciona la desplazando la recta hacia
Se traza el arco capaz de 90º un punto (restarle su radio) y
anterior pero dilatando la cir.
del segmento Po1 su
dilatar la cir. mayor (sumarle el mayor (sumar el radio de la cir recta r (se desplaza el radio de arriba.
os
intersección con o1
o1
hacia
abajo),
el
resto
de
mismo radio) para ir al caso
t
menor).
o1
determina los puntos de
pasos se onservan en la figura
anterior y resolver por A. capaz
o1
t1
tangencia que permiten hallar
o2
P'
o1
rectas las tangentes por su
os
t1
t1
relación de perpendicularidad
P
CENTRO RADICAL
r
P
r
1/2(o1P)
t1
t1
Punto de
P'
ER1
t2
t4
o1
igual
o1
o2
o2 SIMPLIFICACIÓN DE 3 ENTIDADES (1 ENTIDAD CONDICIÓN)
o1
oac
potencia
a
3
o
o2
P
ac
o1
Cir. tang. exterior
Cir. tang. interior o2
t2
t3
cirs dadas
oac
o1
o1
a cir o1 y a la
a cir o1 y a la
t3
CR
P
recta r por el
recta r por el
t3
P
o2 punto P
punto P
t2
o3
1- Se trazan los L.G.E básicos a una de
las entidades, haciendo un barrido por la
zona deseada (ejemplo cir de centro o1 y
radios para que atraviesen la zona).
2- Estos arcos cortan a la recta
perpendicular que une o1 con "r" en los
puntos 1,2,3.
3- Se halla o3 centro de la cir. mínima
que cumple la condición de tangencia
deseada (mitad de la distancia AB)
4- Se trazan arcos de centro o3 y radios
los puntos 1,2,3 hasta que corten a la
recta o1r en los puntos 1',2',3'