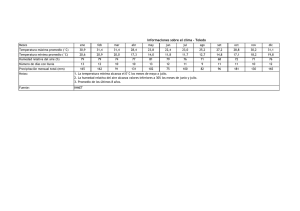
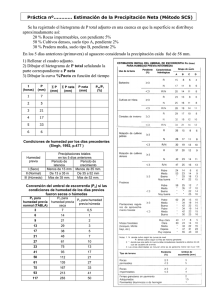
Línea de Acción: Integración de componentes del balance

Línea de Acción: Integración de componentes del balance hidrológico en
zonas de temporal.
Entregable: Algoritmo (diagrama de flujo detallado) del seguimiento para
la obtención y análisis de información documentada.
SECRETARIA DE AGRICULTURA, GANADERÍA, DESARROLLO RURAL, PESCA Y ALIMENTACIÓN
SUBSECRETARÍA DE FOMENTO A LOS AGRO NEGOCIOS
DIRECCIÓN GENERAL DE ESTUDIOS AGROPECUARIOS Y PESQUEROS
1
PRESENTACIÓN
El presente forma parte de la segunda
entrega
programada
del
contrato:
“Generación de Información y Análisis
Integral de la Red Nacional de
Observatorios Agro tecnológicos y
elaboración de bases de datos
estratégicas para apoyar la toma de
decisiones en el sector agrícola del
País”. Se trata de la acción 10:
Integración de componentes del
balance hidrológico en zonas de
temporal. En esta fase se describe el
algoritmo (diagrama de flujo detallado) del
seguimiento para la obtención y análisis
de información documentada. Se parte de
un diagrama de flujo de donde se
describen los componentes del balance
hídrico aplicable a las zonas de estudio.
2
Contenido
I.
Introducción .............................................................................................................. 5
II.
Descripción del Balance de agua en el suelo ........................................................... 5
II.1 El modelo conceptual ............................................................................................. 6
II.2 Definición de variables ........................................................................................... 6
II.2.1 Cambio del contenido de humedad en el suelo (mm).
....................... 7
II.2.2 Precipitación .................................................................................................... 8
II.2.2.1 Cálculo de probabilidad de ocurrencia de lluvia ........................................ 8
II.2.2.2 Cuantificación de la lluvia ........................................................................ 10
II.3 Escurrimiento superficial ...................................................................................... 11
II.3.1 Escurrimiento fuera del área de cultivo .......................................................... 14
II.4 Evapotranspiración .............................................................................................. 14
II.4.1 Evapotranspiración del Cultivo de referencia (ETo)....................................... 15
II.4.2 Evapotranspiración actual (ETc) .................................................................... 18
II.4.2.1 Evapotranspiración del cultivo bajo condiciones de estrés hídrico .......... 19
II.4.2.2 Cálculo del coeficiente Ks ....................................................................... 19
II.5 Capacidad de retención de humedad del suelo ................................................... 20
II.6 Ascenso capilar .................................................................................................... 23
II.7 Percolación profunda ........................................................................................... 24
III.
Alcances de la acción .......................................................................................... 24
IV.
Literatura citada ................................................................................................... 25
3
Índice de tablas
Tabla 1. Valores de la curva numérica según tipo de ecosistema, porcentaje de
cobertura del suelo y potencial de escurrimiento. Tomado de (USDA-NRCS, 2004) .... 14
Tabla 2. Valores k para ciertos cultivos en algunas áreas de E.U.A. ............................ 17
Tabla 3. Porcentaje diario de horas del día con luz, según latitud y mes del año.
Tomado de Brouwer y Heibloem, (1986)....................................................................... 17
Tabla 4. Rangos medios y máximos de las características hídricas del suelo según las
clases texturales del triangulo de texturas. Tomado de Tutorial Soil Water
Characteristics: Hydraulic properties calculator versión 6.02.74 (Saxton y Rawls). ...... 23
Índice de figuras
Figura 1. Modelo conceptual y variables del balance diario de agua del suelo. ............. 6
Figura 2. Procedimiento para generar observaciones aleatorias de una función
probabilística de densidad............................................................................................... 9
Figura 3. Variables incluidas en el método de la servicio de conservación de suelo de
Estados Unidos (SCS). Tomado de (Chow et al, 1988) ................................................ 11
Figura 4.Valores representativos de Humedad Aprovechable (HA) para diferentes tipos
de suelos (Walker, 2003). ............................................................................................. 21
Figura 5. Representación esquemática del contenido volumétrico de humedad a
Capacidad de Campo y Punto de Marchitez Permanente (Sánchez y Catalán 2006). . 22
4
Entregable: Algoritmo (diagrama de flujo detallado) del seguimiento para la obtención y
análisis de información documentada.
I. Introducción
La capacidad de los ecosistemas para mantener una producción sostenida esta
determinada por variables físicas y climáticas del medio como: precipitación, tipo de
suelo, temperaturas, elevación, etc. En ecosistemas áridos las variables climáticas
adquieren relevancia y dentro de éstas la precipitación pluvial define por pucho la
capacidad productiva o potencial productivo de las especies cultivadas.
En la producción agrícola, una sequía puede ser definida como un periodo de clima
seco anormal que causa serios impactos en el balance de agua del área considerada.
Se caracteriza por temperaturas elevadas y falta de precipitación con impactos
económicos de magnitud. En consecuencia, el historial del clima es la base para prever
los escenarios futuros esperados bajo los cuales se puede desarrollar el balance de
humedad y así estar en posibilidades de conocer el rendimiento esperado de los
cultivos.
En esta tesitura, el punto racional de partida para una adecuada planeación de la
agricultura lo constituye el balance de humedad en el suelo para estar en posibilidades
de obtener una apreciación objetiva del riesgo productivo bajo condiciones de
variabilidad climática.
II. Descripción del Balance de agua en el suelo
El balance de agua en el suelo cuantifica los movimientos del agua para un periodo de
tiempo en particular. En agricultura es deseable realizar este balance en forma diaria,
como una manera conveniente de identificar periodos de déficit o exceso de humedad,
que a su vez servirá para calendarizar riegos, o zonificar cultivos en áreas de temporal.
El balance diario se realiza a partir de conocer la humedad antecedente o inicial en el
suelo (
) en un punto de control, añadiendo las entradas al sistema debido a
precipitación (PP), escurrimiento (Q), ascenso capilar (δ), y descontando las perdidas
por evapotranspiración (ET), percolación profunda (Z) y escurrimiento fuera del área de
cultivo (Qo). (Martin de Santa Olalla et al, 2005; Sánchez, 1994). El término pérdidas,
en el caso de la evapotranspiración se refiere a la cantidad de agua que el suelo
“pierde” por este concepto.
El diagrama conceptual del balance de humedad en el suelo es representado en la
Figura 1.
5
Figura 1. Modelo conceptual y variables del balance diario de agua del suelo.
II.1 El modelo conceptual
Como se ha anotado anteriormente, es importante la conceptualización del modelo en
aras de definir los algoritmos ó las relaciones funcionales que cuantificarán cada una
de las variables que intervienen en el balance. En el presente caso, se parte de la
delimitación de una sección de suelo cuyas fronteras, en el eje vertical, son la
superficie del suelo y la profundidad de la zona de raíces. En esta sección quedan
definidas las variables que intervienen en el balance de humedad. Es de notarse la
importancia que juega el tipo de suelo (propiedades físicas) en la disponibilidad de
agua para el desarrollo de los cultivos.
II.2 Definición de variables
La ecuación del balance diario del suelo que actúa sobre el modelo conceptual descrito
anteriormente es representado por:
1
6
Donde
= Cambio en el contenido de humedad en el suelo (mm) en el día i.
Contenido de humedad en el suelo en el día anterior (mm).
= Precipitación en el día i en mm.
= Escurrimiento superficial que se queda en el área de cultivo (mm) en el día i.
= Ascenso capilar (mm) en el día i.
= Evapotranspiración del cultivo (mm) en el día i.
= Escurrimiento superficial que sale del área de cultivo (mm) en el día i.
= Percolación profunda (mm) en el día i.
La precisión de la ecuación está relacionada directamente con la precisión en que se
mide cada componente (Castillo y Sentís, 2001).
A continuación se describe cada uno de los componentes de la ecuación de balance de
agua en el suelo.
II.2.1 Cambio del contenido de humedad en el suelo (mm).
Como su nombre lo indica, este parámetro se refiere al contenido de humedad en el
suelo el día anterior al día en que se realiza el balance, expresado en mm. En el primer
día donde se realiza el balance de agua en el suelo, se considera que el contenido de
humedad es igual a el contenido volumétrico de humedad inicial ( ).
Existen varios métodos para calcular
, el más común y preciso es el método
gravimétrico que consiste en tomar una muestra de suelo pesarla (PSH) y después
dejarla secar en un horno a 105°C por 24 horas para obtener el peso de suelo seco
(PSS) con este valor se obtiene contenido de humedad inicial en base a masa (W).
2
El contenido volumétrico de humedad inicial se obtiene con la formula:
3
7
Donde da es la densidad aparente del suelo, W contenido gravimétrico de humedad
inicial,
se refiere a la densidad del agua (1 gr. cm-3). Este valor es necesario para
iniciar el cálculo del balance de agua en el suelo.
II.2.2 Precipitación
En aras de conocer el riesgo de falla por variaciones en el régimen pluvial en las zonas
de temporal del país, el dato de entrada de lluvia al balance diario de humedad, en el
presente algoritmo se considera aleatorio y representado por una función probabilística
de densidad (fpd). Así, se hace uso de un generador de datos sintéticos de lluvia
partiendo de los parámetros de la “fpd” que describen el comportamiento de esta
variable a través del tiempo.
El generador de precipitación diaria es un modelo cadenas de Markov - distribución
Weibull simplificada y fue utilizada para definir la ocurrencia de periodos secos y
periodos húmedos. Así entonces, cuando en un día, un evento de lluvia ocurre, la
cuantificación del evento se realiza utilizando la ecuación de la distribución Weibull
simplificada.
II.2.2.1 Cálculo de probabilidad de ocurrencia de lluvia
Como se ha asentado, un modelo de cadenas de Markov de primer orden es utilizada
para conocer la ocurrencia de lluvia para un día en particular. Este proceso estocástico
ha sido ampliamente utilizado para la simulación de precipitación. (Nicks et al, 1990;
Sánchez, 1994; Stöckle et al, 1999; Richardson y Wright, 1984).
Para generar los días secos y los días húmedos, fueron utilizadas las probabilidades
PWD (probabilidad de que en un día determinado llueva dado que el día anterior no
llovió) y PWW (probabilidad de que en un día determinado llueva dado que el día
anterior también llovió). De esta manera, si existe un evento lluvioso dado que el día
anterior fue seco, PWD es la probabilidad de precipitación, si existe un evento de lluvia
dado que el día anterior fue húmedo PWW es la probabilidad de precipitación.
Existen otras dos probabilidades complementarias para PWW y PWD y estas son
calculadas a partir de:
4
5
8
Donde PDW, es la probabilidad de ocurrencia de lluvia en un seco, dado que el día
anterior fue húmedo. Y PDD es la probabilidad de ocurrencia de un día seco, dado que
el día anterior fue seco.
Los parámetros PWD y PWW necesarios para simular la ocurrencia de la precipitación
fueron generados a partir de valores diarios de precipitación, y agrupados en valores
mensuales, utilizando el modelo WXPARM (Williams et al, 1992), calculando estos
parámetros para más de 2200 estaciones meteorológicas distribuidos en el país. El
modelo WXPARM fue generado originalmente como una sub rutina del modelo EPIC,
que es usado ampliamente para conocer la productividad del suelo bajo condiciones de
erosión. (Maldonado et al, 2001; Schaub et al, 1998;). Sin embargo, este modelo es
también utilizado de forma independiente del EPIC para sintetizar datos de
precipitación, temperatura, viento y radiación solar.
La generación de datos de lluvia requiere de la generación de observaciones aleatorias
las cuales pueden ser generadas de funciones de probabilidad haciendo válido el
hecho de que la probabilidad acumulada de cualquier función se distribuye
uniformemente en el intervalo de 0 a 1. Así, para cualquier variable aleatoria “Y” con
función de probabilidad py(y), la variable:
Py (y ) =
6
y
∫p
y
( x )∂x
−∞
se distribuye aleatoriamente entre el intervalo 0,1. La Figura 2 ilustra el procedimiento
para generar un valor “y” de la distribución py(x):
Py(y)
1
0.8
0.6
0.4
0.2
Ru
0
y
Py(x)
y
Figura 2. Procedimiento para generar observaciones aleatorias de una función probabilística de
densidad
9
Los pasos de este proceso son:
1. Seleccionar un número aleatorio (Ru) de una distribución uniforme en el intervalo
0,1
2. Hacer Py(y)= Ru en la ecuación 6
3. Resolver para “y”
El paso 3 se conoce como el método de transformación inversa. Acorde a lo anterior, el
proceso de simulación de ocurrencia de lluvia en cualquier día en el presente algoritmo,
consiste en generar un numero aleatorio entre 0 y 1 y compararlo con las probabilidad
de ocurrencia de lluvia generados por el WXPARM, PWW y PWD, dependiendo si el
día anterior fue lluvioso (PWW) o no (PWD) respectivamente, si el numero aleatorio es
menor que la probabilidad condicionante en un día en particular (ya sea PWD o PWW),
un evento de lluvia ocurriría, si esto no se cumple, entonces para ese día no existe
lluvia, siguiendo con el cómputo de las demás variables del modelo. Este proceso se
repite sucesivamente, según el periodo de tiempo a simular en base diaria.
II.2.2.2 Cuantificación de la lluvia
Como se ha asentado anteriormente, para conocer la cantidad de lluvia fue utilizada la
ecuación de distribución Weibull simplificada (Selker et al¸1990)
1
Pd = 0.84 * Pmd * [− ln(Ru )]0.75
7
Donde Pd = Precipitación diaria (mm dia-1), Pmd es la precipitación media diaria para el
mes k, Ru es el numero aleatorio entre 0 y 1. Para el cálculo de Pmd se utiliza:
8
Donde Pm Precipitación media en el mes k en mm mes-1, p (w) es la probabilidad de
días húmedos, y Nm es el número de días que tiene el mes k. p (w) es calculada
utilizando la siguiente fórmula:
9
Donde PWD, como ya se ha establecido, es la probabilidad de ocurrencia de un día
lluvioso dado que el día anterior fue seco, y v es el coeficiente de pendiente, varía entre
10
0 y 1. Este coeficiente controla el intervalo entre eventos de precipitación pero no tiene
efectos sobre el número de días húmedos. Cuando v se aproxima a 1, los días
lluviosos no afectan la probabilidad de precipitación; y al contrario valores pequeños de
v otorgan fuertes efectos de días húmedos o lluviosos. Algunos estudios sugieren que
un valor de v = 0.75 da valores satisfactorios de PWD y PWW. (Geng et al, 1986).
II.3 Escurrimiento superficial
Para estimar el escurrimiento medio por evento lluvioso (Q) el presente algoritmo
resuelve las ecuaciones del método de la curva numérica (CN) que fue desarrollado en
1972 por el servicio de conservación de suelo de Estados Unidos (SCS).
La ecuación del método de la curva numérica se basa en la simplificación del evento de
lluvia, basándose en el siguiente corolario: La cantidad de lluvia en exceso o
escurrimiento directo (Q) es siempre menor o igual a la cantidad de precipitación (Pp);
además, después de que el escurrimiento empieza, la cantidad adicional de agua
retenida en la cuenca (Fa), es menor o igual a algún potencial máximo de retención (S).
(Chow et al, 1988)
Figura 3. Variables incluidas en el método de la servicio de conservación de suelo de Estados Unidos
(SCS). Tomado de (Chow et al, 1988)
11
Antes de iniciar el encharcamiento del suelo hay cierta cantidad de lluvia Ia para el cual
no hay escurrimiento, entonces el potencial de escurrimiento es Pp-Ia. La hipótesis del
método de la SCS es que las dos proporciones de agua actuales son iguales a las dos
cantidades potenciales, esto es:
10
Del principio de continuidad se tiene
11
Combinando las ecuaciones 10 y 11, y despejando Q se obtiene:
12
Esta ecuación es la forma básica para el cálculo de la cantidad de precipitación en
exceso o escurrimiento directo de un evento lluvioso por el método de SCS. (Atkinson,
2001; Chow et al, 1988)
El mismo SCS a través de varios estudios en cuencas experimentales encontró la
siguiente relación empírica:
13
Sustituyendo 13 en 12 se tiene la ecuación 14:
14
Esta última ecuación es la utilizada para calcular escurrimiento, mejor conocido como el
método de la curva numérico o método de la SCS. Los datos de Pp pueden ser
calculados durante el evento lluvioso, pero S varía según el tipo de suelo, la vegetación
existente, además con el tiempo, esta es la razón se creó el concepto de CN
12
Graficando los datos de Pp y Q para numerosas cuencas, la SCS formuló diversas
curvas, que posteriormente fueron estandarizadas a una forma de curva numérica
adimensional (CN) que es definida como 0 ≤ CN ≤ 100. Para superficies impermeables
y superficies de agua CN = 100; para condiciones naturales CN< 100. (Chow et al,
1988)
Existe una relación entre CN y S, que es dada por la ecuación 15:
15
Donde S se expresa en milímetros
La ecuación 15 aplica para cuando existen condiciones antecedentes de humedad
(AMC II). (Rallison, 1980) Para condiciones de secas (AMC I) o húmedas (AMC III) la
curva numérica equivalente puede ser calculada por:
16
17
Los valores de la curva numérica varían de una superficie a otra. En la siguiente tabla
son presentados valores del la curva numérica para distintos tipos de cobertura,
cantidad de cobertura y potencial de escurrimiento.
13
Tabla 1. Valores de la curva numérica según tipo de ecosistema, porcentaje de cobertura del
suelo y potencial de escurrimiento. Tomado de (USDA-NRCS, 2004)
GRUPO
Condición
A
B
C
D
buena
30
55
70
77
Bosques
regular
36
60
73
79
mala
45
66
77
83
buena
30
48
65
73
Arbustos
regular
36
60
73
79
mala
48
67
77
83
buena
39
61
74
80
Pastizales
regular
49
69
79
84
mala
68
79
86
89
Suelo en descanso
77
86
91
94
Grupo “A”: Bajo potencial de escurrimiento, Velocidad de Infiltración (VI)
=8-12 mm hr-1
Grupo “B”: Moderado Bajo potencial de escurrimiento, VI = 4-8 mm hr-1
Grupo “C”: Moderado alto potencial de escurrimiento, VI = 1- 4 mm hr-1
Grupo “D”: Alto potencial de escurrimiento, VI = ≤ 1 mm hr-1
Conductividad Hidráulica Buena: Cobertura vegetal > 75%
Conductividad Hidráulica Regular: Cobertura vegetal 50% - 75%
Conductividad Hidráulica Buena: Cobertura vegetal < 50%
COBERTURA
II.3.1 Escurrimiento fuera del área de cultivo
Se refiere a la cantidad de agua que escurre fuera del área de siembra. Esta variable al
igual que el escurrimiento (Q) es dependiente de las lluvias durante el exceso de
precipitación, capacidad de infiltración, volumen de almacenamiento en las
depresiones, duración del exceso de lluvia, longitud del escurrimiento sobre el suelo,
pendiente del terreno y rugosidad de la superficie. (Prieto, 2004)
El algoritmo considera al componente escurrimiento fuera del área de siembra (Qo) es
igual a cero, debido a que no representa un valor significativo o aún es nulo en áreas
áridas y semiáridas de México. Por otro lado, si ocurriese un evento extremo, el suelo
solo retiene la cantidad de agua que su porosidad le permite asumiendo que el exceso
se infiltra mas allá de la zona de raíces o escurre fuera del arrea del cultivo y así, ese
escurrimiento no es contabilizado.
II.4 Evapotranspiración
La evapotranspiración es la variable que mas impacta al balance de humedad en el
suelo al extraer de ese almacén las cantidades necesarias para el desarrollo del cultivo.
14
Elías y Castellvi (2001) señalan que la Evapotranspiración (ET) es un proceso dinámico
que combina los procesos evaporación del agua en el suelo y transpiración de las
plantas, entonces este concepto se refiere a las pérdidas de vapor de agua en una
superficie con cubierta vegetal.
Los factores que afectan este proceso se agrupan en: (Brouwer y Heibloem, 1986;
Elías y Castellvi, 2001; Allen et al¸2006)
1. Factores climáticos
a. Radiación neta
b. Velocidad del viento
c. Temperatura de la superficie suelo y de la atmosfera
d. Humedad relativa de la atmosfera
2. Factores relacionado con la vegetación
a. Tipo de cubierta vegetal
i. Morfología de las hojas
ii. Albedo
iii. Topología
b. Altura de las plantas
3. Factores edáficos
a. Contenido de humedad en el suelo y su disponibilidad para las plantas
que a su vez es función de las condiciones físicas y químicas del suelo
(textura, estructura, salinidad, pH)
b. Régimen térmico
c. Albedo de la superficie
Cabe destacar que la superficie del suelo con cubierta vegetal esta en un cambio
continuo, así que la evapotranspiración también estará en cambio continuo.
La evapotranspiración incluye tres diferentes conceptos Evapotranspiración de
referencia de un cultivo estándar (ETo), Evapotranspiración del cultivo bajó condiciones
estándares de producción (ETc) y evapotranspiración del cultivo bajo condiciones no
estándares (en este aso, asumidas cuando el suelo presenta niveles de salinidad o
déficit hídrico o ambos), (Allen et al¸2006). Para una revisión exhaustiva sobre
evapotranspiración se sugiere consultar: Sánchez et al, 2004.
II.4.1 Evapotranspiración del Cultivo de referencia (ETo)
Este valor indica la tasa de consumo de agua para un área cubierta por pasto verde de
8-15 cm de altura, el cual crece activamente y que cubre completamente el suelo en
condiciones de no restricción de agua en el suelo. (Brouwer y Heibloem, 1986; Elías y
Castellvi, 2001; Allen et al¸2006). Su valor hace referencia a la influencia del clima
15
sobre las necesidades de agua de los cultivos, y se expresa en mm día-1 o m3 Ha-1
(Brouwer y Heibloem, 1986)
Existen varios métodos para calcular ETo, generalmente estos se agrupan en:
1. Métodos experimentales
a. Tanque evaporímetro
b. Lisímetro
2. Métodos Teóricos utilizando datos de clima
a. Método de Blaney-Criddle
b. Método de Penman
Para fines prácticos y dado que las matrices de transición de probabilidades de lluvia
están en forma mensual, el presente algoritmo utiliza la ecuación empírica propuesta
por Blaney y Criddle en 1950 y que posteriormente fue modificada por la FAO. El
método utiliza como variables de entrada valores mensuales de temperatura,
porcentaje medio diario de horas del día con luz para cierta latitud, y el uso consuntivo
del cultivo. En un principio este modelo fue creado para conocer la evapotranspiración
en áreas áridas y semiáridas del oeste de Estados Unidos. (Blaney y Criddle, 1950;
Blaney y Criddle 1962). Este método ha sido utilizado ampliamente para conocer los
valores del uso consuntivo para múltiples cultivos en distintas regiones del mundo,
dado su simplicidad. Es importante hacer notar que este método provee una estimación
general de la ETo, y bajo ciertas condiciones la ETo puede ser sobreestimada o
subestimada. (Brouwer y Heibloem, 1986; Hauviller et al¸2006; Sánchez, 1999;
Stephens y Stewart, 1963; Xu y Singh, 2002). La literatura menciona que el método fue
desarrollado a partir de la correlación de datos de uso consuntivo con la temperatura
media diaria, porcentajes mensuales de horas-luz diarias, precipitación y temporada de
crecimiento.
El método es representado por:
18
Donde ETo es la evapotranspiración potencial en mm día-1, p es el porcentaje de horas
de sol de un periodo dado (mensual o diario) con respecto al número de horas anual,
Tm es la temperatura media diaria para cierto mes (° C), k es el coeficiente de uso
consuntivo que es dependiente del tipo de vegetación, localización, época del año y
varía de 0.5 para árboles a 1.2 para una densa vegetación natural. (Blaney y Criddle,
1950). Ejemplos de valores k, que representan los coeficiente de evapotranspiración
para los cultivos irrigados son representados en la tabla 2.
16
Tabla 2. Valores k para ciertos cultivos en algunas áreas de E.U.A.
Coeficiente de evapotranspiración k
Duración de la temporada de
Cultivo
crecimiento o periodo entre
Estados del Oeste
Estados del Sureste
estaciones gélidas
de E.U.A.
de E.U.A.
Periodo entre estaciones
a
b
Alfalfa
0.70a – 0.80b
0.80 – 0.85
gélidas
Maíz
4 mese
0.75-0.85
0.60-0.70
Algodón
7 meses
0.60-0.65
0.50-0.55
Cereales de
3 mese
0.75-0.85
0.60-0.65
granos pequeños
Sorgo
4 a 5 meses
0.70
Cítricos, frutales
7 meses
0.50-0.65
Forrajes, Pastos
Periodos entre heladas
0.75
0.65-0.75
Papa
3.5 meses
0.65-0.75
0.60-0.65
Arroz
3 a 5 meses
1.00-1.20
0.85-1.00
Remolacha
6 meses
0.65-0.75
Hortalizas
3 meses
0.60
0.50-0.55
a
Los valores más pequeños son para áreas costeras; los valores más grandes son para áreas con clima
seco o árido
b
Los valores más pequeños son para áreas costeras y para todo el estado de Florida; Los valores más
altos son para las regiones restantes
El parámetro p es puede ser calculado a partir de los valores predeterminados, que
relacionan p con la latitud y el mes del año, ver Tabla 3.
Tabla 3. Porcentaje diario de horas del día con luz, según latitud y mes del año. Tomado de Brouwer y
Heibloem, (1986)
DIC
Lat. Norte ENE FEB MAR ABR MAY JUN JUL AGO SEP OCT NOV
(°)
Sur
JUL AGO SEP OCT NOV
DIC ENE FEB MAR ABR MAY JUN
60
0.15
0.2
0.26
0.32
0.38
0.41
0.4
0.34
0.28
0.22
0.17
0.13
55
0.17
0.21
0.26
0.32
0.36
0.39
0.38
0.33
0.28
0.23
0.18
0.16
50
0.19
0.23
0.27
0.31
0.34
0.36
0.35
0.32
0.28
0.24
0.2
0.18
45
0.2
0.23
0.27
0.3
0.34
0.35
0.34
0.32
0.28
0.24
0.21
0.2
40
0.22
0.24
0.27
0.3
0.32
0.34
0.33
0.31
0.28
0.25
0.22
0.21
35
0.23
0.25
0.27
0.29
0.31
0.32
0.32
0.3
0.28
0.25
0.23
0.22
30
0.24
0.25
0.27
0.29
0.31
0.32
0.31
0.3
0.28
0.26
0.24
0.23
25
0.24
0.26
0.27
0.29
0.3
0.31
0.31
0.29
0.28
0.26
0.25
0.24
20
0.25
0.26
0.27
0.28
0.29
0.3
0.3
0.29
0.28
0.26
0.25
0.25
15
0.26
0.26
0.27
0.28
0.29
0.29
0.29
0.28
0.28
0.27
0.26
0.25
10
0.26
0.27
0.27
0.28
0.28
0.29
0.29
0.28
0.28
0.27
0.26
0.26
5
0.27
0.27
0.27
0.28
0.28
0.28
0.28
0.28
0.28
0.27
0.27
0.27
0
0.27
0.27
0.27
0.27
0.27
0.27
0.27
0.27
0.27
0.27
0.27
0.27
17
Realizando una regresión no lineal multi-parametrica fue encontrada la ecuación que
describe p con respecto al mes del año y la latitud (°) del sitio
0.283092 – [(0.00001099*Mes) – (0.00146046*Latitud)]
19
II.4.2 Evapotranspiración actual (ETc)
A partir la ETo, es posible inferir la evapotranspiración para otros cultivos de interés, la
relación es dada por: (Brouwer y Heibloem, 1986)
20
Donde ETc, es la evapotranspiración actual de cierto cultivo en mm día-1, ETo, es la
Evapotranspiración de referencia mm día-1 y Kc es un coeficiente de cultivo.
Esta ecuación aplica en áreas de cultivo donde se aplica un excelente manejo del
proceso productivo (fertilización adecuada, control de plagas y enfermedades, prácticas
culturales en el momento idóneo, etc.), que se traduce en el logro de la máxima
producción bajo un clima dado. (Allen et al, 2006).
El coeficiente Kc, expresa la relación entre ETo y ETc, en otras palabras la relación
entre el cultivo de referencia y otro cultivo. Además el Kc representa las diferencias
entre el cultivo bajo estudio y el cultivo de referencia, estas diferencias son: (Allen et al,
2006; Brouwer y Heibloem, 1986)
•
•
•
•
Altura del cultivo
Albedo
Resistencias del cultivo a la transferencia de vapor de agua
Evaporación que ocurre en el suelo
La expresión matemática de esta relación es dado por:
21
Este valor varía según las características del cultivo. Esta cualidad permite su uso en
regiones distintas a donde originalmente fue generado. El valor de Kc depende de:
1. Tipo de cultivo.- La diferencias en altura de cultivo, albedo, propiedades
aerodinámicas, además de aspectos fisiológicos como distinta cantidad de
estomas por hoja, diferente cantidad de área foliar, así mismo distintos ciclos
metabólicos, como el caso de algunas plantas suculentas o la piña que abren
18
sus estomas por la noche. Estas diferencias sustanciales, proporcionan a los
cultivos una diferentes ET.
2. Etapa fenológica del cultivo.- Dentro de un mismo cultivo, a lo largo de la etapa
de crecimiento y desarrollo se van presentando diferencias en los requerimientos
de agua y por consiguiente en la ET.
3. Aspectos Climáticos.- Las variaciones en las condiciones del tiempo como
velocidad del viento, temperaturas extremas, afectan el los valores de
resistencia aerodinámica de las plantas, afectando por consiguiente los valores
Kc.
4. Evaporación del suelo.- Las diferencias de evaporación del suelo y transpiración
de la planta, que existe entre un cultivo y el cultivo de referencia, son adheridos
al concepto Kc.
II.4.2.1 Evapotranspiración del cultivo bajo condiciones de estrés hídrico
Este concepto aplica para áreas de cultivo donde durante el desarrollo del mismo
presentan estrés biótico y/o abiótico (por ejemplo salinidad del suelo, falta o exceso de
agua en el suelo, presencia de plagas y enfermedades, nutrición deficiente, etc.) que
reducen el crecimiento y la evapotranspiración del cultivo. Estas condiciones son las
predominantes en las distintas áreas de producción alrededor del mundo. (Allen et al,
2006)
El agua en el suelo se encuentra en constante cambio, llegando en ocasiones a
disminuir hasta cierto punto en que las fuerzas de retención del suelo impiden una
adecuada extracción por parte de las raíces de las plantas, esta situación provoca un
estrés en los vegetales, que generalmente se traduce en el cierre temporal de los
estomas que por consiguiente una menor transpiración. Este componente es
incorporado al cálculo de ET del cultivo con la siguiente ecuación:
22
Donde ETo es la evapotranspiración de referencia, Kc es el coeficiente de cultivo que
expresa la necesidad de agua del cultivo con respecto a la evapotranspiración de
referencia, este valor es dependiente del tipo de cultivo, su estado fenológico, etc., Ks
se refiere a un coeficiente de ajuste dado un estrés hídrico en el suelo.
II.4.2.2 Cálculo del coeficiente Ks
El presente algoritmo ha sido conceptualizado para regiones con escaso regimen
pluvial por lo que la evapotranspiración de los cultivos ocurre bajo condiciones no
estándares de disponibilidad de agua por lo que es necesaria la ponderación del valor
de ETo. Así, la baja fertilidad del suelo, toxicidad por sales, plagas, enfermedades, baja
19
disponibilidad de agua en el suelo y la presencia de capas impermeables en algunos
horizontes del suelo pueden resultar en un desarrollo mermado del cultivo con baja
evapotranspiración. (Allen, et al 2006).
La estimación de Ks requiere de la estimación diaria del balance de humedad en la
zona de raíces de los cultivos como lo señala la ecuación 1. Cuando ocurre estrés
hídrico el valor de Ks representa la magnitud de éste y pondera el valor de ETo por
este efecto. Así, esta variable puede ser cuantificada mediante la siguiente ecuación:
23
Dónde:
DTA = disponibilidad total de agua en la zona de raíces (mm)
DTA = 1000(θcc – θpmp)Zr
θcc= contenido de humedad del suelo a capacidad de campo (m3 m-3)
θpmp = contenido de humedad del suelo a punto de marchites permanente
(m3 m-3)
Zr = profundidad de las raices (m)
∆si = Contenido de humedad en el suelo en el día i (mm)
DFD = humedad fácilmente disponible
DFD = P*DTA
P = 0.55+0.04 (5 – Etc)
II.5 Capacidad de retención de humedad del suelo
Las plantas extraen con sus raíces el agua del suelo, aunque no toda el agua que
existe en el suelo puede ser absorbida por las raíces. La humedad aprovechable por
las plantas es aquella que se encuentra entre dos límites conocidos como Capacidad
de campo y Punto de marchites permanente (véase Figura 4).
20
Para suelos de la misma profundidad, la humedad aprovechable varía grandemente de
una clase textural a otra, por ejemplo desde 25 cm/m en suelos limosos hasta 6 cm/m
en suelos arenosos (Sánchez y Catalán, 2006).
A continuación se tiene una representación esquemática del contenido de humedad a
capacidad de campo y punto de marchites permanente y su variación, según distinta
textura del suelo.
Figura 4.Valores representativos de Humedad Aprovechable (HA) para diferentes tipos de suelos
(Walker, 2003).
Capacidad de campo (CC)
Esta propiedad física del suelo se define como la cantidad de agua que queda en el
suelo después de que un exceso de agua ha drenado y que ha disminuido de forma
importante el movimiento en profundidad, lo cual tiene lugar entre 2 y 3 días después
de una lluvia o del riego en un suelo con textura y estructura uniforme. Se estima que
es un contenido de agua en el suelo correspondiente a un Ψm = -33 KPa = -0.033 Mpa
≡ -0.33 bar.
Punto de Marchites Permanente (PMP)
Este valor corresponde al contenido de agua en el suelo que se encuentra bajo una
tensión de -1500 KPa = -1.5 MPa = -15 bar. Es un valor característico y constante para
un suelo dado. Por debajo de este límite se considera que las plantas no pueden
extraer agua. Así entonces el contenido volumétrico a Capacidad de Campo (θCC) y a
Punto de Marchitez Permanente (θPMP) es:
24
25
21
Por lo que la humedad aprovechable (HA) se encuentra entre θCC y θPMP en el perfil de
suelo que se trate (Pr) (Sánchez y Catalán, 2006)
26
La relación entre CC, PMP y HA es ilustrada en la Figura 5.
ӨS
ӨCC
HA
0%
ӨC
ӨPMP
Figura 5. Representación esquemática del contenido volumétrico de humedad a Capacidad de Campo y
Punto de Marchitez Permanente (Sánchez y Catalán 2006).
Las propiedades hidrodinámicas del suelo se tomaron tomadas de Saxton y Rawls
(2006) y Saxton et al, (1986), ellos generaron ecuaciones que calculan estos valores, a
partir de numerosas correlaciones. Las correlaciones fueron variables como textura,
contenido de materia orgánica, salinidad, compactación y presencia grava en el suelo y
las propiedades hídricas del suelo como punto de marchitez permanente, capacidad de
campo, humedad aprovechable, conductividad hidráulica a saturación.
La siguiente tabla presenta los rangos medios y máximos de las características hídricas
del suelo según textura.
22
Tabla 4. Rangos medios y máximos de las características hídricas del suelo según las clases texturales
del triangulo de texturas. Tomado de Tutorial Soil Water Characteristics: Hydraulic properties calculator
versión 6.02.74 (Saxton y Rawls).
Arena
TEXTURA
Media
Arenoso
Arcilla
Limo
Media
Media
Media
Franco
Media
Limoso
cm cm
mm hr
g cm
92
5
3
5
9.4
46.3
4
114
1.42
3-7
7-12
46-48
4-5
84-157
1.38-1.46
5
9
39
4
65
1.63
2-8
6-12
38-40
3-6
36-99
1.59-1.66
7
16
40
8
44
1.58
3-12
11-22
40-41
5-11
16-79
1.56-1.59
17
26
41
10
8
1.57
13-19
20-32
40-42
7-12
3-17
1.53-1.60
12
25
42
13
13
1.55
7-16
18-31
40-43
11-15
5-29
1.50-1.58
11
29
43
18
13
1.52
3-16
16-36
40-46
13-23
3-47
1.44-1.59
Media
5
13
65
10
25
60
27
13
41
19
40
20
15
65
6
5
89
10
34
56
Rango
Media
Arcillo
arenoso
51
42
7
Rango
Media
Franco
arcilloso
32
34
34
Rango
Media
Arcillo limoso
6
46
48
Rango
Media
Arcilloso
82
Rango
Franco arcillo
limoso
-3
%vol.
Rango
Media
Da
-1
%vol.
Rango
Franco
Limoso
Ks
-1
%vol.
Rango
Media
HA
% peso
Rango
Franco Arcillo
arenoso
Sat.
% peso
Rango
Franco
arenoso
CC
% peso
Rango
Arenoso
franco
PMP
22
Rango
50
28
6
29
40
23
7
1.53
4-8
25-32
39-42
21-25
4-14
1.55-1.61
20
37
47
18
2.9
1.4
17-22
34-40
45-50
16-20
2.1-3.8
1.33-1.47
24
36
43
12
1.2
1.51
20-29
31-43
41-46
10-14
0.1-2.5
1.44-1.57
20
34
44
14
3.2
1.47
17-22
30-37
42-47
13-16
1.6-5.3
1.41-1.53
26
42
51
16
2.2
1.29
23-31
39-45
48-55
15-17
1.8-2.6
1.19-1.38
28
42
49
14
1.24
1.35
23-33
37-47
44-56
13-15
0.01-2.22
1.17-1.48
II.6 Ascenso capilar
En el suelo existe un fenómeno físico en donde las partículas del suelo atraen –por
potencial capilar- las moléculas del agua, venciendo las fuerzas de gravedad,
originando que exista un flujo desde la capa freática hasta el suelo que se encuentra
encima. Este fenómeno se denomina ascenso capilar (δ) y es inversamente
proporcional al tamaño de los poros. (Thompson y Frederick, 1988)
Debido a que el algoritmo fue diseñado para operar en áreas áridas y semiáridas de
México, donde el manto de aguas subterráneas generalmente se encuentra
significativamente por debajo del volumen del suelo utilizado para cultivar, esta variable
se asume igual a cero.
23
II.7 Percolación profunda
Se refiere al movimiento del agua desde el área radicular o área donde crecen los
cultivos a alguna capa inferior del suelo al alguna capa del subsuelo. La percolación
está regida por la cantidad de agua que entra al suelo, las propiedades físicas y
químicas del suelo, estado hídrico del suelo, presencia de horizontes impermeables.
Este fenómeno se presenta en áreas que reciben gran cantidad de precipitación, tierras
de riego con excesivas tasas de aplicación de agua, suelos someros, suelos de textura
gruesa. (Prieto, 2004)
El algoritmo omite el cálculo de este parámetro, debido a que la naturaleza del modelo
es bajo condiciones de temporal en zonas áridas y semiáridas en donde se presentan
eventos de precipitación con características de escaso, aleatorio y torrencial, donde los
suelos son profundos, de textura fina y de poco contenido de humedad.
III. Alcances de la acción
El balance continuo de humedad en el suelo, bajo diferentes condiciones de
precipitación pluvial, es el punto de partida para la adecuada toma de decisiones en
agricultura de temporal. Su valor, es indicativo de déficit o excesos de humedad y
acorde a esto se deberán tomar las acciones pertinentes.
El carácter estocástico de la variable precipitación le imprime un valor agregado a la
metodología ya que se analizan diferentes escenarios de lluvia que pueden ocurrir
acorde al historial climático de la región de interés. Partiendo de esto se pueden tomar
decisiones de cambio en las fechas de siembra, añadir una obra de captación de agua,
u otra práctica que garantice mayor almacenamiento de humedad en el suelo.
Es importante considerar que el método no está diseñado para la predicción de
rendimiento sino que, mediante la simulación continua de varios periodos de
crecimiento del cultivo, se puede obtener una apreciación del déficit o excesos de
humedad que se pudieran esperar en el sitio de interés con impacto en el rendimiento
al verse afectada la evapotranspiración del cultivo.
Lo subsiguiente es la creación de la base de datos climática en términos de las
matrices de transición de lluvia para las estaciones climatológicas de los sitios de
estudio para su posterior sistematización en un modelo de simulación dinámico.
24
IV. Literatura citada
• Allen, R.G., Pereira, L.S., Raes, D. y Smith. M. 2006. Evapotranspiración del
cultivo: guías para la determinación de los requerimientos de agua de los
cultivos. Riego y Drenaje. Volumen 56 de estudio FAO. FAO. Roma. 298 Pág
• Atkinson, Erin L. 2001. Natural Resources Conservation Service curve number
analysis for Texas. Master Science Thesis. Texas Tech University. 104 Pág. [En
línea]
Disponible
para
la
World
Wide
Web
en
:
http://etd.lib.ttu.edu/theses/available/etd-0731200831295017959361/unrestricted/31295017959361.pdf
• Blaney, H. F. y Criddle, W. D. 1950, Determining Water Requirements in Irrigated
Area from Climatological Irrigation Data, US Department of Agriculture, Soil
Conservation Service, Tech. Pap. No. 96, 48 pág.
• Blaney, H. F. y Criddle, W. D. 1962. Determining consumptive use and irrigation
water requirements. No. 1275. Technical Bulletin. USDA. Estados Unidos. 59
pág.
• Brouwer, C. y Heibloem, M. 1986. Irrigation water management: Irrigation water
needs. FAO. Roma, Italia. [En línea] Disponible para la World Wide Web en:
http://www.fao.org/docrep/S2022E/S2022E00.htm
• Castillo F.E.; Sentís F.C.2001. Agro meteorología. Segunda Edición. MundiPrensa. Madrid España. 517 Pág.
• Chow, Ven Te; Maidment, David R.; Mays, Larry W. 1988. Applied Hydrology.
Edición Ilustrada. McGraw Hill. Estados Unidos. 572 Pág.
• Elías Castillo, F. y Castevellí Sentis, F. 2001. Agrometeorología. Segunda
Edición. Mundi-Prensa Libros. Madrid, España. 517 Pág.
• Geng, S., Penning de Vries, F.W. y Supit, I. 1986. A simple method for
generating daily rainfall data. Agric. Forest Meteorol., 36:363-376.
• Hauviller, A.P., Días, H., Pérez, D. y Rodríguez L., M. 2006. Un aporte a la
estimación de la evapotranspiración del cultivo juvenil de Arnadano utilizando
metodología según FAO en localidades de la Mesopotamia Argentina. INTA. pág
[en
línea]
Disponible
para
la
World
Wide
Web
en:
http://www.inta.gov.ar/mendoza/jornadas/Trabajospresentados/Hauviller.pdf
• Maldonado, O.A., Palacios, O.L., Springall, R. y Fernández, D. S. 2001. Empleo
del Modelo SWRRB para generar alternativas de manejo en la cuenca Itzapa,
Guatemala. Agrociencia, mayo-junio, año/vol.35, número 003. Colegio de
Postgraduados.
Texcoco,
México.
Documento
disponible
en
http://redalyc.uaemex.mx/pdf/302/30200308.pdf
25
• Martín de Santa Olalla, Francisco et al. 2005. Agua y Agronomía. Universidad de
Castilla La Mancha. Editorial Mundi-Prensa. Madrid España. 603 Pág.
• Nicks, A.D., Richardson, C.W. y Williams, J.R. 1990. Evaluation of the EPIC
model weather generator. In Sharpley A.N., Williams J.R. (eds.), EPICErosion/Productivity Impact Calculator, 1. Model Documentation, USDA
Technical Bullettin No. 1768, 105-124. Government Printing Office, Washington,
DC, USA.
• Prieto B., C.J. 2004. El agua: Sus formas, efectos, abastecimientos, usos, daños,
control y conservación. Segunda edición. ECOE EDICIONES. Colombia. 280
Pág.
• Rallison, R.E. 1980. Origin and Evolution of the SCS runoff equation. Symp. on
watershed management. 80 ASCE. Boise, Estados Unidos.
• Richardson, C.W. y Wright D.A. 1984. WGEN: A model for generating daily
weather variables: User manual. USDA-ARS. 86 Pág. Documento disponible en
http://soilphysics.okstate.edu/software/cmls/WGEN.pdf
• Sánchez Cohen, I. 1994. Evaluating strip farming systems for arid ecosystems a
stochastic approach. Doctoral Thesis dissertation. University of Arizona. 111
Pág.
• Sánchez Cohen, Ignacio y Catalán Valencia, Ernesto E. 2006. Curso a Técnicos
de CNA. Centro Nacional de Investigación Disciplinaria Relación Agua-SueloPlanta-Atmosfera. Instituto Nacional de Investigación Forestal Agrícola y
Pecuaria. SAGARPA. Gómez Palacio, Durango, México.
• Sánchez Cohen, I., E. Catalan Valencia, M. Villa Castorena. 2004.
Evapotranspiration modeling for irrigation purposes. In: Modeling and Remote
Sensing Applied to Agriculture. Richardson, Baez, Tiscareno Eds. USDA ARS –
INIFAP. Texas, USA. 249 pp
• Sánchez Tienda, J. 1999. Uso consuntivo del cultivo del aguacate: Metodología
Blaney y Criddle modificada relacionando fenología y precipitación. Revista
Chapingo serie Horticultura 5:201-207
• Saxton, K.E. y Rawls, W.J. Tutorial Soil Water Characteristics: Hydraulic
properties calculator versión 6.02.74. USDA-ARS, WSU. Pullman, Estados
Unidos.
[en
línea]
Programa
disponible
en
http://hydrolab.arsusda.gov/soilwater/Index.htm
26
• Saxton, K.E. y Rawls, W.J. 2006. Soil Water Characteristics estimates by texture
and organic matter for hydrologic solutions. Soil Sci. Am. J. 70:1569-1578.
• Saxton, K.E., Rawls, W.J., Romberger, J.S. y Papendick, R.I. 1986. Estimating
generalized soil-water characteristics from texture. Soil Sci. Soc. Am. J.
50(4):1031-1036
• Schaub, D. ; Meier-Zielinsky, E y Goetz, R.E. 1998. Simulating long-term erosion
effects on soil productivity for central Switzerland using the EPIC model.
Modelling soil erosion, sediment transport and closely related hydrological
processes. JAHS no. 195-201.
• Selker, J. S., and D. A. Haith (1990), Development and Testing of SingleParameter Precipitation Distributions, Water Resour. Res., 26(11), 2733–2740.
• Stöckle, C.O., G.S. Campbell, and R. Nelson. 1999. ClimGen manual. Biological
Systems Engineering Department, Washington State University, Pullman, WA.
• Stephen, John C. y Stewart, Ernest H. 1963. A comparison of procedures for
computing evaporation and evapotranspiration. IAHS. Bélgica. Pp.11. [en línea]
Disponible
en
la
World
Wide
Web
en:
http://iahs.info/redbooks/a062/iahs_062_0123.pdf
• Thompson, L.M. y Frederick, R.T. 1988. El suelo y su fertilidad. Cuarta edición.
Reverte. España. 649 Pág.
• USDA-NRCS. 2004. National Handbook. Part 630 Hydrology: Hydrologic soil
cover complexes. USDA. Washington. Estados Unidos. 9-14 Pág.[En línea]
Disponible
para
la
World
Wide
Web
en
http://policy.nrcs.usda.gov/OpenNonWebContent.aspx?content=17758.wba
• Walker, Wynn R. 2003. SIRMOD III Surface Irrigation Simulation, Evaluation and
Design. Utah State University. Logan, Utah, Estados Unidos de América. 146
Pág.
• Williams, J.R. 1992. WXPARM: Weather parameter calculator for EPIC. User
Manual. U.S. Department of Agriculture. Grassland Soil and Water Research
Laboratory, Texas. 6 pp.
• Xu, C.Y. y Singh, V.P. 2002. Cross comparison of empirical equations for
calculating potential evapotranspiration with data from Switzerland. Water
resources Management 16: 197-219.
27