iii. análisis estadístico temporal del oleaje

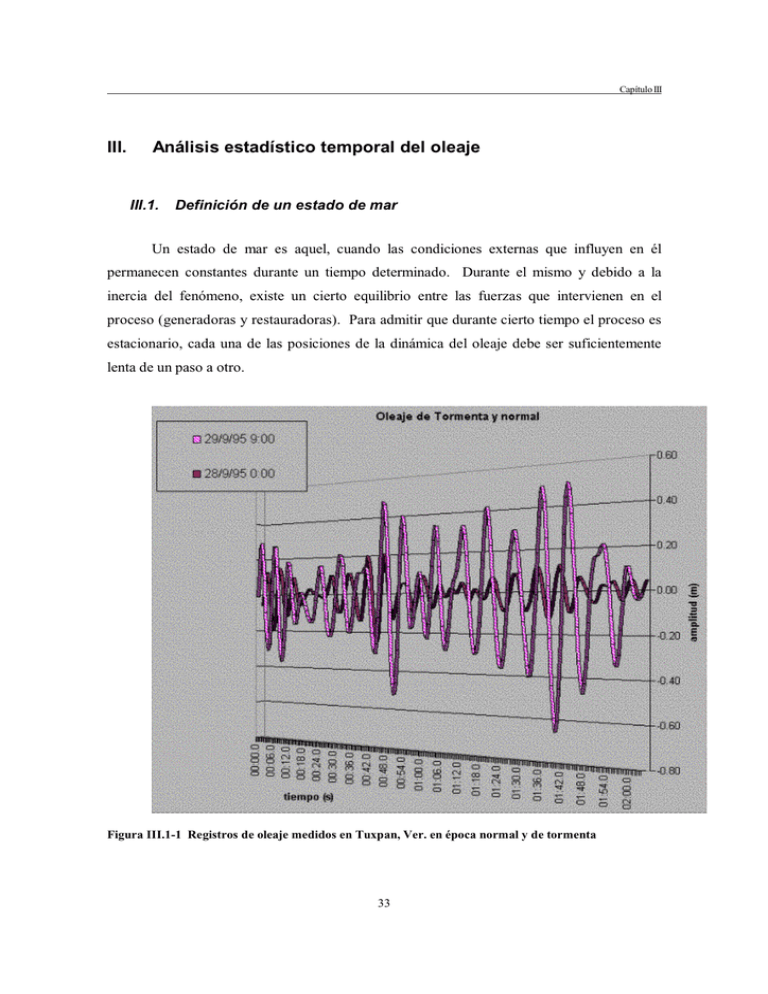
Capítulo III
III.
Análisis estadístico temporal del oleaje
III.1.
Definición de un estado de mar
Un estado de mar es aquel, cuando las condiciones externas que influyen en él
permanecen constantes durante un tiempo determinado. Durante el mismo y debido a la
inercia del fenómeno, existe un cierto equilibrio entre las fuerzas que intervienen en el
proceso (generadoras y restauradoras). Para admitir que durante cierto tiempo el proceso es
estacionario, cada una de las posiciones de la dinámica del oleaje debe ser suficientemente
lenta de un paso a otro.
Figura III.1-1 Registros de oleaje medidos en Tuxpan, Ver. en época normal y de tormenta
33
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
Puede considerarse que el fenómeno del oleaje está formado por dos variaciones:
una de corto periodo (segundos) o estacionaria y otra de largo periodo (horas) o no
estacionaria, y que aparece cuando el estado de mar ha evolucionado.
En la Figura III.1-1 se observan dos registros de oleaje de Tuxpan, Ver.
correspondientes a las siguientes fechas: 28/09/95 00:00 y 29/09/95 9:00; con registros de
8.53 minutos, cada tres horas, con un intervalo de muestreo de 0.5 s lo que hacen 1024
datos. En cada uno se aprecia una variación sobre el nivel medio con diferentes alturas y
periodos, sin embargo al compararlos entre sí, se puede ver que la amplitud de uno es
mayor que el otro, esto significa un cambio del estado del mar provocado probablemente
por el paso de una tormenta.
Considérese η(t) como función de la variación de la superficie libre del agua. Para
definir el periodo y altura de la ola se hará uso del criterio de pasos descendentes por el
nivel medio (zero down crossing) que se muestra en la Figura III.2-3.
III.2.
Descripción estadística de un estado de mar
Se define una muestra al subconjunto de una población. “Una muestra se compone
de algunos de individuos, objetos o medidas de una población” [Ref. 24]. En el caso del
oleaje, una muestra es un conjunto de olas medidas en un tiempo determinado y que
representan el total de ellas.
Las muestras o registros de oleaje que se utilizaron en este trabajo, fueron obtenidos
con equipos instalados en el fondo del mar; con éstos se miden las presiones instantáneas
programadas. Con las mediciones de presión se calcula la columna de agua sobre el sensor
de presión en los aparatos, lo cual hace posible formar la señal del oleaje [Ref. 33]. En el
caso de Tuxpan, la muestras consta de 1024 datos de presión, tomados cada 0.5 segundos;
con este sistema se logran obtener alrededor de 73 olas por muestra.
34
Capítulo III
La razón por la cual se mide con ese criterio, es la de economizar el tiempo de
cálculo para el análisis espectral usando el método de la transformada rápida de Fourier y,
por otro lado, ahorrar costos de baterías y gastos de operación.
Con el intervalo de muestreo de 0.5 s, se define una ola con 14 datos
aproximadamente, ya que el periodo medio en el sitio es alrededor de 7 segundos. Esto se
adapta al criterio comúnmente utilizado que establece que el número de muestras por ola
debe estar entre 10 y 20 elementos, Goda 1985.
CORRECCIÓN DEL NIVEL MEDIO
Existen diversos métodos para sustraer el nivel medio, del mar por marea, de los
registros de oleaje. De estos el más simple es aquel que consiste en sustraer la media
aritmética de todos los datos medidos:
N
η =
∑d
i =1
i
Ecuación III.2-1
N
donde d es la profundidad medida por el aparato (desde el fondo hasta la superficie
libre del agua) y N es el número total de datos.
Ya que la mayoría de los registros contienen la influencia de la variación de la
marea, es mejor incorporar la siguiente corrección lineal por el método de mínimos
cuadrados:
η = A0 + A1n
: n = 1,2,3….,N
Ecuación III.2-2
donde:
35
Victor Rosales Sierra
A0 =
Caracterización del Oleaje aplicada a Tuxpan, Ver.
N 2Y0 − N 1Y1
N 0 N 2 − N 12
A1 =
N
Nr = ∑nr ,
n =1
N 0Y1 − N 1Y0
N 0 N 2 − N 12
Ecuación III.2-3
N
Yr = ∑ n rη n
Ecuación III.2-4
n =1
La fórmula para la corrección del nivel medio con un cambio parabólico por el
método de mínimos cuadrados se define de la siguiente forma:
η = B0 + B1n + B2 n 2
: n = 1,2,3….,N
Ecuación III.2-5
donde:
B0 =
1
[Y0(N2N4-N32)+Y1(N12N3-N1N4)+Y2(N1N3-N22)]
∆
B1 =
1
[Y0(N2N3-N1N4)+Y1(N0N4-N22)+Y2(N1N2-N0N3)]
∆
B2 =
1
[Y0(N1N3-N22)+Y1(N1N2-N0N3)+Y2(N0N2-N12)]
∆
∆ = N0N2N4+2N1N2N3-N23-N0N32-N12N4
Ecuación III.2-6
En las Figuras III.2-1 y III.2-2, se muestran los datos de los registros medidos y su
nivel medio calculado por los “tres métodos” [Ref. 19].
El nivel resultante del método parabólico fue el que mejor representó la variación de
la marea dentro del registro.
36
Capítulo III
Figura III.2-1 Nivel medio calculado con los tres métodos para el registro del 28/09/95 00:00
Figura III.2-2 Nivel medio calculado con los tres métodos para el registro del 29/09/95 09:00
37
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
MÉTODO DE CRUCE POR CERO, NIVELES MÍNIMOS Y MÁXIMOS
Una vez que se corrigió el nivel medio, se realizó el cálculo de cruce por cero para
definir la altura y periodo de cada ola individual del registro; como se describe a
continuación:
Figura III.2-3 Descripción del método de cruces por cero con un registro real
El método de cruces por cero (nivel medio) tiene dos variantes: los pasos
ascendentes y los descendentes. El cálculo con cualquiera de estas variantes arroja los
mismos resultados por las condiciones establecidas en el capítulo II, de que el oleaje es
considerado como un proceso estocástico, estacionario y gausiano donde el nivel medio es
cero y los cruces ascendentes o descendentes son los mismos.
Para este trabajo, se utilizó el método de pasos descendentes por cero con las
siguientes condiciones, (ver Figura III.2-3):
38
Capítulo III
Para definir el periodo de cada ola:
ηi⋅ηi-1<0
y
ηi-1<0
ηi denota el iésimo dato de la elevación de la superficie referida al nivel medio. El
periodo (tiempo transcurrido entre dos pasos descendentes), se determinó calculando la
diferencia entre dos cruces por cero, más un ajuste por medio de una interpolación lineal
entre los tiempos correspondientes a las elevaciones ηi y ηi-1. Si se hubiera utilizado el
método de pasos ascendentes por cero, la segunda condición, para definir el periodo, sería:
ηi-1>0
Para definir la altura de ola se utilizan dos condiciones. El máximo en el perfil de
cada ola individual o cresta, es:
ηi-1<ηi y ηi+1<ηi.
En este caso, también se hace un ajuste parabólico para eliminar la subestimación de
las alturas de ola. Esto se logra con las siguientes ecuaciones:
ηmax = C −
B2
4A
Ecuación III.2-7
donde:
A=½(ηi-1-2ηi +ηi+1),
B=½(ηi+1-ηi-1)
y
C=η
Ecuación III.2-8
El valor ηmin o valle, se calcula con un proceso análogo. La altura de ola se define
como la suma del valor absoluto de ηmin y ηmax.
39
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
PARÁMETROS ESTADÍSTICOS
Los parámetros estadísticos más importantes para definir un estado de mar son los
siguientes [Ref. 44]:
a) La variación del nivel medio del mar:
η(t ) =
1
N
N
∑η
Ecuación III.2-9
i
1
donde ηi es la elevación de la superficie libre del agua en el tiempo ti y N
es el
número de eventos.
b) La variación media cuadrática de la superficie del agua (varianza) que se define
como:
2
=
ηrms
N
1
N
∑η
2
i
Ecuación III.2-10
1
c) La altura y periodo medios de las olas, cuyo cálculo se realiza a partir de las
siguientes expresiones:
1
H=
N0
T=
N
∑H
Ecuación III.2-11
i
1
1 N
∑T
N0 1 i
Ecuación III.2-12
donde N0 es el número de olas individuales de todo el registro; H la altura de ola y T
el periodo de ola.
40
Capítulo III
d) La altura cuadrática media definida por:
H rms =
1
N0
N0
∑H
i =1
2
i
Ecuación III.2-13
e) La asimetría se identifica mediante la siguiente relación:
Skw =
1
3
N 0ηrms
N
∑η
i=i
3
i
Ecuación III.2-14
Existen otros casos específicos para caracterizar el estado de mar con las alturas o
periodos medios 1/n como Hs=H1/3 (altura de ola significante), la altura máxima Hmax o los
estadísticos de orden Hn. En la Tabla III.2-1, se muestran los valores característicos de las
olas resultantes de las series de tiempo que se utilizaron como ejemplo.
41
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
Tabla III.2-1 Parámetros estadísticos de los registros de ejemplo.
42
Capítulo III
III.3.
Análisis estadístico de un estado de mar
Para entender mejor un estado de mar se efectúa un análisis estadístico de sus
variables más importantes que son la altura y periodo de ola. Generalmente nos interesa
conocer la probabilidad (frecuencia relativa), con la que ocurrirá un evento.
Existen
1
diferentes teorías de distribuciones de probabilidad para el oleaje, las cuales se describen
en este capítulo y se comparan posteriormente con los resultados de las mediciones de
campo.
DISTRIBUCIÓN NORMAL DE LA SUPERFICIE LIBRE
Se acepta que la variación de la superficie del mar sigue una distribución de
probabilidad gaussiana [Ref. 24], bajo la suposición de que los componentes de las fases
son arbitrarias pero uniformemente distribuidos en el intervalo (-π,π). El modelo gaussiano
establece explícitamente que existe una simetría alrededor del nivel medio del mar, lo cual
nos lleva a considerar que la media es igual a cero y, por tanto, su función de densidad será:
p(η) =
1
ηrms 2π
−
e
1 η2
2
2 ηrms
Ecuación III.3-1
donde p(η) es la función de densidad.
La función es simétrica alrededor del nivel medio (cero), por tanto, la probabilidad
de una elevación particular positiva es igual a la misma elevación negativa.
Para comprobar lo anterior se presentan en la Figura III.3-1, las distribuciones
normales de la superficie libre de los registros mostrados en la Figura III.1-1.
1
La probabilidad de un evento, en términos del valor numérico de la variable aleatoria, se expresa por la
función de probabilidad
43
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
Figura III.3-1 Distribuciones normales de probabilidad de registros medidos en Tuxpan, Ver.
En ambos casos las funciones son simétricas con media cero. Nótese que en el caso
del oleaje de tormenta la función no es estrecha, sin embargo, permanece simétrica. Se
acepta entonces, que la superficie libre del agua del oleaje sigue una distribución de
probabilidad gaussiana.
DISTRIBUCIONES DE ALTURA DE OLA
Rice [Ref. 36], de 1944 a 1945, encontró una función de altura de crestas para
señales aleatorias de origen electromagnético.
Cartwright[ [Ref. 9] y Longuet-Higgins
[Ref. 27] ampliaron los estudios de Rice y demostraron que la distribución de Rayleigh
[Ref. 35] (desarrollada para fenómenos eléctricos), podría ser utilizada para describir la
distribución de alturas de ola.
44
Capítulo III
Si se tiene un estado de mar SWELL puro con anchura espectral2 ε=0 (espectro de
banda angosta), la descripción de alturas de ola dada por Rayleigh es exacta.
DISTRIBUCIÓN DE RAYLEIGH PARA ALTURAS DE OLA
La distribución de Rayleigh [Ref. 35] supone que hay una correlación exacta entre
una cresta y el siguiente valle; así, la distribución adimensional de alturas de ola se define
como:
p(ξ)=2ξe-ξ²
Ecuación III.3-2
donde:
ξ=H/Hrms
Ecuación III.3-3
A esta expresión se le conoce como la distribución de probabilidad de excedencia de
Rayleigh.
DISTRIBUCIÓN DE LONGUET-HIGGINS PARA ALTURAS DE OLA
Longuet-Higgins [Ref. 27] propuso en 1983 una distribución de crestas de ola que
se pueden aplicar cuando la anchura espectral, ν, es diferente de cero. En el caso ν=0
(espectro de banda angosta), se tiene una distribución Rayleigh, mientras que el extremo
opuesto con un espectro de banda ancha nos indica que existe una distribución normal
truncada en cero. Esta expresión se define de la manera siguiente:
2
La relación entre los anchos espectrales ε y ν se verán con mayor detalle en el capítulo IV.
45
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.

H 
L(ν )HErfc −

 2 2m0ν 
p (H ) =
H2
Ecuación III.3-4
8m0ν ⋅ e 8m0
donde m0 es el momento de orden cero; y Erfc la función de error complementaria,
la cual se define como:


H
 1 2 e
Erfc −
 2 2m ν  = − π ∫
0 
0

∞


H

−
 2 2m ν 
0 

2
dH
Ecuación III.3-5
1
− 
1
1
= 1 + (1 + ν 2 ) 2 
L(ν ) 2 

Ecuación III.3-6
DISTRIBUCIÓN DE TAYFUN PARA ALTURAS DE OLA
En 1981, Tayfun [Ref. 50] propuso una ecuación para alturas de ola que está
limitada por la rotura de la misma, y un parámetro N que combina el estado de mar con la
profundidad. Esta distribución supone que existe una correlación media entre la cresta y el
siguiente valle. Es decir, si se tiene una cresta grande, el próximo valle tiene una alta
probabilidad de ser grande, pero existe una pequeña probabilidad de que pueda ser mediano
o pequeño.
El parámetro N está relacionado con el estado de mar y es función del periodo de
onda y de la profundidad. Si el parámetro N tiende a infinito, entonces se tiene un estado
de mar Swell y la distribución de Tayfun es igual a la de Rayleigh.
∞

 u 
p (ξ , N ) = ξ ∫ uJ 0N  1 / 2  J 0 (ξu )du
0
N 


0≤ξ≤N½
46
Ecuación III.3-7
Capítulo III
 4
 N 1/ 2
p (ξ , N ) = ξ 1 − cos −1 
 ξ
 π
 ∞  N  u 

 ∫ uJ 0  1 / 2  J 0 (ξu ) du
N 

 0 
Ecuación III.3-8
N½≤ξ≤(2N)½
donde N, por una parte, es el parámetro de Tayfun que se define como:
N=
π tanh(k 0 h)
7 2 K0 2m0
Ecuación III.3-9
donde, por otro lado,
ξ=
H
Hrms
Ecuación III.3-10
J0 es la función de Bessel de orden cero y K0 es el número de onda asociado a la
frecuencia media, el cual se puede obtener por iteraciones con la siguiente ecuación:
σ 2h
= k 0 h ⋅ tanh(k 0 h )
g
Ecuación III.3-11
DISTRIBUCIÓN DE CARTER PARA ALTURAS DE OLA
En 1981, Carter [Ref. 8] propuso una ecuación para la distribución de alturas de ola;
en élla se establece que no existe ninguna correlación entre crestas y valles consecutivos.
Es decir, dada una cresta grande, el siguiente valle tiene iguales probabilidades de ser
grande, pequeño o mediano.
La probabilidad de excedencia propuesta por Carter es la siguiente:
47
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
H 
 −8 H0 
 2 H 0 
H0 − 4 H0s 
 Hs 

p( H ≥ H0 ) = 1 − e
e
Erf 
+2 π


Hs
 H s 

2
2
Ecuación III.3-12
donde la función error, Erf, se expresa como:
Erf ( X ) =
2
π
∫
X
0
e− u du
2
Ecuación III.3-13
En 1994, Green concluyó que en un estado de mar SEA (muy desordenado) la
ecuación de Carter es la que representa mejor el fenómeno. En un estado de mar un poco
más ordenado (al salir del área de generación y propagarse el oleaje) la distribución de
Tayfun es la que mejor se ajusta. Por último, en un estado de mar muy ordenado (SWELL)
la distribución de Rayleigh puede expresar adecuadamente dicho comportamiento.
48
Capítulo III
Figura III.3-2 Distribución de probabilidad de excedencia de altura de ola normal
49
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
Figura III.3-3 Distribución de probabilidades de excedencia de altura de ola de Tormenta.
En las Figuras III.3-2 y III.3-3 se aprecia efectivamente que en oleaje normal
(SWELL) la curva de datos medidos se parece mucho a la distribución propuesta por
Rayleigh y también a la establecida por Tayfun, sin embargo el oleaje de Tormenta se
asemeja ligeramente a la distribución de Carter.
50
Capítulo III
DISTRIBUCIONES CONJUNTAS DE PERIODO Y ALTURA DE OLA
En estudios recientes se ha demostrado la importancia del periodo de las olas en
fenómenos tales como el run-up o la estabilidad de las piezas de un rompeolas. Esto ha
generado un gran interés en las distribuciones de probabilidad conjuntas de periodo y altura
de ola.
A continuación se presentan las distribuciones más utilizadas.
DISTRIBUCIÓN DE LONGUET-HIGGINS (1975)
Longuet-Higgins [Ref. 27] propuso en 1975 una función de densidad conjunta de
alturas de ola y periodos, la cual se basa en un modelo de oleaje estacionario y gaussiano
con espectro de banda angosta.
El inconveniente de utilizar un espectro de banda angosta (oleaje SWELL), es que
no se toma en cuenta la asimetría en la distribución de los periodos de ola, situación que sí
se considera, por el contrario, cuando el espectro es de banda ancha.
θ 2 −θ 2
p (θ ,η ) =
e
2π
1+η 2
2
Ecuación III.3-14
donde:
θ=
H
2 m0
Ecuación III.3-15
η=
T − Tm
vTm
Ecuación III.3-16
51
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
donde Tm, asimismo, es el periodo medio.
DISTRIBUCIÓN DE CAVANIÉ ET AL. (1976)
Cavanié, Arhan y Ezraty [Ref. 10] propusieron en 1976 otra distribución teórica,
también basada en un modelo gaussiano de banda angosta, pero donde sí se toma en cuenta
la asimetría de la distribución de los periodos.
Esta fórmula presenta una buena concordancia con los datos observados; sin
embargo, su defecto es utilizar el parámetro de anchura espectral, ε, el cual depende del
cuarto momento de la función de densidad espectral. Este momento tiene el inconveniente
de estar asociado a la cuarta potencia de la función de densidad espectral y cualquier error
pequeño en la distribución se amplifica, sobre todo, para las altas frecuencias.
p(h,τ ) =
α 3h2
4 2π ε (1 − ε )τ τ
2
4
e
5
−
( )−4
h 2 ττ
8ε 2
((τ τ
2 2
)
−α 2 + β 2 α 4
)
Ecuación III.3-17
donde:
h=
H
m0
τ=
T
τ Tc
Tc =
2π
α
Ecuación III.3-18
Ecuación III.3-19
m2
m4
Ecuación III.3-20
52
Capítulo III
T
τ = 
 Tc 
α=
(
si ε<=0.95 →
1
1− 1−ε 2
2
β2 =
τ =1
Ecuación III.3-21
)
Ecuación III.3-22
ε2
1−ε2
Ecuación III.3-23
Como esta ecuación fue obtenida midiendo el periodo de ola entre cresta y cresta,
Tc; no sería correcto aplicar dicha ecuación a olas definidas por el método de cruces por
cero (Battjes 1977). Sin embargo Goda (1978) señala que aún en este caso la distribución
da buenos resultados.
DISTRIBUCIÓN DE LONGUET-HIGGINS (1983)
Longuet-Higgins [Ref. 27] propuso en 1983 otra ecuación basada también en un
espectro de banda angosta, la cual tiene los mismos méritos que la de Cavanié et al, pues
toma en cuenta la asimetría de la distribución de periodos, además que tiene la gran ventaja
de utilizar un parámetro de ancho espectral de orden menor: v (dependiente de segundo y
no del cuarto momento). La distribución se define así:
2
 2   R  −R
p( R , τ ) =  1/ 2   2  e
 νπ   τ 

1  12 
 1+ ν 2  1− τ   L ( ν )


2
Ecuación III.3-24
donde
τ =T
Ecuación III.3-25
T
53
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
H
R=
2
2m0
[
1
1
1
2
= 1 + (1 + v 2 )
L( v ) 2
T=
Ecuación III.3-26
]
Ecuación III.3-27
m0
= T01
m1
Ecuación III.3-28
54
Capítulo III
Figura III.3-4 Distribuciones conjuntas de probabilidad altura - periodo de ola correspondientes al
registro 28/09/95 00:00
55
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
Figura III.3-5 Distribuciones conjuntas de probabilidad altura - periodo de ola correspondientes al
registro 29/09/95 09:00
En el caso de las distribuciones de probabilidad conjunta (altura - periodo), Figuras
III.3-4 y III.3-5, no se aprecia una similitud de los datos medidos respecto de los teóricos,
ni para la señal normal ni para la de tormenta.
56
Capítulo III
DISTRIBUCIONES DE PERIODOS DE OLAS
Las distribuciones de
periodos de ola se derivan de las distribuciones de
probabilidad conjunta citadas anteriormente; por lo tanto, sus parámetros son igualmente
válidos para las ecuaciones que aparecerán a continuación.
DISTRIBUCIÓN DE BRETCHNEIDER (1959)
Bretchneider encontró en 1959, que la distribución de Rayleigh se puede aplicar al
cuadrado de los periodos, lo que lo llevó a proponer la siguiente ecuación:
p(Tz ) = 2.7
Tz3
4
e
T 
− 0.675 z 
 Tz 
4
Ecuación III.3-29
Tz
Tz es el periodo calculado por el método de cruces por cero (zero up cross)
DISTRIBUCIÓN DE CAVANIÉ ET AL. (1976)
Cavanié, Arhan y Ezraty [Ref. 10] propusieron en 1976 la siguiente distribución de
probabilidad de periodos de ola:
p(Tz ) =
2
α 3 β 2 δ Tz
 δ 2 T 2  2

2
z
4 2



Tz  2  +α β
 T z 



Ecuación III.3-30
3/ 2
Las variables α y β se calculan en con las ecuaciones III.3.23 y III.3.24; por otro
lado, se considera δ = 1 .
2
57
Victor Rosales Sierra
Caracterización del Oleaje aplicada a Tuxpan, Ver.
Figura III.3-6 Distribución de probabilidades de excedencia de periodo de ola normal
58
Capítulo III
Figura III.3-7 Distribución de probabilidades de excedencia de periodo de ola de Tormenta.
En las distribuciones de probabilidad de periodo de ola, Figuras III.3-6 y III.3-7, se
aprecia que para el caso de oleaje normal, la curva se ajusta un poco mejor a la distribución
de Cavanié, aunque no es muy diferente de la de Bretchneider. En el caso de oleaje de
Tormenta, ambas distribuciones definen bien la forma de la curva de los datos medidos.
59
Victor Rosales Sierra
III.4.
Caracterización del Oleaje aplicada a Tuxpan, Ver.
Resumen
Se definió un estado de mar, producido por oleaje.
Se describió dicho estado de mar.
Se estableció el método de análisis estadístico de un estado de mar.
Se definieron los parámetros de caracterización estadísticos del oleaje.
Se compararon dos series de tiempo reales, normal y de tormenta, con las diversas teorías
de distribuciones de probabilidad de altura de ola, periodo y conjunción de ambos.
60
Capítulo III
III.
III.1.
III.2.
III.3.
III.4.
ANÁLISIS ESTADÍSTICO TEMPORAL DEL OLEAJE ................................................................33
DEFINICIÓN DE UN ESTADO DE MAR ...................................................................................................33
DESCRIPCIÓN ESTADÍSTICA DE UN ESTADO DE MAR ..........................................................................34
ANÁLISIS ESTADÍSTICO DE UN ESTADO DE MAR ................................................................................43
RESUMEN ............................................................................................................................................60
Figura III.1-1 Registros de oleaje medidos en Tuxpan, Ver. en época normal y de tormenta...........................33
Figura III.2-1 Nivel medio calculado con los tres métodos para el registro del 28/09/95 00:00.......................37
Figura III.2-2 Nivel medio calculado con los tres métodos para el registro del 29/09/95 09:00 ...............37
Figura III.2-3 Descripción del método de cruces por cero con un registro real .................................................38
Figura III.3-1 Distribuciones normales de probabilidad de registros medidos en Tuxpan, Ver........................44
Figura III.3-2 Distribución de probabilidad de excedencia de altura de ola normal ..........................................49
Figura III.3-3 Distribución de probabilidades de excedencia de altura de ola de Tormenta. ............................50
Figura III.3-4 Distribuciones conjuntas de probabilidad altura - periodo de ola correspondientes al registro
28/09/95 00:00 ...............................................................................................................................................55
Figura III.3-5 Distribuciones conjuntas de probabilidad altura - periodo de ola correspondientes al registro
29/09/95 09:00 ...............................................................................................................................................56
Figura III.3-6 Distribución de probabilidades de excedencia de periodo de ola normal ...................................58
Figura III.3-7 Distribución de probabilidades de excedencia de periodo de ola de Tormenta. .........................59
Tabla III.2-1 Parámetros estadísticos de los registros de ejemplo. .....................................................................42
61