CÁLCULOS Vertedores rectangulares de pared delgada sin

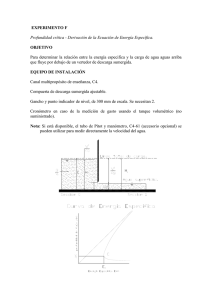
Laboratorio de Hidráulica
Practica 3, del curso de Hidráulica I.
Tema: Vertedores Rectangulares De Pared Delgada Sin Contracciones Laterales
y Con Contracciones Laterales.
Objetivo: Verificar en el laboratorio los diferentes métodos para calcular el
gasto en vertedores rectangulares de pared delgada sin y con contracciones
laterales.
Meta: El alumno deberá de conocer y comprender los diferentes tipos de
vertedores que existen para que se utilizan.
Piezas requeridas:
1. Canal multipropósito de enseñanza, C4.
2.
3.
4.
5.
Vertedor rectangular de pared delgada sin contracciones laterales.
Vertedor rectangular de pared delgada con contracciones laterales.
Medidores de profundidad (Limnímetro). Se necesitan 2.
Tanque volumétrico.
6. Cinta métrica.
7. Cronometro.
VERTEDOR RECTANGULAR DE PARED DELGADA
Ecuación General de Vertedores
Considerando un vertedor de pared delgada y sección geométrica como se observa en la
figura siguiente:
La definición de las variables son:
H=
w=
h=
Carga hidráulica total del agua en el lugar de la estructura
altura de la cresta medida desde la plantilla del canal de alimentación.
desnivel entre la superficie inalterada del agua, antes del vertedor y la
cresta.
de tal modo que,
CH1  CH 2
Aplicando la ecuación de Bernoulli para una línea de corriente entre los puntos 1 y 2 se
tiene
v12
v22
z1 
 z2 
2g
2g
Para la mayoría de las situaciones prácticas,
También se puede suponer que,
v12
0
2g
z 2  Cc( z1 )
donde Cc es un coeficiente de contracción para contemplar que el tirante del agua sobre
la cresta vertedora se contrae cuando se acelera al caer del vertedor.
Haciendo además que,
z1  h
tenemos,
z 2  Cc(h)
y finalmente,
h  Cc(h) 
v2  2 g (1  Cc)h
Despejando v2:
que se puede expresar como
v 2  Cv( h
Para obtener el gasto descargado por el vertedor,
donde el área A2 es
y el gasto es,
v22
2g
Q  v2 A2
A2  z2b  Cc(h)b
Q  Cv( h )Cc(h)(b)  Cv(Cc)bh 3 / 2
Finalmente se considera al producto Cv(Cc)  Cd
como coeficiente de descarga, el cual toma en cuenta las investigaciones realizadas
experimentalmente para diferentes formas geométricas y tipos de vertedores. La
ecuación del vertedor es
Q  Cd bh 3 / 2
Otra forma usual de expresar la ecuación general de vertedores es mediante el uso de la
relación entre la distribución real de velocidades en el vertedor respecto de la
distribución hipotética de velocidades que es de tipo parabólica; este cociente se conoce
como m y tiene diferentes expresiones según los diferentes autores.
De esta manera la ecuación general queda como,
Q
2
2 g bh 3 / 2
3
Se acostumbra agrupar:
Donde,
Cd 
2
3
  0.60
2 g   2 .952 
llamando a Cd el coeficiente del vertedor y finalmente,
Q  Cd bh 3 / 2
PROCEDIMIENTO
Asegúrese de que el canal este nivelado, sin obstrucciones en el extremo final de
descarga del canal. Mida y registre el ancho real b (m) del vertedor de borde afilada
(vertedor rectangular).
Instale el vertedor en el canal con el borde afilado aguas arriba. Revise que el vertedor
está asegurado mediante un gancho de montaje a través del fondo del canal. Para
resultados exactos los espacios entre el vertedor y el canal deben ser herméticamente
sellados en la parte aguas arriba utilizando plastilina. Coloque un gancho y punto
indicador de nivel a los lados del canal, por encima del vertedor, con el punto equipado.
El dato para todas las mediciones será el borde superior de la placa del vertedor. Con
cuidado, ajuste el indicador de nivel para que coincida con la parte superior del
vertedor, cuidando de no dañar el borde del vertedor, y después registre el dato de
lectura. Como alternativa, para evitar daños en el vertedor, abra la válvula de control de
flujo y deje entrar agua al canal hasta que sobre pase el vertedor, luego cierre la válvula
de control de flujo para detener el agua. Cuando el agua deja de correr sobre el vertedor
ajustar el indicador de nivel para coincidir con la superficie del agua y registre el dato
de lectura.
Ajuste el indicador de nivel para medir la posición del fondo en relación con la parte
superior del vertedor y registre la altura del vertedor P (m). Reposicione de alguna
manera el nivel aguas arriba del dique.
Ajuste el flujo de agua dentro del canal para obtener las cargas h, aumente 0.010 m cada
vez. Para cada paso mida el gasto Q, y la carga h. El gasto Q se puede determinar
mediante la lectura directa del caudalímetro o en el tanque volumétrico con un
cronómetro. Para resultados precisos el indicador de nivel debe de estar lo
suficientemente lejos aguas arriba para que sea claro el descenso adyacente al vertedor.
Si la superficie libre tiende a aferrarse a la cara posterior del vertedor entonces los tubos
de ventilación están llenos de agua. Ventilando la superficie libre mediante la inserción
de la punta de un trozo de tubo hueco dentro del espacio detrás del vertedor. La
superficie libre debería separarse del vertedor.
Trace el patrón de flujo cuando el agua pasa sobre el vertedero cuando la superficie
libre es ventilada adecuadamente. Reduzca el gasto ligeramente, entonces bloquee los
tubos de ventilación y trace el patrón de flujo del aferramientote la superficie libre al
vertedor. Mida el gasto Q, y la carga h mientras que la superficie libre se aferra al dique.
CÁLCULOS
𝑽𝒐𝒍.
𝟑
𝑸𝒎𝟏 (𝒎 ⁄𝒔) =
=
𝒕𝒊𝒆𝒎𝒑𝒐
𝑽𝒐𝒍.
𝟑
𝑸𝒎𝟐 (𝒎 ⁄𝒔) =
=
𝒕𝒊𝒆𝒎𝒑𝒐
Vertedores rectangulares de pared delgada sin contracciones laterales.
En esta obra el vertedor rectangular se encuentra al centro de un canal de ancho igual (B, metros)
que la longitud de la cresta b.(B=b)
Fórmulas experimentales para determinar el coeficiente de gasto .
1. Hegly.
Límites de aplicación
Variable
inferior
h(m)
0.1
b(m)
0.5
w(m)
0.2
Datos para una
aplicación
Variable
Valores
Y1(m)
b(m)
w(m)
B(m)
h(m)
superior
0.6
2
1.13
Cálculo de los componentes de la fórmula experimental.
Pr imero  0.6075  0.045(
Segundo 
0.0041
h
Tercero
 0 . 55 (
Cuarto  (
Bb
)
B
Cálculo
(A)
(B)
b 2
)
B
C
h 2
)
hw
(D)
 (A+B)(1+C*D)

Cálculo del gasto:
Cd=
Cd=
Q(m³/s)=
Q(m³/s)=

Cd*b*h(3/2)
m³/s
2. Rehbock (Vertedores sin contracciones laterales)
Datos para una
aplicación
Variable
Valores
Y1(m)
b(m)
w(m)
B(m)
h(m)
h/w
Límites de aplicación (primeras restricciones)
Variable
inferior
superior
h(m)
0.01
0.8
b(m)
0.3
w(m)
0.06
h/w
1
Cálculo de los componentes de la fórmula experimental.
Componente
ecuación
A  0.6035  0.0813(
A
B
Cálculo del gasto
Valor
h  0.0011
)
w
 0.0011
B  1 
h 

3/ 2
Ecuación
 (A)(B)
Cd= 2.952*
Q(m³/s)= Cdbh3/2
Valor
4.- Fórmula de la Sociedad de Ingenieros y Arquitectos Suizos (Fórmula SIAS)
Caso 1.- Vertedores sin contracciones laterales
Datos para una
aplicación
Variable
Valores
Y1(m)
b(m)
w(m)
B(m)
h(m)
h/w
Límites de aplicación (primeras restricciones)
Variable
inferior
superior
h(m)
0.025
0.8
w(m)
0.3
h/w
1
Cálculos
Cálculo de los componentes de la fórmula experimental.
Componente
ecuación
Valor
A  0.578  0.037(b / B)²
A
B
B
3.615  3(b / B)²
1000h  1.6
C  0.5(b / B) 4
C
D
 h 
D

 h  w
2
  A  B1  CD

C d  2 . 952 
Cd
Q  C
Q(m³/s)
d
bh
3 / 2
VERTEDOR RECTANGULAR CON CONTRACCIONES LATERALES
En esta obra el vertedor rectangular se encuentra al centro de un canal de ancho igual
(B, metros) mayor que la longitud de la cresta b.(B>b)

3.- Hamilton-Smith
Límites de aplicación (primeras restricciones)
Variable
inferior
superior
h(m)
0.075
0.6
b(m)
0.3
w(m)
0.3
Datos para una aplicación
Variable
Valores
Y1(m)
b(m)
w(m)
B(m)
h(m)
Límites de aplicación (segundo grupo de restricciones)
Variable
Ecuaciones
Valor límite
h
h(m)
w
2
b  ( B  2h)
b(m)
h
 0.50
b
h/b
Cálculo del gasto:


  0.6161 
b 

10 B 

Cd
Q(m³/s)
 Cd*b*h(3/2)
4.- Fórmula de la Sociedad de Ingenieros y Arquitectos Suizos (Fórmula SIAS)
Caso 2.- Vertedores con contracciones laterales
Límites de aplicación (primeras restricciones)
Datos para una aplicación
Variable
inferior
superior
h(m)
0.025
0.8
Variable
Valores
w(m)
0.3
Y1(m)
h/w
1
b(m)
b
0.3B
w(m)
B(m)
Cálculos
h(m)
h/w
0.3B
Componente
ecuación
Valor
A  0.578  0.037(b / B)²
A
B
C
D

Cd
Q(m³/s)
B
3.615  3(b / B)²
1000h  1.6
C  0.5(b / B) 4
 h 
D

 h  w
2
  A  B1  CD
C d  2 . 952 
Q  C
d
bh
3 / 2