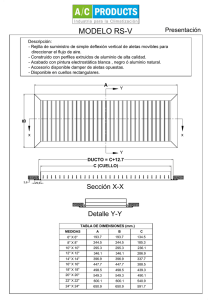
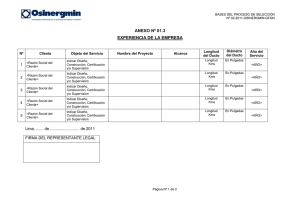
Concepción, Diseño e Implementación de un Laboratorio Virtual

!
UNIVERSIDAD SIMÓN BOLÍVAR
DECANATO DE ESTUDIOS PROFESIONALES
COORDINACIÓN DE INGENIERÍA MECÁNICA
CONCEPCIÓN, DISEÑO E IMPLEMENTACIÓN DE UN LABORATORIO
VIRTUAL PARA FLUJO COMPRESIBLE
Por
Meir Messingher Lang
PROYECTO DE GRADO
Presentado ante la Ilustre Universidad Simón Bolívar
como requisito parcial para optar al título de
Ingeniero Mecánico
Sartenejas, Junio 2008
UNIVERSIDAD SIMÓN BOLÍVAR
DECANATO DE ESTUDIOS PROFESIONALES
COORDINACIÓN DE INGENIERÍA MECÁNICA
CONCEPCIÓN, DISEÑO E IMPLEMENTACIÓN DE UN LABORATORIO
VIRTUAL PARA FLUJO COMPRESIBLE
Por
Meir Messingher Lang
Realizado con la Asesoría del
Prof. Armando Blanco Álvarez
PROYECTO DE GRADO
Presentado ante la Ilustre Universidad Simón Bolívar
como requisito parcial para optar al título de
Ingeniero Mecánico
Sartenejas, Junio 2008
iii
RESUMEN
El presente trabajo desarrolló una herramienta computacional para llevar a cabo prácticas de
laboratorio de flujo compresible utilizando un laboratorio virtual. Este laboratorio permite, por
una parte, la realización de experiencias numéricas complementarias que tocan diversos
tópicos del área de flujo compresible mientras que por otra parte facilita a aquellas personas o
instituciones, sin los recursos para adquirir los equipos necesarios, la realización de
experiencias virtuales que complementan la formación de los futuros ingenieros. El programa
desarrollado permite ofrecer la posibilidad de resolver problemas prácticos, tal como los que
aparecen en cursos y libros de mecánica de fluidos complementado así la experiencia de
estudio de una manera gráfica e interactiva.
El sistema consta de varios módulos que permiten tanto la realización de las prácticas como el
análisis de soluciones “teóricas” que se presentan al estudiar flujo isentrópico, flujo de Fanno,
flujo de Rayleigh y ondas de choque normal. El sistema fue desarrollado empleando el
software MATLAB® 7.0 por su alto poder para calcular solución numérica de sistemas de
ecuaciones no lineales así como por poseer facilidades para la construcción de interfaces
gráficas.
El sistema fue desarrollado de manera que los experimentos numéricos a realizar se
correspondan con experiencias similares que pudieran realizarse en laboratorios reales. Los
parámetros o variables sobre las que el usuario tiene la posibilidad de modificar se
corresponden a aquellas que él podría igualmente controlar en una experiencia real. La
posibilidad en el laboratorio virtual de añadir errores de medición a las soluciones, permite
darle visos realistas a las experiencias a desarrollar.
La metodología aquí seguida se puede aplicar también a otros fenómenos de diversa índole
contribuyendo a la mejora del nivel académico de las Universidades a un costo muy bajo.
Descriptores: Laboratorio virtual, flujo compresible, Matlab.
iv
DEDICATORIA
Dedico este trabajo a mi familia, quienes me han guiado siempre por el camino de la vida.
A la Universidad Simón Bolívar en su constante búsqueda de la excelencia, esperando que
este trabajo aporte un grano de arena en tan esencial y noble tarea.
v
AGRADECIMIENTOS
A mis padres y hermanos por siempre estar para mí, por apoyarme y ayudarme en
absolutamente todo.
Gracias al Profesor Armando Blanco por su excelente labor como tutor, profesor y amigo.
A la Universidad Simón Bolívar por haberme brindado la oportunidad de estudiar y crecer en
tan excelente casa de estudios.
vi
ÍNDICE GENERAL
ACTA FINAL DE PROYECTO DE GRADO........................................................................... ii
RESUMEN ................................................................................................................................ iii
DEDICATORIA.........................................................................................................................iv
AGRADECIMIENTOS...............................................................................................................v
ÍNDICE GENERAL ...................................................................................................................vi
ÍNDICE DE TABLAS................................................................................................................ix
ÍNDICE DE FIGURAS ...............................................................................................................x
LISTA DE SÍMBOLOS Y ABREVIATURAS....................................................................... xiii
1.
INTRODUCCIÓN ...............................................................................................................1
1.1.
DESCRIPCIÓN DEL PROBLEMA .............................................................................3
1.1.1. OBJETIVOS ...........................................................................................................3
1.1.1.1. GENERALES....................................................................................................3
1.1.1.2. ESPECÍFICOS ..................................................................................................3
2.
METODOLOGÍA ................................................................................................................4
2.1.
LABORATORIOS VIRTUALES DE DOMINIO PÚBLICO......................................4
2.2.
PLATAFORMAS PARA EL DESARROLLO DE APLICACIONES
PARA ENSEÑANZA EN INGENIERÍA .....................................................................4
2.3.
DESARROLLO DE ALGORITMOS PARA MODELO UNIDIMENSIONAL
DE FLUJO COMPRESIBLE ........................................................................................5
2.4.
PROGRAMACIÓN DE LOS ALGORITMOS Y ACOPLE CON LA
INTERFAZ GRÁFICA .................................................................................................6
2.5.
VALIDACIÓN DEL CÓDIGO Y FORMULACIÓN DE
EXPERIENCIAS VIRTUALES ...................................................................................6
3.
MARCO TEÓRICO.............................................................................................................8
3.1.
FLUJO COMPRESIBLE ESTABLE Y UNIDIMENSIONAL ....................................8
3.2.
FLUJO ISENTRÓPICO UNIDIMENSIONAL ............................................................8
3.3.
FLUJO DE FANNO ......................................................................................................9
vii
4.
3.4.
FLUJO DE RAYLEIGH .............................................................................................10
3.5.
ONDA DE CHOQUE NORMAL ...............................................................................11
DESCRIPCIÓN DEL LABORATORIO VIRTUAL.........................................................12
4.1.
LABORATORIO VIRTUAL ......................................................................................12
4.2.
GRÁFICAS O SOLUCIÓN EXACTA .......................................................................13
4.3.
PREFERENCIAS ........................................................................................................15
4.4.
GENERALIDADES DE LA INTERFAZ RESPECTO A LOS CASOS
DE FLUJO ISENTRÓPICO........................................................................................16
4.5.
GENERALIDADES DE LA INTERFAZ RESPECTO A LOS CASOS
DE FLUJO DE FANNO..............................................................................................18
4.6.
GENERALIDADES DE LA INTERFAZ RESPECTO A LOS CASOS
DE FLUJO DE RAYLEIGH .......................................................................................18
4.7.
5.
GENERALIDADES ACERCA DEL USO DEL PROGRAMA ................................19
DESARROLLO DEL LABORATORIO VIRTUAL ........................................................20
5.1.
ALGORITMOS ...........................................................................................................20
5.1.1. FLUJO ISENTRÓPICO........................................................................................20
5.1.2. FLUJO DE FANNO..............................................................................................30
5.1.3. FLUJO DE RAYLEIGH .......................................................................................35
5.2.
VALIDACIÓN ............................................................................................................40
5.2.1. FLUJO ISENTRÓPICO CON CONDICIÓN CRÍTICA PRESENTE,
RÉGIMEN SUBSÓNICO Y SUPERSÓNICO.....................................................40
5.2.2. FLUJO ISENTRÓPICO EN RÉGIMEN SUBSÓNICO.......................................43
5.2.3. FLUJO ISENTRÓPICO EN RÉGIMEN SUPERSÓNICO ..................................45
5.2.4. ONDA DE CHOQUE NORMAL .........................................................................45
5.2.5. FLUJO DE FANNO SUBSÓNICO NO ESTRANGULADO..............................46
5.2.6. FLUJO DE FANNO SUBSÓNICO ESTRANGULADO.....................................47
5.2.7. FLUJO DE RAYLEIGH SUBSÓNICO NO ESTRANGULADO
CON REMOCIÓN DE CALOR ...........................................................................48
5.2.8. FLUJO DE RAYLEIGH SUBSÓNICO NO ESTRANGULADO
CON ADICIÓN DE CALOR................................................................................49
viii
5.2.9. FLUJO DE RAYLEIGH SUBSÓNICO ESTRANGULADO
CON ADICIÓN DE CALOR................................................................................49
6.
7.
8.
RESULTADOS..................................................................................................................51
6.1.
FLUJO ISENTRÓPICO ..............................................................................................51
6.2.
ONDA DE CHOQUE NORMAL ...............................................................................58
6.3.
FLUJO DE FANNO ....................................................................................................62
6.4.
FLUJO DE RAYLEIGH .............................................................................................65
CONCLUSIONES Y RECOMENDACIONES.................................................................68
7.1.
CONCLUSIONES.......................................................................................................68
7.2.
RECOMENDACIONES .............................................................................................69
REFERENCIAS BIBLIOGRÁFICAS...............................................................................71!
ix
ÍNDICE DE TABLAS
Tabla 5.1 Comparación de resultados para problema de flujo Isentrópico en régimen
supersónico. .......................................................................................................................45
Tabla 5.2 Comparación de resultados para problema con Onda de Choque Normal................46
Tabla 5.3 Comparación de resultados para problema de flujo de Fanno no estrangulado. .......47
Tabla 5.4 Comparación de resultados para problema de Flujo de Fanno estrangulado. ...........47
Tabla 5.5 Comparación de resultados para problema de flujo de Rayleigh no estrangulado
con remoción de calor........................................................................................................48
Tabla 5.6 Comparación de resultados para problema de flujo de Rayleigh no estrangulado
con adición de calor...........................................................................................................49
Tabla 5.7 Comparación de resultados para problema de flujo de Rayleigh estrangulado
con adición de calor...........................................................................................................50
x
ÍNDICE DE FIGURAS
Figura 4.1 Vista del Laboratorio Virtual. ..................................................................................13
Figura 4.2 Vista de la sección de Gráficas. ...............................................................................14
Figura 4.3 Vista del Panel de Preferencias ................................................................................17
Figura 5.1 Algoritmo empleado en el módulo de Flujo Iséntropico .........................................21
Figura 5.2 Algoritmo empleado en el módulo de Flujo de Fanno.............................................30
Figura 5.3 Algoritmo empleado en el módulo de Flujo de Rayleigh ........................................36
Figura 5.4 Comparación de resultados entre el libro y el programa desarrollado.
Relación p/p0 a lo largo del ducto "A = 0,1 + x2" para flujo isentrópico
subsónico crítico. ...............................................................................................................41
Figura 5.5 Comparación de resultados entre el libro y el programa desarrollado.
Relación T/T0 a lo largo del ducto "A = 0,1 + x2" para flujo isentrópico
subsónico crítico. ...............................................................................................................41
Figura 5.6 Comparación de resultados entre el libro y el programa desarrollado.
Relación p/p0 a lo largo del ducto "A = 0,1 + x2" para flujo isentrópico
supersónico crítico.............................................................................................................42
Figura 5.7 Comparación de resultados entre el libro y el programa desarrollado.
Relación T/T0 a lo largo del ducto "A = 0,1 + x2" para flujo isentrópico
supersónico crítico.............................................................................................................42
Figura 5.8 Comparación de resultados entre el libro y el programa desarrollado.
Relación p/p0 a lo largo del ducto "A = 0,1 + x2" para flujo isentrópico subsónico.........44
Figura 5.9 Comparación de resultados entre el libro y el programa desarrollado.
Relación T/T0 a lo largo del ducto "A = 0,1 + x2" para flujo isentrópico subsónico........44
Figura 5.10 Módulo de Flujo Isentrópico. Vista de la sección Gráficas para una onda de
choque normal dentro del ducto. .......................................................................................46
Figura 6.1 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual. Flujo con
condición crítica presente. Condición aguas arriba del ducto: Régimen Subsónico. ........51
Figura 6.2 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual. Flujo con
condición crítica presente. Condición aguas arriba del ducto: Régimen Supersónico......52
xi
Figura 6.3 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión
representada. Flujo con condición crítica presente............................................................53
Figura 6.4 Módulo de Flujo Isentrópico, vista del Panel de Preferencias.
Ducto Convergente - Divergente seleccionado. ................................................................54
Figura 6.5 Módulo de Flujo Isentrópico, vista del Panel de Preferencias.
Ducto Convergente seleccionado. .....................................................................................54
Figura 6.6 Módulo de Flujo Isentrópico, vista del Panel de Preferencias.
Ducto Personalizado seleccionado. ...................................................................................55
Figura 6.7 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual.
Flujo Subsónico, Primera Medición. .................................................................................56
Figura 6.8 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual.
Flujo Subsónico, Segunda Medición. ................................................................................56
Figura 6.9 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión
representada. Eje vertical seleccionado automático. Flujo Subsónico. .............................57
Figura 6.10 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión
representada. Eje vertical seleccionado Personalizado. Flujo Subsónico. ........................57
Figura 6.11 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con el ducto
representado.......................................................................................................................58
Figura 6.12 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual.
Flujo con Onda de Choque Normal...................................................................................59
Figura 6.13 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con el
Número de Mach representado. Flujo con Onda de Choque Normal. ..............................60
Figura 6.14 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión
representada. Flujo con Onda de Choque Normal.............................................................60
Figura 6.15 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la
temperatura representada. Flujo con Onda de Choque Normal.........................................61
Figura 6.16 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la densidad
representada. Flujo con Onda de Choque Normal.............................................................61
Figura 6.17 Módulo de Flujo de Fanno, vista del Laboratorio Virtual.
Flujo subsónico no estrangulado. ......................................................................................62
xii
Figura 6.18 Módulo de Flujo de Fanno, vista de la sección de Gráficas con el Número de
Mach representado. Flujo subsónico estrangulado............................................................63
Figura 6.19 Módulo de Flujo de Fanno, vista del Panel de Preferencias.
Selección de una sección transversal circular....................................................................64
Figura 6.20 Módulo de Flujo de Fanno, vista del Panel de Preferencias.
Selección de una sección transversal rectangular..............................................................64
Figura 6.21 Módulo de Flujo de Fanno, vista del Laboratorio Virtual. Detalle de
selección del fluido............................................................................................................65
Figura 6.22 Módulo de Flujo de Rayleigh, vista del Laboratorio Virtual.
Flujo subsónico con remoción de calor no estrangulado...................................................66
Figura 6.23 Módulo de Flujo de Rayleigh, vista de la sección de Solución Exacta.
Flujo subsónico con remoción de calor no estrangulado...................................................67
Figura 6.24 Detalle de opción para cambiar de módulo............................................................67
Figura 6.25 Detalle de opciones varias del programa. ..............................................................67
xiii
LISTA DE SÍMBOLOS Y ABREVIATURAS
GENERAL
área_fm:
Área para calcular el flujo másico
apreciación_manómetro:
Apreciación de los manómetros
apreciación_termómetro:
Apreciación de los termómetros
fm:
Flujo másico a través del ducto
imp:
Número de la imagen que se corresponde con la
medición del manómetro
imt:
Número de la imagen que se corresponde con la
medición del termómetro
k:
Relación de calores específicos del gas
L:
Longitud del ducto
Ma:
Vector que contiene el Número de Mach del flujo a lo
largo del ducto
Masal:
Número de Mach en la salida del ducto
Ma_entrada:
Número de Mach en la entrada del ducto
medición_manómetro_valor:
Valor que ha de mostrar un manómetro en específico
medición_termómetro_valor:
Valor que ha de mostrar un termómetro en específico
n:
Número de elementos de los vectores Ma, p, T y ro
p:
Vector que contiene la presión del fluido a lo largo
del ducto
PM:
Peso molecular del gas
precisión_manómetro:
Valor que se sumará o restará al valor exacto de
presión en una sección del ducto dada, para
representar el error del instrumento
precisión_termómetro:
Valor que se sumará o restará al valor exacto de
temperatura en una sección del ducto dada, para
representar el error del instrumento
p_sal:
Presión de salida del ducto
p0:
Presión de estancamiento de gas
xiv
R:
Constante universal de los gases ideales
rango_presiones:
Diferencia entre la presión máxima y mínima
presente en el flujo
rango_temperaturas:
Diferencia entre la presión máxima y mínima
presente en el flujo
ro:
Vector que contiene la densidad del fluido a lo largo
del ducto
ro0:
Densidad de estancamiento de gas
T:
Vector que contiene la temperatura del fluido lo largo
del ducto
T0:
Temperatura de estancamiento de gas
V:
Velocidad del flujo en una sección dada
valores_expe_presión:
Vector que contiene las cinco mediciones de presión
hechas por los cinco manómetros
valores_expe_temperatura:
Vector que contiene las cinco mediciones de
temperatura hechas por los cinco termómetros
velocidad_fm:
Velocidad para calcular el flujo másico
x0 y x0_opuesto:
Vectores que contienen el rango de búsqueda del
Número de Mach
FLUJO ISENTRÓPICO
Aast:
Área crítica del flujo
Aast2:
Área crítica del flujo aguas abajo de la onda de
choque
Acrit_Aast:
Área de criterio dividido por Aast
Acrit_Aast_sup y Acrit_Aast_sub:
Relación entre el área criterio y el área crítica del
flujo para los dos Números de Mach establecidos
como criterio de condición sónica
Amín:
Área mínima del ducto
área:
Vector que contiene la relación área del ducto entre
Aast a lo largo de su longitud
xv
Asal:
Área de salida del ducto
condición_crítica:
Variable que refleja si la solución presenta la
condición sónica
índices_áreas_mínimas:
Vector que contiene el índice correspondientes al
elemento mínimo del vector área. De repetirse este
mínimo, este vector contiene todos los índices
asociados
Ma1:
Número de Mach justo antes de la onda de choque
Ma2:
Número de Mach justo después de la onda de choque
Ma_crit_sup y Ma_crit_sub:
Rango en los Números de Mach que el programa
considera como condición sónica
Ma_opuesto:
Número de Mach aguas arriba de la condición crítica
con el régimen de flujo opuesto al existente aguas
abajo de la misma
Masal_sub:
Número de Mach subsónico en la salida del ducto
cuando la condición crítica está presente en el mismo
Masal_sup:
Número de Mach supersónico en la salida del ducto
cuando la condición crítica está presente en el mismo
Masal_tanteo:
Número de Mach en la sección de salida del ducto,
para la onda de choque que está siendo evaluada en el
tanteo
n_opuesto:
Número entero correspondiente al índice del vector
área que contiene el área mínima más cercano a la
salida del flujo
presión_mínima_onda_choque_salida: Presión que debe haber en la sección de salida del
ducto cuando ocurre una onda de choque normal justo
en esa misma sección
p_opuesto:
Presión aguas arriba de la condición crítica con el
régimen de flujo opuesto al existente aguas abajo de
la misma
p_sal_sub:
Presión en la salida del ducto cuando el Número de
Mach en esa misma sección es Masal_sub
p_sal_sup:
Presión en la salida del ducto cuando el Número de
Mach en esa misma sección es Masal_sup
xvi
p_sal_tanteo:
Presión en la sección de salida del ducto, para la onda
de choque que está siendo evaluada en el tanteo
p02:
Presión de estancamiento del flujo aguas abajo de la
onda de choque
ro_opuesto:
Densidad aguas arriba de la condición crítica con el
régimen de flujo opuesto al existente aguas abajo de
la misma
ro1:
Densidad justo antes de la onda de choque
ro2:
Densidad justo después de la onda de choque
ro02:
Densidad de estancamiento del flujo aguas abajo de la
onda de choque
solución_isentrópica_u_onda_choque: Variable que refleja si el problema tiene solución
tanto isentrópica como con una onda de choque
normal dentro del ducto
T_opuesto:
Temperatura aguas arriba de la condición crítica con
el régimen de flujo opuesto al existente aguas abajo
de la misma
x_tanteo:
Posición donde se está probando si la onda de choque
ocurre
FLUJO DE FANNO
Delta_L:
Distancia entre una sección transversal de flujo dada
y la sección donde ocurre el estrangulamiento (aún
siendo hipotética)
Dh:
Diámetro hidráulico de la sección transversal de
ducto
f:
Coeficiente de fricción de Darcy
L:
Longitud del ducto
l_aux:
Distancia entre la salida del ducto y la sección donde
ocurre el estrangulamiento del tanteo
l_est:
Distancia entre la entrada del ducto y la sección
donde ocurre el estrangulamiento (aún siendo
hipotética)
xvii
l_est_nuevo:
Distancia entre la entrada del ducto y la sección
donde ocurre el estrangulamiento (aún siendo
hipotética) que se genera en cada iteración del tanteo
Ma1:
Número de Mach en la entrada del ducto
Ma2:
Número de Mach en la salida del ducto
pest:
Presión de estrangulamiento del flujo
p1_pest:
Relación entre la presión de entrada al ducto y la
presión de estrangulamiento del flujo
p1_p0:
Relación ente la presión de entrada al ducto y la
presión de estancamiento del flujo
p1:
Presión en la entrada del ducto
régimen_a_medir_aguas_arriba:
Variable que refleja el régimen de flujo aguas arriba
del flujo
ro_entrada:
Densidad en la entrada del ducto
ro_est:
Densidad que tendría el flujo si se estrangulara
solución_fanno:
Variable que refleja si programa puede obtener la
solución del problema
FLUJO DE RAYLEIGH
Cp:
Calor específico del gas
D:
Diámetro del ducto
Ma_entrada:
Número de Mach en la entrada del ducto
Ma_salida:
Número de Mach en la salida del ducto
pest:
Presión que al ser inducida en la salida del ducto
estrangula al flujo
p_entrada:
Presión del fluido en la entrada del ducto
p_salida:
Presión del fluido en la salida del ducto
q:
Calor transferido hacia el flujo por unidad de masa
del mismo
solución_rayleigh:
Variable que refleja si programa puede obtener la
solución del problema
1.
INTRODUCCIÓN
El uso de la computación en la ingeniería es una herramienta que permite resolver problemas
cada vez más complejos y con mayor rapidez de lo que se puede utilizando metodologías
tradicionales. El desarrollo de los método numéricos, el poder de cómputo actual y la relativa
facilidad de programar las operaciones matemáticas asociadas a un problema, permiten el
planteamiento a nivel computacional de problemas muy complejos y la obtención de los
resultados del mismo con relativa rapidez frente a los cálculos manuales, a cualquier persona
con acceso a una computadora y al software apropiado.
Además, la posibilidad de desarrollo de interfaces gráficas ha facilitado aún más el acceso al
poder computacional. Sin necesidad de comprender el funcionamiento interno de una
computadora o un software específico, es posible plantear, resolver y obtener resultados de un
problema empleando una de ellas. La interfaz gráfica interactúa con el usuario a través de la
pantalla de la computadora, brindándole un ambiente que puede comprender y utilizar para
lograr lo planteado. Detrás de la interfaz, está el código que lee los datos ingresados por el
usuario y realiza los cálculos pertinentes para resolver el tipo de problema para el cual fue
diseñada. Posteriormente los resultados son recibidos por el usuario en una diversidad de
formatos tales como tablas de datos, gráficos, etc. de los cuales se puede servir para el análisis
detallado de los problemas planteados.
La gran diversidad de problemas existentes en conjunto con la creatividad humana ha
permitido el desarrollo de interfaces gráficas de variada índole. La posibilidad de desarrollar
una aplicación que simule una práctica de laboratorio es interesante, ya que permite evitar el
costo del equipo físico asociado a la misma. Además, de esta manera, la práctica deja de
requerir ser realizada en un lugar en específico, el laboratorio, dando oportunidad de llevarse a
cabo remotamente donde cada persona tenga acceso a una computadora.
En el curso de Mecánica de Fluidos III de la Universidad Simón Bolívar se estudia el tema de
Flujo Compresible, enfocado el mismo en un análisis unidimensional y en régimen
permanente de los flujos isentrópico, de Fanno, de Rayleigh así como de ondas de choque. Se
trabajará en la posibilidad de realizar una práctica de laboratorio donde se transmitan los
conceptos, ideas y nociones asociadas a dicha área a los estudiantes.
2
En el presente trabajo se desarrolla una metodología que permite, a través del uso de una
interfaz gráfica computacional, llevar a cabo un conjunto de prácticas de laboratorio
enmarcadas en el tema de Flujo Compresible Unidimensional, a través de la manipulación y
observación de tres flujos específicos: Flujo Isentrópico, Flujo de Fanno y Flujo de Rayleigh.
Se considera además, la posibilidad de tener ondas de choque. Cada uno de estos tópicos tiene
condiciones distintas que los definen y que brindan en conjunto al estudiante la oportunidad de
adquirir las nociones básicas de esta área de la Mecánica de Fluidos a través de una actividad
de tipo experimental. Por las características mencionadas del programa, se le denominará
Laboratorio Virtual.
A través de la implementación del software desarrollado en el presente trabajo, la Universidad
Simón Bolívar puede empezar a llevar a cabo dichas prácticas. Se complementará el
aprendizaje, una vez que se cuente con los equipos docentes para la enseñanza de flujo
compresible, y se fomentará el uso de este tipo de herramientas en otras áreas de enseñanza. A
pesar de nunca ser igual una experiencia real a una “virtual” en la pantalla de una
computadora, la falta de los equipos necesarios, vuelve única y positiva a la oportunidad de
interacción entre el estudiante y el fenómeno aún a través de un software.
Es de hacer notar que esta metodología puede extenderse fácilmente a otras áreas y que los
productos aquí desarrollados podrían ser utilizados por todas las universidades nacionales, e
incluso internacionales, impactando de manera positiva el aprendizaje de los futuros
ingenieros.
Este documento se organiza de la manera siguiente. En el capítulo uno se plantea el problema
a resolver, estableciendo los objetivos a cumplir. En el capítulo dos se muestra la metodología
seguida, destacando en particular las distintas etapas que debieron cumplirse para completar el
diseño y la construcción del laboratorio virtual. El marco teórico referencial es detallado para
cada caso de estudio en el capítulo tres. Luego, en el capítulo cuatro se describe el laboratorio
virtual, destacando sus distintos componentes así como el enfoque con el que acometió el
diseño de cada una de los módulos que lo componen. El capítulo cinco desarrolla
extensamente los algoritmos utilizando tanto diagramas de flujo como lenguaje natural o
pseudocódigo, así como la validación del código llevado a cabo. Los resultados obtenidos son
presentados en el capítulo seis para culminar con las conclusiones y recomendaciones.
3
1.1.
DESCRIPCIÓN DEL PROBLEMA
En este trabajo se diseñó e implementó un laboratorio virtual para la enseñanza de flujo
compresible en cursos de Mecánica de Fluidos. Éste laboratorio facilitará en el futuro la
enseñanza de estos cursos al permitir la simulación de experiencias utilizando un computador
personal, a través de un ambiente virtual con equipos y variables controladas equivalentes a
las existentes en laboratorios físicos. El desarrollo de este laboratorio requirió cumplir con los
objetivos que se expresan a continuación.
1.1.1. OBJETIVOS
1.1.1.1.
•
GENERALES
Desarrollar un conjunto de experiencias virtuales en el área de flujo compresible a ser
realizadas a través una interfaz gráfica que permita la simulación de experiencias reales
de laboratorio, permitiendo la fácil variación de los parámetros físicos asociados.
1.1.1.2.
•
ESPECÍFICOS
Desarrollar tres módulos del programa que se correspondan con los tres flujos
compresibles unidimensionales a estudiar en el curso de Mecánica de Fluidos III de la
Universidad Simón Bolívar: Flujo Isentrópico, Flujo de Fanno y Flujo de Rayleigh,
incluyendo la posibilidad de modelar la presencia de ondas de choque.
•
Diseñar y construir la interfaz gráfica que debe permitir al usuario obtener mediciones
de temperatura y presión a lo largo de distintos ductos de prueba mediante
instrumentos que se asemejen a los presentes en laboratorios.
•
Diseñar y construir una interfaz gráfica que permita presentar la solución “exacta”
(desde el punto de vista numérico) del modelo teórico unidimensional de flujo para las
condiciones dadas por usuario y proporcionársela para que éste pueda comparar con
los resultados experimentales obtenidos en el Laboratorio Virtual.
Las etapas seguidas para cumplir con estos objetivos se describen en el capítulo siguiente.
2.
METODOLOGÍA
Durante la realización de este trabajo se cubrieron varias etapas. Estas incluyen los siguientes
pasos:
•
Revisión del estado de arte, en dominio público, del desarrollo de laboratorios virtuales
•
Revisión del uso de plataformas comerciales tales como Excel® o programas similares
en el desarrollo de programas computacionales para la enseñanza en ingeniería
•
Revisión del estado de arte en desarrollo de interfaces gráficas para aplicaciones en
ingeniería
•
Análisis crítico de los flujos isentrópicos, de Fanno y de Rayleigh así como del
modelado de ondas de choque para diseñar algoritmos que permitan analizar
situaciones físicas cuyas variables primarias coinciden con aquellas que pueden ser
controladas en experiencias reales
•
Programación de los algoritmos y acople con la interfaz gráfica
•
Establecimiento de casos base para validación
A continuación se describe brevemente los aspectos cubiertos en cada etapa.
2.1.
LABORATORIOS VIRTUALES DE DOMINIO PÚBLICO
Se realizó una investigación sobre laboratorios de flujo compresible hechos a través de una
computadora y sin necesidad de equipos físicos. Se realizaron búsquedas en Internet y en las
bases de datos EbscoHost® y ScienceDirect®. Del poco material relacionado con el tema, se
pudo encontrar a lo sumo hojas de Excel® o aplicaciones Java que calculaban las relaciones
asociadas a una sección de un flujo isentrópico en función del Número de Mach y otras que
calculaban condiciones de salida en función de las de entrada para ondas de choque normales.
Sin embargo, estas herramientas, muy simples, no tenían aplicación directa en el
cumplimiento de los objetivos, más ambiciosos, del presente trabajo.
2.2.
PLATAFORMAS PARA EL DESARROLLO DE APLICACIONES PARA
ENSEÑANZA EN INGENIERÍA
Dados los resultados obtenidos al revisar el estado de arte en laboratorios virtuales de dominio
público descritos en la sección anterior, se procedió entonces a escoger un programa de
5
desarrollo para crear el software, y se establecieron los elementos básicos que éste debía
contener para representar efectivamente a un laboratorio de flujo compresible orientado al
estudio del flujo isentrópico, flujo de Fanno y flujo de Rayleigh.
Luego de considerar diversas opciones que incluían el uso de compiladores de alto nivel como
FORTRAN y C++ para acoplarlos luego con interfaces gráficas como las proporcionadas por
VISUAL BASIC, se escogió el software MATLAB®, versión 2007b.
Según sus proveedores, entre las ventajas de MATLAB® para esta aplicación se encuentran
(The MathWorks):
•
Es un lenguaje de alto rendimiento para computación técnico-científica.
•
Integra computación, visualización y programación en un ambiente amigable.
•
Su uso típico incluye aplicaciones matemáticas, implementación de algoritmos,
manejo de datos y visualización científica.
•
Permite resolver muchos problemas de ingeniería, especialmente aquellos en cuya
formulación pueden emplearse matrices y vectores en una fracción del tiempo que
tomaría escribir un programa en un lenguaje no interactivo como C o Fortran.
•
Posee una interfaz amigable con la cual es posible probar fácilmente cambios en
programas o ir depurando un programa a medida que se construye.
Realmente, durante el desarrollo de este trabajo se pudo comprobar la veracidad de las
anteriores afirmaciones.
2.3.
DESARROLLO
DE
ALGORITMOS
PARA
MODELO
UNIDIMENSIONAL DE FLUJO COMPRESIBLE
Las ecuaciones que rigen el comportamiento para flujo compresible de gases ideales están
bien establecidas desde hace ya muchos años (Oosthuizen y Carscallen, 1997). En particular,
la aproximación de flujo unidimensional ha sido utilizada como una primera aproximación y
es enseñada en muchas universidades como parte de un primer curso de flujo compresible.
6
Sin embargo, estas ecuaciones son no lineales por lo que se recurre a diversos métodos
aproximados para su solución, empleando desde métodos gráficos y tablas hasta
procedimientos especialmente preparados para tomar en cuenta las no linealidades de las
ecuaciones. Sin embargo, en las aplicaciones que se desarrollan en este trabajo, dado que se
consideró como situación de partida que las variables a prefijar en cualquier experimento
corresponde a aquellas variables sobre las que se tendría control en un experimento real, se
requirió desarrollar algoritmos específicos para cada aplicación.
Así, se desarrollaron algoritmos para cada uno de los flujo estudiados. Estos se expresaron
tanto en términos de Diagramas de Flujo como en Pseudocódigo, de manera que puedan ser
implementados fácilmente por potenciales usuarios de este trabajo.
En cuanto a la programación de los métodos utilizados, se privilegió el uso de las librerías
internas de MATLAB® que incluyen diversas subrutinas tanto para la solución de ecuaciones
no lineales como de sistemas de ecuaciones no lineales. Estas subrutinas fueron validadas en
todos los casos antes de ser utilizadas en las distintas aplicaciones.
2.4.
PROGRAMACIÓN DE LOS ALGORITMOS Y ACOPLE CON LA
INTERFAZ GRÁFICA
Tal como se explicó anteriormente, MATLAB® posee facilidades para generar una interfaz
gráfica y acoplarla con los módulos de cálculo. En esta aplicación se desarrolló una interfaz
gráfica en ambiente Windows™ con el editor de interfaces gráficas de usuario guide de
MATLAB® 2007b
2.5.
VALIDACIÓN DEL CÓDIGO Y FORMULACIÓN DE EXPERIENCIAS
VIRTUALES
El código fue validado a partir de la adaptación de ejemplos encontrados en los textos de
Mecánica de Fluidos utilizados tradicionalmente y citados en la sección de referencias
bibliográficas. Se validó cada uno de los módulos de manera extensiva de manera que se
cubriera el más extenso conjunto posibles de casos.
7
Dado el conjunto de variables utilizadas (variables medibles experimentalmente), todos los
ejemplos debieron ser reformulados y la validación se realizó de manera indirecta. En la
sección 5.2 se detalla este proceso.
Por otra parte, las experiencias propuestas para las prácticas se obtuvieron igualmente de
textos clásicos de mecánica de fluidos. Esto tiene la ventaja de permitirle al estudiante la
comparación con casos ampliamente explicados en la literatura, lo cual debe facilitarle el
proceso de aprendizaje. El programa desarrollado puede utilizarse en clase, utilizando
sencillamente una computadora portátil y un proyector, lo que permite ahondar en
explicaciones al considerar los efectos de realizar variaciones de un parámetro particular (por
ejemplo, disminuir la presión).
En los capítulos siguientes se desarrollan cada una de las distintas etapas descritas
anteriormente.
3.
MARCO TEÓRICO
A continuación se describen los fundamentos teóricos necesarios para la descripción física del
flujo de un gas ideal.
3.1.
FLUJO COMPRESIBLE ESTABLE Y UNIDIMENSIONAL
Para los tres flujos a ser estudiados se tomaron en cuenta un conjunto general de hipótesis.
Resumiendo las consideraciones tomadas por Oosthuizen y Carscallen (1997), se empieza por
tomar en cuenta la compresibilidad del fluido. El comportamiento de este se asume bajo las
condiciones de gas ideal. El régimen de flujo a estudiar es estacionario, es decir que todas las
propiedades son constantes a lo largo del tiempo. Los calores específicos se consideran
constantes para todo el flujo. El flujo puede aproximarse como unidimensional lo que en otras
palabras significa que el estudio se hará considerando relevantes las variaciones de las
propiedades del fluido en una sola dimensión y despreciando las demás. Esta dimensión
coincide con la dirección preferencial de flujo. Se debe agregar también que se desprecia el
trabajo motor y la variación de energía potencial (White, 2004).
Las ecuaciones que aplican a todos los flujos en estudio son las siguientes (White, 2004):
Ma =
V
kRT
˙ = "VA
m
(3.1)
(3.2)
!
3.2.
!
FLUJO ISENTRÓPICO UNIDIMENSIONAL
Tal como expresa White (2004), un flujo puede considerarse isentrópico cuando la variación
de entropía a lo largo del flujo es insignificante. No hay fricción entre el fluido y las paredes
del ducto y el flujo es adiabático (en consecuencia es reversible tomando en cuenta la no
variación de la entropía ya mencionada), lo que significa que la energía es constante a lo largo
del mismo.
Para este flujo en específico el área del ducto es variable, sin embargo el estudio será hecho de
manera unidimensional. Esto se puede hacer “si las variaciones de área son pequeñas y el
9
radio de curvatura de la pared es grande … entonces el flujo es aproximadamente
unidimensional” (White, 2004).
Un resumen de las ecuaciones asociadas al Flujo Isentrópico Unidimensional empleadas en el
presente trabajo puede apreciarse a continuación (White, 2004):
k
!
& k"1
p0 # k "1
= %1+
Ma 2 (
'
p $
2
(3.3)
&
T0 # k "1
= %1+
Ma 2 (
'
T $
2
(3.4)
1
!
' k#1
" 0 $ k #1
= &1+
Ma 2 )
(
" %
2
(3.5)
k +1
!
3.3.
2(k"1)
# k "1
2&
A
1 %1+ 2 Ma (
=
%
(
A* Ma % 1+ k "1 (
$
'
2
(3.6)
!
FLUJO DE FANNO
En el caso particular de Flujo de Fanno, las siguientes consideraciones deben ser tomadas en
cuenta a la hora del análisis de este tipo de flujo. Hay fricción entre el fluido y las paredes del
ducto y la misma se corresponde con los coeficientes de fricción de Darcy. Esta suposición es
cuestionable en el caso de flujo supersónico por lo que este caso no fue considerado en este
laboratorio virtual. Además, el flujo es adiabático. La geometría del ducto corresponde a un
área transversal constante a lo largo del mismo y a una tubería recta, (White, 2004).
Las ecuaciones pertinentes al Flujo de Fanno se presentan a continuación (White, 2004):
)
,
2
+
4 f * # 1" Ma & k + 1
( k + 1) Ma ..
+
l =%
+
ln
2 (
Dh
$ kMa ' 2k +2#%1+ k "1 Ma 2 &(.
+* $
'.2
2
!
(3.7)
10
k +1
p
1
2
=
p * Ma 1+ k "1 Ma 2
2
"
=
"*
!
3.4.
k #1 2
Ma
2
k +1 2
Ma
2
(3.8)
1+
(3.9)
!
FLUJO DE RAYLEIGH
Las condiciones asociadas a este tipo de flujo se pueden resumir en las presentadas a
continuación. No hay fricción entre el fluido y el ducto. Sin embargo el flujo no es adiabático
ya que puede haber transferencia de calor. El área transversal del ducto es constante a lo largo
del mismo, (White, 2004).
Las ecuaciones relacionadas al Flujo de Rayleigh empleadas en el programa son (White,
2004):
q
T
= 01 #1
Cp " T01 T02
!
(3.10)
# k "1
2&
1+
Ma
2
%
(
T02 T2
2
= %
(
T01 T1 %1+ k "1 Ma 2 (
1
$
'
2
2 2
[
[
2
!
(3.11)
T2 Ma2 1+ kMa1
=
T1 Ma 2 1+ kMa 2
1
2
]
]
2
(3.12)
Sustituyendo las ecuaciones 1.12 y 1.11 en la Ecuación 1.10 se obtiene la siguiente expresión:
!
2
[
[
q
Ma2
=
Cp " T01 Ma12 1+ kMa 2
2
!
$ k #1
2'
&%1+ 2 Ma2 )(
#1
2
$ k #1
2'
1+
Ma
1 )
&%
(
2
2 2
1+ kMa1
]
]
(3.13)
11
!
!
3.5.
p2 1+ kMa12
=
p1 1+ kMa2 2
(3.14)
T2 Ma2 2 (1+ kMa12 ) 2
=
T1 Ma12 (1+ kMa2 2 ) 2
(3.15)
" 2 Ma12 (1+ kMa2 2 )
=
"1 Ma2 2 (1+ kMa12 )
(3.16)
!
ONDA DE CHOQUE
NORMAL
Los casos que contemplen la presencia de onda de choque requieren tomar en cuenta las
hipótesis planteadas a continuación. La velocidad del flujo antes y después de la onda de
choque es perpendicular a esta misma. El flujo a través de la onda de choque es adiabático. Se
aplican las mismas hipótesis del flujo unidimensional, es decir que los cambios de las
propiedades del flujo en cualquier dirección que no es la del mismo se desprecian,
(Oosthuizen y Carscallen, 1997).
Las ecuaciones correspondientes a la Onda de Choque Normal empleadas en este trabajo se
presentan a continuación, (Oosthuizen y Carscallen, 1997):
!
p2 2kMa12 " (k "1)
=
p1
k +1
(3.17)
(k "1)Ma12 + 2
Ma2 =
2kMa12 " (k "1)
(3.18)
k +1
!
A2* Ma2 # 2 + (k "1)Ma12 & 2(k"1)
%
(
* =
Ma1 $ 2 + (k "1)Ma2 2 '
A1
(3.19)
k
#
& k"1
"1
k"1
( #) 2k ,
&
)
,
p02 % k + 1
Ma12
k
"1
2
! =%
. Ma1 " +
.(
( %+
k
"1
2
*
*
-'
p01 % 2 1+
k
+
1
k
+
1
$
Ma1 (
$
'
2
(3.20)
La solución numérica de las ecuaciones antes descritas, según sea el caso tratado, permitirá
reproducir virtualmente cada uno de tipos de flujo mencionadas.
!
4.
DESCRIPCIÓN DEL LABORATORIO VIRTUAL
El programa principal se diseñó con tres módulos que permiten el estudio de uno de los tres
tipos de flujo ya mencionados. Cada módulo cuenta con tres paneles o secciones: Laboratorio
Virtual, Gráficas o Solución Exacta y Preferencias, las cuales en conjunto permiten al usuario
tanto observar el comportamiento del flujo bajo las condiciones que él mismo especifica, así
como apreciar el efecto que tiene en el mismo el variar una o varias de éstas.
4.1.
LABORATORIO VIRTUAL
En el Laboratorio Virtual se muestra visualmente el montaje experimental asociado al tipo de
flujo en estudio. Dicho montaje está conformado por un ducto, manómetros, termómetros, un
medidor de flujo másico y una válvula de regulación en el extremo de salida del ducto. Los
medidores de presión y temperatura se diseñaron como una mezcla entre medidores análogos
y digitales para ofrecerle al usuario mayor cantidad de información. Para la parte análoga se
crearon 29 imágenes que representan gráficamente el rango entre la medición mínima y la
máxima. La mínima medida posible en un caso específico de estudio se le asigna a la imagen 1
mientras que la máxima a la 29, y las medidas en cada instrumento se reflejan gráficamente en
proporción lineal a este rango. Para la parte digital del instrumento se coloca la medida en
números con varios decimales justo encima del medidor, dejando al usuario la tarea de
redondear según sea la apreciación correspondiente. Se puede apreciar en detalle lo descrito
anteriormente en la Figura 4.1. Cada medición se genera sumando o restando aleatoriamente al
resultado exacto según el modelo teórico empleado, un valor al azar entre cero y la apreciación
del instrumento apropiado. Dado que en el tipo de fenómeno de trabajo se trabaja con la
presión absoluta, los manómetros reflejarán dicha magnitud. En el presente trabajo cada vez
que se emplee el término de presión se estará haciendo referencia a la presión absoluta.
El medidor de flujo másico es únicamente digital. Se escogió medir temperatura y presión ya
que los medidores para este tipo de magnitudes son comunes en laboratorios. Las mediciones
de presión y temperatura son suficientes en conjunto con los datos del fluido y del ducto para
que el problema quede determinado, en consecuencia se puede calcular a partir de estos la
densidad y el número de Mach así como el flujo másico, ofreciendo este último un punto de
comparación con el medido. Se pueden apreciar dos pequeñas gráficas que muestran las
13
mediciones de los termómetros y manómetros por separado para darle al usuario una idea de
cómo es la distribución de dichas magnitudes a lo largo del ducto. Las apreciaciones de los
termómetros y manómetros se presentan al usuario para su conocimiento.
Figura 4.1 Vista del Laboratorio Virtual.
4.2.
GRÁFICAS O SOLUCIÓN EXACTA
En la sección de Gráficas o Solución Exacta se puede observar la solución exacta del sistema
definido por el usuario según el modelo unidimensional de flujo empleado. Esta permite al
usuario tanto contrastar los datos obtenidos en el Laboratorio Virtual con los esperados según
dicho modelo como apreciar y estudiar el comportamiento del flujo bajo las hipótesis
pertinentes. Además, esta parte del programa permite emplearlo también para resolver
problemas, ejercicios y ejemplos en cuanto a flujo compresible, complementando el contacto
que tiene el usuario con el fenómeno. Se tiene la posibilidad de observar el Número de Mach,
14
presión, temperatura y densidad a lo largo del ducto. También se puede escoger y fijar el rango
del eje vertical de las gráficas para tener un punto de comparación al variar las condiciones del
problema y buscar la nueva solución. Esta opción le da al usuario también perspectiva en
cuanto a la variación en sí de una magnitud respecto a un rango determinado. En la Figura 4.2
se ilustra lo explicado.
Figura 4.2 Vista de la sección de Gráficas.
Tanto en el Laboratorio Virtual como en la sección de Gráficas o Solución Exacta, el usuario
tiene acceso visual y posibilidad de modificar el fluido en estudio, propiedades de
estancamiento del flujo en la entrada del ducto, presión de salida del flujo del ducto y si es el
caso, otras variables que caracterizan el tipo de flujo. De esta manera la persona que usa el
programa tiene siempre presente en la pantalla los valores asociados al caso que está
estudiando.
15
4.3.
PREFERENCIAS
El Panel de Preferencias del programa permite modificar u obtener en detalle otras variables o
valores asociados a la práctica. Se pueden seleccionar las apreciaciones de los instrumentos de
medida, calcular las presiones características del sistema y escoger el régimen de flujo aguas
arriba del ducto para posibilitar el estudio de ambos. En esta sección también se puede
modificar en detalle el ducto a emplear.
El trabajo en conjunto de las características descritas anteriormente permiten al usuario, a
través de la interfaz de cada módulo, seleccionar el fluido a estudiar, modificar las condiciones
de estancamiento del flujo, escoger un tipo de ducto y modificar la presión de salida de la
tubería a través de la válvula quedando determinado el problema. La situación descrita
representa en la realidad un depósito donde las propiedades son medibles y el fluido e trabajo
es escogido, una tubería seleccionada por sus características específicas y cuya descarga está
conectada a través de una válvula a un reservorio donde la presión puede mantenerse en un
valor constante requerido, por ejemplo a través de una bomba de vacío. Mediante la válvula se
puede regular el flujo de salida del ducto induciendo una posible variación de presión en esa
sección y modificando o no aguas arriba las condiciones del mismo. Para el caso en específico
donde el usuario suministre una presión de salida menor a la de estrangulamiento del flujo, el
manómetro en la salida del ducto reflejará la presión de estrangulamiento. Se debe pensar que
el usuario ha tratado de inducir dicho valor de presión a la salida del ducto abriendo la válvula,
pero luego de cierto punto de apertura la presión no puede disminuir debido al
estrangulamiento.
Cabe destacar que se agregó la opción de exportar la data asociada a la solución exacta a
Excel® para posteriores análisis tales como comparación en detalle con las mediciones
experimentales virtuales o con otras soluciones exactas para condiciones diferentes. El usuario
también tiene la opción de reseteo del programa si acaso desease colocar en cero los
instrumentos de medida y vaciar las gráficas. También se puede mover entre los tres módulos
sin necesidad de cerrar el programa. Todos los módulos trabajan en el Sistema Internacional
de unidades y todos los valores en la interfaz están acompañados de su unidad de medición
correspondiente.
16
4.4.
GENERALIDADES DE LA INTERFAZ RESPECTO A LOS CASOS DE
FLUJO ISENTRÓPICO
Específicamente para el flujo isentrópico se escribió un código que permitiese determinar si la
solución presenta o no una onda de choque normal entre la última área crítica en el sentido del
flujo y la salida del ducto. De existir, el usuario ha de notarlo con seguridad en la sección de
Gráficas y probablemente podrá apreciar la discontinuidad en las mediciones del Laboratorio
Virtual. Aguas arriba de la mencionada área crítica se grafican siempre la solución subsónica y
supersónica para brindar al usuario la posibilidad de contrastar ambas. También se agregó la
opción en el Panel de Preferencias de modificar el perfil interno del ducto definido como una
variación del área transversal del mismo a lo largo de su eje axial. Se brindan tanto unos
modelos predeterminados como una opción personalizada en la cual el usuario suple una serie
de par de puntos que corresponden distancia axial con el radio del ducto y que por ende
describen al mismo. El ducto convergente divergente predeterminado se corresponde con la
función “A = 0,1 + x2” donde “A” es el área y “x” la distancia axial. Tanto el ducto
convergente como el ducto divergente predeterminados se corresponden con las mitades del
ducto convergente divergente. El ducto divergente convergente predeterminado se
corresponde con la función “ A = 0,38 – x2 ”. Dado que la opción personalizada interpola los
puntos que el usuario suple, se agregaron unas casillas donde se reflejan el radio mínimo y
área mínima del ducto así como una pequeña imagen del mismo para que el usuario confirme
que el programa está caracterizando el mismo asertivamente. Lo mencionado respecto al Panel
de Preferencias puede observarse en detalle en la Figura 4.3. Todo esto se hizo con la finalidad
de ofrecer la posibilidad de estudiar el efecto que tienen distintas variaciones en el flujo,
además del usuario poder entender y pensar cómo aprovechar las mismas. Se debe resaltar que
el estudio de ondas de choque normales en ductos personalizados debe hacerse con cuidado ya
que el código se pensó para ductos que aguas abajo de la última garganta en el sentido del
flujo tengan un radio creciente hasta la salida.
En el Laboratorio Virtual de este tipo de flujo se observan cinco manómetros y cinco
termómetros a lo largo del ducto que permiten tomar los datos necesarios para observar las
tendencias de la presión y la temperatura y calcular a partir de ellos el número de Mach y la
densidad del fluido a lo largo del mismo como ya ha sido mencionado. En el Panel de
17
Preferencias se puede escoger tanto flujo subsónico como supersónico como condición aguas
arriba del ducto. Es importante destacar que la posibilidad de escoger dicho régimen permite
al usuario obtener medidas para los dos tipos en caso de estar presente la condición crítica. En
caso de no estar, el problema tiene solución única y pudiese pensarse contradictorio una
situación donde el régimen aguas arriba escogido y el régimen de flujo encontrado en el ducto
no fuesen el mismo. En este caso se debe pensar que hay un reacomodo del flujo en algún
tramo entre la condición aguas arriba y la entrada del ducto para poder cumplir con la
condición de salida del mismo. Las presiones críticas asociadas a este tipo de flujo reflejadas
en el Panel de Preferencias son tres: la presión máxima que induce una solución supersónica
completa, la presión mínima que induce una solución subsónica completa, y la presión mínima
que induce una onda de choque a la salida del ducto.
Figura 4.3 Vista del Panel de Preferencias
18
Dado que la presión en el flujo siempre es menor a la presión de estancamiento y que esta
última es constante para este tipo de flujo, si el usuario ingresa una presión de salida mayor a
ésta se le notifica que no es válida. De la misma manera, si ingresa una presión de
estancamiento menor la presión de salida se modifica automáticamente para quedar por debajo
de la misma, evitando errores en el cálculo numérico de la solución.
4.5.
GENERALIDADES DE LA INTERFAZ RESPECTO A LOS CASOS DE
FLUJO DE FANNO
Para el flujo de Fanno se programó la interfaz para permitir modificar la longitud, sección
transversal y coeficiente de fricción de la tubería, posibilitando el estudio del efecto que tienen
dichas variables en el flujo. El Laboratorio Virtual cuenta con la misma cantidad de
manómetros y termómetros que el del flujo isentrópico. La presión crítica asociada a este tipo
de flujo reflejada en el Panel de Preferencias se corresponde con la presión que estrangula al
flujo. Esta primera versión del programa sólo trabaja en régimen subsónico para este tipo de
flujo por lo que es la única opción que se puede seleccionar en las preferencias. En este
módulo no se colocaron restricciones respecto a la relación que hay entre presión en la salida
del ducto y presión de estancamiento de entrada al mismo, por lo que debe emplearse con
cuidado al ingresar dichos valores ya que sí existe una relación entre los mismos.
4.6.
GENERALIDADES DE LA INTERFAZ RESPECTO A LOS CASOS DE
FLUJO DE RAYLEIGH
La interfaz del flujo de Rayleigh permite modificar el calor por unidad de masa de fluido que
se transfiere hacia o desde el flujo. Cabe resaltar que el calor tiene un mínimo y corresponde
con el que al ser extraído lleva a cero la temperatura de estancamiento absoluta del flujo. El
Laboratorio Virtual se hizo únicamente con medidores a la entrada y salida del ducto. Dado
que en la obtención de las ecuaciones de este tipo de flujo no se especifica la forma en la que
ocurre la transferencia de calor (White, 2004) la variación de las propiedades del flujo dentro
del ducto no se puede describir a menos que se establezca alguna forma. Así mismo en la
sección de Solución Exacta sólo se colocan los valores de las mismas a la entrada y salida de
la tubería. La presión crítica asociada a este tipo de flujo reflejada en el Panel de Preferencias
se corresponde con la presión que estrangula al flujo. Esta primera versión del programa sólo
19
trabaja en régimen subsónico para este tipo de flujo por lo que es la única opción que se puede
seleccionar en las preferencias. En este módulo aplica también el cuidado que debe tenerse
con los valores de presión y presión de estancamiento ingresados.
4.7.
GENERALIDADES ACERCA DEL USO DEL PROGRAMA
El código hecho para los tres tipos de flujo se escribió modularmente y se comentó
completamente para facilitar su lectura y entendimiento así como su modificación o
expansión. En grandes rasgos se puede dividir en tres grandes procesos: calcular la solución
según el modelo unidimensional empleado, colocar las medidas en el Laboratorio Virtual y
graficar o colocar los valores exactos en la sección de Gráficas o Solución Exacta. El código
está pensando para agregarle algunos otros casos de estudio tales como el flujo de Fanno y
Rayleigh supersónico así como ondas de choque oblicuas en el flujo isentrópico. El agregar en
los espacios correspondientes el código que calcule estos casos permite fácilmente diversificar
aún más el programa y volverlo más rico en contenido y poderoso en posibilidades de
aplicación.
Para emplear el Laboratorio Virtual como herramienta para llevar a cabo la práctica de Flujo
Compresible Unidimensional, se debe elaborar una debida Guía Práctica de Laboratorio con
algunas condiciones establecidas para obtener las variables del flujo a ser medidas y
posteriormente analizadas. El programa, como se verá más adelante, es suficientemente
flexible como para permitir el diseño de diversas prácticas especialmente concebidas por el
docente o incluso el diseño de actividades de auto aprendizaje. Para realizarlas, el usuario
ingresa los valores pertinentes en la interfaz, obtiene los resultados tanto experimentales como
exactos, y luego los compara por ejemplo a través de gráficos, para poder analizar los
resultados en detalle y aprender de ellos los conceptos básicos asociados al flujo compresible.
5.
DESARROLLO DEL LABORATORIO VIRTUAL
Para cada uno de los casos tratados se desarrolló un módulo del programa. Esta sección
describe los algoritmos desarrollados.
5.1.
ALGORITMOS
Los algoritmos fueron diseñados en función de los casos que se querían estudiar para cada uno
de los tres tipos de flujo en cuestión. Por esta razón hay un algoritmo único para cada módulo
del programa, sin embargo existen ciertas instrucciones comunes a todos.
5.1.1. FLUJO ISENTRÓPICO
Para la simulación de flujo isentrópico se considera como variables de entrada la presión de
salida del ducto, las condiciones de estancamiento del flujo, las propiedades del fluido, las
características del ducto, etc. En la Figura 5.1 se presenta el esquema de funcionamiento del
módulo correspondientes al flujo isentrópico. Las rutinas están enmarcadas en rectángulos y se
explican en detalle a continuación. Para algunos valores particulares de las variables de
entrada el modelo unidimensional podría ser incapaz de predecir soluciones con sentido físico
(por ejemplo la formación de ondas oblicuas a la salida de la tobera). Se ha tomado la
previsión para que en esos casos, la variable solución_isentrópica_u_onda_choque tome el
valor no, y quedará para futuros desarrollos agregar módulos al código para que busque la
solución.
El algoritmo se expresa como:
•
Leer los datos: Lee los datos ingresados por el usuario p_sal, k, PM, p0, T0, !0, L,
Asal.
21
Figura 5.1 Algoritmo empleado en el módulo de Flujo Iséntropico
22
•
Calcular el Área Crítica del ducto: A partir de las condiciones dadas calcula cuál
área debería tener la sección del ducto que presenta flujo sónico.
Calcular Masal de la Ecuación 5.1
k
# k "1
& k"1
p0
= %1+
Masal 2 (
'
p _ sal $
2
(5.1)
Calcular!Aast de la Ecuación 5.2
k +1
2(k"1)
# k "1
2&
1+
Masal
%
(
Asal
1
2
=
%
(
k "1
Aast Masal %
(
1+
$
'
2
•
(5.2)
Calcular!las Presiones Críticas: Calcula la presión límite que genera una solución
subsónica y la presión límite que genera una solución supersónica.
Calcular Masal_sub de la Ecuación 5.3 buscando en el intervalo
x0 = [0,001 ; 1]
k +1
2(k"1)
# k "1
2&
1+
Masal
_
sub
%
(
Asal
1
2
=
%
(
k "1
Amín Masal _ sub %
(
1+
$
'
2
(5.3)
Calcular Masal_sup de la Ecuación 5.4 buscando en el intervalo
!
x0 = [1 ; 10]
k +1
2(k"1)
# k "1
2&
1+
Masal
_
sub
%
(
Asal
1
2
=
%
(
k "1
Amín Masal _ sub %
(
1+
$
'
2
!
(5.4)
23
Calcular p_sal_sub de la Ecuación 5.5
k
# k "1
& k"1
p0
= %1+
Masal _ sub 2 (
'
p _ sal _ sub $
2
(5.5)
Calcular
! p_sal_sup de la Ecuación 5.6
k
# k "1
& k"1
p0
= %1+
Masal _ sub 2 (
'
p _ sal _ sub $
2
•
(5.6)
Calcular la!Presión de Salida que induce Onda de Choque a la salida del ducto:
Calcular presión_mínima_onda_choque_salida de la Ecuación 5.7
presión _ mínima _ onda _ choque _ salida 2kMasal _ sup 2 " (k "1)
=
p _ sal _ sub
k +1
!•
(5.7)
Determinar Acriterio/Aast: Establece un criterio para reconocer la presencia de la
condición sónica.
Dado Ma_crite_sup = 1,01 calcular Acrit_Aast_supde la Ecuación 5.8
k +1
2(k"1)
# k "1
2&
1+
Ma
_
crite
_
sup
%
(
1
2
Acrit _ Aast _ sup =
%
(
k "1
Ma _ crite _ sup %
(
1+
$
'
2
!
(5.8)
Dado Ma_crite_sub = 0,99 calcular Acrit_Aast_subde la Ecuación 5.9
k +1
2(k"1)
# k "1
2&
%1+ 2 Ma _ crite _ sub (
1
Acrit _ Aast _ sub =
%
(
k "1
Ma _ crite _ sub %
(
1+
$
'
2
!
Acrit_Aast = Mínimo valor entre Acrit_Aast_sup y Acrit_Aast_sub.
(5.9)
24
•
Calcular Solución: Calcula la solución asociada al régimen de flujo establecido en
la salida del ducto
Si Masal > 1
x0 = [1 ; 10]
x0_opuesto = [0,001 ; 1]
Si Masal <= 1
xo = [0,001 ; 1]
xo_opuesto = [1 ;10]
Fin
Calcular el Número de Mach, la presión, temperatura y densidad a lo largo del
ducto a partir de las ecuaciones 5.10, 5.11, 5.12 y 5.13 respectivamente.
Número de Mach en el intervalo x0.
Para i: 1 hasta n
k +1
2(k"1)
# k "1
2&
1 %1+ 2 Ma(i) (
área(i) =
%
(
Ma(i) % 1+ k "1 (
$
'
2
(5.10)
k
!
!
& k"1
p0 # k "1
= %1+
Ma(i) 2 (
'
p(i) $
2
(5.11)
# k "1
&
T0
= %1+
Ma(i) 2 (
'
T(i) $
2
(5.12)
1
!
' k#1
" 0 $ k #1
= &1+
Ma(i) 2 )
(
"(i) %
2
(5.13)
Fin
!
•
Calcular Solución Opuesta: Calcula la segunda solución posible cuando la
condición sónica está presente en el ducto.
n_opuesto: Valor máximo del vector índices_áreas_mínimas
25
Calcular el Número de Mach, la presión, temperatura y densidad entre la
entrada y la garganta del ducto a partir de las ecuaciones 5.14, 5.15, 5.16 y 5.17
respectivamente. Número de Mach en el intervalo x0_opuesto.
Para i: 1 hasta n_opuesto
k +1
2(k"1)
# k "1
2&
1+
Ma
_
opuesto(i)
%
(
1
2
área(i) =
%
(
k "1
Ma _ opuesto(i) %
(
1+
$
'
2
(5.14)
k
!
!
# k "1
& k"1
p0
= %1+
Ma _ opuesto(i) 2 (
'
p _ opuesto(i) $
2
(5.15)
# k "1
&
T0
= %1+
Ma _ opuesto(i) 2 (
'
T _ opuesto(i) $
2
(5.16)
1
$ k #1
' k#1
"0
= &1+
Ma _ opuesto(i) 2 )
(
" _ opuesto(i) %
2
!
(5.17)
Fin
•
!
Búsqueda Onda de Choque: Se determina la posición de la onda de choque normal
y se agrega su efecto a la solución supersónica.
Calcular Solución (xo = [1 ; 10])
Calcular Solución Opuesta (xo_opuesto = [0,001 ; 1])
Método de Bisección:
x_tanteo
Calcular Ma1 mediante la Ecuación 5.18
k +1
# k "1
2 & 2(k"1)
1+
Ma
1
%
(
1
2
área(x _ tan teo) =
%
(
Ma1 % 1+ k "1 (
$
'
2
!
(5.18)
Calcular Ma2con la Ecuación 5.19
(k "1)Ma12 + 2
Ma2 =
2kMa12 " (k "1)
!
(5.19)
26
Calcular Aast2 a partir de la Ecuación 5.20
k +1
A2*
Ma2 # 2 + (k "1)Ma12 & 2(k"1)
=
%
(
Aast Ma1 $ 2 + (k "1)Ma2 2 '
(5.20)
Calcular p02 de la Ecuación 5.21
!
k
#
& k"1
"1
2
k"1
%
(
#
&
)
,
)
,
p02
k +1
Ma1
2k
k "1
2
=%
. Ma1 " +
.(
( %+
k
"1
2
* k + 1-'
p0 % 2 1+
Ma1 ( $* k + 1$
'
2
(5.21)
Calcular Masal_tanteo con la Ecuación 5.22 en el rango
x0 = [0,0001 ; 1]
!
(5.22)
Calcular p_sal_tanteo con la Ecuación 5.23
k
# k "1
& k"1
p02
= %1+
Masal _ tan teo 2 (
'
p _ sal _ tan teo $
2
!
(5.23)
Si p_sal_tanteo > p_sal
Mover hacia la salida del ducto x_tanteo
Si p_sal_tanteo < p_sal
Mover hacia la garganta del ducto x_tanteo
Fin
Fin
Calcular !1 con la Ecuación 5.24
1
" 0 $ k #1
2 ' k#1
= &1+
Ma1 )
(
"1 %
2
!
(5.24)
27
Calcular !2 con la Ecuación 5.25
"2
(k + 1)Ma12
=
"1 2 + (k #1)Ma12
(5.25)
Calcular !02 con la Ecuación 5.26
!
1
" 02 $ k #1
2 ' k#1
= &1+
Ma2 )
(
"2 %
2
(5.26)
Para i: n_onda hasta n
!
área(i) = área(i)*Aast/Aast2
Calcular el Número de Mach, la presión, temperatura y densidad entre la
garganta y la salida del ducto a partir de las ecuaciones 5.27, 5.28, 5.29 y 5.30
respectivamente. Número de Mach en el intervalo x0.
k +1
2(k"1)
# k "1
2&
1+
Ma(i)
%
(
1
2
área(i) =
%
(
Ma(i) % 1+ k "1 (
$
'
2
(5.27)
k
!
!
& k"1
p02 # k "1
= %1+
Ma(i) 2 (
'
p(i) $
2
(5.28)
# k "1
&
T0
= %1+
Ma(i) 2 (
'
T(i) $
2
(5.29)
1
!
' k#1
" 02 $ k #1
= &1+
Ma(i) 2 )
(
"(i) %
2
(5.30)
Fin
!
•
Guardar Resultados: Guarda los valores obtenidos para ser empleados por las
rutinas a continuación.
28
•
Colocar Valores en el Laboratorio Virtual: Coloca los valores de temperatura,
presión y flujo másico en los medidores correspondientes. Además grafica en el
Laboratorio virtual las medidas de tanto la presión como la temperatura a lo largo
del ducto.
Si condición_crítica = sí
Según haya escogido el usuario en el panel de preferencias se reflejará
la solución subsónica o supersónica en el Laboratorio Virtual aguas
arriba del punto crítico.
Fin
rango_presiones = (Presión Máxima + apreciación_manómetro) - (Presión
Mínima - apreciación_manómetro)
rango_temperaturas = (Temperaruta Máxima + apreciación_termómetro) (Temperatura Mínima - apreciación_termómetro)
Para i: 1 hasta 5
precisión_manómetro = apreciación_manómetro*[(2(Random(1)-0,5)]
precisión_termómetro = apreciación_termómetro*[(2(Random(1)-0,5)]
j = 1 + [(n-1)/4]*(i-1)
Si i = 5
medición_manómetro_valor = p(n)
Sino
medición_manómetro_valor = p(j) + precisión_manómetro
Fin
medición_termómetro_valor = T(j) + precisión_termómetro
valores_expe_presión(i) = medición_manómetro_valor
valores_expe_temperatura(i) = medición_termómetro_valor
Colocar medición_manómetro_valor
correspondiente al manómetro i.
en
el
cuadro
de
texto
Colocar medición_termómetro_valor
correspondiente al termómetro i.
en
el
cuadro
de
texto
imp = 2 + Redondear[((medición_manómetro_valor – (Presión Mínima
- apreciación_manómetro)) / rango_presiones ) * 29]
29
imt = 2 + Redondear[((medición_termómetro_valor – (Temperatura
Mínima - apreciación_termómetro)) / rango_temperaturas ) * 29]
Cargar la imagen imp de los manómetros en el espacio correspondiente
al manómetro i.
Cargar la imagen imt de los termómetros en el espacio correspondiente
al termómetro i.
Fin
Graficar
en
el
Laboratorio
Virtual
valores_expe_presión
valores_expe_temperatura contra la posición del medidor.
y
Calcular el flujo másico mediante las ecuaciones 5.31, 5.32 y 5.33
área _ fm = "r(1) 2
!
(5.31)
! velocidad _ fm = Ma(1) k 8314,472 T(1)
PM
(5.32)
fm = ro(1) " velocidad _ fm " área _ fm
(5.33)
Colocar fm en el cuadro de texto correspondiente al medidor de flujo másico.
!
• Graficar Solución Exacta: Graficar el Número de Mach, Temperatura, Presión,
Densidad y Radio del ducto según el modelo unidimensional empleado.
•
Reseteo Laboratorio Virtual y Gráficas: Coloca los medidores en cero, resetea los
valores al caso inicial y vacía los cuadros de texto pertinentes.
•
Mensaje al Usuario: Se le notifica al usuario que “No existe una solución
unidimensional para las condiciones especificadas”
30
5.1.2. FLUJO DE FANNO
En la Figura 5.2 se presenta el esquema de funcionamiento del módulo correspondiente al
flujo de Fanno. Las rutinas están enmarcadas en rectángulos y se explican en detalle a
continuación. En el caso que solución_fanno toma el valor de no es donde se debe anexar el
código que busque la solución a los casos no contemplados en este trabajo.
!""#$%&'$()*&'!
3/$$
#45/6"07)76"(/#7
)5-)'7)##/8)$9$:$
3/$0&$
;3-8'<0/,&=!
'&%-,/<07>)00&9$'1!
'&%-,/<07>)00&9$0&!
+)%,-%)#$%)'$.#"'/&0"'$+#12,)'!
+)%,-%)#$3&%-,/<0!
?-)#()#$@"'-%*)(&'!
3/$$
'&%-,/<07>)00&$9$'1!
3/$0&$
+&%&,)#$A)%&#"'$"0$"%$!)8&#)*&#/&$
B/#*-)%!
@"'"*"&$!)8&#)*&#/&$B/#*-)%$
C$?#DE,)'!
?#)E,)#$3&%-,/<0$IJ),*)$
F"0')G"$)%$H'-)#/&$
Figura 5.2 Algoritmo empleado en el módulo de Flujo de Fanno
•
Leer los datos: Lee los datos ingresados por el usuario p_sal, k, PM, p0, T0, !0, f,
L, Dh.
31
•
Calcular las Presiones Críticas: Calcula la presión límite que estrangula al flujo
subsónico.
xo = [0,001 ; 1]
Calcular Ma_entrada en el rango xo de la Ecuación 5.34
)
,
2
+
2&
#
4f
1" Ma
k +1
( k + 1) Ma ..
+
L =%
+
ln
2 (
Dh
$ kMa ' 2k +2#%1+ k "1 Ma 2 &(.
+* $
'.2
!
Calcular p1_pest de la Ecuación 5.35
p1_ pest =
!
(5.34)
k +1
2
1
Ma _ entrada 1+ k "1 Ma _ entrada 2
2
(5.35)
Calcular p1_p0 de la Ecuación 5.36
k
# k "1
&" k"1
p1_ p0 = %1+
Ma 2 (
$
'
2
(5.36)
p1 = p1_p0*p0
!
pest = p1/p1_pest
•
Calcular Solución: Calcula la solución subsónica sea estrangulada o no.
Si p_sal <= pest
Flujo Estrangulado. Calcular el Número de Mach a lo largo del ducto
para esta condición a partir de la Ecuación 5.37 en el rango x0.
Para i: 1 hasta n
Delta_L = L – (i-1)*[L/(n-1)]
)
,
2
+
#1" Ma(i) & k + 1
4f
(k + 1) Ma(i) ..
+
Delta _ L = %
+
ln
2 (
Dh
$ kMa(i) ' 2k + 2#%1+ k "1 Ma(i) 2 &( .
+* $
' .2
2
Fin
!
(5.37)
32
Sino
Flujo no estrangulado. Se determina la longitud de estrangulamiento
desde la entrada del ducto.
l_est = L
Mientras l_est " l_est_nuevo
Calcular Ma1 a partir de la Ecuación 5.38
)
,
2
+
#1" Ma & k + 1
k + 1) Ma1 .
4f
(
1
+
.
l _ est = %
ln
2 (+
Dh
$ kMa1 ' 2k +2#%1+ k "1 Ma 2 &( .
1
+* $
' .2
2
(5.38)
! Calcular p1_pest con la Ecuación 5.39
k +1
1
2
p1_ pest =
k
"1
Ma1 1+
Ma12
2
(5.39)
! Calcular p1_p0 empleando la Ecuación 5.40
k
"
# k "1
2 & k"1
p1_ p0 = %1+
Ma1 (
$
'
2
(5.40)
! pest = p1_p0*p0/p1_pest
Hallar Ma2 de la Ecuación 5.41
k +1
p _ sal
1
2
=
pest
Ma2 1+ k "1 Ma 2
2
2
!
(5.41)
33
Calcular l_aux de la Ecuación 5.42
)
,
2
+
# 1" Ma & k + 1
4f
( k + 1) Ma2 ..
2
+
l _ aux = %
+
ln
2 (
Dh
$ kMa2 ' 2k +2#%1+ k "1 Ma 2 &(.
2
+* $
'.2
2
(5.42)
! l_est_nuevo = l_aux + L
l_est = l_est_nuevo
Fin
Calcular el Número de Mach en el intervalo x0 a lo largo del ducto a
partir de la Ecuación 5.43
Para i: 1 hasta n
Delta_L = l_est – (i-1)*[L/(n-1)]
)
,
2
+
#1" Ma(i) & k + 1
k + 1) Ma(i) .
4f
(
+
.
Delta _ l = %
+
ln
2 (
Dh
$ kMa(i) ' 2k + 2#%1+ k "1 Ma(i) 2 &( .
+* $
' .2
2
(5.43)
Fin
!Fin
Calcular la presión, temperatura y densidad a lo largo del ducto a partir de las
ecuaciones 5.46, 5.47 y 5.48 respectivamente. Número de Mach en el intervalo
x0. La Ecuación 5.44 busca la densidad en la entrada del ducto y la Ecuación
5.45 la densidad de estancamiento.
1
$ k #1
' k#1
"0
= &1+
Ma(1) 2 )
(
" _ entrada %
2
!
!
" _ entrada
=
"est
k #1
Ma(1) 2
2
k +1
Ma(1) 2
2
(5.44)
1+
(5.45)
34
Para i: 1 hasta n
!
!
k +1
p(i)
1
2
=
pest Ma(i) 1+ k "1 Ma(i) 2
2
(5.46)
# k "1
&
T0
= %1+
Ma(i) 2 (
'
T(i) $
2
(5.47)
k #1
1+
Ma(i) 2
" (i)
2
=
k +1
"est
Ma(i) 2
2
(5.48)
Fin
!
•
Guardar Resultados: Guarda los valores obtenidos para ser empleados por las
rutinas a continuación.
•
Colocar Valores en el Laboratorio Virtual: Coloca los valores de temperatura,
presión y flujo másico en los medidores correspondientes. Además grafica en el
Laboratorio virtual las medidas de tanto la presión como la temperatura a lo largo
del ducto. El pseudocódigo es el mismo empleado en la rutina que lleva el mismo
nombre en el módulo de flujo isentrópico pero removiendo la verificación de la
presencia de la condición crítica que para este módulo no aplica.
•
Graficar Solución Exacta: Graficar el Número de Mach, Temperatura, Presión,
Densidad y Radio del ducto según el modelo unidimensional empleado.
•
Reseteo Laboratorio Virtual y Gráficas: Coloca los medidores en cero, resetea los
valores al caso inicial y vacía los cuadros de texto pertinentes.
35
•
Mensaje al Usuario: Se le notifica al usuario que “No existe una solución
unidimensional subsónica para las condiciones especificadas”
5.1.3. FLUJO DE RAYLEIGH
En la Figura 5.3 se presenta el esquema de funcionamiento del módulo correspondiente al
flujo de Rayleigh. Las rutinas están enmarcadas en rectángulos y se explican en detalle a
continuación. En el caso que solución_rayleigh toma el valor de no se debe anexar el código
que busque la solución a los casos no contemplados en este trabajo.
•
Leer los datos: Lee los datos ingresados por el usuario p_sal, k, PM, p0, T0, !0, q,
Cp, D.
•
Calcular las Presiones Críticas: Calcula la presión límite que estrangula al flujo
subsónico.
x0 = [0,001 ; 1]
Si q >= 0
Ma_salida = 1
Calcular Ma_entrada de la Ecuación 5.49
2 2
q
Ma _ salida [1+ kMa _ entrada ]
=
Cp " T0 Ma _ entrada 2 [1+ kMa _ salida 2 ] 2
2
$ k #1
2'
&%1+ 2 Ma _ salida )(
#1
$ k #1
2'
&%1+ 2 Ma _ entrada )(
(5.49)
Calcular p_entrada de la Ecuación 5.50
k
!
# k "1
& k"1
p0
= %1+
Ma _ entrada 2 (
'
p _ entrada $
2
(5.50)
! Calcular p_salida de la Ecuación 5.51
p _ salida 1+ kMa _ entrada 2
=
p _ entrada 1+ kMa _ salida 2
!
pest = p_salida
(5.51)
36
!""#$%&'$()*&'!
3/$$
#45/6"07)76"(/#7
)5-)'7)##/8)$9$:$
3/$0&$
;3-8'<0/,&=!
'&%-,/<07#)>%"/5?9$'1!
'&%-,/<07#)>%"/5?9$0&!
+)%,-%)#$%)'$.#"'/&0"'$+#12,)'!
+)%,-%)#$3&%-,/<0!
@-)#()#$A"'-%*)(&'!
3/$$
'&%-,/<07#)>%"/5?$9$'1!
3/$0&$
+&%&,)#$B)%&#"'$"0$"%$!)8&#)*&#/&$
C/#*-)%!
A"'"*"&$!)8&#)*&#/&$C/#*-)%$
>$@#DE,)'!
A"I"G)#$3&%-,/<0$JK),*)$
F"0')G"$)%$H'-)#/&$
Figura 5.3 Algoritmo empleado en el módulo de Flujo de Rayleigh
Sino
pest No aplica para el caso de enfriamiento en esta versión del
programa
Fin
•
Calcular Solución: Calcula la solución subsónica sea estrangulada o no, tomando
en cuenta si la transferencia de calor es hacia o desde el flujo.
Si p_sal <= pest
Flujo Estrangulado
Si q >= 0
Ma(1) = Ma_entrada
Ma(2) = 1
37
Sino
Esta versión del programa no trabaja el caso de estrangulado con
enfriamiento
Fin
Calcular p(1) de la Ecuación 5.52
k
& k"1
p0 # k "1
= %1+
Ma(1) 2 (
'
p(1) $
2
(5.52)
p(2) =!pest
Calcular T(1) de la Ecuación 5.53
# k "1
&
T0
= %1+
Ma(1) 2 (
'
T(1) $
2
(5.53)
Calcular T(2) de la Ecuación 5.54
!
T(2) Ma(2) 2 (1+ kMa(1) 2 ) 2
=
T(1) Ma(1) 2 (1+ kMa(2) 2 ) 2
(5.54)
! !(1) de la Ecuación 5.55
Calcular
1
' k#1
" 0 $ k #1
= &1+
Ma(1) 2 )
(
"(1) %
2
(5.55)
Calcular
! !(2) de la Ecuación 5.56
"(2) Ma(1) 2 (1+ kMa(2) 2 )
=
"(1) Ma(2) 2 (1+ kMa(1) 2 )
(5.56)
Sino
Flujo !
no estrangulado
p(2) = p_sal
Resolver el sistema lineal conformado por las ecuaciones 5.57, 5.58 y
5.59 para encontrar los valores de p(1), Ma(1) y Ma(2)
38
$ k #1
'
Ma(2) 2 )
2 2 &1+
1+
kMa(1)
] % 2
q
Ma(2) [
(
=
#1
2
2
2
Cp " T0 Ma(1) [1+ kMa(2) ] $ k #1
2'
&%1+ 2 Ma(1) )(
2
(5.57)
(5.58)
!
k
& k"1
p0 # k "1
= %1+
Ma(2) 2 (
'
p(1) $
2
(5.59)
Calcular
! T(1) de la Ecuación 5.60
# k "1
&
T0
= %1+
Ma(1) 2 (
'
T(1) $
2
(5.60)
Calcular
! T(2) de la Ecuación 5.61
T(2) Ma(2) 2 (1+ kMa(1) 2 ) 2
=
T(1) Ma(1) 2 (1+ kMa(2) 2 ) 2
(5.61)
! !(1) de la Ecuación 5.62
Calcular
1
' k#1
" 0 $ k #1
= &1+
Ma(1) 2 )
(
"(1) %
2
(5.62)
Calcular
! !(2) de la Ecuación 5.63
"(2) Ma(1) 2 (1+ kMa(2) 2 )
=
"(1) Ma(2) 2 (1+ kMa(1) 2 )
(5.63)
Fin
!
•
Guardar Resultados: Guarda los valores obtenidos para ser empleados por las
rutinas a continuación.
39
•
Colocar Valores en el Laboratorio Virtual: Coloca los valores de temperatura,
presión y flujo másico en los medidores correspondientes. Además grafica en el
Laboratorio virtual las medidas de tanto la presión como la temperatura a lo largo
del ducto. El pseudocódigo es el mismo empleado en la rutina que lleva el mismo
nombre en el módulo de flujo isentrópico pero tomando en cuenta que sólo hay dos
manómetros y dos termómetros y removiendo la verificación de la presencia de la
condición crítica que para este módulo no aplica.
•
Reflejar Solución Exacta: Coloca el Número de Mach, temperatura, presión y
densidad del flujo según el modelo unidimensional empleado en los cuadros de
texto correspondientes.
•
Reseteo Laboratorio Virtual y Gráficas: Coloca los medidores en cero, resetea los
valores al caso inicial y vacía los cuadros de texto pertinentes.
•
Mensaje al Usuario: Se le notifica al usuario que “No existe una solución
unidimensional para las condiciones especificadas”
40
5.2.
VALIDACIÓN
A continuación se presentan problemas resueltos en las referencias y se comparan los
resultados con los obtenidos en la sección de solución exacta del programa desarrollado a
manera de validación del método de solución empleado en el mismo. Para validarlo
completamente, se presentan problemas con los distintos tipos de caso que se pueden
presentar: flujo isentrópico con condición crítica presente y régimen subsónico, flujo
isentrópico con condición crítica presente y régimen supersónico, flujo isentrópico en régimen
subsónico, flujo isentrópico en régimen supersónico, onda de choque normal, flujo de Fanno
subsónico no estrangulado, flujo de Fanno subsónico estrangulado, flujo de Rayleigh
subsónico no estrangulado con adición o remoción de calor, flujo de Rayleigh subsónico
estrangulado con adición de calor. El caso de flujo de Rayleigh subsónico estrangulado con
remoción de calor no se trabaja en detalle en este programa.
5.2.1. FLUJO ISENTRÓPICO CON CONDICIÓN CRÍTICA PRESENTE, RÉGIMEN
SUBSÓNICO Y SUPERSÓNICO
Uniendo los ejemplos 11.8 y 11.9 del libro de Munson (2004) se puede plantear los siguientes
datos del problema: Aire fluye isentrópicamente a través de un ducto de sección transversal
circular y cuya área es una función de la distancia axial a la garganta de la forma “A = 0,1 +
x2” donde “A” es el área medida en metros cuadrados y “x” es la distancia medida en metros.
Si el ducto se extiende entre valores de “x” -0,5m hasta 0,5m encontrar las relaciones A/A*,
T/T0, p/p0 y el número de Mach a lo largo del ducto, considerando condición de entrada
subsónica o supersónica. Considere que el ducto presenta la condición crítica.
Las relaciones p/p0 y T/T0 en régimen subsónico se presentan en las figuras 5.4 y 5.5
respectivamente mientras que las correspondientes al régimen supersónico se presentan en las
figuras 5.6 y 5.7 respectivamente. Se han agregado la diferencia porcentual respecto a la
solución propuesta por Munson (2004) en un eje secundario.
41
1.20
5.00
4.50
4.00
3.50
3.00
2.50
2.00
1.50
1.00
0.50
0.00
1.00
p/p0
0.80
0.60
0.40
0.20
0.00
-0.6
-0.4
-0.2
0
0.2
0.4
%
Relación p/p0 a lo largo del ducto "A = 0,1 + x2" para flujo
isentrópico subsónico crítico
0.6
x [m]
p/p0 - Programa Desarrollado
p/p0 - Munson (2004)
Diferencia (%)
Figura 5.4 Comparación de resultados entre el libro y el programa desarrollado. Relación p/p0 a lo largo
del ducto "A = 0,1 + x2" para flujo isentrópico subsónico crítico.
1.05
5.00
4.50
4.00
3.50
3.00
2.50
2.00
1.50
1.00
0.50
0.00
1.00
T/T0
0.95
0.90
0.85
0.80
0.75
0.70
-0.6
-0.4
-0.2
0
0.2
0.4
%
Relación T/T0 a lo largo del ducto "A = 0,1 + x2" para flujo
isentrópico subsónico crítico
0.6
x [m]
T/T0 - Programa Desarrollado
T/T0 - Munson (2004)
Diferencia (%)
Figura 5.5 Comparación de resultados entre el libro y el programa desarrollado. Relación T/T0 a lo largo
del ducto "A = 0,1 + x2" para flujo isentrópico subsónico crítico.
42
0.60
5.00
4.50
4.00
3.50
3.00
2.50
2.00
1.50
1.00
0.50
0.00
0.50
p/p0
0.40
0.30
0.20
0.10
0.00
-0.6
-0.4
-0.2
0
0.2
0.4
%
Relación p/p0 a lo largo del ducto "A = 0,1 + x2" para flujo
isentrópico supersónico crítico
0.6
x [m]
p/p0 - Programa Desarrollado
p/p0 - Munson (2004)
Diferencia (%)
Figura 5.6 Comparación de resultados entre el libro y el programa desarrollado. Relación p/p0 a lo largo
del ducto "A = 0,1 + x2" para flujo isentrópico supersónico crítico.
0.90
0.80
0.70
0.60
0.50
0.40
0.30
0.20
0.10
0.00
5.00
4.50
4.00
3.50
3.00
2.50
2.00
1.50
1.00
0.50
0.00
-0.6
-0.4
-0.2
0
0.2
0.4
%
T/T0
Relación T/T0 a lo largo del ducto "A = 0,1 + x2" para flujo
isentrópico supersónico crítico
0.6
x [m]
T/T0 - Programa Desarrollado
T/T0 - Munson (2004)
Diferencia (%)
Figura 5.7 Comparación de resultados entre el libro y el programa desarrollado. Relación T/T0 a lo largo
del ducto "A = 0,1 + x2" para flujo isentrópico supersónico crítico.
43
La concordancia entre los resultados es bastante buena. Una vez encontrado satisfactoriamente
las relaciones de presión y temperatura pedidas, la relación de áreas y el Número de Mach se
pueden calcular en función de éstas. Se determinó que los errores porcentuales respecto a la
solución planteada por Munson (2004) es menor al 1,5% en todos los cálculos. Debe tomarse
en cuenta que los libros resuelven los problemas mediante el uso de tablas e interpolaciones en
las mismas, por lo que los valores que estos presentan tienen cierto grado de error. En cambio
el programa desarrollado halla las soluciones numéricas de las ecuaciones con un alto grado de
precisión, por lo que puede pensarse que los valores se corresponden con el modelo
unidimensional empleado con exactitud. Tomando en cuenta que el error porcentual es
pequeño se puede pensar que si el usuario resolviere el problema mediante tablas obtendría
resultados parecidos a los que calculase con el programa, en consecuencia el programa puede
servir como herramienta para complementar el estudio del tema en cuestión.
5.2.2. FLUJO ISENTRÓPICO EN RÉGIMEN SUBSÓNICO
Resolviendo el Ejemplo 11.10 del libro de Munson (2004) el cual plantea encontrar para el
mismo ducto empleado en el ejemplo de flujo isentrópico con condición crítica presente, la
solución si se cumple que p_sal/p0 = 0,99.
Los resultados se muestran es las figuras 5.8 y 5.9. Se han agregado las diferencias
porcentuales respecto de la solución en el libro en un eje secundario.
44
Relación p/p0 a lo largo del ducto "A = 0,1 + x2" para flujo
isentrópico subsónico
1.01
5.00
4.50
0.96
4.00
3.50
2.50
0.86
%
3.00
p/p0
0.91
2.00
1.50
0.81
1.00
0.50
0.76
0.00
-0.6
-0.4
-0.2
p/p0 - Programa Desarrollado
0
0.2
0.4
x [m]
p/p0 - Munson (2004)
0.6
Diferencia (%)
Figura 5.8 Comparación de resultados entre el libro y el programa desarrollado. Relación p/p0 a lo largo
del ducto "A = 0,1 + x2" para flujo isentrópico subsónico.
1.00
1.00
0.99
0.99
0.98
0.98
0.97
0.97
0.96
0.96
0.95
5.00
4.50
4.00
3.50
3.00
2.50
2.00
1.50
1.00
0.50
0.00
-0.6
-0.4
-0.2
0
0.2
0.4
%
T/T0
Relación T/T0 a lo largo del ducto "A = 0,1 + x2" para flujo
isentrópico subsónico
0.6
x [m]
T/T0 - Programa Desarrollado
T/T0 - Munson (2004)
Diferencia (%)
Figura 5.9 Comparación de resultados entre el libro y el programa desarrollado. Relación T/T0 a lo largo
del ducto "A = 0,1 + x2" para flujo isentrópico subsónico.
45
Nuevamente los resultados obtenidos son muy semejantes. Las diferencias de los resultados
obtenidos comparados con los de Munson (2004) son todos menores al 1,5%. De nuevo se
debe tomar en cuenta que los resultados del libro son obtenidos mediante tablas e
interpolaciones en las mismas por lo que los resultados conllevan un error asociado a este
procedimiento.
5.2.3. FLUJO ISENTRÓPICO EN RÉGIMEN SUPERSÓNICO
Se resolvió el problema 9.40 del libro de White (2004), el cual plantea un flujo isentrópico de
aire con p0 = 800 kPa y T0 = 373.15 K por un conducto y de determina el Número de Mach
cuando el flujo pasa por una sección transversal de área 20 cm2. Los resultados se presentan en
la Tabla 5.1.
Ma1
White (2004)
Programa
Diferencia (%)
2,5
2,5
0,00
Tabla 5.1 Comparación de resultados para problema de flujo Isentrópico en régimen supersónico.
5.2.4. ONDA DE CHOQUE NORMAL
Según el Ejemplo 11.20 del libro de Munson (2004), una onda de choque se puede presentar
para el mismo ducto empleado en el caso de flujo isentrópico con condición crítica presente.
En particular, Munson (2004) plantea determinar la razón de presión de salida del ducto a
presión de estancamiento en la entrada para que se genere una onda de choque normal en la
salida del mismo. Luego, se desea determinar la misma razón si la onda de choque ocurre en x
= 0,3 m.
Variando la presión de salida en el programa hasta que se produzca una onda de choque en los
lugares especificados permite obtener la relación pedida. La Figura 5.10 presenta el caso
particular de la onda de choque ubicada en x=0,3m. Los resultados obtenidos para ambos
casos se presentan en la Tabla 5.2.
46
Munson (2004)
Programa
Diferencia (%)
x = 0,5 m
x = 0,3 m
p_sal/p0
0,331
0,626
0,3304
0,6219
0,18
0,65
Tabla 5.2 Comparación de resultados para problema con Onda de Choque Normal.
Figura 5.10 Módulo de Flujo Isentrópico. Vista de la sección Gráficas para una onda de choque normal dentro
del ducto.
5.2.5. FLUJO DE FANNO SUBSÓNICO NO ESTRANGULADO
La validación del módulo de flujo subsónico no estrangulado se realizó a partir del siguiente
ejemplo, planteado en el libro de Munson (2004) en el ejemplo 11.14. Se considera que aire
atmosférico normal (p0 = 101 kPa, T0 = 288 K) fluye subsónicamente por un ducto adiabático
de área constante. La sección transversal del mismo es circular con un diámetro de 0,1 m. La
longitud del ducto es 1 m y el factor de fricción puede asumirse constante e igual a 0,02. Si la
47
presión de salida se regula en 69,0 kPa calcule el Número de Mach en la entrada y salida del
ducto, así como el flujo másico a través del mismo.
Los resultados se muestran en la Tabla 5.3 y se comparan con los de la referencia.
Ma1
Munson (2004)
Programa
Diferencia (%)
Ma2
0,63
0,6181
1,89
m [Kg/s]
0,70
1,64
0,6925
1,6195
1,07
1,25
Tabla 5.3 Comparación de resultados para problema de flujo de Fanno no estrangulado.
Nuevamente la concordancia entre los resultados obtenidos es excelente, debiéndose la
diferencia a las mismas razones que para los casos antes considerados, es decir, al uso de
tablas para resolver las ecuaciones no lineales.
5.2.6. FLUJO DE FANNO SUBSÓNICO ESTRANGULADO
Para validar lo que ocurre cunado se presenta estrangulamiento por fricción, siguiendo el
ejemplo 11.12 del libro de Munson (2004), se puede plantear la siguiente situación: para las
mismas condiciones utilizadas en el caso de flujo de Fanno subsónico no estrangulado pero
con una longitud del ducto de 2 m, hallar la presión, densidad y temperatura del aire en la
entrada del ducto. Encontrar también el flujo másico y la presión de salida del flujo.
Los resultados obtenidos se reportan en la Tabla 5.4 en conjunto con los hallados por Munson
(2004), reflejando el error respecto a dichos valores.
Munson (2004)
Programa
Diferencia %
m [Kg/s] p1 [kPa] T1 [K] !(1) [kg/m3] p2 [kPa]
1,64
77,3
267
1,016
46,2
1,6293
77,6 266,96
1,0124 45,9173
0,65
0,39
0,01
0,35
0,61
Tabla 5.4 Comparación de resultados para problema de Flujo de Fanno estrangulado.
48
Las diferencias de la Tabla 5.3 y Tabla 5.4 son todos menores al 2%, tomando en cuenta lo
planteado anteriormente referente a la manera de resolución de los problemas en los libros
mediante tablas e interpolaciones, se puede inferir que los resultados que calcula el programa
son realmente exactos según del modelo unidimensional que se emplea en los cálculos.
5.2.7. FLUJO
DE
RAYLEIGH
SUBSÓNICO
NO
ESTRANGULADO
CON
REMOCIÓN DE CALOR
Para validar este módulo se utilizó el ejemplo 10.3 del libro de Oosthuizen y Carscallen
(1997). En este caso se considera que aire con p0 = 240,6 kPa y T0 = 656,6 K fluye
subsónicamente por un ducto al cual se le retira calor a una tasa de 400 kJ/Kg. Si la presión de
salida es de 250,9 kPa calcular el Número de Mach en la entrada y salida del ducto, así como
la presión y temperatura en la entrada del mismo y la temperatura en la salida. Suponer que Cp
tiene un valor de 1,007 kJ/Kg.K.
Para resolver este problema se ingresan los datos en el módulo de flujo de Rayleigh y se
obtienen los resultados reflejados en la Tabla 5.5, acompañados por los que ofrece la
referencia así como de la diferencia porcentual respecto de la misma.
Oosthuizen y Carscallen (1997)
Programa
Diferencia (%)
Ma1
Ma2
p1 [kPa] T1 [K]
T2 [K]
0,52
0,2656
200
623,15
256
0,51531 0,26402
200,65
623,2
255,8
0,90
0,59
0,33
0,01
0,08
Tabla 5.5 Comparación de resultados para problema de flujo de Rayleigh no estrangulado con remoción de calor.
Las diferencias reportadas en la Tabla 5.5 son todos inferiores al 1% y nuevamente se debe
tomar en cuenta que el libro emplea tablas e interpolaciones para resolver el problema,
mientras que el programa resuelve las ecuaciones de manera exacta.
49
5.2.8. FLUJO DE RAYLEIGH SUBSÓNICO NO ESTRANGULADO CON ADICIÓN
DE CALOR
Para validar el caso de flujo de Rayleigh subsónico no estrangulado se utilizó el ejemplo 9.14
del libro de White (2004). En este caso se considera que aire fluye por un ducto con
condiciones de estancamiento en la entrada de p0 = 155 kPa y T0 = 303 K. Se adiciona calor a
una tasa de 900 kJ/Kg. Asumiendo un Cp = 1.005 kJ/Kg.K, si se induce una presión a la salida
del ducto de 109 kPa, se desea determinar el Número de Mach, la presión y la temperatura en
la entrada del mismo así como la temperatura y el Número de Mach en la sección de salida.
Se ingresan los datos en el módulo de Flujo de Rayleigh y se obtienen los resultados reflejados
en la Tabla 5.6 acompañados de los presentes en libro así como del error porcentual respecto a
estos últimos.
White (2004)
Programa
Diferencia (%)
Ma1
Ma2
p1 [kPa] T1 [K]
T2 [K]
0,216
0,573
150
300
1124
0,21661 0,57662
150,00
300,2
1123,1
0,28
0,63
0,00
0,07
0,08
Tabla 5.6 Comparación de resultados para problema de flujo de Rayleigh no estrangulado con adición de calor.
Se puede apreciar en la Tabla 5.6 que las diferencias son menores al 1% al igual que el
ejemplo anterior. La acotación respecto al uso de tablas por parte del libro en la resolución de
los problemas aplica en este caso también.
5.2.9. FLUJO DE RAYLEIGH SUBSÓNICO ESTRANGULADO CON ADICIÓN DE
CALOR
Finalmente, para validar este último caso se utilizó el problema propuesto 11.66 de Munson
(2004) en el que se plantea la siguiente situación: Un flujo de aire entra a un ducto diabático
de área constante. El aire entra con T0 = 288 K y p0 = 101 kPa. Si la adición de calor es de 500
kJ/kg, calcule la presión en la entrada del ducto, así como la temperatura en la entrada y salida
del mismo cuando el flujo másico es máximo.
50
Como se demostrará más adelante, es muy sencillo utilizando este programa determinar la
presión a la cual se estrangula el flujo y en consecuencia, el flujo másico máximo (el cual
ocurre cuando el ducto se estrangula). Con esta presión de salida se puede obtener la solución
al problema planteado. Los resultados se reportan en la Tabla 5.7 acompañados de la solución
de Munson (2004) así como de la diferencia porcentual respecto a esta última.
Munson (2004)
Programa
Diferencia (%)
p1 [kPa]
T1 [K]
T2 [K]
94,5
283
658
94,44
282,5
652,8
0,06
0,18
0,79
Tabla 5.7 Comparación de resultados para problema de flujo de Rayleigh estrangulado con adición de calor.
Las diferencias presentes en la Tabla 5.7 son todos menores al 1% mostrando nuevamente la
similitud entre ambas soluciones.
6.
RESULTADOS
A continuación se muestran aplicaciones de los tres módulos. En éstas se pueden apreciar las
distintas características de cada uno. Las imágenes se corresponden con las situaciones
analizadas en el capítulo cinco.
6.1.
FLUJO ISENTRÓPICO
La Figura 6.1 muestra el Laboratorio Virtual del módulo de Flujo Isentrópico. Se puede
observar el ducto convergente divergente, así como los manómetros por encima y los
termómetros por debajo del mismo. El medidor de flujo másico está en la entrada del ducto. Se
representa también la válvula de regulación en la salida del ducto. En la derecha del montaje
experimental están las dos gráficas de las mediciones hechas de presión y temperatura. El
panel titulado Gas permite al usuario seleccionar el tipo de fluido a estudiar.
Figura 6.1 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual. Flujo con condición crítica presente.
Condición aguas arriba del ducto: Régimen Subsónico.
52
El panel titulado Condiciones de Estancamiento permite al usuario ingresar dichos valores
para el flujo en estudio. La densidad de estancamiento está acompañada de un botón titulado
Calcular, el cual permite computar dicho valor en función de las otras dos magnitudes
mediante la ecuación de estado de gas ideal. En el panel de Condiciones a la Salida el usuario
puede ingresar la presión que desea inducir en dicha sección del ducto mediante la apertura o
cierre de la válvula colocada ahí mismo.
El usuario luego de determinar las variables pertinentes debe oprimir el botón de Medir para
obtener las mediciones. Cabe destacar que el régimen aguas arriba es subsónico en este caso.
En la Figura 6.2 se puede apreciar el mismo pero seleccionando un régimen aguas arriba
supersónico en el Panel de Preferencias.
Figura 6.2 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual. Flujo con condición crítica presente.
Condición aguas arriba del ducto: Régimen Supersónico.
53
En la Figura 6.3 se puede apreciar la sección de Gráficas para el mismo flujo trabajado en las
figuras 6.1 y 6.2. Se observa la duplicidad de soluciones aguas arriba de la garganta del ducto,
lo que se refleja en el Laboratorio Virtual en las dos figuras anteriores. Cabe destacar que en la
sección de Gráficas el botón de Medir ha cambiado por Calcular.
Figura 6.3 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión representada.
Flujo con condición crítica presente.
En la Figura 6.4 y la Figura 6.5 se puede observar el Panel de Preferencias. En el mismo se
puede seleccionar ducto a emplear, las apreciaciones de los distintos instrumentos de medida,
la condición aguas arriba del ducto y se pueden estimar las presiones características del flujo.
En la Figura 6.4 se muestra la selección del ducto convergente-divergente predeterminado,
mientras que en la Figura 6.5 la selección del ducto convergente predeterminado. En la Figura
6.6 en cambio está seleccionada la opción del ducto personalizado y se observa una serie de
puntos que describen al ducto. Se observan en las tres figuras mencionadas un pequeño
recuadro con un esquema del ducto para que el usuario tenga presente cual ha de emplear.
54
Figura 6.4 Módulo de Flujo Isentrópico, vista del Panel de Preferencias.
Ducto Convergente - Divergente seleccionado.
Figura 6.5 Módulo de Flujo Isentrópico, vista del Panel de Preferencias.
Ducto Convergente seleccionado.
55
Figura 6.6 Módulo de Flujo Isentrópico, vista del Panel de Preferencias.
Ducto Personalizado seleccionado.
Para destacar el efecto que tienen las apreciaciones de los instrumentos en las medidas que
muestran, se presentan la Figura 6.7 y 6.8 las cuales se generaron oprimiendo el botón Medir
dos veces seguidas. Se puede observar la variación que hay de una toma de medición a otra en
las imágenes de los instrumentos, así como en los valores digitales que estos mismos reportan
y en las gráficas del lado derecho que muestran la distribución de éstos. Las mediciones se
generan en función de las apreciaciones tal como se detalló en el capítulo cuatro.
La Figura 6.9 y Figura 6.10 presentan la presión en la sección de Gráficas. La primera se
muestra en un eje vertical automático que aprovecha el espacio en pantalla para mostrar la
gráfica, mientras que la segunda se presentan en un eje vertical personalizado que permite
observar en perspectiva la variación de las magnitudes. El eje vertical personalizado
permanece constante entre mediciones, lo que permite observar el efecto que tiene el variar
alguna magnitud en la variable que se está observando.
56
Figura 6.7 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual.
Flujo Subsónico, Primera Medición.
Figura 6.8 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual.
Flujo Subsónico, Segunda Medición.
57
Figura 6.9 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión representada.
Eje vertical seleccionado automático. Flujo Subsónico.
Figura 6.10 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión representada.
Eje vertical seleccionado Personalizado. Flujo Subsónico.
58
En la Figura 6.11 se observa en la sección de Gráficas el ducto. Esta opción permite al usuario
observar en las proporciones correctas el ducto que está siendo empleado para el experimento
virtual.
Figura 6.11 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con el ducto representado.
6.2.
ONDA DE CHOQUE NORMAL
La onda de choque normal se estudia con el programa sólo para flujo isentrópico. Por esto las
figuras presentadas a continuación corresponden con el módulo de dicho tipo de flujo.
En la Figura 6.12 se observa el Laboratorio Virtual con un flujo que presenta una onda de
choque normal. La situación se corresponde con el problema resuelto en el capítulo cinco para
el caso en cuestión.
59
Figura 6.12 Módulo de Flujo Isentrópico, vista del Laboratorio Virtual.
Flujo con Onda de Choque Normal.
En las figuras 6.13, 6.14, 6.15 y 6.16 se presenta la sección de Gráficas representando el
Número de Mach, presión, temperatura y densidad del flujo. Se corresponden al mismo
problema de la Figura 6.12. Las discontinuidades que se observan en las medidas hechas en el
Laboratorio Virtual se pueden confirmar en las gráficas correspondientes a la solución exacta.
60
Figura 6.13 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con el Número de Mach representado.
Flujo con Onda de Choque Normal.
Figura 6.14 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la presión representada.
Flujo con Onda de Choque Normal.
61
Figura 6.15 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la temperatura representada.
Flujo con Onda de Choque Normal.
Figura 6.16 Módulo de Flujo Isentrópico, vista de la sección de Gráficas con la densidad representada.
Flujo con Onda de Choque Normal.
62
6.3.
FLUJO DE FANNO
En la Figura 6.17 se observa el Laboratorio Virtual del módulo de Flujo de Fanno. Se asemeja
al de flujo isentrópico en gran medida. Las diferencias se encuentran en que la presión y
densidad de estancamiento deben ser las de entrada del flujo, y en que se agrega el panel de
Características del Ducto el cual permite modificar sus principales características. El color gris
alrededor del ducto representa el aislamiento que se emplea en experimentos de este tipo para
asegurar la condición de flujo adiabático. En esta figura está resolviendo el problema
correspondiente a flujo de Fano subsónico no estrangulado del capítulo cinco.
Figura 6.17 Módulo de Flujo de Fanno, vista del Laboratorio Virtual.
Flujo subsónico no estrangulado.
En la Figura 6.18 se muestra la sección de Gráficas, resolviendo el problema correspondiente a
flujo de Fanno subsónico estrangulado del capítulo cinco.
63
Figura 6.18 Módulo de Flujo de Fanno, vista de la sección de Gráficas con el Número de Mach representado.
Flujo subsónico estrangulado.
En la Figura 6.19 se observa el Panel de Preferencias, el cual se pueden modificar la sección
transversal del ducto tanto como las apreciaciones de los instrumentos de medida y se pueden
calcular las presiones características del sistema. El ducto de sección circular está
seleccionado y su diámetro ha de ingresarse en el Laboratorio Virtual. En la Figura 6.20 se
muestra en cambio la selección de una sección transversal rectangular, para lo cual debe
ingresarse la medida de su base y su altura. En el Laboratorio Virtual se observará el diámetro
hidráulico del ducto rectangular mas no podrá modificarse directamente, sino a través del
Panel de Preferencias.
64
Figura 6.19 Módulo de Flujo de Fanno, vista del Panel de Preferencias.
Selección de una sección transversal circular.
Figura 6.20 Módulo de Flujo de Fanno, vista del Panel de Preferencias.
Selección de una sección transversal rectangular.
65
En la Figura 6.21 se aprecia la opción del usuario de cambiar el fluido de estudio. Esta opción
está presente para los tres módulos como se puede observar en las imágenes del presente
capítulo.
Figura 6.21 Módulo de Flujo de Fanno, vista del Laboratorio Virtual. Detalle de selección del fluido.
6.4.
FLUJO DE RAYLEIGH
En la Figura 6.22 presenta en Laboratorio Virtual del módulo de Flujo de Rayleigh. Se
observan los dos manómetros y dos termómetros. El caso presente en dicha figura se
corresponde con el de flujo de Rayleigh no estrangulado con enfriamiento resuelto en el
capítulo cinco.
66
Figura 6.22 Módulo de Flujo de Rayleigh, vista del Laboratorio Virtual.
Flujo subsónico con remoción de calor no estrangulado
Se observa en la Figura 6.22 que se ha seleccionado un fluido Personalizado, el cual permite
editar los campos de calor específico, relación de calores específicos y peso molecular del
mismo, opción presente en los módulos de los otros dos tipo de flujo.
En la Figura 6.23 se presenta la vista de la sección de Solución Exacta del mismo problema
referido para la figura anterior. Se observan en ésta las condiciones del flujo en la entrada y
salida del ducto.
En la Figura 6.24 se observa la opción que tiene el usuario para cambiarse de un módulo a otro
sin necesidad de cerrar el programa. Esta figura se extrajo del módulo de Flujo de Fanno por
lo que no se puede seleccionar la opción para acceder al mismo. En la Figura 6.25 se presenta
las opciones que tiene el usuario desde la interfaz: Acceder al Panel de Preferencias, Exportar
la data obtenida a Microsoft Excel®, Restaurar el programa a los valores iniciales y Salir del
programa.
67
Figura 6.23 Módulo de Flujo de Rayleigh, vista de la sección de Solución Exacta.
Flujo subsónico con remoción de calor no estrangulado.
Figura 6.24 Detalle de opción para cambiar de módulo.
Figura 6.25 Detalle de opciones varias del programa.
7.
CONCLUSIONES Y RECOMENDACIONES
En las siguientes páginas se presentan las conclusiones y recomendaciones del presente
trabajo.
7.1.
CONCLUSIONES
El presente trabajo logró desarrollar una herramienta computacional que permite llevar a cabo
prácticas de laboratorio de flujo compresible de manera virtual. Además ofrece la posibilidad
de utilizarse como recurso didáctico en clases teóricas y de resolver problemas planteados en
cursos y libros de mecánica de fluidos complementado así la experiencia de estudio de una
manera gráfica e interactiva. La idea de un Laboratorio Virtual se puede aplicar también a
otros fenómenos de diversa índole por lo que su desarrollo contribuirá a la mejora del nivel
académico de la Universidad a un bajo costo.
Entre las principales conclusiones de este trabajo se tiene que:
Se desarrolló un programa de computadora que ofrece un conjunto de experiencias virtuales
en el área de flujo compresible de una manera gráfica/cuantitativa que permite la variación de
los parámetros físicos asociados para observar su efecto en las mismas.
Es factible la utilización de software de última, tal como MATLAB® para el diseño de
herramienta educativas de alto grado de sofistificación. En particular en esta aplicación se
diseñaron tres módulos correspondientes a los tres tipos de flujos compresibles
unidimensionales estudiados en el curso de Mecánica de Fluidos III de la Universidad Simón
Bolívar: Flujo Isentrópico, Flujo de Fanno y Flujo de Rayleigh.
Se logró construir una interfaz que permite al usuario
•
Obtener mediciones de temperatura y presión a lo largo de distintos ductos de prueba a
través de instrumentos que se asemejan a los que existen en los laboratorios.
•
Variar fácilmente las condiciones que describen al fenómeno y observar los cambios
en su experimento virtual.
•
Presentar la solución exacta del modelo teórico unidimensional de flujo para las
condiciones dadas por el usuario y se la proporciona para que pueda comparar con los
resultados experimentales que obtiene en el Laboratorio Virtual.
69
7.2.
RECOMENDACIONES
A continuación se presentan recomendaciones para futuros trabajos:
a) A nivel general:
En cuanto al desarrollo de un conjunto de experiencias virtuales de manera gráfica se propone
anexar al programa casos específicos correspondientes a los tres tipos de flujo estudiados
mediante una herramienta de análisis tridimensional de dinámica de fluidos computacional
CFD para comparar resultados y consideraciones teóricas empleadas en la derivación de
ecuaciones. Además se propone desarrollar el programa para ocupar la pantalla completa de la
computadora de manera tal que el usuario no tenga fuente de distracción.
b) A nivel específico:
b.1. Con respecto a los módulos desarrollados para el programa se propone complementar el
mismo con otros casos de interés relacionados a diversos tipos de flujo. Además se propone
agregar la opción de poder seleccionar el sistema de unidades a utilizar.
b.2. En referencia a los instrumentos de medida presentes en la interfaz se propone emplear
fotos o imágenes realistas para acercar aún más al usuario a la experiencia de un laboratorio
real. Con respecto a los ductos de prueba se propone mejorar el código de análisis del ducto de
tipo personalizado en el módulo de Flujo Isentrópico para fortalecer el estudio de ondas de
choque en el mismo.
b.3.
En relación a la variación de las condiciones que describen al fenómeno se propone
implementar métodos de interacción con el usuario donde tenga que llevar a cabo acciones
diversas más allá de oprimir botones o ingresar datos tales como arrastrar el ratón por ejemplo
para rotar la válvula.
b.4.
Referente al ofrecerle al usuario la solución exacta para comparar con las medidas del
Laboratorio Virtual se propone desarrollar una sección propiamente dentro de cada módulo
donde se pueda superponer ambas datas para estudiar en detalle las diferencias presentes. En
cuanto a la manera actual de brindar al usuario la solución exacta se propone modificar el
código en el módulo de Flujo Isentrópico para no sustituir la data previamente exportada para
un ducto de tipo personalizado.
70
b.5.
En cuanto al uso del programa desarrollado en la Universidad, se propone formular
experiencias virtuales y generar prácticas de laboratorio donde se contemplen los casos típicos
asociados con flujos subsónicos, supersónicos y cambios de régimen. Además se propone
crear un manual de usuario del programa que contenga instrucciones de instalación y forma de
empleo del mismo, para facilitar y agilizar el proceso de enseñaza sobre el uso del mismo.
8.
REFERENCIAS BIBLIOGRÁFICAS
Munson, Young, y Okiishi. (2004). Fundamentos de Mecánica de Fluidos. Limusa Wiley.
Oosthuizen, P., y Carscallen, W. (1997). Compressible Fluid Flow. McGraw-Hill.
P.I., F., y P.D., D. (2002). Fundamentals of Heat and Mass Transfer. (5. Edición) Wiley.
Shames, I. (1995). Mecánica de Fluidos (3era Edición). McGraw-Hill.
The MathWorks. Extraído Julio de 2008 desde http://www.mathworks.com/
White, F. (2004). Mecánica de Fluidos (5ta Edición). McGraw-Hill.