2 - Estadística
Anuncio

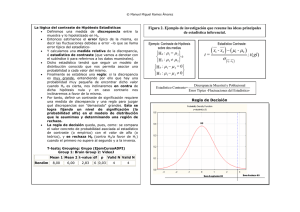
Grado Ciencias Ambientales Facultad Ciencias Departamento Matemáticas Profesor: Santiago de la Fuente Fernández TABLAS INFERENCIA ESTADÍSTICA: INTERVALOS CONFIANZA CONTRASTES HIPÓTESIS INTERVALOS DE CONFIANZA a) Intervalo de confianza para la media μ de una distribución normal N(μ, σ ) de varianza conocida σ 2 σ ⎤ ⎡ I = ⎢x ± z α 2 n ⎥⎦ ⎣ b) Intervalo de confianza para la media μ de una distribución normal N(μ, σ ) de varianza desconocida σ 2 • Muestras superiores a 30, • Muestras pequeñas n > 30 n ≤ 30 s ⎤ ⎡ a I = ⎢x ± zα 2 n ⎥⎦ ⎣ s ⎤ ⎡ a I = ⎢ x ± t α 2; (n −1) n ⎥⎦ ⎣ c) Intervalo de confianza para la varianza σ 2 de una distribución normal ⎡ (n − 1) s 2 ( n − 1) s 2 ⎤ I=⎢ 2 ; 2 ⎥ χ χ ⎢⎣ α 2; (n −1) 1− α 2; (n −1) ⎥ ⎦ d) Intervalo de confianza para la diferencia de medias de dos distribuciones normales • Las varianzas poblaciones σ12 y σ 22 son conocidas ⎡ I = ⎢(x − y ) ± z α 2 ⎣ NOTA.- En todos los intervalos de confianza s2 σ12 n1 + σ 22 n2 ⎤ ⎥ ⎦ es la cuasivarianza • Las varianzas poblaciones - Caso en que la suma σ12 y σ 22 son desconocidas: (n1 + n 2 ) > 30 ⎡ I = ⎢(x − y ) ± z α 2 ⎣ con s12 n1 + n1 ≈ n 2 s 22 n2 ⎤ ⎥ ⎦ - Caso en que los tamaños muestrales son pequeños y las varianzas son desconocidas, pero iguales: I = ⎡(x − y ) ± t α 2; (n1 + n 2 − 2 ) . s p ⎢⎣ s 2p 1 n1 + 1 n2 ⎤ ⎥⎦ s 2p ( n1 − 1) s12 = + (n 2 − 1) s 22 n1 + n 2 − 2 es la media ponderada de las cuasivarianzas muestrales - Caso en que los tamaños muestrales son pequeños y las varianzas son desconocidas y distintas 2 ⎞2 ⎛ s12 s 2 ⎟ ⎜ ⎡ I = ⎢(x − y ) ± t α 2; f ⎣ ⎤ + n1 n 2 ⎥ ⎦ s12 s 22 donde donde f es la aproximación de Welch f = ( ⎜n + n ⎟ 2⎠ ⎝ 1 s12 ) 2 n1 n1 + 1 + ( s 22 ) 2 − 2 n2 n2 +1 e) Intervalo de confianza para la razón de varianzas de dos poblaciones normales ⎡ ⎤ s12 s 22 s12 s 22 I=⎢ ; ⎥ ⎢⎣ Fα 2; (n1 −1), (n 2 −1) F1− α 2; (n1 −1), (n 2 −1) ⎥⎦ NOTA.- Fα; n1 , n 2 = 1 F1− α; n 2 , n1 f) Intervalo de confianza para el parámetro p de una distribución binomial de parámetros n, p, B(n, p) po ( 1 − po ) ⎤ ⎥ n ⎦ ⎡ I = ⎢p o ± z α 2 ⎣ g) Intervalo de confianza para la diferencia de parámetros dos distribuciones binomiales ⎡ I = ⎢(p1 − p 2 ) ± z α 2 ⎣ ( p1 − p2 ) de p1 ( 1 − p1 ) p ( 1 − p2 ) ⎤ + 2 ⎥ n1 n2 ⎦ h) Intervalo de confianza para el parámetro λ de una distribución de Poisson ⎡ λ⎤ I = ⎢λ ± z α 2 ⎥ n⎦ ⎣ i) Intervalo de confianza para la diferencia de datos apareados • Para muestras grandes n > 30 s ⎤ ⎡ I = ⎢d ± z α 2 d ⎥ n⎦ ⎣ • 1 d= n Para muestras pequeñas n ∑ di d i = ξi − ηi i =1 n < 30 s ⎤ ⎡ I = ⎢d ± t α 2, (n −1) d ⎥ n⎦ ⎣ 1 s d2 = n −1 n 2 ( ) d − d i ∑ i =1 CONTRASTE DE HIPÓTESIS a) Contraste de la media de una población normal con varianza conocida • Contraste bilateral H0 : μ = μ0 Hipótesis nula Se acepta H0 Se rechaza si el estadístico H0 Hipótesis alternativa z = si el estadístico z = H a : μ ≠ μ0 x − μ0 ≤ zα 2 σ n x − μ0 σ n > zα 2 σ ⎫ ⎧ R rechazo = ⎨ x − μ 0 > z α 2 . ⎬ n⎭ ⎩ • Contraste unilateral H0 : μ ≤ μ0 Hipótesis nula Se acepta H0 Se rechaza si el estadístico H0 si el estadístico Hipótesis alternativa z= Ha : μ > μ0 x − μ0 ≤ zα σ n z= x − μ0 > zα σ n σ ⎫ ⎧ R rechazo = ⎨ x − μ 0 > z α . ⎬ n⎭ ⎩ b) Contraste de la media de una población normal con varianza desconocida • Contraste bilateral Muestras grandes Hipótesis nula n > 30 H0 : μ = μ0 Hipótesis alternativa Ha : μ ≠ μ0 Se acepta H0 Se rechaza si el estadístico z = H0 x − μ0 s n x − μ0 si el estadístico z = s n ≤ zα 2 > zα 2 s ⎫ ⎧ R rechazo = ⎨ x − μ 0 > z α 2 . ⎬ n⎭ ⎩ Muestras pequeñas Hipótesis nula Se acepta H0 Se rechaza n ≤ 30 H0 : μ = μ0 Hipótesis alternativa si el estadístico t = H0 x − μ0 s n x − μ0 si el estadístico t = s n Ha : μ ≠ μ0 ≤ t α 2; (n −1) > t α 2; (n −1) s ⎫ ⎧ R rechazo = ⎨ x − μ 0 > t α 2; (n −1) . ⎬ n⎭ ⎩ • Contraste unilateral Muestras grandes Hipótesis nula Se acepta H0 Se rechaza n > 30 H0 : μ ≤ μ0 si el estadístico H0 si el estadístico Hipótesis alternativa z= x − μ0 ≤ zα s n z= s ⎫ ⎧ R rechazo = ⎨ x − μ 0 > z α . ⎬ n⎭ ⎩ x − μ0 > zα s n Ha : μ > μ0 Muestras pequeñas Hipótesis nula Se acepta H0 Se rechaza n ≤ 30 H0 : μ ≤ μ0 si el estadístico H0 Hipótesis alternativa Ha : μ > μ0 x − μ0 ≤ t α; (n −1) s n t= si el estadístico t = x − μ0 > t α; (n −1) s n s ⎫ ⎧ R rechazo = ⎨ x − μ 0 > t α; (n −1) . ⎬ n⎭ ⎩ c) Contraste para la varianza de una población normal • Contraste bilateral H 0 : σ 2 = σ 20 Hipótesis nula Se acepta H0 Se rechaza • si el estadístico H0 si el estadístico Hipótesis alternativa χ 2 n − 1) s 2 ( = σ 02 χ 2 n − 1) s 2 ( = σ 02 H a : σ 2 ≠ σ 20 [ ∈ χ12− α 2, ( n −1) ; χ α2 2, ( n −1) [ ∉ χ12− α 2, ( n −1) ; χ α2 2, ( n −1) Contraste unilateral H 0 : σ 2 ≤ σ 20 Hipótesis nula Se acepta H0 Se rechaza si el estadístico H0 si el estadístico Hipótesis alternativa χ 2 χ ( n − 1) s 2 = σ 02 2 ( n − 1) s 2 = σ 02 ] H a : σ 2 > σ 20 < χ α2 , ( n −1) ≥ χ α2 , ( n −1) ] d) Contraste de igualdad de medias de dos poblaciones normales de varianzas conocidas • Contraste bilateral Hipótesis nula Se acepta • H0 H 0 : μ1 = μ 2 Hipótesis alternativa x−y ≤ zα 2 2 2 σ1 σ 2 + n1 n 2 si z = Se rechaza H0 H a : μ1 ≠ μ 2 si z = x−y σ12 σ 22 + n1 n 2 > zα 2 Contraste unilateral Hipótesis nula Se acepta H0 si H 0 : μ1 ≤ μ 2 x−y z= σ12 n1 + σ 22 Hipótesis alternativa ≤ zα Se rechaza H0 si H a : μ1 > μ 2 z= n2 x−y σ12 n1 + σ 22 n2 e) Contraste de igualdad de medias de dos poblaciones normales de varianzas desconocidas • Contraste bilateral Hipótesis nula H 0 : μ1 = μ 2 Muestras grandes Se acepta H0 (n1 + n 2 ) > 30 si el estadístico z = Hipótesis alternativa con n1 ≈ n 2 x−y s12 s2 + 2 n1 n 2 ≤ zα 2 H a : μ1 ≠ μ 2 > zα Se rechaza Muestras pequeñas Se acepta H0 1 + 1 n1 n 2 sp H0 H0 Se rechaza H0 x−y ( n1 − 1) s12 = + (n 2 − 1) s 22 n1 + n 2 − 2 > t α 2 , (n 1 + n 2 − 2 ) 1 + 1 n1 n 2 sp (n1 + n 2 ) ≤ 30 , varianzas desconocidas y distintas σ12 ≠ σ 22 x−y t= si s 2p ≤ t α 2 , (n 1 + n 2 − 2 ) si el estadístico t = Muestras pequeñas Se acepta > zα 2 s12 s2 + 2 n1 n 2 (n1 + n 2 ) ≤ 30 , varianzas desconocidas pero iguales σ12 = σ 22 x−y si t = Se rechaza x−y si el estadístico z = H0 s12 s2 + 2 n1 n 2 ≤ t α 2, f si el estadístico t = f = ( 2 ⎞ ⎛ s12 s 2 ⎟ ⎜ ⎜n + n ⎟ 2⎠ ⎝ 1 ) 2 s12 x−y s12 s2 + 2 n1 n 2 n1 n1 + 1 + ( s 22 2 ) 2 − 2 n2 n2 +1 > t α 2, f • Contraste unilateral Hipótesis nula H 0 : μ1 ≤ μ 2 Muestras grandes Se acepta H0 Hipótesis alternativa (n1 + n 2 ) > 30 si el estadístico z= con n1 ≈ n 2 x−y s12 n1 s 22 +n 2 ≤ zα H a : μ1 > μ 2 Se rechaza H0 Muestras pequeñas Se acepta H0 Se rechaza si x−y t= H0 + > zα s 22 n2 ≤ t α , (n 1 + n 2 − 2 ) x−y 1 n1 sp si H0 1 n2 t= si el estadístico s12 + 1 n2 n1 − 1) s12 ( = + (n 2 − 1) s 22 n1 + n 2 − 2 s 2p > t α , (n1 + n 2 − 2 ) (n1 + n 2 ) ≤ 30 , varianzas desconocidas y distintas σ12 ≠ σ 22 x−y t= n1 Se rechaza + 1 n1 Muestras pequeñas Se acepta s12 n1 (n1 + n 2 ) ≤ 30 , varianzas desconocidas pero iguales σ12 = σ 22 sp H0 x−y z= si el estadístico ≤ t α, f s 22 +n f = 2 si el estadístico x−y t= s12 n1 + s 22 n2 ( ⎛ s12 s 22 ⎞⎟ ⎜ ⎜n + n ⎟ 2⎠ ⎝ 1 s12 ) 2 n1 n1 + 1 + ( s 22 2 ) 2 − 2 n2 n2 +1 > t α, f f) Contraste de igualdad de varianzas de dos poblaciones normales • Contraste bilateral Hipótesis nula Se acepta H0 H 0 : σ 21 = σ 22 si el estadístico F= s12 s 22 Hipótesis alternativa [ H a : σ 21 ≠ σ 22 ∈ F1− α 2; (n1 −1), (n 2 −1) ; Fα 2; (n1 −1), (n 2 −1) ] Se rechaza H0 si el estadístico F= s12 s 22 [ ∉ F1− α 2; (n1 −1), (n 2 −1) ; Fα 2; (n1 −1), (n 2 −1) ] • Contraste unilateral Hipótesis nula Se acepta H0 NOTA.- si F= s12 s 22 Fα; n1 , n 2 = H 0 : σ 21 ≤ σ 22 Hipótesis alternativa ≤ Fα; (n1 −1), (n 2 −1) Se rechaza H0 H a : σ 21 > σ 22 F= si s12 s 22 > Fα; (n1 −1), (n 2 −1) 1 F1− α; n 2 , n1 g) Contraste de igualdad de medias en el caso de datos apareados. • Contraste bilateral H 0 : d = 0 ⇔ μ1 = μ 2 Hipótesis nula Se acepta H0 Se rechaza si el estadístico H0 1 donde d = n si el estadístico n n i =1 i =1 t= Hipótesis alternativa H a : d ≠ 0 ⇔ μ1 ≠ μ 2 d ≤ t α 2 , (n −1) sd n t= d > t α 2 , (n −1) sd n ∑ d i = ∑ (x i − y i ) s d2 1 = (n − 1) n ∑ (di − d ) 2 i =1 • Contraste unilateral Hipótesis nula H 0 : d ≤ 0 ⇔ μ1 ≤ μ 2 Hipótesis alternativa H a : d > 0 ⇔ μ1 > μ 2 Se acepta H0 Se rechaza si el estadístico H0 t= si el estadístico t= d ≤ t α, (n −1) sd n d > t α , (n −1) sd n h) Contraste para el parámetro p de una distribución binomial • Contraste bilateral Hipótesis nula H 0 : p = p o Se acepta H0 si z = p − po po ( 1 − po ) n ≤ zα 2 Hipótesis alternativa H a : p ≠ p o Se rechaza H0 si z = p − po po ( 1 − po ) n > zα 2 • Contraste unilateral Hipótesis nula H 0 : p ≤ p o Se acepta H0 si z = p − po ≤ zα po ( 1 − po ) n Hipótesis alternativa H a : p > p o Se rechaza H0 si z = p − po > zα po ( 1 − po ) n i) Contraste para la igualdad de los parámetros de dos distribuciones binomiales B (n1, p1 ) y B (n2 , p2 ) en muestras grandes • Contraste bilateral Hipótesis nula Se acepta H0 Se rechaza H 0 : p1 = p 2 si el estadístico z = H0 si el estadístico z = Hipótesis alternativa p1 − p 2 p1 ( 1 − p1 ) p ( 1 − p2 ) + 2 n1 n2 p1 − p 2 p1 ( 1 − p1 ) p ( 1 − p2 ) + 2 n1 n2 H a : p1 ≠ p 2 ≤ zα 2 > zα 2 • Contraste unilateral Hipótesis nula Se acepta H0 Se rechaza H 0 : p1 ≤ p 2 si el estadístico H0 z= si el estadístico z = Hipótesis alternativa H a : p1 > p 2 p1 − p 2 ≤ zα p1 ( 1 − p1 ) p2 ( 1 − p2 ) + n1 n2 p1 − p 2 > zα p1 ( 1 − p1 ) p2 ( 1 − p2 ) + n1 n2 Grado Ciencias Ambientales Facultad Ciencias Departamento Matemáticas Profesor: Santiago de la Fuente Fernández