FÍSICA. PRUEBA ACCESO A UNIVERSIDAD +25 TEMA 12. Física

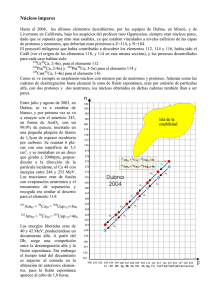
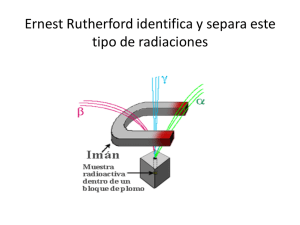
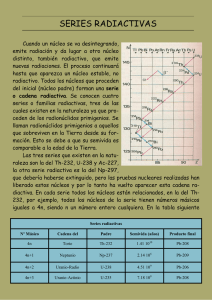
FÍSICA. PRUEBA ACCESO A UNIVERSIDAD +25
TEMA 12. Física nuclear
En 1896 H. Becquerel (1852-1908) se encontraba estudiando el fenómeno de la fluorescencia1 para lo que envolvía
una placa fotográfica en un papel grueso, encima colocaba un material fluorescente y ambos los exponía a la
radiación solar. Cuando desenvolvía la placa fotográfica la encontraba velada, lo que le hacía suponer que la causa
2
era la radiación emitida por el material fluorescente y que ésta debía de ser del tipo de rayos X, pues atravesaba el
grueso papel. Varios días consecutivos nublados detuvieron sus experiencias habiendo dejado su experimento
metido en un cajón; después de lo cual decidió revelar la placa para apreciar que ésta se encontraba totalmente
velada, y no muy poco, como cabría esperar. Este descubrimiento le hizo pensar que la causa del velado de la placa
no era la fluorescencia del material, sino algún tipo de radiación procedente del material que era una sal de uranio.
Finalmente llegó a la conclusión de que la sal de uranio emitía permanentemente una radiación similar a los rayos X y
en todas las direcciones, a las que denominó fluorescencia invisible.
Este fenómeno interesó a Marie Sklodowska3(1867-1934) al que denominaron por primera vez,
radiactividad. Los Curie llegaron a la conclusión, que la causa de la radiactividad eran los átomos de uranio y que su
intensidad era proporcional a la cantidad de uranio presente en la muestra. Ambos, descubrieron que la pechblenda,
mineral de uranio, era cuatro veces más activa que el uranio, y la calcolita dos veces más, concluyendo que estos dos
minerales debían contener pequeñas cantidades de otra sustancia considerablemente más radiactivas que el uranio.
El 27 de junio de 1898 comunicaban el descubrimiento de un nuevo elemento al que denominaron polonio, en honor
del país de origen de Marie, y el 11 de diciembre el descubrimiento del elemento radiactivo por excelencia: el radio.
Los primeros estudios que se realizaron sobre la radiactividad pusieron de manifiesto unas propiedades
generales que podemos resumir:
 Alto poder de penetración en la materia, pudiendo atravesar láminas metálicas.
 Alto poder de ionización de la materia al chocar con los átomos que la constituyen y transformarlos en iones
que se pueden detectar.
 Interacción con campos eléctricos y magnéticos.
 Invariabilidad de la radiactividad ante la acción de factores como la temperatura, la presión, las reacciones
químicas, etc.
 La interacción de la radiactividad con la materia se acompaña de intercambios altamente energéticos.
 La intensidad de la radiactividad en un material es proporcional a la fracción de elemento activo presente.
Tipos de radiaciones
Si la radiactividad emitida por un material natural se hace pasar por un campo
magnético o eléctrico se observa que se descompone en tres radiaciones:
0

Radiación beta 1  : Está formada por partículas con masa pequeña y carga
eléctrica negativa; en concreto se trata de electrones y pueden atravesar
láminas de aluminio con energía entorno a 1 MeV.

Radiación alfa 2  : Está formada por partículas de mayor masa que las beta
y carga eléctrica positiva; en concreto, se trata de núcleos de Helio con masa
equivalente a la de dos protones y dos neutrones y carga equivalente a la de
dos protones. Tienen poco poder de penetración (hoja de papel) y su
energía cinética es del orden de 1 MeV.
Radiación gamma  : No se desvían en campos magnéticos o
eléctricos pues se trata de radiación electromagnética de alta
frecuencia (superior a los rayos X), tiene energía del orden de keV y
son muy penetrantes en la materia.

4
1
La fluorescencia es la luminiscencia producida por ciertos minerales cuando son expuestos a la acción de ciertos
rayos (rayos X, ultravioleta, visibles). Estas radiaciones son transformadas por el mineral en ondas luminosas de
longitud de onda mayor que la de los rayos que inciden en él.
2
No podría tratarse de la radiación solar, pues ésta no atraviesa el grueso papel.
3
Más conocida por Marie Curie, esposa de Pierre Curie, físico que le apoyó en sus investigaciones.
1
El núcleo atómico
En 1907 H.W. Geiger y E. Mardsen, bajo la supervisión de E.
Rutherford, estudiaban el impacto de partículas α sobre
láminas delgadas de oro. Una muestra de Radio se ponía en
un contenedor con un pequeño orificio por el que escapaba
un haz delgado de partículas α que se hacía incidir sobre una
placa de sulfato de zinc, la cual tiene la propiedad de emitir
luz cuando es alcanzada por una partícula α. Al interponer en
su camino una lámina delgada de oro, podían estudiarse las
desviaciones que provocaban los átomos de oro a las
partículas α. En un principio los resultados obtenidos
entraban dentro de lo previsto; la mayoría de las partículas α
atravesaban la lámina de oro sin desviarse y algunas se
desviaban de tal manera que el número de partículas α dispersadas por el oro decrecía rápidamente con el ángulo de
observación, medido respecto a la dirección incidente, y no encontraron evidencia de partículas α que se dispersaran
ángulos mayores de 30º. Rutherford les insistió en que tratasen de encontrar partículas α que se desviasen ángulos
superiores a 30º. La sorpresa ocurrió cuando, poco después, Geiger le comunicó que Mardsen había observado
partículas α dispersadas hacia atrás. Según el propio Rutherford, ".... era como disparar balas sobre un hoja de papel
y ver que rebotan". Geiger y Marsden se dedicaron a medir entonces la distribución de las partículas α con más
cuidado y, en 1909, publicaron sus resultados. La deflexión seguía una función bien definida que decrecía
pronunciadamente con el ángulo, pero que indicaba que la dispersión de las partículas α a ángulos mayores de 90º
era muy superior a la que podría atribuirse a una fluctuación estadística. En 1911, Rutherford dio una explicación a
los resultados de Geiger y Marsden. Según éste, la dispersión a grandes ángulos indicaba que, contrario a lo
pensado hasta entonces, la mayor parte de la masa del átomo, y toda su carga positiva, se encontraba concentrada
en una región muy reducida en el centro del átomo: el núcleo.
http://www.sc.ehu.es/sbweb/fisica/cuantica/rutherford/rutherford.html
Los estudios posteriores para determinar la composición del núcleo, llevaron a pensar que en el núcleo se
1
encontraban los protones ( 1 H ), partícula identificada por Rutherford en 1914 y de la que determinó su masa y su
carga. Pero resultó que no sólo bastaban los protones para justificar la masa del núcleo, lo que llevó a suponer la
existencia de otra partícula cuya masa sería similar a la del protón y no debería tener carga eléctrica, razón por lo que
1
no fue identificada hasta 1932, denominándose neutrón ( 0 n ).
Cada núcleo atómico se identifica por el número de protones o número atómico Z, y por el número de
partículas o nucleones que tiene, llamado número másico A. El número de neutrones será pues, A-Z.
También, llamaremos núclido a cada tipo de núcleo y los representaremos de manera general con el símbolo
químico del elemento químico al que pertenece anteponiéndoles como subíndice Z y como superíndice A.
A
Z
Así por ejemplo:
X
238
92
U se refiere al núclido del Uranio con 92 protones, 238 nucleones de los cuales 238-92=146 son
neutrones.
3
A.1 Describe la composición de los siguientes núclidos: 1 H ,
12
6
C,
60
27
Co ,
137
55
Cs
Existe una gran cantidad de núclidos que podemos clasificar en:

Isótopos: Son núclidos que tienen el mismo Z pero diferente A; es decir, tienen el mismo número de protones
pero diferente número de neutrones. Al tener el mismo número de protones se trata de núclidos del mismo
1
2
3
elemento químico. Por ejemplo: 1 H , 1 H , 1 H se trata de los tres isótopos del elemento químico Hidrogeno y
que se denominan: protio (el más abundante), deuterio y tritio.

Isóbaros: Son núclidos que tienen el mismo A pero diferente Z. Por ejemplo:

Isótonos: Son núclidos que tienen el mismo número de neutrones, pero diferente Z y diferente A. Por
ejemplo:
13
6
Cy
14
7
14
6
Cy
14
7
N
N
A.2 Identifica isóbaros, isótonos e isótopos de entre los siguientes núclidos:
55
26
60
Fe , 2960Cu , 28
Ni , 2656 Fe , 3061Zn , 2760Co
2
Si tenemos en cuenta que la masa del electrón es del orden de 1838 veces menor que la del protón o del
neutrón, podemos considerar que la masa del átomo se encuentra concentrada en un 99% en el núcleo. Por otra
parte, la masa de los átomos debe ser una cantidad muy pequeña por lo que es conveniente definir una unidad de
masa adecuada para medir la masa de los átomos. Desde 1961, se estableció la unidad de masa atómica unificada
u, como la doceava parte de la masa del isótopo
12
6
C que resulta ser 1,66x10-27 kg. Luego podemos concluir que:
1u
lo que nos permite cambiar de escala.
1,66 x1027 kg
A.3 Completa la siguiente tabla:
Partícula
Electrón
Protón
Neutrón
Masa (kg)
9,1x10-31
Masa (u)
1,00783
1,675x10-27
Por lo que respecta a la forma y
volumen de los núcleos, los
resultados experimentales permiten afirmar que, en su mayoría, tienen forma esférica y que su radio se puede
estimar:
r  r0 3 A
-15
donde r0=1,2x10
A.4 Calcula el radio, el volumen y la densidad del núcleo:
137
55
m.
Cs . (Sol: 6,2x10-15 m; 9,9x10-43 m3; 2,3x1017 kg/m3)
3
A.5 Compara la densidad del núcleo anterior con la del Os que es de 22,5 kg/dm . ¿Qué te hace pensar?
A.6 Considera dos protones del núclido
137
55
Cs que se encuentran separados por una distancia igual al radio y calcula:
a) El valor de la fuerza de la interacción gravitatoria. (Sol: 4,8x10-36 N)
b) El valor de la fuerza de la interacción eléctrica. (Sol: 6 N)
c) La aceleración que debería tener cada protón. (Sol: 3,6x1027 m/s2)
d) La energía potencial eléctrica de los dos protones. (Sol: 232 keV)
DATOS: mp=1,00783 u; qp=1,6x10-19 C
Fuerzas nucleares
Una vez establecido que en el núcleo se encuentran los protones y los neutrones quedaba por explicar qué tipo de
fuerzas las mantenían unidas. Estas fuerzas
deberían actuar a muy corta distancia, del orden
de 10-15 m y ser de gran intensidad para justificar
la estabilidad del núcleo. La estabilidad del núcleo
se puede evaluar desde el punto de vista
energético como pasamos a ver.
Se ha observado que para núcleos
estables ligeros, el número de protones es similar
al de neutrones; pero para los núcleos estables
masivos (mayor masa) el número de neutrones
crece sensiblemente por encima del número de
protones. Esto indica que al aumentar el número
de protones, también aumenta la intensidad de las
fuerzas repulsivas de Coulomb, lo que disminuiría
la estabilidad del núcleo. Es por ello que se
necesitan más neutrones para mantener estable
el núcleo ya que entre neutrones, y entre
neutrones y protones, sólo existen fuerzas de atracción. La mayoría de los núclidos estables tienen valores de A par;
además, existen ciertos valores de Z y N (número de neutrones), llamados números mágicos, que corresponden a
núcleos de gran estabilidad.
Por otra parte, también se comprobó que la masa total de un núcleo es menor que la suma de las masas de
los nucleones que lo forman, a esta diferencia de masa se le llama defecto de masa. El principio de equivalencia
masa-energía, E=mc2, establecido por Einstein en su teoría de la relatividad, permite interpretar esta disminución de
masa como la disminución de energía que sufren, los nucleones por separado, al unirse para formar el núcleo y que
será la misma que necesitaremos para separar de nuevo los nucleones del núcleo. Esta diferencia de energía es
conocida como energía de enlace o ligadura y es la que confiere estabilidad al núcleo.
Eligadura  Enucleones  E núcleo
3
El defecto de masa es m  Z  ( m protón )  ( A  Z )  mneutrón  mnúcleo y aplicando el principio de equivalencia:
Eligadura  c 2  m
Para poder realizar comparaciones entre núcleos es interesante
conocer la energía media de enlace por nucleón Eligadura/A para cada
núcleo cuya representación gráfica se muestra al lado y donde
podemos observar:



En los núcleos ligeros se aprecia un aumento brusco de la
energía de enlace por nucleón hasta A=10. La fusión de dos
núcleos ligeros para formar un más pesado, es un proceso en
el que se libera energía. Fusión nuclear.
Los núcleos más estables son los semipesados entorno a
A=62.
Hacia los núcleos pesados, la energía media de enlace por nucleón decrece, de tal manera que la fisión de
un núcleo pesado para formar dos núcleos semipesados, es un proceso en el que se librera energía. Fisión
nuclear.
Finalmente, podemos concluir que para justificar las propiedades de los núcleos hay que pensar en un nuevo tipo de
interacción (además de la gravitatoria y electromagnética) denominada interacción fuerte cuyas características son:




Son fuerzas atractivas entre 1x10-15 y 2x10-15 m, y repulsivas a distancias inferiores a 1x10-15 m.
Son de intensidad muy fuerte para vencer la fuerzas repulsivas eléctricas entre los protones a tan cortas
distancias.
Son de corto alcance, es decir se manifiestan a cortas distancias 1x10-15 m.
Son independientes de la carga eléctrica por lo que se dan entre protones, entre neutrones y entre
protones y neutrones.
A.7 Calcula la energía equivalente de una unidad de masa unificada. (Sol: 934 MeV)
23
A.8 Para el núclido 11 Na de 22,9898 u :
a) Calcula el defecto de masa en su formación. (Sol: 3,4x10-28 kg)
b) Calcula la energía de ligadura por nucleón. (Sol: 83,2 MeV)
c) Calcula la energía necesaria para disociar completamente 1 g de núclidos
DATOS: Busca la masa de los nucleones.
23
11
Na . (Sol: 8,1x1011 J)
Leyes de la desintegración radiactiva
En 1902 E. Rutherford y F. Soddy formularon la ley de la desintegración radiactiva o ley de decaimiento al
comprobar que la actividad radiactiva de una sustancia disminuye exponencialmente con el tiempo. El proceso de
emisión radiactiva es independiente del estado físico o de la combinación química en la que se encuentre la sustancia
radiactiva y se trata de un proceso aleatorio en el que no se puede determinar cuando se desintegrará un núcleo
determinado.
http://www.colorado.edu/physics/2000/isotopes/radioactive_decay3.html
Si tenemos una muestra con N núcleos de un elemento radiactivo. El número de núcleos que se desintegran dN en un intervalo de tiempo infinitesimal dt, es proporcional al número de núcleos presentes y al intervalo de tiempo,
lo que matemáticamente se expresa:
 dN    N  dt
4
donde λ es la constante radiactiva o constante de desintegración (se mide en 1/s) que tiene un valor propio para
cada núclido radiactivo y representa la probabilidad por unidad de tiempo de que un determinado núcleo se
desintegre. Si λ tiene un valor grande, la sustancia radiactiva se desintegrará rápidamente. El signo – (-dN) significa
que el número de núcleos disminuye.
La expresión anterior también la podemos escribir: 
dN
dN
   N donde el valor absoluto 
es la
dt
dt
velocidad de desintegración también conocida como actividad (Ac) de la sustancia radiactiva. La unidad de la
actividad en el SI es el becquerel (Bq) que equivale a una desintegración/segundo. Otras unidades de actividad
4
No confundir con la longitud de onda utilizada en temas anteriores.
4
utilizadas son el curio (Ci) que equivales a 3,7x1010 desintegraciones/segundo y el rutherford que equivale a 106
desintegraciones/segundo.
El número de núcleos radiactivos presentes en una muestra disminuye con el tiempo. Tengamos una muestra
radiactiva que a to=0 (inicialmente) tiene No núcleos radiactivos, ¿cuántos quedarán sin desintegrar al cabo de t
segundos? Veamos:

dN
dN
   N de aquí
    dt e integrando resulta
dt
N
N 
    t que también podemos expresar:
Ln
 N0 
N  N 0  e  t siendo “e” la base de los logaritmos neperianos.
Dado que la masa total de un elemento radiactivo será el producto del número de núcleos por la masa de
estos, podemos escribir
m
Ln      t
 m0 
o también
m  m0  e  t
donde m0 es la masa inicial y m la masa a tiempo t de la sustancia radiactiva.
De igual manera, como la actividad es proporcional a la cantidad de núcleos presentes, también podemos
expresar:
 A 
Ln c     t
 Ac 0 
Un valor característico de los núclidos radiactivos es su periodo de semidesintegración T o tiempo que
tiene que transcurrir para que, en una muestra radiactiva, el número de núcleos radiactivo (o la masa de todos ellos)
 N 
    t tenemos:
 N0 
se reduzca a la mitad, es decir N=N0/2 y sustituyendo en la expresión Ln
1
Ln     T
2
Otro concepto interesante es la vida media
toma el valor:

de donde se deduce
T 
Ln2 

 , que se interpreta como el promedio de vida de cualquier núcleo y que
1

o bien
 
T
Ln 2 
A.9 El número de núcleos de una muestra radiactiva se reduce un 15% en 1,54 días.
a) Calcula la constante radiactiva del núclido radiactivo. (Sol: 1,2x10-6 1/s)
b) Calcula el periodo de semidesintegración del núclido radiactivo. (Sol: 5,8x105 s)
c) Calcula la vida media del núclido radiactivo. (Sol: 8,3x105 s)
234
A.10 Tenemos una muestra de 1012 núcleos de U cuyo periodo de semidesintegración es de 2,5x105 años.
a) ¿Cuál es la actividad inicial de la muestra? (Sol: 0,088 desintegración/s)
234
U quedarán al cabo de 100 años? (Sol: 9,997x1011)
234
8
c) ¿Cuántos núcleos de U se habrán desintegrado en ese tiempo? (Sol: 3x10 )
b) ¿Cuántos núcleos de
A.11 Un gramo de Radio tiene una actividad de 1Ci. Sabiendo que la masa atómica del Radio es 226 u:
a) Calcula la constante de desintegración del Radio. (Sol: 1,4x10-11 1/s)
b) La vida media de los núcleos de Radio. (Sol:7,2x1010 s)
c) El periodo de semidesintegración del Radio. (Sol: 1570 años)
14
A.12 En una excavación arqueológica se encontró un cuenco de calabaza que presentaba una actividad del C de
0,20 desintegraciones/s por cada gramo de carbono. Calcula la antigüedad del cuenco sabiendo que la actividad del
14
C en una planta viva es de 0,27 desintegraciones/s por cada gramo de carbono y que el periodo de
14
semidesintegración del C es de 5570 años. (Sol: 2409 años)
Modos de desintegración radiactiva
Desde un principio se pensó que las radiaciones que constituyen la radiactividad proceden del núcleo del átomo. De
manera natural las sustancias radiactivas emiten los tres tipos de radiaciones antes vistos (α, β, γ) como un
5
mecanismo por el que los núcleos inestables se transforman en otros más estables mediante la liberación de dichas
partículas. En estos procesos de desintegración se cumplen los principios de conservación:
 Conservación de la energía.
 Conservación del momento lineal.
 Conservación de la carga eléctrica.
 Conservación del número de nucleones.
Desde 1913, y como resultado de amplias experiencias se conocen las leyes del desplazamiento de Soddy:



La emisión de una partícula α por un núcleo origina la formación de otro núcleo con un número atómico
inferior de dos unidades y un número másico inferior en cuatro unidades.
La emisión de una partícula β por un núcleo origina otro núcleo con número atómico superior en una unidad y
como el mismo número másico.
La emisión de rayos gamma al ser ondas electromagnéticas no modifica los números característicos del
núcleo.
Después de la desintegración radiactiva es posible que el nuevo núclido que se forma también sea radiactivo y se
proceda a una nueva desintegración. Este proceso continuará hasta que un núclido no sea radiactivo, es decir sea
estable. Un conjunto de estos procesos sucesivos es conocido como serie o familia radiactiva. En la actualidad se
conocen cuatro familias radiactivas que resumimos en la siguiente tabla:
Familia
Torio
Neptunio
Uranio
Actinio
Núclido inicial
232
Th
237
Np
238
U
235
U
T semidesintagración
1,4x1010 años
2,2x106 años
4,5x109 años
7,2x108 años
Núclido final
208
Pb
209
Bi
206
Pb
207
Pb
Emisión alfa α
Se produce en núcleos de elementos pesados o masivos en los que el
número de neutrones y muy superior al de protones. Las partículas α
fueron identificadas como núcleos de Helio que representamos
que están formadas por dos protones y dos neutrones.
Este proceso se puede expresar:
Por ejemplo:
A
Z
4
2
He y
X  AZ42Y  24He
230
90
4
Th 226
88 Ra  2 He
Obsérvese la conservación del número atómico y másico.
Este proceso también va acompañado de un defecto de masa
equivalente a una cantidad de energía que se reparte en forma de
energía cinética entre la partícula α y el nuevo núcleo formado.
Aplicando los principios de conservación de la energía y momento
lineal, se deduce que la velocidad de las partículas α es del orden de 107 m/s que junto con su masa, las hace
idóneas como proyectiles para el estudio de los átomos.
218
84
A.13 Completa las siguientes desintegraciones:
Emisión beta
Po  X  24He
4
X  206
80 Hg  2 He

0
1
e y su emisión se produce en los núcleos que tienen muchos más
A
A
0
neutrones que protones. El proceso se puede expresar: Z X  Z 1Y  1 e
218
218
0
Por ejemplo: 84 Po  85 Ac  1 e
Estas partículas se identificaron como electrones

La emisión de partículas  presentaba varios inconvenientes:
 En el núcleo no hay electrones.
 El principio de conservación del momento lineal.

Para explicar la emisión  , W. E. Fermi (1901-1954) postuló la existencia de una interacción, llamada interacción
débil, por ser de menor intensidad que la interacción fuerte y la electromagnética y cuyo alcance es del orden de 10-15
m. Para hacer compatible esta la emisión β con los principios de conservación, W. Pauli (1900-1958) propuso que la
desintegración daría lugar a la formación de tres partículas:
6
1
0
n 11H  10e  
donde  es el neutrino; partícula sin masa (10000 veces menor que la del electrón) y sin carga por lo que sería difícil
de detectar. El neutrino fue detectado en 1952.
De manera general, la emisión
  se puede expresar: ZA X  Z A1Y  10e  
Dado que el neutrón y el protón tienen una pequeña diferencia de masa la energía equivalente máxima de la partícula
  será: Eβ=(mn-mH)c2 cuyo valor es del orden de 0,78 MeV.
Emisión beta

Cuando un núcleo presenta deficiencia de neutrones, para compensar esta deficiencia, un protón se desintegra:
1
1
siendo
0
1
H  01n  10e  
e el positrón. De manera general para cualquier núcleo que emite   se puede expresar:
A
Z
Por ejemplo:
13
7
X  Z A1Y  10e  
N 136C  10e  
Emisión gamma

Cuando un núcleo emite una partícula alfa o beta queda en un estado energético elevado o excitado y tiende hacia un
estado energético menor mediante la emisión del exceso de energía en forma de fotón de alta energía y que
constituye la radiación gamma. Dado que el fotón no tiene masa ni carga, los números atómico y másico no se
modifican. El proceso lo podemos expresar:
A
Z
X *  ZAX  
Captura electrónica
Se produce en núcleos inestable con defecto de neutrones y consiste en la captura por el núcleo de un electrón de la
capa más cercana al núcleo produciéndose el siguiente proceso:
1
1
H  10e 01n  
La conversión de un protón en un neutrón, disminuye el número atómico del núcleo en una unidad como ocurre en la
emisión del positrón. Por ejemplo:
64
29
64
Cu  10e 28
Ni
El hueco dejado por el electrón capturado en la primera capa de electrones es ocupado por un electrón de las capas
superiores, lo que conlleva la emisión un fotón de rayos X. Por otra parte, el núclido resultante de la captura
electrónica, se encuentra en estado excitado, por lo que al pasar al estado fundamental emite un fotón gamma.
Como hemos visto los procesos nucleares se representan de manera similar a los procesos químicos, llamándoseles
reacciones nucleares; pero ambos procesos debemos diferenciarlos. En las reacciones químicas, las modificaciones
se dan en los electrones que rodean el núcleo; mientras que, en las reacciones nucleares, las modificaciones se dan
en la composición del núcleo y como hemos observado se cumplen el principio de conservación del número atómico y
el número másico.
A.14 Completa los siguientes procesos nucleares:
45
20
Ca  10e   
;
239
93
Np 239
92 U 
;
137
55
Cs137
56 Ba 
;
14
8
O 147 N 
Reacciones nucleares. Radiactividad artificial.
Los procesos radiactivos estudiados hasta ahora tienen carácter espontáneo, es decir se producen por la
inestabilidad de los núcleos. Veamos ahora los procesos nucleares provocados por la acción de una partícula sobre
un núcleo o entre dos núcleos. En estos procesos se dan cambios estructurales en el núcleo y su importancia radica
en que las energías que se ponen de manifiesto, son del orden de un millón de veces de las energías que se ponen
de manifiesto en las reacciones químicas clásicas (enlaces químicos entre átomos); además de la posibilidad de
obtener núcleos de elementos químicos a partir de otros elementos, la deseada transmutación de la materia.
7
En 1919, Rutherford bombardeo nitrógeno con partículas α observando la presencia de partículas de gran alcance,
que identificó como protones, y la formación de isótopos de oxígeno. El proceso lo podemos representar:
14
7
N  24He178O 11H
14
17
o también
7 N ( , p ) 8 O
De nuevo podemos ver que se cumplen la conservación del número másico y del número atómico, además del
momento lineal, energía y momento angular.
En 1934, el matrimonio Joliot-Curie utilizaron partículas α para bombardear láminas de Al, observando el siguiente
proceso:
30
15
27
13
Al  24He 01n 1530P * siendo el fósforo un elemento radiactivo que en pocos minutos se desintegra dando:
P * 1430Si  10e   . Este proceso de desintegración tiene una duración muy corta, lo que puso de manifiesto que en
la naturaleza sólo existen los elementos radiactivos con periodos muy grandes, habiendo desaparecido, por
desintegración, aquellos isótopos radiactivos de pequeños periodos. El matrimonio Joliot-Curie había provocado la
formación de un isótopo radiactivo, es decir, la radiactividad artificial.
A.15 Completa las siguientes reacciones nucleares:
40
18
Ar  24He11H 
11
5
B  X 11H 146C
7
3
Li 11H  47Be 
En los procesos nucleares las variaciones de energía están relacionadas con las variaciones de masa mediante el
2
principio de equivalencia E  m  c
A.16 Calcula la variación de energía asociada al proceso:
14
7
N  24He178O 11H (Sol: 1,9 MeV)
8
DATOS: masas (mN=14,003074 u; mHe=4,002603 u; mH=1,007825 u; mO=16,999131 u); c=3x10 m/s;
-27
1 u=1,66x10 kg
Fisión nuclear
La gráfica de la página 4, en la que se representa la energía de enlace por nucleón, pone de manifiesto que la
energía media de enlace por nucleón decrece, de tal manera que la fisión de un núcleo pesado para formar dos
núcleos semipesados, es un proceso en el que se librera energía. Por otra parte, el descubrimiento del neutrón, por
1932 por J. Chadwick, como partícula sin carga eléctrica le hacía idóneo para ser utilizado como proyectil contra los
núcleos pesados con el fin de provocar su fisión en otros núcleos semipesados y la consiguiente liberación de
energía.
En 1938, O. Hahn descubrió que impactando
núcleos de uranio con neutrones se producía
su fisión, proceso que podemos representar:
235
92
*
92
141
1
U  01n  236
92 U  36 Kr  56 Ba  30 n .
http://www.sagangea.org/hojared_radiacion/paginas/Fision.html
La importancia de este proceso radica:
 La gran liberación de energía en base al principio de
2
equivalencia masa-energía E  m  c .
 La liberación de neutrones que posibilita la continuidad del
proceso (reacción en cadena). Este proceso tiene
algunas variantes de tal manera que el número de
neutrones que se liberar pueden ser 2 o 3.
No todos los neutrones resultantes de una fisión pueden producir otra fisión. Si un sólo neutrón produce fisión en otro
núcleo, tendremos una reacción de fisión en cadena automantenida y controlada; pero si más de un neutrón provoca
nuevas fisiones, el número crece exponencialmente y se produce una explosión nuclear (bomba atómica).
A.17 Calcula la energía liberada en la fisión completa de 1 gramos de U-235 según la reacción:
235
92
92
1
U  01n  36
Kr 141
56 Ba  30 n
DATOS: masas(mU=235,0439 u; mBa=140,9140 u; mKr=91,9250 u; mn=1,008665 u); 1u=1,66x10-27 kg
(Sol: 7,2x1010 J)
Reactor nuclear
8
El aprovechamiento de la energía liberada en las reacciones de fisión nuclear se realiza en el reactor nuclear. El
combustible o material fisionable es el óxido de uranio enriquecido5 entre el 2 y 3,5% de U-235 que se encuentra en
forma de pastillas y metidas en tubos dentro de la vasija del
reactor. La vasija del reactor es una estructura blindada de
hormigón y placas de plomo para evitar la salida de radiaciones
al exterior. Dentro de la vasija del reactor también se encuentra
el moderador (agua, agua pesada o grafito) cuya misión es la de
disminuir la energía cinética de los neutrones hasta hacerlos
235
aptos para provocar fisiones en los núcleos de
U ; y las
barras de control (bario o cadmio), que absorben los neutrones
excedentes dejando la reacción en cadena de manera
automantenida. La energía liberada en la vasija es desalojada
mediante el fluido refrigerante que mediante un intercambiador
de calor pasa a otro circuito en el que agua en forma de vapor
mueve una turbina a la cual está conectado un generador eléctrico.
La fisión nuclear tiene un alto rendimiento energético. Sin embargo, representa un riesgo de contaminación radiactiva
y la eliminación de los residuos radiactivos de las centrales nucleares representa un grave problema medioambiental.
http://www.tecnun.es/Asignaturas/Ecologia/Hipertexto/07Energ/130EnNuclear.htm
http://www1.ceit.es/asignaturas/ecologia/hipertexto/13Residu/150ResRadi.htm
http://omega.ilce.edu.mx:3000/sites/ciencia/volumen1/ciencia2/42/htm/sec_12.html
Fusión nuclear
De igual manera, la gráfica de la página 4, en la que se representa la energía de enlace por nucleón, pone de
manifiesto que la energía media de enlace por nucleón crece a medida que aumenta el número másico. Si
conseguimos acercar dos núcleos ligeros la suficiente para
vencer las fuerzas de repulsión, se fusionarán formando un
núcleo de menor masa que la suma de las masas de los núcleos
que se han fusionado. Esta diferencia de masa se manifiesta
mediante la liberación de una cantidad equivalente de energía. A
estos procesos se les denomina fusión nuclear, que se
caracterizan por la gran cantidad de energía que liberan. Así por
ejemplo, un posible proceso de fusión es:
2
1
H 13H  24He  01n
en el que se liberan 17,7 MeV de energía.
1
4
0
A.18 Calcula la energía que se libera en el proceso de fusión: 41 H  2 He  2 1 e (Sol: 26,3 MeV)
DATOS: masas (mHe=4,002603 u; mH=1,007825 u; me=0,0005485 u); 1u=1,66x10-27 kg
6
La realización de procesos de fusión nuclear, de manera artificial encierra grandes dificultades técnicas pues para
que se inicie el proceso son necesarias temperaturas del orden de 100 millones de ºC, lo cual no es fácil. Desde los
años 50 del siglo XX se han conseguido estos procesos de fusión de manera incontrolada en las explosiones
termonucleares de las llamadas bombas de hidrógeno. En la actualidad se trabaja en distintas líneas para resolver
estos problemas técnicos y poder utilizar la fusión nuclear de manera controlada para la obtención de energía ya que
tiene notables ventajas sobre la fisión nuclear, pues es radiactivamente más limpia y los núcleos fusionables son más
abundantes y fáciles de obtener.
http://www.arrakis.es/~lallave/nuclear/fusion.htm
http://home.earthlink.net/~umuri/_/Main/T_particulas2.html
http://www.noticias.com/articulo/30-06-2005/emil-domec/fusin-nuclear-energia-sustitutiva-sol-que-movera-al-mundo4j68.html
http://www.sagan-gea.org/hojared_radiacion/paginas/Fusion.html
http://thales.cica.es/rd/Recursos/rd99/ed99-0226-01/capitulo5b.html
http://www.invap.net/nuclear/plant_radio/intro.html
5
6
El uranio natural contiene un 0,7% del isótopo U-235, el resto es del isótopo U-238 que no es fisionable.
De manera natural, la fusión nuclear se da en el Sol y las estrellas.
9
AYUDAS PARA LA RESOLUCIÓN DE LOS EJERCICIOS DEL TEXTO



Lee atentamente el ejercicio y piensa que está relacionado con los párrafos anteriores. Piensa que en los casos más
sencillos resolverás el ejercicio aplicando alguna idea o ecuación del párrafo anterior.
Si tienes dificultad con el planteamiento físico del ejercicio, consulta la ayuda correspondiente.
Si no consigues resolver el ejercicio, plantéale al Profesor tus dificultades el próximo día (no al cabo de una semana o de
un mes)
A.1
NÚCLIDO
NUCLEONES
PROTONES( 1 H )
NEUTRONES( 0 n )
H
3
1
2
C
12
6
6
Co
60
27
33
137
55
82
NUCLEONES
PROTONES( 1 H )
NEUTRONES( 0 n )
Fe
55
26
29
Cu
60
29
31
3
1
12
6
60
27
137
55
Cs
1
1
A.2
NÚCLIDO
55
26
60
29
1
1
60
28
Ni
60
28
32
56
26
Fe
56
26
30
61
30
Zn
61
30
29
Co
60
27
33
60
27
A.3
Partícula
Electrón
Protón
Neutrón
Masa (kg)
9,1x10-31
1,67x10-27
1,675x10-27
Masa (u)
0,00055
1,00783
1,00904
A.4 Para calcular el radio aplica:
r  r0 3 A donde
r0=1,2x10-
15
m. Para calcular el volumen supón que el núcleo tiene forma de esfera (busca el volumen de una esfera);
finalmente recuerda que la densidad es d=m/V.
17
13
A.5 2,3x10 /22,5= 1x10 Es decir, la densidad de un núcleo es del orden de 10.000.000.000.000 veces mayor que el
material más denso.
A.6 Recuerda que la interacción gravitatoria de Fg=Gmpmp/r2 ; la interacción eléctrica Fe=KQpQp/r2 . Despreciando la
interacción gravitatoria respecto de la eléctrica a=Fe/mp ; finalmente Ep= KQpQp/r
A.7 Aplica E=c2 Δm =(3x108)2 (1,66x10-27) y ponlo en eV y después en MeV.
A.8 Δm= Suma de la masa de los nucleones – masa del núcleo formado= 11(1,00783 u)+12(1,000904 u) - 22,9898 u=
0,20481 u. Luego aplica E=c2 Δm y exprésalo en eV; finalmente E/A te dará la energía por nucleon.
Para c) recuerda de química que la masa atómica del Na es 23 y que significa que 23 g/mol, luego 1 g serán 1/23=
0,0435 mol de núcleos de Na y como cada mol tiene 6,023x1023 núcleos pues en total tendremos que disociar 0,0435
23
x 6,023x10 núcleos y como antes hemos calculado la energía de formación de un núcleo; entonces:
23
-11
11
0,0435 x 6,023x10 x 3,1x10 = 8,1x10 J
10
A.9 Que se reduce un 15% en 1,54 días significa que al cabo de 1,54 días quedan (N) el 85% de los que había
 N 
    t con los datos Ln0,85    1,54  24  3600  de
inicialmente (N0) luego N/N0=0,85; aplicando Ln
 N0 
donde deducimos
 . Para b) aplicamos T 
A.10 La actividad de una muestra es 
calcular
 aplicamos T 
Ln2 
1
y para c) aplicamos  


dN
dN 0
para la actividad inicial que sabemos que es 
   N 0 para
dt
dt
Ln2 

 N 
    t de donde
En b) queremos saber cuantos núcleos N que quedan al cabo de 100 años; aplicamos Ln
 N0 
12
deducimos N. Para c) los núcleos desintegrados en 100 años serán los que había 10 menos los que hay al cabo de
100 años y que has calculado en el apartado anterior.
-3
-3
A.11 Para a) 1 g de núcleos de Radio son 1/226= 4,42x10 mol de núcleos de radio, donde habrá 4,42x10 x
6,023x1023 = 2,7x1021 núcleos de Radio que tiene una actividad de 1Ci lo que equivale a 3,7x1010 desintegraciones/s
y ahora aplicamos 
dN 0
1
Ln2 
   N 0 para calcular  . Para b) aplicamos   y para c) T 
dt


A.12 Ese cuenco de calabaza en algún momento fue una planta viva cuya actividad del carbono-14 era

dN 0
dN
   N 0  0,27 y actualmente sabemos que la actividad del carbono-14 es 
   N  0,20
dt
dt
N 
Ln2 
  0,741 ; por otra parte aplicando T 
podemos deducir

 N0 
combinando ambas expresiones resulta que 
 N 
 para finalmente aplicar Ln     t de donde podemos deducir t.
 N0 
A.13 Aplicaremos la conservación de los nucleones A y la conservación de la carga Z:
218
84
4
Po 214
82 X  2 He
210
82
4
X  206
80 Hg  2 He
A.14 Igual que A.13
45
20
45
Ca  10 e    21
X
;
239
93
0
Np 239
92 U  1 e   ;
137
55
0
Cs137
56 Ba  1 e  
;
14
8
O 147N  01e  
A.15 Igual que A.13 y A.14
40
18
Ar  24He11H 1943X
11
5
B  24X 11H 146C
7
3
Li 11H  47Be 01n
A.16 Es un proceso nuclear en el que E=c2 Δm; para este proceso Δm=(mO+mH)-(mN+mHe)=1,279x10-3 u. Como
podrás observar hay un aumento de masa que necesita su equivalente cantidad de energía que normalmente es
aportada por el núcleo de Helio.
A.17 Primero calculamos la energía asociada al proceso de fisión de un núcleo de U-235 según la ecuación dada:
235
92
92
1
U  01n  36
Kr 141
56 Ba  30 n
2
23
Con la expresión E=c Δm. Pero en 1 g de U-235 hay (1/235)x6,023x10 núcleos de U-235.
A.18 Aplicamos E=c2 Δm.
EJERCICIOS PROPUESTOS EN LAS PRUEBAS DE ACCESO +25
14
1) Átomos de nitrógeno 7 N atmosférico pueden chocar con un neutrón para transformarse en
por emisión, se convierte de nuevo en nitrógeno.
1.a) Escribe las correspondientes ecuaciones nucleares.
14
6
C . A su vez, éste,
11
1.b) Los restos de animales recientes contienen mayor proporción de
qué se debe este hecho y qué aplicación tiene?
14
6
C
que los restos de animales antiguos. ¿A
2.a) Defina el concepto de isótopo.
2.b) Explique porqué el peso atómico de un elemento expresado en unidades de masa atómica no suele ser un
número entero.
3) Defina los siguientes conceptos: a) nucleones; b) número atómico; c) número másico; d) núclido; e) isótopo.
4) Una sustancia radiactiva, cuya masa inicial m0, posee al cabo de t segundos una masa m  m0  e
4.a) Calcule el periodo de semidesintegración.
4.b) Calcule el valor de m/m0 al cabo de 10 minutos.
0, 02t
.
5) El carbono 14 tiene un período de semidesintegración de 5730 años.
5.a) Calcule su constante de desintegración radiactiva.
5.b) En una mesa de madera se ha desintegrado el 30% del carbono14 que tenía cuando se fabricó. Estime la edad
de la mesa.
6.a) Enuncie la ley de desintegración radiactiva explicando el significado de cada uno de los términos que aparecen
en la misma.
-7
6.b) Se disponen de 0,2 kg de una muestra radiactiva cuya constante de desintegración vale λ=10 1/s . Calcule el
tiempo que tiene que transcurrir para que la muestra final sea de 0,05 kg.
7.a) Indique en qué consisten la fisión y la fusión nucleares.
7.b) Explique los conceptos de energía de ligadura, defecto de masa nuclear y de energía media de enlace por
nucleón.
8.a) Escribir la ley de desintegración radiactiva, explicando el significado de cada uno de sus términos.
51
8.b) Si tenemos 5x1023 átomos del isótopo Cr cuyo periodo de semidesintegración es 27 días, calcule los átomos
que quedaran después de 5 meses.
9.a) Radiactividad natural: Explique el concepto, los tipos, y la naturaleza de las radiaciones emitidas.
9.b) Los núcleos de cierto isótopo radiactivo emiten radiación alfa con un período de semidesintegración de cuatro
horas. Una muestra de ese isótopo contiene inicialmente 8,5x1016 átomos. Calcule la velocidad inicial de
desintegración y el tiempo que tiene que transcurrir para que la muestra radiactiva se reduzca a la décima parte de la
inicial.
10.a) Escribir la ley de desintegración radiactiva, explicando el significado de cada uno de sus términos. Indica
también a qué se llama la actividad radiactiva.
10.b) Se dispone en un laboratorio de 5x1015 núcleos para hacer un experimento de desintegración radiactiva. Treinta
14
días después solamente se tienen 4,7x10 núcleos, indíquese el período de semidesintegración en días.
11.a) Escribir la ley de desintegración radiactiva, explicando el significado de cada uno de sus términos. Indica
también a qué se llama la actividad radiactiva.
b) La constante de desintegración radiactiva de una sustancia vale λ=10-6 1/s. Se dispone inicialmente de 100 g de
dicha sustancia. Calcule el tiempo necesario para que la cantidad de sustancia sea 20 g.
12.a) Indique en qué consisten la fisión y la fusión nucleares.
12.b) Explique los conceptos de energía de ligadura, defecto de masa nuclear y de energía media de enlace por
nucleón.
13.a) Indique en qué consiste la radiactividad natural.
207
13.b) Los núcleos de 84 Po emiten radiación alfa con un período de semidesintegración de 2,80 h. Escriba la
ecuación nuclear del proceso de emisión y calcule el tiempo que debe transcurrir para que una muestra que contiene
ese isótopo radiactivo pierda el 75% del mismo por desintegración radiactiva.
12