termodinámica - Guzlop Editoras

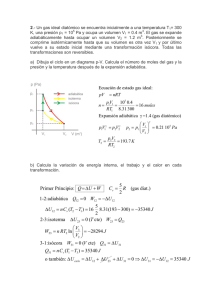
TERMODINÁMICA
PREGUNTAS
1. Si un gas se comprime isotérmicamente, explique si ingresa o sale calor del
sistema.
2. Si tenemos un gas ideal en un recipiente cerrado podemos afirmar:
a) La energía interna aumenta a medida que se comprime isobáricamente.
b) La densidad aumenta a medida que aumenta la presión isotérmicamente.
c) La energía interna aumenta a medida que se comprime isotérmicamente.
d) La densidad disminuye a medida que aumenta la temperatura isobáricamente.
(Ex. Final 2002-II)
a) FFVV
b) VVFF
c) VFVF
d) FFFV
e) FVFV
3.
Cuando un gas ideal se sujeta a un proceso adiabático, es correcto afirmar
I.
la energía interna aumenta bajo una comprensión,
II.
no hay trabajo realizado
III.
el gas se enfría si ocurre expansión
IV.
la temperatura del gas no cambia. (Ex. Sustitutorio 2002-II)
a) FFVV
b) FVFV
c) VFVF
d) VVFF
e) VFFV
4.
Dos moles de un gas ideal monoatómico realizan un ciclo de carnot entre las
temperaturas de 350ºC y 30ºC. Si en el proceso isotérmico de compresión
intercambia 20 cal con el exterior, el trabajo (J) realizado en el ciclo es:
a) 24,2
b) 33,5
c) 52,6
d) 65,7
e) 86,9
(Ex. Sustitutorio 2002-II)
5. ¿Qué es máquina térmica?, ¿tiene limitaciones?
PROBLEMAS
TRABAJO, ENERGÍA Y PRIMERA LEY DE LA TERMODINÁMICA
1. Una máquina de Carnot trabaja entre un depósito caliente a 320 K y un depósito
frío a 260ºK si absorbe 500 joules de calor del depósito caliente. ¿Qué cantidad
de trabajo rinde, si la máquina trabajando a la inversa funciona como
refrigerador entre los mismos depósitos. ¿Qué cantidad de trabajo debe
aplicársele para extraer 1000 joules de calor del depósito frío?
RPTA:a)W = 93.75 Joules, b) W = 230.77 Joules
2.
Cinco moles de un gas ideal se expanden isotérmicamente a 127 C hasta
cuadruplicar su volumen inicial. Encuentre:
a) el trabajo hecho por el gas
b) el calor transferido al sistema, ambos en joules.
Rpta: a) 23040 J ; b) 23040 J
3.
Un gas monoatómico que a la temperatura de 17 0C y a la presión de 2x105
N/m2 ocupa un volumen de 5 litros se calentó y se expandió por
isobáricamente. El trabajo de expansión del gas en estas condiciones resulto
ser igual a 200J ( CP = 5R/2). Hallar:
a) La temperatura final.
(2P)
b) La cantidad de calor intercambiado
(2P)
c) El cambio de la energía interna
(1P)
4.
Un gas ideal monoatómico, ocupa un volumen de 10x10-3 m3 a la presión
de 1x105 pascales y a la temperatura de 27° C, luego se comprime
isotérmicamente hasta que ocupe un volumen de 2 x 10-3 m3 , a continuación
se expande adiabáticamente hasta que ocupe su volumen original (R =_ 8,314
J/mol –°K) .Halle: (Ex. Sust. 2002-1)
a) Las coordenadas de estado P,V,T al final de cada proceso y haga un
diagrama PV;
b) El trabajo realizado en cada proceso y en todo el proceso
Rptas: a) A (10x10-3,1x105Pas, 300°K), B (2x10-3,5x105Pas, 300°K),
C (10x10-3,1x105Pas,300°K)
b) WAB= -1,6x103 J, WBC=9,9x102 J, WTotal= -610 J
5.
Se tienen 5 litros de un gas diatómico (γ=1.4), Cv=5/2R a la temperatura de
600°C y una presión de 20 atm. Si el gas se
expande adiabáticamente hasta 20lt. Siendo
R=0,082lt atm/mol°K. Halle:
a. El trabajo que realiza el gas
b. El cambio de su energía interna
c. Grafique P versus V.
Rpta. a) 212825x103e Joule, b) ∆U= -21,282sat-lt. (Ex.
Sust. 2003-I)
6.
Se tiene inicialmente en un tanque con embolo móvil 2 lt de aire a la presión
de 1atm y a la temperatura 27°C. Si este gas se expande
de acuerdo al grafico mostrado P-V, se pide calcular:
a) El trabajo de i hasta f.
b) El numero de moles n y la temperatura final Tf.;
c) La variación de la energía interna ∆Uif. ;
d) El calor Q recibido. (Ex. Sust. 2003-I)
Rpta: a) 800 J.; b) 0,0813 moles.; Tf = 2700°K c) 4038 J.; d)
4838 J
7.
Un mol de un gas monoatómico ideal, inicialmente a una presión de 1.000
atm y un volumen de 0.025 m3, se calienta hasta un estado final donde la
presión es de 2.000 atm y el volumen es 0.040 m3. Determine el cambio de
entropía en este proceso.
Rpta: 18.4 J/K
8.
Un mol de un gas ideal monoatómico, que ocupa 10-3 m3 a la presión
de 105 pascales, se expande isotérmicamente hasta que su volumen se
duplique, luego a partir de este punto se comprime a presión constante
hasta que alcance su volumen original, luego se comprime isotérmicamente
hasta que llegue a su presión inicial (R= 8,314 J/mol-°K). Halle: (Ex. final.
2002-1)
a) Las coordenadas de estado P, V, T al final de cada etapa y haga un diagrama
PV; b)El trabajo hecho por el gas en todo el proceso
Rpta: a) A (1x105Pa, 1x10-3m3, 12,02°K); B (0,5x105Pa, 2x10-3m3, 12,02°K)
C (0,5x105Pa, 1x10-3m3, 6,01°K); D (1x105Pa, 0,5x10-3m3, 6,01°K)
Un mol de un gas ideal monoatómico(Cv =3R/2, Cp = 5R/2 y γ = 1.67) que se
encuentra inicialmente a 300 K ocupando un volumen de 24 L, experimenta
una expansión isotérmica en la que duplica su volumen, a continuación
experimenta una compresión adiabática en la que su temperatura se eleva a
600 K. Calcular:
a) El volumen y la presión final del gas. (01 pto)
b) Representar el proceso en un diagrama P-V. (01 pto)
c) El calor cedido en el proceso completo. (1,5 pts)
d) El trabajo realizado en el proceso completo. (1,5 pts)
R = 8,31J/mol.K,
1,0 L = 10-3 m3
Rpta. a) 17,1 L; 2,88 atm. C) 1,73x103 J; d) -2,01x103 J
9.
10.
a)
b)
11.
a)
b)
Un sistema termodinámico se lleva del estado a al estado c del
siguiente modo: de a a b lo hace mediante un proceso isovolumétrico, y
de b a c mediante un proceso isobárico. El trabajo W realizado es de
450J. Si hubiera seguido otro proceso adc, de modo que ad sea un proceso
isobarico y dc isócoro el trabajo habría sido 120 J. (5P)
Trace el diagrama presión-volumen de los procesos abc y adc
Si las energías internas fueran Ua=150 J, Ub= 240J, Uc = 680J y Ud= 330J,
determine el calor (considerando el signo) para cada uno de los cuatro
procesos: ab, bc, ad y dc.
Dos moles de un gas ideal diatómico ( • =1.4 ) inicialmente están a 17°C. Se
comprime adiabáticamente a partir de un volumen de 120 litros a 80 litros. Halle:
La temperatura final
Las presiones inicial y final c.-) El trabajo realizado por el gas d.-) La variación de
la energía interna ( 5 p)
CICLOS TERMODINAMICOS Y MAQUINAS TERMICAS
12.
Se tiene 2 moles de helio, el cual se somete a los procesos indicados
en un diagrama P vs. V. Considerando
como gas ideal monoatómico:(R= 8,31
J/mol-°K)(Ex.Fi.2002-1)
a) Hallar: P, V, T en cada uno de los estados A, B y C respectivamente,
b) Hallar el calor y trabajo en cada uno de los procesos, (presente los cálculos
etc.)
c) Que eficiencia tiene una maquina térmica que funciona según este ciclo
Rpta: a)PA=2,07X105 Pa ;VA=0,024 3;TA=300°C
PB =4,15X105 Pa ; VB=0,024 m3;TB=600°C
PC =2,07X105 Pa; VC=0,048 m3;TC=600°C
b) QA-B= 7479 J ; QB-C=6000 J; Qc-a= -12465 J
WA-B= 0 j ; WB-C= 6000 j ; WCA= -4986
c) 7,4%
13.
Un gas ideal monoatómico en cantidad 2 mol efectúa el proceso mostrado, en
un diagrama P vs V, el cual consta de 4 etapas. Si pA=1,5 atm y VA=8,2 lt,
hallar:
(exa.Sus.2002-1)
a) P,V y T, en cada uno de los estados: A, B,C
y D, respectivamente.
b) ¿Qué nombre toma cada una de las etapas
del proceso?, halle la eficiencia de una
máquina térmica que opera según este ciclo.
Rpta: a) PA =1,5 at VA= 8,2 Lt TA= 75°K :
PB=3,0 at VB= 8,2 Lt TB= 150°K
PC =3,0 at VC=24,6 Lt TC= 600°K; PD =1,5
at VD=24,6 Lt TD=300 °K
b) 18%
14.
Cinco moles de un gas monoatómico experimentan un ciclo de Carnot entre
las temperaturas 27 °C y 127 °C, el volumen mínimo que ocupaban es 10 m3
y el volumen máximo es 18 m3. ( CV= 3R/2 , CP= 5R/2 , R = 8,31 J/mol-K ,
1cal = 4,186 J; γ= 5/3) Determinar: (Ex.Fin.2002-1)
a) La mayor presión y la menor presión en el ciclo
b) El volumen y la presión del sistema al final de cada proceso isotérmico
c) El calor absorbido, el calor expulsado y el trabajo efectuado
d) Si cada ciclo lo ejecuta en 0,4 s. Halle la potencia de la maquina
Rpta: a) P1=1662 Pa ; P3= 692,5 Pa ;
b)V2= 11,69 m3, P2= 1421,6 Pa ; V4=15,4 m3 , P4= 809,4 Pa
c)Q1= 2595,2 J , Q2= -1944,5 ; W= 650,7 J
d) P = 1626,75 Watts
15.
Un motor de Carnot funciona entre dos reservorios de calor a las temperaturas
de 260°C y 310°C: (Ex.Sus.2002-1)
a) Que es una maquina ideal?; b)Si en cada ciclo el motor recibe 1400 cal,
cuantas calorías por ciclo salen del sistema; c)Si cada ciclo dura 1,2 s Cual es
la potencia de la maquina?
Rpta: a) Es imposible que calor cedido por el sistema sea cero; b) 1174,1 cal;
c) 788,36 Watt
16.
Una máquina de calor contiene 0,5 moles de un gas diatómico ideal y
evoluciona según la figura mostrada. Los tramos
son: ab isovolumétrico, bc adiabático y ca isobárico;
siendo Ta = 250°K, Tb = 550°K, TC=400°K,
Pa=1,2atm. Calcular:
a)
El trabajo total efectuado en el ciclo
b)
La eficiencia del ciclo
c)
El cambio de entropía en el tramo ab.
Rpta. a) W = 311,3.
b) e = 0,1. c) ∆S = 8.18 J/ºK
17.
El diagrama p-V muestra el ciclo que realiza una masa de aire (diatómico). El
proceso de a a b es adiabático. Si Va = 10 lts. Pa = 1 atm, Ta = 300ºK y Vb= 4
lts., halle:
a)
b)
Pb y Tb.
El cambio de energía interna en el
proceso adiabático.
c) El calor que ingresa al sistema.
d) El calor que sale del sistema
e) El trabajo que realiza el gas en el ciclo
y la eficiencia.
(Ex. Final 2002-II)
Rpta. a) 3,9atm y 468 K, b) 1400J, c)
8190J, d) -7250J, e) 940J, e=0,114
18.
Un gas ideal diatómico realiza el ciclo mostrado en el diagrama p-V. Se sabe
que Ta = 300 K. Halle;
a) El trabajo realizado en el ciclo y la eficiencia del
sistema.
b) El cambio de energía interna ∆Uca y el calor Qca en el
proceso de c hasta a.
c) Cp = 7R/2, Cv = 5R/2. (Ex. Sustitutorio 2002-II)
Rpta. a) W=3x105J, e=0,082, b) Δ U=-27,5x105J, Q=33,5x105J.
19.
Un gas ideal efectúa el proceso cíclico mostrado. En el proceso abc el sistema
absorbe 4500 J de calor. La energía en a es Ua=
600J. a) Determine Uc , b) El calor neto absorbido
en el ciclo completo es 1000 J. para el proceso de
c hacia a halle el trabajo realizado por el gas y el
calor transferido, c) Si Ta , Tb y Tc son las
temperaturas en a, b y c , cual de ellas es la mayor y cuál la menor.
(Ex. Final 2003-I)
Rpta:a) 1100 J, b) 3000 J; 3500 J c) Ta< Tb < Tc
20.
Se tienen 2,34 moles de un gas ideal monoatómico que se utilizan en un ciclo
de Carnot ABCDA de un diagrama p-V. La expansión isotérmica comienza
en el punto A y algunas variables de estado se indican en la siguiente tabla.
a) Dibuje el diagrama p-V de este ciclo
P(k Pa) V(lt)
T(K)
indicando sus procesos isotérmicos y
A
1400
10,0
720
adiabáticos.
b) Calcule los valores desconocidos de p, B
C
24,0
V, T y complete la tabla indicada.
D
15,0
c) Determine la eficiencia del ciclo.
Rpta. TB= 720 K, PC=44,5kPa, TC=53 K, PD=71,2 kPa, TD= 53 K
21.
Una masa de 750 g de oxigeno (diatómico, 32g/mol de peso molecular) es
conducido por el ciclo reversible mostrado en la
figura. Las variables de estado en el punto 1 son:
p1 = 1,4 x 105 N/m2, T1 = 350 K y además se sabe
que V1 = 5 V2. El proceso de 1 a 2 es isotérmico.
R = 8,31 J/mol.K. Determine:
a) El trabajo realizado en cada proceso y en todo el
ciclo.
b) El calor entregado o expulsado en cada proceso y
en el ciclo.
c) La eficiencia del ciclo.
Rpta. a) -1,10x105 J; 2,72x105 J; 0; b) -1,10x105 J; 9,53x105 J; -6,80x105 J
22.
Un gas diatómico (γ = 1,4) es obligado a realizar el ciclo mostrado en la
figura. Si V1 = 8 lt, T1 = 300 K, p1 = 1 atm, y V2 = 3 lt , determine:
a) p2, V3 y T3.
b) El calor que ingresa y el calor que
es expulsado por el gas.
c) El trabajo en el ciclo y la eficiencia.
Rpta. a) p2 = 1,67 atm; V3 = 3,97 lt;
T3=397 K.
b) -785 J; 905 J 0
c) 120 J; 0,133
23.
Un mol de un gas diatómico describe el ciclo de la figura donde la
transformación 2-3 es isoterma. Si P1 = 4 atm; T1 = 1000 K, V2 = 2V1, V3 =
3V1. Se pide:
a) El calor transferido en cada transformación
indicando si se absorbe o se devuelve.
b) Trabajo en cada transformación y trabajo total.
c) La eficiencia del ciclo.
Rpta. a) 2,91x104 J; 6,74x103 J; -3,88x104 J; 6,93x103 J
b) 8,31 x103 J; 6,74x103 J; -1,11x104 J; 0
c) 9,23%
24.
Una maquina térmica que trabaja entre las temperaturas de 300 K y 500K,
utilizando aire (gas diatómico, γ = 1,4), realiza el ciclo de carnot abcda. La
expansión adiabática ocurre de Vb hasta Vc. Si Va = 3,35 lt, pa = 8,95 atm y pb
= 5,98 atm, se pide:
a) Realizar un esquema y describir los procesos que conforman el ciclo de
Carnot.
b) Calcular Vb, Vc, pc, y Vd.
c) Calcular el calor que ingresa y el calor que sale del sistema.
d) Hallar el trabajo cíclico y la eficiencia de la maquina.
Rpta. b) 5,01 Lt, 18,0 Lt, 1,00 atm, 12,0 Lt.
c) 1210 J, -730 J.
d) 480 J,
0,4
25.
La figura muestra el ciclo diessel, en el cual se conocen: p1
= p2 = 3 atm, V1 = 3 L, T1 = 400 K, V2 = 9 L, V3 = 12 L y
siendo aire el gas que trabaja. γ = 1,4 ; cV = 5 cal/mol.K; cp
= 7cal/mol.K. Determine:
a) T2, T3 y T4. (2pts.)
b) El calor que ingresa, el calor que sale del sistema y el trabajo
total realizado por el gas.
c) La eficiencia del ciclo.
Rpta. a) 1200 K, 1070 K, 229 K, b) 6300 J, -720 J, 5580 J.
c) 88,6%
26.
a)
b)
c)
d)
Un gas diatómico es obligado a realizar el ciclo mostrado en la figura, siendo
isotérmico el proceso de A a B y
adiabático el proceso de C a A. Se conocen
TC = 300 K, pC = 1 atm, VC = 8 lt y VA = 2
lt. Halle:
El numero de moles n, pA, TA y pB.
El trabajo que realiza el gas de C hacia A.
Los calores recibido y expulsado por el
gas.
La eficiencia e del ciclo.
Rpta. a) 0,321 moles, 6,96x105 Pa, 522 K y
1,74x105 Pa, b) -1,48x103 J, c) QAB = 1,93x103 J,
QBC = -1,48x103 J y QCA = 0
27.
Un gas ideal diatómico es obligado a realizar un ciclo de Carnot, siendo la
temperatura más alta de 450 K y la más baja de 300 K. En el diagrama p-V,
la expansión isotérmica se realiza del punto (3L, 8 atm) hasta el punto (5L,
4,8 atm).
a) Realice un diagrama p-V de este ciclo de Carnot.
b) Obtenga las variables de estado (p, V y T) de todos los procesos
termodinámicos que ocurren en el ciclo. Anótelos en un cuadro.
c) Calcule el trabajo total y la eficiencia del ciclo.
Rpta.b)
P(atm)
A
8,00
B
4,80
C
1,16
D
1,94
c) 406 J y 0,333
28.
T(K)
450
450
300
300
Dos moles de un gas ideal monoatómico evolucionan según el ciclo mostrado.
El proceso bc es adiabático. pb=9,5 atm, Vb=8,0 m3
y Vc=1,2 m3. Se pide:
La presión en el punto C
El cambio de temperatura en los tramos ca y ab
El calor absorbido, devuelto y la eficiencia del sistema.
Rpta. a) 224 atm b) 91,6x105 K y -103x105 K c)
3,80x108 J, 2,56x108 J y 0,33
a)
b)
c)
29.
a)
b)
c)
d)
30.
V(lt)
3,00
5,00
13,8
8,25
Un dispositivo de cilindro émbolo contiene vapor de agua a 200 kPa y 200 ºC
ocupando 0,5 m3. El embolo se sostiene con un resorte lineal inicialmente no
deformado. Se le transfiere calor lentamente al vapor, lo que provoca que la
presión y el volumen aumenten a 500 kPa y 0,6 m3 respectivamente. Se pide
Muestre el proceso en un diagrama p-v
la temperatura final
el trabajo efectuado por el vapor
el calor total transferido.
Rpta. b) 1,42x103 K c) 0,35x105 J d) 7,35x105 J
Una masa de gas ideal diatómico
reversiblemente el ciclo de la figura
Pa = 2·105 Pa
Va=3m3
Pb = 4·105 Pa
Vb=6m3
Pc = 2·105 Pa
Vc=6 m3
Ta=100 K
Hallar :
a) en cada uno de los procesos W, Q, Δ U
recorre
b) La eficiencia del ciclo
Rpta. a) Wab = 9,0x105 J, Wbc = 0, Wca = -6,0x105 J
Qab = 54x105 J, Qbc = -30x105 J, Qca = -21x105 J
Δ Uab = 45x105 J, Δ Ubc = -30x105 J, Δ Uca =-15x105 J
b) 0,056
31.
Se tienen inicialmente 5 litros de gas ideal diatómico, a la temperatura de
300 K y a la presión de una atmósfera
(Pto. A de la fig. ) y se le somete al ciclo
ABCA mostrado, donde el proceso de B a
C es isotérmico. Si R=0,082 atm.lt/mol.K,
halle :
a) el número de moles.
b) las temperaturas en B y en C, y el
volumen en C; respectivamente. Muestre
sus resultados en una tabla.
c) ∆U, W y Q, en el proceso CA,
respectivamente(responda en atm.lt
d) la eficiencia del ciclo.
Rpta. a) 0,203, b) TB = TC = 1800 K y VC = 30 L, c) -62,5 at-L, -25 at-L y -87,5
at-L.
32.
Cinco moles de un gas ideal monoatómico experimentan un ciclo de Carnot
entre las temperaturas de 37°C y 157°C. Determinar:
a) Las presiones en A y C en (N/m2) (1 pto)
b) El volumen VB y VD en (m3) (2 ptos)
c) El calor absorbido, el calor perdido y el trabajo
efectuado en el ciclo en joule. (2 ptos)
d) Si cada ciclo lo ejecuta en 0,5 s, determine la
potencia y la eficiencia de la máquina. (1 pto)
Rpta. a) 1,79x103 Pa y 716 Pa, b) 11 m3 y 16,3 m3, c)
1703 J, -1278 J y 425 J, d) 850 W y 0,28
33.
Se tienen 0,203 moles de gas ideal monoatómico, que efectúa el proceso
ABCA. Si en A ocupa 5 litros a la presión
de 1 atm y el proceso BC es isotérmico,
halle :
a)
las temperaturas en A, B y C,
respectivamente.
b)
En el tramo BC halle: Q, W y ∆U (en
atm.lt), respectivamente. Ayúdese con
sus datos en una tabla,
c)
la eficiencia del ciclo.
Rpta. a) 300 K, 1800 K y 1800K. b) 5,38x103 J, 5,38x103 J, 0. c) 0,304
34.
Un gas diatómico realiza el ciclo mostrado en la figura. Los procesos ab y cd
son isotérmico y adiabático respectivamente. Si Va = 4 lt, pa = 12,0 atm, Ta =
1400,0K, Vb = 10,0 lt y pd = 5,0 atm, halle:
a) Pb, Td, Tc y pc.
b) El calor que ingresa al gas en todo el ciclo (Q1) y el
calor que sale en todo el ciclo (Q2)
c) El trabajo y la eficiencia del ciclo.
Rpta. a) 4,80 atm, 583 K, 404 K y 1,39 atm, b) 11,4x103 J y
-8,53x103 J, c) 2,8x103 J y 0,25
35.
Un ciclo es seguido por 2 moles de un gas ideal diatómico, cuyo estado inicial
es 1(p1=3 atm, V1=1 m3, T1), pasa a estado 2 en proceso isobárico duplicando
el volumen, a continuación la presión llega a los 2/3 de la anterior en un
proceso isotérmico, luego en forma isobárica retorna al volumen inicial, y por
último regresa al estado inicial con un proceso isócoro. Graficando los
procesos en un diagrama p vs V, se pide :
a) Elabore una tabla que presente los valores de: p, V, T, y U, en cada una de
las esquinas del ciclo; respectivamente.
b) Escoger un proceso y halle cada termino de la 1ª ley, ¿se cumple?,
c) La eficiencia de una máquina térmica que usa este ciclo.
Rpta. b) W12 = 3x105J; Q12 = 1,05x106; ∆U = 7,5x105 J c) 0,0933
36.
Una maquina térmica ideal que funciona según el ciclo de Carnot recibe del
foco caliente 600 cal cada ciclo. La temperatura del foco caliente es de 127 0C
y la del foco frió de 80,6 0 C
a) Dibujar en el diagrama P-V el ciclo.
(1P)
b) Hallar el trabajo que realiza la maquina en cada ciclo. (2P)
c) La cantidad de calor cedido en cada ciclo.
(1P)
d) La eficiencia o rendimiento de la maquina en cada ciclo. (1P)
Rpta. b) 69,6 cal, c) 530 cal, d) 0,116
37.
Una maquina de gas ideal monoatómico (CV = 3R/2) realiza un ciclo
constituido por cinco procesos: El proceso de A-B es isócoro donde VA = 0,5
L, PA = 1 atm y
PB = 12 atm; el proceso de B-C es una expansión
isobárica donde VC = 0,5 L; el proceso de C-D es una expansión adiabática
a)
b)
c)
d)
donde VD = 3,0 L; el proceso de D-E es un enfriamiento isócoro donde PE =
PA y finalmente el proceso E-A es una compresión isobárica.
Dibujar en el diagrama P-V el ciclo completo.
(1P)
Determinar el trabajo que realiza la máquina en cada ciclo.
(2P)
La cantidad de calor absorbido por la máquina en cada ciclo. (2P)
La eficiencia de la máquina.
(1P)
38. Un mol de gas, inicialmente a una presión de 2at y a un volumen de 0.3L tiene
una energía interna de 91 J. En un estado final de
presión es de 1.5at, el volumen de 0.8L y la
energía interna de 182 J. Para los tres caminos
IAF, IBF, IF de la figura halle:
a) El trabajo realizado por el gas.
(2p)
b) El calor neto transferido en cada proceso. (3p)
39. En un ciclo de Carnot, la expansión isotérmica de un mol de un gas ideal
diatómico tiene lugar a 412ºk y la compresión isotérmica a 297ºk. Durante la
expansión isotérmica se transfiere al gas 2090 J de energía calorífica.
Determine:
a)
El trabajo realizado en cada proceso. (1p)
b)
El calor liberado por el gas en J. (2p)
c)
El trabajo neto y la eficiencia del ciclo. (2p)
40. Cinco moles de un gas ideal monoatómico
experimentan un ciclo de Carnot entre las
temperaturas de 37°C y 157°C, según el
grafico que se muestra. Determinar:
a) El volumen Vc y Vd en (m3) (2p)
b) El calor absorbido, el calor perdido y el
trabajo efectuado en el ciclo en joule.
(2p)
c) Si cada ciclo lo ejecuta en 0,5 s,
determine la potencia y la eficiencia de la
máquina. (1p)
P(Pa)
a
b
d
c
0
10
11
41. Dos moles de un gas ideal monoatómico se expande en forma adiabática desde
un volumen de 10 litros y 12 atmósferas de presión, hasta un volumen de 50
litros, a continuación el gas se comprime a presión constante hasta un volumen
de 10 litros y después se hace aumentar su presión a volumen constante,
volviendo al punto inicial.
a) Graficar el diagrama P- V
b) Hallar el trabajo neto en el ciclo
c) Hallar el calor absorbido por el gas en el ciclo
V(m3 )
d) Hallar la eficiencia del ciclo.
Cp = (5/2 ) R Cv = (3/2) R
γ = 5/3
1cal =4.18 J
R = 0,082 atm-lt/mol °K 1 atm = 100 J
42. Una maquina térmica funciona según el ciclo de la figura. La sustancia de
trabajo es un gas ideal monoatómico (γ = 5/3 = 1,67). Si V1 = 8 L, T1 = 300 K,
P1 = 1 atm, y V2 = 3 L, determine:
a)
P2, V3 y T3. (1 pto)
b)
El calor que ingresa y el calor que es expulsado
por el gas en el ciclo. (02 pts)
c)
El trabajo en el ciclo y la eficiencia de la
máquina (02 pts)
d)
(puede considerar 1 atm = 1x105 Pa, 1L = 10-3
m3, R = 8,315 J/mol.K)
43.
a)
b)
Se tiene 10 litros de un gas diatómico a 27 0 C y
una atmósfera de presión. Si se comprime
adiabáticamente hasta 3 litros, luego se expande a presión constante hasta un
volumen final de 10 litros .R = 8,31J / mol 0 k , calcule:
El cambio de temperatura en la compresión adiabática.(3p)
El cambio de energía interna y el trabajo en cada proceso.(2p)
44.
Un mol de un gas monoatómico ideal
experimenta el ciclo reversible mostrado.
a) Si la temperatura en a es de 200ºK, encuentre
las temperaturas en b,c y d. (2p)
b) b) Halle el calor absorbido de a → b . (2p)
c) En que tramos el gas absorbe calor y en que
tramos el gas expulsa calor (1p)
Con las presiones P = 100,0 kpa , 2p = 200,0
kpa , con los volúmenes V = 22,0 dm 3 y 2V=44,0
dm 3 .
45. Una máquina térmica opera empleando el ciclo
de la figura. La sustancia de trabajo es 0,350 moles de un gas diatómico con
comportamiento ideal. El proceso 1-2 es isovolumétrico, el proceso 2-3 es
adiabático y el proceso 3-1 isobárico.
a) Calcule la presión y el volumen en los
estados 1,2 y 3.
b) Calcule Q, W y Δ U para cada uno de los
tres procesos.
c) Calcule el trabajo neto efectuado por el
gas en el ciclo.
d) Calcule el flujo neto de calor hacia la
maquina en el ciclo.
e) Determine la eficiencia térmica de la
máquina y compárela con la de Carnot
que opera entre las mismas temperaturas mínima y máxima T1 y T2.
46. Dos moles de un gas diatómico que se encuentran inicialmente a una presión de
4,00x105 Pa y a una temperatura de 300 K. Se llevan a través del siguiente ciclo
reversible:
• Se expande isotérmicamente hasta que su volumen se duplica.
• Se comprime hasta su volumen original a presión constante.
• Se comprime isotérmicamente hasta una presión de 4,00x105 Pa, y
• Se expande a presión constante hasta su volumen original.
a) Construya una gráfica exacta del proceso cíclico en un diagrama PV.
b) Determine P, V y T para cada uno de los estados involucrados y ordénelos en
una tabla.
c) Determine Q, W y ∆U para cada uno de los procesos.
d) Determine la eficiencia de esta maquina térmica.
47. Un gas ideal es sometido a las siguientes transformaciones representadas.
a) Calcular el valor de las variables P, V, T en los estado 2,3 y 4.
b) Cuál es el trabajo neto realizado por el gas.
RPTA:
a) P2 = 6at V2 = 5lt,
T2 = 500 K
P3 = 3at, V3 = 5lt,
T3 = 250 K
P4 = 3at, V4 = 3lt,
T4 = 150 K
a) W = 600 J
48. Un mol de un gas ideal monoatómico realiza un ciclo de Carnot,
entre las temperaturas de 600 k y 300 k. En el proceso isotérmico de
expansión, el volumen aumenta de 2 litros hasta 5 litros. Calcule:
a) Las coordenadas de estado y haga un gráfico P-V
b) El trabajo en cada etapa y en el ciclo
c) el calor en cada etapa y en el ciclo
d) la eficiencia del gas.
Rpta: PA =24,60 atm;
VA = 2,00 Lt
TA= 600°K
PB = 9,84 atm
VB = 5,00 Lt
TB= 600°K
PC = 1,86 atm
VC = 14,14Lt
TC= 300°K
PD = 4,66 atm
VD = 5,65 Lt
TD= 300°K
49. En el ciclo que se muestra en la figura, un mol de un gas ideal (• = 7/5 =1,4; Cv
= 5R/2; R = 8,31 J/mol.K) se encuentra inicialmente en el estado1, a P1 = 1,00x
105 Pa y T1 = 300 K. El gas se calienta a volumen constante hasta el estado 2
donde T2 = 420 K y luego se expansiona adiabáticamente hasta el estado 3 en
que su presión vuelve a ser igual P1. Luego
se comprime a presión constante hasta su
estado original. Calcular:
a) La temperatura T3 en el estado 3. (2pts)
b) El calor absorbido o cedido en cada uno de
los procesos que conforman el ciclo. (2pts)
c) El rendimiento del ciclo. (1pto)
50. Un gas ideal monoatómico se lleva por el ciclo reversible que indica la figura.
La temperatura en el estado A es de 300 K.
Calcule para los tramos BC y CA:
a) Variación de energía interna
b) Calor y trabajo