Formalización de los Números Reales

Formalización de los Números Reales
M. en I. Gerardo Avilés Rosas
Agosto de 2016
Tema 2
Formalización de los Números Reales
Objetivo: El alumno aplicará las propiedades de los números reales y sus subconjuntos, para
demostrar algunas proposiciones por medio del método de Inducción Matemática y para
resolver inecuaciones.
Contenido
2.1 El conjunto de los números naturales
Concepto intuitivo de número natural
Definición del conjunto de los números naturales mediante los postulados de Peano
Definición y propiedades: adición, multiplicación y orden en los números naturales.
Demostración por Inducción Matemática
2.2 El conjunto de los números enteros
Definición a partir de los números naturales
Definición y propiedades: igualdad, adición, multiplicación y orden en los enteros.
Representación de los números enteros en la recta numérica
2.3 El conjunto de los números racionales
Definición a partir de los números enteros
Definición y propiedades: igualdad, adición, multiplicación y orden en los racionales
Expresión decimal de un número racional
Algoritmo de la división entre enteros
Densidad de los números racionales y representación de éstos en la recta numérica
2.4 El conjunto de los números reales
Existencia de números irracionales (algebraicos y trascendentes)
Definición del conjunto de los números reales
Representación de los números reales en la recta numérica
Propiedades: adición, multiplicación y orden en los reales.
Completitud de los reales
Definición y propiedades del valor absoluto
Resolución de desigualdades e inecuaciones
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
2
El conjunto de los números naturales
2.1 El conjunto de los números naturales
2.1.1 Definición: Postulados de Peano
El conjunto N de los números naturales es tal que:
i)
ii)
iii)
iv)
v)
1N
Para cada n  N existe un único n*  N, llamado el siguiente de n
Para cada n  N se tiene que n* ≠ 1
Si m, n  N y m* = n*, entonces m = n
Todo subconjunto S de N que tenga las propiedades:
a. 1  S
b. Para toda k  S implica que k*  S
es el mismo conjunto N
Definición y propiedades
Adición en N
2.1.2 Definición
Sean m, n  N entonces:
i) n + 1 = n*
ii) n + m* = (n + m)*
La adición, así definida, satisface las siguientes propiedades:
2.1.3 Teorema
Para todo m, n, p  N:
i)
ii)
iii)
iv)
m+nN
m + (n + p) = (m + n) + p
m+n=n+m
Si m + p = n + p, entonces m = n
Cerradura
Asociativa
Conmutativa
Cancelativa
Multiplicación en N
2.1.4 Definición
Sean m, n  N entonces:
i) n ∙ 1 = n
ii) n ∙ m* = (n ∙ m) + n
La multiplicación, así definida, satisface las propiedades que se resumen a continuación:
2.1.5 Teorema
Para todo m, n, p  N:
i)
ii)
iii)
iv)
m∙nN
m ∙ (n ∙ p) = (m ∙ n) ∙ p
m∙n=n∙m
Si m ∙ p = n ∙ p, entonces m = n
Cerradura
Asociativa
Conmutativa
Cancelativa
Tomadas simultáneamente, las operaciones de adición y multiplicación satisfacen la siguiente
ley distributiva:
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
3
El conjunto de los números naturales
2.1.6 Teorema
Para todo m, n, p  N:
m ∙ (n + p) = (m ∙ n) + (m ∙ p)
Orden en N
2.1.7 Definición
Dados dos números naturales n y m, decimos que n es menor que m, lo que representamos
mediante
n < m, si:
∃ x ∈ N tal que n + x = m
Los números naturales satisfacen la siguiente propiedad, llamada ley de la tricotomía.
2.1.8 Teorema
Si m y n son dos números naturales cualesquiera, entonces se verifica una y sólo una de las
siguientes proposiciones:
i)
ii)
iii)
n<m
n=m
m<n
2.1.9 Teorema
Para todo m, n, p ∈ N:
i)
ii)
iii)
m<nm+p<n+p
m < n  mp < np
m<nyn<pm<p
2.1.10 Definición
Dados dos números naturales m y n, decimos que m es mayor que n, lo que representamos
mediante
m > n, si n < m
El proceso de una demostración por inducción matemática consiste en los siguientes pasos:
i) Escribir claramente la proposición P ( n ) cuya validez quiere demostrarse, especificando
la variable de inducción y el conjunto de valores que puede asignarse a dicha variable,
la variable contenida en el paréntesis de P ( ) , denota la variable de inducción.
ii) Si P ( n ) es una proposición enunciada para todos los números naturales, se debe
verificar el cumplimiento de la proposición para el menor valor de n (esto equivale a
verificar que el 1 pertenece a S, según el quinto postulado de Peano).
iii) Demostrar que si P(k ) es verdadera, entonces P (k  1) es verdadera (esto equivale a
demostrar que si k  S entonces k  1  S de acuerdo con el quinto postulado de Peano)
Cuando ii) y iii) se cumplen, se concluye que P ( n ) es verdadera para todo n en el conjunto
de los números naturales.
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
4
El conjunto de los números naturales
Ejemplo. Demostrar por el método de inducción matemática
1 2  3  ...  n 
n  n  1
2
;
 n N
i) Escribiendo claramente la proposición tenemos:
P  n  1 2  3  ...  n 
n  n  1
2
;
 n N
Término enésimo
Variable
de
Inducción
Conjunto
de validez
PROPOSICIÓN
ii) Verificamos si P 1 es verdadero
P 1 :
1
11 1
2
1 1

Por lo tanto P 1 es verdadera
iii) Suponemos que P(k ) es verdadera (hipótesis de inducción) y se tiene que demostrar la
validez de P (k  1) (tesis del problema)
P  k   1 2  3  ...  k 
k  k  1
...(1) Hipótesis
2
P  k  1  1 2  3  ...  k  (k  1) 
(k  1) k  2 
2
…(2) Tesis
Al analizar la expresión (2) nos damos cuenta de que:
1 2  3  ...  k  (k  1) 
(k  1) k  2 
2
P(k)
Sustituyendo (1) en (2):
k  k  1
2
 (k  1) 
(k  1) k  2 
2
Desarrollando el lado izquierdo tenemos:
k  k  1  2(k  1)
2
2

(k  1) k  2 
2
(k  1) k  2 
k  k  2k  2

2
2
k2  3k  2 (k  1) k  2 

2
2
(k  1) k  2  (k  1) k  2 

2
2
... Q.E.D
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
5
El conjunto de los números enteros
2.2 El conjunto de los números enteros
Definición a partir de los números naturales. La diferencia de números naturales
2.2.1 Definición
Sea la ecuación
n + x = m;
con m, n ∈ N
A su solución; es decir, al número x que sumando a n nos da como resultado m, lo llamaremos
la diferencia m – n.
De acuerdo a lo anterior, a los números que se obtienen mediante la diferencia de dos
números naturales les llamaremos números enteros y al conjunto que forma lo
representaremos con Z. Esto es:
2.2.2 Definición
Z = {x | x = m – n; m, n ∈ N}
Es claro que el subconjunto Z+ de Z, definido por: Z+={x | x = m – n; m, n ∈ N; m > n}
Se le conoce como conjunto de los enteros positivos y es precisamente el conjunto de los
números naturales, por lo que N  Z.
Definición y propiedades
Igualdad en Z
2.2.3 Definición
Sean a = m – n, b = p – q dos números enteros, con m, n, p, q ∈ N. Entonces:
a = b sí m + q = n + p
Adición en Z
Como N  Z, la adición en Z debe producir los mismos resultados que la adición en N cuando
los enteros que se suman son positivos, lo que conduce a la siguiente definición:
2.2.4 Definición
Sea a = m – n, b = p – q dos números enteros, con m, n, p, q ∈ N. El número a + b se define
como:
a + b = (m + p) – (n + q)
Cabe mencionar que la adición en Z satisface todas las propiedades establecidas para la
adición en N, sin embargo, la adición en Z cuenta con otras propiedades adicionales:
2.2.4 Teorema
Para todo a, b, c ∈ Z:
i)
ii)
iii)
iv)
v)
vi)
a+b∈Z
a + (b + c) = (a + b) + c
a+b=b+a
Sí a + c = b + c, entonces a = b
a+0=a
∃ –a ∈ Z tal que a + (–a) = 0
cerradura
asociatividad
conmutatividad
cancelación
elemento idéntico
elemento inverso
A partir de la adición y de la propiedad vi) del teorema 2.2.2 se puede definir la sustracción:
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
6
El conjunto de los números enteros
2.2.5 Definición
Sean a, b ∈ Z, el número a – b se define como:
a – b = a + (–b)
Multiplicación en Z
Similar a como se hizo para la adición, la multiplicación en Z puede definirse como sigue:
2.2.6 Definición
Sean a = m – n, b = p – q dos números enteros, con m, n, p, q ∈ N. El número a  b se define
como
a  b  (m  p  n  q)  (n  p  m  q)
La multiplicación, así definida, satisface las propiedades enunciadas a continuación.
2.2.7 Teorema
Para todo a, b, c ∈ N
i)
ii)
ab ∈ Z
a   b  c   a  b  c
cerradura
asociatividad
iii)
iv)
v)
ab  ba
Sí a  c  b  c y c  0 , entonces a = b
conmutatividad
cancelación
elemento idéntico
a 1 a
Tomadas simultáneamente, la adición y la multiplicación satisfacen la siguiente propiedad
distributiva
2.2.8 Teorema
Para todo a, b, c ∈ Z
a   b  c  a  b  a  c
La introducción del cero y los negativos trae como consecuencia la aparición de algunas
propiedades adicionales para la multiplicación en Z:
2.2.9 Teorema
Para todo a, b ∈ Z
vi) a  0  0
vii) (a)  (b)  (a  b)
viii) (a)  (b)  a  b
primera regla de los signos
segunda regla de los signos
Orden en Z
Para los números enteros podemos también definir la relación “menor que”, como una
generalización de la que hemos definido para los naturales
2.2.10 Definición
Sea a, b ∈ Z:
i)
ii)
a < b si ∃ n ∈ N tal que a + n = b
a > b si b < a
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
7
El conjunto de los números enteros
Los números enteros también satisfacen la ley de la tricotomía enunciada para los números
naturales y la relación “menor que” tiene en Z las siguientes propiedades.
2.2.11 Teorema
Para todo a, b, c ∈ Z
i)
ii)
iii)
a<ba+c<b+c
a < b y c > 0  ac < bc
a < b y c < 0  ac > bc
a<byb<ca<c
Representación de los números enteros en la recta numérica.
Como ahora la recta se extiende en ambos sentidos no tiene un punto inicial, como sucede
para los números naturales, por lo que se considera como punto de referencia el punto que
representa al cero. Los números que se encuentran representados a la derecha de dicho
punto se dice que son positivos y a los que están a la izquierda negativos.
2.2.12 Definición
Sea a ∈ Z
a es positivo si a > 0
a es negativo si a < 0
En particular el cero no es positivo ni negativo.
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
8
El conjunto de los números racionales
2.3 El conjunto de los números racionales
El cociente de números enteros
2.3.1 Definición
Sea la ecuación:
bx = a;
con
a, b ∈ Z
A su solución, le llamaremos el cociente de a entre b y lo representaremos con
a
. A los
b
números que se obtienen como el cociente de dos números enteros a, b con b ≠ 0 les
llamaremos números racionales y al conjunto que forman lo representaremos con Q. Esto es:
2.3.2 Definición
Q = {x | x =
a
, a, b ∈ Z, b ≠ 0}
b
Es claro que el subconjunto de Q definido por {x | x =
a
, a, b ∈ Z, b = 1} es precisamente el
b
conjunto de los números enteros, por lo que Z ⊂ Q
Definición y propiedades
La igualdad en Q
La forma más común de trabajar con los números racionales es en forma de quebrados. En
a
es un número racional con a, b ∈ Z y b > 0, y el último factor común de a y b
b
a
es el número uno, decimos que
es la mínima expresión del racional x. De acuerdo con lo
b
a c
anterior, resulta natural considerar que dos números racionales
y
son iguales cuando:
b d
general, si x =
2.3.3 Definición
Sean
a c
,
dos números racionales con a, b, c, d ∈ Z y b, d ≠ 0, entonces
b d
a c
=
b d
si
ad = bc
la cual establece la igualdad de números racionales en términos de la igualdad de números
enteros.
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
9
El conjunto de los números racionales
La adición en Q
2.3.4 Definición
Sean
a c
a c
,
dos números racionales, donde a, b, c, d ∈ Z y b, d ≠ 0. El número
+
se define
b d
b d
como
a c ad  bc
+
=
b d
bd
La adición en Q, así definida, tiene las propiedades que se enuncian a continuación:
2.3.5 Teorema
Para todo x, y, z ∈ Q:
i)
ii)
iii)
iv)
v)
vi)
x+y∈Q
x + (y + z) = (x + y) + z
x+y=y+x
si x + z = y + z, entonces x = y
x+0=x
∃ −x ∈ Q tal que x + (−x) = 0
cerradura
asociatividad
conmutatividad
cancelación
elemento idéntico
elementos inversos
La sustracción en Q puede definirse ahora a partir de la adición y de vi) de la siguiente manera
2.3.6 Definición
Sean
a c
a c
,
∈ Q, el número −
se define como
b d
b d
a c a c
−
=
+
b d b
d
Como consecuencia de i), la sustracción es cerrada en Q; esto es ∀ x, y ∈ Q: x – y ∈ Q
La multiplicación en Q
2.3.7 Definición
Sean
a c
a c
,
dos números racionales, donde a, b, c, d ∈ Z y b, d ≠ 0. El número • se define
b d
b d
como
a c
ac
•
=
b d bd
La multiplicación en Q, así definida, satisface las propiedades que se establecen en el
siguiente teorema:
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
10
El conjunto de los números racionales
2.3.8 Teorema
Para todo x, y, z ∈ Q:
i)
ii)
iii)
iv)
v)
vi)
xy ∈ Q
x(yz) = (xy)z
xy = yx
si xz = yz y z ≠ 0, entonces x = y
x•1 = x
si x ≠ 0 ∃ x−1 ∈ Q tal que x x−1 = 1
cerradura
asociatividad
conmutatividad
cancelación
elemento idéntico
elemento inverso
Al número x−1 se le denomina el inverso de x para la multiplicación. Cabe enfatizar aquí que
todo número racional, con excepción del cero, tiene un inverso multiplicativo en Q.
La división en Q puede definirse ahora a partir de la multiplicación y de vi) de la siguiente
manera
2.3.9 Definición
Sean
a c
c
,
dos números racionales y
≠0
b d
d
El número
a c
÷
se define como
b d
a c
a
d
÷
=
•
b d
b
c
Como consecuencia de i), la división en Q satisface la siguiente propiedad
∀ x, y ∈ Q, y ≠ 0: x ÷ y ∈ Q
Por otra parte, puede demostrarse que los teoremas 2.2.8 y 2.2.9 también son válidos para los
números racionales; esto es
2.3.10 Teorema
Para todo x, y, z ∈ Q
x(y + z) = xy + xz
2.3.11 Teorema
Para todo x, y ∈ Q
i) x • 0 = 0
ii) (−x)(y) = −(xy)
iii) (−x)(−y) = xy
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
11
El conjunto de los números racionales
Orden en Q
2.3.12 Definición
Sean
a c
,
∈ Q, donde b, d ∈ Z+:
b d
a c
si ad < bc

b d
a c
c a
ii)
si


b d
d b
i)
Como consecuencia de esta definición y de la ley de tricotomía en Z, la relación “menor que”
en Q satisface también dicha ley, así como las siguientes propiedades.
2.3.13 Teorema
Para todo x, y, z ∈ Q:
i)
ii)
iii)
x<y⇒x+z<y+z
x < y y z > 0 ⇒ xz < yz
x < y y z > 0 ⇒ xz > yz
x<yyy<z⇒x<z
Similar a la manera como se definió en Z, diremos que un número x ∈ Q es positivo si x > 0 y es
negativo si x < 0.
Expresión decimal de un número racional
Todo número racional tiene una expresión decimal, por ejemplo
3
 0.375,
8
7
 0.212121...,
33
149
 1.12878787...
132
Se dice que una expresión decimal es periódica cuando un dígito, o un grupo de dígitos, se
repiten indefinidamente a partir de un cierto lugar a la derecha del punto decimal. En general,
respecto a la expresión decimal de un número racional podemos establecer el siguiente
enunciado.
2.3.14 Teorema
Todo número racional tiene una expresión decimal periódica.
2.3.15 Teorema
Toda expresión decimal periódica representa a un número racional.
Consideremos la expresión decimal
1.27242424…
Buscamos dos números enteros a, b tales que
a
 1.27242424...
b
Como tenemos dos dígitos antes de presentarse el período por primera vez, multiplicamos por
102 para obtener:
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
12
El conjunto de los números racionales
10 2
a
 127.242424...
b
(i)
En vista de que el período consta de dos dígitos, multiplicamos la expresión (i) por 102 para
obtener:
(10 2 )(102 )
a
 12724.2424...
b
(ii)
Puesto que la parte decimal de estas dos últimas expresiones en la misma, restamos (i) de (ii)
para obtener un número entero; esto es:
a
a
 102  12724  127
b
b
a
104  102
 12597
b
a
9900  12597
b
104


por lo que
a 12597 4199


b 9900 3300
Algoritmo de la división en los enteros
2.3.16 Teorema (Algoritmo de la división para números enteros)
Dados dos números enteros a y b, con b > 0, existen dos enteros únicos q y r, con 0 ≤ y < b,
tales que
a = bq + r
Los números a, b, q y r ∈ Z reciben el nombre de dividendo, divisor, cociente y residuo
respectivamente. La relación a = bq + r, que está planteada en términos de números enteros
exclusivamente, puede ser enunciada en Q como:
a
r
 q
b
b
expresión que nos recuerda la forma como llevamos a cabo el proceso de dividir en
aritmética; esto es, obteniendo el cociente y un residuo.
Consideremos un número racional positivo
a
, con a, b > 0:
b
1. Por el algoritmo de la división para enteros, existen
q0, r0 ∈ Z tales que
a = bq0 + r0, donde 0 ≤ r0 < b
entonces
r
a
 q0  0
b
b
2. Ahora, como r0 ∈ Z, tenemos que 10r0 ∈ Z y existen q1, r1 ∈ Z tales que
10r0 = bq1 + r1, donde 0 ≤ r1 < b
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
13
El conjunto de los números racionales
r0 q1
r

 1
b 10 10  b
q
r
a
entonces
 q0  1  1
b
10 10  b
por lo que
3. Ahora, como r1 ∈ Z, tenemos que 10r1 ∈ Z y existen q2, r2 ∈ Z tales que
10r1 = bq2 + r2, donde 0 ≤ r2 < b
r1
q
r
 22  2 2
10  b 10 10  b
q
q
r
a
entonces
 q0  1  22  2 2
b
10 10 10  b
por lo que
4. Ahora, como r2 ∈ Z, tenemos que 10r2 ∈ Z y existen q3, r3 ∈ Z tales que
10r2 = bq3 + r3, donde 0 ≤ r3 < b
q
r
r2
 33  3 3
10  b 10 10  b
q
r
q
q
a
entonces
 q0  1  22  33  3 3
b
10 10 10 10  b
por lo que
2
En consecuencia, la expresión decimal de
a
será
b
a
 q0 q1q2 q3 ...
b
El proceso puede continuarse indefinidamente; sin embargo, como los residuos r0, r1, r2, r3, …
son números enteros tales que 0 ≤ r1 < b, a lo más, podrán existir b residuos diferentes. Cuando
alguno de los residuos obtenidos se presenta por segunda vez, se inicia el segundo ciclo del
período, el cual se repite indefinidamente.
Si
a
a
a
a
es negativo, entonces escribimos
, donde
es positivo y por tanto tiene una

b
b
b
b
expresión decimal periódica.
Densidad de los números racionales
Los números racionales poseen una propiedad conocida como densidad, según la cual entre
dos números racionales diferentes siempre hay otro número racional, como lo establece el
siguiente teorema.
2.3.17 Teorema
Para todo x, y ∈ Q, con x < y, ∃ z ∈ Q tal que:
x<z<y
Cabe hacer notar que los números naturales y los números enteros no poseen la propiedad
de densidad.
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
14
El conjunto de los números reales
2.4 El conjunto de los números reales
Existencia de los números irracionales (algebraicos y trascendentes)
Los números racionales tienen representación en la recta
numérica, y en virtud de la densidad de Q podría pensarse
que estos son suficientes para “llenar” la recta; es decir,
que todos los puntos de la recta correspondan a algún
número racional, lo cual es falso. Desde la antigüedad los
geómetras griegos se dieron cuenta de que no todos los
puntos de la recta corresponden a números racionales.
Existen muchos números que tienen representación en la
recta numérica y no son racionales. A este tipo de números se les conoce como números
irracionales, los cuales no tienen expresión decimal periódica, característica que los distingue
de los números racionales.
Los números irracionales pueden ser de dos tipos; los que son solución de alguna ecuación
2 ) a los que se les llama irracionales
algebraica con coeficientes enteros (como
algebraicos; y los que no son solución de una ecuación de tal tipo, a los que se les llama
irracionales trascendentes. Como ejemplo de estos últimos tenemos a los números π y e de
relevante importancia en las matemáticas.
Definición del conjunto de los números reales
Al conjunto que contiene tanto a los números racionales como a los números irracionales se
le conoce como el conjunto de los números reales y se le representa con R.
Al conjunto de los números irracionales se le representa comúnmente con Q’, por lo que
podemos escribir
R = Q ∪ Q’
∅ = Q ∩ Q’
y se cumple además que:
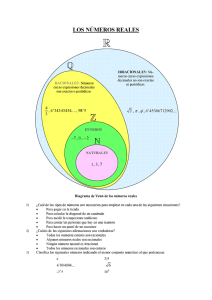
N⊂Z⊂Q⊂R
Propiedades: adición, multiplicación y orden en los reales
2.4.3 Teorema
Para todo x, y, z ∈ R:
i)
ii)
iii)
iv)
v)
vi)
x+y∈R
xy ∈ R
x + (y + z) = (x + y) + z
x(yz) = (xy)z
x+y=y+x
xy = yx
x+0=x
x•1=x
∃ −x ∈ R tal que x + (−x) = 0
∃ x−1 ∈ R tal que x x−1 = 1, si x ≠ 0
x(y + z) = xy + xz
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
cerradura
asociatividad
conmutatividad
elemento idéntico
elementos inversos
distributividad
15
El conjunto de los números reales
2.4.4 Teorema
Para todo x, y ∈ R:
i)
ii)
iii)
x•0=0
(−x)(y) = −(xy)
(−x)(−y) = xy
A partir del teorema 2.4.3 pueden también definirse las operaciones de sustracción y división
en R como sigue:
2.4.5 Definición
Para todo x, y ∈ R:
i)
ii)
El número x – y se define como: x – y = x + (–y)
Si y ≠ 0 el número x ÷ y se define como x ÷ y = xy−1
Orden en R
2.4.6 Teorema
Si x, y ∈ R entonces se verifica una y sólo una de las siguientes proposiciones:
i)
ii)
iii)
x<y
x=y
y<x
2.4.7 Teorema
Para todo x, y, z ∈ R:
i)
ii)
iii)
x<y⇒x+z<y+z
x < y y z > 0 ⇒ xz < yz
x < y y z < 0 ⇒ xz > yz
x<yyy<z⇒x<z
También se definen en R la relación “mayor que” y los términos “positivo y negativo”, de la
misma manera que se definen en Q, es decir:
i)
ii)
iii)
x > y si y < x
x es positivo si x > 0
x es negativo si x < 0
Completitud de los reales
Los teoremas 2.4.3 al 2.4.7 nos muestran que los sistemas de los números reales tienen las
mismas propiedades algebraicas y de orden que en el sistema de los números racionales; sin
embargo, sabemos que el sistema de los números reales es más amplio y más versátil, puesto
que en R podemos resolver ecuaciones para las cuales no existe solución en Q.
2.4.8 Definición
Sea S un subconjunto de R. Un elemento t ∈ R es una cota superior de S si:
x ≤ t, ∀ x ∈ S
Entonces, si t es una cota superior de S, cualquier otro número real mayor que t será también
una cota superior de S. Si un conjunto tiene cota superior se dice que está acotado
superiormente.
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
16
El conjunto de los números reales
2.4.9 Definición
Sea S un subconjunto de R. Un elemento m ∈ R se llama elemento máximo de S si:
i)
ii)
x ≤ m, ∀ x ∈ S; y
m∈S
lo que denotamos mediante max S = m
Es decir, un elemento es máximo de un conjunto S si es una cota superior de S y además
pertenece a S.
A diferencia de las cotas superiores, el elemento máximo de un conjunto, si existe, es único. El
elemento máximo de un conjunto es la menor de sus cotas superiores. Es posible, sin embargo,
hallar conjuntos acotados superiormente para los cuales no existe elemento máximo. Para
tales conjuntos se tiene un concepto que sustituye al de máximo en el sentido de la menor de
las cotas superiores. Tal concepto es el de supremo, que se define a continuación.
2.4.10 Definición
Sea S un subconjunto de R. Un elemento p ∈ R se llama supremo de S si:
iii)
iv)
x ≤ p, ∀ x ∈ S; y
q ∈ R y x ≤ q; ∀ x ∈ S ⇒ p ≤ q
lo que denominamos mediante sup S = p
Es decir; un elemento p es supremo de un conjunto S si p es una cota superior de S y ningún
número menor que p es cota superior de S. El supremo de un conjunto, si existe, es único.
Cabe resaltar aquí que la única diferencia entre los conceptos de elemento máximo y
supremo de un conjunto S, estriba es que el máximo debe ser un elemento del conjunto S,
mientras que el supremo puede ser un elemento de S o no serlo.
2.4.11 Teorema (Completitud de R)
Todo subconjunto no vacío de R que está acotado superiormente tiene un supremo que
pertenece a R.
Este teorema no garantiza la existencia de una mínima cota superior para cualquier conjunto
de números reales acotado superiormente, y establece además que la mínima cota es un
número real, es decir, que pertenece a R.
Definición y propiedades del valor absoluto
2.4.12 Definición
Sea x un número real. El valor absoluto de x, que representaremos con x , se define como:
 x, sí x  0
x 
 x, sí x  0
En general, el valor absoluto de x ∈ R será un número real no negativo, es decir, positivo o
cero. Las principales propiedades del valor absoluto se enumeran en el siguiente teorema:
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
17
El conjunto de los números reales
2.4.13 Teorema
Para todo x, y ∈ R
i)
x ≥ 0. Además x = 0 ⇔ x = 0
ii)
xy = x • y
iii)
xy  x  y
A partir de la definición 2.4.12 y de la representación de los números reales como puntos de
la recta, se observa que mientras más grande es x , más lejos del origen se encuentra el punto
que representa a x. debido a esto, al número x se conoce como la distancia de x al centro.
De acuerdo con lo anterior, si α es un número real positivo, se tendrá que un punto x está
situado entre –α y α cuando (y solamente cuando) x < α. Esta idea puede generalizarse por
medio del siguiente teorema.
2.4.14 Teorema
Sea α ∈ R con α ≥ 0; ∀ x ∈ R se tiene que:
x ≤ α ⇔ −α ≤ x ≤ α
Este teorema tiene la siguiente interpretación geométrica:
{x | x ∈ R, x ≤ α}
—
0

Con ayuda del valor absoluto, la distancia entre dos números reales cualesquiera x y y pueden
definirse como el número real no negativo x  y .
Resolución de desigualdades e inecuaciones
La relación “menor que” y sus propiedades y conceptos relacionados, son de gran utilidad
para describir y manejar intervalos de valores para variables reales. En particular, las
propiedades enunciadas en el teorema 2.4.7 nos permiten “despejar”, cuando es posible, una
variable en una relación de desigualdad.
FORMALIZACIÓN DE LOS NÚMEROS REALES (G€®)
18