t - MC Manuel Amarante - Universidad Autónoma de Nuevo León

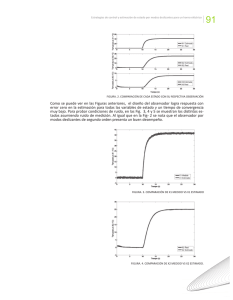
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN
FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA
DEPARTAMENTO DE CONTROL
Práctica N° 10 de Control Moderno
Diseño de Observadores
OBJETIVO
Junto con la teoría vista en clase, las tareas realizadas en casa y el buen uso de los comandos de
Matlab ayudar al alumno a adquirir la competencia para el diseño de Observadores de orden completo
para Sistemas Continuos Monovariable.
MARCO TEÓRICO
En las dos prácticas anteriores se estudió la estructura de la retroalimentación del estado de un
sistema, en el que se supuso que todas las variables de estado de la parte controlable eran medidles y
cuyos valores podían utilizarse de forma inmediata en dicha estructura de control. Las variables de
estado son, sin embargo, en el caso más genérico, variables internas de funcionamiento del sistema
cuyos valores no pueden medirse directamente sobre magnitudes físicas de éste. En este caso general,
los valores de las variables de estado que se desea conocer para efectuar la retroalimentación han de ser
estimadas a partir de la evolución de las señales conocidas del sistema, que son sus salidas y sus
entradas.
.
u(t)
B(t
)
x(t)
∫
x(t)
C(t)
y(t)
A(t)
Observador
xc(t)
Fig. 1 Concepto de Observador
El conjunto de las variables que pueden calcularse a partir de las entradas y las salidas del
sistema forman, como se sabe, el subsistema observable. El cálculo de las variables de estado se realiza
en el sistema denominado Observador, cuyo esquema se muestra en la Figura 1, que en todo momento
es capaz de estimar los valores de las variables de estado reales del sistema, que son necesarias para su
control según la matriz de retroalimentación del estado vista con anterioridad.
Dado un sistema lineal, invariante y observable:
Práctica 10 Laboratorio Control Moderno
o
x(t ) = Ax(t ) + Bu (t )
y (t ) = Cx(t )
(1)
el esquema general de un observador es el representado en la Figura 1, en el que éste proporciona una
medida o estimación dinámica de las variables de estado del sistema a partir de la evolución de sus
entradas y salidas.
Para la realización de un observador, existe un caso trivial en el que las salidas son una
combinación lineal de las variables de estado, caracterizado por una matriz C invariable. En este caso el
observador del estado se resuelve simplemente invirtiendo esta matriz:
x(t ) = C −1 y (t )
Si se desea obtener de forma continua la evolución de las variables de estado del sistema en
cada instante, se implementa un sistema dinámico que tiene como entradas las entradas y salidas del
sistema, y que responde a las condiciones enunciadas por el siguiente teorema:
Dado u sistema lineal, invariante y observable:
o
x(t ) = Ax(t ) + Bu (t )
y (t ) = Cx(t )
(1)
se dice que el sistema definido por las ecuaciones:
o
x c (t ) = Fxe (t ) + Gu (t ) + Hy (t )
es un observador del anterior, si verifica las dos condiciones siguientes:
1. Si los estados de ambos sistemas coinciden en un instante t0, xe(t0) = x(t0), entonces los
estados coinciden para todo instan te posterior xe(t) = x(t) para cualquier entrada u(t)
aplicada sobre el sistema.
2. xe(t) debe tender asintoticamente al estado x(t) para cualquier entrada u(t) y para
cualesquiera estados iniciales xe(t0) y x(t0).
lim xe (t ) − x(t ) = 0
t →∞
(2)
Estas dos condiciones imponen diversas restricciones a las matrices del observador. Así, si se
forma la diferencia entre la evolución del estado del observador y del sistema:
o
o
x e (t ) − x(t ) = Fxe (t ) − Ax(t ) + (G − B )u (t ) + HCx(t )
(3)
se deduce que:
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
2
Práctica 10 Laboratorio Control Moderno
Por la primera condición, se sabe que si se parte de un mismo estado inicial, ante cualquier
entrada, los estados deben coincidir en todo instante. Para que la entrada no influya en la
diferencia entre ambos se debe cumplir:
G=B
(4)
con lo que la Ec. (3) queda Ec. (5):
o
o
x e (t ) − x(t ) = Fxe (t ) − Ax(t ) + HCx(t )
(5)
Dada esta ecuación, para que los estados coincidan en todo instante se debe cumplir Ec. (6):
F = A − HC
(6)
con lo que la Ec. (5) pasa a valer Ec.(7):
o
o
x e (t ) − x(t ) = ( A − HC )( xe (t ) − x(t ))
(7)
Como puede observarse de esta expresión, la dinámica de la diferencia entre las variables
estimadas y las variables de estado viene gobernada por la matriz A-HC.
Si los estados iniciales no coinciden xe(0) ≠ x0, el estado estimado debe tender
asintoticamente al estado del sistema, por lo que los valores propios de la matriz A-HC
deben estar en el semiplano negativo.
Adicionalmente, en la práctica se necesita que la dinámica del observador dado por F sea más
rápida que la del sistema dado por A, para que el observador estime las variables de estado más
rápidamente que la variación de éstos y, por lo tanto, puedan ser utilizadas de forma eficaz como una
buena estimación de las variables de estado en la retroalimentación del estado del sistema. Esto se
consigue si la parte real de los valores propios de la matriz A-HC es significativamente menor que la de
los valores propios de la matriz A.
El objetivo final de la utilización de un observador es diseñar un control por retroalimentación
del estado a partir del estado estimado. Cabe, por lo tanto, analizar la controlabilidad al sistema en
forma conjunta con el observador, tanto antes de realizar la retroalimentación del estado como después.
Las ecuaciones tanto del sistema inicial como del observador son:
o
x(t ) = Ax(t ) + Bu (t )
(8)
o
x e (t ) = ( A − HC )xe (t ) + Bu (t ) + HCx(t )
(9)
escrito en forma matricial:
o   A
 ox(t )  = 
 x e (t )  HC


  x(t )   B 
+
u (t )
A − HC   xe (t )  B 
0
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
(10)
3
Práctica 10 Laboratorio Control Moderno
cuya representación gráfica se observa en la Figura 2.
Si se estudia la controlabilidad del sistema conjunto, mediante la construcción de la matriz Q:
 B AB A2 B L An −1B 
Q=
(11)
2
n −1 
 B AB A B L A B 
Como puede verse fácilmente, el conjunto formado por los dos grupos de variables es no
controlable.
Dado que se parte de que el sistema inicial es controlable, el rango de esta matriz sigue siendo
n, por lo que se puede se puede hacer una separación de la parte no controlable, mediante el cambio:
~
 I 0  x(t )   x(t ) 
x(t ) = 
=


− I I   xe (t )  xe (t ) − x(t )
Con lo que la nueva expresión de la ecuación de estado es:
 o
 A
 o x(t )o  = 
 x e (t ) − x(t )  0


(12)
  x(t )   B 
+
u (t )
A − HC   xe (t ) − x(t )  0 
0
(13)
Ecuación de la que puede extraerse las siguientes conclusiones:
La parte no controlable es la diferencia entre el estado estimado y el estado real: actuando
sobre la entrada no se modificará el comportamiento de esta diferencia, como cabe esperar de
las condiciones impuestas en la definición del observador.
u(t)
B
∫
x(t)
C
y(t)
A
H
B
∫
xe(t
)
A-HC
Fig. 2 Esquema del sistema con observador.
La evolución de la parte no controlable es:
xe (t ) − x(t ) = Φ A − HC (t , t0 )( xe 0 − x0 )
(14)
que corrobora lo ya conocido: será cero, si el estado inicial para las variables reales y para las
estimadas es el mismo, y tendera a cero, si siendo el estado inicial distinto, los valores propios
de A-HC tienen parte real negativa.
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
4
Práctica 10 Laboratorio Control Moderno
El hecho de retroalimentar el estado x(t) no afecta la dinámica del observador, sólo a la del
sistema observado. Sin embargo, no hay que olvidar que no es posible retroalimentar x(t), al
no tener acceso a estas variables, sino xe(t), el conjunto de variables estimadas.
El objetivo de este apartado es, dado un sistema lineal, invariante, observable y monovariable,
diseñar un observador que estime el estado. Conocidas las matrices A, B y C del sistema, y según se vio
con anterioridad, el observador debe cumplir.
G=B
F = A-HC, siendo H tal que los valores propios de F deben estar en el semiplano negativo, y
además, de parte real significativamente menor que los valores propios dominantes de la
matriz A ó Ar, en caso de un sistema con retroalimentación del estado.
El objetivo es calcular H de forma que se cumplan las anteriores condiciones. La representación
del estado estimado obtenido dependerá de la representación del estado elegida para expresar A, B, y C.
al igual que sucederá con el mecanismo elegido para diseñar la retroalimentación del estado, es
interesante elegir una representación que simplifique los cálculos. Así si se elige la llamada forma
canónica observable.
Calcular los elementos de la matriz H a partir de los coeficientes de la ecuación Expresar el
sistema en su forma canónica observable; para ello es necesario determinar la matriz de
transformación, mediante el método que se describe en el siguiente subapartado.
Determinar la posición que deben ocupar los polos del observador y obtener, a continuación,
los coeficientes de su ecuación característica (fn, fn-1,…,f0). La posición elegida para dichos
polos dependerá de la posición de los polos del sistema, de forma que la dinámica del
observador sea significativamente más rápida que la del sistema observado.
característica de F y de la ecuación característica de A, según las siguientes expresiones
h1 = −a0 + f 0
h2 = − a1 + f1
(15)
M
hn = − an −1 + f n −1
Montar el observador según la Figura 3 permite obtener una estimación del estado
expresado en la forma canónica observable, a partir de las matrices B, F y H anteriormente
calculadas.
y(t)
u(t)
x(t)
B
∫
C
A
H
~
Bo
∫
~
xe(t)
~ ~
~
F=Ao-HCo
Fig. 3 Esquema del sistema con el Observador expresado en la forma canónica observable.
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
5
Práctica 10 Laboratorio Control Moderno
Obsérvese que todas las matrices involucradas en el esquema de la Figura 3 están expresadas
en la forma canónica observable.
DESARROLLO
Para el sistema, del cual se muestran a continuación las matrices que determinan su dinámica,
que no e tienen accesibles las variables de estado es necesario diseñar un Observador del Estado que las
estime.
•
x = Ax(t ) + Bu (t )
y (t ) = Cx(t )
Donde
1
0 
 0

A= 0
0
1 
− 35.85 − 11.28 − 8.8
0 
B = 0
1
C = [25 0 0]
Para iniciar con el diseño primero probamos la dinámica del sistema determinando sus valores
propios, la Observabilidad para saber cuantas variables de estado tiene, cuantas son observables y si es
estable.
En Matlab:
%Cargando las matrices que determinan la dinámica del sistema
>> A=[0 1 0;0 0 1;-35.85 -11.28 -8.8]
A=
0 1.0000
0
0
0 1.0000
-35.8500 -11.2800 -8.8000
>> B=[0;0;1]
B=
0
0
1
>> C=[25 0 0]
C=
25
0
0
>> D=[0]
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
6
Práctica 10 Laboratorio Control Moderno
D=
0
%Determinación de estabilidad
>> eig(A)
ans =
-7.9483
-0.4259 + 2.0806i
-0.4259 - 2.0806i
%Determinación de la Controlabilidad y la Observabilidad
>> Co=ctrb(A,B)
Co =
0
0
1.0000
0
1.0000 -8.8000
1.0000 -8.8000 66.1600
>> rank(Co)
ans =
3
>> rank(A)
ans =
3
>> Ob=obsv(A,C)
Ob =
25 0 0
0 25 0
0 0 25
>> rank(A)
ans =
3
>> rank(Ob)
ans =
3
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
7
Práctica 10 Laboratorio Control Moderno
De los cálculos en Matlab nos damos cuenta que el sistema es estable, que tiene tres Variables
de Estado y que las tres son controlables y observables, de aquí determinaremos la dinámica del
Observador debiendo tenerla más rápida que la del sistema por lo que colocaremos sus valores propios
en s1=-10, s2=-10 y s3=-15, cálculo de H con el comando >>acker para obtener F=A-HC que determina
la dinámica del observador.
En Matlab:
%Cargando la matriz P que contiene los polos de lazo cerrado del observador
>> P=[-10 -10 -15]
P=
-10 -10 -15
%Cálculo de H para obtener F que determina la dinámica del Observador
>> L=acker(A',C',P)'
L=
1.0480
6.3264
-8.9278
>> H=L
H=
1.0480
6.3264
-8.9278
>> F=A-H*C
F=
-26.2000 1.0000
0
-158.1600
0
1.0000
187.3440 -11.2800 -8.8000
>> eig(F)
ans =
-15.0000
-10.0000 + 0.0000i
-10.0000 - 0.0000i
Observando los valores propios que determinan la dinámica del Observador, s1=-15, s2=-10 y
s3=-10, nos damos cuenta que la dinámica del observador está basada en los valores propios con que lo
diseñamos.
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
8
Práctica 10 Laboratorio Control Moderno
Para estimar la calidad del diseño simularemos con Simulink la dinámica de las variables de
estado del sistema, visualizándolas en gráficas de Matlab, la dinámica de las variables de estado
estimadas y la diferencia entre ambas, de acuerdo a la Figura 3. Los diagramas de Simulink Figura 4 y
las respectivas gráficas que las tenemos en las Figuras 5, 6, 7 y 8
Fig. 4 Diagrama de Simulink para simular el sistema con su Observador de Estado (obsérvese que
aquí la notación de las Matrices A, B, y C del Observador continúan en la forma original sin
expresarse en la Forma Canónica Observable)
Fig. 5 Variables generadas por la simulación Figura 4 y los comandos para realizar las gráficas de
las figuras 6, 7 y 8
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
9
Práctica 10 Laboratorio Control Moderno
Fig. 6 Gráfica de respuesta al escalón de las Variables de Estado
Fig. 7 Gráfica de respuesta al escalón de las Variables de Estado Estimadas
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
10
Práctica 10 Laboratorio Control Moderno
Fig. 8 Gráfica de respuesta al escalón de la diferencia de las Variables de Estado Reales y las
Estimadas
REPORTE
Sea el siguiente sistema, del cual se presentan sus ecuaciones de estado en seguida, en donde las
Variables de Estado no están disponibles y necesitan ser estimadas:
o

1
0   x1 (t )  0 
 xo 1 (t )  0
 x 2 (t ) =  0
0
1   x2 (t ) +  0 u (t )
o
 
 x 3 (t ) 1.244 0.3956 − 3.145  x3 (t ) 1.244


 x1 (t )
y (t ) = [1 0 0] x 2 (t )
 x3 (t )
Diseñe un Observador que las estime con una dinámica en la que los polos dominantes del
mismo tengan la parte real negativa el triple de los del sistema a estimar.
La entrada r(t) es una función escalón unitario.
a. Obtenga la matriz de ganancia del Observador H.
b. Obtenga la matriz que determina la dinámica del Observador F=A-HC.
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
11
Práctica 10 Laboratorio Control Moderno
c. Compruebe que los Polos dominantes de la dinámica del observador tiene parte real
negativa el triple de la del sistema a estimar
d. Obtenga el desempeño en el tiempo de las Variables de Estado reales y las estimadas en
una misma gráfica comparando ambos desempeños para una entrada escalón unitario y
un tiempo de 0 a 5 seg. con incrementos de 0.05.
e. Obtenga una gráfica del desempeño en el tiempo de los estados reales en forma
individual para una entrada en escalón unitario utilizando Simulink. Las gráficas
deberán realizarse con el comando >>plot.
f. Obtenga una gráfica del desempeño en el tiempo de los estados estimados en forma
individual, para una entrada escalón unitario utilizando Simulink. Las gráficas deberán
realizarse con el comando >>plot.
g. Obtenga una gráfica que muestre el desempeño en el tiempo del error de estimación de
las variables de estado.
h. Haga un informe detallado del procedimiento seguido en la práctica con su debida
fundamentación matemática.
i. Explique cada comando utilizado en la práctica.
j. Conclusiones
M.C. Manuel Amarante Rodríguez
28 de Julio del 2011
12