T.P Diciembre 5º Eco Matemática

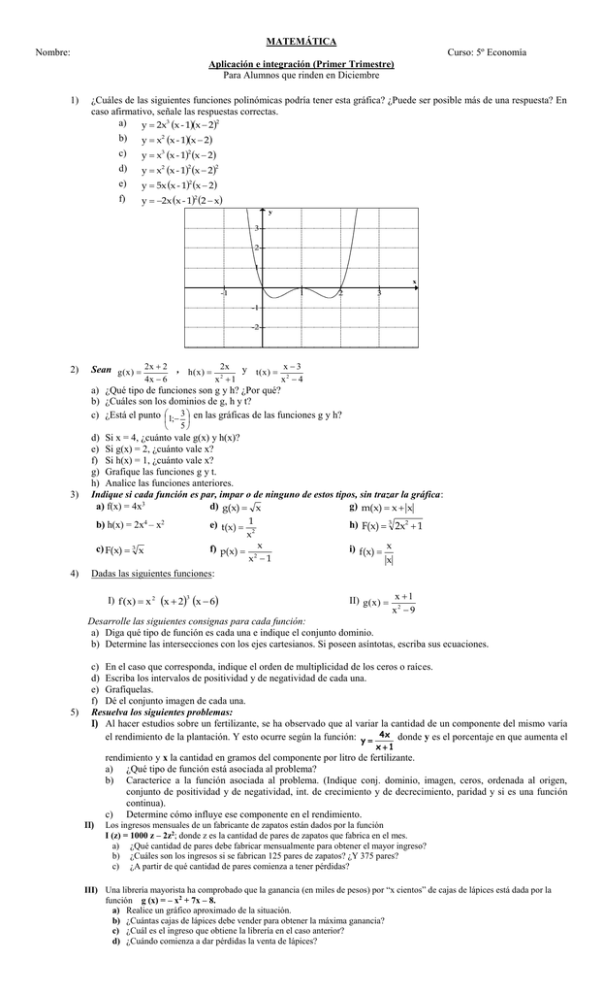
MATEMÁTICA
Nombre:
Curso: 5º Economía
Aplicación e integración (Primer Trimestre)
Para Alumnos que rinden en Diciembre
1)
¿Cuáles de las siguientes funciones polinómicas podría tener esta gráfica? ¿Puede ser posible más de una respuesta? En
caso afirmativo, señale las respuestas correctas.
a)
y  2x3 x - 1x  22
b)
y  x2 x - 1x  2
c)
y  x3 x - 12 x  2
d)
y  x2 x - 12 x  22
e)
y  5x x - 12 x  2
f)
y  2x x - 12 2  x
y
3
2
1
x
-1
1
2
3
-1
-2
2)
Sean g ( x )  2 x  2 , h ( x )  2x
2
4x  6
x 1
y t(x)  x  3
2
x 4
a) ¿Qué tipo de funciones son g y h? ¿Por qué?
b) ¿Cuáles son los dominios de g, h y t?
c) ¿Está el punto 1; 3  en las gráficas de las funciones g y h?

3)
4)
5
d) Si x = 4, ¿cuánto vale g(x) y h(x)?
e) Si g(x) = 2, ¿cuánto vale x?
f) Si h(x) = 1, ¿cuánto vale x?
g) Grafique las funciones g y t.
h) Analice las funciones anteriores.
Indique si cada función es par, impar o de ninguno de estos tipos, sin trazar la gráfica:
a) f(x) = 4x3
d) g(x)  x
g) m(x)  x  x
b) h(x) = 2x4 – x2
e) t( x )  1
2
c) F(x)  3 x
f) p( x ) 
x
x
x2  1
h) F(x)  3 2x2  1
i) f(x)  x
x
Dadas las siguientes funciones:
I) f (x)  x 2 x  23 x  6
II) g ( x )  x  1
x2  9
Desarrolle las siguientes consignas para cada función:
a) Diga qué tipo de función es cada una e indique el conjunto dominio.
b) Determine las intersecciones con los ejes cartesianos. Si poseen asíntotas, escriba sus ecuaciones.
5)
c) En el caso que corresponda, indique el orden de multiplicidad de los ceros o raíces.
d) Escriba los intervalos de positividad y de negatividad de cada una.
e) Grafíquelas.
f) Dé el conjunto imagen de cada una.
Resuelva los siguientes problemas:
I) Al hacer estudios sobre un fertilizante, se ha observado que al variar la cantidad de un componente del mismo varía
el rendimiento de la plantación. Y esto ocurre según la función: y  4x donde y es el porcentaje en que aumenta el
x1
rendimiento y x la cantidad en gramos del componente por litro de fertilizante.
a) ¿Qué tipo de función está asociada al problema?
b) Caracterice a la función asociada al problema. (Indique conj. dominio, imagen, ceros, ordenada al origen,
conjunto de positividad y de negatividad, int. de crecimiento y de decrecimiento, paridad y si es una función
continua).
c) Determine cómo influye ese componente en el rendimiento.
II)
Los ingresos mensuales de un fabricante de zapatos están dados por la función
I (z) = 1000 z – 2z2; donde z es la cantidad de pares de zapatos que fabrica en el mes.
a) ¿Qué cantidad de pares debe fabricar mensualmente para obtener el mayor ingreso?
b) ¿Cuáles son los ingresos si se fabrican 125 pares de zapatos? ¿Y 375 pares?
c) ¿A partir de qué cantidad de pares comienza a tener pérdidas?
III) Una librería mayorista ha comprobado que la ganancia (en miles de pesos) por “x cientos” de cajas de lápices está dada por la
función g (x) = – x2 + 7x – 8.
a) Realice un gráfico aproximado de la situación.
b) ¿Cuántas cajas de lápices debe vender para obtener la máxima ganancia?
c) ¿Cuál es el ingreso que obtiene la librería en el caso anterior?
d) ¿Cuándo comienza a dar pérdidas la venta de lápices?
MATEMÁTICA
Nombre:
Curso: 5º Economía
Aplicación e integración (Segundo Trimestre)
Para Alumnos que rinden en Diciembre
1)
a)
Siendo f(x)  2x
y g (x )  log 1 2 x
Grafica ambas funciones, analiza ambas funciones y completa el siguiente cuadro
f(x)  2x
Caracterización
g (x )  log 1 x
2
Dominio
Imagen
Intervalo de Crecimiento
Intervalo de Decrecimiento
Ecuaciones de asíntotas
Ceros
Ordenada al origen
Conjunto de Positividad
Conjunto de Negatividad
3


Si A  5 m .a  ; log m = 0,5; log a = -1,5; log u = 2,5. ¿Cuánto vale A?
2
 u 
4) Resuelve las siguientes ecuaciones exponenciales.
1
a) 4 x 
g) 2 x  2x  4
4
b) 2 x 1  8
h) 2 . 3x + 5 . 3x – 3x = 6
c) 9 . 3 x  27
i) 2 x = 10
3)
d) 3 2 x 1  1
x
j) 5 .  1   2 3  0
2
1
x
a) e) 2
k) e + 3 ex = 4

8
1
x2
f) 27 . 3   0
l) 3 x = 21
3
5) Resuelve las siguientes ecuaciones logarítmicas.
a) log x 27 = 3
e) log 5 (x + 12) – log 5 (x + 3) = 1
b) log 1/2 (-x + 5) = 2
f) log (x – 8) + log (x – 2) = log (-8 – x)
c) log 3 x = 5 . log 3 2
g) 20 . log (x2 – 15) = 0
2
d) log 2 (8 . x) + log 2 (4 . x ) = 8
h) 2 . log 7 x – log 7 (x + 6) = 3 . log 7 2
1 x 2
6)
Plantee y resuelva los siguientes problemas:
1) A una persona se le inyectan 250 mg de penicilina. La cantidad de penicilina (en mg) presente en el cuerpo al

2
t
transcurrir el tiempo está dada por f(t) = 250. e 3 , siendo t el tiempo en hora.
a) Realice un gráfico aproximado de la situación.
b) ¿Cuántos mg de penicilina posee el cuerpo en el momento de aplicarse la inyección?
c) ¿Cuántos mg se encuentran en el cuerpo pasada 3 horas?
d) Si el cuerpo contiene 80 mg de penicilina ¿cuánto tiempo pasó desde que se le aplicó la inyección?
2) Una sustancia radiactiva pierde el 3% de su masa cada día. Diez días después de comenzada la observación, se tiene
150 g.
a) ¿Cuántos gramos de sustancia había al comenzar la observación?
b) Escriba la ley de la función que modela la situación.
c) ¿Después de cuánto tiempo se reduce la masa de la sustancia a la mitad?
MATEMÁTICA
Nombre:
Curso: 5º Economía
Aplicación e integración (Tercer Trimestre)
Para Alumnos que rinden en Diciembre
1) Marcar con una cruz la/s respuesta/s correcta/s
a)
b)
c)
d)
El ángulo 34º 5’ 2” expresado en sistema centesimal es:
 37𝐺 87𝑀 9𝑆
 37𝐺 52𝑀 16𝑆  32𝐺 20𝑀 5𝑆  40𝐺 2𝑀 15𝑆
𝐺 𝑀
𝑆
113 7 32 expresado en sistema sexagesimal es:
 101º 47’ 48”  103º 20’ 4”
 101º 48’ 47”  95º 20’ 57”
El ángulo exterior de un triángulo equilátero, expresado en sistema centesimal tiene una amplitud de:
 140𝐺 20𝑀 5𝑆  133𝐺 33𝑀 33𝑆  66𝐺 66𝑀 66𝑆  133𝐺 20𝑀
𝜋
¿Cuánto mide la amplitud de un ángulo de un triángulo, si sus otros dos ángulos miden 50º y rad
 111𝐺 11𝑀 11𝑆
 111𝐺 6𝑀 40𝑆
 1, 47 rad
6
 1, 74 rad
2) Graficar y resolver los siguientes problemas:
I) Desde un helicóptero que vuela a 500 m de la tierra se divisa una casa. La visual dirigida desde el helicóptero a la
casa forma con la vertical un ángulo de 47º. Calcular a qué distancia de la casa se encuentra el helicóptero.
II) Una persona de pie sobre un acantilado de 50 m de altura observa 2 boyas con ángulos de depresión de 18º y 20º
respectivamente, como muestra el esquema. Calcular:
a) La distancia entre las boyas
b) La distancia entre la persona y la boya más cercana.
III) Un mástil tiene 15 m de alto. ¿Cuánto mide la sombra que proyecta cuando el ángulo de elevación del Sol es de 57º?
¿Qué distancia hay entre el extremo del mástil hasta el de su sombra?
IV) Desde lo alto de un árbol se tensan dos cables y se atan al piso, como se ve en la figura. El más alejado queda a 40 m
de la base del árbol. Calcular:
a) La altura del mismo.
b) La longitud de ambos cables.
c) La distancia, a nivel del piso, entre ambos cables.
V) Para calcular la altura de un edificio, Mariela se ubica a una distancia de 40 m de éste. La línea de la visual del punto
más alto del edificio sabiendo que los ojos de Mariela están a 1,6 m del piso.
VI)
Se necesita construir una rampa para acceder a una plataforma que está a 9 m de altura. Si la rampa forma un ángulo de 20º con la
horizontal: ¿Cuál es la longitud de la rampa? ¿A qué distancia está el pie de la rampa del lugar en el que comienza la plataforma?
VII) ¿Cuál es la medida de la base de un triángulo isósceles, si la medida de su altura es de 4 m y la medida de cada uno de sus lados
congruentes es de 12 m? ¿Cuál es la amplitud de sus ángulos interiores?
VIII) Desde un globo a 2 km de altura, los ángulos de depresión de dos poblaciones alineadas con el globo son 81º 30’ y 13º 40’. ¿A
qué distancia se encuentran las poblaciones entre sí? (el ángulo de depresión es el ángulo entre la horizontal y la línea de la
visual, cuando ésta se encuentra por debajo de la horizontal)
IX) Tres pueblos X, W, Z, están unidos por carreteras rectas. La distancia entre X y W es de
6 km; a los
pueblos W y Z los separan 9 km. El ángulo que forman las carreteras que unen X y con W y W con Z es de
120º. ¿Qué distancia hay entre X y Z?
X) En una plazoleta de forma triangular, los lados miden 60 m, 75 m y 50 m. ¿Qué ángulos se forman en las
esquinas de la misma?
XI) Los puntos A y B se encuentran en los lados opuestos de un cráter lunar. El punto C se halla a 50 m de A.
Se determina que las medidas de los ángulos BAC y ACB son 112º y 42º, respectivamente. ¿Cuál es el
ancho del cráter?
XII) Un trozo de alambre de 5,5 m de largo se dobla formando un triángulo. Uno de los lados mide 1,5 m y el
otro 2m. Encuentre las amplitudes de los ángulos del triángulo.
XIII) Se construye un puente sobre un cañón. La longitud del puente es de 1 537 m. Desde el punto más bajo
del cañón, los ángulos de elevación de los extremos del puente son 78º y 72º. ¿Cuál es la profundidad
del cañón?
3) Verifique las siguientes identidades trigonométricas:
a)
ˆ  sec 2 
ˆ
1  tg2 
f) cotg2 
ˆ  cos2 
ˆ  cos2 
ˆ . cotg2 
ˆ
b)
ˆ  cosec 2 
ˆ
1  cot g 2 
ˆ
ˆ
sen   1 sen   1   cos2 ˆ
ˆ  cot g ˆ . senˆ . cosˆ  1
g) tg
ˆ . tg
ˆ  sec 
ˆ
cosec
1
cos ˆ

 tg ˆ
sen ˆ . cosˆ sen ˆ
i) sen ˆ  cos ˆ
c)
d)
e)






  cos ˆ  sen ˆ 
h) 1  tg
ˆ 1  tg
ˆ   sec 2 
ˆ 2
j)
1
2
2
2
ˆ . tg
ˆ cotg
ˆ cos
ˆ
sen 
ˆ
 cos 
ˆ . cosec 
ˆ
cos