RAZONES TRIGONOMÉTRICAS DEFINICIÓN La razón

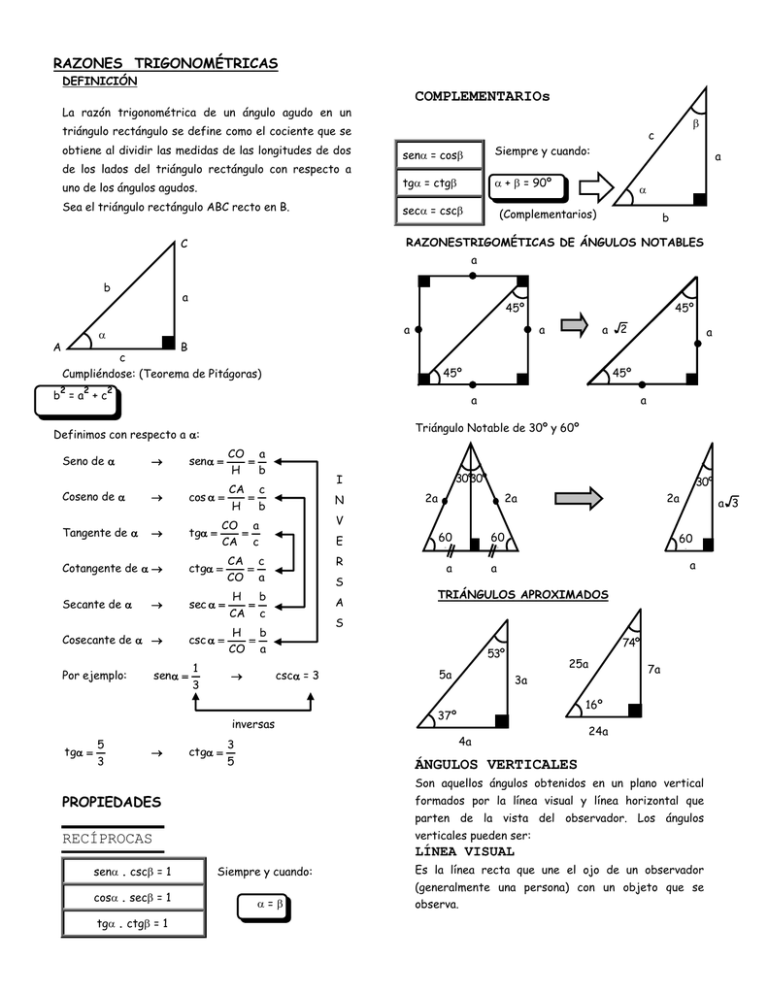
RAZONES TRIGONOMÉTRICAS
DEFINICIÓN
COMPLEMENTARIOs
La razón trigonométrica de un ángulo agudo en un
triángulo rectángulo se define como el cociente que se
obtiene al dividir las medidas de las longitudes de dos
sen = cos
Siempre y cuando:
uno de los ángulos agudos.
tg = ctg
 +  = 90º
Sea el triángulo rectángulo ABC recto en B.
sec = csc
de los lados del triángulo rectángulo con respecto a

c
a

(Complementarios)
b
RAZONESTRIGOMÉTICAS DE ÁNGULOS NOTABLES
C
a
b
A
a
45º
a

a
2
b =a +c
45º
2
2
a

sen 
CO a

H
b
Coseno de 

cos  
CA c

H
b

tg 
Secante de 

H
b
sec  

CA c
Cosecante de  
H
b
csc  

CO a
sen 
1
3
N
E
R
S
A
60
º
a
2a
60
º
a
60
º
a
TRIÁNGULOS APROXIMADOS
74º
53º
inversas

2a
S
csc = 3

2a
30º
V
CA c

CO a
ctg 
30º30º
I
CO a

CA c
Cotangente de  
Por ejemplo:
a
Triángulo Notable de 30º y 60º
Seno de 
Tangente de 
45º
a
Definimos con respecto a :
5
tg 
3
a
B
c
Cumpliéndose: (Teorema de Pitágoras)
2
45º
5a
25a
16º
37º
4a
3
ctg 
5
7a
3a
24a
ÁNGULOS VERTICALES
Son aquellos ángulos obtenidos en un plano vertical
PROPIEDADES
formados por la línea visual y línea horizontal que
RECÍPROCAS
verticales pueden ser:
sen . csc = 1
cos . sec = 1
tg . ctg = 1
parten de la vista del observador. Los ángulos
LÍNEA VISUAL
Siempre y cuando:
=
Es la línea recta que une el ojo de un observador
(generalmente una persona) con un objeto que se
observa.
a 3
Calcular:
LÍNEA HORIZONTAL
Es la línea recta paralela a la superficie horizontal
2
a) a b) b
ÁNGULO DE ELEVACIÓN
Es el ángulo formado por la línea horizontal y la
c) c
d) 1 e) 1/2
4.-Del gráfico calcular tg
Si: tg 
línea visual cuando el objeto a observar se
encuentra por encima de la línea horizontal.
3
10

Línea Visual
VVisual
a) 0,2

Línea Horizontal
hHorizontal
2
E = sen A + sen B
referencial que pasa por el ojo del observador.
b) 0,4
5,.-Calcular “x”
Si: ctg  ctg 

c) 0,6 d) 0,8
e) 1,2
6
5
C
ÁNGULO DE DEPRESIÓN
x
Es aquel ángulo formado por la línea horizontal y
la línea visual cuando el objeto se encuentra por

debajo de la línea horizontal.
Línea
A
a) 11
Horizontal
1.
bHH
HHHHHHHHh
HHorizontal

Si: sen 
18
b) 13

D
c) 14 d) 15
B
e) 18
7
4
Calcular: E  3 sec   7 tg
Línea
Visual
a) 1/3
b) 2/3 c) 5/3 d) 7/3
e) 1
II.-PROPIEDADES
1.
: Ángulo de Depresión.
1.
Si:  es un ángulo agudo tal que cos  
 1
2
Calcular : Sec
2.-Del gráfico calcular “x”
Si: tgB 
3
2
B
a) 1
4x + 2
b) 2
c) 3
d) 4
e) 5
A
7x + 1
3.-En un triángulo rectángulo ABC recto en C.
C
1
.
3
Indicar lo incorrecto:
a) sen20º = cos70º
b) tg10º ctg10º = 1
c) sec(x + 40º) = csc(50º - x)
d) tg(x + y) ctg(x + y) = 1
e) tg20º = ctg20º
2,.Indicar lo incorrecto:
a) sen15º = cos75º
b) sec28º = csc62º
c) tg20º ctg20º = 1
d) sen42º csc42º = 1
e) cos8º = cos82º
3.-Señale el valor de “x”
Si: sen2x csc40º = 1
a) 10º
d) 20º
b) 5º
e) 40º
c) 15º
sec60º
4.-Sabiendo que tg5x ctg(x + 40º) = 1
Calcular: cos3x
1
2
a) 1
b)
c) 2 d) 3
e)
2
3
2
5.-Hallar “x”
Si: cos(3x – 12º) sec(x + 36º) = 1
a) 12º b) 24º c) 36º d) 48º
6.-Calcular “tg3x”
5.-Calcular: E = (tg60º + sec30º - sen60º)
a) 25/12
Calcular: E 
e) 8º
a)
Si: cos(x + 25º) sec(65º - x) = 1
a) 1
3
3
b)
3 d)
c)
3
4
a) 1
b) 2
tg10º
sen20º

cos 70º ctg80º
c) 3 d) 2/3
tg30º sec 60ºsen37º cos 30º
sen2 45º
3 3
11 3
c)
5
5
d)
5 3
3
e)
2 3
5
6.-Evaluar: E 
7.-Calcular:
E
b)
e) 7/18
sen2 45º cos 60º
csc 30º
senx
7.-Del gráfico calcular: E 
seny
4
3
e)
3
5
b) 25/24 c) 49/12 d) 49/24
e) 3/2
8.-Si: sen(2x + 10º) = cos(x + 20º)
Calcular:
E = sec3x + tg(2x + 5º)
a)
4 2
5
b)
4
5
c)
2
5
d) 4 2
x
y
53º
45º
e) 1
a) 2
b) 3
c) 4 d) 5
e) 6
2.
III. RT. ÁNGULOS NOTABLES
Determine tg en el gráfico.
1,-Calcular:
E  6tg30º . sec 45º  5 cos 53º
a) 1
b) 0
c) -1 d) 2
e) -2
2.-Calcular:
E = 2sen30º + tg45º (sen53º + sen37º)
a) 1,2
b) 3,2
c) 3,4 d) 4,5
e) 5,2
3.-Determine: tg
5x - 2
a)
3
b)
3
3
c)
3
2
d)
3
6
e)
3 3
2
2x + 1
a) 1
b) 2
x-1
c) 3 d) 4
1.-A una distancia de 20 m de un poste se observa su
e) 5
parte alta con ángulo de elevación 37º. Determinar la
visual.
3.-Calcular:
E = (sec245º + tg45º) ctg37º - 2cos60º
a) 0
b) 1
c) 2 d) 3
a) 5 m
b) 15
c) 25 d) 35
e) 40
2.-Un niño de 1,5 m de estatura divisa una piedra en el
e) 4
suelo con un ángulo de depresión de 37º. ¿A qué
4.- Calcular: “x”
distancia del niño se encuentra la piedra?
3xsec53º - tg45º = sec60º(sec45º + sen45º)
a) 1

IV.ÁNGULOS VERTICALES

30º
30º
b) 2
c) 3 d) 4
csc30º
a) 1 m
b) 2
c) 3
d) 2,5
e) 4
e) 5
3.-Una persona de 2 m de estatura divisa lo alto de una
torre de altura de 32 m con un ángulo de elevación de
15º. Se acerca una distancia “x” y el ángulo de elevación
se duplica. ¿Cuánto vale “x”?
a) 15 m b) 30
c) 60
d) 120
e) 150
4.-Desde lo alto de un faro, se observa a un mismo lado,
dos barcos anclados, con ángulos de depresión de 53º y
11.-calcular la altura de un monte
a)600m
b)325m
37º. Si los barcos están separados una distancia de 14
c)400n
m. ¿Cuál es la altura del faro?
d)320m
a) 16 m b) 12
c) 24 d) 32
e) 8
5.-Una persona de 2 m de estatura observa lo alto de un
poste con un ángulo de elevación de 37º, si el poste mide
14 m, ¿a qué distancia del poste se encuentra la
persona?
a) 12 m b) 16
c) 18 d) 24
e) 36
6.-Desde lo alto y bajo de un muro se observa lo alto de
un poste con ángulos de elevación de 37º y 45º,
respectivamente. Si la distancia entre muro y poste es 8
m, halle la suma de sus alturas.
a) 6 m
b) 8
c) 10
d) 12
e) 16
7.-En la figura, BD = 100 dm. Entonces AC mide:
a)
150
b)
100
c)
50
3 dm
3 dm
3 dm
3 dm
3 dm
C
12.-Para medir la altura de una montaña se miden ángulos
de elevación desde dos puntos distantes 480 m y situados
a 1200 m sobre el nivel del mar. ¿Cuál es la altura si los
ángulos son de 45º y 76º?
13.-Un barco sale de un puerto y durante 4 horas sigue un
curso de 78ª a 18 nudos .Después ,la nave cambia al curso
de 168ª y lo sigue durante 6h a 16 nudos .Después de 10
horas, a) ¿Cuál es la distancia del barco al puerto? b) ¿Cuál
es la orientación del puerto con respecto a la nave ?
14.-El ángulo de elevación del sol es 42º ,¿Cuál es la
longitud de la sombra proyectada sobre el suelo de una
persona que mide 6,1 pie de altura ?
15.-Una torre de 135 pie de altura está situada a la orilla
de un lago, Desde la punta de la torre , el ángulo de
30º
A
e) 15
D
depresión de un objeto en la orilla opuesta del lago es
B
36.3º ¿Cuál es la anchura del lago?
16.- Dos embarcaciones salen del puerto al mismo tiempo.
8.-Un observador se encuentra en un faro al pie de un
La primera navega con un curso de 35º a 15 nudos , ,ientra
acantilado. Esta a 687m sobre el nivel del mar, desde este
que la segunda lo hace con un curso de 125º a 20 nudos
punto observa un barco con un ángulo depresión de 23º. Se
.Obtenga , después de 2 horas a) la distancia entre las
desea saber a que distancia de la base del acantilado se
naves , b) La orientación de la primera embarcación
encuentra el barco.
respecto a la segunda c) la orientación de la segunda
respeto a la primera
9. Dos personas distantes entre sí 840 m, ven simultáneamente un
avión con ángulos de elevación respectivos de 60º y 47º, ¿a qué
17.- Una persona se encuentra en la ventana de su
altura vuela el avión?
apartamento que está situada a 8m. del suelo y observa el
edificio de enfrente. La parte superior con un ángulo de
30 grados y la parte inferior con un ángulo de depresión
de 45 grados. Determine la altura del edificio señalado.
h
d)
25
47º
60º
840
10.-Para medir la anchura
de un río se han medido los
ángulos de la figura desde
dos puntos de una orilla
distantes 160 m. ¿Qué
anchura tiene el rio?
60º
18.-Al observar desde el último piso de un edificio de
18.3m de altura , el ángulo de elevación del extremo
superior de un poste vertical, es de 14º.Desde la base del
edificio el ángulo de elevación del extremo del poste es
28º . Obtenga a) la altura del poste b) la distancia del
edificio al poste
19,-Se observa dos objetos que están en una misma recta
con el pie de una colina y los ángulos de depresión de estos
objetos desde la cima son 30º y 23º, respectivamente .Sila
distancia entre los objetos es 75m. ¿Cuál es la altura de la
colina?