3 propiedades ópticas en el infrarrojo

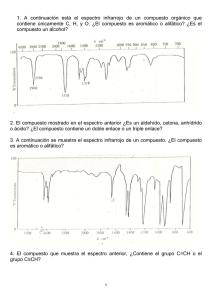
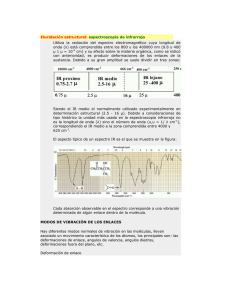
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades ópticas en el infrarrojo
3 PROPIEDADES ÓPTICAS EN EL INFRARROJO
3.1 INTRODUCCIÓN
La región espectral del infrarrojo se extiende desde el dominio visible (0.75 μm) hasta el de las
microondas (1000 μm). La espectrofotometría del infrarrojo es una técnica de amplia utilización en el
estudio e identificación de la estructura molecular de sustancias, tanto orgánicas como inorgánicas. Esto
es debido a que las moléculas y redes iónicas de dichas sustancias poseen modos normales de vibración
en el dominio infrarrojo. Por un fenómeno de resonancia, cuando se ilumina con luz de la misma energía
que la de uno de los modos normales de vibración, el campo eléctrico de la onda electromagnética excita
dicho modo, observándose un pico de absorción de la energía de la onda.
Podemos distinguir tres zonas dentro del dominio infrarrojo, cada una de ellas caracterizada por
un tipo de absorción determinada (vibraciones intramoleculares, vibraciones colectivas de la red):
−
Infrarrojo próximo : 0.75-2.5 μm
−
Infrarrojo fundamental: 2.5-25 μm
−
Infrarrojo lejano : 25-1000 μm
El objetivo del trabajo consiste en la familiarización con los instrumentos y técnicas de
caracterización en el infrarrojo fundamental, y en obtener los espectros de absorción de ciertas sustancias,
que nos permitirán determinar la contribución de la polarizabilidad iónica en el material.
3.2 FUNDAMENTO TEÓRICO
En una red cristalina, los núcleos de la red constituyen un sistema de osciladores acoplados de
manera que no pueden vibrar independientemente, sino según unos ciertos modos normales de vibración
colectiva o fonones. Estos modos normales tienen varias ramas que pueden clasificarse en acústicas y
ópticas. En el modo acústico todos los núcleos de la celda unidad se mueven en fase. En el modo óptico
hay una diferencia de fase que vale π en el caso más simple de dos átomos por celda unidad. Además las
vibraciones pueden ser longitudinales o transversales, según la vibración sea en la dirección de la
propagación o perpendicular a ella.
3.2.1
Redes iónicas
Cuando una onda electromagnética se propaga en una red cristalina iónica, el desplazamiento de
los iones positivos (A) y negativos (B) de su posición de equilibrio por la acción de un campo eléctrico
produce un momento dipolar inducido por cada par de iones y, por tanto, una contribución a la
polarización P - y consecuentemente a la permitividad ε del material - que se añade a la contribución de
la polarización electrónica. Las soluciones de tipo armónico para t conducen a una relación entre P iónica
y el campo E, que en el caso de un único modo de vibración es del tipo:
r
r
Pion = Nα ion Eloc
α ion (ω ) =
2
eeff
/μ
(1)
ω02 − ω 2
siendo Eloc el campo local, αion la polarizabilidad iónica, ωo la frecuencia propia de las vibración
cristalina característica de cada material, N la densidad de pares AB por unidad de volumen, eeff la carga
eléctrica eficaz del momento inducido por el desplazamiento, y μ la masa reducida de los iones que
forman la red:
3-1
Laboratorio de Física de Materiales Dieléctricos y Ópticos
1
μ
=
Propiedades ópticas en el infrarrojo
1
1
+
M1 M 2
(2)
La polarización total incluye además la contribución electrónica:
r
r
Pe = Nα e Eloc
(3)
con lo que la polarización total resulta:
r r
r
r
P = Pion + Pe = N (α ion + α e )Eloc
(4)
r
r
Igualando la conocida expresión macroscópica de P = ε 0 (ε r − 1) E con (4) y utilizando la
expresión del campo local de Lorentz [Eloc=E(εr+2)/3] resulta la ecuación de Clausius-Mossotti:
ε r (ω ) − 1 N
[α (ω ) + α e (ω )]
=
ε r (ω ) + 2 3ε 0 ion
(5)
Si la frecuencia es menor que ωo (ec.1), la onda electromagnética se propaga de acuerdo con una
permitividad εs que corresponde a las contribuciones estáticas iónica αion(0) y electrónica. Para ω = ωo,
ocurre la resonancia, que se manifiesta en una banda de absorción. Para frecuencias más altas que ωo
(ec.1),αion=0, y la onda electromagnética se propaga de acuerdo con una permitividad ε¶ que corresponde
únicamente a la contribución electrónica (mientras su energía sea inferior a la umbral de las transiciones
interbandas, las cuales se encuentran en la región del visible o el ultravioleta).
El caso de una única frecuencia de resonancia se presenta en los materiales con redes cristalinas
muy simples como la red cúbica. En general, el material será anisótropo, y además puede presentar
distintos modos de vibración, lo que da lugar a diferentes bandas de absorción.
3.2.2
Redes covalentes
Cuando una onda electromagnética se propaga en una red cristalina covalente, el campo E de la
onda electromagnética no provoca dipolos inducidos (eeff =0 ⇒ αion=0). Por tanto, la única contribución a
la permitividad de estos materiales es la de la polarizabilidad electrónica (constante en el IR), y su
espectro de transmisión en el infrarrojo fundamental es prácticamente plano.
Los materiales a estudiar son una oblea de silicio monocristalino (c-Si), y de dos capas de nitruro
de boro (BN) depositadas sobre c-Si en nuestro Laboratorio mediante la técnica de magnetrón sputtering,
bajo condiciones distintas de bombardeo iónico.
Es bien conocido que el silicio monocristalino es un material importante en electrónica y otros
campos. Este material presenta típicamente un pico de absorción bastante débil debido a impurezas de
oxígeno, localizado en el infrarrojo fundamental en el valor k = 620 cm-1.
El BN presenta dos posibles fases cristalinas: hexagonal y cúbica. La fase cúbica del BN es
especialmente atractiva ya que presenta la propiedad de ser el segundo material conocido más duro
después del diamante, y le aventaja incluso en algunos aspectos. Los coeficientes de absorción para
ambas fases, en el caso de material monocristalino (ref.5), se muestran en la figuras 1 y 2. Se observa
que:
−
El BN hexagonal es anisótropo y presenta dos frecuencias de resonancia diferentes para los
modos transversales según sea la orientación del campo eléctrico E respecto al eje c (eje
perpendicular al plano que contiene los hexágonos):
o
Si E es paralelo a c: k1 = 783 cm-1 (B-N-B bending) y k2 = 1510 cm-1.
o
Si E es perpendicular a c: k1 = 767 cm-1 y k2 = 1367 cm-1 (B-N stretching).
3-2
Laboratorio de Física de Materiales Dieléctricos y Ópticos
−
Propiedades ópticas en el infrarrojo
El BN cúbico es isótropo, con una sola frecuencia de resonancia en k = 1065 cm-1.
Una de las importantes aplicaciones actuales de la técnica de espectrofotometría IR consiste en la
determinación de la estructura de capas finas (≈ 1 μm) de nitruro de boro (BN). Los materiales en capa
fina son policristalinos, y por tanto presentan picos de absorción algo más anchos y menos intensos que
en el material monocristalino, aunque localizados en las mismas frecuencias. A partir del espectro
vibración al infrarrojo puede deducirse el tipo de enlace entre el B y N.
Figura 1. BN Hexagonal
Figura 2. BN Cúbico
3.3 REALIZACIÓN EXPERIMENTAL
3.3.1
Dispositivo experimental
Para medir las diferentes muestras se utilizará un espectrofotómetro de infrarrojo fundamental
(2.5 - 25 μm) UNICAM SP1100, de tipo dispersivo, y que consta esencialmente de:
−
fuente de energía radiante.
−
monocromador, para aislar una banda estrecha de energía radiante.
−
detector, para medir la energía radiante transmitida a través de la muestra.
El instrumento es de doble haz, y utiliza como fuente un hilo de NiCr incandescente. La luz se
divide en dos haces, uno de los cuales se hace incidir sobre la muestra y el otro se utiliza como referencia.
Ambos entran en el monocromador a través de rendijas de abertura variable. Seguidamente son
modulados por un troceador ("chopper"), que hace pasar alternativamente el haz de la muestra y el de
referencia. Tras pasar por uno de los filtros de interferencia, cada uno de los haces entra al
monocromador donde las distintas longitudes de onda son separadas por una red de difracción, y a la
salida la longitud de onda seleccionada llega a un detector de tipo térmico. El espectrofotómetro realiza el
cociente entre las intensidades de los dos haces, y de esta manera determina la transmitancia,
obteniéndose el espectro de forma gráfica (ver con detalle el esquema óptico en la figura 5.1 del manual).
3.3.2
−
Mandos del espectrofotómetro
Selector PROGRAMME:
3-3
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades ópticas en el infrarrojo
En posición SURVEY el espectro se adquiere de manera más rápida que en modo
NORMAL. Esta mayor rapidez comporta una menor precisión. El modo LOW-NOISE es
aún más preciso pero no debe utilizarse si no es necesario por ser a la vez más lento.
−
Palanca SCAN/STOP:
La posición SCAN sirve para iniciar un registro, o bien para reanudarlo en el caso de que
éste se haya detenido llevando la palanca a la posición STOP.
−
Selector del tipo de SCAN:
En posición NORMAL, un scan puede, en cualquier momento, ser detenido (posición STOP
de la palanca) i reanudado (palanca en posición SCAN). Por el contrario, en posición
AUTORETURN, cuando se detiene un scan, el espectrofotómetro se reposiciona
automáticamente, volviendo al inicio del espectro.
3.3.3
−
Manejo del espectrofotómetro
Ajuste de la base (BASELINE) y del fondo de escala (EXPANSION):
Hacer avanzar (sin rotulador) el registro del espectrofotómetro hasta la posición λ≈10 μm del
espectro y detenerlo. Comprobar que, con las ventanas MUESTRA y REFERENCIA vacías,
el índice del registro se sitúa cerca del 80%. Corregir, en caso de que convenga, este valor
mediante el potenciómetro EXPANSION. Tapar la ventana MUESTRA. El índice del
registro ha de situarse en 3 %. Corregir, en caso de que convenga, esta posición mediante el
potenciómetro BASELINE. IMPORTANTE: Hay que tener en cuenta que el detector es de
respuesta lenta, por lo cual, los cambios de posición del índice del registro al tapar (o
destapar) no son instantáneos. Testear y corregir alternativamente BASELINE y el
EXPANSION hasta que adquieran las posiciones deseadas. Al acabar volver, seleccionando
la posición AUTORETURN, al principio del espectro.
−
Punto de inicio de un espectro:
El primer tramo del espectro (desde 25 hasta 18 μm) presenta el inconveniente de que los
detectores de infrarrojo no funcionan correctamente para estas longitudes de onda, por lo que
todos los espectros que se adquieran han de empezar en 18 μm. Para ello, estando el selector
de tipo de scan en posición NORMAL y sin registrar, se hará avanzar (Palanca SCAN) el
espectro desde la posición inicial (25 μm) hasta 18 μm.
−
Obtención de un scan:
El material a estudiar se encuentra a veces en forma de capa fina (espesor del orden de la
micra) depositado sobre un sustrato. Para determinar la contribución del modo de vibración
a la absorción, hay que eliminar todas las demás contribuciones al espectro de transmisión
procedentes del sustrato y del aire, por lo que debemos realizar dos operaciones.
En primer lugar corregir las posibles desviaciones del 100% del instrumento. Se trata de
normalizar el espectro experimental TE(λ) al espectro del 100%, T100(λ):
TN (λ ) = TE (λ ) / T100 (λ )
(6)
En segundo lugar, para eliminar la influencia del sustrato se obtiene la transmisión del pico
T(λ) normalizada a la transmisión del sustrato:
T (λ ) = TN (λ ) / TN 0 (λ )
Este proceso se ilustra de modo esquemático en la figura 3.
3-4
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades ópticas en el infrarrojo
Figura 3
3.3.4
Muestras
−
A: Oblea de c-Si.
−
B: Capa fina BN18 (0.3 μm) sobre oblea de c-Si, bajo bombardeo iónico débil.
−
C: Capa fina BN86 (0.1 μm) sobre oblea de c-Si, bajo bombardeo iónico fuerte.
Con un rotulador colocado en su soporte, con el selector de scan en modo AUTORETURN, y
habiendo situado en las ventanas REFERENCIA y MUESTRA las muestras que corresponda, iniciar el
scan (palanca en posición SCAN). Detenerlo cuando convenga.
3.3.5
Procedimiento experimental
Obtener los siguientes espectros recordando que, en todos ellos, el punto de inicio ha de ser 18
μm (ver manejo del espectrómetro: punto de inicio de un espectro):
Nº PROGRAMME
3.3.6
Zona
Ventana REFERENCIA Ventana MUESTRA
1
NORMAL
18-2.5μm
-
-
2
NORMAL
18-2.5μm
-
Muestra A
3
NORMAL
18-2.5μm
-
Muestra B
4
18-2.5μm
-
Muestra C
5
Picos
Muestra A
Muestra B
6
Picos
Muestra A
Muestra C
Elementos de discusión
−
¿A qué mecanismos físicos se deben los picos de absorción en las distintas regiones del
infrarrojo?.
−
¿Cómo se consigue variar la longitud de onda en el espectrofotómetro?. ¿Para qué sirven los
filtros?.
−
A partir del espectro experimental del c-Si, deducir el carácter iónico o covalente de la red, y
determinar el valor de su permitividad relativa (Ver Anexo 1).
3-5
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades ópticas en el infrarrojo
−
Indique las diferencias entre los espectros obtenidos cuando se utiliza el aire o el c-Si como
referencia. Justifíquelas, y razone la utilidad del procedimiento seguido en la obtención de los
espectros 5 y 6.
−
Obtener las longitudes de onda de los picos de absorción observados en las diferentes muestras
de BN y su energía correspondiente. Identificar los tipos de enlace y los modos de vibración a
que corresponden.
−
En el espectro normalizado, calcular aproximadamente el valor del coeficiente de absorción en
los picos mediante la expresión: I=exp(-αd), siendo I el valor de la transmitancia normalizada en
el pico y d el valor del espesor de la capa en cm. Comparar con los valores del material
monocristalino.
−
Discutir la orientación cristalina de la capa de BN hexagonal.
−
A partir del valor experimental de ω0 para el BN cúbico, y sabiendo que su densidad es 3.48
g/cm3 y el índice de refracción en el visible es 2.0, determinar el valor de la permitividad
estática.
3.4 BIBLIOGRAFÍA
−
Apuntes de la asignatura.
−
C. Kittel, "Introducción a la física del estado sólido"; Ed. Reverté.
−
E.D. Olsen."Métodos ópticos de análisis"; Ed. Reverté, Barcelona, 1986.
−
Manual del espectrofotómetro.
−
S. Jager, K. Bewilogua, C.P. Klages, Thin Solid Films 245 (1994) 50.
−
S. Gimeno, J.L. Andújar, A. Lousa, Diamond and Related Materials, 6 (1997) 604.
3-6