Propulsión. Problemas

Andrés Zarabozo Martínez
Propulsión. Problemas
Ingeniería Aeronáutica
ETSEIAT
2011
Andrés Zarabozo Martínez
Propulsión. Problemas
Acerca de estos apuntes
Estos apuntes se han realizado para cubrir el temario de la asignatura “Propulsión”, que se imparte
en el cuarto curso de Ingeniería Aeronáutica, en la Escola Tècnica Superior d’Enginyeries Industrial i
Aeronàutica de Terrassa, de la Universitat Politècnica de Catalunya (ETSEIAT – UPC).
Licencia
Esta obra está bajo una licencia Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0) de
Creative Commons. Para ver una copia de esta licencia, visite:
http://creativecommons.org/licenses/by-sa/3.0/deed.es_ES
En líneas generales:
Es libre de:



Compartir – Copiar, distribuir y comunicar públicamente la obra.
Transformar la obra y crear obras derivadas.
Hacer un uso comercial de esta obra.
Bajo las condiciones siguientes:


Reconocimiento — Debe reconocer al autor de la obra original (pero no de una manera que
sugiera que tiene su apoyo o apoya el uso que hace de su obra).
Compartir bajo la Misma Licencia — Si altera o transforma esta obra, o genera una obra
derivada, sólo puede distribuir la obra generada bajo una licencia idéntica a ésta.
-2-
Andrés Zarabozo Martínez
Propulsión. Problemas
0. Índice
0.
Índice ............................................................................................................................................... 3
1.
Aerorreactores ................................................................................................................................ 4
2.
Problema 1.
Consumo específico respecto al peso del motor ........................................................ 4
Problema 2.
Parámetro de flujo de masa en función de Mach ....................................................... 7
Problema 3.
Variaciones del flujo en función del Mach ................................................................ 11
Problema 4.
Problema teórico ...................................................................................................... 14
Problema 5.
Boeing 707 ................................................................................................................ 17
Problema 6.
Turbofán para el B707............................................................................................... 22
Problema 7.
Variaciones del empuje adimensional e impulso específico .................................... 27
Problema 8.
Estatorreactor ........................................................................................................... 33
Problema 9.
Resistencia de entrada .............................................................................................. 36
Problema 10.
Compresor............................................................................................................. 39
Problema 11.
Turbina .................................................................................................................. 44
Problema 12.
Actuaciones de un UAV ......................................................................................... 47
Problema 13.
Actuaciones de un caza ......................................................................................... 51
Motor cohete ................................................................................................................................ 56
Problema 1.
Calculo de empujes y de áreas de un motor cohete................................................. 56
Problema 2.
Aplicación de la segunda ley de Newton .................................................................. 63
Problema 3.
Sistema de defensa antiaérea basado en misiles ..................................................... 66
Problema 4.
Perdidas por efecto de la no uniformidad ................................................................ 70
Problema 5.
Tobera aerospike ...................................................................................................... 72
Problema 6.
Estudio de tobera utilizando el método de las características ................................. 76
Problema 7.
Cohete de agua ......................................................................................................... 85
Problema 8.
Diseño de una tobera ideal bidimensional ............................................................... 88
Problema 9.
Efecto de partículas en el flujo .................................................................................. 95
-3-
Andrés Zarabozo Martínez
Propulsión. Problemas
1. Aerorreactores
Problema 1. Consumo específico respecto al peso del motor
El principal objetivo de los desarrolladores de motores es obtener un consumo específico de
combustible mínimo. Menos combustible quemado permite más carga de pago en los aviones. Pero
desafortunadamente la reducción en el consumo específico de combustible implica motores más
grandes y pesados (debido a relaciones de presiones mayores y relaciones de derivación).
Asumiendo que la masa de la aeronave al principio del vuelo en crucero es
, y que tanto la
relación entre la sustentación y la resistencia ( ) y el consumo específico del empuje
son
constantes para todo el vuelo de crucero. Se pide lo siguiente
a. Encontrar la masa de combustible en crucero
como una función de
y .
b. Para el caso de un vuelo de corto/medio alcance (con
), simplificar la expresión
anterior, considerando una masa media de la aeronave ̅
(
Asumiendo que el incremento del peso y la reducción de afectan a ̅ y
factores
y
, y usando la expresión encontrada en b, se pide
)⁄ .
, respectivamente con
c. Encontrar la relación entre
y , y otros parámetros (según sea necesario) que impliquen
que una mejora en no sea interesante (el incremento en el peso del motor no implica un
ahorro en combustible).
-4-
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a.
(
)
Se utiliza la ecuación de Breguet para el caso de turborreactor
Se busca ahora despejar la masa de combustible
.
⁄
⁄
(
⁄
)
⁄
Finalmente
⁄
(
)
b.
La ecuación obtenida puede simplificarse mediante series de Taylor. La serie de Taylor de la función
exponente es
En esta serie cuando
es muy pequeño (
) se pueden eliminar términos. Una primera
simplificación sería utilizando solo un término de la serie para la función de la masa de combustible.
⁄
⁄
(
Ahora se simplifica otra vez la función
⁄
)
⁄
pero con dos términos
⁄
-5-
(
⁄
)
Andrés Zarabozo Martínez
Propulsión. Problemas
[
(
⁄
(
⁄
)
⁄
(
⁄
) ]
⁄
)
⁄
El término que está entre paréntesis se puede reemplazar utilizando la simplificación de un solo
término.
(
⁄
Considerando una masa media de la aeronave ̅
)
)⁄ .
(
̅
⁄
c. Ahorro de combustible con motor nuevo
Se utiliza la siguiente simbología, para el nuevo motor su gasto de combustible es
. Se
considera que el nuevo motor tiene un incremento de peso
y una disminución en el consumo
específico.
̅
⁄
̅(
⁄
)
(
)
Cogiendo primero la ecuación del nuevo motor
̅(
⁄
⁄
⁄
)
̅
(
̅
(
(
)
)
)
El ahorro de combustible es
⁄
̅
(
)
El incremento de peso tiene que ser menor al ahorro de combustible para que sea útil el nuevo
motor.
̅
⁄
(
̅
⁄
-6-
(
)
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 2. Parámetro de flujo de masa en función de Mach
Considerando un flujo unidimensional a través de un conducto con variaciones leves de su área
transversal ( ), demuestra que el flujo de masa ̇ puede expresarse como una función del Mach
local , la presión total , la temperatura total y el área:
̇
̅(
)
√
) se denomina parámetro de flujo de masa. Grafica esta función y encuentra el
La función ̅ (
) llega a su máximo.
número de Mach donde ̅(
-7-
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Consideramos un depósito como el que se ve en la Figura 1.1. Las condiciones son estacionarias, se
desprecia la fricción de las paredes y no hay adición de calor (por lo que las condiciones de remanso
se mantienen constantes).
̇
Figura 1.1. Diagrama de la sección del flujo
Se busca que condiciones tiene el fluido respecto a las condiciones de remanso.
El flujo másico se define como ̇
. De la ecuación de continuidad se puede afirmar que el
flujo másico es constante para todo el tubo de salida. Suponiendo la teoría de gas perfecto.
̇
√
√
√
Se estudia ahora la presión y la temperatura respecto a las condiciones de remanso
[
]
Introduciéndolo en la ecuación del flujo
̇
√
√
[
]
√
√
[
]
(
)
Esta ecuación es general tanto si se conserva o no la presión de remanso. La diferencia es que si se
conserva se puede poner en función de la presión de remanso en la condición (inicial). Con esta
-8-
Andrés Zarabozo Martínez
Propulsión. Problemas
expresión se puede relacionar el número de Mach de una sección con el número de Mach en otra
sección, ya que las únicas variables no constantes serían y .
√
√ [
]
[√ (
)
(
)
√ [
√
(
)
]
[√ (
̅
̅
(
]
)
(
)
)
]
Donde ̅ es el parámetro de flujo de masa.
Para un valor dado de , en términos de número de Mach, el parámetro de flujo de masa varía como
se observa en la Figura 0.1 (tabulada para
). La Tabla 0.1 muestra valores de la función de
parámetro de flujo de masa y es muy útil para otros ejercicios, sobre todo en el estudio de
actuaciones.
Buscando el máximo de la función se encuentra que el máximo coincide con condiciones sónicas.
̅
(
)
(
)
(
)
(
)
(
)
(
)
γ = 1.4
0.80000
Parámetro de flujo de masa
0.70000
0.60000
0.50000
0.40000
0.30000
0.20000
0.10000
0.00000
0.00
1.00
2.00
3.00
Número de Mach
-9-
4.00
5.00
6.00
Andrés Zarabozo Martínez
Propulsión. Problemas
Figura 1.2. Gráfico de ̅ en función de
̅
̅
̅
̅
Tabla 1.1. Valores de ̅ en función de
- 10 -
̅
̅
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 3. Variaciones del flujo en función del Mach
De la ecuación de continuidad y conservación de cantidad de movimiento para un flujo casi
unidimensional e isentrópico, obtener una relación diferencial en términos de la velocidad , sección
y número de Mach .
-
Ecuación de continuidad:
Ecuación de conservación de la cantidad de movimiento:
Flujo isentrópico:
- 11 -
⁄
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
De la ecuación de continuidad se puede hacer una ecuación diferencial
(
)
Se quiere combinar la ecuación diferencial con la de conservación de cantidad de movimiento.
Se multiplica la ecuación de continuidad por ⁄
Estas dos ecuaciones se pueden restar.
Se toma ahora la ecuación del flujo isentrópico y se crea una ecuación diferencial.
Ya que la velocidad del sonido es √
. Ahora se junta con la relación derivada de la resta entre la
ecuación de continuidad y conservación de cantidad de movimiento
(
)
(
)
(
)
Y también utilizando
- 12 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Se obtiene
(
)
Utilizando la ecuación de conservación de cantidad de movimiento (
(
) se tiene
)
(
)
De estas últimas ecuaciones se puede deducir que si el régimen es subsónico los signos del
diferencial de densidad y el área van en paralelo, o sea aumento de área significa un aumento de
densidad. También se deduce que si el área aumenta la velocidad disminuye
En cambio si el régimen es supersónico pasaría al revés, un aumento de área disminuiría la densidad,
y también un aumento de área implica un aumento de velocidad.
También se puede llegar a la conclusión que para Mach igual a uno el diferencial de área es cero. Eso
significa que la condición sónica ocurre en el tramo de área mínima(o también denominado en las
toberas, cuello).
- 13 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 4. Problema teórico
). Encontrar la función de la
Graficar el ciclo ideal de un motor turborreactor en un diagrama (
eficiencia térmica en términos de las temperaturas de las etapas del turborreactor. Simplificar la
expresión lo máximo posible considerando aplicable las relaciones termodinámicas, e indicando,
para unas condiciones de vuelo dadas, el efecto de y en la eficiencia térmica.
Nota: y deben considerarse independientemente (en el análisis del diseño), en otras palabras,
no están relacionados.
- 14 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
El diagrama (
) para un motor ideal es el mismo que el estudiado en el libro “Propulsión. Teoría”.
La Figura 1.3 muestra el ciclo de un motor ideal.
Figura 1.3. Diagrama del ciclo de un motor ideal
El rendimiento térmico es un concepto teórico que expresa una relación entre la energía cinética de
un flujo y la energía calorífica de la combustión. Es una forma de cuantificar la eficiencia del motor
en el cambio de tipo de energía.
( ̇
̇ )
̇
̇(
̇
)
̇
̇
̇
Haciendo la hipótesis de que
(
)
̇
(
(
̇
)
(
)
)
- 15 -
(
(
De la igualdad de trabajos compresor-turbina (despreciando el
(
)
(
) establece
)
)
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Volviendo al rendimiento térmico
En el ciclo ideal la entropía solo varía en la combustión. Entre el punto
pasa lo mismo entre el punto y . Se puede decir que
(
)
(
y
la isobára es la misma;
)
Finalmente el rendimiento térmico queda
Debido a que el
hace variar otros rendimientos, la solución de compromiso es el ( )
desarrollado en los apuntes de teoría.
- 16 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 5. Boeing 707
El Boeing 707 fue un avión de pasajeros de finales de los años . Tiene cuatro turborreactores Pratt
& Whitney JT3C-7 con las siguientes características en condiciones de nivel de mar
-
Ratio de presión
Temperatura de entrada de la turbina
Empuje
Asumiendo comportamiento ideal de todos los componentes, tobera convergente y aproximando
, se pide lo siguiente:
a. Flujo de aire ̇
b. Consumo de combustible ̇
Considerando un vuelo a
a una altitud de
, y considerando que se tiene la
misma relación de presiones del compresor ( ) y de la turbina ( ) de las operaciones a nivel de
mar, se pide:
c. El empujo unidimensional
d. El consumo específico de combustible
- 17 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Las condiciones estáticas significan que el avión está quieto en el suelo con los motores puestos en
marcha.
a. Caudal másico
Con la relación de compresión
se puede encontrar
.
Como se tienen condiciones ideales de todos los componentes
Se busca
sabiendo que esta en condiciones estáticas (
.
).
En la cámara de combustión se tiene
Del balance de potencia compresor-turbina se obtiene la relación de temperaturas y presiones de la
turbina
(
⁄(
)
(
)
)
⁄(
)
Como no se sabe qué tipo de tobera se tiene (solo se sabe que es convergente), se busca la relación
de presiones (ya simplificado por ser un motor ideal)
Si la tobera fuese adaptada
√
[(
)
(
)
]
√
[
(
)⁄
]
Este Mach no puede existir ya que la tobera es convergente, y en una tobera convergente el máximo
Mach posible es . Por lo tanto la tobera es crítica. Como regla general, para toberas convergentes,
se puede verificar que la tobera es crítica si la relación de presiones es mayor que
(
)
- 18 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Aunque en exámenes es necesario hacer el procedimiento anterior completo.
Se sabe que la tobera es crítica. Se debe calcular ahora la relación de presiones de salida y de
temperatura.
⁄
(
)
(
)
⁄
El empuje adimensional es
̇
√
√
√
√
(
)
El flujo másico se puede calcular de la siguiente forma
̇
( ⁄ ̇
)
⁄
√
b. Flujo de combustible
El flujo de combustible es
̇
̇
Donde
(
)
Si no se especifica otra cosa el valor de
(
⁄
es de
)
.
⁄
̇
c. Empuje adimensional
Se van a suponer los siguientes valores
-
se mantiene igual al calculado antes
y también se mantienen (debido a las suposiciones anteriores)
Para saber si la tobera está en condiciones críticas o no, como regla general si la tobera al nivel del
mar es crítica, en vuelo de crucero es “aún más crítica”.
También se deben calcular
y
- 19 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Del balance de potencia compresor – turbina se tiene
(
(
)
)
(
)
La relación de temperaturas queda
La de presiones (inversa)
(
)
(
)
El empuje adimensional se calcula de forma similar que en los primeros apartados.
̇
√
√
(
)
√
(
√
d. Consumo específico
Sabiendo que para las condiciones de vuelo dadas (ISA)
⁄
√
Se calcula ahora el coeficiente
(
)
(
)
El impulso específico es
̇
̇
̇
- 20 -
̇
)
Andrés Zarabozo Martínez
Propulsión. Problemas
̇
El consumo específico es
⁄
̇
Otra forma de escribir este consumo específico pero en otras unidades es
⁄
Esto significa que para dar un kilo de fuerza consume
- 21 -
de combustible por hora.
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 6. Turbofán para el B707
Considera un turbofán que reemplace los motores del Boeing 707 del Problema 5, asumiendo:
-
el mismo empuje
los mismos parámetros
y
estáticas
una relación de derivación
una relaciones de presión del fan
operando a nivel del mar en condiciones
Asumiendo un comportamiento ideal de todos los componentes, toberas convergentes y
aproximando
, se pide lo siguiente
a. Flujo másico ̇ (flujo primario)
b. Consumo de combustible ̇
Considerando un Mach de vuelo
ratio de presiones del compresor
y turbina
a una altura de
, y asumiendo el mismo
de las operaciones a nivel del mar, se pide
c. El consumo específico de combustible
- 22 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a. Flujo másico
La relación de temperaturas es igual que en el caso del turborreactor.
Se recuerda que pese a que se sabe que el motor tiene componentes ideales siempre se debe
escribir la ecuación completa e indicar que
.
La relación de temperaturas del fán es
Sabiendo que se está en condiciones de nivel del mar y estáticas
{
De la relación de potencias compresor – turbina se sabe
[
(
[
)]
(
)
(
Las relaciones de presiones son
Se debe verificar que toberas se tienen
(
)
(
)
Tanto la tobera primaria como la secundaria son adaptadas.
- 23 -
(
)
)]
Andrés Zarabozo Martínez
Propulsión. Problemas
√
)
[(
√
)
[(
√
]
[
]
√
}
{ √
(
)
]
[
]
{
{
El empuje adimensional queda
̇
{√
[
(
)]
[
(
)]
}
√
̇
√
̇
̇(
)
⁄
b. Consumo de combustible
Se calcula primero el coeficiente de presión
(
)
̇
(
)
⁄
̇
̇
c. Consumo específico de combustible
Se mantienen constantes los siguientes parámetros
Al cambiar de altura se debe calcular la nueva temperatura ambiente y la nueva velocidad del sonido
( )
(
)
- 24 -
Andrés Zarabozo Martínez
Propulsión. Problemas
⁄
√
√
Al cambiar la velocidad de vuelo se cambian los parámetros
y
.
De la relación de potencia compresor – turbina se obtiene
[
(
[
)]
(
)]
Se calculan las relaciones de presiones de remanso en la tobera.
{
Ambas toberas son críticas ya que ambas relaciones son mayores que
relaciones de temperatura y presión en la tobera
.Se calculan las
{
(
)
(
{
(
)
)
(
)
El empuje adimensional es
{√
̇
(
[
{√
El factor
[
)]
(
)]
}
{ √
}
{
√
[
(
[
)]
(
)]
es
(
)
(
- 25 -
)
}
}
Andrés Zarabozo Martínez
Propulsión. Problemas
Finalmente se puede calcular el consumo específico.
̇
̇
̇
⁄ ̇
- 26 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 7. Variaciones del empuje adimensional e impulso específico
Dadas las siguientes condiciones de vuelo
-
Altitud de crucero,
Número de Mach de crucero,
Se pide encontrar los valores óptimos (en términos del máximo impulso específico para máximo
empuje) de
y
y los valores de los parámetros adimensionales de
y , cuando se
incremente de a
(en una gráfica).
Usar los siguientes valores
⁄
⁄(
- 27 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Se resolverá el problema tomando un solo valor de
. El problema pide hacer lo mismo para
poder ver gráficamente la variación del impulso específico y el empuje adimensional en función del
parámetro .
Para
y
Ahora se busca el valor de
sabiendo que el motor es óptimo.
(
Se reemplaza √
)(
(√
)
)
√
por
(
[(
)(
)(
(
)
)](
)
)
(
)
Esta ecuación se resuelve de forma iterativa. Dará dos soluciones, pero como
se descarta una
de las soluciones. Normalmente se prueba aislando el valor de de mayor potencia.
√[(
)(
√[(
)(
√
)](
)](
(
El vuelo se desarrolla a
La temperatura ambiente a esa altura es
(
)
( )
Se puede sacar la temperatura de entrada de las turbinas
- 28 -
)
)
)
Andrés Zarabozo Martínez
El
Propulsión. Problemas
correspondiente es el óptimo y queda
√
( )
Se calcula ahora
y
(
)
(
(
)
)
(
[
⁄(
)
(
⁄(
)
[
)]
)
(
)]
Las toberas en este problema son adaptadas ya que es caso óptimo
La tobera del primario es convergente ya que el valor es menor que la relación crítica (
).
La tobera del flujo secundario es convergente – divergente. En contrario a lo que dice la teoría (aquí
calculada), en la práctica no se emplearía una tobera convergente – divergente ya que solo serviría
para estar en condiciones óptimas en estas condiciones en concreto. Una tobera con geometría
variable tampoco sería una buena solución. Por compromiso se usa una tobera convergente ya que
la pérdida de potencia no es tan significativa en comparación con los problemas que causaría utilizar
el otro tipo de tobera.
Para verificar que lo que se ha hecho está bien se comprueban las velocidades de escape (deben de
ser iguales ya que son ambas adaptadas), se calcula primero el número de Mach y luego la velocidad
de escape
- 29 -
Andrés Zarabozo Martínez
Propulsión. Problemas
[
√
√
[
]
√
[
]
]
√
[
]
(
√
√
)
⁄
√
√
(
)
Efectivamente ambas velocidades son iguales.
El empuje adimensional es
̂
(
̇
(√
[√
)
)
(
)(
](
)
)
̂
El impulso específico es
√
(√
√
)
(
)(
)
Se han usado los siguientes valores
⁄
⁄(
)
√
El impulso específico adimensional es
√
̂
√
(√
(
)
)(
̂
- 30 -
)
⁄
⁄
Andrés Zarabozo Martínez
Para valores distintos de
Propulsión. Problemas
se sigue el mismo procedimiento obteniendo los siguientes resultados
̂
̂
Tabla 1.2. Valores del problema para distintos
Empuje adimensional
7
6
5
4
F
3
2
1
0
0
2
4
6
8
α
Figura 1.4. Empuje adimensional respecto a
- 31 -
10
12
14
Andrés Zarabozo Martínez
Propulsión. Problemas
Impulso específico
9000
8000
7000
6000
5000
Isp
4000
3000
2000
1000
0
0
2
4
6
8
10
12
14
α
Figura 1.5.Impuslo específico respecto a
Impulso específico adimensional
0.3
0.25
0.2
Îsp 0.15
0.1
0.05
0
0
2
4
6
8
10
α
Figura 1.6. Impulso específico adimensional respecto a
- 32 -
12
14
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 8. Estatorreactor
Se supone un avión equipado con un estatorreactor en vuelo supersónico en la estratosfera. Se le
añade un buen diseño de la entrada de aire con geometría variable para evitar fuertes ondas de
choque. En vez de una onda de choque aparecen muchas ondas de menor potencia, y la velocidad se
reduce hasta el motor a una velocidad subsónica con perdida negligible de la presión de remanso.
Además, una geometría variable de la tobera permite un flujo de salida adaptado a la presión de
ambiente para cualquier condición de vuelo.
Considerando conocidos todos los datos relacionados con el motor, comportamiento ideal de los
componentes del motor y una fracción de flujo de combustible negligible, se pide
a. Representar en un diagrama
el ciclo del motor, y encontrar el número de Mach de
salida
b. Calcular el área de captura
como una función del número de Mach de vuelo ( ) y otros
parámetros si fuese necesario
c. Calcular el ratio ⁄ como función de
y de otros parámetros si fuese necesario
Entrada
Cámara de combustión
Figura 1.7. Diagrama de etapas del estatorreactor
- 33 -
Tobera
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a. Diagrama
El diagrama (
) para un motor ideal es parecido que el estudiado en el libro “Propulsión. Teoría”,
pero adaptado a un estatorreactor ideal. La Tabla 1.3 muestra las distintas etapas del
estatorreactor. La Figura 1.8 muestra el ciclo del estatorreactor ideal.
Etapa
Proceso
características
Compresión adiabática sin trabajo añadido
crecen, constante
Adición de calor
constante,
crecen
Expansión adiabática sin trabajo extraído, cambio de
disminuyen,
volumen
constante
Tabla 1.3. Etapas de un estatorreactor ideal
Figura 1.8. Diagrama del ciclo de un estatorreactor ideal
b. Calcular el área de captura
Al ser tobera adaptada
.
√
[(
- 34 -
)
]
Andrés Zarabozo Martínez
Propulsión. Problemas
√
)
[(
]
Pese a que los números de Mach sean iguales no significa que las velocidades lo sean
√
√
Hay que introducir ahora la condición de que el flujo de entrada es igual al flujo de salida por las
toberas (ya que se ha despreciado la adición del combustible). Se elige el punto 8 que es la garganta
de la tobera, en este punto el número de Mach es 1.
̅(
̇
)
√
Se calcula ahora el flujo en la sección 0. Al ser supersónico se puede elegir ese punto donde se
quiera ya que la información del flujo supersónico no viajas aguas arriba. Se decide que el punto está
en la punta.
̇
̅
√
Los flujos son iguales
̅
̅
√
)
̅(
̅(
√
̅(
)
) √
̅(
√
)
Los valores de ̅ se obtienen a través de tablas tabuladas para el .
c. Calcular el ratio
⁄
La relación de áreas es igual a la relación de ̅ , ya que
̇
̅(
)
̅
√
̅
̅
- 35 -
̅
√
̅(
̅(
)
)
√
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 9. Resistencia de entrada
Asumiendo un flujo unidimensional, aplicar la ecuación de conservación de cantidad de movimiento
en el tune de flujo mostrado en la figura, entre los puntos (0) y (1), y obtener la resistencia de
entrada dada por la integral
( )
∫
(
)⃗
( )
Obtener una expresión asintótica para
.
Figura 1.9. Volumen de control utilizado
- 36 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Se empieza calculando la ecuación de conservación de cantidad de movimiento
(
∫
∫ (
)
∫ (
)(
(
∫
)⃗
∫
∫ (
)
)[
(
⃗( ⃗
⃗ )⃗
)[
(
)⃗
)
(
∫
)(
)]
∫ ⃗ ( ⃗ ⃗)
El último término es cero ya que la superficie 2 se define por unas líneas de corriente donde la
velocidad es perpendicular al vector normal del plano.
∫ (
)⃗
Físicamente la integral de la normal por la superficie en un volumen cerrado es nula.
∫
⃗
∫ ⃗
Volviendo a la ecuación de conservación de la cantidad de movimiento
∫ (
)⃗
Se multiplica escalarmente por .
(
)
(
(
)
(
)
(
)
)
Esta expresión es siempre positiva aunque ya se fijó el signo según el convenio de signos del empuje.
Ahora se fija el
para ver como afecta el flujo de entrada. Se adimensionaliza la expresión
(
)
(
)
La relación de presiones se encuentra de la siguiente forma
(
)
(
- 37 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
(
(
(
)
)
)
La relación de áreas es igual a la relación de ̅ (parámetro de flujo de masa), ya que
̇
̅
̅(
)
√
̅
√
√
̅
̅
Se introducen estos valores en el Excel y se obtiene la siguiente gráfica mostrando que la resistencia
de entrada es siempre positiva.
- 38 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 10. Compresor
Se quiere realizar un proyecto preliminar de un compresor axial para un turborreactor bajo los
siguientes criterios:
-
Relación de presión:
Etapas repetidas
Filas repetidas
Velocidad axial constante a lo largo del compresor
Angulo de entrada:
Temperatura de entrada:
Número de mach de entrada:
La tecnología accesible permite los siguientes valores:
-
Eficiencia politrópica de la etapa:
-
Eficiencia politrópica del rotor:
-
Máximo incremento de temperatura por etapa:
( )
)⁄
(
Se pide lo siguiente
a.
b.
c.
d.
e.
f.
g.
La eficiencia politrópica global (para el compresor entero)
La eficiencia isentrópica global
El número mínimo de etapas
La velocidad del compresor
La distribución de presiones totales a lo largo del compresor
La distribución de la presión y temperatura (estática) a lo largo del compresor
La distribución de áreas de paso de las palas a lo largo del compresor
- 39 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a. Eficiencia politrópica global
En este tipo de problema se suele utilizar la terminología con subíndice que significa “inlet” (o de
entrada) para la primera etapa.
( )
Se puede encontrar primero
⁄
√
√
Se hace la suposición que el compresor tiene etapas. Se define el
del motor como la relación de
presiones de salida de la última etapa y la presión de entrada de la primera etapa.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
Estos valores de relación de presión de cada etapa no son iguales.
(
( )
)
(
( )
( )
( )
( )
( )
( )
( )
( )
( )
(
(
( )
)
(
( )
)
)
)
Obteniendo una demostración de lo que se estudió en el tema del turborreactor. Es importante
notar que esto no es extrapolable para el rendimiento isentrópico.
b. Eficiencia isentrópica global
Como se sabe
⁄(
- 40 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
La eficiencia isentrópica es
c. Número mínimo de etapas
Se sabe que el incremento de temperatura total es
( )
( )
( )
( )
( )
[
]
Por lo tanto el número de etapas es
( )
(
[
]
)
Utilizando valores numéricos
( )
(
( )
(
)
)
(
(
)
)
(
)
Este es el incremento que se tiene que conseguir con la suma de etapas. Como máximo cada etapa
puede producir solo
.
(
)
d. Velocidad del compresor
La velocidad se consigue mediante la ecuación de Euler.
(
)
Donde
Además
Queda una ecuación lineal de segundo orden. La
tienen todos los datos para calcularla.
( )
La ecuación para encontrar
√
( )
es la velocidad tangencial a la entrada y se
√
queda
- 41 -
⁄
Andrés Zarabozo Martínez
Propulsión. Problemas
Esta ecuación tiene dos soluciones pero una será negativa por lo que directamente se pone la
solución positiva.
√
⁄
También es interesante calcular la velocidad absoluta a la salida del rotor.
√
(
√
)
(
√
)
⁄
e. Distribución de presiones totales a lo largo del compresor
La distribución se obtiene a partir de la distribución de temperaturas totales. Como son etapas
repetidas, entre estaciones homólogas de la etapa ( ) y la etapa ( ) se tiene
( )
( )
(
)(
)
(
)
(
(
)
)
Como son filas repetidas, entre estaciones de una misma etapa se tiene
( )
( )
( )
(
)
La presión total en la salida del rotor de la etapa ( ) respeto la presión total a la entrada de la etapa
( ) es
( )
( )
( )
( )
( )
( )
( )
(
(
f.
)
(
(
)
)
( )
( )
)
(
( )
(
)
(
)
)
Distribución de presiones y temperaturas estáticas
La temperatura estática en la entrada de la etapa ( ) respecto a la temperatura estática en la entrada
de la etapa ( ) es
( )
( )
(
)(
)
(
)
Entre estaciones de una misma etapa
( )
( )
( )
(
( )
)
(
(
)
)
Las presiones estáticas se obtienen a partir de las presiones totales, Mediante las correcciones por
número de Mach. Debido a que las velocidades se repiten de etapa en etapa, y que hay similitud
geométrica entre álabes del rotor y estator, los números de Mach se calculan de la siguiente forma
- 42 -
Andrés Zarabozo Martínez
Propulsión. Problemas
( )
( )
( )
( )
( )
√
√
( )
( )
√
(
)
( )
( )
√
√
√
( )
(
)
La presión estática en la entrada de la etapa ( ) respecto la presión estática a la entrada de la etapa
( ) es
( )
( )
( )
( )
[
(
( )
)
(
( )
)
( )
]
( )
[
(
( )
]
)
La presión estática en la salida del compresor de la etapa ( ) respecto a la presión estática en la
entrada de la etapa ( ) es
( )
( )
( )
( )
[
(
( )
)
(
( )
)
( )
]
( )
[
(
( )
]
)
g. Distribución de áreas de paso
De la ecuación de continuidad se tiene
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
La velocidad axial es constante.
( ) ( )
( ) ( )
( ) ( )
( ) ( )
Utilizando ahora la ecuación de los gases perfectos, se busca la relación de densidades.
( )
( )
( ) ( )
( )
( )
( ) ( )
( )
( )
( ) ( )
( )
( )
( ) ( )
( )
( )
( ) ( )
( )
( )
( ) ( )
Se pueden calcular a partir de las relaciones obtenidas en el apartado anterior. Como la densidad
aumenta a lo largo el compresor, las áreas de paso son cada vez más pequeñas. Cuanto más se
quiera comprimir se tiene que hacer álabes (o sección de paso) cada vez más pequeños y los efectos
viscosos son más notables haciéndolos menos eficientes.
Cuando el radio medio
es el mismo para todas las etapas, las relaciones de alturas de paso
coinciden con la relación de áreas, debido a las siguientes proporcionalidades
( )
( )
( )
( )
- 43 -
( )
( )
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 11. Turbina
Se pide diseñar una etapa de turbina (encontrar
asumiendo las siguientes condiciones:
-
Flujo axial en la entrada y la salida
constante
⁄
⁄
Calcular también el valor de ( ̇ ⁄ ̇ )
- 44 -
y
) para potencia máxima ( ̇ ⁄ ̇ ),
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Se calcula el número de mach del movimiento del rotor.
√
√
De la ecuación del grado de reacción
(
Se multiplica la ecuación de
por
)
(
)
, obteniendo
(
)
Utilizando ahora la igualdad derivada de la optimización del parámetro
(
)
(
)
Se obtiene
(
(
)
)
Esto es un polinomio de orden dos, por lo que se obtienen dos soluciones para
una por ser negativa.
Se puede encontrar el ángulo
Se busca ahora
partiendo de la siguiente ecuación
- 45 -
, pero se descarta
Andrés Zarabozo Martínez
Propulsión. Problemas
(
(
)
)
(
(
)
(
(
)
)
(
(
)
(
)
)
)
(
(
)
Haciendo un cambio de variable
(
)
(
)
(
)
(
)
(
)
Este polinomio tiene seis ecuaciones pero se toman solo la solución real
√
√
Se calcula la temperatura de remanso en el punto entre el estator y el rotor.
El ratio ̇ ⁄ ̇ se determina mediante su definición como
̇
( )
̇
√
√
√
√
̇
( )
̇
⁄
- 46 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
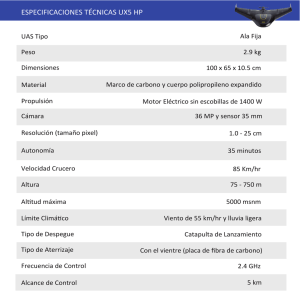
Problema 12. Actuaciones de un UAV
Para propulsar un UAV de reconocimiento se considera la posibilidad de utilizar como planta
propulsora un turborreactor de flujo simple. Los requisitos de diseño en operación estática a nivel
del mar ISA son:
-
Empuje
Relación de compresión
Temperatura de entrada a turbina
Toberas convergentes
De acuerdo con estos requisitos y suponiendo componentes ideales, se pide:
a. Comprobar que la tobera es crítica y calcular el caudal másico de aire
b. Determinar la temperatura
por debajo de la cual, operando en estático a nivel del mar
ISA, la tobera deja de ser crítica.
Solo para el apartado siguiente, suponer que para cada etapa completa del compresor el
rendimiento politrópico vale
, con una configuración de etapas repetidas, filas repetidas y
velocidad axial constante. Suponiendo también que el incremento máximo de temperatura total por
etapa es ( )
, y el flujo de entrada a cada etapa es axial, y a la entrada del comresor es
, calcular:
Número mínimo de etapas necesarias para conseguir la relación de compresión de diseño y área de
entrada al compresor, teniendo en cuenta el caudal másico encontrado en el apartad a. (si no se ha
⁄ ).
calculado, tomar ̇
- 47 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a. Comprobación de la tobera y caudal másico
Lo primero que se busca es
Sabiendo la temperatura en la entrada del compresor
De la ecuación de la relación de potencia compresor – turbina (sabiendo que en operación estática
.
(
)
(
)
Se comprueba que tobera se tiene
Se tiene tobera crítica.
(
)
(
√
√
√
)
El empuje adimensional para tobera crítica queda
̇
√
√
(
(
)
)
Se obtiene el flujo másico
̇
⁄
⁄ ̇
⁄√
⁄
b. Temperatura
Se sabe que la tobera es crítica
- 48 -
Andrés Zarabozo Martínez
Propulsión. Problemas
(
Por otro lado, sabiendo que
)
(
)
es constante, y como hay condiciones estáticas (
), se tiene que
Si la tobera fuese adaptada
(
)
(
)
Utilizando la ecuación del balance de potencia
Obteniendo, multiplicando por la temperatura ambiente
c. Número mínimo de etapas y área de entrada
Ahora se tiene que considerar un rendimiento por lo que los cálculos se tienen que hacer desde el
principio.
(
)
(
La temperatura en la salida del compresor (tomando
)
) es
Obteniendo una diferencia de temperaturas entre la entrada y la salida del compresor de
El número de etapas por lo tanto queda
[
(
)
]
[
El caudal másico se obtiene como
- 49 -
]
[
]
Andrés Zarabozo Martínez
Propulsión. Problemas
̇
̅(
)
√
En el problema 2, se obtiene una tabla con los valores de la función parámetro de flujo de masa
tabulados para
̇
̅(
√
(
̅
)
√
)
- 50 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 13. Actuaciones de un caza
Un caza de combate está propulsado por un motor turbofán, con una geometría variable
convergente – divergente, teniendo siempre condiciones de tobera adaptada. Inicialmente la
aeronave vuela a
con las siguientes características
Asumiendo comportamiento ideal en todos los componentes y despreciando el flujo de masa de
combustible con respecto al flujo de aire, se pide lo siguiente
a. Calcular el consumo de combustible en las condiciones de operación descritas
b. Obtener la relación de áreas
El piloto precede a interceptar un avión enemigo que vuela a una altitud de
y avanza la
palanca de potencia para obtener potencia máxima (con
). La operación consiste en dos
fases: ascender con Mach constante (
) hasta la altitud final (
), seguido de una
aceleración horizontal hasta llegar a un Mach de
. Se pide lo siguiente
c. El empuje del motor a
El flujo de aire a
y
y
con
con
- 51 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a. Consumo de combustible
Se utiliza el modelo ISA para encontrar la presión y la temperatura ambiental.
(
(
)
)
(
(
)
)
(
)
El coeficiente de presión se obtiene de la siguiente forma
⁄(
También se calcula
)
y
( )
(
)
La fracción de combustible se calcula de la siguiente forma
(
)
Recordar que en esta fórmula
⁄ .
contrario
(
)
no es la altitud sino que es el poder calorífico, si no se dice lo
De la ecuación del balance de potencia se aísla
(
)
(
)
( )
Al ser tobera adaptada
√
[(
)
]
√
- 52 -
[(
)
]
Andrés Zarabozo Martínez
La relación
⁄
Propulsión. Problemas
es
√
√
Donde
El flujo de masa se calcula utilizando la fórmula del empuje adimensional
̇
[(
̇
)
]
[
√
⁄
]
Por lo tanto el consumo de combustible
( ̇ )
⁄
̇
b. Relación de áreas
Debido a la conservación de masa se puede utilizar la ecuación de continuidad (por lo tanto flujo de
masa entrante igual a saliente)
̇
̅(
)
√
√
̅(
√
)
√
La relación de áreas queda
̅(
̅(
)
)
( )
(
)
(
)
(
)
c. Empuje del motor a
Debido a que se ha empujado la palanca de gas para dar más potencia, se han cambiado las
condiciones de vuelo. Generalmente lo que cambia la palanca de gas es la temperatura en la salida
de la combustión. Ahora se tiene
La fuerza a
con el nuevo ajuste de temperatura se denomina
se utilizara para otras variables con el nuevo ajuste.
̇
(
̇
, este tipo de connotación
)
Debido a que se han cambiado las condiciones, la relación de compresión del compresor también
habrá cambiado. Hay que recordar que solo se mantiene constante la relación de presiones de la
turbina.
- 53 -
Andrés Zarabozo Martínez
Propulsión. Problemas
(
)
(
)
( )
Para el cálculo del flujo másico se suele utilizar el parámetro de flujo para
unidad.
̇
̅(
)
̅(
)
̇
√
̇
√
ya que este es la
√
√
√
√
⁄
Al ser tobera adaptada
(
)
√
)
[(
]
√
[(
( )
La relación
⁄
es
√( )
√
Se calcula el empuje adimensional (teniendo tobera adaptada)
(
̇
)
(
)
- 54 -
)
]
Andrés Zarabozo Martínez
Propulsión. Problemas
Finalmente el empuje es
(
)
̇
√
̇
d. Flujo másico a
En este apartado se vuelven a cambiar las condiciones de vuelo. Como también se cambia la altura
se debe volver a calcular la presión y la temperatura ambiente. Hay que tener cuidado ya que la
altura en la que se desarrolla este apartado es
y se está por encima del límite de la
troposfera.
(
(
)
(
)
(
)
Se vuelven a calcular
(
)
(
)
ya que ahora se tiene
(
)
)
y
(
)
⁄
√
√
La nueva relación de compresión del compresor se calcula otra vez utilizando el balance de
potencias
(
)
(
(
)
)
Se calcula ahora el flujo másico de forma similar al apartado anterior
̇
̅(
)
̇
( )
( )
̅(
√
( )
( )
√
)
( )
( )
̇
√
⁄
- 55 -
√
√
̇
√
√
Andrés Zarabozo Martínez
Propulsión. Problemas
2. Motor cohete
Problema 1. Calculo de empujes y de áreas de un motor cohete
Un motor cohete para un lanzador orbital tiene las siguientes características:
-
⁄
⁄
Se pide
a. Calcular la velocidad característica y el gasto por unidad de área de garganta
b. Calcular el coeficiente de empuje al despegue. Nota: verificar que existe desprendimiento
del flujo en esta condición
c. Dimensionar las áreas
y
tal que el empuje al despegue sea
. Calcular el
flujo másico y el impulso específico correspondientes.
d. Determina a qué altitud (atmósfera ISA) dejará de desprenderse el flujo, y calcular el empuje
y el impulso específico en este punto.
e. Determinar a qué altitud estará adaptada la tobera, y calcular el empuje y el impulso
específico en este punto
f. Determinar el empuje y el impulso específico en el vacío
- 56 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a. Velocidad característica
y gasto ̇ ⁄
Se calcula primero el factor ( ), sabiendo que
( )
La constante del gas
√ (
)
(
)
√
(
)
(
)
se calcula a partir de la constante universal
Nota: son más eficientes los propulsantes con una constante
propulsantes con peso molar bajo.
alta, y por lo tanto son mejores los
La velocidad característica se obtiene a partir de la siguiente ecuación
√
(
El gasto ̇ ⁄
√
⁄
)
es
⁄
̇
b. Coeficiente de empuje al despegue
Cuando las toberas están demasiado sobre expansionadas (se asume que en este punto la tobera
está sobre expansionada ya que se está lanzando el cohete al nivel del mar) aparece un
desprendimiento de flujo en la tobera.
El coeficiente de empuje es
(
)
( (
))
Todos los parámetros del coeficiente de empuje dependen del número de Mach (como se ha
demostrado en la teoría), por lo tanto es lo primero que se debe calcular.
La relación de áreas es un dato del enunciado ⁄
. Como se sabe que la relación de
áreas solo depende del Mach y de se tiene una expresión para obtener el número Mach.
(
(
)
- 57 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Para resolver el valor del número de Mach se pueden utilizar métodos numéricos iterativos o utilizar
los valores tabulados de las tablas del parámetro de flujo, ya que también esta expresión es igual a la
relación del parámetro de fulo de masa. Para casos de motores cohete es muy útil utilizar tablas
tabuladas del parámetro del flujo de masa para valores de
y
.
̅
̅
̅
̅
Se sabe que el parámetro ( ) coincide con el valor de parámetro de flujo de masa para el caso
sónico. En la garganta se tienen esas condiciones.
(
̅
De las tablas tabuladas para
)
se obtiene que el Mach de salida es
Si se resolviese de forma iterativa
(
(
)
(
(
)
)
)
√(
)
Empezando por un valor supersónico de por ejemplo
las iteraciones
, se obtienen los siguientes valores en
Por lo que la solución coincide con la obtenida en las tablas,
.
Calculando el coeficiente de empuje en el vacío se obtiene
(
)
(
)
(
)
(
)
√
√
- 58 -
⁄
Andrés Zarabozo Martínez
Propulsión. Problemas
Obteniendo finalmente el coeficiente de empuje
( )
Pero como se dijo antes la tobera está sobreexpansionada y es posible que haya desprendimiento de
flujo. Si hubiese desprendimiento de flujo este valor del coeficiente de empuje no sería el correcto.
Se debe comprobar que no haya desprendimiento y si lo hubiese recalcular el coeficiente de empuje.
La relación de presiones entre la salida y la cámara es
(
)
(
)
Debido a que la presión de salida es menor a
veces la presión ambiente (
),
tiene desprendimiento de flujo y por lo tanto el coeficiente de empuje es incorrecto.
Se debe buscar la relación de áreas ⁄ , donde
de choque y empieza el desprendimiento.
Se sabe que en esta sección
, se
es la sección de salida donde se genera la onda
, por lo tanto
Utilizando la expresión de la relación de presiones se obtiene el Mach de salida (corregido debido al
desprendimiento).
(
√
[(
⁄
)
)
]
√
[(
)
]
El coeficiente de empuje en vacío cambia ya que el número de Mach se ha modificado
(
)
(
)
(
)
(
)
√
√
- 59 -
Andrés Zarabozo Martínez
Propulsión. Problemas
La relación de áreas es
̅
̅
(
)
√
√
(
(
)
)
(
)
(
)
Finalmente se puede recalcular el coeficiente de empuje
(
)
(
)
c. Dimensionar las áreas, calcular el flujo másico y el impulso específico
El empuje es seiscientas toneladas.
Además se puede definir el empuje como
Donde
Por lo tanto
(
)
Físicamente el área de salida es la que da el enunciado (con la relación de áreas), el área efectiva
solo se utiliza para encontrar el empuje.
El flujo másico Queda
̇
(
̇
⁄
)
El impulso específico queda
̇
Con este impulso específico se podría afirmar que el cohete utiliza combustible líquido.
d. Altitud, empuje e impulso, cuando deja de haber desprendimiento
Se debe calcular la altura en la cual la presión de salida (en la sección del final de la tobera) sea
. En el apartado b se obtuvo el número de Mach y la relación de presiones ⁄ . Se debe
calcular la altura donde la presión ambiente es
. En el apartado de b se obtuvo que
- 60 -
Andrés Zarabozo Martínez
Propulsión. Problemas
[
(
])
(
)
De las ecuaciones ISA se sabe
(
(
)
)
(
)
⁄
El coeficiente de empuje en el vacío que se obtuvo en el apartado b sin la corrección de
desprendimiento coincide con el coeficiente a esta altura.
[
]
(
)
En toneladas
(
)
El empuje ha aumentado debido a que se reduce el efecto de estar sobreexpansionada a medida
que aumenta la altura y disminuye la presión. El impulso específico aumentará también en la misma
proporción ya que el flujo másico y la aceleración de la gravedad se mantienen constantes
(
e.
)
(
)
(
)
(
)
Altitud para tener tobera adaptada, calcular empuje e impulso específico
Se sabe que
. De las ecuaciones ISA se debe encontrar el punto en el que la presión
atmosférica es igual a esta presión
(
) (
)
Se hace una hipótesis: suponer que la altura no excede los
otra ecuación de la ISA.
(
)
(
ya que si no habría que utilizar
)
⁄
El coeficiente de empuje cuando se tiene tobera adaptada es igual a
- 61 -
Andrés Zarabozo Martínez
( )
(
)
(
Propulsión. Problemas
)
(
)
(
)
√
√
El empuje queda
(
)
El impulso específico queda (nota: el parámetro de flujo de masa se mantiene constante y el impulso
específico es proporcional al empuje).
(
f.
)
(
(
)
)
(
)
Empuje e Impulso específico en el vacío
El impulso específico queda
(
)
(
)
(
)
- 62 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 2. Aplicación de la segunda ley de Newton
Aplicar la segunda ley de Newton a un vehículo lanzador propulsado por un motor cohete y obtener
la ecuación dinámica que rige su movimiento.
Nota: Considerar el sistema formado por el vehículo y el motor
- 63 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Se considera un vehículo como el representado en la siguiente figura
Figura 2.1. Vehículo del problema
En un instante la cantidad de movimiento que tiene el vehículo es
( )
( )
( )
Se debe encontrar cual es la cantidad de movimiento al pasar un diferencial de tiempo
.
El vehículo pierde masa pero gana velocidad. Al sistema se le debe de sumar un término que incluye
la cantidad de movimiento que tiene el combustible cuando es expulsado.
(
)
( ( )
)
( ( )
)
(
)
Según el principio fundamental del cálculo de Newton, la derivada es
(
)
( ( )
[
( )
) ( ( )
)
(
)
( )
( )
]
̇
Los términos como por ejemplo
superiores.
se aproximan a cero ya que son infinitesimales de órdenes
Se consideran ahora las fuerzas externas al vehículo
∫
⃗
Esto podría considerarse como la causa del movimiento donde el efecto, el cambio de cantidad de
movimiento (segunda ley de Newton), es lo que se ha obtenido antes.
- 64 -
Andrés Zarabozo Martínez
Propulsión. Problemas
La ecuación de la segunda ley de newton queda
∫
⃗
̇
̇
Donde
es la fuerza propulsiva y es igual a la expresión obtenida en los apuntes
̇
(
- 65 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 3. Sistema de defensa antiaérea basado en misiles
El nuevo sistema de defensa antiaérea basado en misiles tierra aire basado en misiles tierra aire
lanzados oblicuamente. Los requisitos de diseño son:
-
Masa máxima en lanzamiento
Masa al final del tramo acelerado
Tiempo del tramo acelerado
Velocidad final del tramo acelerado
⁄
Se pide
a. Plantear la ecuación del movimiento, despreciando el peso y la resistencia aerodinámica, y
bajo la hipótesis preliminar que el impulso específico se mantiene constante así como ̇ ,
determinar el valor del impulso específico. Determinar también la velocidad en función del
tiempo.
Suponiendo que inicialmente la presión en la cámara de combustión es de
temperatura de combustión es
, el coeficiente adabático es
⁄(
). Se pide
, la
con
b. Obtener el impulso específico en el momento de lanzamiento, considerando que se
pretende optimizar las prestaciones a baja altura.
- 66 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a. Plantear las ecuaciones del movimiento
La ecuación del movimiento para motores cohetes es
Se recuerda que esta ecuación es válida siempre y cuando se introduzcan las fuerzas propulsivas en
el termino . Además se desprecia el peso, por lo que la contribución de las fuerzas másicas son
nulas.
̇
(
)
̇ [
(
)
̇
]
En este punto no se puede aún resolver la ecuación, por ejemplo utilizando una masa media (no se
indica nada parecido en el enunciado).
La ecuación también se puede escribir como
̇
(
)
Queda una EDO inmediata que se puede resolver.
∫
∫
Esta es la ecuación de Tsiokovsky, muy utilizada en el estudio de maniobras espaciales.
El impulso específico queda
Sabiendo que
( )
̇ , y volviendo a la ecuación de Tsiokovsky
( )
( )
- 67 -
̇
Andrés Zarabozo Martínez
Propulsión. Problemas
( )
(
)
̇
Se sabe que el tramo acelerado tiene una duración de
(
̇
y que la velocidad final es de
)
⁄ .
⁄
La velocidad queda entonces
( )
(
)
⁄𝑠 800
700
600
500
400
300
200
100
0
0
0.5
1
1.5
2
Figura 2.2. Velocidad respecto al tiempo
b.
Impulso específico en el lanzamiento
La ecuación de la velocidad en función de Mach es
√
Se busca primero el número de Mach, al estar optimizada a baja altura, la presión de salida es igual a
la presión atmosférica al nivel del mar (tobera adaptada).
√
[( )
]
√
La temperatura de salida es
- 68 -
[(
)
]
Andrés Zarabozo Martínez
Propulsión. Problemas
La velocidad de salida queda
√
⁄
√
El impulso específico se puede definir como la velocidad de salida partido por la gravedad.
- 69 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 4. Perdidas por efecto de la no uniformidad
Evaluar las perdidas por el efecto de las no uniformidades en la tobera axisimétrica de la figura, de
acuerdo con la configuración de flujos indicada.
̇
̇
̇
Figura 2.3. Figura del problema
- 70 -
̇⁄
̅
̇⁄
̅
̇⁄
̅
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Es recomendable hacer un par de comprobaciones primero para ver que no haya errores en el
enunciado. Hay que comprobar que las facciones de flujo másico cumplen la ecuación de
continuidad.
̇
̇
∑ ̇
̇
̇
̇
Hay que comprobar también que la media de la entalpia media coincide con la media de las
entalpias del flujo
∑ ̇
̅
̇(
̅
̅ )
̇̅
Dividiendo ahora ambos lados por el flujo másico se obtiene
̅
∑ ̇
̇
El problema está bien planteado.
Se calcula ahora el rendimiento por la no uniformidad
̇
( ) (√
̇
̇
̅
(
( ) [(√
̅
√
̅
̅
√
√
̅ )
̅ )
)
√̅ ]
) ̅
(
(√
√
√
√
)
Este es el tipo de no uniformidad debido a lo variación de la entalpia en el flujo de salida. Otro tipo
de no uniformidad es la no uniformidad debido a distribuciones de presiones y temperatura en la
salida.
- 71 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 5. Tobera aerospike
Calcular el coeficiente de fuerza
de la tobera bidimensional de tipo Aerospike que se observa en
la siguiente figura. La relación de calores específicos
. Encontrar también las relaciones
⁄ y ⁄ .
Nota: Se recomienda considerar previamente el funcionamiento en diseño.
Velocidad del flujo al final de la expansión
Plano de simetría
Figura 2.4. Esquema de la tobera Aerospike
- 72 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Se puede observar que hay una desviación de flujo de
. Esto significa que la tobera está
trabajando fuera de las condiciones de diseño. Como dice el enunciado, es recomendable estudiar
primero las condiciones de diseño.
Como se conserva el invariante
se tiene
(
Hay que recordar que (
)
y
(
Conociendo
)
(
)
.
)
se tiene
√
√
Además se tiene la siguiente expresión que depende del número de Mach.
(
Utilizando las tablas de (
)
√
√
) se obtiene el número de Mach
Conociendo el número de Mach se puede obtener
El ángulo
y posteriormente .
se obtiene observando la siguiente figura
Figura 2.5. Diagrama de la tobera con los ángulos
- 73 -
Andrés Zarabozo Martínez
Propulsión. Problemas
De la figura
Pudiendo ahora encontrar
.
(
)
(
)
La altura final es entonces
Por lo tanto la relación de áreas de la tobera es
Se puede utilizar el parámetro de flujo para comprobar el resultado anterior
̅(
̅(
̅(
)
)
)
̅(
̅(
̅(
)
)
)
( ) . Cuando se tiene
Se plantea ahora de nuevo el problema pero considerando ahora que
esta condición el flujo se expande más de lo deseado. Como el flujo es supersónico, la información
solo viaja en una dirección y por lo tanto la información en la pared es la misma que en la condición
de diseño (por ejemplo la presión en la pared de la tobera).
Se genera una variación en el coeficiente de empuje.
( )
(
( )
)
Esta expresión se puede demostrar aplicando la conservación de la cantidad de movimiento e los
dos casos.
∫
(
)
Como las condiciones en la pared son las mismas ya que se tiene flujo supersónico y haciendo la
resta entre el caso de diseño y fuera se obtiene
∫
(
)
(
)
Hay que tener cuidado ya que en el caso de que la presión sea mayor que la de diseño esto no se
podría usar. Eso es debido a que la distribución de presiones en la pared es distinta al caso de diseño
(a partir de cierto punto, en el principio de la tobera si que es la misma).
- 74 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Como regla general el coeficiente de empuje aumenta cuando la presión exterior aumenta.
Considerando expansión isentrópica
(
)
( ) el invariante
Cuando se tiene
(
se mantiene igual que en condición de diseño.
(
(
(
)
Obteniendo una un Mach para esta
)
)
(
)
(
)
)
a partir de las tablas.
La relación de presiones para el caso de estudio se puede ahora calcular
(
)
(
)
El coeficiente de empuje de diseño es
̇
(
( )
(
(
)
)
(
)
(
)
√
)
√
Finalmente se obtiene el coeficiente de empuje
( )
( )
(
(
)
- 75 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 6. Estudio de tobera utilizando el método de las características
Cuando una tobera, que ha sido diseñada para tener condiciones uniformes y flujo axial a la salida,
opera con presión ambiente inferior de la de diseño (para la cual sería igual a la ambiente), el flujo
aguas abajo experimenta una sucesión de expansiones y compresiones, dando lugar a una
configuración de flujo que comúnmente se conoce con el nombre de “diamantes”. Todo ello, hasta
que, a suficiente distancia aguas abajo, el flujo se estabiliza en unas condiciones transversales
uniformes de presión (realmente, no está tan claro que la velocidad sea también exactamente
uniforme, si las ondas de choque presentan una curvatura apreciable, ya que el incremento de
entropía será distinto para cada línea de corriente).
a) Haciendo uso de la ecuación de la cantidad de movimiento (formulación integral), obtener la
velocidad suficientemente aguas debajo de la tobera, donde puede suponerse uniformidad
tanto de presión como de velocidad en función de las variables del flujo en la sección de
salida de la tobera.
Considérese una tobera bidimensional diseñada para que a la salida el flujo se axial y uniforme, con
.
b) Indicar la Figura 2.6 la configuración de líneas características en el chorro de salida en
condiciones de diseño.
Plano de simetría
Figura 2.6. Diagrama de la tobera
( ) y que
Supóngase ahora que la presión ambiente es
.
c) Indicar qué fenómeno va a tener lugar a la salida, así como las condiciones de contorno que
deben considerarse. Justificar razonadamente que, a partir de la sección de salida , la
configuración del flujo hasta cierta distancia equivaldría a la impuesta por una placa plana de
cierta longitud, deflectada cierto ángulo , tal como se muestra en la Figura 2.7.
d) Encontrar el ángulo .
Plano de simetría
Figura 2.7.tobera con plano en la salida
- 76 -
Andrés Zarabozo Martínez
Propulsión. Problemas
e) Dibujar las líneas características, e indicar cuáles de ellas son rectas. ¿Puede tener lugar
algún tipo de incompatibilidad en alguna zona del flujo? Justificarlo. Físicamente, ¿en qué se
traduciría esta incompatibilidad?
Recomendación: en caso de recurrir a una solución numérica, generar la malla a partir de sólo 2
características, numerado las características de una familia, con números, y los de la otra, con letras.
- 77 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
a) Condición en el infinito
Se utiliza el teorema de conservación de la cantidad de movimiento. El volumen de control utilizado
se puede observar en la Figura 2.8.
⃗
⃗
⃗
Plano de simetría
Figura 2.8. Volumen de control utilizado para la formulación integral
La formulación integral queda
⃗( ⃗
∫
∫ ⃗( ⃗
⃗)
∫ ⃗( ⃗
⃗( ⃗
∫
⃗)
∫
⃗)
∫
⃗)
∫
∫
Viendo la Figura 2.8 se pueden desarrollar las integrales
(
)
(
)
∫
∫
̇
⃗
⃗
̇
La presión sobre la superficie lateral es siempre la presión ambiente
∫
̇
⃗
̇
Si se tiene una integral cerrada se debe cumplir que
∫
∫
⃗
⃗
∫ ⃗
∫
∫ ⃗
⃗
Obteniendo
̇
̇
- 78 -
(
)
Andrés Zarabozo Martínez
Propulsión. Problemas
(
)
̇
b) Configuración de las líneas características para la condición de diseño
Si las condiciones uniformes se mantienen (y se considera mezcla turbulenta, dominio uniforme), las
líneas características
y
son rectas y las propiedades del flujo son uniformes.
Plano de simetría
Figura 2.9.Lineas características para la condición de diseño
c) Operación con presión ambiente por debajo de la presión de ambiente de diseño
Como la presión ambiente es menor que la de diseño, hay una expansión de Prandtl – Meyer. El
abanico de expansión empieza con
(es decir
) correspondiendo a una relación
de presiones
(
)
(
)
Al final de la expansión se tiene presión ambiente (igual a
√
[( )
]
√
[(
)
).
]
√
[(
)
Plano de simetría
Figura 2.10. Tobera equivalente con plano inclinado
- 79 -
]
Andrés Zarabozo Martínez
Propulsión. Problemas
Dado que en las expansiones de Prandtl – Meyer bidimensionales la presión es constante a lo largo
de las líneas características, el problema a efectos prácticos equivale a considerar la configuración de
la Figura 2.10.
d) Ángulo
Se calcula la variable
que solo depende de
√
√
Siguiendo el invariante
se tiene (ver Figura 2.10)
(
√
(
Mirando el invariante
)
√
(
√
)
)
√
se tiene
(
)
Además al ser una zona uniforme
(
(
Se encuentra fácilmente el valor de (
√
(
)
Finalmente el ángulo
)
(
)
)
√
(
)
(
√
)
√
)
es
e) Dibujar las líneas características, buscar incompatibilidades en alguna zona del flujo
El proceso de cálculo se basa en ir buscando los parámetros de los puntos de cruce entre las líneas
características como se observa en la Figura 2.11. Se toman una serie de líneas y puntos en sus
cruces. Cuantas más líneas se tomen más precisión se tiene.
- 80 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Línea de
corriente
divisoria
Plano de
simetría
Figura 2.11. Selección de putos en los cruces de las líneas características
Ya se conocen las propiedades de las primeras líneas características, como por ejemplo
Además siguiendo las líneas características se sabe que
Lo más simple es confeccionar una tabla con los distintos puntos e ir calculando los distintos
parámetros que se van obteniendo.
Se calcula
para los dos primeros casos
√
√
Como el punto
√
viene de un invariante negativo salido directamente de
(sin cruzarse con otra
línea característica) se puede ver fácilmente que los valores son iguales, hay que recordar que el
número de Mach se mantiene constante en la línea de corriente divisoria.
En el punto
al estar en la línea de simetría se conoce el ángulo
esa línea (nulo).Se miran primero los datos que se tienen
que es igual al ángulo que tiene
Punto
-
-
-
-
-
Tabla 2.1. Valores iniciales de los puntos conocidos
- 81 -
-
-
Andrés Zarabozo Martínez
Propulsión. Problemas
Se escoge ahora El punto con más información (punto
ángulo por lo que se puede obtener y a su vez .
). Se conoce tanto el invariante como el
Obteniendo según las tablas
Los otros valores ya son triviales
√
Se actualiza ahora la tabla, hay que recordar que además se conserva el invariante encontrado en las
otros puntos.
Punto
-
-
-
-
-
-
-
Tabla 2.2. Tabla con primera actualización
Se podrían ahora resolver tanto el punto
como el punto
ya que se tienen dos datos en cada
punto. Se muestra a continuación la resolución del punto
que consiste en el punto donde se
cruzan dos invariantes conocidos. Se forma un sistema de dos ecuaciones con dos incógnitas
{
{
Como
y
son iguales que en el punto
Para el caso del punto
, todos los valores restantes son también los mismos.
la resolución es casi idéntica a la resolución del punto
- 82 -
.
Andrés Zarabozo Martínez
Propulsión. Problemas
Se muestran todos los resultados en la tabla ya acabada.
Punto
Tabla 2.3. Tabla finalizada
Si se hiciese con mayor precisión al aumentar el número de características se obtendría un resultado
parecido al siguiente.
Figura 2.12. Resultado del análisis más intensivo
Se puede ver como las líneas características
se entrecruzan. Esto es una irregularidad
caracterizada por la aparición de una onda de choque oblicua, situada en el cruce que esté más a la
izquierda. La onda de choque tiene la pendiente de la primera característica afectada.
A partir de ese punto es necesario recurrir a las ecuaciones de ondas de choque oblicuas para
conocer las condiciones del flujo inmediatamente después de la onda de choque. La generación de
entropía a través de la onda de choque dificulta la utilización del método de las características, ya
que se tiene que aplicar por zonas y naturalmente solo donde el flujo sea supersónico. La siguiente
figura muestra el desarrollo de las líneas características.
- 83 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Línea de corriente divisoria
Ondas
de
choque oblicuas
Expansión
Expansión
Plano de simetría
Figura 2.13. Aparición de ondas de choque en la expansión
Dependiendo de las condiciones particulares (
y ⁄
), se podría dar el caso de que las ondas
de choque oblicuas no lleguen al eje de simetría, sino que apareciese una onda de choque normal,
dando lugar a una configuración en Y. Esto pasa cuando el ángulo que forma la onda de choque
oblicua con el eje de simetría sea demasiado grande.
Figura 2.14. Configuración de onda de choque en Y
En el caso de tobera con flujo sobre expansionado también se puede tener una configuración tipo
diamante. Esto pasa cuando la presión de salida sea ligeramente inferior al ambiente de manera que
también se forme una onda de choque en Y justo a la salida.
Figura 2.15. Configuración de onda de choque de tipo diamante
Si la relación de presiones fuese tal que se produjese una onda de choque normal en la salida, el
flujo posterior a la onda de choque sería subsónico y no se tendría configuración de diamante. Se
tendría una tobera crítica.
Figura 2.16. Tobera crítica
- 84 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 7. Cohete de agua
La figura adjunto representa un cohete propulsado por agua a presión utilizando botellas de 2 litros
de plástico. Inicialmente, el volumen de agua es
y el resto es aire. Mediante una bomba
de aire se eleva la presión dentro de la botella hasta
con
, a partir de la cual
el tapón cede y sale disparado y comienza a salir el agua a presión. Se considera que el cohete deja
de propulsar cuando se acaba el agua de su interior.
Se pueden usar las siguientes hipótesis:
-
En todo momento dentro de la botella la presión de aire y de agua es uniforme (gradiente de
presión por fuerzas de gravedad y de inercia negligible)
El gas experimenta una expansión adiabática y sin degradación de energía (proceso
isentrópico)
El agua es un fluido incompresible
La presión de estancamiento del agua se mantiene constante hasta la salida (teorema de
Bernouilli)
Se pide encontrar el empuje y razonar que efectos tendría sobre las actuaciones del cohete la
utilización de un líquido con mayor densidad. Además se pide encontrar la variación del impulso
específico en función de la masa de propulsante
Nota: el líquido siempre descarga a la atmosfera con una presión estática igual a la presión ambiente
Aire
Agua
Figura 2.17. Cohete de agua
- 85 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
La ecuación del empuje es también valida para fluidos líquidos
(
̇
)
Todos los líquidos (al ser incompresibles) se descargan a la atmosfera a presión atmosférica.
̇
La velocidad de escape se obtiene utilizando el teorema de Bernouilli. Se evalúa la presión de
estancamiento en el límite superior del agua (condición , con presión igual del gas interior) y en el
tapón (condición de salida).
√
(
)
El flujo másico de salida es
̇
Se han despreciado los efectos viscosos en el agujero de la botella (
).
Obteniendo el empuje
(
)
El impulso específico queda
(
)
̇
Se observa que el empuje no es función de la densidad del fluido. Se utiliza agua ya que se consigue
un flujo másico pequeño obteniendo mayor duración de tiempo de empuje. En el caso de poner por
ejemplo solo aire, todo el flujo se expulsaría de golpe y el cohete apenas obtendría un impulso.
Mirando ahora la variación de la velocidad de salida respecto al tiempo
√
(
)
Se puede relacionar la presión del gas con su volumen.
( )
(
- 86 -
( )
)
Andrés Zarabozo Martínez
Propulsión. Problemas
√
(
(
( )
)
)
Como se obtuvo antes el impulso específico es igual a la velocidad
√ (
(
( )
)
)
El volumen varía en el tiempo de la siguiente forma
∫
Esta integral se debe resolver numéricamente. Se puede ver como la integral es el flujo másico
partido por la densidad.
∫
∫
̇
El hecho de utilizar un fluido con mayor densidad, aumenta el tiempo de descarga para una
velocidad de escape igual. Es obvio que también aumenta drásticamente el peso. Además hasta que
el líquido que sale adquiere la velocidad de escape
se obtiene un transitorio con un bajo.
El hecho de tener un área de salida mayor aumenta el empuje per también aumenta el flujo de
salida por lo que disminuye el tiempo de impulso.
- 87 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 8. Diseño de una tobera ideal bidimensional
Se pide diseñar una tobera ideal bidimensional para expandir el fluido desde unas condiciones
cercanas a las sónicas, desde
hasta
. Utilizad cuatro líneas características con
.
Figura 2.18. Tobera con las cuatro líneas características
- 88 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Según la numeración de la Figura 2.18, se identifican las diferentes regiones





uniforme
simple
simple
no simple
uniforme si el panel es recto, aunque aún no se ha determinado la geometría
Como cálculo preliminar al conocer
se puede encontrar .
√
√
Siguiendo las líneas características, se pueden identificar los puntos con invariantes iguales
Y también
Además se conoce el ángulo en los puntos de la pared inferior
El punto con mayor información es el punto . Se empieza buscando la información de ese punto.
Como se conoce el número de Mach se pueden encontrar fácilmente y .
√
(
√
)
(
√
√
√
)
√
También se pueden obtener fácilmente los invariantes y las direcciones
(
(
)
)
Al conocer el Mach de salida se pueden calcular valores para el punto
(
√
)
√
(
√
- 89 -
y
)
.
√
Andrés Zarabozo Martínez
Propulsión. Problemas
√
√
También se pueden obtener fácilmente los invariantes
(
(
)
)
Y de forma similar a antes, las direcciones
Es muy útil en este tipo de ejercicio utilizar tablas para ir almacenando la información e ir pudiendo
elegir los siguientes puntos que se deben calcular. En la primera tabla se pueden ver los valores
obtenidos hasta ahora y así como las igualdades debidas a los invariantes.
Punto
0
Tabla 2.4. Primeros datos obtenidos
Se debe ahora buscar un punto donde se tengan suficientes datos. Por ejemplo el punto , se
conocen los dos invariantes.
{
{
A partir de este número
y utilizando tablas se puede obtener el número de Mach y a partir de ese
número se puede encontrar . Finalmente se obtienen las direcciones
y
.
√
√
- 90 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Punto
0
Tabla 2.5. Datos actualizados de la segunda iteración
Mirando la línea característica que va des
hasta
, se observan cuatro puntos. Se obtiene
primero la diferencia entre y y se divide por la cantidad de puntos en la línea menos uno.
A partir de este valor se pueden obtener los invariantes de los otros dos puntos de la línea
Al tener ahora los dos invariantes de esos puntos se pueden obtener el resto de parámetros de esos
puntos.
{
{
√
√
Similarmente para el punto .
{
{
- 91 -
Andrés Zarabozo Martínez
Propulsión. Problemas
√
√
Se vuelve a actualizar la tabla.
Punto
0
Tabla 2.6. Datos actualizados de la tercera iteración
Como se tiene que
y además se sabe que
y se tienen dos variables para resolver el
sistema de dos ecuaciones y cuatro incógnitas para el punto .
{
(
{
√
)
√
De forma similar se encuentra el punto
{
(
{
√
√
- 92 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Punto
0
Tabla 2.7. Actualizado el punto 5 y
y los invariantes iguales
Se pueden encontrar ahora el resto de puntos ya que se conocen todos los invariantes. Se empieza
por el punto .
{
{
√
√
Se continua con el punto .
{
{
√
√
- 93 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Finalmente se obtiene el punto .
{
{
√
√
Se muestra a continuación la tabla finalizada.
Punto
0
Tabla 2.8. Tabla finalizada
Los puntos se obtienen como coordenadas (
utilizada.
(
), la siguiente figura muestra la nomenclatura
)
(
(
)
)
(
(
)
)
Figura 2.19. Nomenclatura utilizada para puntos y ángulos
Las ecuaciones para obtener un punto en un cruce de dos líneas características, conociendo las
coordenadas de los puntos anteriores son
(
- 94 -
)
Andrés Zarabozo Martínez
Propulsión. Problemas
Problema 9. Efecto de partículas en el flujo
El efecto de que el flujo lleve una fracción de masa de partículas solidas en un gas en expansión se
puede representar utilizando un coeficiente de dilatación adiabática medio y una masa molecular
media.
̅
Para
(
(
)
)
̅
el calor específico de alta temperatura es
⁄
⁄ .
Se considera un cohete solido con
-
⁄
⁄
Para una proporción del
de aluminio en la carga del propergol, es del orden de
. Calculad
el impulso específico del cohete con tobera adaptada y comparadlo con el que se obtendría para la
misma
pero sin partículas.
- 95 -
Andrés Zarabozo Martínez
Propulsión. Problemas
Resolución
Se calculan primero los calores específicos de presión constante y volumen constante del gas si
estuviese libre de partículas.
⁄
⁄
⁄
⁄
Se sabe que el calor específico del solido (o líquido) es
aluminio es del
. Por lo tanto el coeficiente ̅ medio es
(
(
̅
)
)
(
(
̅
⁄
⁄ y que la proporción de
)
)
Y la masa molecular media es
̅
⁄
Se calcula ahora la velocidad de salida para la relación de presiones y temperatura de cámara dadas
̅
√
̅
[
̅
̅
( )
̅
√
]
(
[
)
]
⁄
Alternativamente se puede calcular utilizando el calor específico a presión constante medio. Se
recomienda calcularlo también así como método de comprobación. El calor específico a presión
constante medio es
(
̅
)
(
)
⁄
⁄
Obteniendo la velocidad
̅
√
̅
[
( )
̅
]
√
[
(
)
]
⁄
Bajo las condiciones de tobera adaptada, no hay contribución de presiones en el empuje o en el
impulso específico.
̇
̇
Sin tener en cuenta las partículas pero con la misma relación de presiones y la misma temperatura
de cámara se obtiene
- 96 -
Andrés Zarabozo Martínez
√
[
Propulsión. Problemas
( )
√
]
(
[
)
]
⁄
̇
̇
La perdida es por lo tanto
Se puede comprobar la precisión de la aproximación lineal dada por la hipótesis de
factor es
(
( )
pequeño. El
)
La relación de velocidades considerando o no las partículas se puede aproximar (linealizar) de la
siguiente forma
[
[
Esto equivale a una pérdida del
porcentaje de .
(
(
(
(
)
)
(
(
)
)]
)
)]
, que no se separa mucha de la calculada antes a pesar del alto
- 97 -