Greta Navas - prof.usb.ve. - Universidad Simón Bolívar
Anuncio

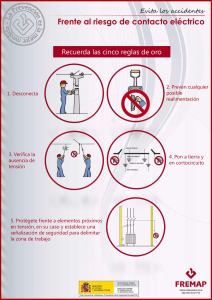
Universidad Simón Bolívar Departamento de Conversión y Transporte de Energía CT-4311 Conversión de Energía Eléctrica IV Prof. José Manuel Aller . Trimestre Enero-Marzo 2014 TAREA 3 Greta Navas 10-10493 Sartenejas, junio de 2014 CT4311 Máquinas Eléctricas III USB Enunciado Modelar el comportamiento dinámico de una motor sincrónico de polos salientes con devanados amortiguadores de 6 kVA, 416 V, factor de potencia nominal 0.8, y corriente de campo nominal de 5 A. Los datos de la máquina en el sistema adimensional de unidades, son los siguientes: Re 0,05 Rad 0,03 Rf 0,08 Raq 0,03 Lσve 0,15 Lad 1,5 Lσvf 0,2 Laq 1 Ld 1,5 Lad-d 1,35 Lq 1 Laq-q 0,85 Ldf 1,35 Lad-f 1,3 2HωB 400 Lσva 0,15 La corriente de campo nominal produce la tensión nominal en la condición de vacío. El motor sincrónico acciona una bomba cuya característica es: Tm = 0, 2 + 0, 1 ∗ ωm + 2, 7 ∗ ω2m La máquina sincrónica se arranca conectándola a la red trifásica, mientras se mantiene la bobina de campo en cortocircuito hasta alcanzar el punto de equilibrio. Una vez alcanzado este punto se inyecta la corriente de campo máxima. 1. Determine las bases coherentes del sistema adimensional de unidades. 2. Realice un análisis de los resultados obtenidos cuando se integran las ecuaciones dinámicas por medios numéricos. 3. Determine con el modelo las corrientes de campo que hacen operar a la máquina en factor de potencia capacivo e inductivo de 0.85. 4. Calcule las corrientes de cortocircuito brusco en la barra de alimentación durante los primeros 10 ciclos si la máquina se encuentra previo al cortocircuito en un punto de operación donde consume la potencia nominal a factor de potencia 0.85 inductivo considerando que la velocidad no cambia durante el transitorio electromagnético. 5. Repita el cálculo de las corrientes de cortocircuito brusco en la barra de alimentación en el instante inicial si la máquina se encuentra previo al cortocircuito en un punto de operación donde consume la potencia nominal a factor de potencia 0.85 capacitivo no cambia durante el transitorio electromagnético. 6. Compare los resultados obtenidos en los puntos 3 y 4 con el método transitorio y subtransitorio aproximado. 7. Determine la frecuencia y amortiguamiento de las oscilaciones de pequeña señal ante pequeños escalones de la carga mecánica 3 %. 8. Si la red es una barra infinita, cuanto tiempo puede mantenerse el cortocircuito en bornes del motor antes de perder estabilidad si inicialmente se encointraba en su punto nominal de operación 2 CT4311 Máquinas Eléctricas III USB 1. Determine las bases coherentes del sistema adimensional de unidades. Con los valores de los parámetros: Lmd = Ld − Lq = 0, 5H L2 df Lmf = Lmd = 3, 646H q Nd Lmd Nf = Lmf = 0, 3703 La siguiente tabla contiene los valores correspondientes a las bases en el sistema adimensional de unidades en variables del estator y en variables de campo. Sbase [kVA] Vbase [kV] Ibase [A] Zbase [Ω] Lbase [mH] ωbase [rad/s] Vbase-f [V] Ibase-f [A] Zbase-f -f [Ω] Zbase-e-f [Ω] 2 240,1778 8,3272 28,8427 76,5058 377 648,5715 3,0837 210,3225 77,8862 2. Realice un análisis de los resultados obtenidos cuando se integran las ecuaciones dinámicas por medios numéricos. Las ecuaciones dinámicas de la máquina son las siguientes: di −1 dt =L dω dt (v − Ri − ωGi) T e−T m = 2Hω base dθ = ω dt Se utilizó el siguiente código para la integración de estas ecuaciones en Matlab arrancando la máquina con el campo cortocircuitado y alimentándolo a los 2,65 segundos (1000 pu) a tensión nominal: global Re Rf Rad Raq Lse Lsf Ld Lq Ldf J Lad Laq Ladd Laqq Ladf Lsa Lf Re=0.05; Rf=0.08; Rad=0.03; Raq=0.03; Lse=0.15; Lsf=0.2; Ld=1.5; Lq=1; Ldf=1.35; J=400; Lad=1.5; Laq=1; Ladd=1.35; Laqq=0.85; Ladf=1.3; Lsa=0.15; Lf=1.55; st=[0 1200]; y0=[0 0 0 0 0 0 0]; [t,X]=ode23(@funmaq,st,y0); figure plot(t,X(:,1)); figure plot(t,X(:,2)); figure plot(t,X(:,3)); figure plot(t,X(:,4)); figure plot(t,X(:,5)); figure plot(t,X(:,6)); figure plot(t,X(:,7)); 3 CT4311 Máquinas Eléctricas III USB function pX=funmaq(t,X) global Re Rf Rad Raq Lse Lsr Ld Lq Ldf J Lad Laq Ladd Laqq Ladf Lsa Lf Id=X(1); Iq=X(2); If=X(3); Iad=X(4); Iaq=X(5); w=X(6); theta=X(7); I=[X(1);X(2);X(3);X(4);X(5)]; Va=sqrt(3)*cos(t); Vb=sqrt(3)*cos(t-2*pi/3); Vc=sqrt(3)*cos(t-4*pi/3); alfa=exp(1i*2*pi/3); v=sqrt(2/3)*(Va+alfa*Vb+alfa^2*Vc); Vdq=v*exp(-1i*X(7)); V=zeros(5,1); L=[Ld 0 Ldf Ladd 0; 0 Lq 0 0 Laqq; Ldf 0 Lf Ladf 0; Ladd 0 Ladf Lad 0; 0 Laqq 0 0 Laq]; Li=inv(L); R=[Re 0 0 0 0; 0 Re 0 0 0; 0 0 Rf 0 0; 0 0 0 Rad 0; 0 0 0 0 Raq]; G=[0 -Lq 0 0 -Laqq;Ld 0 Ldf Ladd 0; 0 0 0 0 0; 0 0 0 0 0 ; 0 0 0 0 0]; if t<1000 V(3)=0; else V(3)=1.0853*Rf; end Te=(Ld-Lq)*X(1)*X(2)+Ldf*X(3)*X(2)+Lad*X(4)*X(2)-Laq*X(5)*X(1); Tm=0.2+0.1*X(6)+2.7*X(6)^2; pI=L\(V-R*I-X(6)*G*I); pw=(Te-0.8*Tm)/(3*J); ptheta=X(6); pX=[pI(1);pI(2);pI(3);pI(4);pI(5);pw;ptheta]; Se obtuvieron las siguientes señales: 4 CT4311 Máquinas Eléctricas III 5 USB CT4311 Máquinas Eléctricas III USB 3. Determine con el modelo las corrientes de campo que hacen operar a la máquina en factor de potencia capacivo e inductivo de 0.85. Se halla el punto de operación a tensión y potencia nominal pero con factor de potencia 0,85 capacitivo e inductivo, resolviendo el problema directo y obteniéndose los siguientes datos de operación en convención motor: V (pu) I (pu) P (pu) Q (pu) cos(fp) if (pu) if (A) δ Fp capacitivo 1 0,9412 0,8 -0,4958 31,79° 2,0861 10,4303 -29,53° Fp inductivo 1 0,9412 0,8 0,4958 -31,79° 1,1194 5,5971 -59,09° 4. Calcule las corrientes de cortocircuito brusco en la barra de alimentación durante los primeros 10 ciclos si la máquina se encuentra previo al cortocircuito en un punto de operación donde consume la potencia nominal a factor de potencia 0.85 inductivo considerando que la velocidad no cambia durante el transitorio electromagnético. En este caso, se toma como condición prefalla, el punto de operación hallado en el punto anterior en el caso de factor de potencia 0,85 inductivo y se utiliza el programa del punto 2 para calcular las nuevas corrientes transitorias y subtransitorias luego de un cortocircuito brusco que ocurre a los 4 segundos (1500 pu) y reestableciendo las tensiones del eje directo y cuadratura a los 5,3 segundos (2000 pu). 6 CT4311 Máquinas Eléctricas III 7 USB CT4311 Máquinas Eléctricas III USB 5. Repita el cálculo de las corrientes de cortocircuito brusco en la barra de alimentación en el instante inicial si la máquina se encuentra previo al cortocircuito en un punto de operación donde consume la potencia nominal a factor de potencia 0.85 capacitivo no cambia durante el transitorio electromagnético. Se toma como condición prefalla el punto de operación hallado en el punto 3 para el caso de factor de potencia capacitivo y se corre nuevamente el programa para calcular las corrientes luego del cortocircuito brusco que ocurre a los 4 segundos, exactamente igual al caso anterior. 8 CT4311 Máquinas Eléctricas III USB 6. Compare los resultados obtenidos en los puntos 4 y 5 con el método transitorio y subtransitorio aproximado. Se calculan la reactancia transitoria del eje directo y las subtransitorias del eje directo y cuadratura tomando en cuenta las condiciones iniciales de operación, ya que el flujo se mantiene constante en los tiempo 0- y 0+ del análisis transitorio: Xd’ (pu) Xd” (pu) Xq” (pu) 0,3242 0,2850 0,2775 Ahora se consiguen las corrientes transitorias y subtransitorias con las condiciones prefalla y postfalla establecidos anteriormente: Ef 0 = V e0 − ReIe0 − jXd0 Id0 − jXqIq 0 Ef 00 = V e00 − ReIe00 − jXd00 Id00 − jXq 00 Iq 00 Obteniéndose las siguientes corrientes: 9 CT4311 Máquinas Eléctricas III Id’ (pu) Iq’ (pu) Ie’ (pu) Id” (pu) Iq” (pu) Ie” (pu) Fp inductivo 0,9694 0,5249 1,1024 1,6554 2,6213 3,1002 USB Fp capacitivo 4,5579 0,8370 4,6342 2,9740 0,6866 3,0523 7. Determine la frecuencia y amortiguamiento de las oscilaciones de pequeña señal ante pequeños escalones de la carga mecánica 3 %. La siguiente expresión define el comportamiento dinámico de la oscilación: Δδ (s) = 2H ωB ΔT m s2 + ωD s+ dP dδ (δo ) B De donde: δo = −64, 25° (δo ) = 2, 0105 D = Tsnn ≈ 100 dP dδ Los polos de la expresión serán: s1 = −9, 315rad/s s2 = −40, 685rad/s Por lo tanto: Δδ (s) = 0,03 (s+9,315)(s+40,685) Cuyo comportamiento será el siguiente: 10 CT4311 Máquinas Eléctricas III USB 8. Si la red es una barra infinita, cuanto tiempo puede mantenerse el cortocircuito en bornes del motor antes de perder estabilidad si inicialmente se encontraba en su punto nominal de operación Tomando el criterio de áreas iguales y siendo δc el ángulo critico de despeje y δmax el ángulo máximo que puede tener la máquina para no perder el equilibrio, como se observa en la siguiente figura, donde realmente nuestro par mecánico está representado por la curva dada en el enunciado: ´ δc δo ´ δmax T mdδ = δc (T e − T m)dδ δmax = π − δo Además, como el área bajo la curva representa la energia cinética que gana o pierde la máquina: 2 − 12 Jωs2 = T m(δc − δo) 4W k1 = 12 Jωm 1 2 2 4W k2 = 2 Jωs − 12 Jωm = T m(δmax − δc) Despejando, se obtiene el ángulo critico: δc = π 2 Con esto, es posible despejar el tiempo critico: q tc = (δc−δo)4H ωs2 T m =⇒ tc = 10, 45seg 11