( + - = ( ) 2 ln fxxx =

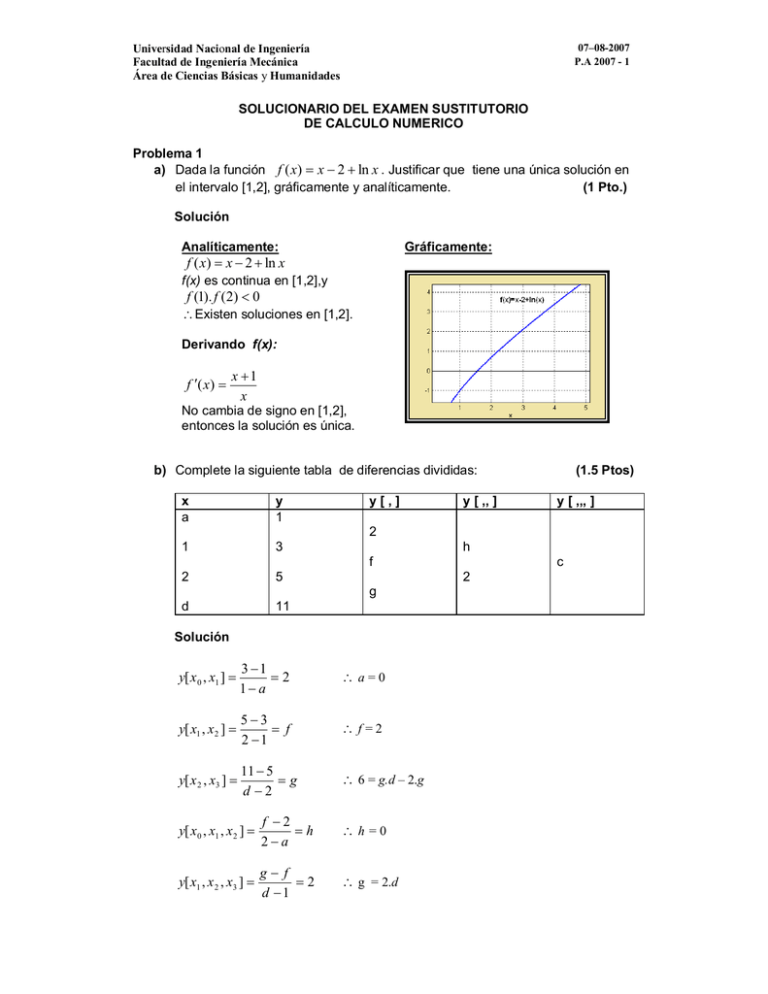
07–08-2007
P.A 2007 - 1
Universidad Nacional de Ingeniería
Facultad de Ingeniería Mecánica
Área de Ciencias Básicas y Humanidades
SOLUCIONARIO DEL EXAMEN SUSTITUTORIO
DE CALCULO NUMERICO
Problema 1
a) Dada la función f ( x)  x  2  ln x . Justificar que tiene una única solución en
el intervalo [1,2], gráficamente y analíticamente.
(1 Pto.)
Solución
Analíticamente:
Gráficamente:
f ( x)  x  2  ln x
f(x) es continua en [1,2],y
f (1). f (2)  0
 Existen soluciones en [1,2].
Derivando f(x):
f ( x) 
x 1
x
No cambia de signo en [1,2],
entonces la solución es única.
b) Complete la siguiente tabla de diferencias divididas:
x
a
y
1
1
3
y[,]
y [ ,, ]
(1.5 Ptos)
y [ ,,, ]
2
h
f
2
5
d
11
c
2
g
Solución
y[ x 0 , x1 ] 
3 1
2
1 a
 a=0
y[ x1 , x2 ] 
53
 f
2 1
 f=2
y[ x 2 , x3 ] 
11  5
g
d 2
 6 = g.d – 2.g
y[ x0 , x1 , x2 ] 
f 2
h
2a
 h=0
y[ x1 , x 2 , x3 ] 
g f
2
d 1
 g = 2.d
y[ x0 , x1 , x2 , x3 ] 
2h
2
c  c
d a
d
Resolviendo:
a=0
f=2
h=0
d1 =3
g1 =6
c1=2/3
d2 = -1
g2 = -2
c2= -2
c) Desarrolle un programa que permita buscar todas las raíces de una función
cualquiera fun. La búsqueda se realizara en el intervalo [a, b], considere un
paso de h, verificando si existe un cambio de signo, en caso afirmativo, aplique
10 iteraciones usando el Método de la Bisección para mejorar la precisión de la
raíz.
Complete la función en Matlab.
function r=raices(fun,a,b,h)
%r: Vector que contiene las raíces calculadas
%fun: Cadena de caracteres que definen la función a resolver
f=inline(fun);
for x=a:h:b
x1=x;x2=x+h;
if(
Solución
function r=raices(fun,a,b,h)
%r:Vector que contiene las raíces calculadas
%fun: Cadena de caracteres que definen la función a resolver
f=inline(fun);
r=[];
for x=a:h:b
x1=x;x2=x+h;
if(feval(f,x1)*feval(f,x2))<0
for i=1:10
xm=(x1+x2)/2;
fx=feval(f,xm);
fa=feval(f,x1);
if fa*fx<0
x2=xm;
else
x1=xm;
end
end
r=[r,xm];
end
end
(1 Pto.)
d) Una placa de 12 cm. de lado tiene sus bordes mantenidos a las temperaturas
mostradas en la figura. Se desea saber la distribución de temperatura en el
interior de la placa. Se escogerá un
y
espaciamiento de h = 4 cm.
u=0
La ecuación de transferencia de calor en
estado estacionario se reduce a Laplace:
12
u =100
u =100
 2u  2 u

0
x 2 y 2
R
x
0
12
u =100
Plantee el sistema de ecuaciones lineales
luego aplicar diferencias finitas.
(1.5 Ptos.)
Solución
y
u=0
12
NODO P1
P1
P2
P3
P4
u =100
0
8
2
u (8,8)  2u (4,8)  u (0,8) P2  2 P1  100
 u
(4,8) 

2
x
42
16
u =100
0
4
x
0
4
8
u ( 4,12)  2u ( 4,8)  u ( 4, 4) 0  2 P1  P3
 2u
( 4,8) 

y 2
42
16
12
u =100
0
NODO P1
NODO P3
P2  2 P1  100 0  2 P1  P3

0
16
16
P4  2 P3  100 P1  2 P3  100

0
16
16
NODO P2
NODO P4
100  2 P2  P1 0  2 P2  P4

0
16
16
100  2 P4  P3 P2  2 P4  100

0
16
16
1
0   P1    100 
 4 1
 1 4 0
1   P2    100 

.

1
0  4 1   P3   200

  

1
1  4  P4   200
0
 P1  62.5
P2  62.5
P3  87.5
P4  87.5
Problema 2
La densidad de energía radiada, a la frecuencia  , por unidad de volumen en un
“cuerpo negro” que se encuentra a temperatura absoluta T, que denotaremos por
u ( , T ) , viene determinada por la ecuación de Planck:
8h  3
u ( , T )  3 . h
c
e kT  1
Donde “h” es la constante de Planck h  6.626 .10
Boltzmann con k  1.38066 . 10
c  3 . 10
8
-23
-34
J.s , “k” es la constante de
J /º K y “c” es la velocidad de la luz en vacío
m / s . Se desea determinar la frecuencia (positiva) a la que se hace
máxima la emisión de energía radiante a una temperatura fija T, Utilice el método de
bisección, determinando un intervalo inicial de búsqueda de solución. (Realice 3
Iteraciones).
(5 Ptos.)
Sugerencia: Efectúe un cambio de variable M 
8h
h
y N 
3
k
c
Solución
Para una temperatura fija T, y siguiendo la sugerencia, tenemos:
u ( )  M .
3
, para que la función alcance su máximo valor:
N

e T 1
du
 0 , derivando:
d
N
N

N 
( )( e T )  (.e T  1).(3 2 )
du
T
 M .
N

d
(e T  1) 2
3
Igualando a cero y simplificando para
N
N

N 
 ( e T )  (.e T  1).(3)  0
T
  0 , tenemos:
Método de Bisección, en el intervalo [2,3]:
Sea: x 
N

T
Entonces:
f ( x)  x.e x  3.e x  3
Para: a = 2, b = 3
f(a) .f(b) < 0
Iteración
0
1
2
3
a
2
2.5
2.75
2.75
b
3
3
3
2.875
x
2.5
2.75
2.875
2.8125
De la última iteración:
N
  2.8125
T
x
  2.8125
T
N
[s 1 ]
Donde:
N
h
 4.7992.10 11
k
[º K .s ]
T: temperatura del “cuerpo negro” fija: [ºK]
Constante de Planck: h  6.626 . 10
-34
[ J .s ]
Constante de Boltzmann: k  1.38066 .10
- 23
 J 
º K 
 
Problema 3
Un sistema dinámico presenta la siguiente respuesta en el tiempo:
t(seg.)
y(m)
0
0.871
0.2
0.921
0.4
0.952
0.6
0.972
0.8
0.994
1.2
0.999
1.6
0.999
2
0.999
 b.t
a) Realice un ajuste por mínimos cuadrados usando la función: y  1  a.e
Indique a su criterio que tan buena la función de ajuste obtenida.
(2 Ptos)
b) Determine para que tiempo el sistema alcanza el 95% de su posición máxima.
(1 Pto)
c) Determine el área bajo la curva y(t) en [0,2] usando el método del trapecio a
partir de la tabla dada y luego integre la función de ajuste. Compare los
resultados e indique a su criterio cual de ellos es el más fiable.
(2 Ptos)
Solución
y  1  a.e  b.t
Entonces:
Ln(1  y )  Ln(a.e  b.t )
 b.t
 Ln (1  y )  Ln( a)  Ln (e )
Haciendo cambio de variable:
Y  Ln(1  y)
xt
B  Ln(a)
A  b
Tenemos la nueva tabla:
Y  A.x  B
x (seg.)
Y  Ln(1  y)
0
-2.048
0.2
-2.5383
0.4
-3.0365
2
 x  9 .2
 x  6.8
0.6
-3.5755
0.8
-5.1160
1.2
-6.9078
1.6
-6.9078
2
-6.9078
 x.y  41.1176
 y  37.0376
n=8
Reemplazando en:
 x 2

  x
 x. A   xy 
n   B    y 
Obtenemos:
9.2 6.8  A  41.1176
6.8 8 . B     37.0376

  

Resolviendo
A  2.8174
B  2.2349
Entonces:
a  0.1070
b  2.8174

y  1  0.1070.e2.8174.t
Factor de Regresión para diversos ajustes:
AJUSTE LINEAL
AJUSTE CUADRATICO
y  0.0549.t  0.9167
R2 = 0.6739
2
y  0.0642.t  0.1826.t  0.882
R2 = 0.9633
AJUSTE EXPONENCIAL
y  1  0.1070.e 2.8174.t
R2 = 0.6633
Graphics:
AJUSTE CUADRATICO
2
y  0.0642.t  0.1826.t  0.882
AJUSTE EXPONENCIAL
y  1  0.1070.e 2.8174 .t
El factor de regresión indica que la aproximación no es muy buena, sin embargo si se
conoce que el comportamiento del sistema dinámico es del tipo exponencial, entonces
se hace necesario el ajuste por medio de esta función, se puede mejorar el ajuste
agregando más datos a la tabla.
b)
Posición máxima: y= 0.999 [m]
Para calcular el tiempo en que alcanza 95% de su posición máxima, usaremos la
función de ajuste obtenida anteriormente:
Entonces:
95 % (0.999)  1  0.1070.e 2.8174.t

t  0.2634
c)
Por el Método de Trapecio Simple:
I
[seg ]
h
y 0  y 7  = (2  0) 0.871  0.999  1.87
2
2
Por el Método del Trapecio Compuesto:
h1
 yo  2( y1  y2  y3 )  y4   h2 y4  2( y5  y6 )  y7  =
2
2
(0.2)
I
0.871  2.(0.921  0.952  0.972)  0.994  0.4 0.994  2.(0.999  0.999)  0.999
2
2
I
I  1.9533
Integrando la función de ajuste:
2
I   1  0.1070.e  2.8174.t  1.9622
0
Regla del Trapecio
1.87
Trapecio Compuesto
1.9533
Integral de fun. de ajuste
1.9622
Si la función presentara dificultades de integración, el método del trapecio compuesto
seria una alternativa fiable, dada la cercanía de los puntos de la tabla.
Problema 4
Resuelva la ecuación dinámica del circuito considerando que antes de cerrar la llave
S, no había ninguna energía almacenada en el circuito, R=2Ω, L=2H, C= 0.5F.
Al cerrar la llave S, se puede analizar el comportamiento dinámico del circuito a partir
de la Ley de Kirchoff para corriente:
V(t )  R.i(t )  L.
d .i(t )
dt

1
. i( t ) .dt
C 
Se desea estudiar la conducta dinámica de
este circuito en el tiempo 0 a 1 seg.
S
Se pide:
a) Formule el sistema EDO de primer
orden incluyendo las condiciones
iniciales.
(1 Pto)
V(t)=sin(3.5*t)
b) Resuelva usando el algoritmo de Heun
con h1 = 0.5 y muestre los valores de i(t)
aproximados en t = 0 ,0.5 ,1 seg. (1 Pto)
c) Resuelva usando el mismo algoritmo anterior con h2 = h1/2 y muestre los
valores de i(t) en t = 0 ,0.5 ,1 seg.
(1.5 Ptos)
d) Si se conoce que i(1)  0.130168 usando h3 = 1 / 8 por el método de Heun,
determine una mejor aproximación de la intensidad en el tiempo de 1 segundo,
usando la extrapolación de Ríchardson. Comente su respuesta. (1.5 Ptos)
Solución
a) La corriente i(t ) y la carga q (t ) se relacionan mediante:
 i(t ).dt  q
(t )
Entonces la E.D.O se transforma en:
V(t )  R.i( t )  L.i(t ) 
1
.q (t )
C
Condiciones Iniciales:
 La llave S esta abierta en t=0 :

 i(0)  0
La energía inicial almacenada en el circuito esta dada por:
E0 
1
1
2
2
.q 0  L.i0
2C
2
Antes de cerrar el interruptor S, E 0  0 ,
 q (0 )  0
El sistema de E.D.O de primer orden será:
q   f ( x, y, z )  i
1
i   g ( x, y, z )  . sin(3.5 * t )  q  i
2
q (0 )  0
i (0 )  0
b)
Usando h1 = 0.5
t (seg.)
0
0.50
1.00
q(t)
0
0
0.0769
i(t)
0
0.1230
0.0484
q(t)
0
0
0.0135
0.0485
0.0936
i(t)
0
0.0480
0.1245
0.1602
0.1146
c)
Usando h2 = 0.25
t (seg.)
0
0.25
0.50
0.75
1.00
d)
Usando la extrapolación de Ríchardson
D j ,k 
4 k 1 D j 1,k 1  D j ,k 1
4 k 1  1
Para k=2,3,….. y j = 1,2,3,…..
Los valores D1,1, D 2,1 , D 3,1 ... son los valores aproximados de un algoritmo numérico
con h1, h2 ,h3 ….
Pasos
h=0.5
h=0.25
h=0.125
i(1)
0.048400
0.114592
0.130168
D,1
D,2
0.136656
0.13536
0.1352736
La figura muestra la variación de la corriente
i(t) con el tiempo, como se ve, con la
extrapolación de Ríchardson se obtiene
valores que se aproximan bastante al
comportamiento real.
Cabe señalar que la solución mediante el
algoritmo de Heun converge cada vez más
para h≥0.125.
i(t) vs. t