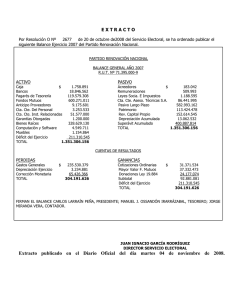
Campo eléctrico F = q E, distrib.discreta E = k qi r2 ˆri, distrib

Formulario 1r cuatrimestre.
Fonaments Fı́sics de l’Enginyeria
Campo eléctrico
Z
qi
dq
~
k 2 rˆi , distrib.continua E = k
r̂,
ri
Q r2
i
dq
dq
dq
, ρ=
,
densidades de carga λ = , σ =
dl
dS
dV
elementos de lı́nea
dl = dx (eje), dl = dr (radial), dl = Rdϕ (arco de circunferencia)
elementos de superficie dS = 2πr dr (capa circular),
dS = r2 /2dϕ (sector circular),
elementos de volumen dV = 2πrh dr (capa cilı́ndrica), dV = 4πr2 dr (capa esférica),
σ
L/2
2kλ
kQx
q
, plano Ez =
,
hilo recto (mediatriz) Ey =
, eje anillo Ez = 2
2
3/2
x
(x + R )
2ǫ0
(L/2)2 + x2
~ distrib.discreta E
~ =
F~ = q E,
X
ley de Gauss Φ = qint /ǫ0 , ǫ0 = 1/(4πk),
flujo Φ =
Z
S
~ ΦEcte = E
~ · dS,
~ · S,
~
E
interfaz entre medios E2n − E1n = σ/ǫ0 , material conductor E = 0, V = cte.
Potencial eléctrico
V =
X qi
i
k , V =
ri
Z
Q
k
dq
, Ep elect = qV,
r
Esfera metálica V = k
~ = −∇V (3D),
relación campo − potencial E
El = −
Q
,
R
dV
(1D),
dl
1
1
1
1
condensadores Q = CV, ǫ = κǫ0 , Econd = QV, Cparalelo = C1 + C2 ,
=
+
,
2
Cserie
C1 C2
σ
2πǫl
ǫS
, V = Ed, E =
cond. cilı́ndrico C =
.
cond. placas paralelas C =
d
ǫ
ln(R2 /R1 )
Campo magnético
~ ω = qB/m,
partı́cula F~ = q ~v × B,
voltaje Hall VH = vport Bd,
~ (B cte.),
hilo de corriente F~ = I ~l × B
F~ = I
Z
L
~
d~l × B,
Z
µ0 I Z d~l × r̂
~ · d~l = µ0 Iint ,
~
B
Biot − Savart B =
,
Ampere
4π L r2
L
µ0 I
µ0 I
µ0 N I
Bhilo =
, Bespira =
, Bbobina =
2πrZ
2R
l
~ · dS,
~ ΦB cte = B
~ · S,
~ autoinducción Φ = LI, Lbobina = µ0 N 2 S/l,
flujo Φ = B
S
fem inducida (Faraday) Vind = −
dΦ
,
dt
l
Ohm V = IR, R = ρ .
S
Cinemática y mecánica
d~x
d~v
d|v|
v2
, ~a = , a2 = a2t + a2n , at =
, an =
dt
dt
dt
R
MRU s(t) = s0 + v0 t, MRUA v(t) = v0 + at, s(t) = s0 + v0 t + 1/2at2 ,
movimiento circular T = 2π/ω, f = 1/T, s = ϕR, v = ωR, a = αR,
F~ = m~a, Fr = µN, muelle F = −k∆x.
~v =
Formulario 2o cuatrimestre.
Fonaments Fı́sics de l’Enginyeria
Trabajo y energı́a
W =
Z
S
~
F~ · ds,
F~ = cte ⇒ W = F~ · ~s,
Em = Ec + Ep ,
Ec = 1/2mv 2 , Ep g = mgh, Ep el = 1/2kx2 ,
Wfnc = ∆Em , Fl = −dU/dl.
Centro de masas y sistemas de partı́culas
M~rCM =
X
mi~ri , M~vCM =
i
X
X
mi~vi , M~aCM =
i
F~ext = M~aCM ,
choques ∆~p = ∆(m~v ) = 0,
X
mi~ai , sist.continuos M~rCM =
i
Z
M
~ri dm
choque elástico ∆E = 0.
Rotación
I=
X
mi ri2 , I =
i
Z
M
r2 dm, Ec rot = 1/2Iω 2 ,
τ = F r sin φ,
X
τ = Iα,
X
τext = IαCM ,
ejes paralelos I = ICM + M h2 , Ianillo = M R2 , Icilind. = 1/2M R2 , Iesfera = 2/2M R2 ,
Ibarra centro = 1/12M L2 , Ibarra extremo = 1/3M L2 , Iprisma rectang. = 1/12M (b2 + h2 ),
momento angular L = pr sin φ = mvr sin φ, Lrot = Iω, fuerzas centrales L = cte.
Fluidos
ρ = m/V, p = F/A, ph = ρgh, Arquimedes B = ρf gVsub , patm = 1, 013 · 105 kPa = 1 atm
Bernouilli p + 1/2ρv 2 + ρgh = cte, continuidad Iv = Av = cte.
Termodinámica
pV = nRT, Ēc = 3/2kT, Calor Q = mce ∆T, cambio fase QL = mcL ,
R = 8, 31 J/(molK) = 0, 082 atm l/(molK), 1r principio Q = ∆U + W,
W =
Z
pdV , ∆U = nCv ∆T, Qp=cte = nCp ∆T, Qv=cte = nCv ∆T, γ = Cp /Cv , Cp − Cv = nR,
proc.adiabático Q = 0, pV γ = cte, entropı́a, proc.quasiestático ∆S = Q/T,
W
Tfrio
|Qc |
|Qc |
rendimiento ciclo ǫ =
, rend. óptimo (Carnot) ǫc = 1 −
=1−
, η=
.
Qa
Qa
W
Tcaliente
Oscilaciones
2
2
x(t) = Acos{ωt + ϕ0 }, T = 2π/ω, f = 1/T, ωmuelle
= k/m, ωpend
= g/L,
−t/(2τ
amortiguadas x(t) = Ae
cos{ωt + ϕ0 }, F~vis = −b~v , τ = m/b, Q = ω0 τ = 2π/(∆E/E)ciclo
F0
, ∆ω/ω0 = 1/Q.
forzadas A = q
m2 (ω 2 − ω02 )2 − b2 ω 2
Ondas
1D x(t) = Acos{ωt + kx + ϕ0 }, λ = 2π/k, v = T /λ,
vcuerda =
q
F/µ, vsonido =
q
γp/ρ,
3D I = P/(4πr2 ), β = 10logI/I0 , I0 = 10−12 W/m2 , Doppler f ′ = f (1 − uf /v)/(1 + ur /v).
Luz, interferencia, difracción y Óptica
n = c/v, ni sin φi = nr sin φr , ángulo crítico sin φc = n2 /n1 ,
interf. δ = 2π∆r/λ, δ = 2πm (const), δ = 2πm + π (destruct.),
2 rendijas mλ = d sin φ ≈ dym /L,
1 rendija asinφ ≈ y1 /L,
′
′
′
1/s + 1/s = 1/f, y /y = −s /s, espejo f = r/2, lente delgada 1/f = (n − 1) · (1/r1 − 1/r2 ),
Interfaz n1 /s + n2 /s′ = (n1 − n2 )/r, y ′ /y = −(n1 s′ )/(n2 s).