descargar

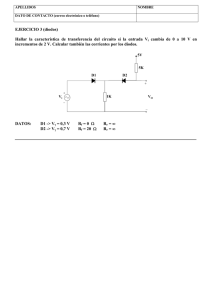
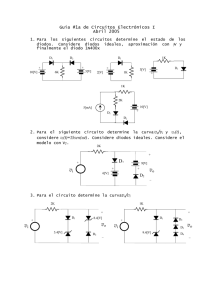
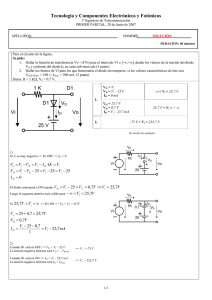
Tema 3. Circuitos con diodos.
Tema 3
CIRCUITOS CON DIODOS.
1.- Aplicación elemental.
2.- Circuitos recortadores (limitadores).
2.1.- Resolución de un circuito recortador utilizando las cuatro aproximaciones del
diodo.
2.1.1.- Resolución utilizando la primera aproximación.
2.1.2.- Resolución utilizando la segunda aproximación.
2.1.3.- Resolución utilizando la tercera aproximación.
2.1.4.- Resolución utilizando la aproximación de diodo ideal.
2.2.- Otros circuitos recortadores.
2.3.- Circuito recortador a dos niveles.
3.- Circuitos rectificadores.
3.1.- Rectificador de media onda.
3.1.1.- Cálculo de la corriente.
3.1.2.- Cálculo de la tensión en el diodo.
3.2.- Rectificador de onda completa.
3.2.1.- Circuito con dos diodos.
3.2.1.1.- Cálculo de las corrientes.
3.2.1.2.- Cálculo de las tensiones en los diodos.
3.2.2.- Circuito con puente de diodos.
3.2.2.1.- Cálculo de las corrientes.
3.2.2.2.- Cálculo de las tensiones en los diodos.
4.- Filtrado de condensador.
39
Tema 3. Circuitos con diodos.
1.- APLICACIÓN ELEMENTAL.
Supongamos el circuito del apartado 4 del tema anterior. La señal de entrada es
vi = VM sen t. Vamos a calcular la función de transferencia del circuito (vo = f(vi)) y la
tensión de salida vo.
ID (mA)
m=1/Rf
vi
RL
i
vo
VD (V)
m=1/Rr
A
V
Los pasos a seguir para la resolución de este tipo de circuitos serán los
siguientes:
1.-
Suponer un estado del diodo.
2.-
Sustituir el diodo por su modelo y resolver el circuito (cálculo de tensiones e
intensidades.
3.-
Comprobar qué condición debe de cumplir la entrada para que el diodo esté en el
estado supuesto.
a/.- Suponemos que el diodo está en inversa (vD  0).
Sustituimos el diodo por su modelo equivalente. En este caso una resistencia de
valor Rr.
Rr
vi
i
i
RL
vo
vi
RL  Rr
vo  R L  i  R L 
vi
RL

 vi
RL  Rr RL  Rr
La condición que se debe de cumplir para que el diodo esté en inversa es que la
corriente circule en el sentido de cátodo a ánodo, es decir:
40
Tema 3. Circuitos con diodos.
vi
 0  vi  0
RL  Rr
i0
Por tanto:
Si v i  0  v o 
RL
 vi
RL  Rr
b/.- Suponemos que el diodo está en directa pero no hay conducción (0  vD  V)
Sustituimos el diodo por su modelo equivalente. En este caso un circuito abierto.
A
C
RL
vi
vo  0
vo
La condición para que el diodo esté en corte es 0vDV
vD  vA  vC 

v A  vi
 v D  vi

vC  0

Por tanto
Si 0  vi  V
 vo  0
c/.- Suponemos que el diodo está en conducción (vD  V)
Sustituimos el diodo por su modelo equivalente. En este caso una resistencia de
valor Rf en serie con una fuente de tensión de valor V.
A
vi
V
Rf
1
i
2C
RL
i
vo
v i  V
Rf  RL
vo  R L  i 
41
RL
 ( v i  V )
Rf  RL
Tema 3. Circuitos con diodos.
La condición que se debe de cumplir para que el diodo esté en conducción es
que la corriente circule en el sentido de ánodo a cátodo, es decir:
i0
v i  V
 0  vi  V
Rf  RL
Por tanto
Si vi  V
 vo 
RL
 (vi  V )
RL  Rf
En resumen:
RL
 vi
RL  Rr
 vo  0
Si vi  0  v o 
Si 0  vi  V
Si vi  V
 vo 
RL
 ( vi  V )
RL  Rf
La curva característica del circuito es la representada a continuación:
vo
vo 
RL
(vi V )
RL Rf
vi
vo 
RL
 vi
RL  Rr
D. Inversa
V
D. Corte
D. Conducción
A continuación representamos la tensión de salida vo (t) cuando la tensión de
entrada es vi =sen(t)
42
Tema 3. Circuitos con diodos.
Vo
Vo
RL
 (VM  V )
RL  Rf
vi
T/2
t1
V
T/4
3T/4
T
t
t2
RL
 VM
R L  Rr
VM
-VM
vi
t1
T/4
t2
T/2
3T/4
T
t
2.- CIRCUITOS RECORTADORES (LIMITADORES).
2.1.- Resolución de un circuito recortador utilizando las cuatro aproximaciones del
diodo.
Vamos a resolver el circuito de la siguiente figura.
R=1K
vi
vo
v i  20  sent
VR= 10 V
Y vamos a resolverlo para cada una de las cuatro aproximaciones del diodo.
43
Tema 3. Circuitos con diodos.
2.1.1.- Resolución utilizando la primera aproximación
ID (mA)
Rf = 20 
m=1/Rf
Rr = 100 K
V = 0,7 V
VD (V)
m=1/Rr
A
V
a/.- Suponemos que el diodo está en inversa (vD  0).
R
i
A
vi
Rr
i
vo
v i  VR
R Rr
v o  VR  R ri  VR  R r
C
VR
v i  VR
R Rr
R r v i  R  VR
R Rr
vo 
La condición que se debe de cumplir para que el diodo esté en inversa es que la
corriente circule en el sentido de cátodo a ánodo, es decir:
v i  VR
 0  v i  VR
R  Rr
R v  RVR
Por tanto, si vi  VR  v o  r i
R  Rr
Dando valores
i0
Si
v i  10 V

vo 
100v i  10
101
b/.- Suponemos que el diodo está en directa pero no hay conducción (0  vD  V)
R
A
vi
C
vo
v o  vi
VR
44
Tema 3. Circuitos con diodos.
La condición para que el diodo esté en corte es 0vDV
v D  0
vD  vA  vC 
v  V  0  v  V

 i
R
i
R
v A  vi
 v D  vi  VR 

v D  V
v C  VR

vi  VR  V  vi  VR  V
Por tanto, si VR  vi  VR  V
 v o  vi
Dando valores:
Si 10  vi  10,7 V  vo  vi
c/.- Suponemos que el diodo está en conducción (vDV)
R
A
i
Rf
vi
i
V
vo
vi  VR  V
R  Rf
v o  VR  V  R f i  VR  V 
C
VR
vo 
Rf
vi  VR  V 
R  Rf
Rf
R
VR  V 
vi 
R  Rf
R  Rf
La condición que se debe de cumplir para que el diodo esté en conducción es
que la corriente circule en el sentido de ánodo a cátodo, es decir:
i0
v i  VR  V
 0  vi  VR  V
R  Rf
Por tanto, si vi  VR  V
 vo 
Rf
R
VR  V 
vi 
R  Rf
R  Rf
Dando valores
Si
v i  10, 7 V

45
vo 
v i  535
51
Tema 3. Circuitos con diodos.
La curva de transferencia del circuito será:
vo
vo 
10,7
10,5
10
v i  535
51
vo  vi
vi
0,099
0,1
vo 
100 v i  10
101
10
10,7
D. Inversa
D. Conducción
D. Corte
Si representamos la tensión de salida vo en función del tiempo
vo, vi
20
10,88
10,7
10
t
0,099
-19,7
-20
46
Tema 3. Circuitos con diodos.
2.1.2.- Resolución utilizando la segunda aproximación.
ID (mA)
Rf = 20 
Rr = 
m=1/Rf
V = 0,7 V
VD (V)
V
a/.- Suponemos que el diodo está en corte (vD  V)
R
A
vi
C
vo
v o  vi
VR
La condición para que el diodo esté en corte es vDV
v D  v A  vC 

v A  vi
 v D  vi  VR  V

v C  VR

Por tanto, si vi  VR  V
 vi  VR  V
 v o  vi
Dando valores
Si
vi  10,7 V  vo  vi
b/.- Suponemos que el diodo está en conducción (vD  V)
Este caso es exactamente igual que el visto en el apartado c del punto 2.1. Por
tanto
47
Tema 3. Circuitos con diodos.
Si
v i  10, 7 V

vo 
v i  535
51
La curva de transferencia del circuito será:
vo
vo 
v i  535
51
10,7
10,5
vo  vi
vi
10,7
D. Corte
D. Conducción
Si representamos la tensión de salida vo en función del tiempo
vo, vi
20
10,88
10,7
10
t
-20
48
Tema 3. Circuitos con diodos.
2.1.3.- Resolución utilizando la tercera aproximación.
ID (mA)
Rf = 0
Rr = 
V = 0,7 V
VD (V)
V
a/.-
Suponemos que el diodo está en corte (vD  V)
Este caso es exactamente igual que el visto en el apartado a del punto 2.2. Por
tanto
Si
b/.-
vi  10,7 V  vo  vi
Suponemos que el diodo está en conducción (vD  V)
R
A
i
V
vi
i
vi  VR  V
R
vo
C
v o  VR  V
VR
La condición que se debe de cumplir para que el diodo esté en conducción es
que la corriente circule en el sentido de ánodo a cátodo, es decir:
i0
v i  VR  V
 0  vi  VR  V
R
Por tanto, si vi  VR  V
 vi  VR  V
Dando valores
Si
vi  10,7 V  vo  10,7 V
49
Tema 3. Circuitos con diodos.
La curva de transferencia del circuito será:
vo
10,7
vo  vi
vi
10,7
D. Corte
D. Conducción
Si representamos la tensión de salida vo en función del tiempo
vo, vi
20
10,7
10
t
-20
50
Tema 3. Circuitos con diodos.
2.1.4.- Utilizando la aproximación de diodo ideal.
ID (mA)
Rf = 0
Rr = 
V = 0
VD (V)
a/.-
Suponemos que el diodo está en corte (vD  0)
R
A
vi
C
v o  vi
vo
VR
La condición para que el diodo esté en corte es vD 0
v D  v A  vC 

v A  vi
 v D  vi  VR  0  vi  VR

v C  VR

Por tanto, si vi  VR
 v o  vi
Dando valores
Si
b/.-
vi  10 V  vo  vi
Suponemos que el diodo está en conducción (vD  0)
R
i
A
vi
i
C
vo
vi  VR
R
v o  VR
VR
51
Tema 3. Circuitos con diodos.
La condición que se debe de cumplir para que el diodo esté en conducción es
que la corriente circule en el sentido de ánodo a cátodo, es decir:
i0
vi  VR
 0  vi  VR
R
Por tanto, si v i  VR
 v i  VR
Dando valores
vi  10 V  vo  10 V
Si
La curva de transferencia del circuito será:
vo
10
vo  vi
vi
10
D. Corte
D. Conducción
Si representamos la tensión de salida vo en función del tiempo
vo, vi
20
10
t
-20
52
Tema 3. Circuitos con diodos.
2.2.- Otros circuitos recortadores.
53
Tema 3. Circuitos con diodos.
2.3.- Recortadores a dos niveles
R
Suponemos diodos ideales
D1
v i  20  sent
D2
vo
vi
VR1=10 V
VR2=20 V
Como ahora tenemos dos diodos, en principio tendremos cuatro estados
posibles.
a/.- Suponemos que los dos diodos D1 y D2 están en corte.
R
vi
VR1
A1
C2
C1
A2
v o  vi
vo
VR2
La condición que se debe de cumplir para que el diodo D1 esté en corte
v D1  0
v D1  v A1  v C1 

v A1  vi
 vi  VR1  0  vi  VR1

v C1  VR1

La condición que se debe de cumplir para que el diodo D2 esté en corte
vD2  0
v D 2  v A 2  vC 2 

v A 2   VR 2
  VR 2  vi  0  vi   VR 2

v C 2  vi

Por tanto, si  VR 2  vi  VR1  v 0  vi
54
Tema 3. Circuitos con diodos.
Dando valores
Si
 20  vi  10 V  v0  vi
b.- Suponemos que D1 está en conducción y D2 en corte.
R
v o  VR1
i
vi
VR1
A1
C2
C1
A2
i
vo
VR2
vi  VR1
R
La condición que se debe de cumplir para que D1 esté en conducción es que la
intensidad circule en el sentido de ánodo a cátodo, es decir:
vi  VR1
 0  vi  VR1
R
i0
La condición que se debe de cumplir para que el diodo D2 esté en corte
vD2  0
vD 2  vA 2  vC2 

v A 2   VR 2
  VR 2  VR1  0  Se cumple siempre

v C 2  VR1

Esto quiere decir que siempre que el diodo D1 esté en conducción, es decir,
siempre que vi  VR1 el diodo D2 estará en corte. Por tanto ya podemos adelantar que
no será posible el caso de que los dos diodos estén simultáneamente en conducción.
Por tanto, si vi  VR1  vo  VR1
Dando valores
Si
vi  10 V  vo  10 V
55
Tema 3. Circuitos con diodos.
c.- Suponemos que D1 está en corte y D2 en conducción.
R
A1
C2
C1
A2
i
vi
VR1
v o  VR 2
vo
i
VR2
vi  VR 2
R
La condición que se debe de cumplir para que el diodo D1 esté en corte
v D1  0
v D1  v A1  v C1 

v A1   VR 2
  VR 2  VR1  0  Se cumple siempre

v C1  VR1

La condición que se debe de cumplir para que D2 esté en conducción es que la
intensidad circule en el sentido de ánodo a cátodo, es decir:
i0
vi  VR 2
 0  vi   VR 2
R
Esto quiere decir que siempre que el diodo D2 esté en conducción, es decir,
siempre que vi  -VR1 el diodo D1 estará en corte. Por tanto, volvemos a comprobar, al
igual que en el caso anterior que no será posible el caso de que los dos diodos estén
simultáneamente en conducción.
Por tanto, si vi  VR 2
 v o  VR1
Dando valores
Si
vi  20 V  vo  20 V
d.- Suponemos que D1 está en corte y D2 en conducción.
56
Tema 3. Circuitos con diodos.
No sería necesaria la resolución de este caso, ya que con los tres anteriores
tenemos completamente resuelto el problema. Lo vamos a resolver, de todas formas,
para comprobar que es un caso imposible como ya hemos adelantado.
R
Se debería de cumplir que
vi
A1
C2
C1
A2
VR1
VR1   VR 2
vo
Lo cual es imposible (10  -20)
VR2
Dibujamos la curva de transferencia del circuito.
La tensión de salida será
57
Tema 3. Circuitos con diodos.
3.- CIRCUITOS RECTIFICADORES.
3.1.- Rectificadores de media onda.
El circuito de la figura es un típico rectificador de media onda. El circuito se
alimenta de la red eléctrica ( típicamente tensión alterna de 220 V eficaces y 50 Hz ). A
nosotros nos interesará la tensión vi de entrada al rectificador propiamente dicho. Esta
vendrá determinada por la relación de transformación del transformador.
N2
N1
Vred
220 V
vi
RL
vo
Vred N1

vi
N2
La tensión vi será una tensión sinusoidal de
VM
0
valor máximo VM.
t
Supondremos para la resolución de todos
T
T/2
los circuitos rectificadores la aproximación de
diodo ideal
Vamos a resolver el circuito.
a.- Suponemos que el diodo está en conducción.
vo
A
C
VM
vi
i
RL
vo
i
vi
Obtenemos que si vi  0, es decir, si 0  t 
58
T
2
RL
vo
 v o  vi
0
t
T/2
Tema 3. Circuitos con diodos.
b.- Suponemos que el diodo está en corte.
vo
A
C
VM
vi
RL
vo
vi
Obtenemos que si vi  0, es decir, si
RL
vo
0
T
T/2
t
T
 t  T  vo  0
2
Podemos observar como a partir de una tensión que tiene valores positivos y
negativos obtenemos una que únicamente toma valores positivos. En esto precisamente
consiste la rectificación.
vi
VM
t
vo
0
vo = vi
vo = 0
vi
vo
VM
t
0
T
Si hubiésemos elegido la tercera aproximación, es decir, si hubiésemos tenido en
cuenta la tensión umbral, el resultado hubiese sido el siguiente
vi
A
V
vo
C
VM
VM-V
VM
0,7 V
V = 0,7 V
0
T/2
t
vi
RL
vo
0
T
59
t
T/2
Tema 3. Circuitos con diodos.
3.1.1.- Cálculo de la corriente.
Conocida como es la tensión de salida vo, será fácil conocer la corriente que
circula por la resistencia que, en este caso es, evidentemente, la misma que circula por
el diodo.
i
T
VM

0  t  2  i  R  sen (t )
L

T
 tT  i0
 2
vo
RL
i
IM
I dc
0
T/2
T
t
A la hora de realizar el circuito deberemos colocar un diodo cuya corriente
máxima rectificada promedio sea superior a la que debe de soportar el diodo en el
circuito.
Idc 
T
T
 1 T2
1  T2
I M (1)
2
i
dt

i
dt

I

sen
(

t)
dt


cos
(

t)


T

 2  T  0 M
0
T 0
T 
Teniendo en cuenta que   2f 
Idc 
2
T
 T  2  y   
T
2
IM
Vdc 

VM

El valor eficaz de esta corriente será:

1
I2  
T

I2
 M
T


T
2
0
T
2
0
i 2dt 


1
i dt  
T
 T
2

T
2

T
2
0
1
i 2dt 
T

T
2
0
I2
I 2M sen 2 (t ) dt  M
T
T
1  cos (2t )
I2 
1
2
dt  M  t 
sen (2t ) 
2
2 T  2
0
2
I T
1
1
 IM
sen 2 
sen 0 

0
2 T  2
2
2
 4
2
M
I
IM
2
V
60
VM
2

T
2
0
sen 2 (t ) dt 
Tema 3. Circuitos con diodos.
3.1.2.- Cálculo de la tensión en el diodo.
Tendremos que calcular la tensión a la que está sometido el diodo, fijándonos
sobre todo, en el valor máximo de la tensión que soporta el diodo cuando está
polarizado en inversa.
vD
VM
vi
RL
0
T/2
t
T
vD
-VM
Si observamos el circuito, en todo momento se cumple v D  vi  v o
Por tanto
T

0  t  2
v D  vi  v o 
T
 tT
2
v o  vi
 vD  0
vo  0  v D  vi
En consecuencia vemos que el diodo debe ser capaz de aguantar la tensión VM.
3.2.- Rectificadores de onda completa.
3.2.1.- Circuito con dos diodos.
vi VS
D1
N1
vi
Vred
VSM
N2
VM =VSM/2
vo
VS
RL
0
T/2
T
t
vi
D2
En la figura aparece el circuito para obtener un rectificado de onda completa
utilizando únicamente dos diodos. Notar que para poder hacer este tipo de rectificado se
necesitan dos tensiones idénticas vi, lo cual se consigue fácilmente con un
61
Tema 3. Circuitos con diodos.
transformador que tenga una toma central en el secundario. De tal forma que si la
tensión que tenemos en el secundario es de la forma VS  VSM sen (t ) la tensión de
VSM
sen (t )
2
entrada al rectificador será vi 
Para resolver el circuito,
a.- Suponemos que el diodo D1 está en conducción y el diodo D2 en corte.
A1
N1
C1
N2
vi
vo
i1
vi
Vred
vo
VM
VM
VS
RL
vi
0
A2
t
T/2
0
t
T/2
C2
En este caso vemos como v o  vi
Para que D1 esté en conducción i1 
vi
 0  vi  0
RL
Para que D2 esté en corte v D 2  v A 2  v c 2  0   vi  vi  0  vi  0
Por tanto
0t
T
2
 v o  vi
b.- Suponemos que el diodo D1 está en corte y el diodo D2 en conducción.
A1
N1
vi
vi
vi
Vred
C1
N2
VM
vo
VS
RL
vi
0
i2
A2
T/2
T
t
0
VM
C2
Ahora vemos como v o   vi
62
T/2
T
t
Tema 3. Circuitos con diodos.
Para que D1 esté en corte v D1  v A1  v C1  0  vi  ( vi )  0  vi  0
Para que D2 esté en conducción i 2 
vi
 0  vi  0
RL
Por tanto
T
 t  T  v o   vi
2
Ahora estamos en condiciones de representar la curva de transferencia del
circuito así como las tensiones de entrada y de salida.
vo
vo
vi
VM
VM
vo = -vi
vo = vi
vi
0
T
T/2
t
0
T/2
T
t
VM
3.2.1.1.- Cálculo de las corrientes.
Cada uno de los diodos está en conducción un semiperiodo, mientras que por la
carga circula corriente durante el periodo completo.
Como se puede apreciar en la gráfica, el valor de las corrientes i1 e i2 que
circulan por D1 y D2 respectivamente es igual que en el caso anterior del rectificado de
media onda. Por tanto vamos a centrarnos en calcular los valores de la intensidad en la
carga. Calcularemos como hemos hecho en el caso anterior tanto el valor máximo como
el valor medio o de continua y su valor eficaz.
63
Tema 3. Circuitos con diodos.
i1
IM
Idc
0
T/2
t
T
i2
IM
Idc
0
T
T/2
t















IM 
VM
RL
I dc 
IM







IM 
VM
RL
Idc 
2I M

I
IM
2
i
IM
Idc
0
T
T/2
t
IM
2
I
Para el cálculo del valor medio de la corriente en la carga:

1
I dc 
T


T
2
i dt 
0

T
T
2

2
i dt  
 T

T
2

Idc 
2 I (1)
cos (t )02
I M  sen (t ) dt  M 
T

T
0
2 IM
Vdc 

2 VM

El cálculo del valor eficaz de la corriente será:

1
2
I 
T


T
2
0
i 2dt 


2
i dt  
T
 T
2

T
2

I
T
2
0
2
i 2dt 
T

T
2
0
2 I2
I 2M sen 2 (t ) dt  M
T
IM
V
2
3.2.1.2. Cálculo de las tensiones en los diodos.
64
VM
2

T
2
0
sen 2 (t ) dt 
I 2M
2
Tema 3. Circuitos con diodos.
N1
N2
vi
Vred
vD1
Del circuito observamos que en
vo
todo momento se cumple
RL
v D1  vi  v o
vD2
v D2   vi  v o
VS
vi
En el primer semiperiodo:
0t
 v  vi  v o  0
T
 v o  vi   D1
2
 v D2   vi  v o  2 vi
En el segundo semiperiodo
 v  vi  v o  2 vi
T
 t  T  v o   vi   D1
2
 v D2   vi  v o  0
Si las representamos gráficamente
VM
0
vo
T
T/2
t
vi
vD2
VSM = 2 VM
vD1
Es importante observar como cuando los diodos están en inversa deben soportar
una tensión máxima de valor 2 VM. Es decir, deben de soportar toda la tensión del
secundario del transformador, mientras que a la carga llega una tensión de valor
máximo VM o, lo que es lo mismo, la mitad de la tensión del secundario.
3.2.2.- Circuito con puente de diodos.
65
Tema 3. Circuitos con diodos.
En la figura se representa un circuito rectificador de onda completa utilizando un
puente de diodos. A diferencia del caso anterior no necesitamos dos tensiones vi
idénticas, por tanto no necesitaremos un transformador con toma intermedia. Por otra
parte, podemos observar como ahora necesitamos 4 diodos en una configuración típica
conocida como puente de diodos.
4
+
D1
vi
D2
VM
N1
RL
N2
D4
D3
t
0
T/2
-
2
vi
Vred
vo
T
La tensión de entrada al circuito rectificador es una sinusoidal de valor máximo
VM.
vi  VM sen (t )
Resolvemos el circuito. Los casos posibles son:
a.- Suponemos que los diodos D1 y D3 están en conducción y D2 y D4 en corte.
vi
VM
+
C1
C2
A1
N1
N2
i
A2
RL vo
C3
t
A4
vo
-
2
vi
T/2
C4
A3
Vred
0
VM
0
Para este caso v o  vi
66
T/2
t
Tema 3. Circuitos con diodos.
Para que D1 y D3 estén en conducción i 
vi
0
RL
 vi  0
Para que el D2 esté en corte v D 2  v A 2  v C 2  0  0  vi  0  vi  0
Para que el D4 esté en corte v D 4  v A 4  v C 4  0  0  vi  0  vi  0
Por tanto
0t
T
2
 v o  vi
b.- Suponemos que los diodos D1 y D3 están en corte y D2 y D4 en conducción.
vi
+
C1
C2
A1
N2
vi
Vred
0
A2
T
T/2
t
RL vo
C4
C3
A4
-
VM
A3
2
N1
i
vi
VM
0
T/2
T
Para este caso v o   vi
Para que D2 y D4 estén en conducción i 
 vi
0
RL
 vi  0
Para que el D1 esté en corte v D1  v A1  vC1  0  vi  0  0  vi  0
Para que el D3 esté en corte v D3  v A 3  vC3  0  vi  0  0  vi  0
Por tanto
T
 t  T  v o   vi
2
67
t
Tema 3. Circuitos con diodos.
Tanto la curva de transferencia del circuito como la tensión en la carga son
exactamente iguales a las que teníamos en el apartado anterior.
vo
vo
vi
VM
VM
vo = -vi
vo = vi
vi
0
T
T/2
t
0
T/2
T
VM
3.2.2.1.- Cálculo de las corrientes.
Si las tensiones son iguales a las del caso anterior, lo mismo ocurrirá con las
intensidades. (Obviamos su cálculo por haber sido realizado en el apartado anterior).
i1
IM
Idc
0
T/2
T
t
i2
IM
Idc
0
T/2
T
t
i















IM 
VM
RL
I dc 
IM







IM 
VM
RL
I dc 
2I M

I
IM
2
IM
Idc
0
T/2
T
t
I dc 
I
2 IM

Vdc 
IM
2
V
68
I
2 VM

VM
2
IM
2
t
Tema 3. Circuitos con diodos.
3.2.2.2. Cálculo de las tensiones en los diodos.
4
+
vD1
D1
D4
D3
vi    v D4  v o  v D2 
-
2
vi
vo
vi  v D1  v o  v D3
vD3
vD4
Vred
Podemos observar como:
D2
RL
N2
N1
vD2
1

 v D1  v D3  v D1  v D3  2  vi  vo 
Como 
1
v  v
 v D2  v D4    vi  v o 
D2
D4

2
En el primer semiperiodo
0t
T
2

v o  vi
 v D1  v D3  0

 v D2  v D4   vi
En el segundo semiperiodo
T
tT
2

v o   vi
 v D1  v D3  vi

 v D2  v D4  0
Si lo representamos gráficamente.
VM
vo
t
0
-VM
T
T/2
vD2 vD4
vD1 vD3
A diferencia del caso anterior, ahora toda la tensión del secundario llega a la
carga. Los diodos, en inversa, deberán de ser capaces de aguantar una tensión VM.
69
Tema 3. Circuitos con diodos.
4.- FILTRADO DE CONDENSADOR.
A los circuitos rectificadores vistos hasta ahora, vamos a añadirles un
condensador en paralelo con la carga.
Vamos a suponer en un primer análisis que no existe resistencia de carga. Es
decir, suponemos que RL = . Supondremos también diodo ideal.
En el instante inicial todas las tensiones son cero, vi =0 y vo = 0. A medida que
aumenta vi tendríamos:
v Anodo  vi 
  Diodo en conducción  v o  vi
v Cátodo  0 
En el instante t = T/4 la tensión de entrada alcanza su valor máximo VM. En este
instante el condensador estará cargado con una tensión igual a VM. A partir de este
instante vi comienza a disminuir. Sin embargo, la tensión en bornes del condensador se
mantiene, ya que éste no tiene un camino a través del cual pueda descargarse. Por tanto:
70
Tema 3. Circuitos con diodos.
v Anodo  vi ( VM )
 v Anodo  v Cátodo
v Cátodo  VM

 Diodo en corte  v o  v condensador  VM
Esta situación se mantendrá indefinidamente ya que la tensión de entrada nunca
podrá tener un valor superior a VM que haga que el diodo se ponga en conducción.
Si ahora colocásemos la resistencia en paralelo con el condensador le estamos
proporcionando un camino de descarga al condensador.
Al ir descargándose el condensador su tensión decrece a un ritmo exponencial.
Esta situación se mantendrá mientras el diodo se mantenga en corte, es decir, mientras
vánodo < vcátodo . En el momento en el que vánodo > vcátodo el diodo se pone nuevamente
en conducción de forma que la tensión en el condensador se iguala a la de entrada
( vO = vi ). En resumen, el condensador se carga cuando el diodo esta en conducción y
se descarga a través de la resistencia cuando el diodo está en corte, de forma que ahora
siempre habrá tensión en la salida.
D ON
D OFF
VM
D ON
D OFF
vo
vi
0
t1
t2
0
T/4
-VM
vD
71
Tema 3. Circuitos con diodos.
En cuanto a las corrientes que van a circular por el circuito, podemos distinguir
igualmente dos casos en función del estado del diodo.
Así, cuando el diodo está en conducción
iD = iC + iL
Como conocemos la tensión en los bornes de la resistencia y del condensador
iL 
vO VM

 sen t
RL RL
iC  C
dv O
 C    VM  cos t  2f  C  VM  cos t
dt
Directamente proporcional a C cuanto mayor sea la capacidad del condensador
que pongamos para realizar el filtrado, la tensión de salida será más continua (menor
rizado) pero como contrapartida, la tensión por el condensador y, por tanto, la corriente
por el diodo será mayor.
En el caso en el que el diodo está en corte, la corriente que circula por la
resistencia proviene de la descarga del condensador
iC =- iL
iL 
vO VM
t

 exp
RL RL
RC
72
Tema 3. Circuitos con diodos.
iL
0
t1
t2
iD
0
T/4
iC
D ON
D ON
Un resultado similar obtendríamos si hubiésemos analizado el caso de un
circuito rectificador de onda completa. En las figuras siguientes se presentan las
tensiones y corrientes para los dos casos de rectificadores de onda completa analizados
en este tema (circuito con dos diodos y puente de diodos
73
Tema 3. Circuitos con diodos.
VM
vo
vi
0
t1
t2
T/4
vD1
vD3
-VM
D1
D3
ON
vD2
vD4
D2
D4
D1
D3
ON
74
ON
D2
D4
ON
Tema 3. Circuitos con diodos.
Una vez que hemos visto de forma cualitativa las tensiones y corrientes por los
circuitos con filtrado, vamos a pasar a analizar cuantitativamente los valores de dichas
magnitudes.
En primer lugar, para simplificar, se aproxima la tensión de salida por una onda
triangular.
Vrp
V
VM
Vdc
0
t1
t
T/4 t2
T
El valor medio de esta tensión triangular será:
Vdc 
Vdc 
1
T
v
O
dt Donde
T
v
O
dt  Area encerrada por la curva
T
1
1
V








V
V
T
V
T
V


M
M

T 
2
2
Definimos para la onda de salida los siguientes parámetros:
Vrp = Tensión de pico o de cresta de ondulación o rizado
Vrp 
V
2
Vr = Tensión eficaz de rizado o de ondulación
Vr 
Vrp
3
 = Factor de ondulación
75
Tema 3. Circuitos con diodos.

Vr
100
Vdc
%
Este factor de ondulación nos da una idea de lo bueno o malo que es el rizado, es
decir, de lo que se aproxima la tensión de salida a una tensión continua.
Por otra parte, cuando el condensador se descarga, la carga proporcionada por el
mismo es
QC  C  V
El condensador se está descargando desde el instante
T
durante un tiempo
4
T

T    t1  , es decir, aproximadamente durante el tiempo en el que el diodo está en
4

corte.
Si tenemos en cuenta que el diodo está en conducción durante un tiempo t2-t1 (o
T

aproximadamente   t1  ) y que este tiempo es muy pequeño frente al periodo,
4

podemos suponer que el condensador se descarga en un tiempo igual al periodo.
Cuando el condensador se descarga, lo hace a
través de la resistencia. La carga en la resistencia
viene dada por
T
T
QL 
 i dt  I  T
c
T
(ya que hemos supuesto que el condensador se descarga en un tiempo T).
Si suponemos, que toda la carga que llega a la resistencia la proporciona el
condensador. Es decir, si despreciamos la carga que llega a la resistencia durante el
intervalo de tiempo en el que los diodos están en conducción. Tendremos
QC  Q L
Donde

C  V  Idc  T
C = Capacidad del condensador (F)
V = Tensión de descarga del condensador (V)
76
Tema 3. Circuitos con diodos.
Idc = Valor medio o de continua de la intensidad. Idc 
Vdc
(A)
RL
T = Periodo de la tensión de entrada (s)
Por otra parte, toda la carga ha tenido que pasar previamente por el diodo.
IDmáx
IDmáx
La carga que atraviesa el diodo será
QD 
i
d
T
QD 
t1 T/4 t2
dt 

T
4
i d dt  Area sombreada
t1
1
T

I D max   t1 
2
4

t1 T/4 t2
Donde t1 es el instante tras la descarga en que vo = vi.
Para
t  t1
v o  VM  V 

vi  VM sen t1 
t1 
1
V  V
arc sen M
VM

t1 
1
V  V
arc sen M
2f
VM
Para calcular la intensidad máxima por los diodos (IDmax) haremos:
QD  QL
o
77
Q D  QC