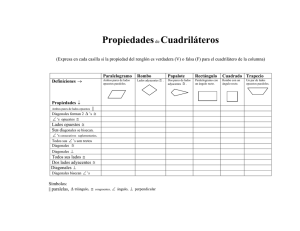
CUADRILATEROS: · Los ángulos interiores suman 360º · Los

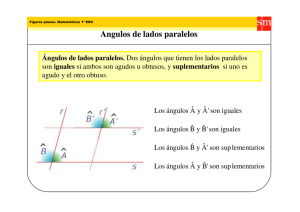
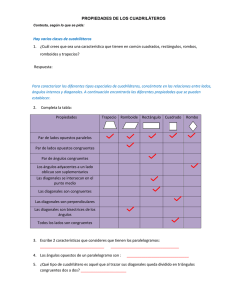
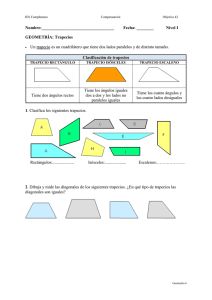
CUADRILATEROS:
· Los ángulos interiores suman 360º
· Los ángulos exteriores suman 360º
· Clasificación según par de lados opuestos paralelos:
> Paralelogramos (2 pares)
> Trapecios (1 par)
> Trapezoides (ningún par)
A. PARALELOGRAMOS:
· Tienen 2 pares de lados opuestos paralelos.
· Cuadrado – Rectángulo – Rombo – Romboide
1. CUADRADO:
· 4 ángulos interiores rectos
· 4 lados iguales
· Lados opuestos paralelos
· Las diagonales son iguales y son perpendiculares
· Las diagonales se dimidian (÷ en partes iguales)
· Las diagonales bisectan los ángulos
· Se puede inscribir una circunferencia
· Se puede circunscribir una circunferencia
·d= a 2
· p = 4a
· A = a2
2. RECTANGULO:
· 4 ángulos interiores rectos
· Lados opuestos de igual medida
· Lados opuestos paralelos
· Las diagonales son iguales y se dimidian
· Se puede circunscribir una circunferencia
· p = 2a + 2b
· A = ab
3. ROMBO:
· 4 lados iguales
· Lados opuestos paralelos
· Ángulos opuestos iguales
· Ángulos contiguos suplementarios
· Las diagonales son perpendiculares
· Las diagonales se dimidian y bisectan los ángulos
· Se puede inscribir una circunferencia
· p = 4a
· A = a  h o bien A =
ef
2
D
C
d1
d2
A
B
a
D
C
d1
b
d2
A
B
a
D
C
d2
d1
h
e
A
f
a
B
D
d1
h
b
d2
A
4. ROMBOIDE:
· Lados opuestos de igual medida
· Lados opuestos paralelos
· Ángulos opuestos iguales
· Ángulos contiguos suplementarios
· Las diagonales se dimidian
· p = 2a + 2b
· A = ah
C
B
a
B. TRAPECIOS:
· Tienen 1 par de lados opuestos paralelos llamados basales.
· Trapecio Escaleno – Trapecio Isósceles – Trapecio Rectángulo
b
D
c
γ
δ
1. TRAPECIO ESCALENO:
· Lados no paralelos no son congruentes.
· AB // CD
· α + δ = 180º
· β + γ = 180º
·p=a+b+c+d
C
M
N
d
h
α
β
A
a
D
b
δ
d1
γ
d
M
N
d2
h
A
β
B
a
A=
3. TRAPECIO RECTANGULO:
· Uno de sus lados no paralelos es
perpendicular a las bases.
· AB es perpendicular a AD
· DA es perpendicular a DC
· AB // CD
· c = h = altura
· Ángulos en A y D son rectos
· β + γ = 180º
·p=a+b+c+d
· A = MN  h
(a  b)
A=
h
2
ab
(a  b)
 h y MN 
2
2
2. TRAPECIO ISOSCELES:
· Lados no paralelos son iguales (AD = BC)
· AB // CD
· Las diagonales son iguales
· Ángulos contiguos suplementarios
·α=β
·γ=δ
· p = a + b + 2c
· A = MN  h
C
c
α
· A = MN  h / A =
B
(a  b)
h
2
b
D
γ
C
c
M
d
N
h
A
β
a
B
4. MEDIANA DE UN TRAPECIO:
· Segmento que une los puntos medios de los lados no
· Es paralela a las bases.
· MN = AB + DC
2
D
C
paralelos.
M
N
A
B
D
C. TRAPEZOIDES:
δ
b
γ C
c
· No tienen lados opuestos paralelos.
d
α
A
β
a
B